Abstract
Studies on estimating cumulative fire intensity from spreading wildland fires based on fire radiative energy density (FRED) have primarily been conducted through controlled experiments. The objective of this study was to assess the potential for estimating FRED for freely-burning wildfires at landscape scales. Airborne thermal infrared image sequences collected 8 and 9 December 2017 during the Thomas Fire were used for surface temperature derivation and FRED estimation. Sensitivity of varying ambient temperatures, and a newly developed method that adjusts for ash radiances on fire radiative flux density (FRFD) and FRED estimates were tested. Pixel-level image classification was run to identify FRFD time sequences that were complete or incomplete because of cloud obscuration and provided the basis for an obscuration gap filling technique. Variations in estimated ambient temperature used to estimate FRFD had little impact on FRED estimates, while our ash adjustment led to notable differences. An exponential decay model characterized FRFD time sequences well, providing a basis for gap filling irregular sequences caused by atmospheric obscuration. FRED estimates were regressed on rate of spread (ROS) magnitudes and found to be positively and significantly correlated. FRED magnitudes were higher on 9 December when the Thomas Fire burned under higher wind speeds and lower relative humidity levels (Santa Ana weather conditions) than on 8 December.
1. Introduction
Because of their potentially catastrophic impacts to humans and ecosystems, wildland fires elicit a range of societal and governmental actions and costly investment in emergency response, fire suppression, community and infrastructure adaptation, fuel management, and postfire recovery. With the wide range of wildfire impacts, understanding the behavior of actively progressing and future wildfires is important for planning and implementing each of these actions, to minimize losses and maximize potential benefits.
Wildfire behavior variables of primary interest are fire intensity and the rate of fire spread [1]. Each of these could attain values ranging across orders of magnitude depending on wind, terrain, and fuel characteristics. Instantaneous fire intensity is typically specified as fire-line intensity, the energy release rate per unit length of the fire front, or as the reaction intensity, the energy release rate from a unit area of active combustion [2]. In practice, because of smoke, terrain, and difficulty in approaching active wildfires, a large fire’s behavior is often not known beyond its daily progress, and predictions are often based on extrapolations from mathematical descriptions of fire behavior in laboratory settings [3,4,5,6]. Despite their mathematical foundation, researchers have collected validation data for their models through controlled experimentation [7,8].
Airborne remote sensing at infrared wavelengths of electromagnetic radiation can quantify both the rate of spread and the radiant portion of fire intensity. The latter may be directly related to fire environmental effects or indicative of the total intensity that impacts other attributes such as resistance to control or suppression effectiveness [9].
How can we deduce these fire properties from remote measurements? A remote sensor viewing a fire target generates a digital number that is highly and linearly related to the spectral radiance of radiation (in units of J m−2 s−1 sr−1 um−1), impinging upon its detector; the relation of that radiance to the digital number is provided by a calibration in the laboratory, made by viewing a standard, high-temperature, black-body cavity across a range of appropriate temperatures [9,10]. Radiance at an airborne sensor will be influenced by some atmospheric attenuation of the radiation emitted at the ground [8,11]. Apparent fire-target temperatures can be estimated from upwelling target radiance and the Planck function, with the assumption that the target is indeed a black-body or gray-body radiator [9,12,13,14]. That assumption is reasonable for surfaces covered by black ash either beneath or without flaming combustion [11]. Within the flaming zone, the radiance of very hot ash beneath flames may dominate the direct radiance from low emissivity flames [11], depending on the wavelength of light observed.
A fire radiative flux density (FRFD) or exitance (with units of J m−2 s−1) associated with energy emitted by the fire and hot ash can be calculated, with reference to the Stefan–Boltzmann relation, as follows:
where Tf is burning surface temperature, Tb is ambient temperature (constant) adjacent to fire, and σ is the Stefan–Boltzmann constant [11].
FRFD = σ (Tf4 − Tb4)
The integration of the radiative flux density with time, as depicted in Figure 1, provides the fire radiative energy density (FRED) [14,15,16], a measure of the total radiative energy emitted from the fire environment, including flames, heated fuel elements, and the hot soil surface.
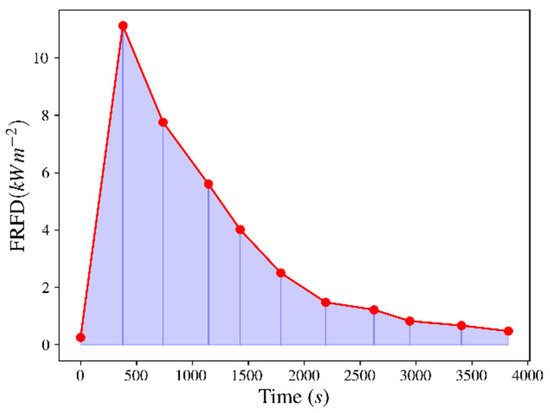
Figure 1.
Temporal profile of FRFD (each dot in the profile at t time) for a plot under a free burning wildfire. Fire energy radiative density (FRED) is the time integrated FRFD over the profile (i.e., area under curve).
A time sequence of FRFD can be used to calculate FRED (Jm−2) [10,11] based on Equation (2):
where FRFDi is the FRFD from each time sequence image i, and t is time.
Upwelling radiation from fires may be detected and has been measured using both satellite-based and airborne sensors [11,14,15,17]; the former give wide-area, infrequent coverage at relatively low resolution, while the latter provide potentially frequent, high-resolution observations over more limited areas.
A drawback of satellite-based systems is the difficulty in separating contributions of radiation from sub-pixel areas of unburned and burned ground or discriminating extensive sub-pixel areas of low-intensity combustion from smaller areas of high-intensity burning [11]. Higher-resolution satellite-based sensors (e.g., Landsat8 OLI, Ball Aerospace, Broomfield, CO, USA) will also saturate over high-radiance fire targets, yielding artificially low radiance and temperature estimates. Lower-resolution sensors may avoid saturation by diluting the high-temperature signal with uncertain amounts of radiation from unburned or cooled ground [14]. FRED, nonetheless, has been estimated based on satellite imagery [14,15].
Time-sequential, airborne thermal-infrared (ATIR) sensors have been used to monitor wildfire temperatures and progression [11], estimate rates of spread across time intervals of a few minutes [18], and estimate the radiant energy flux from fires over time [11,19]. Energy measurements have required specialized imagers that accommodate the very high radiances associated with wildland fires [11]. For example, the USDA Forest Service Pacific Southwest Research Station (PSW) and Space Instruments, Inc. (Encinitas, CA, USA) co-developed the FireMapper and FireMapper 2.0 (FM2) imagers, which employ microbolometer focal-plane arrays with band-pass filters, to provide unsaturated fire measurements at thermal-infrared wavelengths of approximately 9 and 12 μm [11].
Using repeat-pass imagery collected using FireMapper sensors from chaparral wildfires, Riggan et al. [11] noted that there is often a qualitative and local spatial association of peak fire radiance with pre-fire biomass. Hudak et al. [19] examined FireMapper imagery collected by PSW, over a burnout operation on the perimeter of the 2003 Cooney Ridge wildfire in Montana, and compared FRFD and FRED estimates from remote sensing with those derived from temperature measurements at the ground. FRED has also been estimated from ATIR imagery collected over prescribed fires including the 2011 and 2012 RxCADRE experiments [10,17]. In the latter, the total fire radiant energy was four times higher from a forested plot than from one composed of dry grass, because of differences in fuel load [10,18]. Results from RxCADRE also highlighted the influence of the rate of spread and residence time on FRED estimates. If a fire spreads rapidly with low residence time relative to the ATIR imaging frequency, some areas of active burning may not be imaged, yielding underestimates of FRED [20].
Controlled experiments like RxCADRE and the Cooney Ridge fire measurements implemented repeated ATIR imaging to estimate and map the intensity of relatively controlled and small-scale fires [10,18]. However, such observations of fire dynamics for small-scale experimental fires may not be representative of actively progressing, high-intensity, large-scale wildfires.
For this study, we assess procedures and their sensitivity when estimating FRED for the 2017 Thomas Fire in southern California, a rapidly expanding, large wildfire that burned primarily in chaparral during dry, Santa Ana weather conditions, and examine the spatial distribution of FRED. In the context of the Thomas Fire, we address the following research questions:
- How sensitive are FRED estimates to the choice of ambient surface temperature, variations in FRFD time series shape, and incorporation of an adjustment for ash and char heating?
- How do the magnitudes and spatial distributions of FRED vary for windy and less-windy wildfire spread conditions?
- How does the spatial distribution of FRED co-vary with wildfire ROS?
2. Data and Methods
2.1. Study Area and Wildfire Context
The study area consists of portions of the Thomas Fire that were imaged repetitively using an ATIR system on 8 December (Sequences 1 and 2) and 9 December 2017 (Sequence 3) [18], provided in Figure 2. The Thomas Fire burned from 4 December 2017 to 18 January 2018 across Santa Barbara and Ventura Counties, California, USA. At the time, it was the largest wildfire in Californian history. It mostly burned shrubby fuels in dense chaparral, with some subshrubs and grass fuels within coastal sage scrubs and trees, as well as herbaceous fuels of riparian and oak woodland communities also burning. The topography of the Thomas Fire burn extent is complex, consisting of hilly and mountainous terrain. The sequences for both dates were captured when the Thomas Fire was mostly spreading upslope [18]. Sustained wind speeds during a Santa Ana (low humidity, high wind speeds) weather condition were estimated with the FireBuster model [21], ranging from 1.3 to 1.8 ms−1 for 8 December and 6.7 to 8.9 ms−1 for 9 December [18].
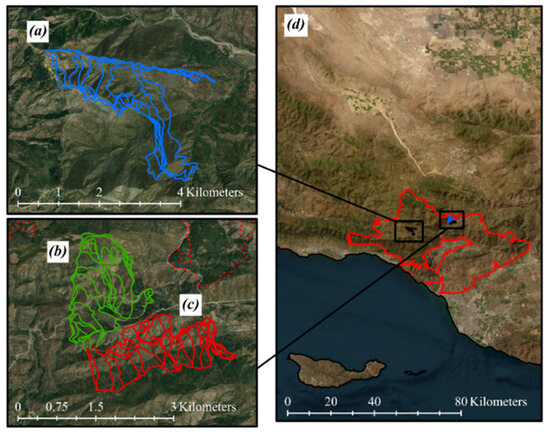
Figure 2.
Study area maps associated with the Thomas Fire that burned in December 2017 in Santa Barbara and Ventura counties, California, USA. (a) Sequence 3 (blue), (b) Sequence 2 (green), (c) Sequence 1 (red) are fire front lines delineated by Schag et al. [20]. The Thomas Fire Extent (d) is identified in red.
2.2. Image Data
We used time sequences of ATIR images of the Thomas Fire to estimate and analyze FRED distributions for the Thomas Fire. An FM2 imager owned and operated by Kolob Canyon Aerial Services was flown on their Aero Commander twin-propeller aircraft. Most of the imagery was captured using a racetrack pattern, with the imaging flightline oriented perpendicular to the predominant fire spread direction and the active fire front within image frame coverage. The FM2 imager uses a microbolometer frame-based imaging sensor that measures thermal-infrared radiation, without requiring cryogenic cooling, and typically does not saturate [11]. The FM2 sensor captured TIR radiance with a broadband (8.0–12.5 μ) and two narrowband (centered at 8.95 μ and 11.86 μ) channels, typical for land surface temperatures emissions. For this study, we exclusively used the IR3 narrowband, centered at 11.86 μ. The spatial resolution of the FM images varies as a function of altitude above ground level and was 10.4 m for the 8 December imaging sequences and 11.4 m for the 9 December sequence. The temporal resolution of the imagery is determined by the time between passes, which is determined by the ground speed of the aircraft flying and the size of the racetrack flight pattern [18]. Table 1 contains image acquisition details for the three sequences.

Table 1.
Imagery acquisition details for 8 December and 9 December.
FM2 images were georeferenced and orthorectified by USFS PSW, using Agisoft Metashape software (Version 1.8.4). Mosaics of the image frames were created using the maximum pixel value for overlapping orthoimages. Images were converted from digital number values to at-sensor radiances using a blackbody calibration curve with a radiance offset to control sensor drift that is caused by small changes in sensor temperature during imagery collection. Atmospheric correction was not applied to the imagery. Images were converted from radiances to apparent temperature values (in Kelvin).
2.3. General Methodological Approach
We assessed the sensitivity of FRED estimates to the selection of inputs and the spatial distribution of FRED for different weather conditions during the Thomas Fire, including ambient temperatures, a temperature adjustment associated with heating of ash and char surfaces, and atmospheric obscurations causing missing or attenuated FRFD values. We also characterized FRFD temporal trajectories using exponential decay functions and compared exponential decay coefficients for differing fire behaviors. Sensitivity and temporal profile analyses were based on repetitive FM2 image data for 9 December 2017 only. We estimated and compared FRED distributions and analyzed the spatial association between FRED and ROS for both the 08 and 09 December 2017 datasets.
The calibrated surface temperatures were processed to estimate FRFD in MJm−2 and FRED in kWm−2, based on Equations (2) and (3) [19]. The time intervals used to estimate FRED estimations were based on the recorded FM2 acquisition times for sequential images.
2.4. Ambient Temperature Selection
Since FRFD is derived from the difference between the burning and ambient (adjacent, non-burning) apparent surface temperatures, we evaluated the sensitivity of FRED estimates to ambient temperature selection. Ambient temperatures were estimated based on two sampling approaches, by extracting samples from several topographic aspect orientations for adjacent unburned areas and from a single long transect oriented traversing through a range of slope aspects and angles (and therefore, solar illumination conditions).
The slope aspect was derived using a USGS NED 10 m digital elevation model available through Google Earth Engine. The aspect raster was transformed and resampled to conform with FM2 pixels. Aspect was classified into the following four aspect classes: North (315° to 45°), East (45° to 135°), South (135° to 225°), and West (225° to 315°). Mean ambient temperature values across all image passes were calculated for pixels within each of the four slope aspect classes.
For the single transect approach, a 1.26 km transect was delineated across unburned vegetation adjacent to the burn scar and apparent temperature values were sampled for all pixels of the image time series. The criteria for delineating the transect included areas that did not burn throughout the duration of imagery and a line that transect a representative range in slope aspects orientations and, therefore, varying surface illumination conditions. The impact of ambient temperature uncertainty on FRFD and FRED was tested by estimating FRED and FRFD with a range of ambient temperatures. We used the minimum and maximum temperatures sampled (across all images) along the transect to determine the range of ambient temperatures.
2.5. Ash Temperature Adjustment
Due to the high emissivity and brightness temperature and low albedo of deposited ash and char during and immediately following smoldering combustion, the warmer background may erroneously contribute to FRED estimation [11,22]. An alternative function to control for ash depositions during low temperature smoldering is defined as follows:
where Ta is the temperature of ash in direct sunlight postfire, which was estimated by Riggan et al. [23] to be 343 K.
The ash adjustment was applied for the portion of the FRFD temporal profile when Tf < 473 K, where 473 K was deemed to be the minimum temperature for chaparral to ignite based on the work of Engstrom et al. [24]. Temperatures below this threshold were assumed to be associated with smoldering combustion and not flaming combustion. The adjustment was not applied for temperatures > 473 K, the temperature at which Riggan et al. [11] found that flaming combustion is the predominant influence on TIR radiance, such that radiant energy from solar-heated ash radiance is negligible.
To evaluate the impact of applying an ash adjustment, we compared ash-adjusted with non-ash-adjusted FRED estimates. The ash- and non-ash-adjusted estimates were based on an initial ambient temperature of 289 K. Percent change in mean and median FRED was estimated, as well as percent change in the mean FRED for the highest intensity fires (95th percentile).
2.6. Temporal Profile Analyses
2.6.1. Profile Classification
Binary classifiers were implemented to characterize FRFD temporal profiles, facilitating the selection of the most complete samples for analyzing peak FRFD, decay coefficient estimation, and atmospheric obscuration adjustments. Pixels were classified sequentially into four classes, in the following order: Unburned, Burned, Complete, and Obscured, based on the rule sets shown in Table 2. The minimum ignition temperature of chaparral, 473 K [25], was used as the threshold temperature for the Burned classifier. Pixels were classified as Complete when subsequent images provided negligible increases in total FRED and were classified as Obscured when there is a 40% increase in FRFD after the onset of exponential FRFD decay. A threshold of 40% was chosen based on empirical observations of FRFD temporal profiles. Pixels classified as Burned were further classified as Incomplete or Complete, while pixels classified as Complete were further classified as Obscured or not Obscured. Ash and non-ash adjusted profiles were classified to identify variations in their temporal shape.

Table 2.
Binary classifiers and associated rulesets.
2.6.2. Peak FRFD Analysis
Hudak et al. [10] noted the importance of capturing the peak FRFD within a time series to accurately estimate FRED. Peak FRFD are associated with the zone behind the active fire front. They comprise a large proportion of the total energy density and not capturing the peak can lead to a substantial underestimation of FRED. To assess the importance of peak FRFD on estimated FRED, we estimated the peak FRED (FREDpeak) as follows:
where FREDpeak is the partial FRED associated with the peak FRFD, tpostΔ is the time change (in seconds) between the peak FRFD and the next image, tpreΔ is the time change between the image prior to the peak and the peak FRFD, is the mean change in time, and FRFDpeak is the maximum FRFD in the temporal profile. Percent attribution of the FRFDpeak to the cumulative FRED is not possible without converting from flux density (Watts) to energy density (Joules). FREDpeak was calculated for all profiles that were classified as Complete. To reduce the processing times of our analysis, peak FRFD and cumulative FRED were analyzed for profiles that peaked at image pass 2.
We also calculated FRFD over shorter time intervals and determined what percentage of FRED was contributed to by specific time segments. For a hypothetical FRFD temporal profile, 60% of the FRED was accumulated 40 min post-peak and 90% 56 min post-peak.
2.6.3. Exponential Decay Coefficients
Based on the general temporal temperature progressions of fires [26] and empirical observations of temporal progression of FRFD reconstructed from FM2 imagery, FRFD profiles exhibit an exponential decay shape following peak burn temperature. Thus, the post-peak profile of FRFD progression can be approximated using the following exponential decay equation:
where A is the peak FRFD (amplitude/FRFD at ignition) (kWm−2), c is the time at ignition (s), t is the time post-ignition (s), and b is the exponential decay coefficient, commonly referred to as the half-life.
FRFD = Ae(c − t)/b)
We assumed that the peak FRFD (FRFDmax) occurs the first time a pixel is imaged burning, when solving for the exponential decay coefficient (rate) (b) using ordinary least squares regression. Both ash- and non-ash-adjusted profiles were regressed. Figure 3 shows the steepness of the exponential decay curves with varying exponential decay coefficients and a sample outcome for decay function fitting. The decay coefficient was used as a metric for comparison, such as for determining the sensitivity of FRED estimates to the use of ash adjustments. Decay coefficients were only calculated for pixels classified as Complete and not as Obscured. Maximum and minimum decay coefficients were also calculated to establish a range of decay coefficients. The mean and median decay coefficient for the 95th percentile of FRED was calculated to approximate the temporal characteristics of the highest intensity fires.
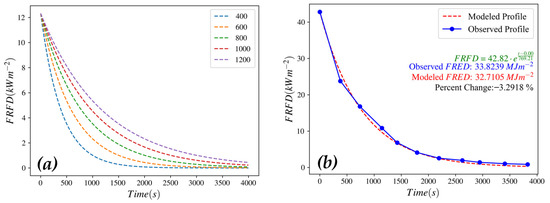
Figure 3.
(a) Sample of exponential decay functions (A = 12 kWm−2). Varying steepness in functions is due to differing decay coefficients (identified using the legend). (b) Example of function matching for an FRFD temporal profile.
2.6.4. Obscuration Adjustment
Atmospheric obscuration from high water vapor concentrations or pyrocumulus clouds occurring during imaging of the Thomas Fire represented within FRFD temporal profiles likely leads to the underestimation of FRED [11]. Despite these obscurations, profiles still exhibit exponential decay post-peak, when FRFDpeak is not obscured. To adjust for obscuration, we fit exponential decay functions to the FRFD temporal profiles classified as obscured and replaced the obscured FRFD values with that estimated by the exponential decay models for the same time step. Obscuration adjustments were applied to both ash- and non-ash-adjusted temporal profiles. Figure 4 illustrates the obscuration adjustment approach carried out by filling in the obscured gap with the modeled value. To approximate the effectiveness of adjusting for atmospheric obscurations, we calculated the mean FRED for all obscured profiles prior to adjustment. The mean FRED and percent difference were calculated for the adjusted temporal profiles and were compared with the FRED estimates based on unadjusted profiles.
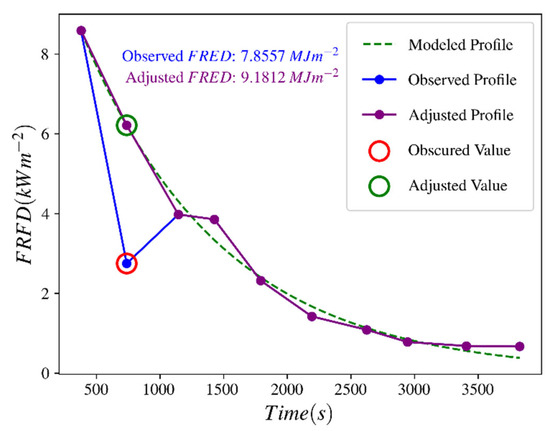
Figure 4.
Function matching for an obscured FRFD temporal profile. The red circle in the profile corresponds to an obscured observation and was removed before decay function determination. The purple profile is the adjusted profile with the gap filled value. The green circle corresponds to the new value.
2.7. Spatial Distribution of FRED Estimates
We analyzed FRED magnitudes and spatial distributions, as well as the relationship of FRED with wind speed and ROS for the 8 December and 9 December ATIR sequences. An ambient temperature of 289 K was used for both dates. All pixels classified as Complete and not Obscured were compared between the two dates. To compare estimates between areas where active fire progression was observed, FRED, FRFD, and classification statistics were derived for samples adjacent to fire fronts delineated by Schag et al. [20].
We generated and overlaid grid cells larger than the ground sampling distance of FM2 imagery, to sample FRFD and FRED estimates for comparison with the ROS estimates made by Schag et al. [20], to facilitate analysis of ROS and fire intensity relationships. Two grid cell sizes were tested, as follows: 22.75 m × 22.75 m (2 × 2 pixels) and a 34.13 m × 34.13 m (3 × 3) grid. Mean temperature and FRFD values were calculated for each grid cell using zonal statistics in ArcGIS Pro. Grid cell sampling was restricted to non-ash-adjusted FRFD. Centroids of ROS vectors were assigned a 2 × 2 and 3 × 3 grid cell, using a spatial join in ArcGIS Pro. We ran an ordinary least squared regression to compare assigned FRED and ROS for grid cells.
Previous studies by Riggan et al. [11] and Hudak et al. [10,19] highlighted the importance of pixel proximity to fire front location during image sampling. Higher FRFD and FRED were observed near the flaming front’s location during imagery collection. To assess the impact of fire front proximity to measured FREDs and FRFDs, we identified four locations (two for 8 December and two for 9 December) across fire fronts delineated by Schag et al. [18]. Criteria for fire front locations were based on the frequency of Complete and not Obscured pixels within 250 m of the fire front. For each of these four locations, we drew buffers extending 225 m away from the fire front location, with each buffer having a width of 25 m.
2.8. Toolsets and Software
Modules for FRFD and FRED estimation and pixel classification were developed in Python 3.10, using the GDAL and rasterio python libraries. Exponential decay coefficients were approximated using the curve fitting function from the SciPy python library. Sampling grids were created using the OGR and geopandas python libraries, and a zonal statistics tool in ArcGIS Pro was used to select FRFD samples. A transect for ambient temperatures was delineated and sampled using a custom GIS GUI developed in Python 3.10, built with the folium and PyQT5 libraries. All graphs and plots were created using the matplotlib python library. All Python code is available on GitHub as an ArcGIS Pro Python Toolbox (Version 3.9).
3. Results
3.1. Sensitivity to Ambient Temperature Estimation and Ash Adjustment
The sensitivity of FRED estimates to ambient temperature selection for varying slope aspects is summarized in Table 3. A 1.8% lower mean FRED and a 2.2% lower median FRED were estimated for southern exposures relative to northern aspects. When examining the highest intensity fires (95th percentile), the difference in mean FRED decreased to a negligible 0.55%.

Table 3.
Difference in measured FRED when using topographically derived ambient temperatures.
A temperature range of 13 K was found along the transect used to sample a range of ambient temperatures, with a minimum temperature of 284 K and a maximum of 297 K. A +1 K difference in ambient temperature led to a 0.35% lower mean FRED and 0.45% lower median FRED. With a range of 284 K and 298 K, a 13 K difference in ambient temperature led to a 4.56% difference in mean FRED and a 5.85% difference in median FRED. The highest intensity fires (95th percentile) were not sensitive to a 13 K difference in ambient temperature, with a 1.53% lower mean FRED.
When ash adjustments were applied to FRFD temporal profiles estimated using an ambient temperature of 289 K, the mean FRED was 8.69% lower, while the median FRED was 15.51% lower. The mean FRED for the highest intensity (95th percentile) fires was 2.97% lower.
The application of an ash control had a substantial impact on whether an FRFD temporal profile was classified as Complete or Incomplete. Of all pixels within the burn extent, 60.28% were classified as Burned. Of the pixels classified as Burned, the percentage of Complete profiles was 15.03% (63.75% or 25,972 pixel, to 75.78% or 30,728 pixels) higher when applying an ash control. Figure 5 shows the distribution of classified pixels within the burn extent and differences in classification results between the two methods.
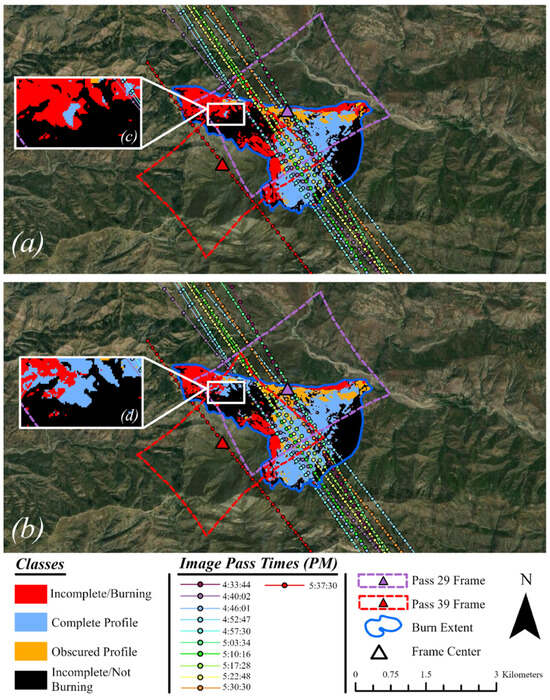
Figure 5.
Classifications of pixels within the burned area. Flight paths are included to indicate the location of the sensor during image collection. (a) Non-ash-adjusted. (b) Ash-adjusted. Inset maps (c,d) show changes in pixel classifications between FRFD profiles.
3.2. Importance of Capturing Peak FRFD on FRED
Histograms of the percentage of the total FRED accounted for by the peak FRFD, for FRFD temporal profiles classified as Complete (not obscured), are presented in Figure 6a,b. The application of an ash control impacted the influence of the peak FRFD on calculated FRED, since the mean percentage is higher when applying an ash adjustment (15.86% to 18.51%). Minimum and maximum percentages varied between ash and non-ash adjusted. The range of percentages for non-ash-controlled was 6.82% to 57.81%, and 7.05% to 69.53% for ash-adjusted.
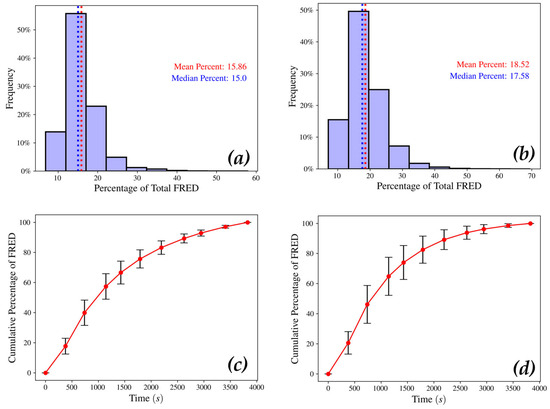
Figure 6.
Frequency of percentage of calculated FRED determined by peak FRFD for (a) non-ash-adjusted and (b) ash-adjusted. Cumulative percentage of FRED over time for (c) non-ash-adjusted and (d) ash-adjusted. Bars extending from points indicate the range of cumulative percentage values for each time.
The progression of mean percent cumulative FRED as image passes are added and FRFD values are accumulated are illustrated in Figure 6c,d. Cumulative FRED plots for both ash- and non-ash-adjusted profiles exhibit a logistic shape, with FRED increasing quickly for the first few image passes before slowly leveling out and reaching 100%. By the 8th image pass (on average, 43 min into image collection), over 90% of the contribution to FRED is observed for both profiles.
3.3. Obscured Apparent Temperature Observations
The FRFD temporal profile classifier identified areas where obscuration was readily apparent. When compared with non-ash-adjusted profiles, the percentage of completed profiles identified as Obscured was higher for ash-adjusted profiles. Figure 5 illustrates a greater extent of where obscurations occurred, regardless of ash adjustment. Of the non-ash-adjusted profiles, 18.04% were classified as Obscured, while 23.60% of ash-adjusted profiles were classified as Obscured, a 5.54% difference.
3.4. Exponential Decay Models of FRFD Profiles
Ignoring all obscured profiles, we analyzed 21,280 non-ash-adjusted profiles and 23,436 ash-adjusted profiles. Figure 7 illustrates that the decay rate coefficients are unimodal, with a slight right skew. Table 4 provides general statistics for all calculated decay rates, as well as statistics for the highest intensity fires (95th percentile of FRED). Applications of an ash adjustment led to a steeper temporal profile post-peak, indicated by the 20% lower mean decay coefficient for the ash-adjusted temporal profiles. Despite the lower model coefficients for all temporal profiles, decay coefficients for the highest intensity (95th percentile) fires were closer between ash- and non-ash-adjusted profiles, with the ash-adjusted mean decay coefficient being 4.89% lower.
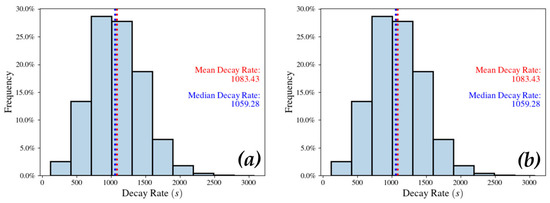
Figure 7.
Frequency of decay rates for all pixels classified as Complete. Both non-ash-adjusted (a) and ash-adjusted (b) skew right.

Table 4.
General statistics for calculated decay coefficients. All decay coefficients (DC) were calculated using least squared regression.
Comparison of modeled FRED through the reconstructed exponential decay functions with the observed FRED indicates that the function fits characterized the expected FRFD temporal profile shape. Figure 8 provides a scatter plot of modeled and observed FRED. The non-ash-adjusted regression coefficient is 0.986, while the ash-adjusted regression coefficient is 0.991. The mean difference between observed and modeled FRED is 5.28% for ash-adjusted temporal profiles and 5.92% for non-ash-adjusted temporal profiles. For ash-adjusted profiles, 0.91% of modeled FRED is lower than observed FRED, while 0.95% of modeled FRED is lower than observed FRED for non-ash-adjusted profiles.
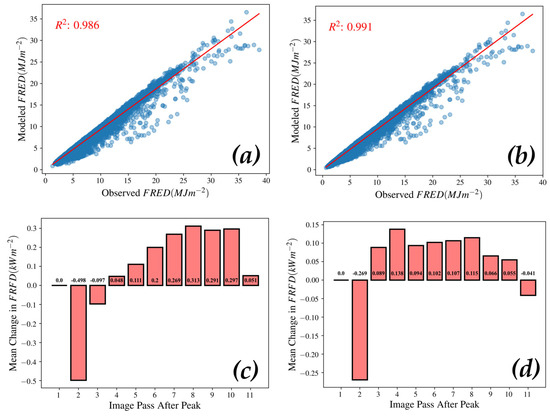
Figure 8.
Observed FRED calculated from observed FRFD temporal profiles vs. reconstructed FRFD temporal profiles using exponential decay function. (a) Non-ash adjusted. (b) Ash-adjusted. Mean residual between observed FRFD and modeled FRFD post-peak. Positive value indicates that the observed value is higher. (c) Non-ash-adjusted. (d) Ash-adjusted.
The agreement of the decay rate model relative to the FRFD temporal profile varies for different image passes. Figure 8c,d show the mean residual between observed FRFD and their modeled FRFD separated based on image pass post-peak temperature. For both profiles, the mean modeled FRFD is, on average, larger than the observed FRFD for image pass 2. However, the residual is 50% smaller for the ash-adjusted profiles (0.50 kWm−2 to 0.25 kWm−2). Similarly, the pattern of increasing residuals later in the time series is exhibited between both ash- (Figure 8d) and non-ash-adjusted (Figure 8c) profiles, but the residuals are smaller for the ash-adjusted profiles. For the last image, the residual is negative (overestimated) for the ash-adjusted profiles and positive (underestimated) for the non-ash-adjusted profiles.
The distribution of FRED and shift in skew (towards the left) in Figure 9c,d after the obscuration adjustment indicates that the adjustment successfully gap-filled the FRFD temporal profile and adjusted for energy density lost. Non-ash-adjusted and ash-adjusted profiles yielded different FRED estimates, and mean FRED values for both are greater by 0.9 MJm−2, when the obscuration adjustment was applied. On average, FRED is 21.89% higher for the ash-adjusted profiles and 16.86% higher for the non-ash-adjusted profiles, when an obscuration adjustment was applied. Frequency of percent changes are shown in Figure 9a,b.
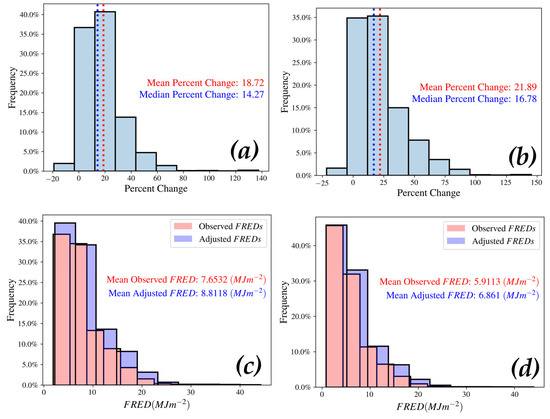
Figure 9.
Percent difference in FRED associated with the obscuration adjustment. (a) Non-ash-adjusted. (b) Ash-adjusted. Frequency of observed and adjusted FRED. Distribution of FRED shifts to the left post adjustment. (c) Non-ash-adjusted. (d) Ash-adjusted.
In total, we analyzed 4692 non-ash-adjusted profiles and 7292 ash-adjusted profiles. The application of the decay function for smoothing provided mixed results. Modeled FRED was lower than observed FREDs for 4.49% of non-ash-adjusted profiles and 7.26% of ash-adjusted profiles. The maximum difference between observed and adjusted FRED is 145.22% for the ash-adjusted profiles and 137.44% for the non-ash-adjusted profiles. The minimum difference from observed to adjusted FRED is −21.65% for the ash-adjusted profiles and −29% for the non-ash-adjusted profiles, when functions were fitted poorly.
Obscuration adjustment led to a negative change from the observed FRFD 9.82% of the time for ash-adjusted profiles and 6.79% of the time for non-ash-adjusted profiles. Based on empirical observations of obscured pixels, this may be a product of poor function fitting near the tail end of the temporal profile. Residuals in Figure 8c,d indicate that modeled FRFD was commonly lower than observed FRFD. If points in the time series were identified as Obscured near the tail end, the FRFD would likely be lower.
3.5. Relationship of FRED to ROS
The apparent relationship between FRED and ROS was analyzed for the two grid cell sizes for the 9 December dataset. Of the 469 samples where ROS could be reliably sampled, 72 contain Complete and Non-obscured pixels for 2 × 2 grid cells and 76 for 3 × 3 grid cells. Most of the samples used for this analysis were selected from the ROS centroids delineated between image passes 2–5, since centroids after image pass 5 were often assigned a grid cell that was classified as Incomplete. Of the samples for the 2 × 2 grid, 84.72% and 81.57% for the 3 × 3 grid came from this set of image passes.
Scatter plots and regression results for both 2 × 2 (Figure 10a) and 3 × 3 (Figure 10b) grid cells, including coefficients of determination and p values are illustrated in Figure 10. The coefficients of determination for both grid cell sizes are 0.70 for 2 × 2 and 0.51 for 3 × 3, indicating a positive co-variability between ROS and FRED, with both regression outputs exhibiting statistical significance (p < 0.05).
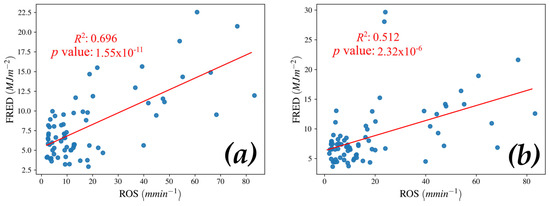
Figure 10.
Scatter plots and linear regression results for grid cell FRED and ROS vector centroids. (a) 2 × 2 grid cells and (b) 3 × 3 grid cells.
3.6. FRED Magnitudes and Spatial Distributions
Descriptive statistics of FRED distributions derived for 8 December (moderate wind speeds) and 9 December (high wind speeds) image sequences are provided in Table 5. Without controlling for variable topography, mean FRED for 8 December is higher by 12.5%. The 95th percentile for measured FRED is also 6.4% higher for 8 December. Despite the higher energy densities across the burn extent for 8 December, the peak FRFD across the burn extent is lower. The max peak FRFD for 9 December is 85.4% higher than 8 December and the mean peak FRFD is 28.5% higher. The 95th percentile of measured FRFD for 9 December is 38.5% larger than 8 December.

Table 5.
FRED and FRFD Statistics for 8 December and 9th. Topographic control FRED and FRFD were restricted to pixels within the fire front area delineated by Schag et al. [18].
When restricting the analysis to areas near the active advancing fire fronts, observations from stagnating fire fronts near ridge tops and spot fires for the 8 December dataset are removed and FRED statistics were altered. When comparing the entire burn extent for both days, 8 December FRED and FRFD estimates are lower, likely due to the removal of a stationary front west of the delineated fire fronts, while 9 December estimates are higher. With the area restriction, the mean FRED for 9 December is 4.9% higher than the mean FRED for 8 December. While the mean FRED is higher on 9 December, the difference between the median FRED is negligible (0.10 MJm−2). The mean peak FRFD is 21.9% higher for 9 December and 0.02 MJm−2 lower for 8 December. The 95th percentile of peak FRFD is 33.7% higher when applying an area restriction for 9 December and is 0.11 kWm−2 lower for 8 December.
Maps of estimated FRED for both dates, as well as their respective histograms are depicted in Figure 11. Spot fires behind the actively progressing front (pixels east of the fire front area) were more prevalent on 9 December (Figure 11b) than 8 December sequences (Figure 11a). The highest recorded FRED (95th percentile) for the 8 December burn extent was outside of the fire front area, located northwest of the burn extent, where a fire front remained stationary as it crested a hill. The opposite was the case for 9 December, with the 95th percentile of FRED located within the southern portion of the fire front area where ROS was high. However, when comparing the distribution of FRED within the fire front areas of 8 December and 9 December, fewer pixels were (1) imaged burning and (2) classified as Complete for 9 December. When restricting samples to the fire front areas, 70% of pixels on 8 December were classified as Burning and 30% as Complete, while 58% of pixels were classified as Burning and 23% as Complete for the December dataset.
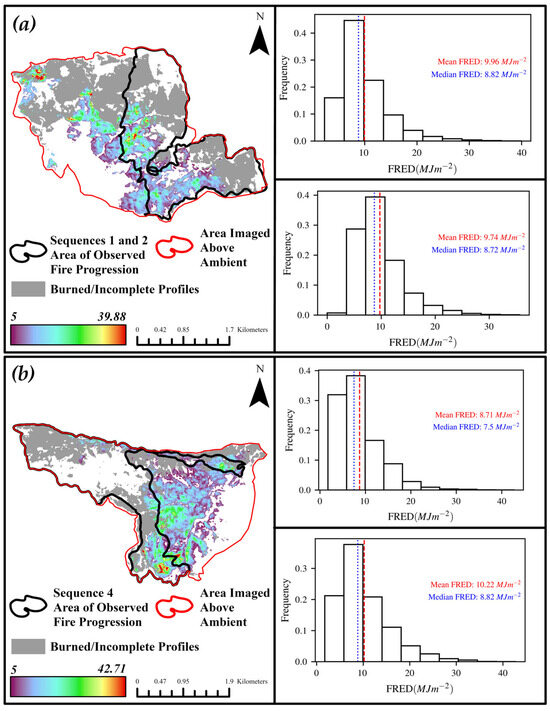
Figure 11.
Estimated FRED (MJm−2). Red area indicates where temperatures were above ambient (289 K) and near ash temperatures (343 K) during imagery collection. Black area indicates where active fire progression was observed. Gray pixels reached the 473 K threshold but were classified as Incomplete or Obscured. White pixels did not reach this 473 K threshold. For each map, the upper FRED histogram is for the entire burn extent and the lower histogram is for the fire front area. (a). For 8 December and (b) 9 December.
Statistics for each fire front, as well as the mean FRED and peak FRFD across all fronts are listed in Table 6. Figure 12 illustrates the mean FRED results for Fire Front 2. Resulting mean FRED and mean Peak FRFD were variable across all four fire fronts. The highest calculated mean FRED between all fire fronts varies; however, on average, there is a gradient descent when heading towards the final 225 m buffer. The ideal distance away from the fire front is not easy to identify, but the buffer average across all fire fronts in Table 6 may indicate that the ideal range is between 25 and 150 m. While the highest recorded MEAN Peak FRFD is highly variable across all fire fronts, each fire front indicates that the lowest recorded MEAN Peak FRFD is located 25 m away from the fire front. Fire Front 3 provides a trend that is different in comparison to the other fire fronts. The mean peak FRFD increases with distance from the active fire front. Table 6 indicates that, on average, the ideal distance away from the fire front for the highest mean peak FRFD is 125–150 m.

Table 6.
Mean FRED and Mean Peak FRFD for each fire front and buffer distance. All fronts section indicates the average for each distance across all fronts.
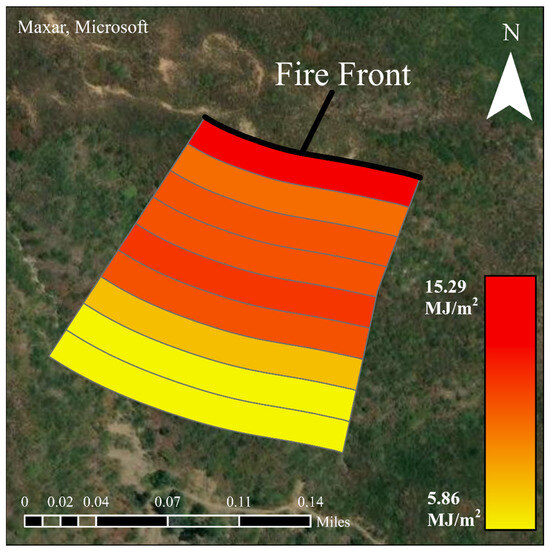
Figure 12.
Buffer zones and their mean FRED for Fire Front 2.
4. Discussion
Studies pertaining to the estimation and analysis of fire intensity metrics, such as FRED, based on repetitive ATIR imaging have primarily been conducted during controlled experiments, including the RxCADRE [10,17] and Cooney Ridge campaigns [19]. Other studies have used multi-temporal satellite image data with low spatial and temporal resolution [27,28,29]. A notable gap in the literature exists for fire intensity estimation at landscape-scales using ATIR imagery. The main research objectives of this study were to determine the procedural approaches and their sensitivities for the reliable estimation of FRED using time sequential ATIR image data for 9 December (Sequence 3), and to assess how FRED varies spatially and in comparison with ROS for both 8 December and 9 image sequences captured during the Thomas Fire.
The outcomes of this research add to findings of Boschetti and Roy [27] and Hudak et al. [10,19] by bridging the gap between small-scale, experimental studies to a landscape-scale study of a free-burning wildfire. We developed new methods and tools to address the implications of atmospheric obscuration, ash radiances, and co-registration errors to improve the reliability of FRED calculations. We also developed methods for properly characterizing FRFD temporal profiles (through classification and function fitting) to help improve imagery collection, processing, and analysis in the future. This work builds upon the works of Schag et al. [20] by exploiting ATIR image sequences for estimating fire ROS and assessing its covariation with FRED.
4.1. Sensitivity of FRFD and FRED Estimation Procedures
While ground-based systems for ambient temperature determination were employed in fire intensity studies based on experimental fires [10,19], our results indicate that an image-based approximation of ambient temperatures is suitable for estimating FRED. Controlling for variations in slope aspect illumination were found to be not important unless the difference in illumination leads to a substantial difference in surface temperatures (>30 K). Lower FRFD estimates resulting from higher ambient temperatures were most apparent near the end of FRFD temporal profiles, where surfaces reach temperatures < 400 K and begin to level off. However, this had little impact on FRED estimates due to >90% of the energy density being accumulated prior. More reliable ambient temperature determination may be required for studies focused on low temperature smoldering combustion.
Riggan et al. [11] noted the low impact of ash depositions during flaming combustion, so a background adjustment for ash depositions was deemed unnecessary for their fire intensity estimation. However, in this study, FRFD for low temperature smoldering combustion was found to be influenced by radiance from heated ash, such that applying an ash adjustment led to a substantial difference in the FRFD temporal profile shape and accumulated FRED. The end of the FRFD temporal profile dips substantially for ash-temperature-adjusted profiles compared to those using ambient temperature subtraction. When compared to non-ash-adjusted profiles, the application of the ash adjustment led to a lower FRED estimate, a greater number of Completed and Obscured profiles, a greater impact of the peak FRFD on FRED, and steeper exponential decay models. Ash adjustments applied to FRFD profiles were based on values from a previous study conducted in a tropical savanna [11]. Other approaches could include controls for slope aspect due to variations in solar irradiance [11], or controls for varying ash colors [23]. High-intensity fires deposit a thick layer of white/gray ash, while low-intensity fires consume less vegetation and leave a dark (gray or black) ash layer [23]. These variations in ash layer color affect the solar absorption and emitted radiance of surfaces, such that a characterization of ash background temperature based on fire intensity (e.g., peak FRFD) may be a useful indicator of ash radiances during smoldering combustion [23].
Hudak et al. [10,19] noted the importance of sampling the peak temperature within the temporal profile, since a large portion of the estimated energy density is attributed to the peak. While capturing the peak temperature of the temporal profile is key to reliably estimating the total energy density, we found that the degree to which the total energy density is attributed to the peak temperature is highly variable. For example, the peak temperature contributed > 60% of the measured FRED for some temporal profiles and as low as 20% for others. Achieving an adequate sampling frequency is key to capturing the peak temperature, but the duration of sampling is also important for properly estimating FRED.
Another important consideration regarding capturing the peak temperature of the temporal FRFD profile is that the maximum recorded temperature may not represent the true peak temperature. This may occur because a pixel during a TIR image pass was not sensed at or near the passing of the active fire front, or because of the relatively low emissivity values associated flames, which are gray body radiators [9,15]. The latter means that the true “peak” for a temperature temporal profile may be underestimated, unless the emissivity of the flaming zone was known and used to modify surface temperature estimates. Riggan et al. [11] proposed a multiband method to adjust for surface emissivity, but such a method is not feasible for the single, narrow-band TIR data utilized for this study.
FRFD temporal profiles were numerically characterized using an exponential decay model, particularly through the exponential decay coefficient. While Hudak et al. [10,19] noted the exponential decay shape of FRFD temporal profiles for the RxCADRE and Cooney Ridge experiments, no metric was utilized to quantify the form of the profiles. Modeled and observed FRED estimates in this study are highly correlated (R2 > 0.98 for both ash- and non-ash-adjusted), providing a proxy measurement for the accuracy of decay function fit. Alexander [26] reported temperature temporal profiles exhibiting a similar exponential decay shape, which support the reliability of our findings. Despite the high degree of fit with modeled FRED, residuals between the modeled and observed FRFD values are greater for FRFD measurements later in the time series. This may result from the exponential decay function being strongly influenced by the peak amplitude, a parameter that is not calculated through least squared regression.
We demonstrated that atmospheric obscuration is a source of missing or reduced surface temperature observations for ATIR imaging of active fires [11], which influences the ability to adequately sample FRFD for FRED estimation. Riggan and Tissell [11] state that pyrocumulus clouds and water vapor produced by flaming combustion can obscure radiances within the TIR spectral range (8–12 um). Our obscuration classification results suggest that obscuration was not common for the passes over the Thomas Fire incorporated in this study, though obscuration associated with the high-intensity, rapidly spreading fire captured during Sequence 3 was evident.
Other studies concerned with the estimation of FRED based on ATIR imaging have not identified or adjusted for obscured pixels in temporal profiles, possibly because they were based on experimental burns that do no generate large plumes of water vapor and/or pyrocumulus clouds [10,17,19]. By identifying obscured pixels and fitting an exponential decay function to temporal FRFD profiles, obscured values can be adjusted and associated energy density losses can be compensated.
In some instances, poor exponential decay model fits or poorly identified obscured profiles lead to unreliable FRED estimates. This stemmed from errors in classifying obscured profiles, where small variations in measured FRFD during smoldering combustion (when the temporal profile flattens out) were identified as an obscuration. Based on FRFD residuals results from Complete and non-Obscured profiles, modeled FRFD values later in the time series were lower than observed FRFD. Since Obscured values in the temporal profile occurred later in the time series, the modeled FRFD was lower.
Exponential decay function fitting was shown to be a useful alternative to commonly used gap-filling or anomaly smoothing methods to account for gaps caused by Obscured values, such as Savitzky–Golay or Whitaker filtering [24]. Future applications of the exponential decay function may include value predictions later in the time series. If the decay coefficient from an FRFD temporal profile can be determined based on an incomplete temporal sequence, particularly with a few key clear images captured near the start of the time sequence, the distance decay modeled shape may be sufficient for reliably estimating FRED.
4.2. FRED Distributions and Relationships
When including the entire burn extent captured by repetitive ATIR imaging, which includes spot fires and stagnating fire fronts, FRED magnitudes were estimated to be higher for the 8 December passes that burned during moderate wind speed conditions than for the 9 December passes. After restricting sampled pixels to the fire front area (where fire progression is active), FRED and peak FRFD statistics are higher on 9 December than 8 December. The Rothermel model of fire propagation includes reaction intensity (Wm−2) as a variable that increases ROS, so a higher ROS may be associated with a higher intensity heat source [30]. Therefore, peak FRFD statistics may be a helpful approximator for fire rate of spread.
Despite the higher estimated cumulative fire intensities for 9 December, the frequency at which pixels were imaged burning was lower. Only 50% of pixels within the fire area were classified as Burning for 9 December, while 70% were classified as Burning for 8 December. This is likely due to active fire progression being fast relative to the repetitive imaging frequency for 9 December, preventing the flaming combustion to be captured during image passes. This is emphasized by a large extent, seen in Figure 11b, with a lack of pixels classified as Burned within the active fire front zones imaged at that time.
Spatial distributions of estimated fire intensity in previous studies by Hudak et al. [10] and Riggan et al. [11] indicated that the higher fire intensities were located near the actively progressing head. Using our buffer approach, such an association is not evident in our FRED estimates. However, the progressive decrease in measured FRED as the buffer distance increases may provide an indication of an ideal zone for FRED estimation.
Maps depicting spatial distributions of FRED can be important datasets for studying fire behavior and the impacts of FRED on burn severity and postfire recovery. For example, Hudak et al. [19] found that ash deposition postfire was positively correlated with measured energy densities during the Cooney Ridge Fire Experiment. Ash deposition influences could be compared by using a coarse grid to sample Landsat-derived NBR/dNBR. FRED distributions could also be examined relative to distributions of postfire recovery trajectories, such as those derived from Landsat time series. [31,32,33].
Results from this thesis research indicate that ROS is positively correlated with FRED for burned areas of the Thomas Fire where adequate temporal sampling of ATIR-derived brightness temperatures was achieved. The spatial extent of the sampled area was limited due to a lack of Complete and non-Obscured profiles spatially associated with ROS vectors. The application of decay coefficients for completing incomplete profiles is useful for gap filling and increasing the number of samples for ROS and FRED analysis. Portions of the active fire where ROS was estimated to be spreading fastest (95th percentile of spread vectors) were not included in the sample since they were not classified as Burned or Complete. This is consistent with the observation of Hudak et al. [10] that when ROS is high, flaming combustion may not be imaged for many locations, leading to an underestimation of FRED for those locations [10].
5. Conclusions
This study addresses procedures and their sensitivity and reliability for reconstructing time sequences of TIR flux densities and estimating FRED for active wildland fires through aerial thermal-infrared imagery at a landscape scale, a shift away from previous studies that calculated FRFD and FRED through controlled experiments [10,19]. We addressed the impact of ambient temperature approximations on fire intensity measurements and conclude that variable approximations of ambient temperature do not impact the discrimination of high- and low-intensity fires. We provided an alternative approach to background temperature subtraction that controls ash radiances during low temperature smoldering combustion. Using the fire temperature time series developed by Alexander [26] as a reference, we developed and fit an exponential decay model to FRFD temporal profiles to properly characterize how flux densities decay over time. We used these decay models to adjust for classified instances of obscuration within FRFD temporal profiles. ROS vectors and FRED comparisons between 8 and 9 December 2017 imaging passes for the Thomas Fire provide an indication of how ROS covaries with FRED.
While the outcomes from this study are promising, some challenges and limitations were faced when conducting the research. First, the imagery for this study was originally used for ROS research. The racetrack flight method makes it possible for repeat passes to be consistent and fast; however, the tracking of numerous flaming fronts can extend the return interval. The tradeoff for a longer return interval is providing a larger area of coverage. This leads to a tradeoff researchers must consider; the return interval can be decreased by focusing on a smaller area (individual front), but coverage is limited. A fast ROS and long return interval may prevent imaging during peak combustion. As previously mentioned, variations in surface emissivity and obscurations provide a level of uncertainty in estimating FRED [11].
Future studies should consider the refinement of flight patterns and repeat frequency when collecting ATIR imagery. While the sampling duration is important for accurate approximations of FRED, a higher sampling frequency would increase the likelihood of collecting the peak and provide more samples for FRFD temporal profiles. A racetrack flight pattern that covers a small area would increase the sampling frequency and prevent mischaracterizations of FRED due to missing instances of flaming combustion, especially for fast-spreading fire fronts. The tradeoff for increasing the sampling frequency would be a reduction in spatial coverage.
Studies of cumulative fire intensity should be conducted with airborne sensors utilizing additional infrared wavebands. Riggan and Tissell [11] noted the importance of using SWIR or MIR in conjunction with LWIR for accurate approximations of fire intensity. An appropriate research direction would be analyzing FRED distributions relative to image-derived metrics for prefire fuel load and/or moisture and postfire burn severity maps derived from satellite spectral vegetation indices [32]. Assessing spatial correspondence of FRED relative to topographic variables such as directional slope [18] would be another worthwhile objective. Fuel loads and moisture in southern California chaparral vary based on slope aspect, specifically northern- and southern-facing slopes [34]. Southern slopes are less dense with vegetation than northern-facing slopes [34], so spatial distributions of FRED may reflect topographic differences across landscapes.
Author Contributions
Conceptualization, A.J.M., D.A.S., P.J.R., J.O. and H.S.; Methodology, A.J.M., D.A.S., J.O. and H.S.; Software, A.J.M.; Validation, A.J.M.; Formal analysis, A.J.M.; Resources, R.T.; Data curation, A.J.M., P.J.R. and R.T.; Writing—original draft, A.J.M.; Writing—review & editing, D.A.S., P.J.R., R.T., J.O. and H.S.; Visualization, A.J.M.; Supervision, D.A.S.; Funding acquisition, D.A.S. and P.J.R. All authors have read and agreed to the published version of the manuscript.
Funding
Funding to support this research was provided by the USDA Forest Service, Pacific Southwest Research Station grants: G00012222 (Effects of Drought Stress and Forest Management on Fire Behavior and Post-Fire Forest Structure in Western Coniferous Forest) and grant G000147000 (Remote Sensing of Forest Health and Fire Effects).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rothermel, R.C.; Deeming, J.E. Measuring and Interpreting Fire Behavior for Correlation with Fire Effects; Intermountain Forest and Range Experiment Station, US Department of Agriculture: Ogden, UT, USA, 1980.
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Intermountain Forest & Range Experiment Station, Forest Service: Ogden, UT, USA, 1972; Volume 115.
- Bradstock, R.; Auld, T. Soil Temperatures during Experimental Bushfires in Relation to Fire Intensity: Consequences for Legume Germination and Fire Management in South-Eastern Australia. J. Appl. Ecol. 1995, 32, 76–84. [Google Scholar] [CrossRef]
- Weise, D.R.; Zhou, X.; Sun, L.; Mahalingam, S. Fire Spread in Chaparral—‘Go or No-Go?’. Int. J. Wildland Fire 2005, 14, 99. [Google Scholar] [CrossRef]
- Emery, S.M.; Uwimbabazi, J.; Flory, S.L. Fire Intensity Effects on Seed Germination of Native and Invasive Eastern Deciduous Forest Understory Plants. For. Ecol. Manag. 2011, 261, 1401–1408. [Google Scholar] [CrossRef]
- Kreye, J.K.; Brewer, N.W.; Morgan, P.; Varner, J.M.; Smith, A.M.S.; Hoffman, C.M.; Ottmar, R.D. Fire Behavior in Masticated Fuels: A Review. For. Ecol. Manag. 2014, 314, 193–207. [Google Scholar] [CrossRef]
- Cheney, N.P.; Gould, J.S.; McCaw, W.L.; Anderson, W.R. Predicting Fire Behaviour in Dry Eucalypt Forest in Southern Australia. For. Ecol. Manag. 2012, 280, 120–131. [Google Scholar] [CrossRef]
- Cruz, M.G.; Cheney, N.P.; Gould, J.S.; McCaw, W.L.; Kilinc, M.; Sullivan, A.L. An Empirical-Based Model for Predicting the Forward Spread Rate of Wildfires in Eucalypt Forests. Int. J. Wildland Fire 2022, 31, 81–95. [Google Scholar] [CrossRef]
- Veraverbeke, S.; Dennison, P.; Gitas, I.; Hulley, G.; Kalashnikova, O.; Katagis, T.; Kuai, L.; Meng, R.; Roberts, D.; Stavros, N. Hyperspectral Remote Sensing of Fire: State-of-the-Art and Future Perspectives. Remote Sens. Environ. 2018, 216, 105–121. [Google Scholar] [CrossRef]
- Hudak, A.T.; Dickinson, M.B.; Bright, B.C.; Kremens, R.L.; Loudermilk, E.L.; O’Brien, J.J.; Hornsby, B.S.; Ottmar, R.D. Measurements Relating Fire Radiative Energy Density and Surface Fuel Consumption—RxCADRE 2011 and 2012. Int. J. Wildland Fire 2016, 25, 25–37. [Google Scholar] [CrossRef]
- Riggan, P.; Tissell, R. Chapter 6 Airborne Remote Sensing of Wildland Fires. Dev. Environ. Sci. 2009, 8. [Google Scholar] [CrossRef]
- Thornberry, T.D.; Gao, R.-S.; Ciciora, S.J.; Watts, L.A.; McLaughlin, R.J.; Leonardi, A.; Rosenlof, K.H.; Argrow, B.M.; Elston, J.S.; Stachura, M.; et al. A Lightweight Remote Sensing Payload for Wildfire Detection and Fire Radiative Power Measurements. Sensors 2023, 23, 3514. [Google Scholar] [CrossRef] [PubMed]
- Allison, R.S.; Johnston, J.M.; Craig, G.; Jennings, S. Airborne Optical and Thermal Remote Sensing for Wildfire Detection and Monitoring. Sensors 2016, 16, 1310. [Google Scholar] [CrossRef] [PubMed]
- Wooster, M.; Zhukov, B.; Oertel, D. Fire Radiative Energy for Quantitative Study of Biomass Burning: Derivation from the BIRD Experimental Satellite and Comparison to MODIS Fire Products. Remote Sens. Environ. 2003, 86, 83–107. [Google Scholar] [CrossRef]
- Wooster, M.J.; Roberts, G.; Perry, G.L.W.; Kaufman, Y.J. Retrieval of Biomass Combustion Rates and Totals from Fire Radiative Power Observations: FRP Derivation and Calibration Relationships between Biomass Consumption and Fire Radiative Energy Release. J. Geophys. Res. Atmos. 2005, 110, 1–24. [Google Scholar] [CrossRef]
- Kremens, R.L.; Dickinson, M.B.; Bova, A.S. Radiant Flux Density, Energy Density, and Fuel Consumption in Mixed-Oak Forest Surface Fires. Int. J. Wildland Fire 2012, 21, 722–730. [Google Scholar] [CrossRef]
- O’Brien, J.J.; Loudermilk, E.L.; Hornsby, B.; Hudak, A.T.; Bright, B.C.; Dickinson, M.B.; Hiers, J.K.; Teske, C.; Ottmar, R.D. High-Resolution Infrared Thermography for Capturing Wildland Fire Behaviour: RxCADRE 2012. Int. J. Wildland Fire 2016, 25, 62. [Google Scholar] [CrossRef]
- Schag, G.M.; Stow, D.A.; Riggan, P.J.; Tissell, R.G.; Coen, J.L. Examining Landscape-Scale Fuel and Terrain Controls of Wildfire Spread Rates Using Repetitive Airborne Thermal Infrared (ATIR) Imagery. Fire 2021, 4, 6. [Google Scholar] [CrossRef]
- Hudak, A.; Freeborn, P.; Lewis, S.; Hood, S.; Smith, H.; Hardy, C.; Kremens, R.; Butler, B.; Teske, C.; Tissell, R.; et al. The Cooney Ridge Fire Experiment: An Early Operation to Relate Pre-, Active, and Post-Fire Field and Remotely Sensed Measurements. Fire 2018, 1, 10. [Google Scholar] [CrossRef]
- Klauberg, C.; Hudak, A.; Bright, B.; Boschetti, L.; Dickinson, M.; Kremens, R.; Silva, C. Use of Ordinary Kriging and Gaussian Conditional Simulation to Interpolate Airborne Fire Radiative Energy Density Estimates. Int. J. Wildland Fire 2018, 27, 228–240. [Google Scholar] [CrossRef]
- Benoit, J.W.; Chen, S.C. FireBuster: A Tool for Fire Management; Pacific Southwest Research Station General Technical Report; USDA Forest Service: Ogden, UT, USA, 2019; Volume 261, pp. 25–37.
- Riggan, P.J.; Hoffman, J.W.; Brass, J.A. Estimating Fire Properties by Remote Sensing. In Proceedings of the 2000 IEEE Aerospace Conference. Proceedings (Cat. No. 00TH8484), Hyderabad, India, 25 March 2000; Volume 3, pp. 173–179. [Google Scholar]
- Brass, J.A.; Ambrosia, V.G.; Riggan, P.J.; Sebesta, P.D. Consequences of Fire on Aquatic Nitrate and Phosphate Dynamics in Yellowstone National Park. Int. Assoc. Wildland Fire 1996, 6, 53–57. [Google Scholar]
- Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A Comparison of Methods for Smoothing and Gap Filling Time Series of Remote Sensing Observations—Application to MODIS LAI Products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
- Engstrom, J.D.; Butler, J.K.; Smith, S.G.; Baxter, L.L.; Fletcher, T.H.; Weise, D.R. Ignition Behavior of Live California Chaparral Leaves. Combust. Sci. Technol. 2004, 176, 1577–1591. [Google Scholar] [CrossRef]
- Alexander, M.; Stocks, B.; Wotton, M.; Lanoville, R.A. An Example of Multi-Faceted Wildland Fire Research: The International Crown Fire Modelling Experiment. In Joint III International Conference on Forest Fire Research and 14th Conference on Fire and Forest Meteorology; University of Coimbra: Coimbra, Portugal, 1998. [Google Scholar]
- Boschetti, L.; Roy, D.P. Strategies for the Fusion of Satellite Fire Radiative Power with Burned Area Data for Fire Radiative Energy Derivation. J. Geophys. Res. Atmos. 2009, 114, D20302. [Google Scholar] [CrossRef]
- Freeborn, P.H.; Wooster, M.J.; Roberts, G. Addressing the Spatiotemporal Sampling Design of MODIS to Provide Estimates of the Fire Radiative Energy Emitted from Africa. Remote Sens. Environ. 2011, 115, 475–489. [Google Scholar] [CrossRef]
- Roberts, G.; Wooster, M.J.; Perry, G.L.W.; Drake, N.; Rebelo, L.-M.; Dipotso, F. Retrieval of Biomass Combustion Rates and Totals from Fire Radiative Power Observations: Application to Southern Africa Using Geostationary SEVIRI Imagery. J. Geophys. Res. Atmos. 2005, 110, 6018. [Google Scholar] [CrossRef]
- Andrews, P.L. The Rothermel Surface Fire Spread Model and Associated Developments: A Comprehensive Explanation; Technical Report; Rocky Mountain Research Station, Forest Service: Fort Collins, CO, USA; United States Department of Agriculture: Fort Collins, CO, USA, 2018.
- Pickell, P.D.; Hermosilla, T.; Frazier, R.J.; Coops, N.C.; Wulder, M.A. Forest Recovery Trends Derived from Landsat Time Series for North American Boreal Forests. Int. J. Remote Sens. 2016, 37, 138–149. [Google Scholar] [CrossRef]
- Hislop, S.; Jones, S.; Soto-Berelov, M.; Skidmore, A.; Haywood, A.; Nguyen, T.H. Using Landsat Spectral Indices in Time-Series to Assess Wildfire Disturbance and Recovery. Remote Sens. 2018, 10, 460. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. Landscape Assessment: Remote Sensing of Severity, the Normalized Burn Ratio, in FIREMON: Fire Effects Monitoring and Inventory System; Lutes, D.C., Ed.; USDA Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2005.
- Barbour, M.; Keeler-Wolf, T.; Schoenherr, A.A. Terrestrial Vegetation of California; University of California Press: Berkeley, CA, USA, 2007; ISBN 0-520-93336-2. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).