Activation Energy of Hydrogen–Methane Mixtures
Abstract
1. Introduction
2. Methodology for Determining the Activation Energy
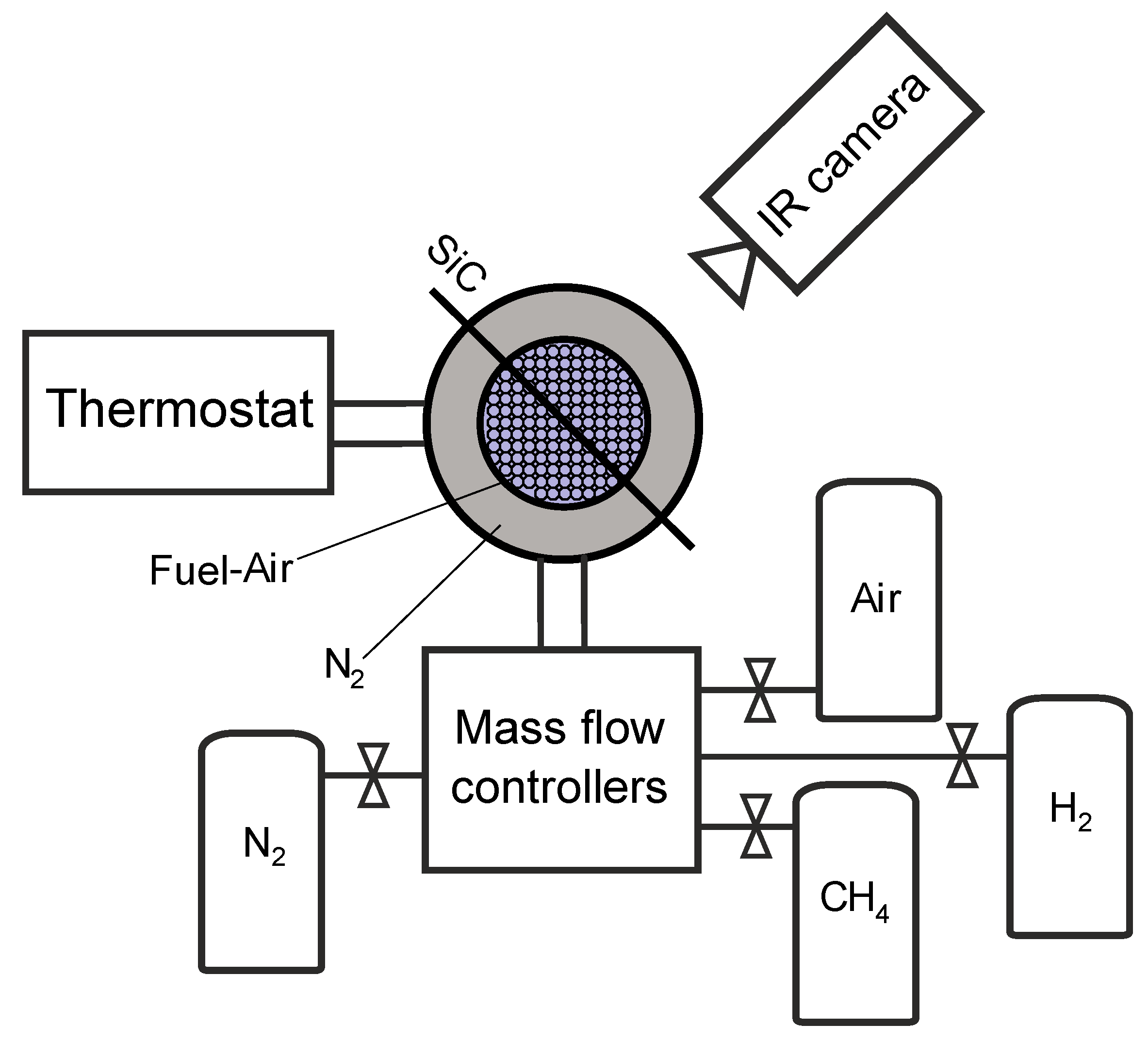
2.1. Experimental Setup
2.2. Modelling with the Detailed Reaction Mechanism
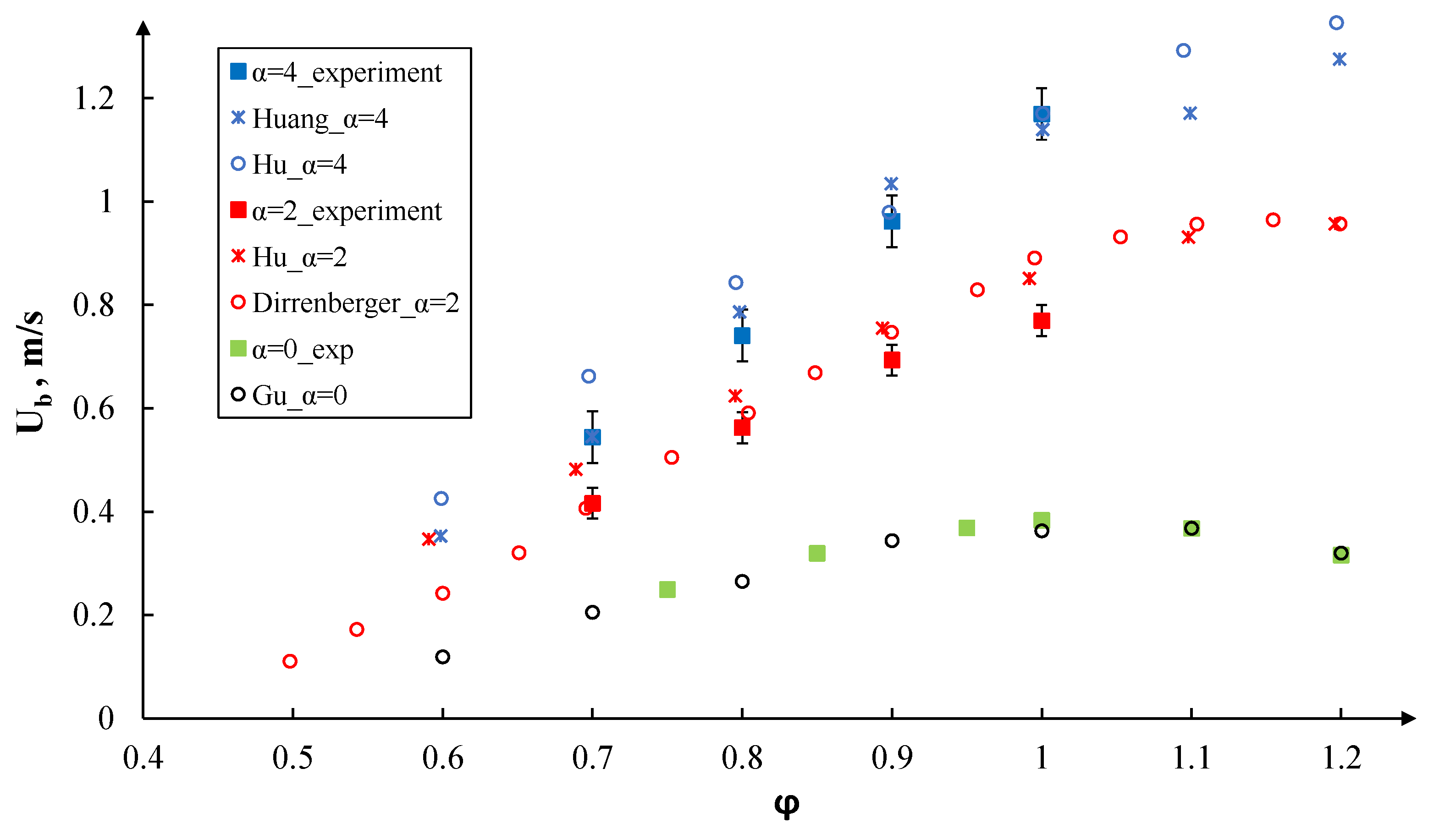
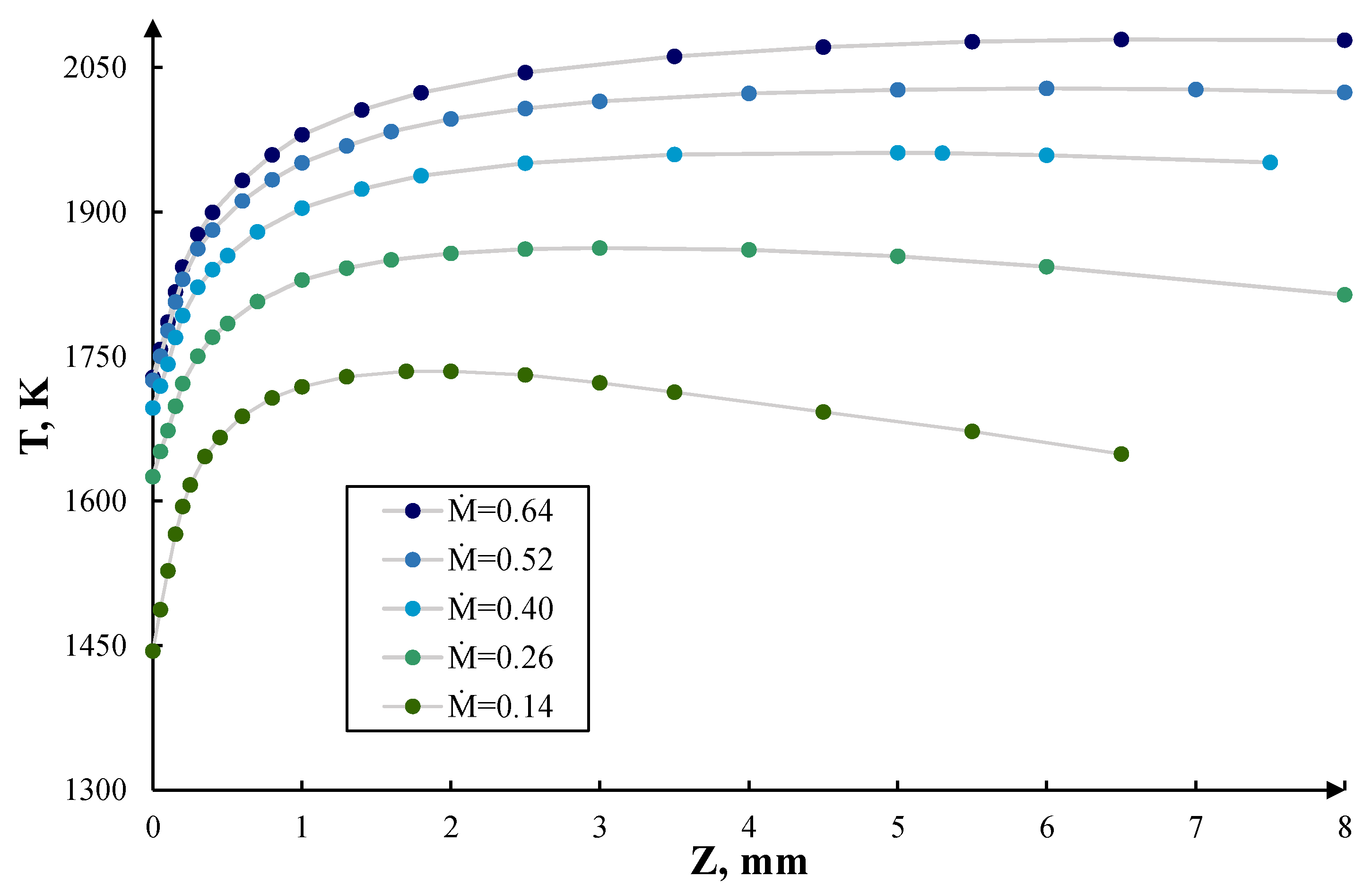
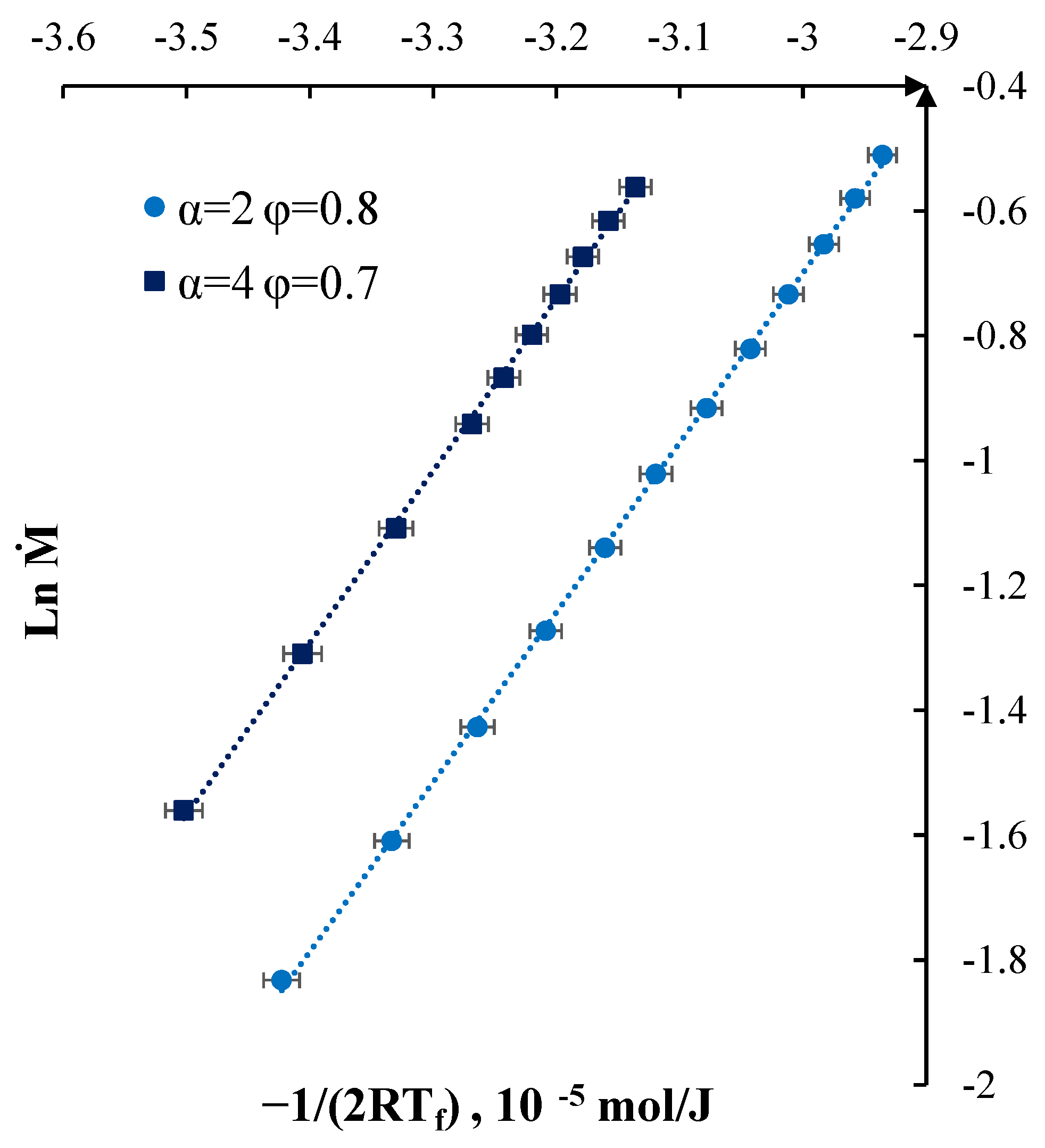
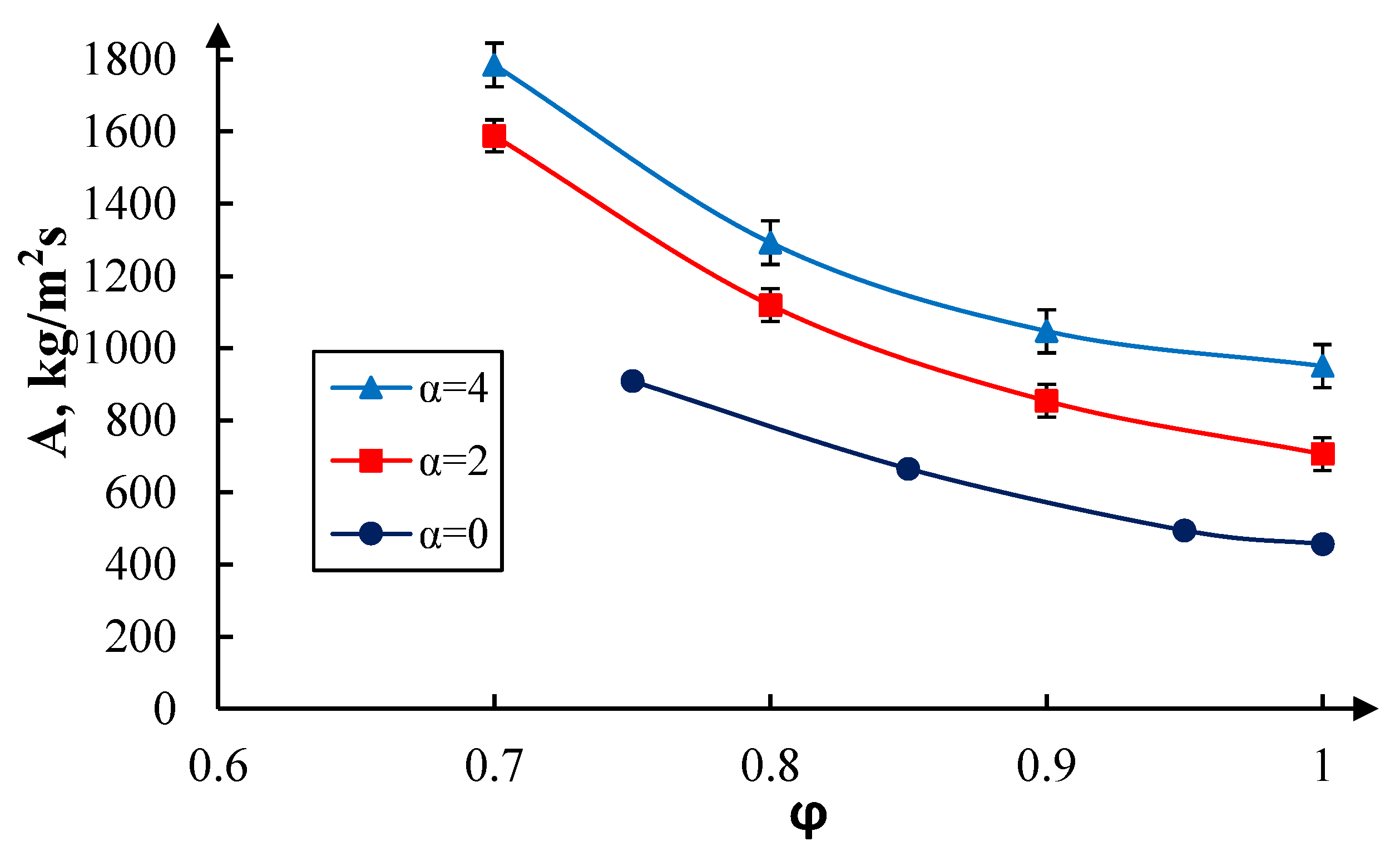
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature and Abbreviations
Nomenclature
| p | pressure |
| T | temperature |
| flame front temperature | |
| adiabatic flame temperature | |
| gas temperature |
Abbreviations
| density | |
| R | universal gas constant |
| overall activation energy | |
| A | correlation factor |
| molar fuel concentration | |
| K | standard pre-exponential factor of the bimolecular reaction rate |
| laminar burning velocity | |
| mass flow rate of the fresh mixture | |
| critical mass flow rate at which there is flame blow-off | |
| equivalence ratio | |
| ratio of the molar fractions of hydrogen to methane | |
| molar fraction of i-th species | |
| Z | height above the burner |
| d | filament diameter |
| emissivity | |
| Stefan–Boltzmann constant | |
| heat exchange coefficient | |
| thermal conductivity | |
| thermal diffusivity | |
| Nusselt number | |
| Zeldovich number | |
| Lewis number |
References
- Sher, E.; Refael, S. A simplified reaction scheme for the combustion of hydrogen enriched methane/air flame. Combust. Sci. Technol. 1988, 59, 371–389. [Google Scholar] [CrossRef]
- Refael, S.; Sher, E. Reaction kinetics of hydrogen-enriched methane-air and propane-air flames. Combust. Flame 1989, 78, 326–338. [Google Scholar] [CrossRef]
- Gauducheau, J.; Denet, B.; Searby, G. A numerical study of lean CH4/H2/air premixed flames at high pressure. Combust. Sci. Technol. 1998, 137, 81–99. [Google Scholar] [CrossRef]
- El-Sherif, S. Control of emissions by gaseous additives in methane—Air and carbon monoxide—Air flames. Fuel 2000, 79, 567–575. [Google Scholar] [CrossRef]
- Park, J.; Keel, S.I.; Yun, J.H. Addition effects of H2 and H2O on flame structure and pollutant emissions in methane–air diffusion flame. Energy Fuels 2007, 21, 3216–3224. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Z.; Tang, C.; Miao, H.; Wang, X. Numerical study of the effect of hydrogen addition on methane—Air mixtures combustion. Int. J. Hydrogen Energy 2009, 34, 1084–1096. [Google Scholar] [CrossRef]
- Bougrine, S.; Richard, S.; Nicolle, A.; Veynante, D. Numerical study of laminar flame properties of diluted methane-hydrogen-air flames at high pressure and temperature using detailed chemistry. Int. J. Hydrogen Energy 2011, 36, 12035–12047. [Google Scholar] [CrossRef]
- Li, Q.; Hu, G.; Liao, S.; Cheng, Q.; Zhang, C.; Yuan, C. Kinetic effects of hydrogen addition on the thermal characteristics of methane—Air premixed flames. Energy Fuels 2014, 28, 4118–4129. [Google Scholar] [CrossRef]
- Ying, Y.; Liu, D. Detailed influences of chemical effects of hydrogen as fuel additive on methane flame. Int. J. Hydrogen Energy 2015, 40, 3777–3788. [Google Scholar] [CrossRef]
- Ren, F.; Chu, H.; Xiang, L.; Han, W.; Gu, M. Effect of hydrogen addition on the laminar premixed combustion characteristics the main components of natural gas. J. Energy Inst. 2019, 92, 1178–1190. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Ju, D.; Huang, Z.; Han, D. Analysis of exergy losses in laminar premixed flames of methane/hydrogen blends. Int. J. Hydrogen Energy 2019, 44, 24043–24053. [Google Scholar] [CrossRef]
- Xiang, L.; Jiang, H.; Ren, F.; Chu, H.; Wang, P. Numerical study of the physical and chemical effects of hydrogen addition on laminar premixed combustion characteristics of methane and ethane. Int. J. Hydrogen Energy 2020, 45, 20501–20514. [Google Scholar] [CrossRef]
- Law, C.K.; Kwon, O. Effects of hydrocarbon substitution on atmospheric hydrogen—Air flame propagation. Int. J. Hydrogen Energy 2004, 29, 867–879. [Google Scholar] [CrossRef]
- Halter, F.; Chauveau, C.; Djebaïli-Chaumeix, N.; Gökalp, I. Characterization of the effects of pressure and hydrogen concentration on laminar burning velocities of methane–hydrogen—Air mixtures. Proc. Combust. Inst. 2005, 30, 201–208. [Google Scholar] [CrossRef]
- Ilbas, M.; Crayford, A.; Yılmaz, I.; Bowen, P.; Syred, N. Laminar-burning velocities of hydrogen—Air and hydrogen—Methane—Air mixtures: An experimental study. Int. J. Hydrogen Energy 2006, 31, 1768–1779. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Zeng, K.; Liu, B.; Wang, Q.; Jiang, D. Measurements of laminar burning velocities for natural gas—Hydrogen—Air mixtures. Combust. Flame 2006, 146, 302–311. [Google Scholar] [CrossRef]
- Halter, F.; Chauveau, C.; Gökalp, I. Characterization of the effects of hydrogen addition in premixed methane/air flames. Int. J. Hydrogen Energy 2007, 32, 2585–2592. [Google Scholar] [CrossRef]
- Hu, E.; Huang, Z.; He, J.; Jin, C.; Zheng, J. Experimental and numerical study on laminar burning characteristics of premixed methane—Hydrogen—Air flames. Int. J. Hydrogen Energy 2009, 34, 4876–4888. [Google Scholar] [CrossRef]
- Hu, E.; Huang, Z.; He, J.; Miao, H. Experimental and numerical study on lean premixed methane—Hydrogen—Air flames at elevated pressures and temperatures. Int. J. Hydrogen Energy 2009, 34, 6951–6960. [Google Scholar] [CrossRef]
- Eckart, S.; Pizzuti, L.; Fritsche, C.; Krause, H. Experimental study and proposed power correlation for laminar burning velocity of hydrogen-diluted methane with respect to pressure and temperature variation. Int. J. Hydrogen Energy 2022, 47, 6334–6348. [Google Scholar] [CrossRef]
- Yilmaz, H.; Schröder, L.; Hillenbrand, T.; Brüggemann, D. Effects of hydrogen addition on combustion and flame propagation characteristics of laser ignited methane/air mixtures. Int. J. Hydrogen Energy 2023, 48, 17324–17338. [Google Scholar] [CrossRef]
- Yu, G.; Law, C.; Wu, C. Laminar flame speeds of hydrocarbon + air mixtures with hydrogen addition. Combust. Flame 1986, 63, 339–347. [Google Scholar] [CrossRef]
- Ren, J.Y.; Qin, W.; Egolfopoulos, F.; Tsotsis, T. Strain-rate effects on hydrogen-enhanced lean premixed combustion. Combust. Flame 2001, 124, 717–720. [Google Scholar] [CrossRef]
- Ren, J.Y.; Qin, W.; Egolfopoulos, F.; Mak, H.; Tsotsis, T. Methane reforming and its potential effect on the efficiency and pollutant emissions of lean methane—Air combustion. Chem. Eng. Sci. 2001, 56, 1541–1549. [Google Scholar] [CrossRef]
- Jackson, G.S.; Sai, R.; Plaia, J.M.; Boggs, C.M.; Kiger, K.T. Influence of H2 on the response of lean premixed CH4 flames to high strained flows. Combust. Flame 2003, 132, 503–511. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, X.; Wei, W.; Qiu, L.; Wu, H. Effects of hydrogen addition on laminar flame speeds of methane, ethane and propane: Experimental and numerical analysis. Int. J. Hydrogen Energy 2017, 42, 24055–24066. [Google Scholar] [CrossRef]
- Coppens, F.; De Ruyck, J.; Konnov, A.A. Effects of hydrogen enrichment on adiabatic burning velocity and NO formation in methane + air flames. Exp. Therm. Fluid Sci. 2007, 31, 437–444. [Google Scholar] [CrossRef]
- Coppens, F.; De Ruyck, J.; Konnov, A.A. The effects of composition on burning velocity and nitric oxide formation in laminar premixed flames of CH4 + H2 + O2 + N2. Combust. Flame 2007, 149, 409–417. [Google Scholar] [CrossRef]
- Konnov, A.; Riemeijer, R.; De Goey, L. Adiabatic laminar burning velocities of CH4 + H2 + air flames at low pressures. Fuel 2010, 89, 1392–1396. [Google Scholar] [CrossRef]
- Hermanns, R.; Konnov, A.A.; Bastiaans, R.; De Goey, L.; Lucka, K.; Köhne, H. Effects of temperature and composition on the laminar burning velocity of CH4 + H2 + O2 + N2 flames. Fuel 2010, 89, 114–121. [Google Scholar] [CrossRef]
- Dirrenberger, P.; Le Gall, H.; Bounaceur, R.; Herbinet, O.; Glaude, P.A.; Konnov, A.; Battin-Leclerc, F. Measurements of laminar flame velocity for components of natural gas. Energy Fuels 2011, 25, 3875–3884. [Google Scholar] [CrossRef]
- Zahedi, P.; Yousefi, K. Effects of pressure and carbon dioxide, hydrogen and nitrogen concentration on laminar burning velocities and NO formation of methane-air mixtures. J. Mech. Sci. Technol. 2014, 28, 377–386. [Google Scholar] [CrossRef]
- Nilsson, E.J.; van Sprang, A.; Larfeldt, J.; Konnov, A.A. The comparative and combined effects of hydrogen addition on the laminar burning velocities of methane and its blends with ethane and propane. Fuel 2017, 189, 369–376. [Google Scholar] [CrossRef]
- Volkov, D.; Moroshkina, A.; Mislavskii, V.; Sereshchenko, E.; Gubernov, V.; Bykov, V.; Minaev, S. Relaxational oscillations of burner-stabilized premixed methane—Air flames. Combust. Flame 2024, 259, 113141. [Google Scholar] [CrossRef]
- Scholte, T.; Vaags, P. Burning velocities of mixtures of hydrogen, carbon monoxide and methane with air. Combust. Flame 1959, 3, 511–524. [Google Scholar] [CrossRef]
- Lafay, Y.; Renou, B.; Cabot, G.; Boukhalfa, M. Experimental and numerical investigation of the effect of H2 enrichment on laminar methane—Air flame thickness. Combust. Flame 2008, 153, 540–561. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, M.; Feng, M.; Zhu, Y. Study on mechanisms of methane/hydrogen blended combustion using reactive molecular dynamics simulation. Int. J. Hydrogen Energy 2023, 48, 1625–1635. [Google Scholar] [CrossRef]
- Westbrook, C.; Dryer, F. Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Coffee, T.; Kotlar, A.; Miller, M. The overall reaction concept in premixed, laminar, steady-state flames. I. Stoichiometries. Combust. Flame 1983, 54, 155–169. [Google Scholar] [CrossRef]
- Coffee, T.; Kotlar, A.; Miller, M. The overall reaction concept in premixed, laminar, steady-state flames. II. Initial temperatures and pressures. Combust. Flame 1984, 58, 59–67. [Google Scholar] [CrossRef]
- Barenblatt, G.; Librovich, V.; Makhviladze, G. The mathematical theory of combustion and explosions. In Consultants Bureau; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Clavin, P. One-dimensional mechanism of gaseous deflagration-to-detonation transition. J. Fluid Mech. 2023, 974, A46. [Google Scholar] [CrossRef]
- Fernández-Tarrazo, E.; Sánchez, A.; Liñán, A.; Williams, F. A simple one-step chemistry model for partially premixed hydrocarbon combustion. Combust. Flame 2006, 147, 32–38. [Google Scholar] [CrossRef]
- Polifke, W.; Geng, W.; Döbbeling, K. Optimization of rate coefficients for simplified reaction mechanisms with genetic algorithms. Combust. Flame 1998, 113, 119–134. [Google Scholar] [CrossRef]
- Grenkin, G.; Chebotarev, A.; Babushok, V.; Minaev, S. Determination of global kinetic parameters by optimization procedure using burning velocity measurements. Math. Model. Nat. Phenom. 2018, 13, 50. [Google Scholar] [CrossRef]
- Zakharov, A.D.; Fursenko, R.V.; Minaev, S.S. Optimisation method for automatic selection of rate constants of global reaction mechanisms. Combust. Theory Model. 2022, 27, 153–167. [Google Scholar] [CrossRef]
- Christiansen, E.; Sung, C.; Law, C.K. Pulsating instability in near-limit propagation of rich hydrogen/air flames. Symp. (Int.) Combust. 1998, 27, 555–562. [Google Scholar] [CrossRef]
- Law, C.; Sung, C. Structure, aerodynamics, and geometry of premixed flamelets. Prog. Energy Combust. Sci. 2000, 26, 459–505. [Google Scholar] [CrossRef]
- Gu, X.J.; Haq, M.Z.; Lawes, M.; Woolley, R. Laminar burning velocity and Markstein lengths of methane–air mixtures. Combust. Flame 2000, 121, 41–58. [Google Scholar] [CrossRef]
- Vandenabeele, H.; Corbeels, R.; Van Tiggelen, A. Activation energy and reaction order inmethane-oxygen flames. Combust. Flame 1960, 4, 253–260. [Google Scholar] [CrossRef]
- Bane, S.; Ziegler, J.; Shepherd, J. Development of One-Step Chemistry Models for Flame and Ignition Simulation; GALCIT Report GALCITFM:2010.002; Graduate Aerospace Laboratories, California Institute of Technology: Pasadena, CA, USA, 2010; p. 53. [Google Scholar]
- Arutyunov, V.; Belyaev, A.; Arutyunov, A.; Troshin, K.; Nikitin, A. Autoignition of Methane–Hydrogen Mixtures below 1000 K. Processes 2022, 10, 2177. [Google Scholar] [CrossRef]
- Kaskan, W. The dependence of flame temperature on mass burning velocity. Symp. (Int.) Combust. 1957, 6, 134–143. [Google Scholar] [CrossRef]
- Francisco, R.W.; Oliveira, A.A.M. Simultaneous Measurement of the Adiabatic Flame Velocity and Overall Activation Energy using a Flat Flame Burner and a Flame Asymptotic Model. Exp. Therm. Fluid Sci. 2018, 90, 174–185. [Google Scholar] [CrossRef]
- Moroshkina, A.D.; Ponomareva, A.A.; Mislavskii, V.V.; Sereshchenko, E.V.; Gubernov, V.V.; Bykov, V.V.; Minaev, S.S. Determining the global activation energy of methane—Air premixed flames. Combust. Theory Model. 2023, 27, 909–924. [Google Scholar] [CrossRef]
- Ferguson, C.; Keck, J. Stand-off distances on a flat flame burner. Combust. Flame 1979, 34, 85–98. [Google Scholar] [CrossRef]
- Kurdyumov, V.; Matalon, M. The porous-plug burner: Flame stabilization, onset of oscillation, and restabilization. Combust. Flame 2008, 153, 105–118. [Google Scholar] [CrossRef]
- Moroshkina, A.; Mislavskii, V.; Kichatov, B.; Gubernov, V.; Bykov, V.; Maas, U. Burner stabilized flames: Towards reliable experiments and modelling of transient combustion. Fuel 2023, 332, 125754. [Google Scholar] [CrossRef]
- Vilimpoc, V.; Goss, L.; Sarka, B. Spatial temperature-profile measurements by the thin-filament-pyrometry technique. Opt. Lett. 1988, 13, 93–95. [Google Scholar] [CrossRef]
- Maun, J.D.; Sunderland, P.B.; Urban, D.L. Thin-filament pyrometry with a digital still camera. Appl. Opt. 2007, 46, 483–488. [Google Scholar] [CrossRef]
- Nechipurenko, S.; Miroshnichenko, T.; Pestovskii, N.; Tskhai, S.; Kichatov, B.; Gubernov, V.; Bykov, V.; Maas, U. Experimental observation of diffusive-thermal oscillations of burner stabilized methane-air flames. Combust. Flame 2020, 213, 202–210. [Google Scholar] [CrossRef]
- Goodwin, D.G. Cantera C++ User’s Guide; California Institute of Technology: Pasadena, CA, USA, 2002; Volume 32. [Google Scholar]
- Smith, G.; Golden, D.; Frenklach, M.; Moriarty, N.; Eiteneer, B.; Goldenberg, M.; Bowman, C.; Hanson, R.; Song, S.; Gardiner, W., Jr.; et al. GRI-Mech 3.0. 1999. Available online: http://combustion.berkeley.edu/gri-mech/ (accessed on 17 December 2023).
- Konnov, A.A.; Mohammad, A.; Kishore, V.R.; Kim, N.I.; Prathap, C.; Kumar, S. A comprehensive review of measurements and data analysis of laminar burning velocities for various fuel + air mixtures. Prog. Energy Combust. Sci. 2018, 68, 197–267. [Google Scholar] [CrossRef]
- Franzelli, B.; Riber, E.; Gicquel, L.Y.; Poinsot, T. Large eddy simulation of combustion instabilities in a lean partially premixed swirled flame. Combust. Flame 2012, 159, 621–637. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moroshkina, A.; Ponomareva, A.; Mislavskii, V.; Sereshchenko, E.; Gubernov, V.; Bykov, V.; Minaev, S. Activation Energy of Hydrogen–Methane Mixtures. Fire 2024, 7, 42. https://doi.org/10.3390/fire7020042
Moroshkina A, Ponomareva A, Mislavskii V, Sereshchenko E, Gubernov V, Bykov V, Minaev S. Activation Energy of Hydrogen–Methane Mixtures. Fire. 2024; 7(2):42. https://doi.org/10.3390/fire7020042
Chicago/Turabian StyleMoroshkina, Anastasia, Alina Ponomareva, Vladimir Mislavskii, Evgeniy Sereshchenko, Vladimir Gubernov, Viatcheslav Bykov, and Sergey Minaev. 2024. "Activation Energy of Hydrogen–Methane Mixtures" Fire 7, no. 2: 42. https://doi.org/10.3390/fire7020042
APA StyleMoroshkina, A., Ponomareva, A., Mislavskii, V., Sereshchenko, E., Gubernov, V., Bykov, V., & Minaev, S. (2024). Activation Energy of Hydrogen–Methane Mixtures. Fire, 7(2), 42. https://doi.org/10.3390/fire7020042






