Abstract
Building fires pose a critical threat to life and property. Therefore, accurate fire risk prediction is essential for effective building fire prevention and mitigation strategies. This study presents a novel approach to predicting fire risk in buildings by leveraging advanced machine learning techniques and integrating diverse datasets. Our proposed model incorporates a comprehensive range of 34 variables, including building attributes, land characteristics, and demographic information, to construct a robust risk assessment framework. We applied 16 distinct machine learning algorithms, integrating them into a stacking ensemble model to address the limitations of individual models and significantly improve the model’s predictive reliability. The ensemble model classifies fire risk into five distinct categories. Notably, although the highest-risk category comprises only 22% of buildings, it accounts for 54% of actual fires, highlighting the model’s practical value. This research advances fire risk prediction methodologies by offering stakeholders a powerful tool for informed decision-making in fire prevention, insurance assessments, and emergency response planning.
1. Introduction
1.1. Background and Motivation
Building fires remain a critical global threat, resulting in significant loss of life and property, as well as economic damage. Accurate prediction models are essential for identifying high-risk buildings and enabling targeted fire-prevention strategies. Traditional fire-prevention strategies have relied heavily on historical data and expert-driven risk assessments. However, these approaches often fall short in complex, evolving urban environments where a wide array of variables must be considered.
With the advent of artificial intelligence (AI) and machine learning (ML), more sophisticated methods of fire risk prediction are emerging. These techniques have demonstrated remarkable success in other fields, leveraging complex datasets to enhance their predictive accuracy. For instance, [1,2] developed a real-time fire-detection and flashover-prediction model using time-series temperature data integrated with deep learning, enhancing the precision and timeliness of fire detection systems. Similarly, [3,4] achieved a high prediction accuracy in wildfire risk prediction through a stacking ensemble learning model that integrates diverse data types and exhibits enhanced interpretability and reliability. Furthermore, [5,6,7] demonstrated the effectiveness of probability-based Monte Carlo life-risk analysis models in predicting the life-risk during fire emergencies.
1.2. Machine Learning in Predictive Modeling
Recent advancements in machine learning have significantly enhanced predictive modeling across various disciplines. These improvements have been achieved by incorporating more comprehensive datasets and employing advanced modeling techniques. For example, [8,9,10] used a spatial Markov chain model combined with an indicator system to assess the risk high-rise building fires, considering both the probability of fire occurrence and the potential consequences. [11,12,13] proposed optimized fire risk indexing models using statistical machine learning, achieving superior prediction accuracy by addressing data sparsity and incorporating diverse risk factors. Additionally, [14,15] integrated building information modeling (BIM) with real-time fire data to enhance fire disaster management and response strategies. [16] developed a dynamic pipeline for spatio-temporal fire risk prediction, integrating time-varying data from various sources to predict fire risks more accurately. [17] combined neuro-fuzzy systems and metaheuristic optimization algorithms to improve the spatial prediction of wildfire probability. [18] applied gradient boosting to predict the compressive strengths of sustainable concrete materials, achieving high accuracy and highlighting the robustness of this method in integrating diverse datasets. Similarly, [19] employed soft computing techniques, such as Random Forest and genetic programming, to predict the bond strengths of FRP bars in concrete, further demonstrating the adaptability of AI-based models in structural prediction tasks. These models have proven highly effective in predicting outcomes where multiple factors must be analyzed simultaneously. By incorporating variables like the building characteristics, land use, and demographic data, machine learning algorithms are uniquely positioned to address the complexities inherent in fire risk prediction. The versatility of these techniques is exemplified by their successful application across various domains, including in construction and urban planning.
1.3. Limitations of Traditional Fire Risk Models
Despite these advancements, current fire-prediction research still faces several limitations. Traditional fire risk models often suffer from two major limitations: their reliance on a narrow set of variables (e.g., building characteristics or fire history) and their use of single-model approaches. These limitations can result in overfitting, reduced generalizability, and an inability to capture the complexity of modern fire risk environments, where demographic, geographic, and structural factors all play significant roles.
Previous work in fire risk prediction has shown some success using machine learning models, but many studies focus on a limited range of input variables, thereby underperforming when generalized to larger datasets. Single-model approaches, such as those using decision trees or simple regression, struggle to balance the trade-off between precision (minimizing false positives) and recall (minimizing false negatives), both of which are crucial in fire prevention systems.
Most studies have focused on limited variables such as the physical building characteristics, fire history, and weather data without sufficient consideration of broader factors like the building location, surrounding environment, and demographic characteristics [20,21,22,23,24,25,26]. Furthermore, the accuracy of these models has been hampered by issues related to data bias and missing values. Many previous models are based on single machine learning algorithms, which have a limited predictive power and a tendency to overfit.
1.4. Objectives of This Study
This study aims to address the limitations of traditional fire risk prediction models by developing a more robust and accurate approach utilizing ensemble machine learning techniques. Specifically, this research focuses on creating a stacking ensemble model that integrates the predictions of 16 different machine learning algorithms, including decision trees, neural networks, and support vector machines. By leveraging the complementary strengths of these algorithms, the model is designed to overcome the challenges of single-model approaches, such as overfitting and limited generalizability.
The model incorporates 34 independent variables, covering key dimensions such as the building attributes (e.g., type of building usage, total floor area), land characteristics (e.g., land price, land area), and demographic factors (e.g., population density, number of buildings in the district). This comprehensive dataset enables the model to capture the complex interplay of various factors contributing to the fire risk. By integrating diverse data sources, this study aims to improve both the predictive accuracy and practical applicability of fire risk models.
This research focuses on buildings classified as “Special Buildings” (SBs) in the Republic of Korea, which are subject to regular fire safety inspections due to their elevated fire risk. The model classifies these buildings into five distinct fire risk categories, providing actionable insights for stakeholders involved in fire prevention, insurance risk assessments, and emergency response planning. Figure 1 conceptualizes the research framework for building fire risk forecasts using the stacking ensemble method.
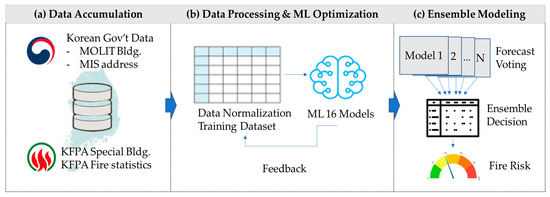
Figure 1.
Research Framework for Building Fire Risk Prediction Using Stacking Ensemble Methods.
The key objectives of this study are as follows:
- To develop and compare fire risk prediction models using 16 machine learning algorithms, evaluating their individual strengths and weaknesses in predicting fire incidents;
- To enhance the prediction performance of these models by incorporating a comprehensive range of building, environmental, and demographic variables;
- To validate the model’s predictive performance and reliability using real-world fire incident data, ensuring its applicability in practical settings;
- To create a stacking ensemble model capable of classifying fire risk into five distinct grades, providing a more reliable and accurate risk-classification system.
By fulfilling these objectives, this study contributes to the advancement of fire risk prediction methodologies, offering improved tools for risk assessment and fire prevention strategies.
1.5. Structure of the Paper
This paper is structured as follows:
- Section 2: Describes the data collection and preprocessing methods used in this study, including a detailed explanation of the independent variables and machine learning algorithms employed;
- Section 3: Presents the results of the model development and evaluation process, including performance metrics such as precision, recall, and F1-score for each algorithm;
- Section 4: Provides an in-depth discussion of the findings, highlights the strengths and limitations of the models, and suggests potential areas for future research;
- Section 5: Concludes the paper by discussing the practical implications of the model for fire prevention, insurance risk assessments, and fire safety management, along with recommendations for further refinement and application.
2. Materials and Methods
2.1. Data Collection
This study focuses on special buildings (SBs) in the Republic of Korea, which are subject to safety inspections by the Korea Fire Protection Association (KFPA). Under the Fire and Disaster Compensation and Insurance Act, SBs are defined as facilities where large numbers of people gather, work, or reside. Examples include government buildings, schools, hospitals, lodging facilities, performance venues, broadcasting stations, commercial facilities, multi-use facilities, apartments, factories, buildings over 11 stories, bathhouses, movie theaters, railway stations, and indoor shooting ranges. These buildings typically have a gross floor area exceeding 1000 square meters, reflecting their substantial sizes and potential fire risks.
Approximately 8 million buildings (ranging from 8,508,355 to 8,730,004 between 2018 and 2022) are available for analysis through Geographic Information System (GIS) data in the Republic of Korea, with a fire occurrence rate of less than 1% (0.84% to 0.97%). However, the dataset for all buildings contains issues such as missing values and incomplete records, which can adversely affect model performance. Therefore, we focus on the more reliable SB dataset maintained by the KFPA. Although SBs comprise less than 2% of all buildings (1.62% to 1.85%), they exhibit a fire occurrence rate over 14 times higher than that of all buildings. This higher incidence rate makes SBs a more suitable dataset for machine learning analysis, as the extremely low fire occurrence rate in the general building dataset could lead to model bias and poor predictive performance.
Due to limitations in the data, we could determine fire occurrences only at the address level rather than at the individual building level. In some cases, multiple buildings share the same address, and if a fire occurred at that address, all buildings were marked as having experienced a fire. This may result in an overestimation of fire occurrences in our dataset. Future research should aim to obtain more granular data to improve the accuracy of fire incident attribution. Table 1 shows fire incident information for all buildings and specialty buildings.

Table 1.
Fire Incidents in All Buildings and Special Buildings.
The dependent variable in this study is the occurrence of a fire, framed as a binary classification problem (fire occurrence = 1, no fire occurrence = 0). Our objective is to predict whether a fire will occur in a building based on a set of independent variables.
To ensure that the model development process does not infringe on anyone’s privacy or require extensive field surveys, we utilized only publicly available databases and accessible data sources. During the data collection process, we identified numerous erroneous values that could not have originated from the corresponding items. To improve the data quality, we removed outliers by excluding values beyond the 99th percentile of the normal distribution for each variable.
The independent variables consist of a comprehensive set of 34 features, encompassing various building, land, and demographic characteristics. These variables were selected based on their potential influence on fire risk and their availability in public records. Table 2 provides detailed descriptions of these variables, including their abbreviations, definitions, units, and ranges.

Table 2.
Description of Independent Variables.
2.2. Data Preprocessing
2.2.1. One-Hot Encoding
Categorical variables, including ‘Type of building usage’ (B_usg), ‘Type of building structure’ (B_str), ‘Categorical land type’ (L_type), ‘Primary land zoning category’ (L_zon1), ‘Secondary land zoning category’ (L_zon2), ‘Current land use condition’ (L_cond), ‘Elevation of the land’ (L_elev), ‘Shape of the topography’ (L_shape), and ‘Type of adjacent road’ (L_road), were converted into binary variables using one-hot encoding. This process transforms each categorical variable with n categories into n binary variables, each indicating the presence (1) or absence (0) of a category. One-hot encoding is essential for algorithms that cannot handle categorical variables directly, and it ensures that the model does not assume any ordinal relationship among categories. Table 3 shows an example of One-Hot encoding results.

Table 3.
Example of One-Hot Encoding Results.
2.2.2. Standardization
Numerical variables were standardized using z-score normalization to have a mean of 0 and a standard deviation of 1. This step eliminates scale differences between variables, ensuring that features with larger magnitudes do not dominate the model training process. Standardization is particularly important for algorithms sensitive to the scale of input data, such as support vector machines and neural networks. Table 4 shows an example of the standardization results.

Table 4.
Example of Standardization Results.
2.2.3. Handling Class Imbalance
The dataset exhibited a significant imbalance between ‘fire’ and ‘non-fire’ instances, with ‘non-fire’ cases vastly outnumbering ‘fire’ cases. To address this, we employed random undersampling to achieve a 1:1 ratio between ‘fire’ and ‘non-fire’ data. While undersampling reduces the size of the majority class, it helps prevent the model from becoming biased toward predicting the majority class. We acknowledge that undersampling may lead to the loss of potentially valuable information in the majority class.
Alternative methods such as the synthetic minority over-sampling technique (SMOTE) or ensemble techniques designed for imbalanced datasets were considered. However, undersampling was chosen for computational efficiency and to maintain a manageable dataset size, given the large volume of data available.
2.2.4. Splitting Train and Test Data
After balancing the dataset, we divided it into training and testing subsets using an 80/20 split. The splitting was performed randomly with stratification to maintain the class balance in both subsets. The training set was used to develop the models, while the test set was reserved for evaluating their performance on unseen data. This approach ensures that the models’ predictive capabilities are assessed fairly and reduces the risk of overfitting. Figure 2 shows a conceptual diagram of splitting training and test datasets.
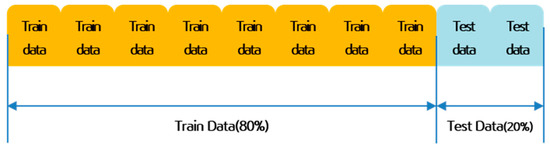
Figure 2.
Conceptual Diagram of Train and Test Dataset Splitting.
2.3. Modeling
A total of 16 machine learning algorithms were employed to develop the prediction models. These algorithms were selected based on their proven effectiveness in classification tasks, and their ability to capture complex nonlinear relationships. Table 5 lists the techniques used along with their abbreviations.

Table 5.
Machine Learning Techniques Used for Modeling.
These models encompass a variety of machine learning paradigms, including ensemble methods, neural networks, support vector machines, and probabilistic classifiers. Their diversity allows for a comprehensive evaluation of different modeling approaches in predicting building fire risk.
Based on the literature review in Section 1, which highlighted the effectiveness of various machine learning models in achieving high prediction accuracy and robustness, we selected these models for this study. They have demonstrated strong performance in previous research on fire risk prediction and related domains.
All models were implemented using Python and relevant machine learning libraries such as scikit-learn, TensorFlow, and PyTorch. Hyperparameter tuning was performed using grid search and cross-validation methods to optimize model performance. The code for the model development process can be found on GitHub: https://github.com/jswon0803/Fire_AI/blob/main/AI_Model_Baseline_Code.ipynb (accessed on 20 September 2024).
2.4. Model Evaluation
The performance of the prediction models was rigorously evaluated using the 20% reserved test dataset. To validate the predictive accuracy and reliability of the models, we employed several evaluation metrics derived from a confusion matrix, which includes four possible outcomes:
- True Positive (TP): Correctly classified fire instances;
- True Negative (TN): Correctly classified non-fire instances;
- False Positive (FP): Non-fire instances incorrectly classified as fires;
- False Negative (FN): Fire instances incorrectly classified as non-fires.
The following metrics were calculated:
- Accuracy: Measures the proportion of correct predictions among all instances.
- Precision: Indicates the proportion of true positive predictions among all positive predictions.
- Recall (Sensitivity): Reflects the proportion of actual positives correctly identified.
- F1-score: The harmonic mean of precision and recall.
These metrics offer a comprehensive evaluation of the models’ effectiveness, particularly in handling the imbalanced nature of the original dataset. By focusing on metrics like precision and recall, we ensure that the models are not only accurate but also effective in identifying fire incidents without excessive false alarms.
3. Results
3.1. Model Training Results
The training of the 16 machine learning models yielded varying levels of performance across the different evaluation metrics: accuracy, precision, recall, and F1-score. These metrics provide a comprehensive understanding of each model’s effectiveness in predicting fire incidents. Table 6 shows the prediction results for each model, sorted by F1 score in descending order.

Table 6.
Model Training Results (Sorted in Descending Order by F1-score).
- Accuracy measures the proportion of correct predictions (both fire and non-fire incidents) among all predictions. Models such as the Random Forest (RF), Bagging Classifier (BC), and XGBoost (XGB) models demonstrated higher accuracy. However, in the context of imbalanced datasets, accuracy alone can be misleading, as a model may achieve high accuracy by predominantly predicting the majority class (non-fire incidents).
- Precision indicates the proportion of true positive predictions among all positive predictions made by the model. Models like the RF, XGB, and CatBoost (CB) models showed higher precision, suggesting they have a lower rate of false positives. High precision is crucial when the cost of false positives is significant.
- Recall (also known as sensitivity) reflects the model’s ability to identify actual fire incidents among all actual positive cases. Models such as the Long Short-Term Memory (LSTM) model, Artificial Neural Networks (ANNs), and Decision Trees (DTs) exhibited high recall, indicating effectiveness in detecting actual fires but potentially producing more false positives.
- The F1-score is the harmonic mean of precision and recall, providing a balance between the two metrics. Models like the Gradient Boosting (GB), LightGBM (LGB), and XGB models achieved higher F1-scores, suggesting they maintain a good balance between detecting fires and minimizing false positives.
- High Recall, Low Precision: Models like LSTM and ANNs have high recall but low precision, meaning they are good at detecting actual fires but also predict many false positives;
- High Precision, Lower Recall: Models like RF and XGB have higher precision but lower recall, indicating they make fewer false positive predictions but may miss some actual fire incidents;
- Balanced Performance: The GB, LGB, and XGB models achieve a better balance between precision and recall, as reflected in their higher F1-scores.
Given the imbalanced predictive abilities of the individual models, an ensemble method is proposed to capitalize on the strengths and mitigate the weaknesses of the individual models.
3.2. Analysis of Individual Models
3.2.1. Random Forest (RF)
The Random Forest model aggregates predictions from multiple decision trees, improving the robustness and reducing overfitting. The RF models showed relatively high precision but lower recall, indicating accurate predictions with some missed incidents, resulting in fewer false positives but potentially more false negatives.
3.2.2. Decision Tree (DT)
Decision Trees use a tree-like structure to split data based on feature values, making them useful for interpretability. DT models exhibited high recall but low precision, indicating that they are good at detecting fires but are prone to false positives due to overfitting, especially with noisy or unbalanced data.
3.2.3. CatBoost (CB)
CatBoost is a gradient boosting algorithm that handles categorical features efficiently, reducing overfitting with built-in features. The CB model showed moderate performance with balanced precision and recall but slightly lower F1-scores compared to other boosting models.
3.2.4. XGBoost (XGB)
XGBoost is an optimized gradient boosting framework designed for speed and performance. The XGB models had relatively high precision but a lower recall, suggesting they can accurately predict fires but may miss some incidents, resulting in fewer false positives but potentially more false negatives.
3.2.5. K-Nearest Neighbors (KNN)
KNN is a non-parametric method that classifies instances based on the majority class among the k-nearest neighbors. The KNN models showed moderate performance with a high recall, indicating strength in predicting actual fires but with a risk of false positives. They are simple and intuitive but can be computationally intensive with large datasets.
3.2.6. Naive Bayes (NB)
Naive Bayes classifiers are probabilistic models based on Bayes’ theorem, assuming independence between features. The NB models showed a high recall but low precision, resulting in moderate F1-scores. They effectively detect fires but produce many false positives, possibly due to the violation of the independence assumption in real-world data.
3.2.7. Artificial Neural Networks (ANN)
ANNs are computational models inspired by the human brain, capable of capturing complex patterns. The ANNs showed a high recall but low precision, indicating a tendency to predict many false positives while effectively detecting actual fires. They require extensive training time and can be prone to overfitting.
3.2.8. Deep Neural Networks (DNN)
DNNs with multiple hidden layers can model complex nonlinear relationships. They showed a very high recall but lower precision, similar to ANNs, suggesting a strong fire-prediction capability but with many false positives. They require significant computational resources and careful tuning to prevent overfitting.
3.2.9. Long Short-Term Memory (LSTM)
LSTM networks are a type of recurrent neural network suitable for sequence data, capable of capturing temporal dependencies. The LSTM models showed a very high recall but low precision, leading to many false positives. In this context, since the data may not have temporal dependencies, LSTM’s advantages might not be fully utilized, possibly explaining the lower precision.
3.2.10. Support Vector Machines with Polynomial Kernel (SVMPs)
Support Vector Machines (SVM) are widely used for classification tasks. Polynomial kernels map data into higher dimensions to form nonlinear decision boundaries. The SVMPs showed a balanced performance in terms of precision and recall, making them suitable for ensemble methods to provide balanced predictions. However, they can suffer from the curse of dimensionality, which may reduce performance in high-dimensional spaces.
3.2.11. Support Vector Machines with Radial Basis Function (SVMRs)
The Radial Basis Function (RBF) kernel computes similarities between data points using a Gaussian function, allowing for nonlinear classification. The SVMRs showed a very high recall but lower precision, leading to a moderate F1-score. This suggests that they are effective at detecting actual fires but produce many false positives. In ensemble methods, this characteristic can be advantageous, as other models may offset the false positives.
3.2.12. Support Vector Machines with Sigmoid Kernel (SVMSs)
Sigmoid kernels map data nonlinearly for binary classification but often require careful parameter tuning. The SVMSs had lower performance metrics compared to other SVM variants, which may limit their utility in isolation. Nevertheless, they can contribute valuable diversity in an ensemble model.
3.2.13. AdaBoost (AB)
AdaBoost is an ensemble method that combines weak learners to form a strong classifier by focusing on misclassified samples. The AB models showed lower performance with a low precision and recall, resulting in low F1-scores. This indicates limited effectiveness in predicting fire risk accurately, possibly due to sensitivity to noisy data and outliers.
3.2.14. Light Gradient Boosting Machine (LGB)
LightGBM enhances gradient boosting with efficient tree-based learning, known for handling large datasets and categorical features effectively. The LGB models showed a strong overall performance, balancing precision and recall effectively, and achieved one of the highest F1-scores among the models tested.
3.2.15. Bagging Classifier (BC)
The Bagging Classifier model is an ensemble method that builds multiple models from different subsamples and aggregates their predictions. The BC model showed a lower precision and recall, making it less effective than other models in predicting fire risk accurately. It may struggle with imbalanced data.
3.2.16. Gradient Boosting (GB)
Gradient Boosting builds models sequentially, minimizing the errors of the previous models using gradient descent for optimization. The GB models showed a high recall and moderate F1-scores, indicating strong performance in detecting actual fires but with higher false positives. Extensive hyperparameter tuning is required to prevent overfitting.
3.3. Rationale for Choosing the Ensemble Method
Given the variability in the individual model performances, particularly in balancing precision and recall, an ensemble approach is warranted. The ensemble method leverages the strengths of multiple models while mitigating their weaknesses, leading to an improved overall predictive performance.
- Improved Accuracy: Combining predictions reduces the likelihood of errors being made by the individual models;
- Enhanced Robustness: Diversity among models ensures that the ensemble is less sensitive to anomalies and variations in the data;
- Balanced Precision and Recall: Models with a high recall compensate for those with high precision, achieving a better overall balance that is essential for fire risk prediction.
3.4. Ensemble Voting Methodology
The stacking ensemble model combines the predictions of the 16 individual models using a voting mechanism. Each model casts a “vote” on whether a building is at risk of fire. The total number of votes is then used to classify the building’s fire risk level. Table 7 is an example of individual model predictions for some buildings, where ‘O’ stands for ‘fire’ and ‘X’ stands for ‘no fire’. Figure 3 is a conceptualization of the ensemble voting methodology. Buildings with a higher number of models predicting a fire are considered at higher risk. Table 8 shows the results of fire prediction by the number of predictive models.

Table 7.
Example of Individual Model Predictions for Selected Buildings.
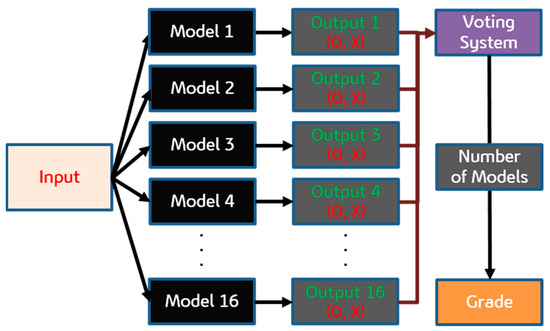
Figure 3.
Concept of Ensemble Voting Methodology.

Table 8.
Fire-Prediction Results Based on Number of Predictive Models.
Methodology Steps:
- Prediction Aggregation: For each building, collect the predictions from all models;
- Vote Counting: Tally the number of models predicting a fire for a given building;
- Risk Level Assignment: Classify buildings into risk levels based on the number of votes they receive.
As the number of models predicting a fire increases, the fire occurrence rate also increases, indicating that buildings classified with higher grades have a higher likelihood of experiencing a fire. This pattern demonstrates the effectiveness of the ensemble model in identifying varying levels of fire risk. Figure 4 shows the change in fire rate by the number of models predicting fire.
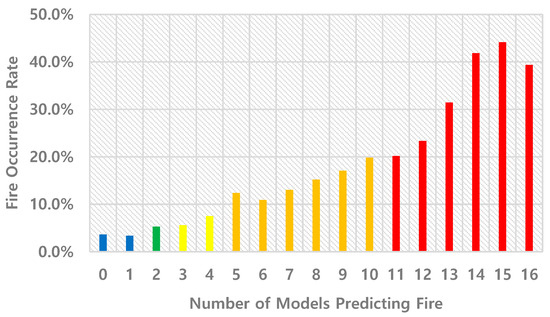
Figure 4.
Fire Occurrence Rate by Number of Models Predicting Fire.
To make the risk classification more practical for real-world applications, the initial 17 grades were consolidated into five broader risk categories. The equal intervals method was employed to reclassify the risks into five distinct classes:
- Grade 1 (Extremely Low Risk, Blue color): 0–1 models predicting a fire;
- Grade 2 (Low Risk, Green color): 2 models predicting a fire;
- Grade 3 (Medium Risk, Yellow color): 3–4 models predicting a fire;
- Grade 4 (High Risk, Orange color): 5–10 models predicting a fire;
- Grade 5 (Extremely High Risk, Red color): 11–16 models predicting a fire.
This simplification facilitates the easier interpretation and implementation of fire prevention strategies. The classification was adjusted to maintain an approximately equal share of 20% for each risk grade. Table 9 summarizes the prediction performance by fire hazard class. Figure 5 shows the fire occurrence rate by grade.

Table 9.
Fire Hazard Rating Grades.
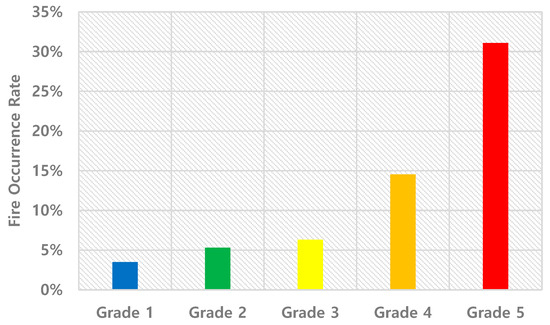
Figure 5.
Fire Occurrence Rate by Grade.
Analyzing the grades individually:
- Grade 1 (Lowest Risk): Only about 3.5% of the buildings experienced actual fires, representing 6.9% of all fire occurrences, indicating this as the safest category;
- Grade 5 (Highest Risk): While comprising only 21.5% of the predicted buildings, it accounted for 54.5% of actual fire occurrences, marking it as the highest risk category.
Although the share of predicted buildings remains relatively consistent at around 20% across all grades, the fire occurrence rate and the share of actual fire occurrences increased significantly with each grade. This pattern confirms the effectiveness of the grading system in accurately stratifying fire risk levels. Figure 6 shows the predicted percentage of buildings by class and Figure 7 shows the actual percentage of fires by class.
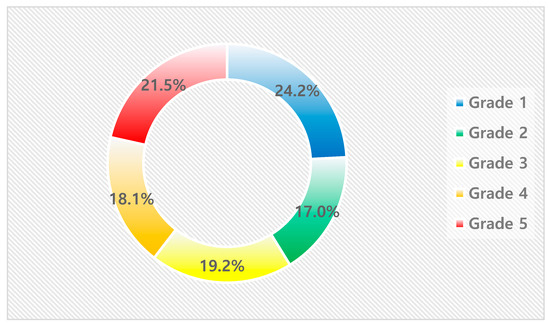
Figure 6.
Share of Predicted Buildings by Grade.
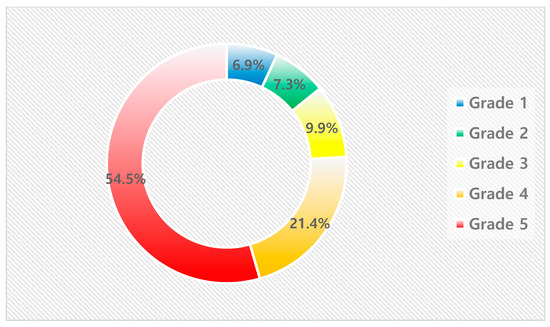
Figure 7.
Share of Actual Fire Occurrences by Grade.
4. Discussion
4.1. Model Evaluation and Performance
The evaluation of the various machine learning models revealed distinct strengths and weaknesses in predicting building fire risks. While the precision was generally low across the models, ranging from 15.42% to 36.76%, the recall was considerably high, ranging from 28.69% to 90.29%. This trend indicates that the models tend to overpredict fires, resulting in a higher number of false positives. In the context of fire risk prediction, this characteristic is crucial because missing an actual fire (false negative) can have severe consequences, including the loss of life and property.
- High Recall Models: Models such as the LSTM, ANN, and DT models exhibited a high recall, effectively identifying most actual fire incidents. However, their low precision means they also produced many false positives, which can lead to unnecessary alarms and strain on resources;
- High Precision Models: Models like the RF, XGB, and CB models demonstrated higher precision, indicating a lower rate of false positives. Nevertheless, their recall was lower, suggesting that they might miss some actual fire incidents, which is undesirable in safety-critical applications;
- Balanced Models: The GB, LGB, and XGB models achieved higher F1-scores, reflecting a better balance between precision and recall. These models are particularly valuable because they maintain a reasonable detection rate of actual fires while minimizing false alarms.
The variability in model performance underscores the trade-offs between precision and recall in fire risk prediction. While a high recall is essential to ensure that most fire incidents are detected, maintaining an acceptable precision is also important to prevent resource wastage due to false positives. In fire safety applications, a balance must be struck to maximize detection while minimizing unnecessary interventions.
4.2. Effectiveness of the Ensemble Method
To address the imbalanced predictive abilities of the individual models, a stacking ensemble method was employed. This approach combines the predictions of multiple models to improve the overall accuracy and reliability.
- Improved Balance: The ensemble method effectively balances precision and recall by leveraging the strengths of different models. Models with a high recall compensate for those with high precision, resulting in a more balanced overall prediction;
- Enhanced Robustness: Aggregating multiple models reduces the impact of any single model’s biases or errors, leading to more reliable and consistent predictions.
By consolidating the predictions, the ensemble model classified fire risk levels into five distinct grades. This grading system simplifies the interpretation of results and facilitates practical implementation in real-world fire prevention strategies. The effectiveness of the ensemble method is further evidenced by the distribution of actual fire occurrences across the risk grades:
- Grade 1 (Lowest Risk): Comprised 24% of the predicted buildings but only accounted for 7% of the actual fire occurrences, indicating a low risk and validating the model’s ability to identify safer buildings;
- Grade 5 (Highest Risk): Represented 22% of the predicted buildings but accounted for 54% of the actual fire occurrences, demonstrating the model’s proficiency in accurately pinpointing high-risk buildings.
These findings confirm the ensemble model’s effectiveness in stratifying buildings according to fire risk, allowing for targeted interventions and more efficient resource allocation.
4.3. Practical Implications for Fire Risk Management
The developed fire hazard rating grades offer a practical framework for various stakeholders involved in fire risk management:
- Policy Makers: Regulatory authorities can prioritize inspections and enforce stricter safety regulations for buildings identified as high-risk. This targeted approach can enhance the effectiveness of fire safety policies and resource allocation’
- Insurance Companies: Risk-based premium adjustments can be made, promoting fair and accurate insurance policies that reflect the actual risk levels of buildings. This can incentivize property owners to invest in fire safety measures;
- Building Managers: Resources can be allocated more efficiently by focusing on maintenance and safety measures in higher-risk buildings. Proactive measures can be implemented to mitigate identified risks;
- Emergency Services: Fire departments can optimize response planning by identifying areas with higher predicted fire risks. This allows for the strategic placement of resources and quicker response times to high-risk areas.
4.4. Limitations
Despite these promising results, several limitations should be acknowledged:
- Data Limitations: Reliance on publicly available data may limit the model’s accuracy due to potential issues like missing values, the data quality, and the inability to capture all relevant factors. The overestimation of fire occurrences due to address-level data aggregation is a specific concern;
- False Positives: The ensemble model, while improving the overall performance, still produces a considerable number of false positives, which could lead to unnecessary resource allocation and potential desensitization to fire alarms;
- Model Complexity: The stacking ensemble approach increases the computational complexity, potentially hindering real-time implementation and scalability, especially in resource-constrained environments;
- Generalizability: The model was developed based on data from the Republic of Korea’s special buildings and may require adaptation for use in other regions or building categories due to differences in building codes, environmental factors, and demographic characteristics.
4.5. Future Research Directions
To enhance the model’s applicability and address its limitations, future research should focus on:
- Data Enrichment: Incorporating additional data sources, such as real-time sensor data (e.g., smoke detectors, temperature sensors) or maintenance records, to improve the model’s predictive accuracy and capture dynamic risk factors;
- Model Optimization: Simplifying the model to reduce the computational demands without sacrificing performance. Techniques like feature selection, dimensionality reduction, or using more efficient algorithms can be explored;
- Cross-Regional Validation: Testing the model in different geographical contexts and building types to assess its generalizability and adaptability to other regions;
- Stakeholder Collaboration: Working with industry experts, policymakers, and fire safety professionals to refine the fire risk grading system, ensuring its practical relevance and facilitating its adoption in policy and practice.
5. Conclusions
This study presents a novel approach to building fire risk prediction by leveraging advanced machine learning techniques and a comprehensive dataset encompassing 34 variables related to building characteristics, land features, and demographic information. By employing a stacking ensemble model that integrates 16 different machine learning algorithms, this research addresses the limitations of individual models and enhances their predictive performance.
5.1. Key Contributions
- Comprehensive Data Integration: Incorporating diverse variables captures the complex factors contributing to fire risk, improving the model’s robustness and applicability in various contexts. This holistic approach enhances our understanding of fire risk factors;
- Practical Risk Stratification: Classifying the fire risk into five distinct grades provides a usable framework for stakeholders to implement targeted fire-prevention measures. The grading system simplifies complex predictive outputs into actionable insights, facilitating decision-making.
5.2. Implications for Stakeholders
- Policy Implementation: Authorities can utilize the model to prioritize safety inspections, allocate resources effectively, and update regulatory standards based on the identified risk levels. This can lead to the more efficient use of public resources and improved safety outcomes;
- Insurance Assessment: Insurance companies can adjust their premiums and coverage options based on the risk grades, leading to fairer and more accurate policies that reflect the actual risk. This approach can promote risk-mitigation efforts by building owners;
- Resource Allocation: Emergency services and building managers can allocate resources more efficiently by focusing on higher-risk buildings, enhancing the overall fire safety and response effectiveness. This targeted approach can improve emergency preparedness and reduce response times.
5.3. Limitations and Recommendations
While the model shows significant promise, several limitations need to be addressed:
- Data Quality and Availability: Future work should aim to incorporate more detailed and high-quality data to improve the model’s accuracy. Collaborations with governmental agencies and private organizations could facilitate access to better data and enable the inclusion of additional relevant variables;
- False Positives Reduction: Further research is needed to refine the model to reduce the false-positive rates without compromising the recall. Techniques such as cost-sensitive learning, adjusting classification thresholds, or employing more sophisticated ensemble methods could be explored;
- Model Simplification: Simplifying the ensemble model can make it more accessible for real-time implementation. Investigating methods to reduce the model’s computational complexity, such as pruning less-impactful models from the ensemble or using more efficient algorithms, is recommended.
Author Contributions
Conceptualization, C.C. and S.A.; methodology, C.C.; software, J.W.; validation, J.W., J.L. and C.C.; formal analysis, J.W.; investigation, J.L.; resources, J.L.; data curation, S.A.; writing—original draft preparation, C.C. and S.A.; writing—review and editing, C.C.; visualization, J.W.; supervision, C.C.; project administration, S.A.; funding acquisition, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank the editors and reviewers for their valuable opinions and suggestions that improved this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, T.; Wang, Z.; Wong, H.Y.; Tam, W.C.; Huang, X.; Xiao, F. Real-time Forecast of Compartment Fire and Flashover based on Deep Learning. Fire Saf. J. 2022, 130, 103579. [Google Scholar] [CrossRef]
- Tam, W.C.; Fu, E.Y.; Li, J.; Peacock, R.D.; Reneke, P.A.; Cleary, T.; Ngai, G.; Leong, H.V.; Huang, M.X. Real-Time Flashover Prediction Model for Multi-Compartment Building Structures Using Attention Based Recurrent Neural Networks. Expert Syst. Appl. 2023, 223, 119899. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Wang, K.; Wang, Z.; Chen, Y. Forest Fire Risk Prediction Based on Stacking Ensemble Learning for Yunnan Province of China. Fire 2024, 7, 13. [Google Scholar] [CrossRef]
- Akyol, K. Robust stacking-based ensemble learning model for forest fire detection. Int. J. Environ. Sci. Technol. 2023, 12, 13245–13258. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Mehaffey, J.; Hadjisophocleous, G. A Probability-Based Monte Carlo Life-Risk Analysis Model for Fire Emergencies. Fire Saf. J. 2017, 89, 51–62. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Park, H. Probabilistic Analysis of Occupant Safety During Fire Emergencies Using Monte Carlo Simulation. Saf. Sci. 2017, 95, 1–12. [Google Scholar]
- Lu, C.; Li, Q. Monte Carlo Simulation for Life-Risk Assessment in Fire Scenarios. J. Fire Prot. Eng. 2018, 28, 347–360. [Google Scholar]
- Zhang, Y.; Wang, G.; Wang, X.; Kong, X.; Jia, H.; Zhao, J. Regional High-Rise Building Fire Risk Assessment Based on the Spatial Markov Chain Model and an Indicator System. Fire 2024, 7, 16. [Google Scholar] [CrossRef]
- Zhu, W.; You, Q. High-Rise Building Group Regional Fire Risk Assessment Model Based on AHP. J. Risk Anal. Crisis Response 2021, 6, 31–37. [Google Scholar] [CrossRef]
- Zhu, W.; You, Q. Comprehensive Evaluation of Fire Risk for High-Rise Civil Buildings Based on Fuzzy Analytic Hierarchy Process. In Proceedings of the 2019 IEEE 11th International Conference on Advanced Infocomm Technology (ICAIT), Jinan, China, 18–20 October 2019; pp. 179–185. [Google Scholar]
- Manikandan, K.; Nakkeeran, E. Safety Analysis Improvement in Fire Risk Assessment Model and Optimized Risk Indexing Using Deep Learning Approach. Int. J. Intell. Syst. Appl. Eng. 2024, 12, 732–742. [Google Scholar]
- Li, S.; Tao, G.; Zhang, L. Fire Risk Assessment of High-Rise Buildings Based on Gray-FAHP Mathematical Model. Procedia Eng. 2018, 211, 395–402. [Google Scholar] [CrossRef]
- Rezaei, S.; Shokouhyar, S.; Zandieh, M. A Neural Network Approach for Retailer Risk Assessment in the Aftermarket Industry. Benchmarking: Int. J. 2019, 26, 1631–1647. [Google Scholar] [CrossRef]
- Kim, D.; Cha, H.; Jiang, S. The Prediction of Fire Disaster Using BIM-Based Visualization for Expediting the Management Process. Sustainability 2023, 15, 3719. [Google Scholar] [CrossRef]
- Wehbe, R.; Shahrour, I. A BIM-Based Smart System for Fire Evacuation. Future Internet 2021, 13, 221. [Google Scholar] [CrossRef]
- Mutakabbir, A.; Lung, C.-H.; Ajila, S.A. Forest Fire Prediction Using Multi-Source Deep Learning. In Proceedings of the 13th EAI International Conference, BDTA 2023, Edinburgh, UK, 23–24 August 2023; pp. 123–134. [Google Scholar]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. For. Meteorol. 2019, 266–267, 198–207. [Google Scholar] [CrossRef]
- Al-Hamd, R.K.S.; Albostami, A.S.; Alzabeebee, S.; Al-Bander, B. An optimized prediction of FRP bars in concrete bond strength employing soft computing techniques. J. Build. Eng. 2024, 65, 105835. [Google Scholar] [CrossRef]
- Albostami, A.S.; Al-Hamd, R.K.S.; Al-Matwari, A.A. Data-driven predictive modeling of steel slag concrete strength for sustainable construction. Buildings 2024, 14, 2476. [Google Scholar] [CrossRef]
- Hong, S.G.; Jeong, S.R. Development and Comparison of Data Mining-Based Prediction Models of Building Fire Probability. Korean Soc. Internet Inf. 2018, 19, 101–112. [Google Scholar]
- Yoon, D.W.; Hwang, H.; Pak, T.Y.; Kim, B.T.; Li, X.; Lee, J. Fire Risk Prediction Using Building Information and Machine Learning Methods. Adv. Inf. Commun. 2022, 1, 22–30. [Google Scholar]
- Ryu, J.W.; Kim, Y.J.; Kim, E.J.; Kim, M.W. A Generation Method of Fire Probability Prediction Model Based on Weather Forecast. J. KIISE: Comput. Pract. Lett. 2014, 20, 68–79. [Google Scholar]
- Sterne, J.A.; White, I.R.; Carlin, J.B.; Spratt, M.; Royston, P.; Kenward, M.G.; Wood, A.M.; Carpenter, J.R. Multiple Imputation for Missing Data in Epidemiological and Clinical Research: Potential and Pitfalls. BMJ 2009, 338, b2393. [Google Scholar] [CrossRef] [PubMed]
- Nugroho, H. A Review: Data Quality Problem in Predictive Analytics. Int. J. Appl. Inf. Technol. 2023, 7, 79–91. [Google Scholar] [CrossRef]
- Tam, W.C.; Fu, E.Y.; Mensch, A.; Hamins, A.; You, C.; Ngai, G.; Leong, H.V. Prevention of cooktop ignition using detection and multi-step machine learning algorithms. Fire Saf. J. 2021, 120, 103043. [Google Scholar] [CrossRef] [PubMed]
- Ngai, M.; Fu, E.Y.; Tam, A.; Yang, A.; Ngai, G. Finding the signal from the smoke: A real-time, unattended fire prevention system using 3D CNNs. J. Stud. Res. 2022, 11, 1–12. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).