Abstract
Identifying the underlying factors derived from geospatial and remote sensing data that contribute to forest fires is of paramount importance. It aids experts in pinpointing areas and periods most susceptible to these incidents. In this study, we employ the geographically and temporally weighted regression (GTWR) method in conjunction with a refined continuous invasive weed optimization (CIWO) algorithm to assess certain spatially relevant drivers of forest fires, encompassing both biophysical and anthropogenic influences. Our proposed approach demonstrates theoretical utility in addressing the spatial regression problem by meticulously accounting for the autocorrelation and non-stationarity inherent in spatial data. We leverage tricube and Gaussian kernels to weight the GTWR for two distinct temporal datasets, yielding coefficients of determination (R2) amounting to 0.99 and 0.97, respectively. In contrast, traditional geographically weighted regression (GWR) using the tricube kernel achieved R2 values of 0.87 and 0.88, while the Gaussian kernel yielded R2 values of 0.8138 and 0.82 for the same datasets. This investigation underscores the substantial impact of both biophysical and anthropogenic factors on forest fires within the study areas.
1. Introduction
Many ecosystems worldwide undergo natural disturbances triggered by fire [1]. Whether resulting from human activities or natural processes, forest fires are considered a major factor contributing to the significant loss of forest ecosystems globally [2]. Forest fires can affect the biodiversity, species composition, and ecosystem structure of forests [3]. Moreover, they also influence human lives, environmental health, and economies [4]. While fires can have both short- and long-term beneficial and negative consequences, when an ecosystem is already disturbed, there may be a higher chance of unfavorable and unpredictable repercussions. These may include large pulse emissions of CO2 and particulate matter into the atmosphere, the loss of natural resources like forest cover, the extinction of wildlife, and the possibility of massive socioeconomic consequences [1]. Recently, forest fire occurrences have been increasing due to global warming, high rates of population growth, and anthropogenic interference in forest areas [5] and, annually, about 10 million hectares of worldwide forests are damaged by fire [6]. Forests cover about 1.2 million hectares of land in northern Iran, and over 300 hectares of this is burned yearly [7]. Forest management systems must be able to prevent, detect, and respond to forest fires and they require recognition of the effective spatial driving factors [8].
Numerous studies have investigated the detection of key spatial driving factors in forest fires, categorizing them into two significant types: biological and biophysical, alongside socioeconomic factors [9]. The biophysical factors have primarily been the intended focus of fire disaster management [9,10]. However, it is worth noting that humans can also ignite forest fires through actions such as arson, smoking and discarding cigarettes, sparks from power lines, the use of explosives or fire during hunting, picnic fires, shepherds’ fires, and stubble burning [11]. Mukunga et al. [12] utilized datasets encompassing global climate, vegetation, land cover, and socioeconomic factors such as cropland fraction, GDP, road density, livestock density, and grazed lands. Their evaluation of ignition occurrences, employing a random forest machine learning technique, led them to the conclusion that incorporating human factors enhances the accuracy of predicting fire occurrences in most regions of the world. Most forest fires in Europe are initiated by human activities, yet the exact anthropogenic driving factors remain unidentified [13] because human-related factors, such as land use, accessibility to forests, fuel management, legal restrictions, economic, and cultural context can be complex [14,15]. Roman-Cuesta and Martinez-Vilalta [16] demonstrated that in Mexico the maximum wind speed, the number of producers, and the degrees thereof are the most critical factors in forest fire regimes. [17] concluded that there is a significant relationship between forest fires, the road network, and farms in Chiapas, Mexico. In southwestern China, Murthy et al. [18] identified forest fire policy as a crucial factor influencing the occurrence of forest fires. Calcerrada et al. [19] explored a spatial pattern of fire ignitions and frequency on the Southern California landscapes using human-related and biophysical variables as well as a multiple logistic regression model for fire ignitions and Poisson univariate and multiple regressions for fire frequency. According to their results, biophysical variables mostly affected the fire frequency pattern and human-related variables explained most of the variations in fire ignition. Erten et al. [20] used the weights of evidence (WofE) model and concluded that the accessibility of forests to people is the most effective factor in fire ignitions in Central Spain. By using the wildfire–urban interface fire dynamics simulator (WFDS), Bufacchi et al. [21] determined the vegetation moisture, surface area-to-volume ratio, and bulk density as the most critical factors in the rate of fire spread. Zhang et al. [22] concluded that wildfires are most likely to occur in forests, mountainous areas, savannas, and lands with high vegetation coverage and areas near human-built infrastructure. Joseph et al. [23] used a spatiotemporal Bayesian statistical model to show that the temperature and moisture of air can forecast significant wildfire size probabilities and that housing density has a close relationship with fire frequency. In a study conducted by Jafari and Pourghasemi in 2019 [24], a random forest model was employed to identify the key driving factors for a regional-scale wildfire in the Zagros Mountains of Iran. Their findings indicated that factors such as proximity to residential areas, precipitation, elevation, and proximity to roads were the most influential in predicting forest fires. [6] found that the density of the roads and the length of the boundary between a forest and residential areas were the most effective factors for predicting forest fires among 28 identified factors. Milanović et al. [25] identified coniferous forests, proximity to agricultural land, and the amount of leaf litter as the main factors affecting forests using the gradient boosted machine algorithm.
Moreover, Avila-Flores et al. [26] and Koutsias et al. [27] concluded that the effective driving factors for forest fires are spatially dependent and, in such cases, the results of geographically weighted regression (GWR) are better than ordinary regressions. Ref. [28] employed GWR and recognized land use, rainfall, and vegetation type as the most significant factors affecting forest fires in Durango, Mexico. Sa et al. [29], using GWR, showed that in sub-Saharan Africa, climate-driven variables are more effective for fires than human-related variables. The effective driving factors derived from geospatial and remote sensing data on forest fires are also time dependent, but in most of the research projects that used GWR, they were overlooked. Traditional GWR only considers two dimensions of location and it does not support any temporal variations in the problem. For accurately solving these problems with temporal variations, it is essential to consider time as a dimension. Therefore, traditional GWR must be adapted with time.
The primary objective of this research is to identify the significant spatially related driving factors of wildfires in the Golestan forest, located in Golestan Province, Iran. This will be accomplished using geographically and temporally weighted regression (GTWR) in conjunction with a modified continuous invasive weed optimization (CIWO) algorithm. Fires occur in the Golestan forest every year and most of them are set by humans. Hence, both anthropogenic and biophysical variables have been used in this study and we hypothesize that human-related variables are the major effective factors for fires in the case study. Any combination of the explanatory variables leads to a different answer. Hence, a modified CIWO algorithm has been proposed to find the best combination of factors.
2. Materials and Methods
2.1. Study Area
The Golestan forest is one of the most important forests in Iran and is situated in the north of the country. With an average elevation of 1378 m, the Golestan forest is primarily a transitional mountainous region situated between the western Khorasan–Kopet Dagh Mountains and the eastern Alborz Mountains [30]. This forest is among the principal tourist regions in Iran, with numerous roads passing through it. According to statistical records, most registered fires have occurred in the vicinity of these roads, and humans have been implicated in most of them [31]. The Golestan forest encompasses seven general categories of vegetation types, including closed forests, steppes, halophytic communities, fern communities, hygrophilous and aquatic communities, open woodlands and scrubs, and mountain meadows [31]. It experiences three different climate types, classified according to Emberger’s system as cold-arid, temperate semi-arid, and temperate sub-humid [32]. The study area is located at 37°20′–37°47′ N and 55°87′–56°12′ E (Figure 1) in the cold-arid region. The area covers approximately 681.553 km2, chosen due to the frequent occurrence of fires in the Golestan forest over the past few years.
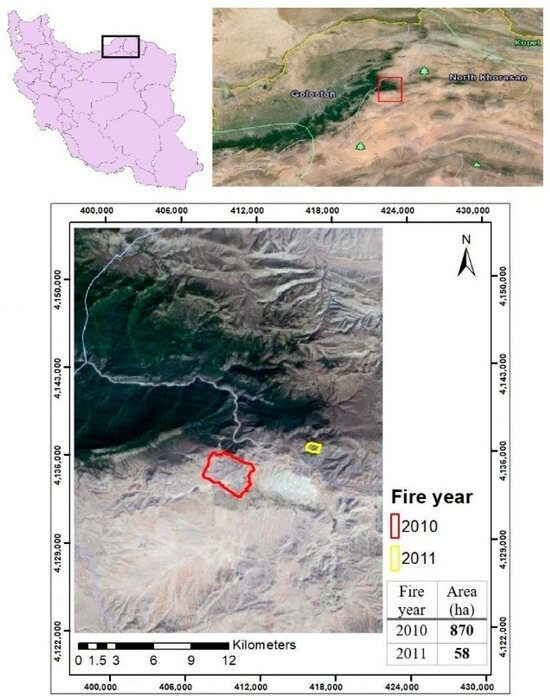
Figure 1.
The study area.
2.2. Datasets
Two large fires occurred in the study area on 17 November 2010 and 15 July 2011, covering areas of 870 and 57 hectares, respectively (Figure 1), and are used as the dependent variables of the current study. The actual burned area, road network, rivers, soil types, land uses, and residential zones in the study area were acquired from Department of Natural Resources of Golestan, North Khorasan and Semnan Provinces (https://frw.ir/, accessed on 16 January 2016) and are shown in Figure 2. Also, the geographic coordinates of the synoptic weather stations close to the area (Figure 3) and their data, including the maximum, minimum, and mean temperature, the total rainfall, as well as the maximum wind speed and the azimuth in November 2010 and July 2011 were provided from the Meteorological Organization of Iran (https://www.irimo.ir/, accessed on 25 January 2016). For a generalization of these data to the whole area, the ordinary Kriging method [33] with the exponential semivariogram model was used [34] with a resolution of 30 m (Figure 4 and Figure 5). This model was used because the values of mean bias error, mean absolute error, and global standard deviation for these datasets were, respectively, 0.35, 8.36, and 11.50% of the other variogram models.
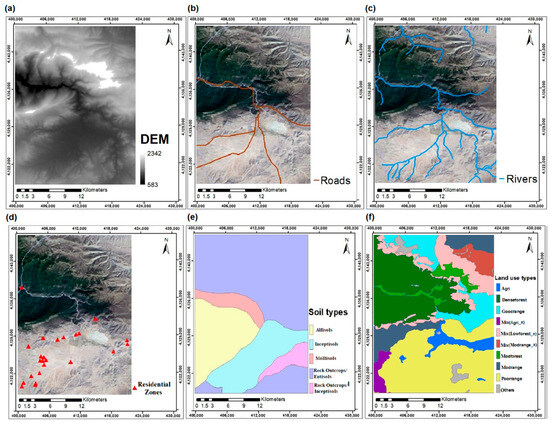
Figure 2.
Used data layers in this research (a) DEM, (b) the road network, (c) the rivers, (d) the residential zones, (e) the soil types, and (f) land use.
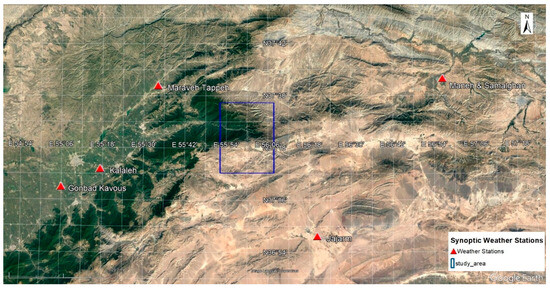
Figure 3.
The synoptic weather stations close to the study area.
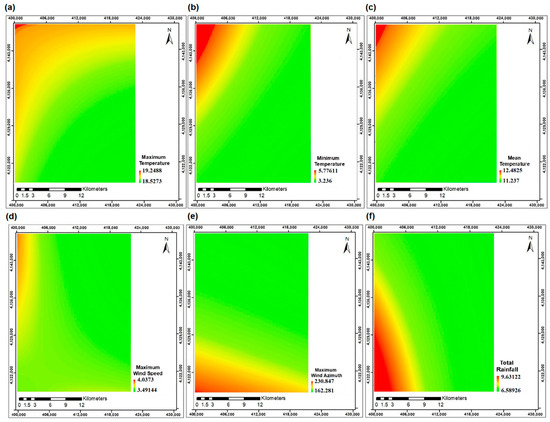
Figure 4.
The rasters generated from interpolating (a) maximum temperature (°C), (b) minimum temperature (°C), (c) mean temperature (°C), (d) maximum wind speed (m/s), (e) maximum wind azimuth, and (f) total rainfall (mm) on 17 November 2010.
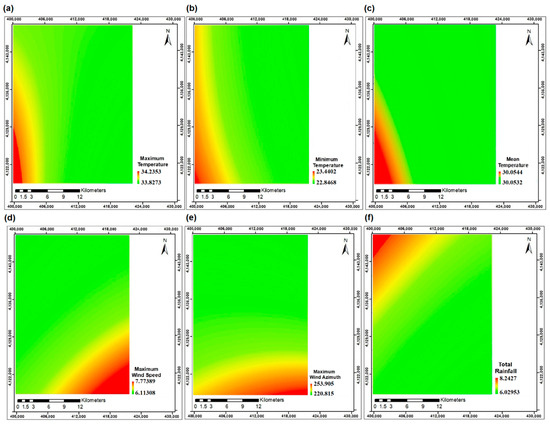
Figure 5.
The rasters generated from interpolating (a) maximum temperature (°C), (b) minimum temperature (°C), (c) mean temperature (°C), (d) maximum wind speed (m/s), (e) maximum wind azimuth, and (f) total rainfall (mm) on 15 July 2011.
The land use and soil type information layers were on a scale of 1:100,000 and the road network and rivers information layers were on a scale of 1:5000; all of which were acquired in 2006. We used the ASTER 30 m GDEM to generate the slope and aspect layers (Figure 6). The road network, the rivers, and the residential zones information layers were in the vector format. Hence, the Euclidean distance analysis was used to generate raster layers with a resolution of 30 m so that each cell of these layers shows the distance from the nearest road, river, and residential zone (Figure 7).
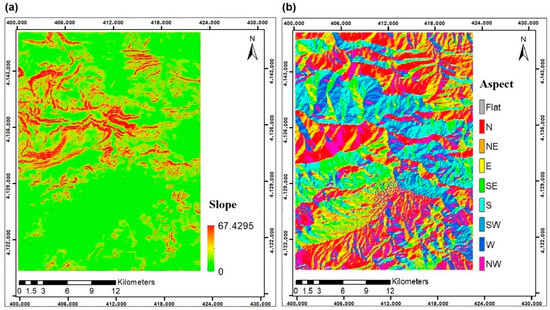
Figure 6.
Data layers of (a) slope and (b) aspect.
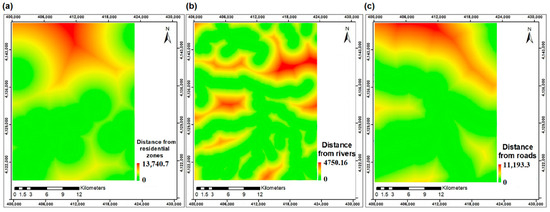
Figure 7.
Data layers of distance from (a) residential zones (m), (b) rivers (m), and (c) roads (m).
Before executing the algorithm, the correlation among the spatial factor layers was analyzed using Equations (1) and (2):
where n is the number of observations, and are two datasets with covariance , and are the mean values, and are standard deviations, and r is the correlation coefficient. All values of the correlation coefficients are in the range [−0.7, 0.7]; hence, there is no significant correlation among the data. Accordingly, all of them were used in the GTWR algorithm. Figure 8 and Figure 9 present the correlation matrix among the datasets that is used in this study.
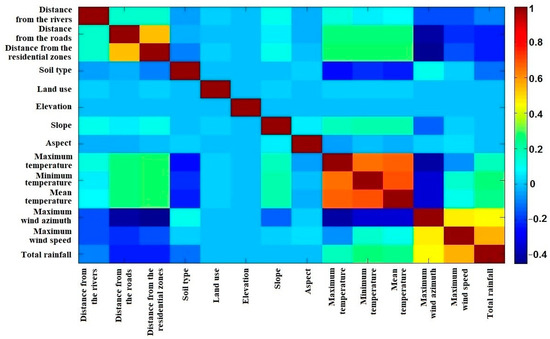
Figure 8.
The correlation matrix for 17 November 2010 data.
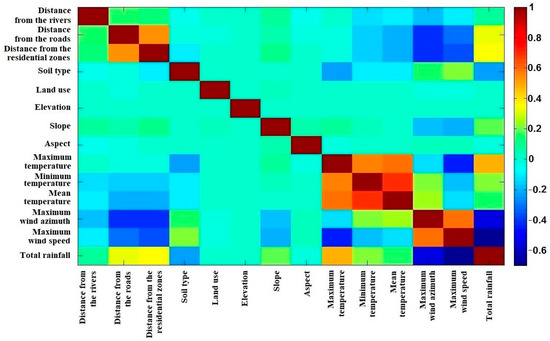
Figure 9.
The correlation matrix for 15 July 2011 data.
2.3. Geographically Weighted Regression (GWR)
The spatial data have exceptional specifications that make working with them difficult. Two significant properties of spatial data are (a) autocorrelation or spatial dependency based on Tobler’s law, which is “Everything is related to everything else, but near things are more related than distant things” and (b) spatial heterogeneity or non-stationarity means the spatial autocorrelation is variable in space. The ordinary least squares (OLS) method cannot handle these properties and presumes that the data are independent and homogeneous. Thus, it computes only one set of answers that may be wrong. Accordingly, the GWR method was introduced by [35] to handle these problems. This method allows the data to be dependent on location and non-stationary, also it obtains regression coefficients locally for each position and extracts variable relationships in space. The general formula of GWR is seen below [36]:
where is a dependent variable, is the jth explanatory variable, is the number of explanatory variables, is the residual of the model, and is the coefficient of regression that is a function of position .
GWR is a weighted least squares method against OLS. The coefficients of regression are obtained by Equation (4) [36]:
where is the weight matrix that is dependent on position , and it is a diagonal matrix containing geographical weights as follows [36]:
where i is the ID of observation and n is the number of observations.
The most significant part of the GWR method is the definition of geographical weights and several kernels have been proposed to compute these weights, two of which that have proven high performance being the Tricube and the Gaussian kernels shown below, respectively [37]:
where is the geographical weight of the jth observation in the ith position, is the Euclidean distance between these two points shown in Equation (8), is the bandwidth parameter, is the standard normal distribution function and is the standard deviation of values for each point.
The distance is often Euclidean, but other types of distance can also be used. Selecting proper bandwidth is vital, because if it is too large, results will tend toward OLS results, and if the bandwidth is too small, the variance of the results will grow strongly [36].
There are several methods for optimizing the bandwidth parameter, and one of them is cross-validation as follows [35]:
where n is the number of observations, is the ith observation, and is the predicted observation in the ith point using only the other point observations. The bandwidth parameter relates to through , and each bandwidth that minimizes the is the optimal bandwidth [35].
GWR outputs include some parameters for evaluating the model. The most important one is the coefficient of determination, R2, known as a measure of goodness of fit [33]. It is in the range [0, 1] and higher values are preferable for it. R2 is obtained by Equation (10) as follows [34]:
where n is the number of observations, is the ith observation, is the ith predicted observation, and is the mean of the observations.
As mentioned in Section 1, GWR can handle local variations and spatial non-stationarity. A statistic that can be used to determinate the size of the variations in regression coefficients in the study area is the standard deviation of regression coefficients computed through Equation (13) [35]:
where is the regression coefficient of the jth factor in the ith observation, is the mean of regression coefficients of the jth factor in all observations, and n is the number of observations.
The two other statistics used to evaluate the distribution of residuals are the root mean squares error () and the normalized () as shown below:
where n is the number of observations, is the ith observation, is the ith estimated observation, and is the standard deviation of the estimated observations.
2.4. Geographically and Temporally Weighted Regression (GTWR)
In cases involving the inclusion of time, it is imperative to account for temporal variations in addition to local ones. As discussed in Section 1, traditional GWR faces limitations in handling time. Consequently, GWR was adapted into a temporal version, referred to as GTWR. In this context, it is adequate to introduce time to the conventional equations as an additional dimension. As a result, Equations (3)–(5) undergo changes as follows [38]:
The other equations will be the as same as the traditional ones with a change in the definition of distance. The distance in GWR is a spatial distance in two dimensions that is achieved by Equation (8) but the distance in GTWR is a spatiotemporal distance that is defined by [38] as follows:
where and are scale factors to balance the various effects that occurred due to measuring the spatial and temporal distances in their respective metric systems. This distance is used in Equations (6) and (7) to compute the geographical weights. Algorithm 1 shows the pseudo-code of the proposed GTWR method used in this study.
| Algorithm 1 The proposed GTWR pseudo-code for this study |
| Select the optimal bandwidth parameter using Cross Validation. Calculate the spatiotemporal distance among all pairs of the points. Calculate the geographic weights using Tricube kernel. Calculate the coefficients of regression Calculate the Coefficient of Determination. return the coefficients of regression; the Coefficient of Determination; the residuals; the estimated values of observations; the used kernel type; the optimal bandwidth; the t-statistics matrix; the iteration of Cross Validation; the estimated standard deviation of residuals; the input parameters of the GTWR method. |
2.5. Selection of the Optimum Spatial Factors
It is necessary to choose a set of spatial factors that will optimize the performance of GWR/GTWR. To achieve this, this study introduces a modified version of continuous invasive weed optimization (CIWO) for the purpose of selecting the most suitable subset of spatial factors. A position vector of a weed k, , as an individual, was initialized with uniformly random values for i = 1 to d, where d is the number of spatial factors. For a weed, those factors with would be selected for calculating the weed’s fitness function where is a predefined threshold. The fitness function of the kth weed, fk, in the present research is 1-R2 (Equation (10)), which must be minimized. The number of seeds that a weed k can produce in every iteration is calculated as follows:
where fb and fw are the best and the worst weed fitness values from the first to the present iteration, Nmin and Nmax are the predefined minimum and maximum number of seeds that a week could produce during evolution. The closeness of a seed to its parent weed is determined by:
where itmax is the maximum number of iterations, and m is the modulation index, ci and cf are the predefined initial and final closeness value from the parent weed at the first and the last iteration, respectively. The new position vector of weed k is achieved by:
In each iteration of the proposed modified CIWO, the weeds with the lower fitness produce seeds, but the others are removed until the maximum predefined weed population (Pmax) in each iteration is reached. Accordingly, Algorithm 2 shows the pseudo-code of the proposed modified CIWO.
| Algorithm 2 The pseudo-code of the proposed algorithm for selecting spatial factors with the most effects on forest fires |
| Create a d-dimenonal weed position vector P times (P < Pmax) with a uniformly random values αi ∈ (0,1) for i = 1 to d, where d is the number of spatial factors do for each iteration (it = l to itmax) do Calculate cit based on Equation (21); end for for each weed (k = l to P) do Calculate the fiuess, i.e., the l-R2, based on Equation (10) for αi where αi> σth; end for while it <= itmax do for each weed k do Calculate the number of seeds [Equation (20)]; Randomly disperse the generated seeds over the search-space Equations (21)–(23); Add the generated seeds at the end of the population; Calculate the fitess of the generated seeds, i.e., the l-R2, based on Equation (10) for αi where αi> σth; end for if P > Pmax then Sort the population in deseending order of their l-R²; Eliminate population of weeds with higher l-R² till P = Pmax; end if end while return the selected spatial factors (αi where αi > σth) for the weed with the best fitness; |
3. Results
In the current study, we examined the influence of 14 distinct factors on forest fires in the study area. These factors encompass variables such as proximity to rivers, distance from roads, proximity to residential zones, soil type, land use, elevation, slope, aspect, maximum temperature, minimum temperature, mean temperature, maximum wind azimuth, maximum wind speed, and total rainfall. As mentioned before, we considered both biophysical and human factors to obtain better results. The observations were imported in binary format (1 for fire and 0 for non-fire). Spatial distances were measured in meters, and temporal intervals were measured in days.
The kernels of Equations (6) and (7) were used in both the GWR and GTWR algorithms, and the bandwidth parameter was optimized using Equation (9). The properties of the proposed modified CIWO are shown in Table 1.

Table 1.
The modified CIWO-based spatial factor selection parameter values.
After applying the GTWR algorithm with tricube and Gaussian kernels, we obtained R2 values of 0.9985 and 0.9740, respectively. In the first case, six factors, including distance from rivers, soil type, maximum temperature, maximum wind azimuth, maximum wind speed, and total rainfall, were identified as effective factors. In the second case, all factors except soil type were found to be significant. Moreover, the GWR algorithm using the tricube kernel resulted in an R2 equal to 0.8731 and 0.8888 for the fires that occurred on 17 November 2010 and 15 July 2011, respectively. In the first case, eight factors including distance from residential zones, soil type, land use, elevation, slope, aspect, minimum temperature, and maximum wind azimuth, and in the second case, seven factors, including distance from residential zones, soil type, elevation, slope, aspect, minimum temperature, and maximum temperature, were recognized as the most effective factors. In addition, the GWR algorithm using the Gaussian kernel resulted in an R2 equal to 0.8138 and 0.8203 for the fires that occurred on 17 November 2010 and 15 July 2011, respectively. In the first case, eight factors, including distance from rivers, distance from roads, land use, aspect, minimum temperature, mean temperature, maximum wind speed, and total rainfall, and in the second case, seven factors, including distance from residential zones, land use, elevation, maximum temperature, minimum temperature, mean temperature, and maximum wind azimuth, were recognized as the most effective factors. Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 display the outcomes of the modified CIWO algorithm, presenting both the best and mean fitness values, the last best individuals, the average distance between individuals, and the fitness of each individual in the last iteration, with corresponding properties detailed in Table 1.
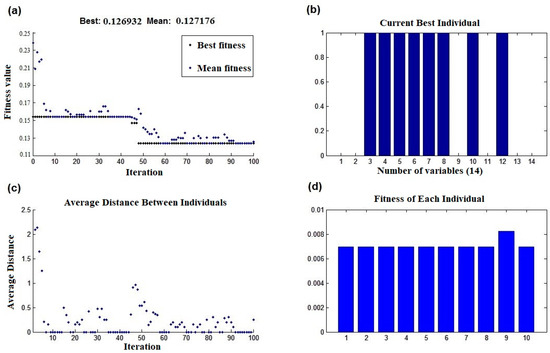
Figure 10.
(a) The best and the mean values of fitness, (b) the last best individuals, (c) the average distance between individuals, (d) the fitness of each individual in the last iteration using the GWR method with the tricube kernel and the modified CIWO for 17 November 2010 data.

Figure 11.
(a) The best and the mean values of fitness, (b) the last best individuals, (c) the average distance between individuals, (d) the fitness of each individual in the last iteration using the GWR method with the Gaussian kernel and the modified CIWO for 17 November 2010 data.
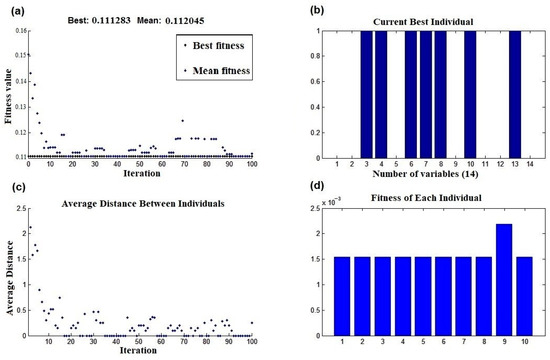
Figure 12.
(a) The best and the mean values of fitness, (b) the last best individuals, (c) the average distance between individuals, (d) the fitness of each individual in the last iteration using the GWR method with the tricube kernel and the modified CIWO for 15 July 2011 data.
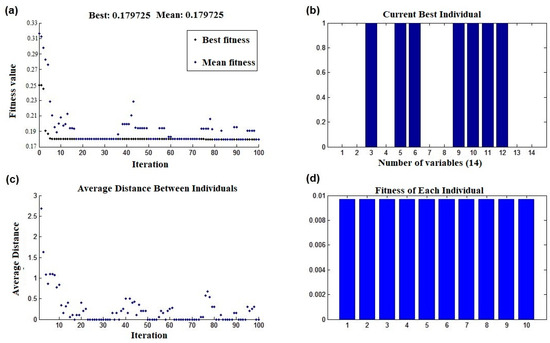
Figure 13.
(a) The best and the mean values of fitness, (b) the last best individuals, (c) the average distance between individuals, (d) the fitness of each individual in the last iteration using the GWR method with the Gaussian kernel and the modified CIWO for 15 July 2011 data.
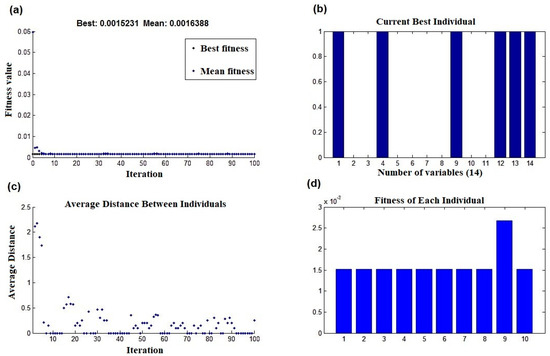
Figure 14.
(a) The best and the mean values of fitness, (b) the last best individuals, (c) the average distance between individuals, (d) the fitness of each individual in the last iteration using he GTWR method with the tricube kernel and the modified CIWO.

Figure 15.
(a) The best and the mean values of fitness, (b) the last best individuals, (c) the average distance between individuals, (d) the fitness of each individual in the last iteration using the GTWR method with the Gaussian kernel and the modified CIWO.
The standard deviation of regression coefficients was computed, and the results are shown in Table 2, Table 3 and Table 4. The number 0 is related to the constant coefficient of regression and the dash marks are related to the regression coefficients of ineffective factors, and were obtained as presented in Table 5, Table 6 and Table 7.

Table 2.
The standard deviation of regression coefficients for the important spatial factors using GWR and the modified CIWO method (see Algorithm 2) for 17 November 2010 data.

Table 3.
The standard deviation of regression coefficients for the important spatial factors using GWR and the modified CIWO method (see Algorithm 2) for 15 July 2011 data.

Table 4.
The standard deviation of regression coefficients for the important spatial factors using GTWR and the modified CIWO method (see Algorithm 2).

Table 5.
RMSE and NRMSE of the residuals of the model using GWR and the modified CIWO method for 17 November 2010 data.

Table 6.
RMSE and NRMSE of the residuals of the model using GWR and the modified CIWO method for 15 July 2011 data.

Table 7.
RMSE and NRMSE of the residuals of the model using GTWR and the modified CIWO method.
As depicted in Table 5, Table 6 and Table 7, the GTWR method with the tricube kernel demonstrated superior performance compared to the other methods. Given this superior performance, the estimated observations () derived from the GTWR method with the tricube kernel were selected. Subsequently, the estimated fire observations for the entire study area were obtained using ordinary kriging interpolation with a resolution of 30 m and an exponential variogram. This decision was based on the mean bias error, mean absolute error, and global standard deviation values for this dataset, which accounted for 0.001, 10.41, and 16.20% of the values observed with other variogram models, respectively. The resulting outputs are presented in Figure 16. To assess the model’s performance, classification confusion matrices and evaluation metrics are computed, as shown in Table 8, Table 9 and Table 10.
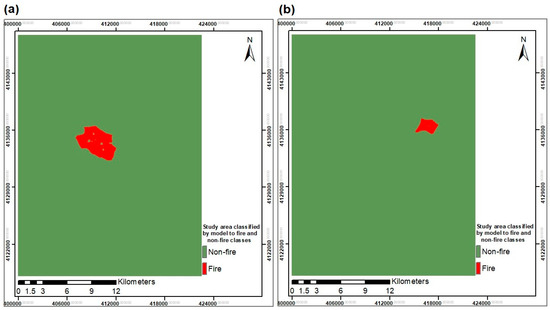
Figure 16.
The predicted class of cells in the study area using the GTWR method with the tricube kernel and the modified CIWO method for (a) 17 November 2010 and (b) 15 July 2011.

Table 8.
The confusion matrix using GTWR with the tricube kernel and the modified CIWO method for 17 November 2010.

Table 9.
The confusion matrix using GTWR with the tricube kernel and the modified CIWO method for 15 July 2011.

Table 10.
The evaluation measures of the model.
4. Discussion
According to Figure 12a and Figure 14a, displaying the best fitness function values obtained using the GWR method with the tricube kernel for 17 November 2010, and 15 July 2011, the data are 0.127 and 0.111, with mean values of 0.127 and 0.112, respectively. Similarly, Figure 13a and Figure 15a illustrate the best fitness function values achieved using the GWR method with the Gaussian kernel for 17 November 2010, and 15 July 2011, as 0.186 and 0.179, with mean values of 0.187 and 0.179, respectively. Lastly, Figure 14a and Figure 15a show the best fitness function values using the GTWR method with the tricube and Gaussian kernels as 0.001 and 0.026, with mean values of 0.001 and 0.026, respectively. In all cases, the fluctuations in the fitness function are minimal, and in some instances, convergence occurs rapidly (refer to Figure 10b). The average distance between individuals, displayed in Figure 10c, Figure 11c, Figure 12c, Figure 13c, Figure 14c and Figure 15c, decreases, albeit with some fluctuations. Generally, the GTWR algorithm with the tricube kernel achieves superior fitness function values compared to both the GWR algorithm and GTWR with the Gaussian kernel.
The factors identified as effective drivers of forest fires in this case study area through geographically weighted regression (GWR) using the tricube kernel include six biophysical and two human factors for 17 November 2010 data. Additionally, for 15 July 2011 data, the tricube kernel identifies six biophysical and one human factor. Furthermore, the factors identified as effective drivers of forest fires in our study area by GWR using the Gaussian kernel comprise six biophysical and two human factors for 17 November 2010 data. For 15 July 2011 data, the Gaussian kernel highlights five biophysical and two human factors.
Finally, the factors that are identified by GTWR as the effective factors for forest fire drivers in our study area include only six biophysical factors using the tricube kernel and ten biophysical and three human factors using the Gaussian kernel. According to the forest fire statistics in recent years, most of the fires that occurred in the Golestan province were near roads and residential zones and, in our study, both of these are recognized as significant factors in some cases. Also, some biophysical factors are identified as important factors. Hence, both of these factors affect forest fires in our study area and fire management strategies should consider them simultaneously.
The estimated fires depicted in Figure 16 closely resemble the actual fires, and the model exhibits high accuracy, sensitivity, and specificity, as evidenced by the data presented in Table 10. Additionally, our study area displays considerable non-stationarity, with the constant coefficient of regression exhibiting the maximum standard deviation, as indicated in Table 2, Table 3 and Table 4. Moreover, the residuals, as demonstrated in Table 5, Table 6 and Table 7, consistently approach zero. It is noteworthy that in all instances, GTWR employing the tricube kernel outperformed both GWR and GTWR utilizing the Gaussian kernel.
5. Conclusions
Determining the effective factors for forest fire drivers, derived from geospatial and remote sensing data, is so important because many forest areas around the world are destroyed every year by fire. Many of the driving factors of forest fires can be prevented by law enforcement, efficient forest management policies, and more supervision. In the current study, we tried identifying the factors affecting forest fires using the GTWR method integrated by the modified CIWO algorithm. The tricube and the Gaussian kernels were used for weighting GTWR, which resulted in R2 = 0.9985 and R2 = 0.9740, respectively. However, the traditional GWR using the tricube kernel resulted in R2 = 0.8731 and R2 = 0.8888, and the Gaussian kernel resulted in R2 = 0.8138 and R2 = 0.8203 for two sets of data, separately. This study demonstrates that both biophysical and anthropogenic factors exert significant effects on forest fires. The inclusion of time in the geographically and temporally weighted regression (GTWR) method, compared to the traditional GWR, yields improved results. Consequently, forest management systems can leverage this proposed technique with more forest fire data to derive more operational insights in the study area.
For future research endeavors, the number of driving factors, particularly human-related ones, can be expanded. This includes considerations of educational, cultural, and economic levels, tourist numbers, regulations, and forest management strategies. However, collecting such data poses a challenge. Additionally, there are other crucial factors, like vegetation type, fuel characteristics, moisture, and the duration of sunny hours, which we lacked comprehensive datasets for in this study. The incorporation of these factors could enhance the analysis. Our technique has the potential for improvement by incorporating more field and remotely sensed data on forest fires. Furthermore, it can be extended to predict fire dynamics and development in forests, contributing to a faster and more effective emergency evacuation response.
Author Contributions
Conceptualization, P.P. and A.R.; methodology, P.P., A.R., B.B. and O.G; software, P.P. and A.R.; validation, B.B. and O.G.; investigation, P.P., B.B. and O.G.; resources, P.P. and A.R.; data curation, P.P. and A.R.; writing—original draft preparation, P.P., A.R. and B.B.; writing—review and editing, P.P., A.R., B.B. and O.G; visualization, A.R., B.B. and O.G; supervision, P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data is unavailable due to privacy restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Eskandari, S.; Miesel, J.R.; Pourghasemi, H.R. The temporal and spatial relationships between climatic parameters and fire occurrence in northeastern Iran. Ecol. Indic. 2022, 118, 106720. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Y.; Feng, Z.; Feng, Z.; Zhao, Z.; Chen, S.; Zhang, H. Forest fire occurrence prediction in China based on machine learning methods. Remote Sens. 2022, 14, 5546. [Google Scholar] [CrossRef]
- Ma, W.; Feng, Z.; Cheng, Z.; Chen, S.; Wang, F. Identifying Forest Fire Driving Factors and Related Impacts in China Using Random Forest Algorithm. Forests 2020, 11, 507. [Google Scholar] [CrossRef]
- McKenzie, D.C.; Shankar, U.; Keane, R.E.; Stavros, E.N.; Heilman, W.E.; Fox, D.G.; Riebau, A.C. Smoke Consequences of New Wildfire Regimes Driven by Climate Change. Earth’s Future 2014, 2, 35–59. [Google Scholar] [CrossRef]
- Saha, S.; Bera, B.; Shit, P.K.; Bhattacharjee, S.; Sengupta, N. Prediction of Forest Fire Susceptibility Applying Machine and Deep Learning Algorithms for Conservation Priorities of Forest Resources. Remote Sens. Appl. Soc. Environ. 2023, 29, 100917. [Google Scholar] [CrossRef]
- Kolanek, A.; Szymanowski, M.; Raczyk, A. Human Activity Affects Forest Fires: The Impact of Anthropogenic Factors on the Density of Forest Fires in Poland. Forests 2021, 12, 728. [Google Scholar]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Aryal, J. Forest Fire Susceptibility and Risk Mapping Using Social/infrastructural Vulnerability and Environmental Variables. Fire 2019, 2, 50. [Google Scholar] [CrossRef]
- Su, Z.; Tigabu, M.; Cao, Q.; Wang, G.; Hu, H.; Guo, F. Comparative Analysis of Spatial Variation in Forest Fire Drivers between Boreal and Subtropical Ecosystems in China. For. Ecol. Manag. 2019, 454, 117669. [Google Scholar] [CrossRef]
- Massetti, A.; Rudiger, C.; Yebra, M.; Yebra, M.; Hilton, J.E.; Hilton, J.E. The Vegetation Structure Perpendicular Index (VSPI): A Forest Condition Index for Wildfire Predictions. Remote Sens. Environ. 2019, 224, 167–181. [Google Scholar]
- Dickson, B.G.; Prather, J.W.; Xu, Y.; Hampton, H.M.; Aumack, E.N.; Sisk, T.D. Mapping the Probability of Large Fire Occurrence in Northern Arizona, USA. Landsc. Ecol. 2006, 21, 747–761. [Google Scholar]
- Arif, M.; Alghamdi, K.K.; Sahel, S.A.; Alosaimi, S.O.; Alsahaft, M.E.; Alharthi, M.A.; Arif, M. Role of Machine Learning Algorithms in Forest Fire Management: A Literature Review. J. Robot. Autom. 2021, 5, 212–226. [Google Scholar]
- Mukunga, T.; Forkel, M.; Forrest, M.; Zotta, R.M.; Pande, N.; Schlaffer, S.; Dorigo, W. Effect of Socioeconomic Variables in Predicting Global Fire Ignition Occurrence. Fire 2023, 6, 197. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; Chuvieco, E.; Koutsias, N. Modelling Long-term Fire Occurrence Factors in Spain by Accounting for Local Variations with Geographically Weighted Regression. Nat. Hazards Earth Syst. Sci. 2013, 13, 311–327. [Google Scholar] [CrossRef]
- Mercer, D.E.; Prestemon, J.P. Comparing Production Function Models for Wildfire Risk Analysis in the Wildland–urban Interface. For. Policy Econ. 2005, 7, 782–795. [Google Scholar] [CrossRef]
- Moritz, M.A.; Keeley, J.E.; Johnson, E.A.; Schaffner, A. Testing a Basic Assumption of Shrubland Fire Management: How Important Is Fuel Age? Front. Ecol. Environ. 2004, 2, 67–72. [Google Scholar]
- Roman-Cuesta, R.M.; Martínez-Vilalta, J. Effectiveness of Protected Areas in Mitigating Fire within Their Boundaries: Case Study of Chiapas, Mexico. Conserv. Biol. 2006, 20, 1074–1086. [Google Scholar]
- Syphard, A.D.; Radeloff, V.C.; Keuler, N.S.; Taylor, R.S.; Hawbaker, T.J.; Stewart, S.I.; Clayton, M.K. Predicting Spatial Patterns of Fire on a Southern California Landscape. Int. J. Wildland Fire 2008, 17, 602–613. [Google Scholar]
- Murthy, K.K.; Sinha, S.K.; Kaul, R.; Vaidyanathan, S. A fine-scale state-space model to understand drivers of forest fires in the Himalayan foothills. For. Ecol. Manag. 2019, 432, 902–911. [Google Scholar] [CrossRef]
- Romero-Calcerrada, R.; Novillo, C.J.; Millington, J.D.A.; Gomez-Jimenez, I. GIS Analysis of Spatial Patterns of Human-caused Wildfire Ignition Risk in the SW of Madrid (central Spain). Landsc. Ecol. 2008, 23, 341–354. [Google Scholar] [CrossRef]
- Erten, E.; Kurgun, V.; Musaoglu, N. Forest fire risk zone mapping from satellite imagery and GIS: A case study. In Proceedings of the XXth Congress of the International Society for Photogrammetry and Remote Sensing, Istanbul, Turkey, 12–23 July 2004. [Google Scholar]
- Bufacchi, P.; Krieger, G.C.; Mell, W.; Alvarado, E.; Santos, J.C.; de Carvalho, J.A. Numerical Simulation of Surface Forest Fire in Brazilian Amazon. Fire Saf. J. 2016, 79, 44–56. [Google Scholar]
- Zhang, Y.; Lim, S.; Sharples, J.J. Modelling Spatial Patterns of Wildfire Occurrence in South-eastern Australia. Geomat. Nat. Hazards Risk 2016, 7, 1800–1815. [Google Scholar]
- Joseph, M.B.; Rossi, M.W.; Mietkiewicz, N.; Mahood, A.L.; Cattau, M.E.; St. Denis, L.A.; Nagy, R.C.; Iglesias, V.; Abatzoglou, J.T.; Balch, J.K. Spatiotemporal Prediction of Wildfire Size Extremes with Bayesian Finite Sample Maxima. Ecol. Appl. 2019, 29, e01898. [Google Scholar] [PubMed]
- Jaafari, A.; Pourghasemi, H.R. Factors influencing regional-scale wildfire probability in Iran: An application of random forest and support vector machine. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 607–619. [Google Scholar]
- Milanović, S.; Kaczmarowski, J.; Ciesielski, M.; Trailović, Z.; Mielcarek, M.; Szczygieł, R.; Milanović, S.D. Modeling and mapping of forest fire occurrence in the Lower Silesian Voivodeship of Poland based on Machine Learning methods. Forests 2023, 14, 46. [Google Scholar]
- Ávila-Flores, D.Y.; Pompa-García, M.; Antonio-Nemiga, X.; Rodríguez-Trejo, D.A.; Vargas-Perez, E.; Santillan-Perez, J. Driving Factors for Forest Fire Occurrence in Durango State of Mexico: A Geospatial Perspective. Chin. Geogr. Sci. 2010, 20, 491–497. [Google Scholar] [CrossRef]
- Koutsias, N.; Martínez-Fernández, J.; Allgöwer, B. Do Factors Causing Wildfires Vary in Space? Evidence from Geographically Weighted Regression. GIScience Remote Sens. 2010, 47, 221–240. [Google Scholar] [CrossRef]
- Ávila-Flores, D.Y.; Pompa-Garcia, M.; Vargas-Perez, E. Spatial analysis of forest fire occurrence in the state of Durango. Rev. Chapingo Ser. Cienc. For. Ambiente 2010, 16, 253–260. [Google Scholar]
- Sá, A.C.L.; Pereira, J.M.C.; Charlton, M.; Mota, B.; Barbosa, P.; Fotheringham, A.S. The Pyrogeography of Sub-saharan Africa: A Study of the Spatial Non-stationarity of Fire–environment Relationships Using GWR. J. Geogr. Syst. 2011, 13, 227–248. [Google Scholar]
- Akhani, H. Plant Biodiversity of Golestan National Park, Iran; OÖ Landesmuseum, Biologiezentrum: Linz, Austria, 1998; Volume 53. [Google Scholar]
- Jahdi, R.; Bacciu, V.; Salis, M.; Del Giudice, L.; Cerdà, A. Surface Wildfire Regime and Simulation-Based Wildfire Exposure in the Golestan National Park, NE Iran. Fire 2023, 6, 244. [Google Scholar]
- Akhani, H. Studies on the flora and vegetation of the Golestan National Park, NE Iran. III. Three new species, one new subspecies and fifteen new records for Iran. Edinb. J. Bot. 1999, 56, 1–31. [Google Scholar] [CrossRef]
- Ziary, Y.; Safari, H. To Compare Two Interpolation Methods: IDW, Kriging for Providing Properties (Area) Surface Interpolation Map Land Price. District 5, Municipality of Tehran area 1. In Proceedings of the FIG Working Week, Hong Kong, China, 13 May 2007; Volume 13. [Google Scholar]
- Shekhar, S.; Xiong, H. Encyclopedia of GIS; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression-Modelling Spatial Non-Stationarity. Statistician 1998, 47, 431–443. [Google Scholar]
- McMillen, D.P.; McDonald, J.F. Locally Weighted Maximum Likelihood Estimation: Monte Carlo Evidence and an Application. In Advances in Spatial Econometrics: Methodology, Tools and Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Charlton, M.; Fotheringham, S.; Brunsdon, C. Geographically Weighted Regression; White Paper; National Centre for Geocomputation, National University of Ireland Maynooth: Kildare, Ireland, 2009. [Google Scholar]
- Huang, B.; Wu, B.; Barry, M. Geographically and Temporally Weighted Regression for Modeling Spatio-temporal Variation in House Prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).