Abstract
Efficient evacuation route planning during underground coal mine fires is essential to minimize casualties. This study addresses current shortcomings by proposing a real-time method that integrates a multifactor coupling analysis and the optimized multilayer perceptron regressor-shortest path faster algorithm (MSPFA). This research aims to enhance evacuation route planning by overcoming factors such as inadequate consideration, low accuracy, and information lag in existing methods. This study improves the shortest path faster algorithm (SPFA) for dynamic route planning, mitigates the impact of fixed walking speed parameters using the particle swarm algorithm, and selects the optimal model (MLPRegressor) through the Bootstrap algorithm for estimating personnel walking speeds. Validated through smoke-spread experiments, the MSPFA algorithm dynamically adjusts evacuation routes, preventing toxic passages. Visualization via drawing interchange format (DXF) successfully enhances route comprehension. The MSPFA algorithm outperforms the Dijkstra algorithm with a runtime of 78.5 msand a personnel evacuation time of 3344.74 s. This research establishes a theoretical foundation for intelligent evacuation decision making in underground fire disasters. By introducing the MSPFA algorithm, it provides crucial technical support, significantly reducing the risk of casualties during emergencies.
1. Introduction
In coal mines, disasters such as gas explosions, mine fires, dust explosions, flooding, and roof collapses often lead to casualties and property losses. Incidents resulting in injuries and fatalities still occur. On 27 September 2020, a major fire accident occurred in the Songzao coal mine, a subsidiary of Chongqing Energy Investment Group in China. The incident resulted in 16 fatalities, 42 injuries, and an economic loss of CNY 25.01 million. In 2023, a belt conveyor caught fire at Shujiao Coal Mine in Shanjiao Village, Panzhou City, Guizhou Province, China, resulting in 16 fatalities. An underground emergency evacuation system in mines is necessary to ensure mine safety and normal production. A rapid and efficient mine evacuation route is an indispensable component of this system. Therefore, the rational planning of mine evacuation routes plays a crucial role in ensuring the safety of underground personnel. In the event of a mine fire, the interconnected and complex network of mine tunnels forms a highly intertwined and branched topological structure. In disaster situations, it is essential to dynamically plan evacuation routes in real time to ensure the safety of underground workers.
The current methods for planning evacuation routes in underground coal mines mainly include graph theory algorithms, swarm heuristic algorithms [1,2], K-shortest path algorithms [3], the A* algorithm [4], and genetic algorithms [5]. Among them, graph theory algorithms [6] are considered the most stable and the fastest. In the planning of evacuation routes, Liu Xiaoxiao, Wang Yunjia, and others [7] conducted three-dimensional evacuation route planning based on fire temperature, wind speed and direction, and smoke quality score. They added the influence of fire wind pressure to the original fire evacuation route plan and made breakthrough progress in the visualization of mine evacuation routes. Wang Yukun, Wu Feng, and others [8] constructed an improved Dijkstra graph theory algorithm, enhancing the speed of searching for the shortest path. Zhao Zuopeng, Zong Yuanyuan, and others [9] introduced the concept of personnel walking speeds for the first time in mine flood evacuations, making evacuation routes more reasonable under flood conditions. Wang Jinhua, Wang Yougang, and others [10] achieved dynamic route planning by integrating underground sensor data into evacuation route planning. Early mine fire simulation software, including MFIRE [11], POZAR, uQEM, CFIRE [12], and MFRDSS, were used to simulate ventilation conditions in mine fires. After a fire occurs, the first step in mine evacuation route planning is to calculate the equivalent length of the tunnels under disaster conditions. The calculation of the equivalent length involves both static and dynamic parameters. Adjusting the dynamic parameters allows for a more reasonable determination of the equivalent length of mine tunnels [13,14]. In the process of calculating equivalent length, there is often a tendency to overlook changes in personnel walking speeds, a failure to consider real-time updating edge weights in tunnels under underground disaster conditions, and neglect of real-time changes in air composition within tunnels, the variations in personnel walking speed during disasters, and the direction of smoke spread. This leads to variability in evacuation routes. Additionally, equivalent length calculations do not use the shortest time as a computation metric [8,15], resulting in a lag in evacuation route planning. All these factors contribute to a disparity between the actual movement of personnel and the calculated shortest equivalent length [16]. Different disaster scenarios lead to different evacuation routes, requiring the planning of distinct evacuation routes for varying situations. During the underground smoke-spreading process, to minimize harm caused by smoke, it is essential to dynamically update the equivalent length of tunnels based on real-time conditions by using sensors such as gas, temperature, CO, dynamic parameters, and static parameters. This real-time update facilitates the dynamic adjustment of evacuation routes. The current planning method for evacuation routes under fire conditions is not optimal, and improvements are needed in real-time dynamic planning, visualization, personnel walking speed estimations, and other aspects of mine fire evacuation routes.
Based on these issues, real-time evacuation routes in the event of a mine fire are planned in this study. The optimization of mine evacuation algorithms, the visualization of mine evacuation routes, and rationalization of the equivalent length of mine evacuation routes are explored. Building upon the current research foundation, this study establishes a multi-factor coupling evacuation route algorithm based on the multilayer perceptron regressor shortest path faster algorithm (MSPFA). Through the analysis of evacuation routes under fire and smoke conditions, estimations of real-time personnel walking speeds, and the construction of reasonable equivalent lengths for pathways, real-time planning is achieved, resulting in favourable outcomes in evacuation experiments.
2. Materials and Methods
2.1. Shortest Path Faster Algorithm
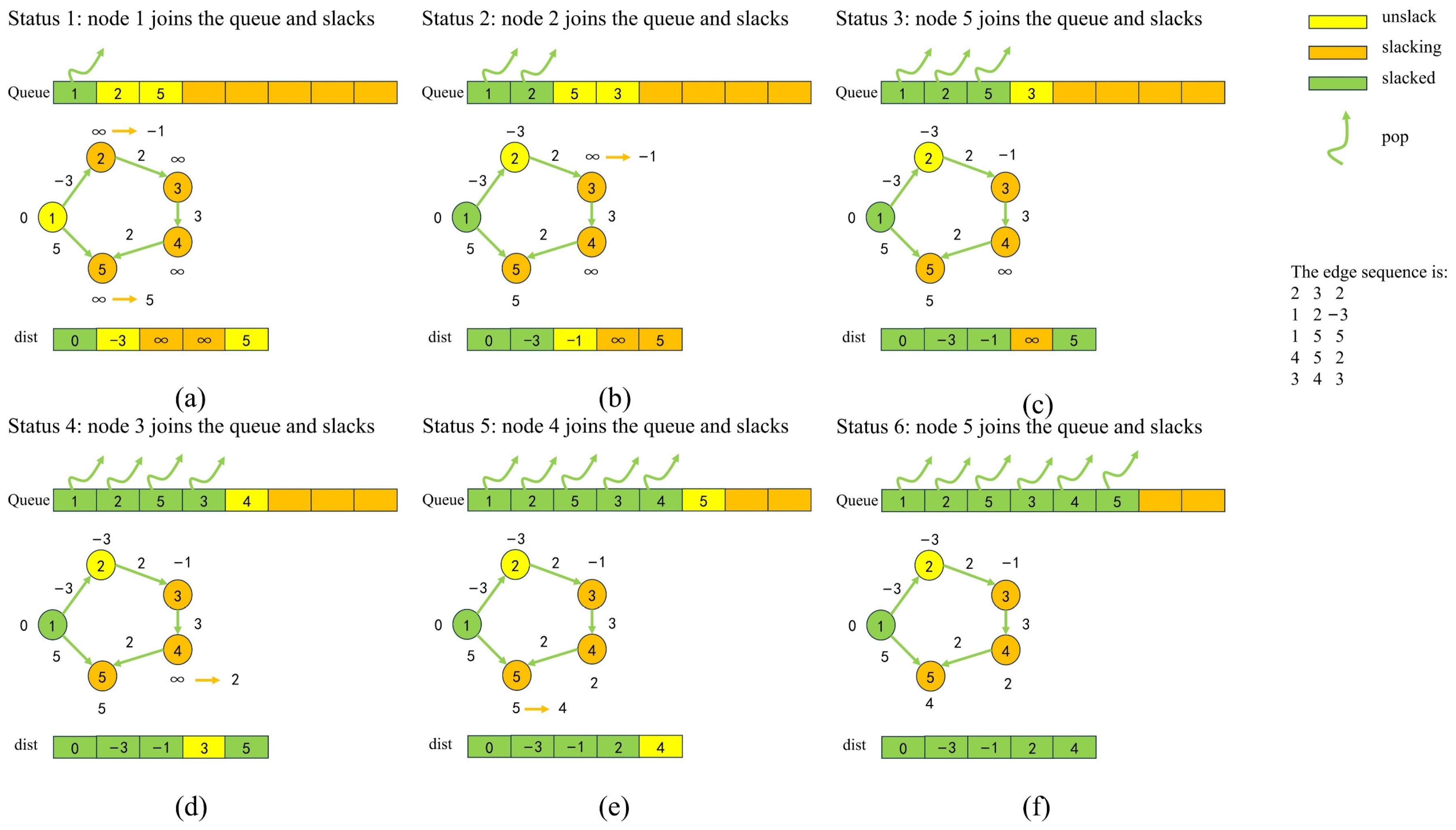
The Shortest Path Faster Algorithm (SPFA) is a single-source shortest path algorithm used for solving single-direction weighted graphs. Compared to the traditional Dijkstra algorithm [17,18], the SPFA employs relaxation operations, resulting in less time complexity. It is suitable for directed graphs, undirected graphs, and graphs with negative edge weights, enabling faster real-time dynamic path planning [19,20]. The connectivity of the mine tunnel network is complex, and during a mine fire, the equivalent lengths of certain tunnels can dynamically change due to smoke propagation. The real-time planning of paths using algorithms such as A*, swarm heuristic optimization, and genetic algorithms may result in slower solution speeds. Therefore, the SPFA from graph theory is employed for addressing this problem, particularly due to its efficiency in handling real-time changes in mine tunnel equivalent lengths caused by smoke spread during a mine fire. A specific illustration of the SPFA algorithm is shown in Figure 1. The operational process of the SPFA algorithm is as follows:
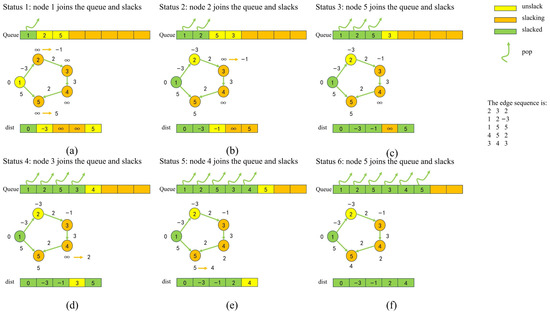
Figure 1.
SPFA algorithm using queue-based relaxation optimization.
Take out the top point in the queue, scan every edge sent from vertex , set the end point of each edge as , and the weight of edge as . If , update , update the path to ; if vertex is not in the queue, put vertex into the queue; if is not true, then nothing is done to the vertex .
Repeat Step 1 until the queue is empty.
When a mine tunnel fire occurs, the propagation of smoke in mine tunnels is complex, and the equivalent lengths of mine tunnels need to be updated in real time. The use of the traditional SPFA algorithm is slow. Building upon this algorithm, the evacuation route can be replanned more quickly by determining the current tunnel in which personnel are located. Therefore, during the process of storing tunnel equivalent lengths, a real-time database is utilized to ensure the rapid reading and writing of tunnel equivalent lengths. Additionally, in the tunnel where personnel are currently located, the optimal evacuation route is re-planned. Figure 1 illustrates the process of the SPFA algorithm for calculating the shortest path. In (a), the process begins with node 1 being placed in the queue, while the other nodes are initialized to infinity. Optimization is performed for neighbouring nodes, and this cycle continues until all nodes are optimized.
2.2. Multifactor Coupling Fire Evacuation Route Planning Model
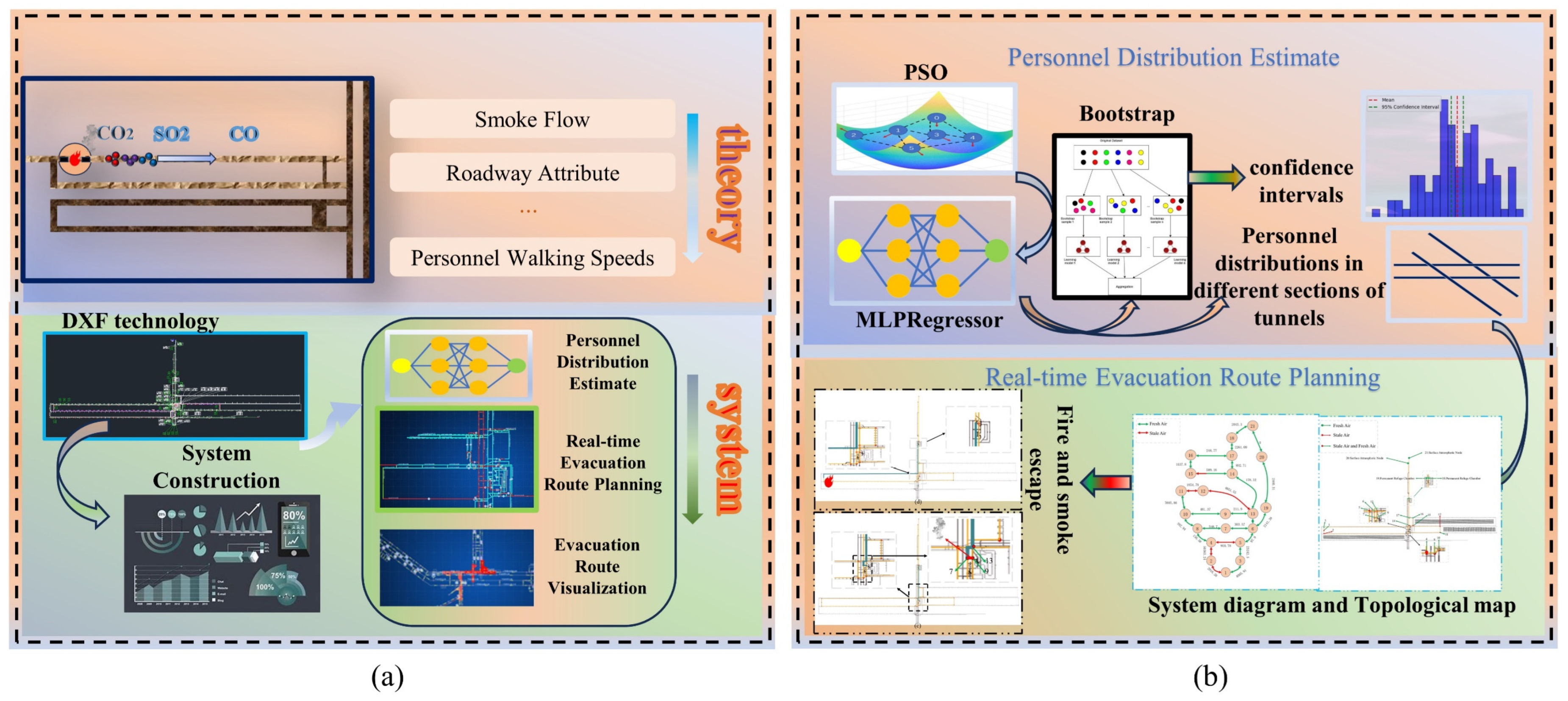
Multifactor coupling fire evacuation route planning combines fixed basic parameters such as the concentration of disaster gases such as CO and CO2, tunnel slope, and length, along with indicators related to the spread of smoke in the tunnel during a fire, personnel walking speed [21], and other metrics [22]. Using the multilayer perceptron regressor-shortest path faster (MSPFA) algorithm, a multifactor coupling fire evacuation route planning model is constructed, enabling real-time planning and analysis in the event of a fire. The MSPFA algorithm framework is depicted in Figure 2.
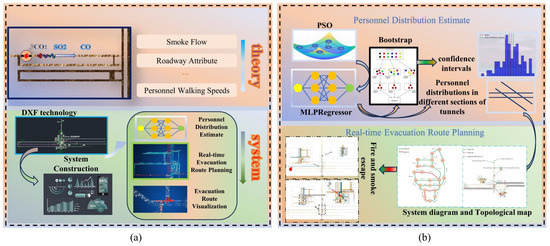
Figure 2.
Diagram of the multifactor coupling fire evacuation route planning model.
In (a), the theory analyzes various toxic and harmful gases, designs roadway attributes, and integrates personnel walking speeds. In the system design, it involves the conversion of drawing exchange format (DXF) mine maps and personnel distribution, real-time evacuation route planning, and evacuation route visualization. Based on this analysis, in (b), the personnel distribution estimate processes the data, incorporating PSO, MLPRegressor, and Bootstrap algorithms to estimate personnel distribution. Finally, real-time evacuation route planning calculations are designed.
Estimation of Personnel Walking Speeds Based on the Multilayer Perceptron Regressor Algorithm
During normal mining operations, underground personnel may experience congestion during shift changes or in the event of a fire, similar to traffic jams [23]. The walking speed of personnel is likely to be lower than normal due to impaired-vision movement. Using a traditional fixed value for walking speed can lead to significant distortions. Therefore, it is essential to estimate the real-time distribution of personnel and calculate their corresponding walking speeds.
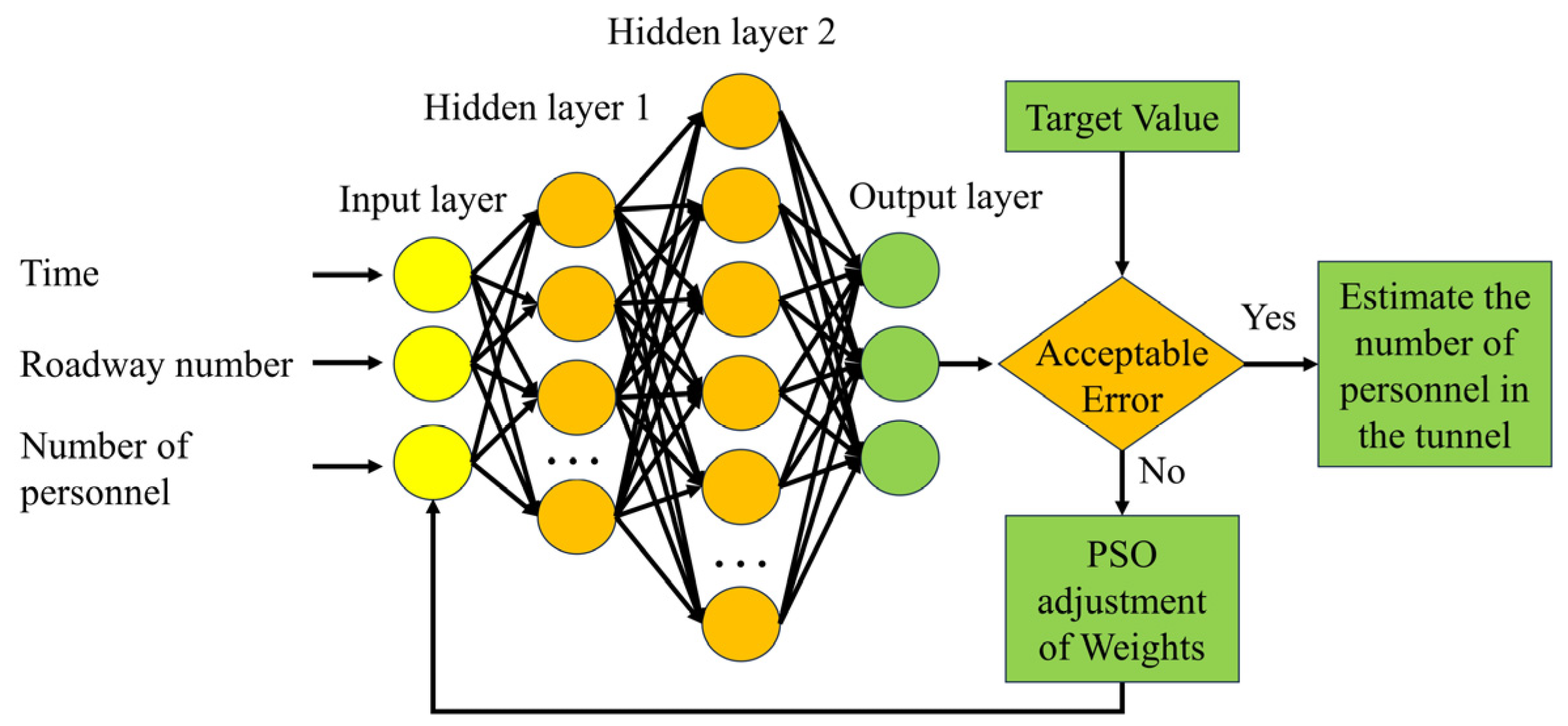
The multilayer perceptron regressor algorithm (MLPRegressor) is a type of multioutput regression model that is a feedforward neural network consisting of one or more hidden layers and an output layer. Each hidden layer has multiple neurons, and each neuron is connected to all the neurons in the previous layer. The MLPRegressor can be employed to learn complex relationships between input and output values and is applied to regression problems involving continuous prediction values. Due to the limited data on personnel distributions in tunnels, the MLPRegressor parameters are optimized using the Particle Swarm Optimization (PSO) algorithm. Cross-validation is employed to mitigate the risk of model overfitting. Figure 3 shows a neural network diagram of the MLPRegressor model used for predicting patient distribution. In this diagram, the input parameters include the number of tunnels in significant tunnels, the quantity of personnel distributed in the tunnel, and the historical time. The output parameter is the number of personnel in a specific tunnel at various times in a significant tunnel.
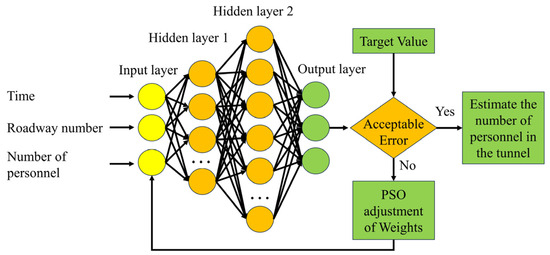
Figure 3.
Regression model of the ability of the MLPRegressor to estimate personnel distribution.
Due to the limited and less apparent data on the distribution of personnel in the tunnel, the original sequence is first cumulatively summed to generate an accumulated sequence. Based on this accumulated sequence, predictions for the average number of personnel in future time periods are made. This prediction is subsequently combined with real-time pedestrian density data. Finally, the real-time speed of personnel is calculated by using the three-parameter relationship formula for traffic flow [9,24].
2.3. MSPFA Model
To ensure the accurate calculation of tunnel equivalent lengths during a mine fire, the process involves a comprehensive consideration of factors such as tunnel length, slope, concentrations of CO and CO2, smoke propagation during a fire, the congestion level, and personnel walking speeds in the tunnel [21]. Based on these considerations, the MSPFA algorithm was developed to dynamically calculate the equivalent length of a tunnel in real-time.
During a mine fire, there are five main indicators, namely smoke propagation, personnel walking speeds, tunnel intrinsic parameters, wind speed, and the source of the fire [22]. Among these factors, smoke is one of the most crucial factors during a fire outbreak. Smoke propagation during a fire can lead to poisoning and even death. The key monitored indicators include temperature, CO concentration, CO2 concentration, and SO2 concentration. Personnel walking speeds considers the congestion level in the tunnel, while the intrinsic parameters of the tunnel include its length, type, slope, height, and obstacles. Formulas (1) and (2) represent the basic formulas for calculating the tunnel equivalent length.
In these two formulas, is the influence coefficient of the roadway height. is the influence coefficient of the roadway slope. is the influence coefficient of the obstacles in the roadway. is the roadway length, m. is the predicted escape speed of personnel without smoke spreading in the roadway, m/s. is the predicted escape speed of personnel when smoke spreads along roadways, m/s. is the predicted time needed for personnel pass through the roadway in the case of smoke spreading, s. is the temperature threshold. is the influence coefficient of different toxic and harmful gas concentrations in the roadway. is the coefficient of the end points of the roadway, and when there are toxic and harmful gases in the connecting roadway; the coefficient is a multiple of 1.5 when the same toxic and harmful gases exist in the connecting roadway.
In a high-temperature environment, temperature plays a crucial role in increasing the heat load on individuals, leading to an increase in body temperature. When the environmental temperature reaches a certain level, the human body may experience heat stress, resulting in a significant increase in transit time. Formulas (3) and (4) represent the relationships between the allowable passage time for individuals in high-temperature tunnels and the temperature, respectively [25]:
In these formulas, is the time when the roadway is allowed to reach high temperatures, min. is the temperature, . is the maximum endurance time of the human body in a high-temperature environment. The weight table for calculating the equivalent length of various toxic and harmful gases during smoke propagation is shown in Table 1 [26].

Table 1.
Determination of coefficients for tunnel equivalent length based on poisoning conditions and concentrations of various toxic gases.
During a fire in a mine, the inherent parameters of the tunnel include the tunnel length, tunnel slope, tunnel height [27], and obstacles, which are also important factors affecting the equivalent length of the tunnel. Table 2, Table 3 and Table 4 analyse the impact of inherent parameters on personnel evacuation during a fire.

Table 2.
Influence of roadway height on the equivalent length of the roadway.

Table 3.
Influence of roadway slope on the equivalent length of the roadway.

Table 4.
Influence of local obstacles on the equivalent length of the roadway.
The above explanation describes the method of calculating the equivalent length in mine tunnels. In real-world scenarios, sensor data in mine tunnels change in real time, and when a certain hazardous factor reaches a given threshold, the route is no longer passable. Therefore, based on the original equivalent length calculation, it is necessary to determine whether the road is feasible and to increase its equivalent length. Table 5 shows the impassable concentrations and reasons for CO, CO2, and SO2 gas emission. Different types of toxic and harmful gases can cause severe suffocation or even death when present at certain concentrations.

Table 5.
Impassable concentrations of different types of toxic and harmful gases.
Similarly, high temperature is a crucial factor leading to casualties. In the process of calculating the time taken for personnel to traverse the tunnel, the temperature is considered through the maximum allowable time, integrating Equations (1)–(4). Based on the maximum temperature that the human body can endure, if the time needed for personnel to traverse the tunnel exceeds the maximum permissible time under high-temperature conditions, it is assumed that the personnel do not survive. Therefore, the final equivalent length of the tunnel is determined according to Equation (5):
3. Mine Tunnel Real-Time Evacuation Route Experiment
3.1. Basic Computer Lab Experimental Design
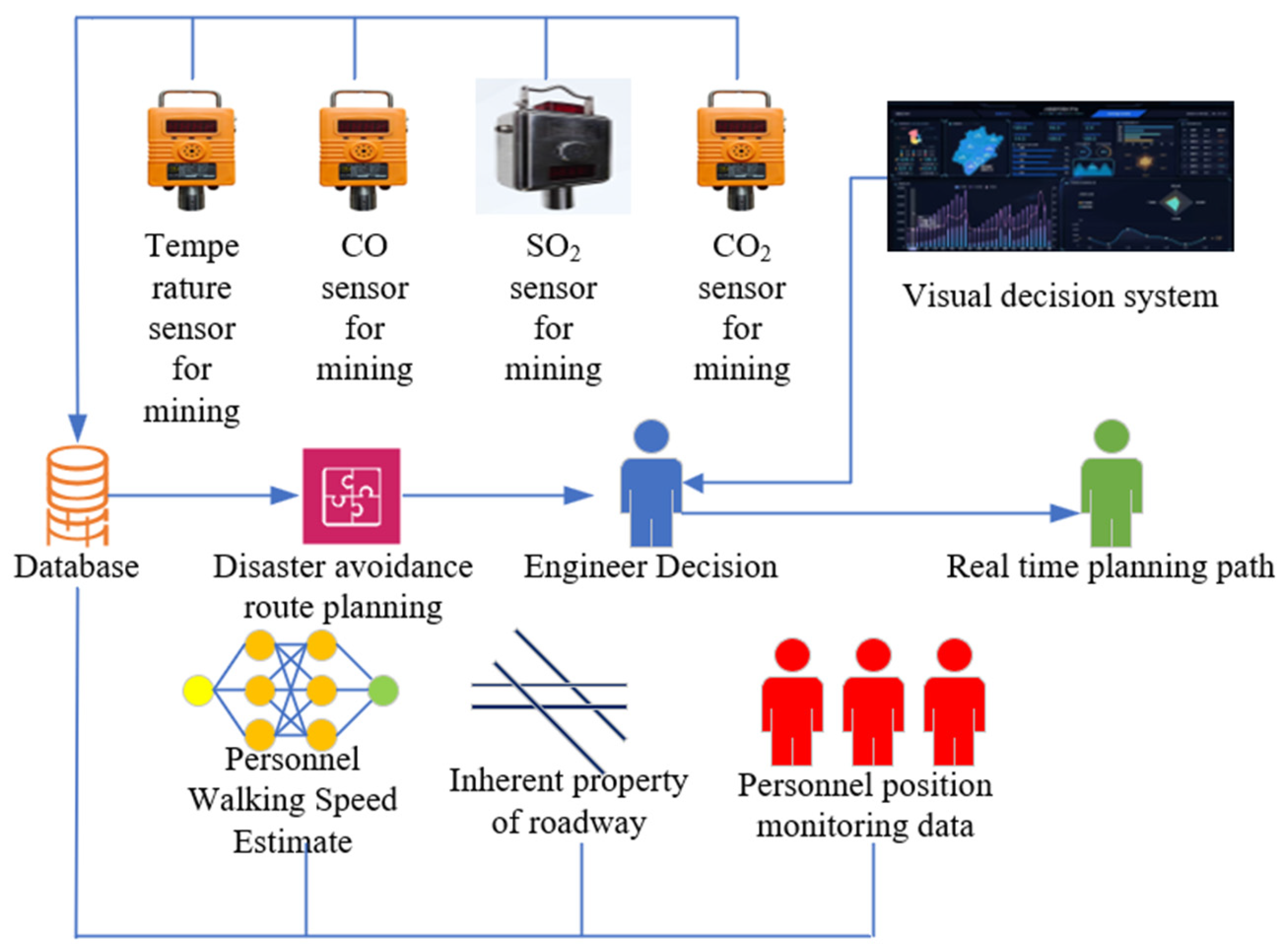
Due to the changing location of personnel, a new route must be reconfigured within the current tunnel to achieve real-time planning of a mine evacuation route. The ezdxf library in Python can be used to extract key features from a CAD mine map. With the aid of key feature data extraction and drawing tools, it is possible to visualize evacuation routes during mine fires. Additionally, by using the Rust programming language, an SPFA dynamic programming method is developed to achieve the real-time planning of mine evacuation routes. Figure 4 illustrates the design of the real-time evacuation route experiment in mine tunnels, considering factors such as personnel walking speeds, tunnel intrinsic attributes, current personnel location, and sensor parameters. At different time intervals, real-time data transmission from the mine collects current underground data, including gas concentrations, tunnel lengths, heights, slopes, and other intrinsic attributes, which are subsequently stored in an SQLite database. Based on historical data collection, the current walking speed of personnel in underground tunnels is estimated. On this basis, the real-time planning of mine evacuation routes is implemented, and engineers make decisions and analyse the situation to determine the evacuation route for personnel, with instructions sent to underground evacuees.
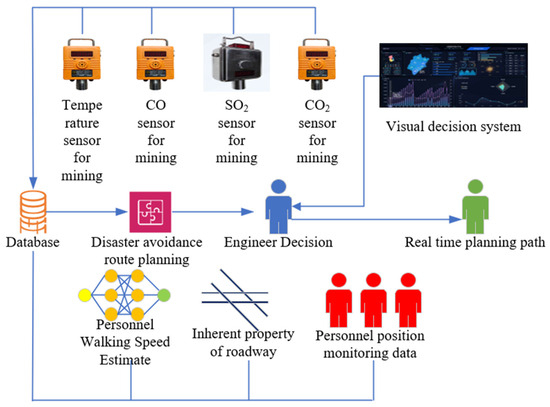
Figure 4.
Design of real-time evacuation route experiment in mine tunnels.
A simulated evacuation experiment is designed based on an actual production mine. Dynamic evacuation route solving and a visual analysis are implemented in computer software. The initial mine evacuation route tunnel system diagram and topological graph are shown in Figure 5 and Figure 6, respectively.
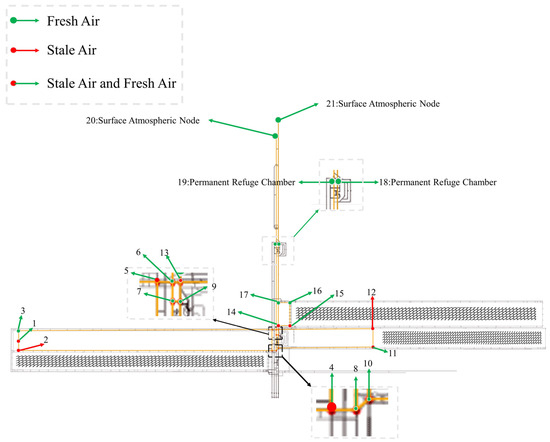
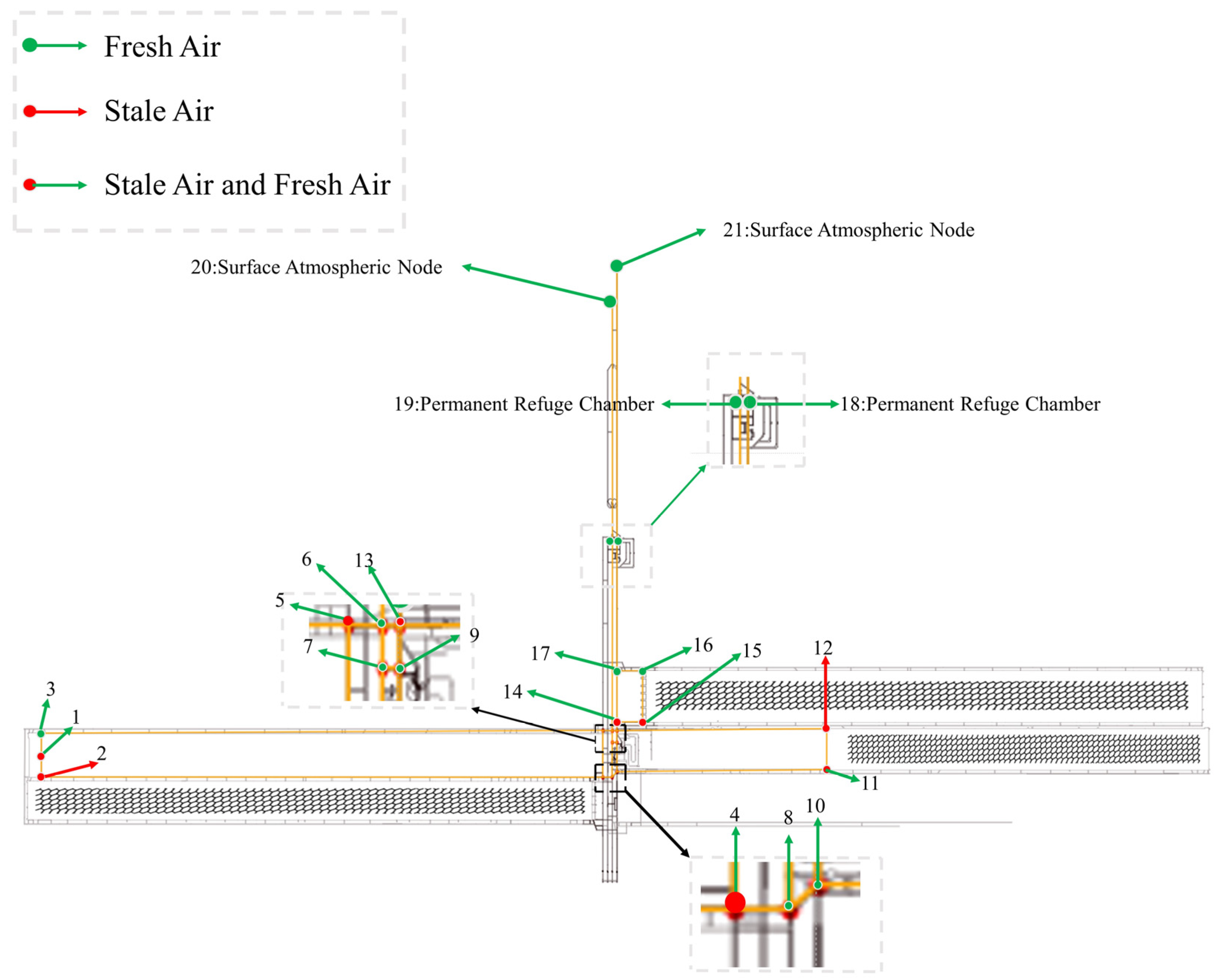
Figure 5.
System diagram of the mine tunnel fire evacuation route tunnel.
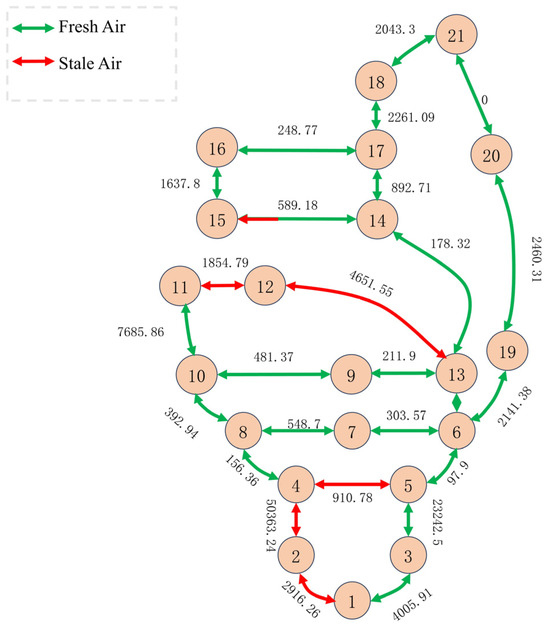
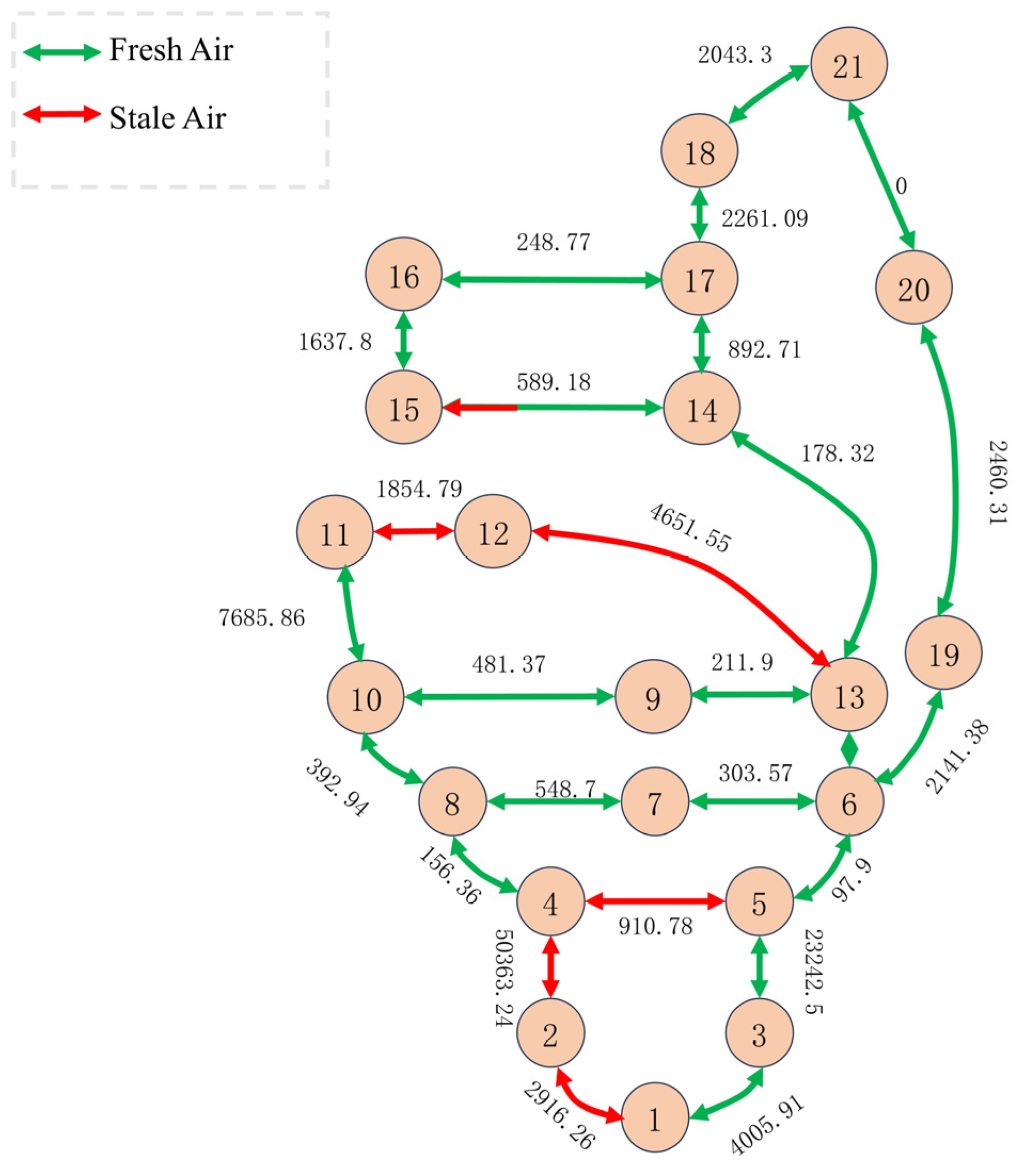
Figure 6.
Topological map of mine tunnel evacuation routes in case of fire.
The system diagram in Figure 5 corresponds to the mine tunnel topological graph in Figure 6, providing a detailed display of key information in the mine tunnels.
Nodes 1, 2, and 3 represent the front-end nodes of the coal mining face. Node 4 is the return airway connection point, while node 5 serves as the transport airway connection point. Nodes 6 and 13 denote a connecting roadway, and nodes 7 and 9 represent another connecting roadway. Nodes 8 and 10 form a connecting roadway leading to the transport airway. Node 11 connects the coal mining face to the transport airway, and node 12 connects it to the return airway. Nodes 14 and 15 are internal transport airway nodes for the coal mining face, while nodes 16 and 17 are transport airway nodes. Nodes 1 and 2, 4 and 5, 11 and 12, and 14 and 15 all have contaminated airflow. Nodes 2 and 12 are directly connected, and the entire airflow in the tunnel between them is contaminated. In the graphics, the yellow area represents accessible regions, and the black grid lines indicate mined-out areas.
Figure 6 consists of virtual nodes and real nodes and the edges between them, with the calculated equivalent lengths of the tunnels labelled on the edges. In Figure 6, clearly shows that except for the areas formed by nodes 1–4 and 11–16, which constitute polluted airflows in the coal mining face, the remaining locations are supplied with fresh airflow.
3.2. Estimation of Different Tunnel Personnel Walking Speeds
In this section, an analysis and comparison of three methods, MLPRegressor, XgbRegressor (extreme gradient-boosting regressor), and RFR (random forest regressor) is conducted. The optimal algorithm is selected for predicting personnel distribution. Table 6 shows the personnel distribution at various time intervals. The first four time intervals are chosen as the training period, and the personnel distribution for the latter two intervals between 8:41 and 9:00 is predicted.

Table 6.
Personnel distributions in different sections of tunnels at various time intervals.
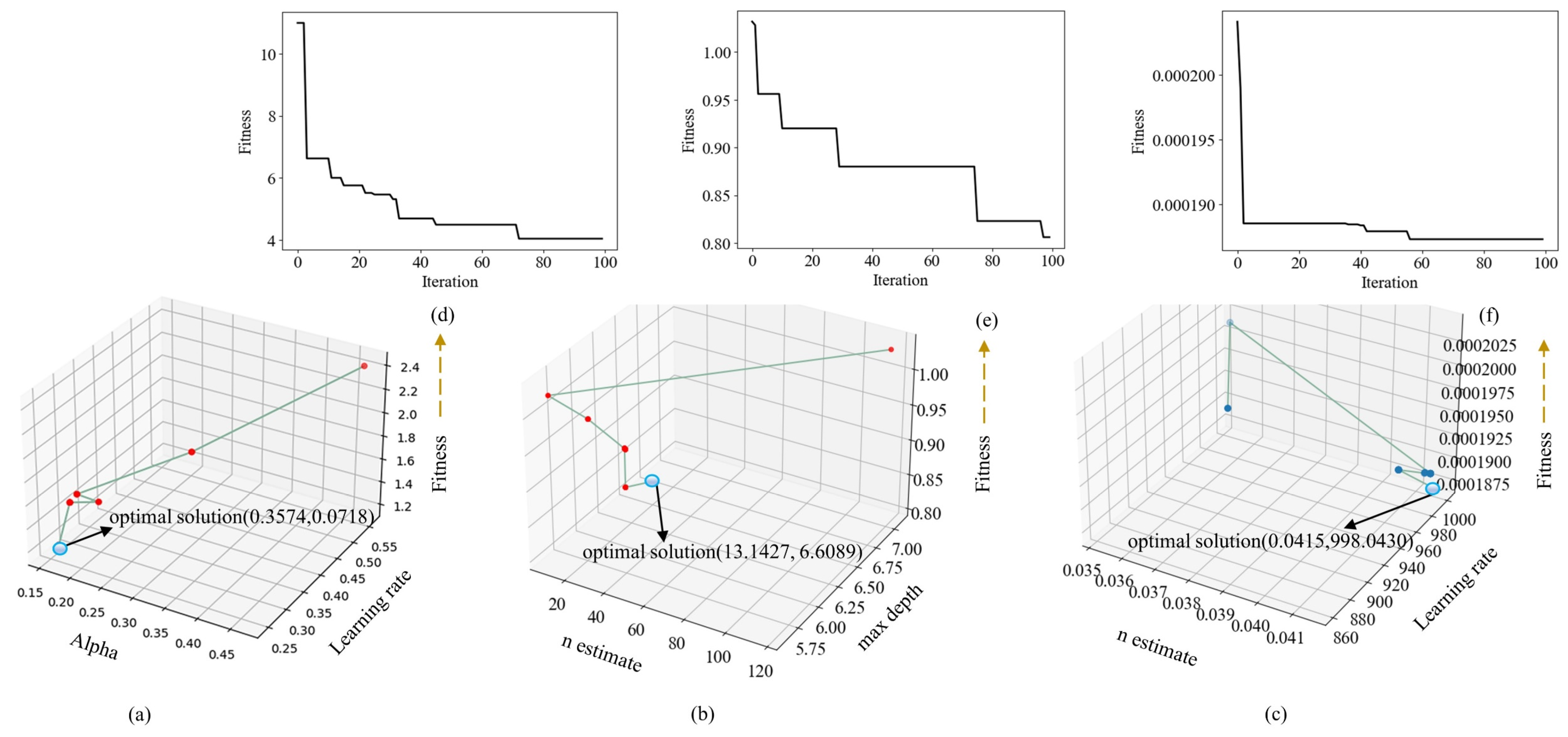
Figure 7 shows the optimization process for the three neural network models. Different colored bullets represent the optimal optimization nodes. Subfigure a represents the MLPRegressor neural network with optimized parameters (alpha, learning rate), yielding 0.3574 and 0.0718. Subfigure b corresponds to the random forest regressor with optimized parameters (n_estimators, max_depth), resulting in (13.1427, 6.6089). Subfigure c shows the XgbRegressor neural network with optimized parameters (n_estimators, learning rate) (0.0415, 998.0430). In subfigure d, the fitness value of MlpRegressor reaches below 4 and remains essentially unchanged in the last 20 iterations. In subfigure e, the fitness value of the random forest regressor drops below 0.80, and in subfigure f, the fitness value of xgbregressor reaches below 0.00019. Overall, the fitness iterations of the three subfigures have reached optimal values, indicating that the parameter selection is reasonable.
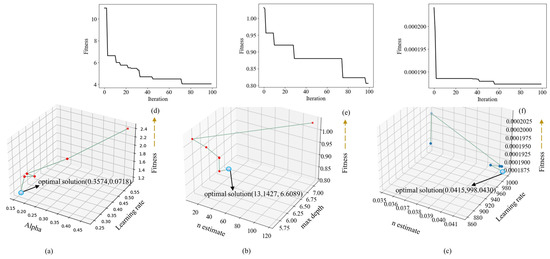
Figure 7.
Comparison of the optimization processes for the three algorithms.
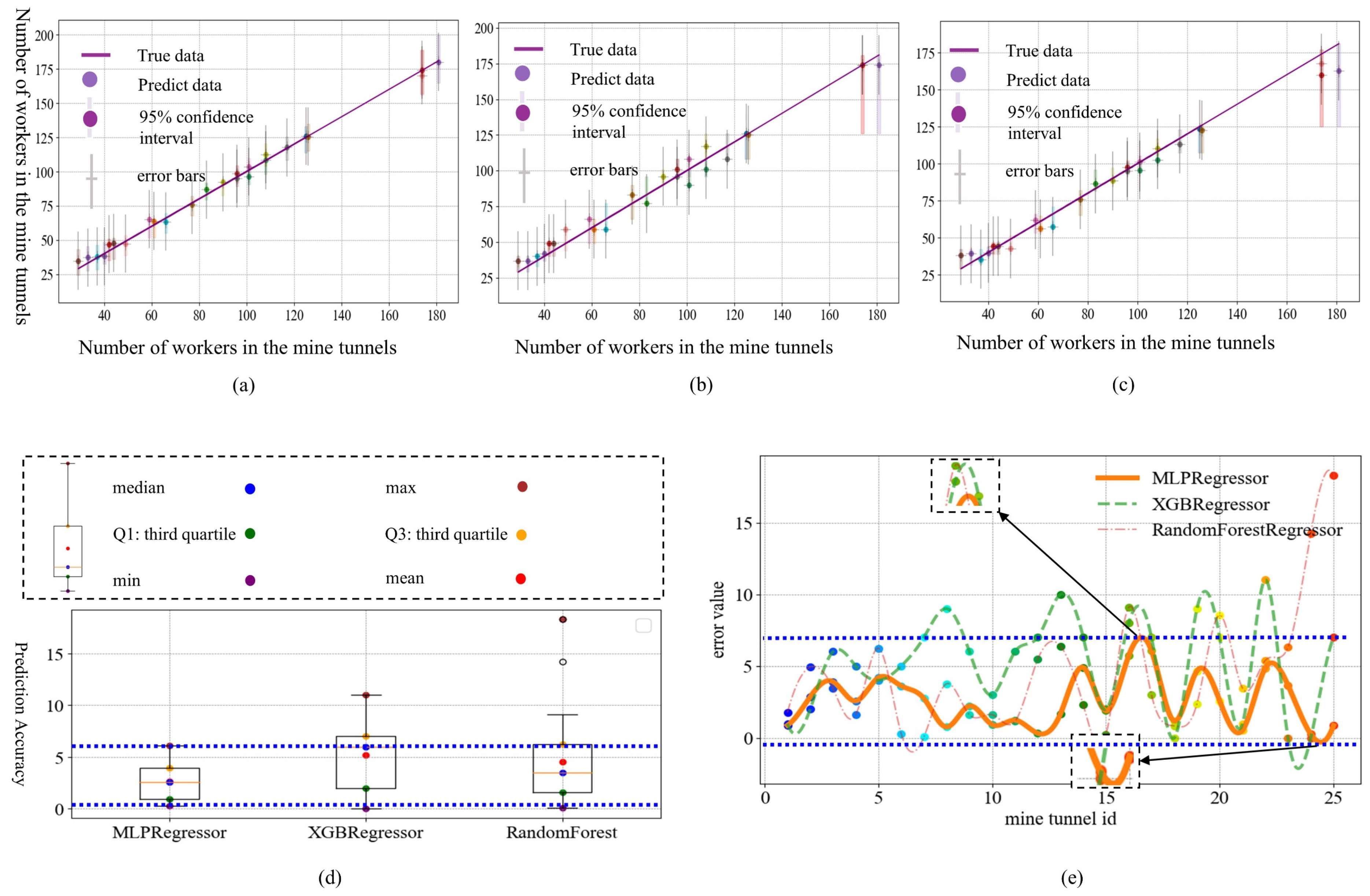
Following the optimization, the MLPRegressor, XgbRegressor, and RFR were used to predict personnel distribution, and the results are shown in Figure 7 and Table 7. In Figure 8, Panels a–c depict the prediction error plots for the three algorithms, with the 95% confidence intervals calculated using the BootStrap [23,28] algorithm. Each tunnel is represented by bullets of different colors. In Panel d, a boxplot analysis of the error plots for the three algorithms is presented. The blue interval represents the maximum and minimum ranges for the MLPRegressor, which exhibited the smallest prediction gap and the most uniform distribution, followed by those of the the XgbRegressor and RFR. Panel d corresponds to the values in Table 8. In Panel e, the yellow solid line represents the MLPRegressor, the green dashed line represents the XgbRegressor, and the orange dashed line represents the RFR. The middle region between the two blue dashed lines represents the maximum and minimum ranges for the MLPRegressor, with the differences for the other two algorithms being less than those for the MLPRegressor. Different colored bullets located above the yellow solid line represent the error nodes for MlpRegressor, those above the green dashed line represent the error nodes for XgbRegressor, and those above the orange dashed line represent the error nodes for RFR. In the upper subplot of subfigure e, MLPRegressor exhibits the smallest error value, while in the lower subplot of subfigure e, the error value for RFR remains higher than that of MLPRegressor.Table 8 clearly shows that the MLPRegressor has smaller maximum and minimum error values, and the Q1 and Q3 errors are also smaller than those of the other two algorithms. Therefore, the MLPRegressor is chosen for further study. An analysis of the prediction results for the three methods is provided in Table 7, where the MLPRegressor outperforms the others in terms of R2, MAE, MSE, RMSE, and other metrics. Considering these factors, the MLPRegressor is selected for prediction.

Table 7.
Analysis of the prediction effects of the different methods.
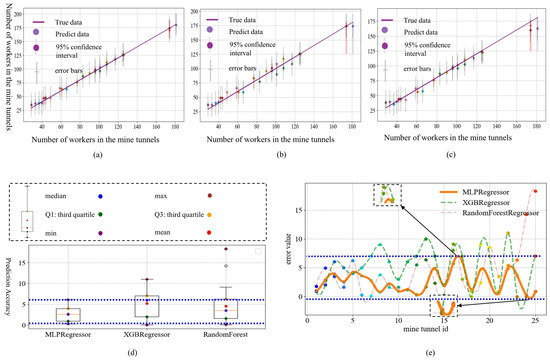
Figure 8.
Comparison of the optimization processes for the three algorithms.

Table 8.
Boxplot result distribution chart.
After predicting the average number of people in the tunnel by using the MLPRegressor in Table 9, the real-time flow speed is estimated based on the traffic flow three-parameter relationship [9,24] , where represents the crowd density, represents the walking speed of people, and represents the flow rate of people. Table 10 represents the estimated flow speed.

Table 9.
Results of different method predictions.

Table 10.
Estimated flow speed.
3.3. Real-Time Planning of Mine Evacuation Routes
Based on real-time updates from personnel location monitoring and sensor data at each moment, evacuation routes are replanned within the personnel’s current tunnel. Evacuation experiments are designed, and computer software is used to calculate personnel evacuation routes. In the simulated tunnels, the viable evacuation points include the intake air shaft and permanent refuge chambers. As personnel move underground, evacuation routes are dynamically planned in real time. The following figures depict the real-time evacuation route calculation results and the visualization of personnel evacuation routes when using the MSPFA algorithm.
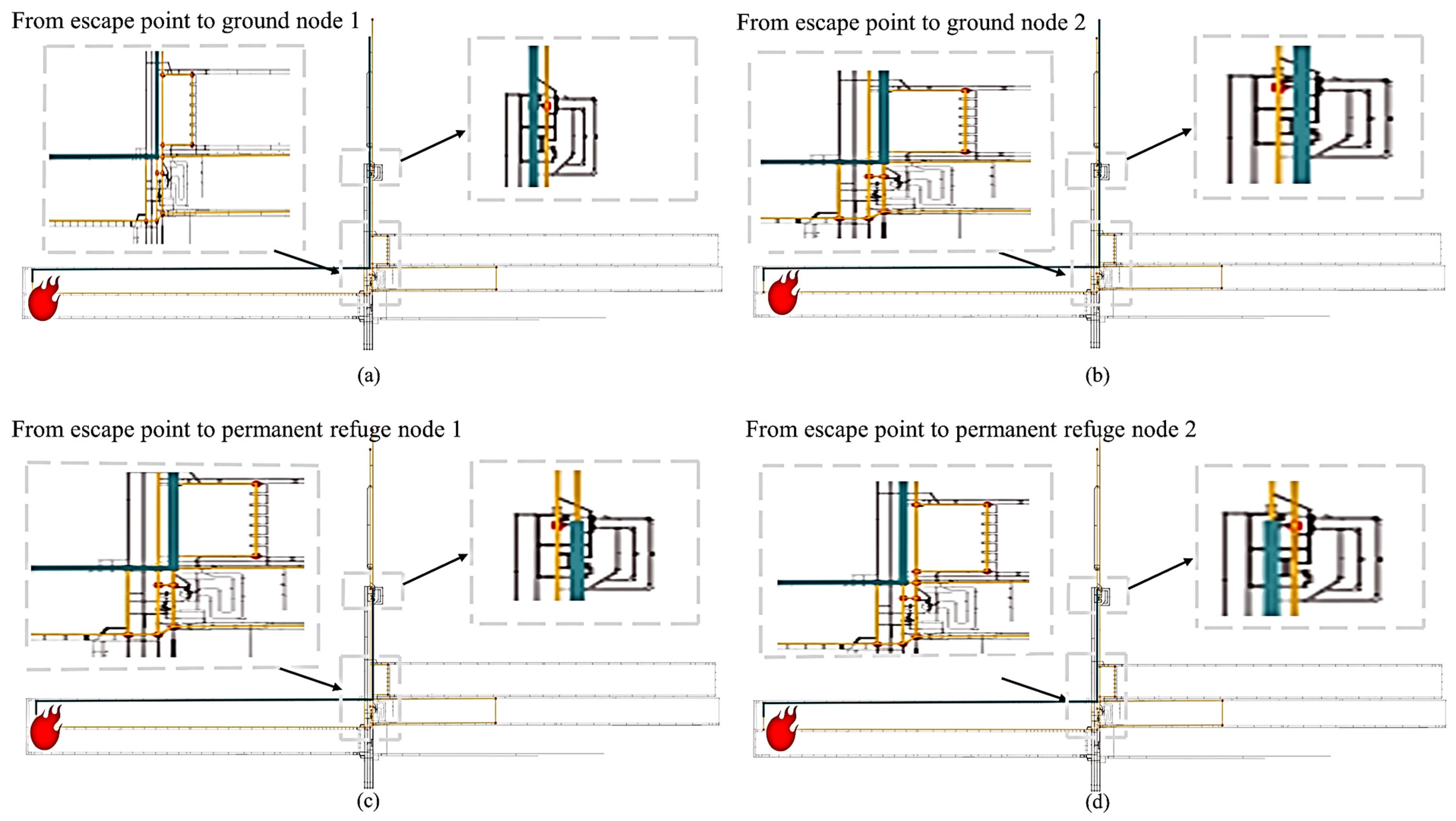
Table 11 shows the shortest distance table for evacuating to safe areas when a fire occurs on the workface where Node 1 is located. Figure 6 depicts the personnel evacuation route system in the mine, where paths (a), (b), (c), and (d) correspond to subfigures a, b, c, and d, respectively, in Figure 9. The evacuation endpoints include permanent refuge chambers and the surface. The computer automatically generated the graphics in Figure 9, providing better support for engineer decision analysis and evacuation path planning. In the figure, deep green indicates the evacuation route, while yellow represents the passable route in the absence of a fire. Subfigures a and b illustrate the minimum paths to different surface nodes, while c and d depict the minimum paths to different permanent refuge chambers.

Table 11.
Evacuation paths for personnel and target refuge areas.
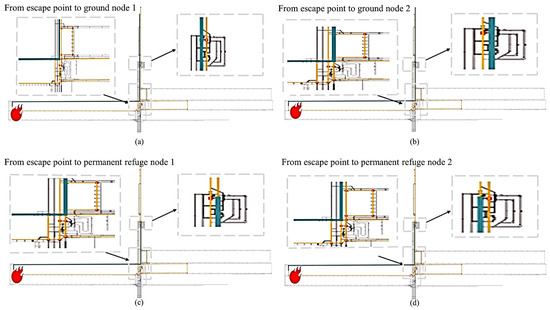
Figure 9.
A diagram of the evacuation route for mine tunnel personnel.
4. Results and Discussion
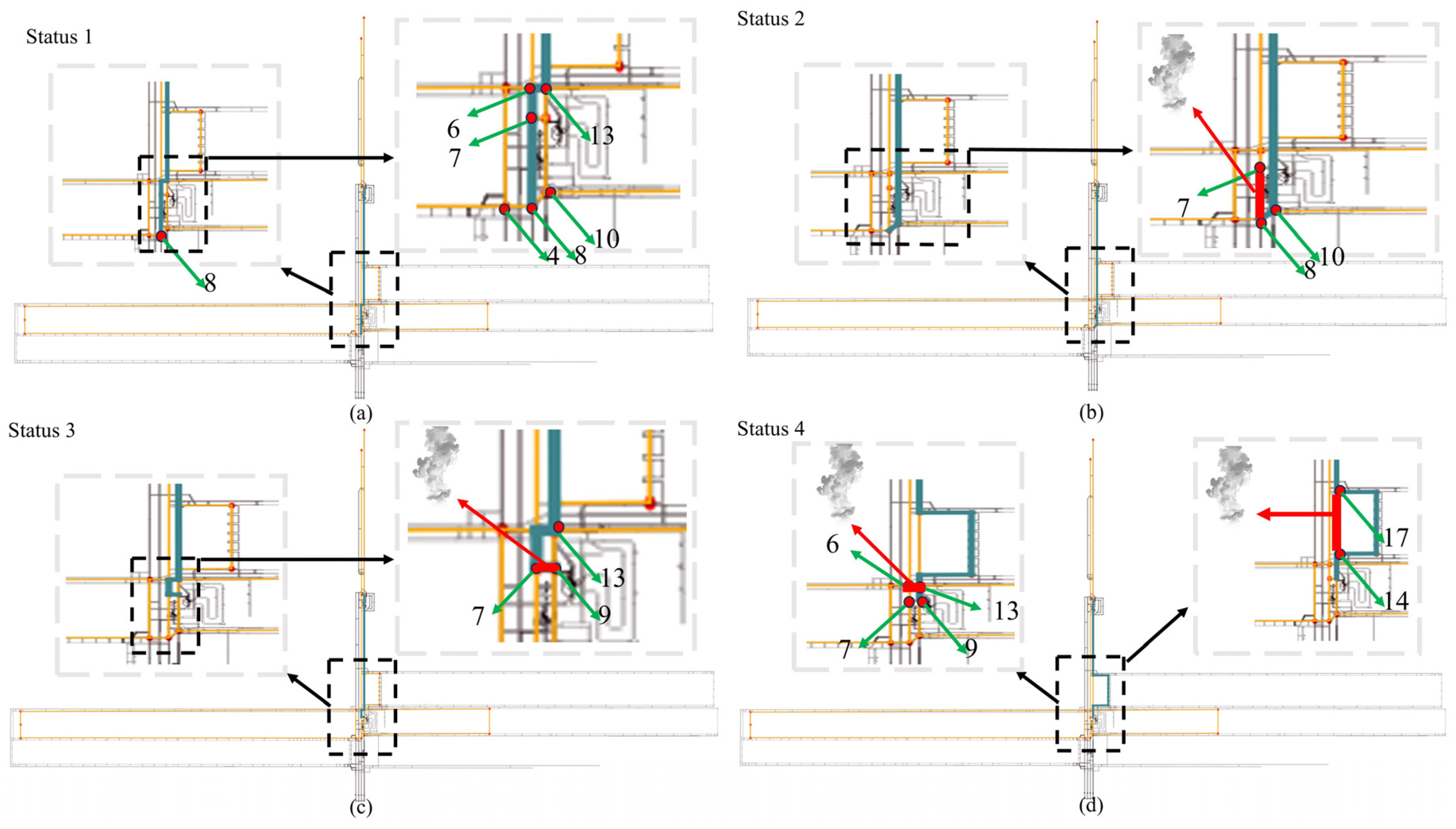
In this paper, an MSPFA algorithm based on the topological and system diagrams of a mine is described. By estimating personnel walking speeds and by receiving data from underground sensors, the algorithm understands the current location of personnel and dynamically plans escape routes in real time, effectively avoiding smoke-filled tunnels. In practical mining applications, the MSPFA algorithm adapts to changes during simulated mine fire smoke propagation. Table 12 and Figure 10 show the real-time planning results of the MSPFA algorithm under fire-smoke-propagation conditions. Table 12 presents an experiment of evacuation path planning for a simulated moment in which smoke continues to spread from point 8. Figure 10 shows the mine tunnel personnel evacuation route planning diagram, where dark green represents the evacuation route and yellow represents the passable route when there is no fire. The four plots depict real-time planning results for personnel evacuation paths under various scenarios of smoke propagation in different areas. In the subplot a, the planning path for the current time period is represented by blue lines, from node 8 to 6 to 13. As the smoke spreads from node 8 to 7, the route is adjusted in subplot b, where the red region in the subplot indicates an impassable area, while the blue area remains passable, leading from node 8 to 10. In subplot c, the subplot annotates the current passable area as the smoke spreads from node 9 to 7, represented by blue lines from node 7 to 13. Subplot d illustrates the passable area as smoke expands from node 6 to 13, 14, and 17. The red lines indicate impassable areas, including nodes 14 to 17 and the path from node 6 to 13, while the blue curves represent passable areas.

Table 12.
Evacuation paths of personnel in the context of smoke propagation.
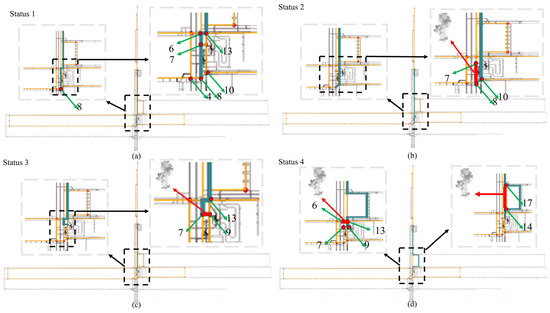
Figure 10.
Mine tunnel personnel evacuation route system diagram.
After the improved MSPFA algorithm was implemented, it was compared with the traditional Dijkstra algorithm. The path from node 8 to node 18 was selected, and the results are shown in Table 13.

Table 13.
Path planning results of different algorithms.
Table 13 shows that the personnel evacuation time for the MSPFA algorithm is 3344 s, while for the Dijkstra algorithm, the personnel evacuation time is 4291 s. Therefore, in terms of finding evacuation routes, the MSPFA algorithm outperformed the Dijkstra algorithm. In terms of algorithm efficiency, the MSPFA algorithm, with the initial parameters determined, had a runtime of 78.5 ms, while the Dijkstra algorithm had a runtime of 103.6 ms. The efficiency of the MSPFA algorithm is superior to that of the Dijkstra algorithm. Both algorithms successfully avoided contaminating airflows in their evacuation paths, indicating that the quality of the paths generated by both the MSPFA and Dijkstra algorithms was generally good. However, according to Figure 10 and Table 12, the MSPFA algorithm can adapt to different environments, can dynamically adjust to changes in the path, and exhibits real-time adaptability. This validates the feasibility of the algorithm under varying conditions.
5. Conclusions
In this study, experimental research on real-time evacuation route planning in the event of a mine fire was conducted by using computer experimental methods and algorithm design. The primary focus was on the development of a real-time evacuation-route-planning model based on a multifactor coupling analysis and the construction of the multilayer perceptron regressor shortest path faster algorithm (MSPFA) algorithm. The results of this study indicate the following:
- (1)
- A real-time evacuation-route-planning model based on a multifactor coupling analysis was proposed, and the MSPFA algorithm was constructed. This algorithm can real-time estimate personnel walking speeds, determine the direction of delayed propagation, and dynamically optimize paths based on the real-time location of underground personnel. The inclusion of real-time underground influence data in the multifactor coupling analysis model, combined with multiple data factors and a theoretical analysis, facilitated the development of a real-time equivalent length calculation method.
- (2)
- Compared to XgbRegressor and RFR, the MLPRegressor demonstrated more accurate personnel walking speed estimations. This superiority is evident in the box plots, confidence intervals, and R2, MAE, MSE, and RMSE values, where the MLPRegressor outperformed the other algorithms.
- (3)
- The MSPFA algorithm effectively avoids toxic and harmful gases in real-time mine evacuation routes. Additionally, the efficiency of the MSPFA algorithm in real-time mine evacuation route planning exceeds that of the Dijkstra algorithm, possibly due to the sparse graphical representation of mine tunnel networks.
Technical guidance for intelligent evacuation decision making in mines for reducing casualties in the event of a fire was provided in this study. Future research should include delving into the propagation trends of fires in various tunnel topologies, analysing the specific impacts of fire wind pressure and airflow reversal, proposing more rational indicators, and further advancing the development of intelligent mining.
Author Contributions
Conceptualization, Z.Y. and J.F.; methodology, Z.Q.; software, Z.Q.; validation, Z.Q., Y.H. and Y.W.; formal analysis, Y.C.; investigation, L.Z.; resources, J.Z.; data curation, Z.Q.; writing—original draft preparation, Z.Q.; writing—review and editing, Z.Y.; visualization, Y.H.; supervision, J.F.; project administration, Z.Y.; funding acquisition, J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Research and Development Program of Shaanxi Province, grant numbers 2020GY-139 and 2022GY-150.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data are not publicly available due to commercial confidentiality, as they contain information that could compromise the privacy of research participants.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gong, X.; Chang, X.; Jia, P. Optimization method for mine rescue path based on ant colony algorithm. Ind. Mine Autom. 2018, 44, 76–81. [Google Scholar]
- Fan, W.; Lu, C. Determination of Underground Mine Fire Optimal Path of Multi Rescue Teams by Swarm Intelligence Algorithm. Met. Mine 2014, 1, 133–136. [Google Scholar]
- Cheng, S.; Zhang, X.; Li, F. Application of K Shortest Path Algorithm in Avoiding from Mine Water Disaster. Met. Mine 2014, 1, 137–140. [Google Scholar]
- Liu, M.-J.; Zhu, X.-A.; Wang, Z.-G. Application Research of Mine Flood Escape Route Based on Bidirectional A* Algorithm. Coal Eng. 2019, 9, 42–47. [Google Scholar]
- Li, N.; Wu, Y.; Ye, H.; Wang, L.; Wang, Q.; Jia, M. Scheduling optimization of underground mine trackless transportation based on improved estimation of distribution algorithm. Expert Syst. Appl. 2023, 245, 123025. [Google Scholar] [CrossRef]
- Yu, D.; Yan, W. Research overview on underground escape path in coal mine. China Coal 2022, 48, 40–47. [Google Scholar]
- Liu, X.; Wang, Y. Study on route planing and 3D simulation of escape from mine fire. China Saf. Sci. J. 2017, 27, 26. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, F. Implementation of Improved DijkStra Algorithm for Choosing the best Escape Route in Mine’s Emergency Rescue. Ind. Mine Autom. 2008, 34, 13–15. [Google Scholar]
- Zhao, Z.; Zong, Y. A multi-path algorithm implemented with bidirectional search of mine water inrush hedge. J. China Univ. Min. Technol. 2015, 44, 590–596. [Google Scholar]
- Wang, J.; Wang, Y.; Zhang, L. Dynamic programming and release system of underground emergency escape route based on real-time data. China Coal 2015, 41, 67–71+83. [Google Scholar]
- Greuer, R.E. Mining Publication: Study of Mine Fires and Mine Ventilation: Part I, Computer Simulation of Ventilation Systems Under the Influence of Mine Fires. Engineering 1977. Available online: https://api.semanticscholar.org/CorpusID:134513630 (accessed on 15 December 2023).
- Han, C.; Nie, S.; Zhang, H.; Chen, C. Study on Highly Stable Biomass Gel Foam with Ultra-Strong Film-Forming Performance Based on the Double Network Structure to Inhibit Coal Spontaneous Combustion. Combust. Sci. Technol. 2023, 1–17. [Google Scholar] [CrossRef]
- Lundberg, D.J.; Kim, J.; Parviz, D.; Strano, M.S. Mitigation of ventilation air methane (VAM) using novel methanotrophic coating materials: A technical analysis. Environ. Res. Lett. 2023, 18, 114039. [Google Scholar] [CrossRef]
- Xu, Z. Analysis of underground gas spreading trend and dynamic planning method of disaster avoidance route. Inn. Mong. Coal Econ. 2017, 13, 128–129. [Google Scholar] [CrossRef]
- Xu, S.; Li, M.; Mao, S. Study on escape route algorithm with constraints during coal mine fire. Coal Sci. Technol. 2018, 46, 173–178+59. [Google Scholar]
- Huang, Y.; Liu, Y.; Zhang, L. Human Evacuation Model of Coal Mine Stope Disasters and Refuge Chamber Layout. Saf. Coal Mines 2017, 6, 112–115. [Google Scholar]
- Tong, X.; Yuan, S.; Fang, W. Classification and calculation of the best escape route of coal mine based on Dijkstra algorithm. Ind. Mine Autom. 2018, 44, 94–99. [Google Scholar]
- Khakzad, N. A methodology based on Dijkstra’s algorithm and mathematical programming for optimal evacuation in process plants in the event of major tank fires. Reliab. Eng. Syst. Saf. 2023, 236, 109291. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, L.; Wang, L. Mine shaft based on Dijkstra Research on search method of emergency disaster avoidance path. Min. Mach. 2014, 9, 133–138. [Google Scholar]
- Cai, M.; Zhu, X.; Liu, D. Mine water inrush rescue model based on optimized SPFA algorithm. Coal Geol. Explor. 2019, 47, 78–83. [Google Scholar]
- Bi, L.; Cui, J.; Lin, G. Construction and Realization of Optimal Mathematical Model of Mine Fire Escape Route. Gold Sci. Technol. 2017, 25, 104–109. [Google Scholar]
- Chen, R.-X. Analysis of Movement of Fire Smoke Flow and Determination of Route for Avoiding Disaster Based on Information Platform of 3DGIS Digital Mine. Ind. Mine Autom. 2012, 38, 45–51. [Google Scholar]
- Xu, X.; Keoh, S.L.; Seow, C.K. Towards Prediction of Bus Arrival Time using Multi-layer Perceptron (MLP) and MLP Regressor. In Proceedings of the 2023 8th International Conference on Business and Industrial Research (ICBIR), Bangkok, Thailand, 18–19 May 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Dehman, A.; Farooq, B. Capacity characteristics of long-term work zones on signalized intersection approaches. Transp. Res. Part A Policy Pract. 2023, 175, 103791. [Google Scholar] [CrossRef]
- Li, Y.; Gao, S.-J.; Hong, Y.-L. Underground Escaping Routes Based on Single-source Shortest Path Algorithm. Saf. Coal Mines 2013, 44, 191–193. [Google Scholar]
- Fu, E.; Tang, A. Selection of the best escape route during underground fire. Saf. Coal Mines 2006, 32–34. [Google Scholar]
- Shen, Y. Environmental Risk and Escape Route Optimization for Mine Fire Personnel. Master’s Dissertation, China University of Mining and Technology, Xuzhou, China, 2020. [Google Scholar]
- Jung, C.; Lee, Y.; Lee, J. Performance Evaluation of the Multiple Quantile Regression Model for Estimating Spatial Soil Moisture after Filtering Soil Moisture Outliers. Remote Sens. 2020, 12, 1678. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).