Abstract
Unmanned aerial vehicles (UAVs) equipped with RGB, multispectral, or thermal cameras have demonstrated their potential to provide high-resolution data before, during, and after wildfires and prescribed burns. Pre-burn point clouds generated through the photogrammetric processing of UAV images contain geometrical and spectral information of vegetation, while active fire imagery allows for deriving fire behavior metrics. This paper focuses on characterizing the relationship between the fire rate of spread (RoS) in prescribed burns and a set of independent geometrical, spectral, and neighborhood variables extracted from UAV-derived point clouds. For this purpose, different flights were performed before and during the prescribed burning in seven grasslands and open forest plots. Variables extracted from the point cloud were interpolated to a grid, which was sized according to the RoS semivariogram. Random Forest regressions were applied, obtaining up to 0.56 of R2 in the different plots studied. Geometric variables from the point clouds, such as planarity and the spectral normalized blue–red difference index (NBRDI), are related to fire RoS. In analyzing the results, the minimum value of the eigenentropy (Eigenentropy_MIN), the mean value of the planarity (Planarity_MEAN), and percentile 75 of the NBRDI (NBRDI_P75) obtained the highest feature importance. Plot-specific analyses unveiled distinct combinations of geometric and spectral features, although certain features, such as Planarity_MEAN and the mean value of the grid obtained from the standard deviation of the distance between points (Dist_std_MEAN), consistently held high importance across all plots. The relationships between pre-burning UAV data and fire RoS can complement meteorological and topographic variables, enhancing wildfire and prescribed burn models.
1. Introduction
Wildfires often have severe impacts on a wide range of valued assets, including natural ecosystems [1], wildlife [2], firefighters [3], and nearby communities [4]. The development of a wildfire depends on variables such as weather conditions (wind, rainfall, relative humidity, and temperature), fuel properties (structure, fuel moisture, and distribution), and site factors (soil moisture and topography) [5]. Of these, only fuels can be modified through management actions; the pattern and timing of ignition, fire suppression activities, or fuel treatments may all play a key role in influencing wildfire regimes [6]. In many parts of the world, the increasing risks and impacts of wildfires have led to a greater emphasis on proactive fuel and fire management approaches, such as fuel treatments or prescribed fires, to mitigate the negative effects of a wildfire [7]. In many cases, prescribed burning can be one of the most effective methods of fuel reduction [8]. Nevertheless, prescribed burning can be challenging, requiring prior knowledge of the regulations, an evaluation of the burning area, and the preparation of a burning technical plan [7,8]. This planning model relies on predicted fire behavior, which informs how the burn should be implemented (firing sequence) [8]. In this regard, one of the critical factors for the success and safety of these operations is the fire rate of spread (RoS) [9]. The RoS is therefore an essential metric for the useful modeling of prescribed burns and wildfires [10].
In recent decades, the scientific community has developed several models to predict the RoS of fires using different concepts and methodologies. These models are mainly based on biophysical variables (terrain fragmentation, vegetation type, topography, or meteorological variables) and fuel variables (fuel continuity, fuel amount, or fuel moisture) [11,12,13]. Therefore, fire modeling requires, in addition to knowledge of meteorological and topographic conditions, the characterization of fuels. In this context, the role of live and dead fuels plays an important role in inhibiting or promoting the spread of fire [14].
In recent years, Earth observation products have been increasingly applied to improve our understanding of wildfire occurrence, underlying drivers, and behavior [15,16]. Current applications include the use of coarse-scale MODIS multispectral satellite imagery to examine how live fuel moisture might affect ROS distributions [14]. Related work, also with coarse-scale data, have leveraged advances in machine learning techniques to examine phenology effects on fire occurrence [17]. More recently, Hodges and Lattimer developed a wildland fire spread model based on convolutional neural networks using the model of Rothermel and results from FARSITE as input [18]. Similarly, Khanmohammadi et al. applied machine learning methods to predict the RoS in grasslands using seven environmental variables (meteorological and biophysical) [19].
Wildland and prescribed firefighting operations have traditionally relied on manned aerial vehicles or ground crews for control, ignition, and suppression, with inherent risks to human life [3]. In recent years, unmanned aerial vehicles (UAVs) have been increasingly used to monitor, detect, and fight forest fires [3,16,20]. Rapid advances in electronics, computer science, and digital cameras have allowed UAV-based remote sensing systems to provide a promising substitute for conventional fire monitoring on all phases of a wildfire (pre-fire, active fire, and post-fire). The versatility of this equipment allows it to be equipped with cameras (RGB, thermal, multispectral, or hyperspectral) or LiDAR sensors while being able to meet critical spatial and spectral resolution requirements. The high spatial resolution of UAVs enables the identification of patterns and features that may remain imperceptible at lower resolutions [16]. This is achieved by capturing data from a closer distance from the object, in contrast to other platforms like satellites or airplanes, where such flexibility is either impossible or very costly. Currently, UAVs equipped with thermal cameras are widely adapted for tasks such as the identification of hotspots, the early detection of wildfires, monitoring fire behavior, or nighttime operations [3,20]. The use of thermal imaging cameras is being combined with conventional methods for data collection in wildfires, since variables such as the fire RoS that were traditionally measured visually by technicians can now be measured through thermal cameras equipped in UAVs [9]. UAVs allow the acquisition of coincident data on fuels (pre-burn) and fire behavior (active fire) with higher spatial and temporal resolution. UAVs can also be used to measure post-fire impacts [9].
The development of the use of UAVs has been accompanied by improvements in digital image processing techniques. Algorithms such as Structure from Motion (SfM) allow the extraction of point clouds, 3D objects, or orthophotos [21]. Point clouds derived from UAV-based digital aerial photogrammetry (UAV-DAP) provide 3D information, useful for the detection of differences in vertical structures (i.e., plant height, plant patterns, and leaf distribution). In addition to geometric information, UAV-DAP point clouds can contain spectral information extracted from the original pixel value [22]. Thus, from overlapping images, it is possible to obtain a spectral point cloud, which provides both geometric and spectral information of the analyzed environment [23,24]. The integration of spectral and geometric information in photogrammetric point clouds increases the diversity of variables and can improve classifications and segmentations compared to the exclusive use of orthophotography or traditional LiDAR data [25,26]. However, compared to LiDAR data, UAV-DAP is more sensitive to light conditions and does not have the same levels of accuracy and penetration capability [22]. In recent years, LiDAR sensors that combine RGB cameras to colorize clouds have become commercially available [27], combining the advantages of both technologies, but their price remains a constraint.
Based on these recent developments, it seems likely that the use of geometric and spectral information obtained from UAV-DAP point clouds could be useful for the improvement of current fire RoS prediction models. Accordingly, this study aimed to analyze the relationship between fire RoS and optical and geometric data obtained prior to prescribed burning. For this purpose, we explored the relationship between the observed fire RoS obtained during several prescribed burns (active fire) as the dependent variable and geometrical and spectral variables extracted from UAV-DAP point clouds prior to prescribed burning (pre-burn) as independent variables. Once the regression models were calculated, the most influential variables for predicting the fire rate of spread were studied. We hope that the outcomes of this study can contribute to improving the planning and execution of prescribed burns at fine scales, as well as enhancing wildfire modeling and understanding the relationships between fuel and fire behavior.
2. Materials and Methods
2.1. Study Sites
Our study focused on data collected from seven plots on prescribed burns at two study sites in western Montana (USA) and southern Oregon (Figure 1). The two plots were located at The Nature Conservancy’s Sycan Marsh Preserve (referred to as Sycan henceforth), and five plots in the University of Montana’s Lubrecht Experimental Forest (Lubrecht henceforth). Lubrecht’s study area plots range from 45 to 209 m2, while plot sizes in the Sycan study area were 2269 m2 for plot 1 and 4070 m2 for plot 2 (Table 1).
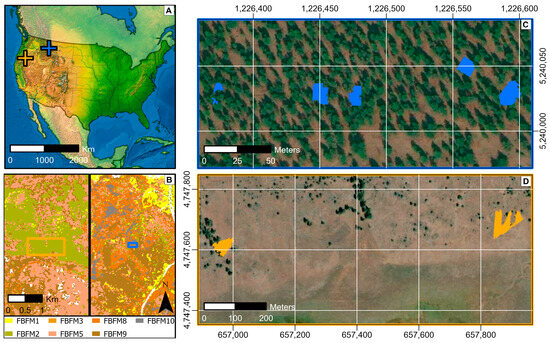
Figure 1.
Locations of the study areas in the northwest of the USA, visualizing Lubrecht’s plots with a blue cross and Sycan’s plots with an orange cross (A). Thirteen Anderson fire behavior fuel models (FBFM) of Sycan (left) and Lubrecht (right) (B). Areas where RoS was obtained in the five Lubrecht plots (C) and the two Sycan plots (D). The coordinate reference system was EPSG:32610 (C,D).

Table 1.
Description of the data acquisition conditions in the plots, specifically including the following: study area, plot number, plot dimensions, acquisition date, slope, weather conditions, ambient temperature, wind speed, and wind direction obtained from RTMA [28].
The Sycan Preserve is a 12,000 ha wetland located in the headwaters of the Klamath Basin in southern Oregon. The elevation of the plots located in this ecological site is around 1500 m with respect to the ellipsoidal WGS84 vertical datum, with an average annual temperature of 5.9 °C and an average annual rainfall of about 405 mm. On the other hand, Lubrecht is a forest of almost 9000 ha, located around 50 km northeast of Missoula, Montana, in the Blackfoot River drainage. The elevation of this study area is around 1280 m, with an average annual temperature of 5.3 °C and an average annual rainfall of about 430 mm. The similar climatic conditions in the two study areas allowed the development of a similar forest typology, dominated by Pinus ponderosa subsp. ponderosa Douglas ex C. Lawson (commonly called Columbia ponderosa pine) in the upper stratum and grass species in the lower stratum, mainly Pseudoroegneria spicata (Pursh) Á. Löve and Festuca idahoensis Elmer. Specifically, the Sycan study area is a grassland, dominated by grasses with a low presence of ponderosa pine and other shrubs, while the Lubrecht study area is an open forest, dominated by ponderosa pine in its upper stratum. The chosen plots represent a variety of western USA surface fuels that typically experience low- and mixed-severity fire.
2.2. Overview of the Methods
A general overview of the methodology is shown in Figure 2. The methodology is divided according to the data collection time (before or during prescribed burning) [8].
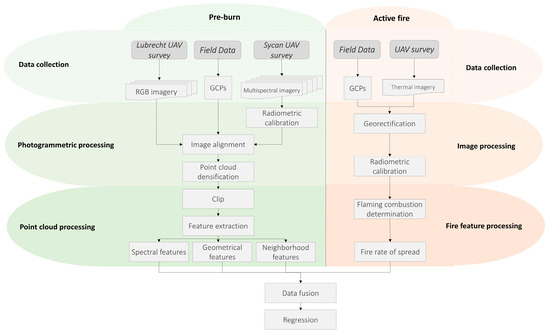
Figure 2.
Workflow of the proposed methodology. Abbreviations: UAV: unmanned aerial vehicle, GCPs: ground control points.
In the pre-burn phase, a UAV flight was performed using an RGB camera at the Lubrecht site and a multispectral camera at the Sycan study area. The objective was to compare the values of the RoS using different spectral, radiometric, and spatial resolution data. Before the UAV flights, eight ground control points (GCPs) per plot were placed, and their positions were measured using a GPS receiver. A photogrammetric process was carried out using Agisoft Metashape software version 1.7.1 (Agisoft, St. Petersburg, Russia) to obtain the point clouds of the study areas. This process involved four steps: the radiometric calibration of the multispectral images, the reconstruction of the flight scene through the alignment of the images, the point cloud densification, and then the extraction of spectral, geometric, and neighborhood variables from the point cloud. During prescribed burning, a static, hovering UAV flight with a thermal camera was flown to the center of each plot. To georeference these data, additional GCPs were placed. Next, the radiometric calibration and georectification of the images were carried out. Finally, flaming combustion was thresholded, and the fire RoS was derived in vector format. Only the most relevant steps in obtaining the fire RoS are explained here. Additional methodology can be found in Moran et al. [9]. The polygonal data representing the fire RoS were interpolated to a grid, sized according to their semivariogram range, and integrated with a set of variables derived from the pre-burn point cloud. Finally, a regression per plot was performed in which the dependent variable was the RoS and the independent variables were the spectral, geometric, and neighborhood variables obtained from the photogrammetric point cloud.
2.3. Plot Selection
Fieldwork was carried out in May 2017 in Lubrecht and in October 2018 in Sycan, performing an aerial data collection with an unmanned aerial vehicle (UAV). For this study, the methodology was tested at two different scales, so the plots of the Lubrecht and Sycan areas were of different sizes (Table 1). These areas were defined by the zones where the fire RoS values were obtained in the study conducted by Moran et al. [9]. The locations of these plots were chosen to minimize the occlusion of the tree canopy and on the basis of adequate surface fuel continuity.
2.4. Data Collection
A total of eight GCPs were placed in each plot. Initially, four points were placed in the corners of each square plot. The remaining four GCPs were then positioned in a smaller square, maintaining the same shape but with dimensions reduced to 1/3 of the original. Distances between GCPs were measured with measuring tape and a TruPulse 360°B laser rangefinder (Laser Technology Inc., Centennial, CO, USA). The accuracy of this rangefinder is ±0.2 m within a maximum range of 2000 m. Once the plot dimensions were measured, the GCPs were placed at the corners. Their coordinates were obtained using two GNSS receivers, Emlid Reach RS (Emlid Tech Kft., Budapest, Hungary), with an RTK setup. According to the manufacturer, this setup has a nominal accuracy of 7 mm + 1 ppm horizontally and 14 mm + 2 ppm vertically.
The data acquisition was different depending on the study area. At Sycan, multispectral and thermal data were collected. At Lubrecht, RGB and thermal data were collected. For the collection of multispectral (Sycan) and thermal (Sycan and Lubrecht) data, we used a DJI Matrice M100 UAV (SZ DJI Technology Co., Shenzhen, China). The M100 was equipped with a Micasense RedEdge camera (Micasense Inc., Seattle, WA, USA) for the multispectral pre-burning data acquisition at Sycan. This camera has five sensors with different bands: blue (475 nm), green (560 nm), red (668 nm), red edge (717 nm), and near infrared (840 nm). These five sensors (4.8 × 3.6 mm) have a resolution of 1.2 MP with a focal length fixed at 5.5 mm, a sensor pixel size of 3.75 μm, and a color depth of 16 bits. For the pre-burning collection of RGB data in Lubrecht, we used a DJI Phantom 4 (SZ DJI Technology Co., Shenzhen, China). The Phantom 4 has a built-in camera with a CMOS sensor (1/2.3″), a resolution of 12.4 MP, a focal length of 20 mm, and a color depth of 8 bits. Regarding the pre-burning flight plan, the two Sycan plots followed a cross-grid flight pattern with a nadir camera angle. The flight height was 180 m above the ground for plot 1 and 120 m for plot 2. On the five Lubrecht plots, a more detailed data acquisition was performed using the Phantom 4. A cross-grid flight pattern with a nadir camera angle was also performed in this shot, but an oblique perimeter shot was added, changing the camera angle to 15° off-nadir. This shot was taken at a height of 10 m above the ground.
Once these data were collected, the plots were burned using a drip torch to achieve a coherent and stable fire front, extending it perpendicularly to the plot edge and the expected spread direction. During the burning of the plots, the M100 was equipped with a DJI Zenmuse XT (SZ DJI Technology Co., Shenzhen, China), an uncooled VOx microbolometer sensor with a spectral range between 7.5 and 13 μm. This camera has a resolution of 0.3 MP with a focal length fixed at 9 mm, with a sensor pixel size of 17 μm. In this case, the UAV was positioned at the center of the plots at a fixed altitude above ground (18–20 m), and the temporal resolution was fixed at 5 s at Sycan and 1 ± 0.13 s at Lubrecht.
2.5. Photogrammetric and Thermal Image Processing
Photogrammetric processing was applied to RGB and multispectral images taken prior to prescribed burning. The workflow starts with a radiometric calibration of the multispectral images. Radiometric calibration compensates for sensor black level, sensor gain, exposure settings, sensor sensitivity, and lens vignette effects. This calibration was conducted using MicaSense’s algorithms [29]. The radiometrically calibrated images of Sycan were input into the software Agisoft Metashape, while the RGB images of Lubrecht’s plots were input into Pix4D version 4.3.27 (Pix4D SA, Prilly, Switzerland). The processes within both software are similar, with relatively consistent results in our experience, dependent more on image quality and GCPs than the algorithmic differences in the software. The photogrammetric processes in both software starts with identifying, matching, and monitoring the movement of common features between images using a custom algorithm [30] derived from the scale-invariant variable transform (SIFT) algorithm [31]. The next step is to determine the interior orientation parameters of the camera (focal length, main point, and lens distortion) and the exterior orientation parameters (projection center, coordinates, and rotation angles around the three axes), subsequently improving their positions with a bundle-adjustment algorithm [30]. This process is a particular optimization of the SfM algorithm [32]. The GCPs collected in the field were used in this phase to improve the orientation of the images, as well as to scale the photogrammetric block and provide it with absolute coordinates. These processes were carried out in Agisoft by setting the alignment process to “Highest”, while in Pix4D, the “Keypoints image scale” option was set to “Full”. During this process, the 3D coordinates of the features extracted in the first processing step were obtained, creating a point cloud commonly referred to as a tie point cloud. Finally, once we obtained the final position and orientation of the images, a pair-wise depth map computation was performed [30] using the tie point cloud to generate an approximate digital terrain model from which new points were obtained, creating a dense point cloud. This process was set to “Ultra high” in Agisoft and “High” in Pix4D.
For the active fire thermal imagery obtained from the Zenmuse XT sensor, processing followed the methods described by Moran et al. [9]. Fire and tree occlusion caused variable strategies for image stabilization and rectification. The lower altitudes for the Lubrecht plots meant GCPs could be used in nearly all cases to georectify and stabilize in one step. For the Sycan plots, GCP visibility was inconsistent and necessitated video stabilization techniques and a georectification of the image stacks rather than individual images. For this purpose, the warp stabilizer algorithm included in Adobe After Effects (Adobe Inc., San Jose, CA, USA) was applied to stabilize the images. For the radiometric calibration of thermal images, proprietary software was used to calculate the radiant temperature utilizing factory calibrations and verification with black-body emitters in laboratory settings. The software was parameterized with an emissivity constant at 0.98, entering average values of ambient temperature and relative humidity taken during data capture.
2.6. Fire Variable Processing
Once the images were georectified and radiometric calibration was applied, the flaming combustion was determined. For this purpose, temperature thresholding and edge detection techniques were combined. First, edge detection following Canny’s method [33] was applied to each thermal image. This method identified the flaming front, transient flames, and pre-frontal heat. Then, pixel values along the defined edge of the flame front were extracted, and a two-class k-means clustering was applied to determine the flaming combustion threshold automatically [34].
A vector-based approach was applied to obtain the fire RoS, which relied on pairing points defined as fire lead or fire back edge. This approach first calculated the progression of the fire breakthrough polygons, and then, these polygons were enhanced based on the focal points, lead edge points, and back edge points (Figure 3A). Once the RoS estimates were derived, the thermal pixels were aggregated to analytical units (polygons) based on the method described in Moran et al. [9].
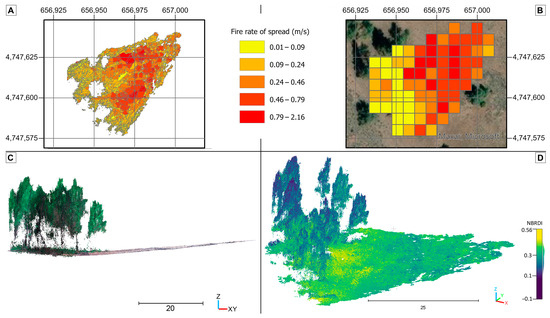
Figure 3.
Visualization of Sycan plot 2: 2D vector information of fire rate of spread (RoS) polygons, EPSG:32610 (A). RoS polygons interpolated to a 7 m grid (B), EPSG:32610. Side view of the RGB 3D point cloud (C). 3D point cloud visualizing the normalized blue–red difference index (NBRDI) (D).
2.7. Point Cloud Processing
The clouds were clipped within the area of each plot where the fire RoS was calculated, and variables were subsequently extracted from the point clouds. These variables were divided into geometric, spectral, and neighborhood variables. Neighborhood variables were further divided into neighborhood spectral and geometric variables, calculated at point level.
From the Lubrecht RGB point clouds, a total of 16 spectral variables were obtained, the blue, green, and red band values, together with the spectral indices described in Table 2. From the Sycan multispectral point clouds, 27 spectral variables were calculated, which were the values of the blue, green, red, RedEdge, and NIR bands, along with the spectral indices listed in Table 2.

Table 2.
Spectrum (RGB or multispectral (MS)), name, description, equation, and references of the spectral neighborhood variables.
The neighborhood of a point was defined as p ∈ R3, with R3 being the set of points inside a sphere s, of center p, and a radius of 0.10 m for Sycan plots and 0.01 m for Lubrecht plots. The different radius chosen in each study area was due to the different point densities. Two neighborhood spectral indices were calculated for each point cloud. If the point cloud was RGB, the mean and standard deviation of the NGRDI of the neighborhood of each point were obtained. In the case of multispectral clouds, the mean and standard deviation of the NDVI were calculated. The latter vegetation index was chosen due to its relationship with fuel moisture content [60].
The same geometric variables were obtained for the RGB and multispectral point clouds, since the geometric information of the point cloud is independent of the type of spectral information that it contains. These neighborhood geometric variables are described in Table 3. Therefore, a total of 44 variables were obtained from Sycan multispectral clouds and 34 variables from Lubrecht RGB clouds.

Table 3.
Name, description, and equation of the geometrical neighborhood variables, where Sp is the set of points in a neighborhood.
2.8. Data Fusion and Regression
Once the point cloud variables and the fire RoS vector polygons were obtained (Figure 3A), we performed a spatial interpolation, homogeneously distributing the variables on a grid to sample the data spatially. Semivariograms of the RoS polygons were computed to determine the appropriate grid scale [61]. In considering the centroid of each RoS polygon, a semivariogram for the centroids of the RoS was calculated, fitting it to three different curve models (Gaussian, exponential, and stable) [62]. These models provide additional information on the scale of the spatial correlation and assist in the selection of the optimum grid size. The model (Gaussian, exponential, or stable) was selected based on the root mean square error (RMSE) (3) of the fitted curve. The optimum grid size was selected based on the adjusted semivariogram range of each model. After selecting the grid size for each plot, an interpolation of the RoS polygons was performed, assigning the interpolated value to the grid (Figure 3B). The point cloud analysis yielded a comprehensive set of grid metrics, including the maximum, minimum, mean, and the 25th, 50th, 75th, and 90th percentiles. Specifically, 294 variables were derived from the Sycan multispectral plots, which is an increase from the initial 44 variables calculated from these multispectral clouds. Similarly, the analysis of the Lubrecht RGB plots resulted in 224 variables obtained from the original 34 variables calculated from the RGB clouds. This process was carried out using an ad hoc algorithm written in the Python programming language, using the pandas [63] and geopandas [64] libraries.
After the extraction of variables, a dimensional reduction process was carried out by applying univariate linear regression models and screening the variables using the F and p-values. Through dimensional reduction, the number of variables was reduced to 50 per plot. The regression process was carried out using Random Forest (RF) [65], implemented using the Python Sci-kit library [66]. The RF regression algorithm is an ensemble learning method that fits several decision trees on subsamples of the input dataset, averaging them to improve the predictive accuracy and control overfitting [65,66,67]. The dataset was randomly split to obtain 80% of training samples and 20% of testing samples. To obtain a better model fit, a hyperparameter optimization was performed for the following parameters: number of trees in the forest (200 or 500), number of variables to consider when looking for the best split (“auto”, “sqrt” or “log2”), and maximum tree depth (5, 10, or “None”). The accuracy of each combination of hyperparameters was assessed using cross-validation with 10 folds. The chosen hyperparameters for each method were those with the highest mean cross-validated score. To evaluate the accuracy of the regression, the coefficient of determination (R2), mean absolute error (MAE), and RMSE were calculated:
where n is the number of observations; yi is the value of the fire RoS of observation i; is the fire RoS value approximated through the model regression of observation i; is the mean of the fire RoS observations; ymax is the maximum value of the fire RoS in all the observations; and ymin is the minimum value of the fire ROS in all the observations.
3. Results
3.1. Photogrammetric Point Cloud Processing
Seven point clouds were obtained during the photogrammetric process, one per plot. Due to the different cameras and flight plans used, point clouds with different characteristics were obtained depending on the study area (Table 4). Thus, the Sycan multispectral point clouds had an average of 29,878,242 points, while that of the Lubrecht clouds was 242,800,056 points. The plot dimensions, camera model, and flight height were the main parameters affecting the number of points per cloud. The average point cloud density in Sycan was 354.17 points·m−2, and in Lubrecht, it was 737,066.62 points·m−2.

Table 4.
Study area, plot number, flight pattern, camera, flight height (m), total points, density (points·m−2), and number of points after the clipping of the point clouds processed.
3.2. Grid Size Determination
From the derived RoS polygons, the fire RoS varied between 0 and 2.7 m·s−1 at the two Sycan plots, while it ranged from 0 to 0.1 m·s−1 at the Lubrecht plots. Figure 4 shows the semivariograms obtained from the Sycan plots. In plot 1, the curve with the best fit was obtained with the stable model (semivariogram RMSE, 0.10), obtaining a range of 1.47 m. Plot 2 obtained a better fit with the Gaussian model (semivariogram RMSE, 0.07) with a range of 7.34 m. Finally, plots 1 and 2 combined obtained a better fit using the Gaussian model (semivariogram RMSE, 0.08) with a range of 6.64 m. The range value was rounded to integers for all plots. The range value obtained for all Lubrecht plots was 1 m.
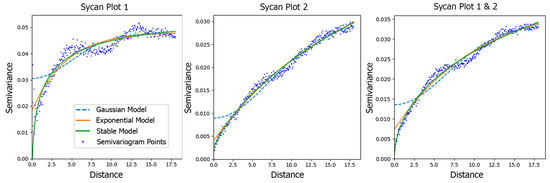
Figure 4.
Semivariograms of the fire rate of spread from Sycan plots 1, 2, and 1 and 2 combined with the curves fitted to the Gaussian, exponential, and stable models.
3.3. Fire Rate of Spread Regression
Table 5 shows the hyperparameters used in the regression model that generated the highest coefficient of determination. The most repeated combination of hyperparameters were the maximum number of variables in auto, 500 decision trees (estimators), and no limit on the tree depth for the Sycan plots and the maximum number of variables in auto, the number of estimators being 200, and the maximum tree depth set to 10 for the Lubrecht plots. The models obtained a range of R2 between 0.56 (combined plots 1 and 2 of Sycan) and −0.23 (plot 4 of Lubrecht). Analyzing the results by study area, we can see that the most significant determination coefficients were obtained from the Sycan plots, highlighting plot 2 (R2 = 0.48) and the combination of plots 1 and 2 (R2 = 0.56). For these plots, low values of MAE and RMSE were obtained, considering the range of fire advance velocities detected (between 0.01 and 2.70 m·s−1). Similarly, in the Lubrecht plots, low values of MAE and RMSE were also obtained, being the values obtained close to the arithmetic mean of the velocities detected during the prescribed burning. Despite the statistics of the Lubrecht plots, negative or very low values of R2 suggest that the predictions made by the models are close to random, tending to be around the mean of the observations.

Table 5.
Study area, plot, fire RoS range, and grid size hyperparameters used in the RoS regression model that obtained the highest coefficient of determination (R2), mean absolute error (MAE), and root mean square error (RMSE).
3.4. Feature Importance and Performance of the Models
To determine the variables providing the most information to the models, we computed the importance of the permutation obtained for each variable in each plot [65]. Figure 5 shows that the variables with the highest importance of the normalized permutation across all plots were mainly 13: Eigenentropy_MIN, Planarity_MEAN, NBRDI_P75, Dist_std_MEAN, Dist_std_MAX, Anisotropy_MEAN, NGBDI_P50, SARVI_MIN, Omnivariance_MEAN, ARVI_MIN, NGBDI_P25, Verticality_P90, and Planarity_MIN, repeating the point cloud neighborhood variables Dist_std and Planarity twice. Conducting a separate analysis for each plot revealed that the model associated with plot 2 employs a more extensive combination of geometric and spectral variables than the other models. Conversely, the model combining information from plots 1 and 2 had a lower number of variables, indicating more efficient modeling using a smaller set of features. In this study area, which achieved the highest R2 (0.56), we found eight geometric neighborhood variables (Eigenentropy_MIN, Planarity_MEAN, Dist_std_MEAN, Dist_std_MAX, Anisotropy_MEAN, Omnivariance_MEAN, Verticality_P90, and Planarity_MIN) and five spectral variables (NBRDI_P75, NGBDI_P50, SARVI_MIN, ARVI_MIN, and NGBDI_P25) with a normalized permutation importance greater than 0.05. From these variables, several were used independently of the plot, such as Planarity_MEAN (used in plots 1, 2, and 1 and 2 combined), Dist_std_MEAN (used in plots 1 and 1 and 2 combined), Dist_std_MAX (plots 1 and 2) and Planarity_MIN (plots 1 and 2). The variables extracted from the point cloud that were most frequently repeated were the eigenentropy (MAX, MEAN, MIN, P25, P50, and P90), linearity (MAX, MEAN, P25, P50, P75, and P90), planarity (MEAN, MIN, P25, P50, P75, P90), and NBRDI variables (MEAN, P25, P50, P75).

Figure 5.
Permutation variable importance for the models obtained from Sycan plots 1, 2, and 1 and 2 combined. The permutation importance was normalized for each plot by assigning a value of one to the sum of the permutation importance of all variables.
The performances of the models can be analyzed in Figure 6, which plots the predicted versus observed results of the Sycan plots. In these graphs, the number of samples varies depending on the plot due to the use of a different grid size in plot 1 (1 m), compared to plots 1, and 1 and 2 combined, where the grid size was 7 m. No graph shows outliers in the prediction, obtaining close results to the line of perfect agreement. Figure 6 shows the learning curves of the plots, after calculating the R2 obtained for the models by adding each of the variables analyzed. Features were entered into the model based on their permutation importance. The plot 2 curve stabilizes using eight variables, obtaining an R2 of 0.31. In the case of plots 1 and 2 combined, the learning curve stabilizes when using 10 variables, obtaining an R2 of 0.41.
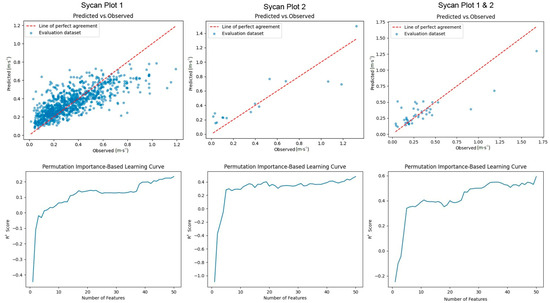
Figure 6.
Predicted vs. observed plots of regression models of Sycan field plots 1, with a grid size of 1 m (top left); 2, with a grid size of 7 m (top middle); and 1 and 2 combined, with a grid size of 7 m (top right), showing the results for the test (evaluation) datasets. Learning curves of Sycan plots 1 (bottom left), 2 (bottom middle), and 1 and 2 combined (bottom right), showing the evolution of the coefficient of determination score (R2) as new features were added.
3.5. Result Summary
In summarizing the results, photogrammetric processes were applied to obtain seven point clouds. Each one corresponds to a specific plot in two study areas, with variations in camera characteristics and flight plans (Table 4). Plot dimensions (mean size of 128 m2 in Lubrecht and 3169.67 m2 in Sycan) and flight height (10 m in Lubrecht and 120–180 m in Sycan) significantly influenced the number of points obtained in each cloud (mean ≈ 242.8 M in Lubrecht plots and mean ≈ 29.88 M in Sycan). Camera characteristics (RGB in Lubrecht and multispectral in Sycan) caused a difference in the number of RoS-related features (224 in Lubrecht and 294 in Sycan). The fire RoS polygons were adjusted to a grid based on the range parameter of their semivariogram, obtaining a grid size in all plots of 1 m, except in plot 2 and plots 1 and 2 combined of Sycan, where the grid size was 7 m (Table 5). The R2 values for the RoS models ranged from 0.24 to 0.56 in Sycan and −0.23 to 0.15 in Lubrecht. The features with the highest normalized permutation importance in the three models of Sycan were Eigenentropy_MIN, Planarity_MEAN, and NBRDI_P75 (Figure 5). Plot-specific analyses unveiled distinct combinations of geometric and spectral features, although certain features, such as Planarity_MEAN and Dist_std_MEAN, consistently held high importance across all plots, proving relevant for all regression models. The training curves of the models (Figure 6) show how the regression models stabilized after incorporating ten variables, achieving an R2 of 0.34 in plot 2 and 0.41 in the combination of plots 1 and 2.
4. Discussion
The use of new technologies in fire modeling allows us to obtain fine-scale features, helping to obtain more accurate predictions of fire behavior. Rapid advances in computational, sensing, and processing techniques require new studies to help in processing and interpreting the increased amount of available data at finer scales. This study analyzed pre-burning fine-scale UAV-DAP data to predict fire RoS. The primary objective was to establish relationships between the fire RoS and features derived from point clouds.
4.1. RoS Spatial Correlation
Geometric, spectral, and spatial neighborhood metrics at fine scales extracted from the point cloud were interpolated to a grid for which its size was determined using the semivariogram of the fire RoS variable (Figure 4). Data availability influences the precision of spatial variability representation; therefore, semivariograms may exhibit distinct curves based on the mathematical models they fit [61]. Specifically, the Gaussian model assumes a smooth and continuous spatial process, while the stable model accommodates heavy-tailed distributions and significant skewness, making it more robust to outliers. In practice, semivariograms from different plots exemplify this variability: Sycan plot 1, with fewer data points, obtained a better fit to the stable model, resulting in a range of 1 m. A low range indicates that spatial correlation between data points diminishes rapidly with distance. In contrast, plot 2 and the combined plots exhibit a better fit with the Gaussian model, suggesting a smoother spatial process due to potentially larger datasets, resulting in a range of 7 m. Conversely, a high range indicates that spatial correlation between data points extends over longer distances. Thus, the choice of model and observed range in the semivariogram reflect the interplay between data availability and spatial correlation characteristics.
4.2. Data Acquisition and Model Generation
Different spectral, radiometric, and spatial resolution data were utilized from the two test sites, including RGB and multispectral data, and 8-bit and 16-bit radiometric resolution images for Lubrecht and Sycan, respectively. In the tests carried out, promising results were obtained for the Sycan plots, whereas inconsistent outcomes were found for the Lubrecht plots. Weather conditions were almost constant during the prescribed burns in both study areas, and the wind speed was very low (Table 1), which does not explain the different results obtained. The different results obtained can be explained as follows:
- Plots size. The plots have a total area of 6339.35 m2 in Sycan and 641.18 m2 in Lubrecht. The lack of model training data (means of 112 samples from the Lubrecht plots vs. 2810 samples from the Sycan plots) reduces the capacity of the models. This fact was observed in the Sycan plots, where the combination of the data from the two plots with a 7 m grid obtained the best fit.
- Plot characteristics. The different characteristics of the study areas (grasslands in Sycan and open forest in Lubrecht) may have affected the correct modeling of the RoS. In Lubrecht, we found less fuel type variability within the plots, while in Sycan, we found higher variability. This higher variability is related to the different RoS velocities detected in the plots. At Sycan, mean velocities of 0.18 m·s−1 and peak velocities of 2.7 m·s−1 were reached, while in the Lubrecht plots, mean velocities of 0.01 m·s−1 and maximum velocities of 0.139 m·s−1 were obtained.
- Spatial and spectral resolution. The different scales of the data collection at Lubrecht (very fine scale), with a flight height of 10 m, and Sycan (fine scale), with a flight height of 180 (plot 1) and 120 m (plot 2), may have affected the results obtained. The higher spatial resolution of Lubrecht did not imply an improvement of the results, so a significant increase in the spatial resolution does not necessarily improve the RoS prediction models. On the other hand, the difference in spectral resolution between the captures with an RGB camera and a multispectral camera does not seem to have affected the results, since the spectral features with the greatest permutation importance can be obtained with both cameras (e.g., the NBRDI, which only needs information from the blue and red bands).
4.3. Importance of the Features
The extraction of metrics from the UAV-DAP point cloud allowed us to estimate the fuel from geometric, spectral, and spatial neighborhood metrics at fine scales. The results obtained for the Sycan models reveal the remarkable potential of the structure and greenness of the vegetation, as defined through UAV-DAP-derived geometric and spectral metrics, to explain RoS variability.
Spectral variables allowed us to record and identify the status of the fuel (greenness), providing information to the model of the vegetation through vegetation indices. The positive results observed for Sycan stem from the execution of more extensive prescribed burns, which allowed for greater heterogeneity in both fuel composition and fire propagation velocities. This fuel heterogeneity has been key to modeling fire RoS behavior. In this sense, Figure 3A,D show the inverse relationship between fire RoS and vegetation indices, such as NBRDI. Relating the NBRDI values of grass cover (Figure 3D) to surface fire (Figure 3A), we found that higher NBRDI values were associated with live fuels, explaining why they have a lower RoS value. Conversely, herbaceous areas with lower NBRDI values were related to higher RoS. These results are in accordance with previous studies in which MODIS images were used, demonstrating the capability of spectral variables to predict the RoS using the perpendicular moisture index (PMI). They found that the RoS shows significant decreasing trends with an increasing PMI [14]. Despite the notable difference in scale with respect to our study (the pixel size of MODIS is 500 m), the inverse relationship between the fire RoS and vegetation indices has the same behavior.
The results obtained underscore the importance of the geometric variables such as the planarity, which obtained the greatest permutation importance in the models. These geometric variables capture the landscape’s spatial arrangement and distribution, including topographical features and the structure of vegetation. The inclusion of such geometric variables enhances the predictive accuracy of RoS models by accounting for the heterogeneity of the landscape and its influence on the behavior of wildfires. Regarding geometric and spatial neighborhood metrics, to the best of the authors’ knowledge, this is one of the first investigations to study the relationship between variables extracted from the spatial distribution of points in a point cloud (LiDAR or photogrammetric) with the fire RoS.
The results suggest the potential of variables derived from UAV-DAP to understand fire behavior. Nevertheless, the use of UAV-DAP variables alone cannot fully explain the fire RoS, but they provide relevant information that can complement meteorological, topographical, and biophysical data. The findings of this study provide promising insights toward understanding the relationships between fuel and fire behavior at fine scales. This information may contribute to planning and implementing safer and more effective prescribed burns.
4.4. Model Comparison
The complexity of fire behavior makes it challenging to model. Pioneer models such as the Mk 3/4 Grassland Fire Danger Meter [13] obtained a MAE of 1.58 m·s−1, within a RoS ranging from 0.01 to 9.3 m·s−1, resulting in a MAE% of 17.01% in the estimation of RoS in 187 Australian fires [10]. The RoS error of the Mk 5 Grassland Fire Danger Meter [68] and the CSIRO Grassland Fire Spread Model [69] have also been measured with the same wildfire dataset, resulting in MAEs of 0.64 m·s−1 and 0.95 m·s−1 and MAE%s of 6.89% and 10.23%, respectively. American models, such as the one published by Rothermel in 1972 [12], obtained a MAE of 0.22 m·s−1 in grasslands, within a RoS ranging from 0.06 to 0.5 m·s−1, resulting in a MAE% of 50%. More recently, Anderson et al. [70] published a model for temperate shrublands, obtaining a MAE of 0.15 m·s−1 ranging from 0.08 to 1.67 m·s−1, yielding a MAE% of 9.43%. Khanmohammadi et al. [19] obtained a MAE of 0.65 m·s−1 using a Gaussian support vector machine (SVM) for regression in 238 grassland wildfires, with a RoS range from 0.14 to 4.72 m·s−1, yielding a MAE% of 14.19%. Comparing with the results obtained in this study, specifically from the combination of Sycan plots 1 and 2, we obtained a MAE of 0.16 m·s−1, with a RoS range between 0.01 m·s−1 and 2.70 m·s−1, which results in a MAE% of 6.02%. These statistics are consistent with the results previously obtained by other authors.
4.5. Key Findings
In this study, we focused solely on the variables obtained from the UAV-DAP point cloud, excluding the consideration of other factors, including meteorological variables, that play a fundamental role in the fire RoS [71]. Our objective was to provide a unique, fine-scale perspective on fuels that could complement models relying on meteorological variables in future work. Geometric variables are indicators of the structure and density of the vegetation, whereas spectral indices are related to the physiological status and density of the vegetation, so they complement others not considered in this study, such as meteorological variables.
One of the most critical parameters for obtaining efficient variables derived from the UAV-DAP point cloud was the extension of the study area. Data obtained from small areas are not sufficient to establish a proper relationship with the RoS; a minimum area is needed, and this is a constraint when using drones, due to their limited autonomy [3]. We recommend that, for model generation, the training data should cover an extent greater than or equal to that flown in Sycan. The extent of the data capture mainly depends on the technical characteristics of the drone, as well as the flight plan followed. For instance, when assuming a flight plan similar to the one used in Sycan, with a height range of 120–180 m following a cross-grid pattern, some multispectral drones, such as the DJI Mavic 3M, can map an area of up to 80 hectares in a single flight by following the flight plan software Drone Deploy version 5.14.0 (DroneDeploy, Inc., San Francisco, CA, USA). This represents a significantly larger area than that flown in this study. The models generated were plot specific, requiring the creation of new ones when fuel conditions and topographies differ. In this sense, the good results obtained for Sycan demonstrate the effectiveness of the methodology for fuels categorized under the Anderson Fire Behavior Fuel Model 2 (Figure 1), making it possible to apply the models generated in this study to other environments with similar characteristics. From the results obtained, the fire RoS can be predicted without the use of meteorological predictions. Based on the results obtained, RoS prediction is promising even without the inclusion of biophysical, topographic, or meteorological variables. However, mainly with respect to meteorological conditions, it should be noted that the impact of their variation with respect to model training conditions needs to be further investigated. This is something that should be deeply studied in future work.
5. Conclusions
This study aimed to analyze relationships between the fire RoS and UAV-DAP data obtained prior to prescribed burning. The dependent variable, the fire RoS, was derived from thermal images captured using UAVs during a prescribed burn. Independent variables were extracted from RGB images, and multispectral 3D point clouds were generated before the burn.
We found that geometric and spectral variables extracted from the point clouds are related to the fire RoS, such as the planarity or the NBRDI variables. The fine scale with which the variables derived from the point clouds were obtained allowed us to characterize the fire RoS with a high level of detail. The fuel heterogeneity and extension of the study area were key to the correct generation of the models. These results encourage further research on combining the variables with the greatest importance obtained in this study, which provide relevant information about the structure, density, and state of the vegetation, as well as meteorological, topographical, and biophysical data in order to predict the fire RoS. In future work, we will compare models generated using variables derived from UAV-DAP point clouds with other fire RoS models.
The incorporation of UAV-DAP data into fire RoS models improves our understanding of fire behavior and fuel dynamics. The fine scale of UAV-DAP data enables the development of new techniques and methodologies that can improve prescribed burning management strategies, mitigating associated risks.
Author Contributions
Conceptualization, J.P.C.-R., C.J.M., C.A.S. and R.A.P.; methodology, J.P.C.-R. and C.J.M.; software, J.P.C.-R.; formal analysis, J.P.C.-R., C.J.M. and C.A.S.; data collection, C.J.M., C.A.S. and V.H.; writing—original draft preparation, J.P.C.-R.; writing—review and editing, J.P.C.-R., J.E., J.T., L.Á.R., C.J.M., C.A.S., V.H. and R.A.P.; funding acquisition, L.Á.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was primarily supported by grants BES-2017-081920 and PID2020-117808RB-C21 from MCIN/AEI/10.13039/501100011033 and ESF Investing in your future. Additional support was provided by the US National Science Foundation under Grant No. OIA-2119689 and the Strategic Environmental Research and Development Program (SERDP), grant number RC20-1025.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Botella-Martínez, M.A.; Fernández-Manso, A. Estudio de la Severidad Post-Incendio en la Comunidad Valenciana Comparando los Índices DNBR, RdNBR y RBR a Partir de Imágenes Landsat 8. Rev. Teledetección 2017, 49, 33–47. [Google Scholar] [CrossRef]
- Weise, D.R.; Wright, C.S. Wildland Fire Emissions, Carbon and Climate: Characterizing Wildland Fuels. For. Ecol. Manag. 2014, 317, 26–40. [Google Scholar] [CrossRef]
- Twidwell, D.; Allen, C.R.; Detweiler, C.; Higgins, J.; Laney, C.; Elbaum, S. Smokey Comes of Age: Unmanned Aerial Systems for Fire Management. Front. Ecol. Environ. 2016, 14, 333–339. [Google Scholar] [CrossRef]
- Blanchi, R.; Leonard, J.; Haynes, K.; Opie, K.; James, M.; de Oliveira, F.D. Environmental Circumstances Surrounding Bushfire Fatalities in Australia 1901–2011. Environ. Sci. Policy 2014, 37, 192–203. [Google Scholar] [CrossRef]
- Syphard, A.D.; Rustigian-Romsos, H.; Mann, M.; Conlisk, E.; Moritz, M.A.; Ackerly, D. The Relative Influence of Climate and Housing Development on Current and Projected Future Fire Patterns and Structure Loss across Three California Landscapes. Glob. Environ. Chang. 2019, 56, 41–55. [Google Scholar] [CrossRef]
- Salis, M.; Laconi, M.; Ager, A.A.; Alcasena, F.J.; Arca, B.; Lozano, O.; Fernandes de Oliveira, A.; Spano, D. Evaluating Alternative Fuel Treatment Strategies to Reduce Wildfire Losses in a Mediterranean Area. For. Ecol. Manag. 2016, 368, 207–221. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Botelho, H.S. A Review of Prescribed Burning Effectiveness in Fire Hazard Reduction. Int. J. Wildland Fire 2003, 12, 117. [Google Scholar] [CrossRef]
- Indiana Department of Natural Resources Prescribed Burning. Available online: https://www.in.gov/dnr/fish-and-wildlife/files/HMFSPrescribedBurn.pdf (accessed on 3 July 2023).
- Moran, C.J.; Seielstad, C.A.; Cunningham, M.R.; Hoff, V.; Parsons, R.A.; Queen, L.; Sauerbrey, K.; Wallace, T. Deriving Fire Behavior Metrics from UAS Imagery. Fire 2019, 2, 36. [Google Scholar] [CrossRef]
- Cruz, M.G.; Gould, J.S.; Alexander, M.E.; Sullivan, A.L.; McCaw, W.L.; Matthews, S. Empirical-Based Models for Predicting Head-Fire Rate of Spread in Australian Fuel Types. Aust. For. 2015, 78, 118–158. [Google Scholar] [CrossRef]
- Faivre, N.R.; Jin, Y.; Goulden, M.L.; Randerson, J.T. Spatial Patterns and Controls on Burned Area for Two Contrasting Fire Regimes in Southern California. Ecosphere 2016, 7, e01210. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Intermountain Forest & Range Experiment Station, Forest Service, US Department of Agriculture: Ogden, UT, USA, 1972.
- McArthur, A.G. Weather and Grassland Fire Behaviour; Leaflet (Forestry and Timber Bureau); no. 100; Forestry and Timber Bureau: Canberra, Australia, 1966. [Google Scholar]
- Maffei, C.; Menenti, M. Predicting Forest Fires Burned Area and Rate of Spread from Pre-Fire Multispectral Satellite Measurements. ISPRS J. Photogramm. Remote Sens. 2019, 158, 263–278. [Google Scholar] [CrossRef]
- Chuvieco, E.; Aguado, I.; Salas, J.; García, M.; Yebra, M.; Oliva, P. Satellite Remote Sensing Contributions to Wildland Fire Science and Management. Curr. For. Rep. 2020, 6, 81–96. [Google Scholar] [CrossRef]
- Bailon-Ruiz, R.; Lacroix, S. Wildfire Remote Sensing with UAVs: A Review from the Autonomy Point of View. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 412–420. [Google Scholar]
- Bajocco, S.; Guglietta, D.; Ricotta, C. Modelling Fire Occurrence at Regional Scale: Does Vegetation Phenology Matter? Eur. J. Remote Sens. 2015, 48, 763–775. [Google Scholar] [CrossRef]
- Hodges, J.L.; Lattimer, B.Y. Wildland Fire Spread Modeling Using Convolutional Neural Networks. Fire Technol. 2019, 55, 2115–2142. [Google Scholar] [CrossRef]
- Khanmohammadi, S.; Arashpour, M.; Golafshani, E.M.; Cruz, M.G.; Rajabifard, A.; Bai, Y. Prediction of Wildfire Rate of Spread in Grasslands Using Machine Learning Methods. Environ. Model. Softw. 2022, 156, 105507. [Google Scholar] [CrossRef]
- Yuan, C.; Zhang, Y.; Liu, Z. A Survey on Technologies for Automatic Forest Fire Monitoring, Detection, and Fighting Using Unmanned Aerial Vehicles and Remote Sensing Techniques. Can. J. For. Res. 2015, 45, 783–792. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Arévalo-Verjel, A.N.; Lerma, J.L.; Prieto, J.F.; Carbonell-Rivera, J.P.; Fernández, J. Estimation of the Block Adjustment Error in UAV Photogrammetric Flights in Flat Areas. Remote Sens. 2022, 14, 2877. [Google Scholar] [CrossRef]
- Carbonell-Rivera, J.P.; Torralba, J.; Estornell, J.; Ruiz, L.Á.; Crespo-Peremarch, P. Classification of Mediterranean Shrub Species from UAV Point Clouds. Remote Sens. 2022, 14, 199. [Google Scholar] [CrossRef]
- Hoffrén, R.; Lamelas, M.T.; de la Riva, J. UAV-Derived Photogrammetric Point Clouds and Multispectral Indices for Fuel Estimation in Mediterranean Forests. Remote Sens. Appl. 2023, 31, 100997. [Google Scholar] [CrossRef]
- Danson, F.M.; Sasse, F.; Schofield, L.A. Spectral and Spatial Information from a Novel Dual-Wavelength Full-Waveform Terrestrial Laser Scanner for Forest Ecology. Interface Focus. 2018, 8, 20170049. [Google Scholar] [CrossRef]
- Carbonell-Rivera, J.P.; Estornell, J.; Ruiz, L.Á.; Crespo-Peremarch, P.; Almonacid-Caballer, J.; Torralba, J. Class3Dp: A Supervised Classifier of Vegetation Species from Point Clouds. Environ. Model. Softw. 2024, 171, 105859. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Línková, L. A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner. Remote Sens. 2021, 13, 4811. [Google Scholar] [CrossRef]
- De Pondeca, M.S.F.V.; Manikin, G.S.; DiMego, G.; Benjamin, S.G.; Parrish, D.F.; Purser, R.J.; Wu, W.-S.; Horel, J.D.; Myrick, D.T.; Lin, Y.; et al. The Real-Time Mesoscale Analysis at NOAA’s National Centers for Environmental Prediction: Current Status and Development. Weather. Forecast. 2011, 26, 593–612. [Google Scholar] [CrossRef]
- MicaSense Incorporated RedEdge Camera Radiometric Calibration Model. Available online: https://support.micasense.com/hc/en-us/articles/115000351194-RedEdge-Camera-Radiometric-Calibration-Model (accessed on 5 August 2021).
- Dmitry Semyonov Algorithms Used in Photoscan. Available online: https://www.agisoft.com/forum/index.php?topic=89.0 (accessed on 28 June 2023).
- Lowe, D.G. Object Recognition from Local Scale-Invariant Features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Ullman, S. The Interpretation of Structure from Motion. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1979, 203, 405–426. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Lloyd, S. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically Resistant Vegetation Index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Fraser, R.H.; van der Sluijs, J.; Hall, R.J. Calibrating Satellite-Based Indices of Burn Severity from UAV-Derived Metrics of a Burned Boreal Forest in NWT, Canada. Remote Sens. 2017, 9, 279. [Google Scholar] [CrossRef]
- Kataoka, T.; Kaneko, T.; Okamoto, H.; Hata, S. Crop Growth Estimation System Using Machine Vision. In Proceedings of the Proceedings 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume 2, pp. b1079–b1083. [Google Scholar]
- Richardson, A.J.; Wiegand, C.L. Distinguishing Vegetation from Soil Background Information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Huete, A.; Justice, C.; Van Leeuwen, W. MODIS Vegetation Index (MOD13); NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1999; Volume 3.
- Dong, Y.X. Review of Otsu Segmentation Algorithm. Adv. Mat. Res. 2014, 989–994, 1959–1961. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Ray, T.W.; Farr, T.G.; Blom, R.G.; Crippen, R.E. Monitoring Land Use and Degradation Using Satellite and Airborne Data. In Proceedings of the Summaries of the 4th Annual JPL Airborne Geoscience Workshop, Washington, DC, USA, 25–29 October 1993. [Google Scholar]
- Barbosa, B.D.S.; Ferraz, G.A.S.; Gonçalves, L.M.; Marin, D.B.; Maciel, D.T.; Ferraz, P.F.P.; Rossi, G. RGB Vegetation Indices Applied to Grass Monitoring: A Qualitative Analysis. Agron. Res. 2019, 17, 349–357. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A Modified Soil Adjusted Vegetation Index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of Vegetation Indices and a Modified Simple Ratio for Boreal Applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Carbonell-Rivera, J.P.; Estornell, J.; Ruiz, L.A.; Torralba, J.; Crespo-Peremarch, P. Classification of UAV-Based Photogrammetric Point Clouds of Riverine Species Using Machine Learning Algorithms: A Case Study in the Palancia River, Spain. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B2-2020, 659–666. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA/GSFC Type III Final Report; NASA/GSFC: Greenbelt, MD, USA, 1974; Volume 371.
- Shimada, S.; Matsumoto, J.; Sekiyama, A.; Aosier, B.; Yokohana, M. A New Spectral Index to Detect Poaceae Grass Abundance in Mongolian Grasslands. Adv. Space Res. 2012, 50, 1266–1273. [Google Scholar] [CrossRef]
- Hunt, E.R.; Cavigelli, M.; Daughtry, C.S.T.; Mcmurtrey, J.E.; Walthall, C.L. Evaluation of Digital Photography from Model Aircraft for Remote Sensing of Crop Biomass and Nitrogen Status. Precis. Agric. 2005, 6, 359–378. [Google Scholar] [CrossRef]
- Stricker, R.; Müller, S.; Gross, H.-M. Non-Contact Video-Based Pulse Rate Measurement on a Mobile Service Robot. In Proceedings of the 23rd IEEE International Symposium on Robot and Human Interactive Communication, Edinburgh, UK, 25–29 August 2014; pp. 1056–1062. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR Absorbed by Vegetation from Bidirectional Reflectance Measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Gamon, J.A.; Surfus, J.S. Assessing Leaf Pigment Content and Activity with a Reflectometer. New Phytol. 1999, 143, 105–117. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Biging, G.S.; Larrieu, M.R. Estimation of Forest Leaf Area Index Using Vegetation Indices Derived from Hyperion Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1355–1362. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel Algorithms for Remote Estimation of Vegetation Fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Costa, L.; Nunes, L.; Ampatzidis, Y. A New Visible Band Index (VNDVI) for Estimating NDVI Values on RGB Images Utilizing Genetic Algorithms. Comput. Electron. Agric. 2020, 172, 105334. [Google Scholar] [CrossRef]
- Chuvieco, E.; Cocero, D.; Riaño, D.; Martin, P.; Martínez-Vega, J.; de la Riva, J.; Pérez, F. Combining NDVI and Surface Temperature for the Estimation of Live Fuel Moisture Content in Forest Fire Danger Rating. Remote Sens. Environ. 2004, 92, 322–331. [Google Scholar] [CrossRef]
- Hiers, J.K.; O’Brien, J.J.; Mitchell, R.J.; Grego, J.M.; Loudermilk, E.L. The Wildland Fuel Cell Concept: An Approach to Characterize Fine-Scale Variation in Fuels and Fire in Frequently Burned Longleaf Pine Forests. Int. J. Wildland Fire 2009, 18, 315. [Google Scholar] [CrossRef]
- Balaguer, A.; Ruiz, L.A.; Hermosilla, T.; Recio, J.A. Definition of a Comprehensive Set of Texture Semivariogram Features and Their Evaluation for Object-Oriented Image Classification. Comput. Geosci. 2010, 36, 231–240. [Google Scholar] [CrossRef]
- Mckinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference (SciPy 2010), Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Jordahl, K.; Van den Bossche, J.; Fleischmann, M.; Wasserman, J.; McBride, J.; Gerard, J.; Tratner, J.; Perry, M.; Badaracco, A.G.; Farmer, C.; et al. Geopandas/Geopandas: V0.8.1. 2020. Available online: https://geopandas.org/en/stable/about/citing.html (accessed on 5 March 2024).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- McArthur, A.G. Grassland Fire Danger Meter Mark V; Country Fire Authority: Melbourne, VIC, Australia, 1977.
- Cheney, N.P.; Gould, J.S.; Catchpole, W. Prediction of Fire Spread in Grasslands. Int. J. Wildland Fire 1998, 8, 1–13. [Google Scholar] [CrossRef]
- Anderson, W.R.; Cruz, M.G.; Fernandes, P.M.; McCaw, L.; Vega, J.A.; Bradstock, R.A.; Fogarty, L.; Gould, J.; McCarthy, G.; Marsden-Smedley, J.B.; et al. A Generic, Empirical-Based Model for Predicting Rate of Fire Spread in Shrublands. Int. J. Wildland Fire 2015, 24, 443. [Google Scholar] [CrossRef]
- Linn, R.R.; Winterkamp, J.L.; Furman, J.H.; Williams, B.; Hiers, J.K.; Jonko, A.; O’Brien, J.J.; Yedinak, K.M.; Goodrick, S. Modeling Low Intensity Fires: Lessons Learned from 2012 RxCADRE. Atmosphere 2021, 12, 139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).