Research on Multi-Objective Optimization on Explosion-Suppression Structure-Nonmetallic Spherical Spacers
Abstract
1. Introduction
2. Analytical Method
2.1. Multi-Factor Analysis of Variance
2.2. The Novel Fuzzy Analytic Hierarchy Process (FAHP) Method
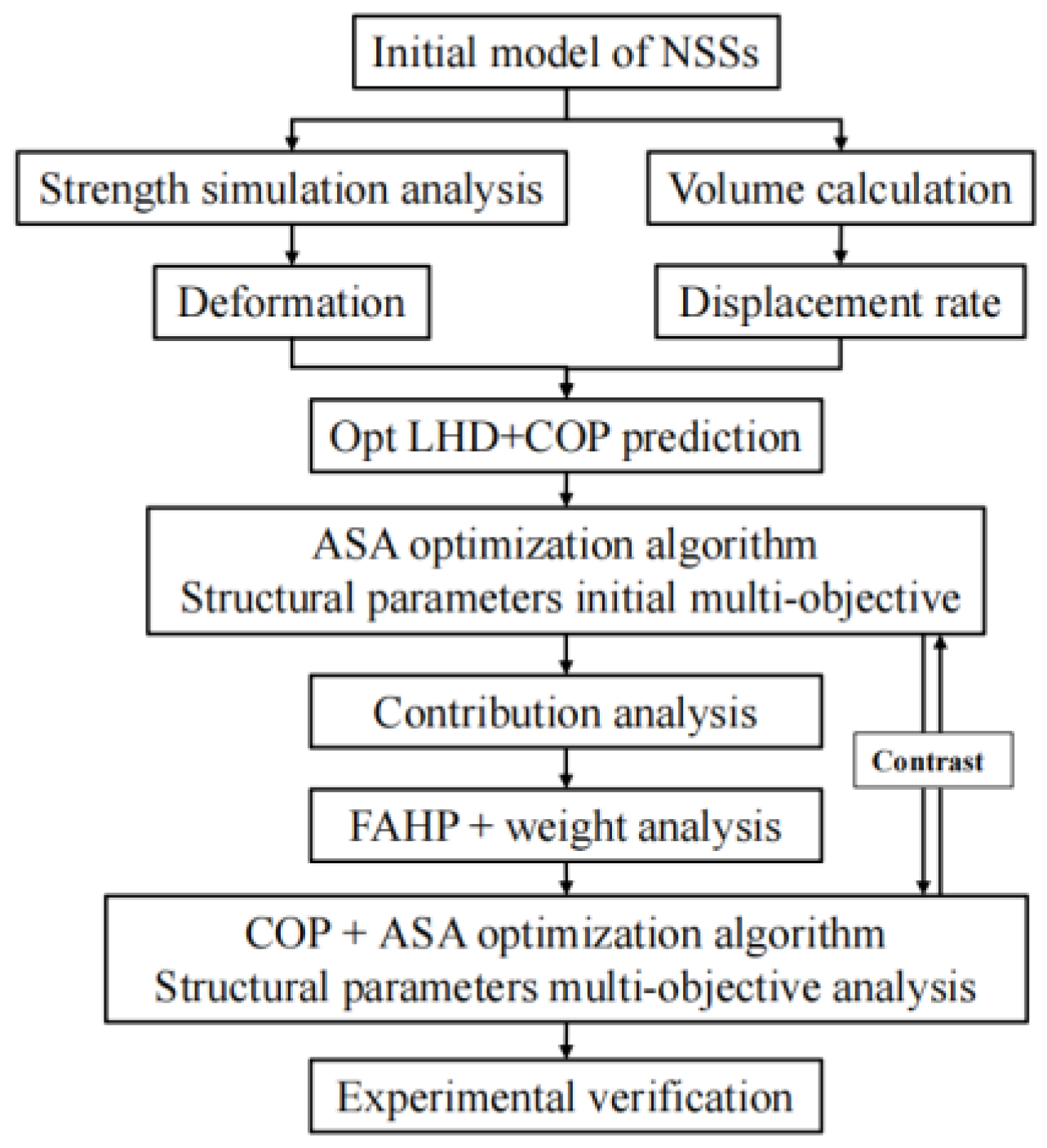
3. Multiple-Objective Optimization Method
3.1. Multiple Objective Optimizations of NSS Structure
3.2. The Optimization Goals of NSSs
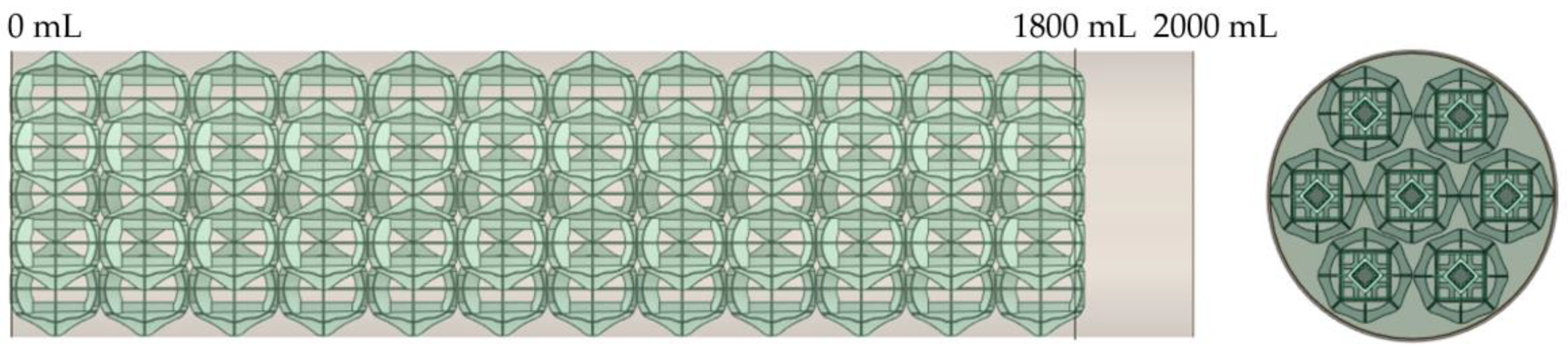
3.3. Sampling Structural Parameters
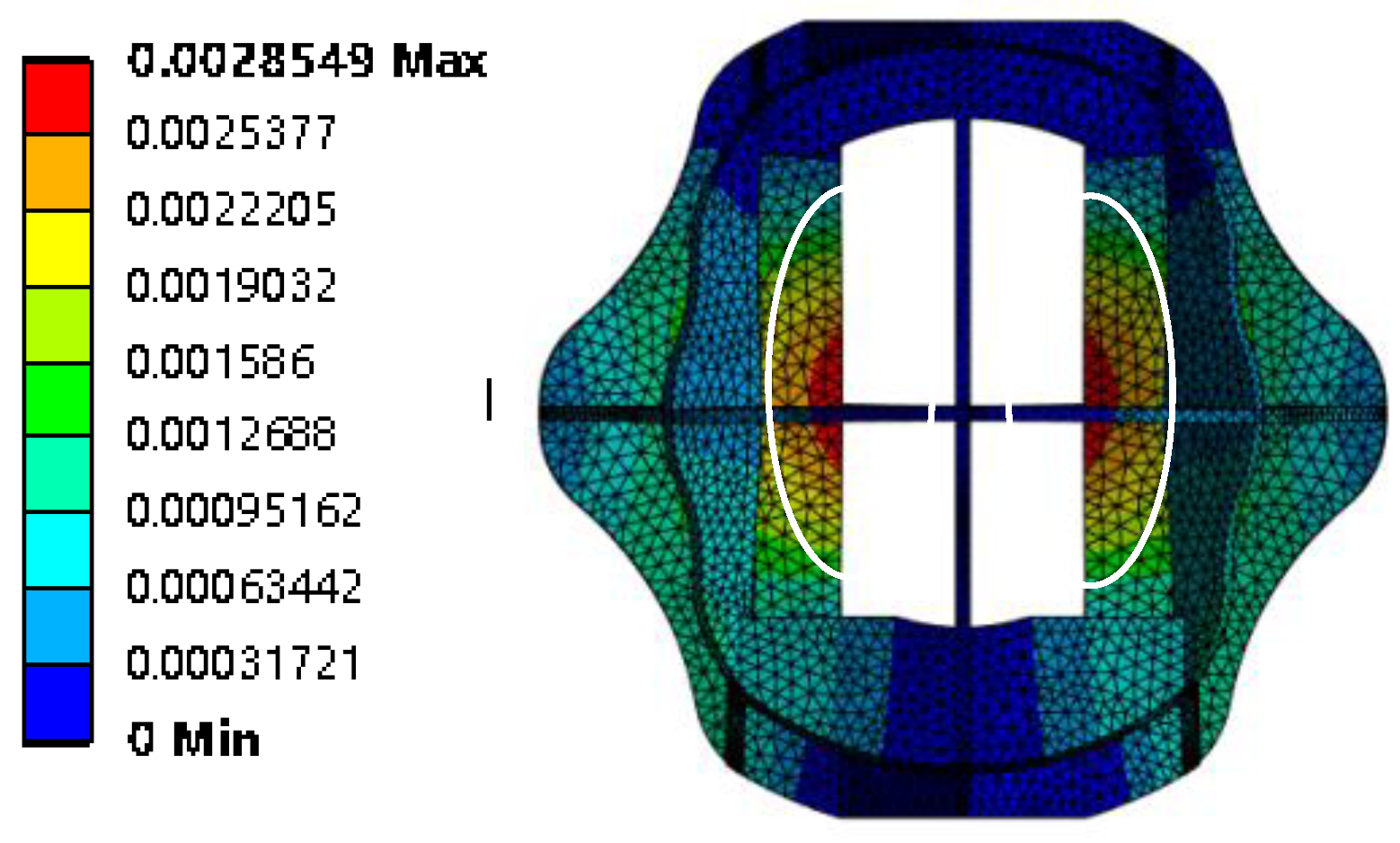
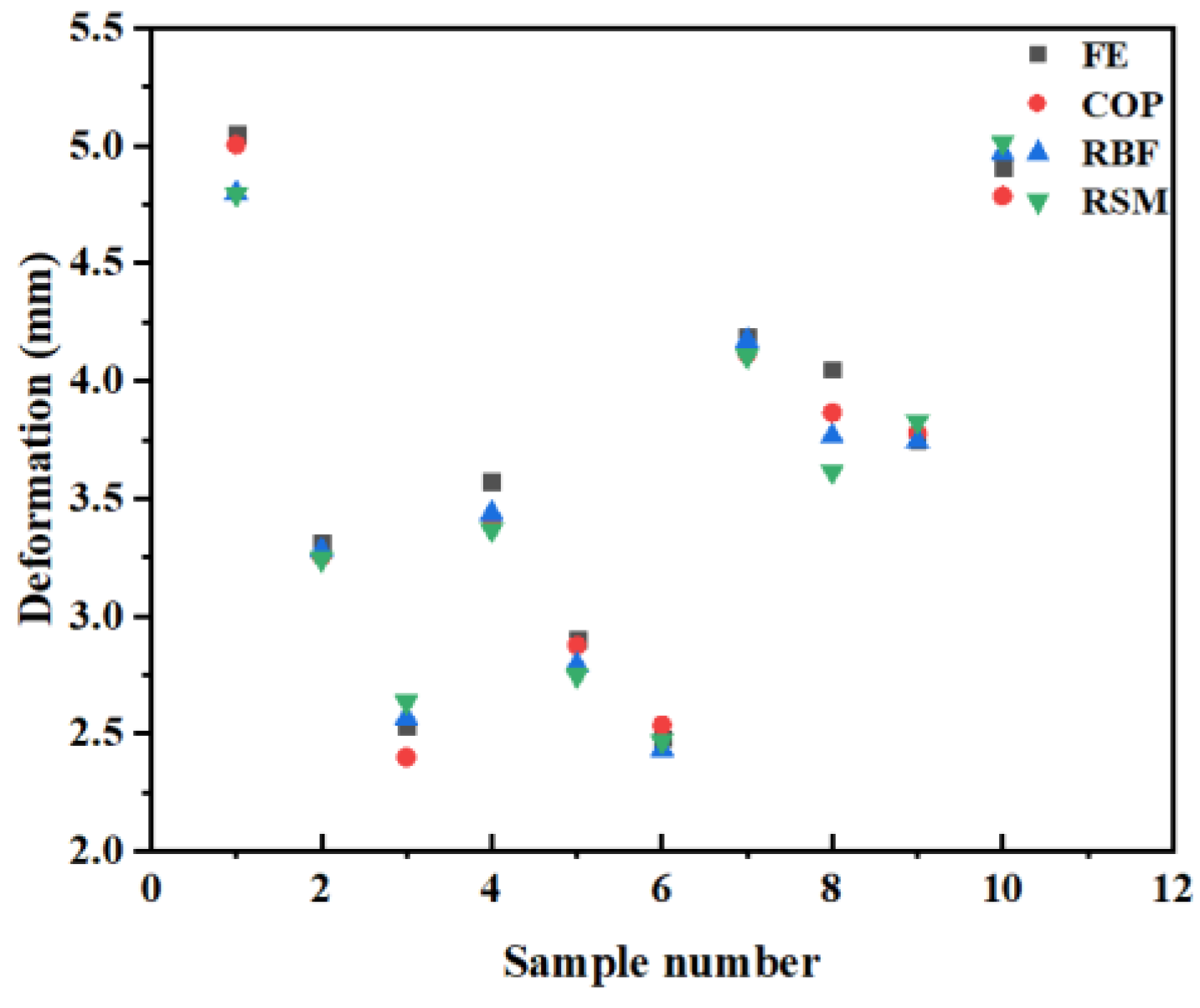
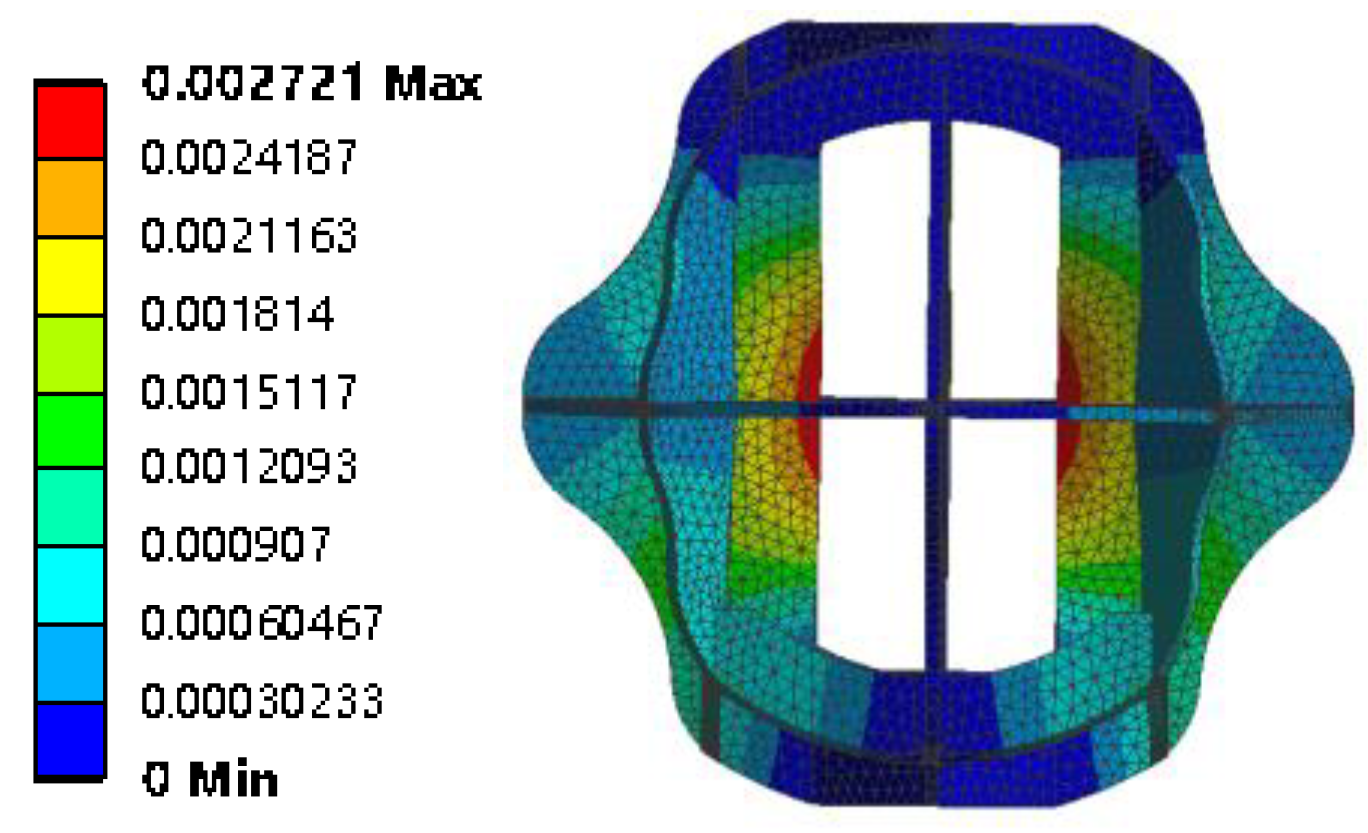
3.4. Deformation and Displacement Rate Prediction
3.5. Multi-Objective Optimization of NSS Structural Parameters
4. The Application of Improved FAHP Method to Multi-Objective Optimization
5. Experimental Verification of NSS Explosion Suppression Performance
6. Conclusions
- (1)
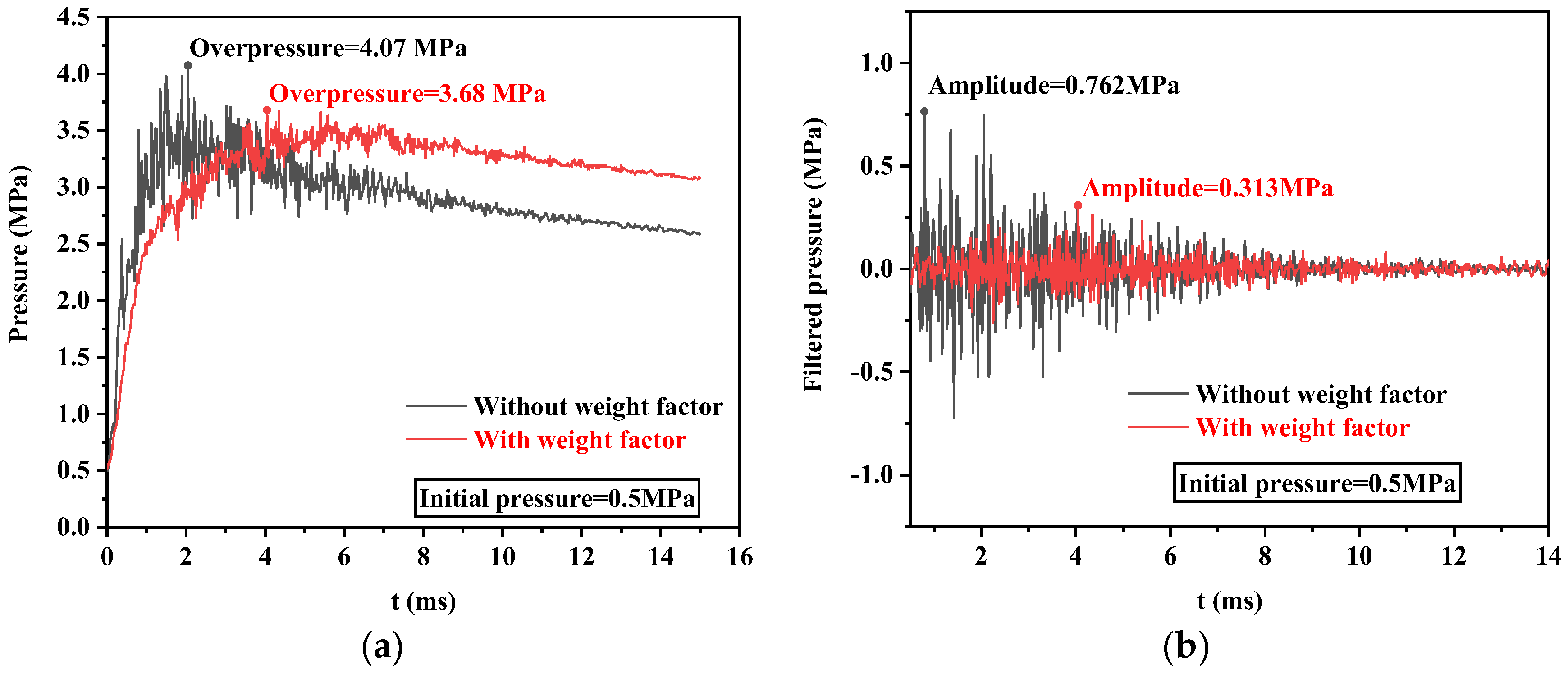
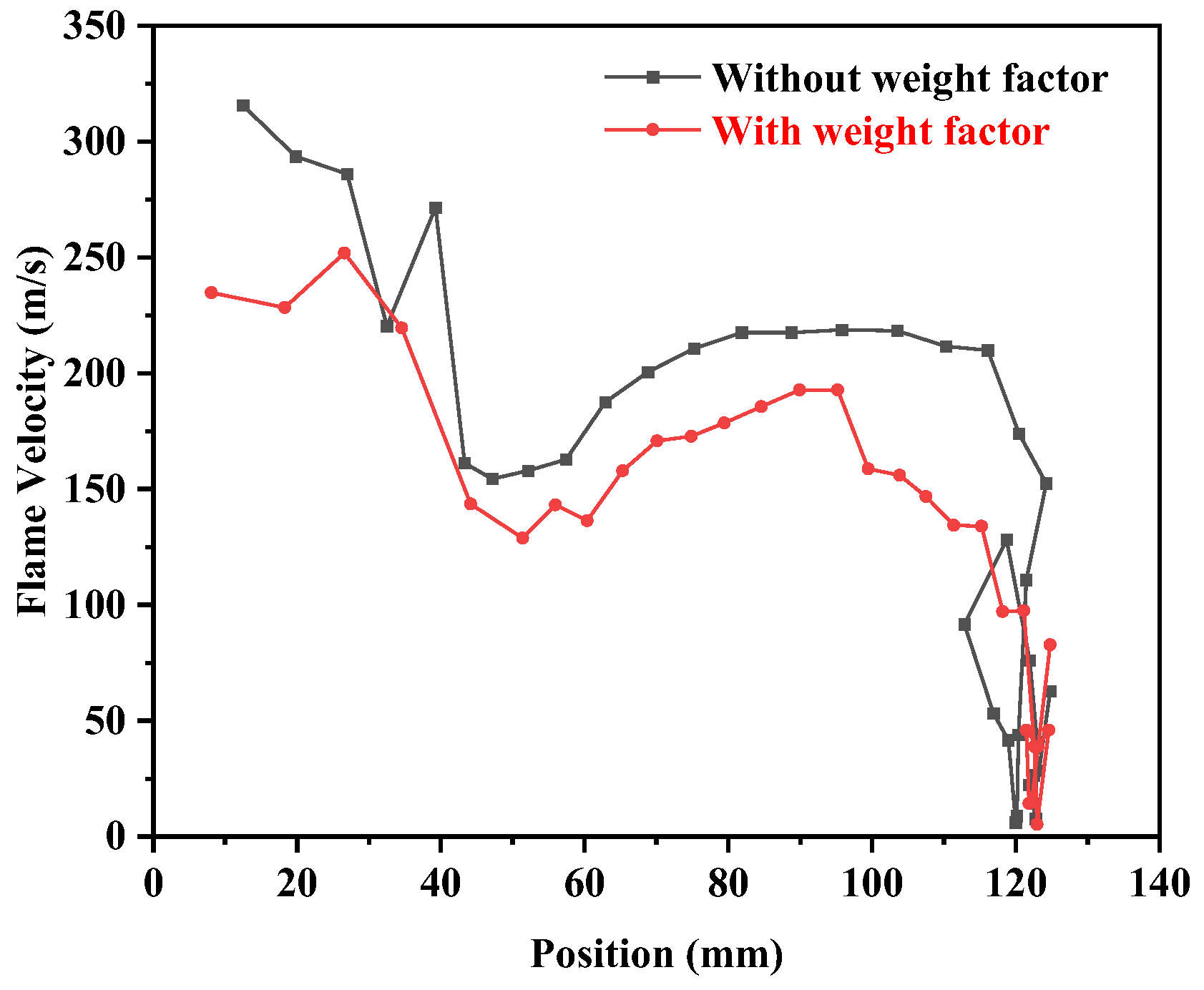
- The multi-objective optimization method with weight analysis was proposed to optimize the structure of NSSs. The displacement rate and explosion suppression performance were optimized simultaneously. Compared with the original NSS model with a deformation of 2.85 mm and a displacement rate of 3.63%, the deformation is improved by 12.98%, and the displacement rate is improved by 6.1%. Compared with the optimized design model of NSSs without weight factor with a deformation of 2.75 mm and a displacement rate of 3.48%, the deformation has been optimized by 9.82% and the displacement rate has been optimized by 2.0%. The optimized performance objectives show significant improvement compared with the optimization results without considering weights.
- (2)
- One of the multiple objectives was considered a factor; the fuzzy judgment matrix was reconfigured to better reflect actual working conditions, then transformed by membership function conversion. A fuzzy consistency matrix was obtained. Weight allocation was then reassigned, and a multi-objective weight distribution matrix was calculated. The novel FAHP method is proposed to address the weight allocation problem in multi-objective optimization and achieve optimal solutions.
- (3)
- The conflicting multi-objective weight allocation is resolved by MANOVA and the novel FAHP method. Integrating Opt LHD, COP, and ASA, the multi-objective optimization method of structural parameters was developed and applied to the problem of multi-objective optimization of NSSs. The low displacement rate and high explosion suppression performance of NSSs were achieved simultaneously.
- (4)
- This method was developed and applied to the multi-objective optimization of NSSs. At the same time, it was also applied to other structures. But it is not certain whether it can be applied to multi-objective optimization in other areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Di Sarli, V.; Di Benedetto, A.; Russo, G. Large Eddy Simulation of transient premixed flame–vortex interactions in gas explosions. Chem. Eng. Sci. 2012, 71, 539–551. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A.; Russo, G. Sub-grid scale combustion models for large eddy simulation of unsteady premixed flame propagation around obstacles. J. Hazard. Mater. 2010, 180, 71–78. [Google Scholar] [CrossRef]
- Wei, H.; Gao, D.; Zhou, L.; Feng, D.; Chen, R. Different combustion modes caused by flame-shock interactions in a confined chamber with a perforated plate. Combust. Flame 2017, 178, 277–285. [Google Scholar] [CrossRef]
- Zhou, L.; Zhong, L.; Zhao, J.; Gao, D.; Wei, H. Flame propagation and combustion modes in end-gas region of confined space. Combust. Flame 2018, 190, 216–223. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, J.; Zhou, L.; Gao, D.; Xu, Z. Effects of the equivalence ratio on turbulent flame–shock interactions in a confined space. Combust. Flame 2017, 186, 247–262. [Google Scholar] [CrossRef]
- Wei, H.; Xu, Z.; Zhou, L.; Gao, D.; Zhao, J. Effect of initial pressure on flame–shock interaction of hydrogen–air premixed flames. Int. J. Hydrogen Energy 2017, 42, 12657–12668. [Google Scholar] [CrossRef]
- Wen, X.; Xie, M.; Yu, M.; Li, G.; Ji, W. Porous media quenching behaviors of gas deflagration in the presence of obstacles. Exp. Therm. Fluid Sci. 2013, 50, 37–44. [Google Scholar] [CrossRef]
- Ibrahim, S.; Masri, A. The effects of obstructions on overpressure resulting from premixed flame deflagration. J. Loss Prev. Process Ind. 2001, 14, 213–221. [Google Scholar] [CrossRef]
- Mittal, V.; Pielichowski, K.; Leszczyńska, A.; Njuguna, J.; Kamal, M.R.; Uribe-Calderon, J.; Manias, E.; Heidecker, M.J.; Nakajima, H.; Costache, M.C.; et al. Thermally Stable and Flame Retardant Polymer Nanocomposites; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Fony, Z. Fundamentals of Engineering Thermodynamics; McGraw-Hill Book Co.: New York, NY, USA, 1998. [Google Scholar]
- Yang, Z.; Zhao, K.; Song, X.; Li, B.; Zhang, D.; Xie, L. Effects of mesh aluminium alloys and propane addition on the explosion-suppression characteristics of hydrogen-air mixture. Int. J. Hydrogen Energy 2021, 46, 34998–35013. [Google Scholar] [CrossRef]
- Lu, C.B.; Zhu, X.D.; Wang, H.Z. Comprehensive evaluation on explosion proof performance of non-metallic barrier and explosion proof material. J. Saf. Sci. Technol. 2014, 10, 125–130. [Google Scholar]
- Zhao, Y.D.; Jiang, X.S.; Xie, W.; He, D.H. Experimental study on suppression of gasoline-air mixture explosion in narrow-confined space using non-metallic spherical anti-explosion material. Contemp. Chem. Ind. 2020, 49, 1017–1022. [Google Scholar]
- Dai, H.; Yao, D.; Yu, Y.; Zhang, J.; Wang, D. Energy attenuation behavior on propane–air premixed combustion on account of nonmetallic spherical spacers in confined space with two perforated plates. Energy Sci. Eng. 2023, 11, 3855–3868. [Google Scholar] [CrossRef]
- Song, X.Z.; Zuo, X.C.; Yang, Z.K.; Chen, J.; Xie, L.F.; Li, B. The explosion-suppression performance of mesh aluminum alloys and spherical nonmetallic materials on hydrogen-air mixtures. Int. J. Hydrogen Energy 2020, 45, 32686–32701. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, J.; Wang, J.; Wang, D. Flame propagation behavior of propane–air premixed combustion in a confined space with two perforated plates at different initial pressures. Energy Sci. Eng. 2022, 10, 2940–2953. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, L.; Zhang, J.; Wang, J.; Meng, X.; Wang, D. Explosion-Suppression Characteristics of Nonmetallic Spherical Spacers on Propane-Air Mixtures in Confined Space. Appl. Sci. 2021, 11, 9238. [Google Scholar] [CrossRef]
- Saaty, T.L. The analytic hierarchy process: Planning, priority setting, resource allocation. In Fe Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980; Volume 15, pp. 97–98. [Google Scholar]
- Saaty, T.L. How to Make a Decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 2–26. [Google Scholar] [CrossRef]
- Ooi, J.; Promentilla, M.A.B.; Tan, R.R.; Ng, D.K.; Chemmangattuvalappil, N.G. Integration of Fuzzy Analytic Hierarchy Process into multi-objective Computer Aided Molecular Design. Comput. Chem. Eng. 2018, 109, 191–202. [Google Scholar] [CrossRef]
- Nallusamy, S.; Ganesan, M.; Balakannan, K.; Shankar, C. Environmental Sustainability Evaluation for an Automobile Manufacturing Industry Using Multi-Grade Fuzzy Approach. Int. J. Eng. Res. Afr. 2016, 19, 123–129. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Liu, Y.; Qin, Z.; Ma, L.; Hong, F.; Chu, F. Dynamic analysis of magnetorheological damper incorporating elastic ring in coupled multiphysical fields. Mech. Syst. Signal Process. 2024, 208, 111040. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy Set Feory—And Its Applications; Kluwer-Nijhoff Pub: Leiden, The Netherlands, 1985. [Google Scholar]
- Krej, J. On Additive Consistency of Interval Fuzzy Preference Relations; Pergamon Press Inc.: Oxford, UK, 2017. [Google Scholar]
- Zhou, H.; Jia, M.; Feng, Y.; Liu, Y. Evaluation system for automatic fare gate capacity based on delphi and improved FAHP. In Proceedings of the 2017 IEEE 6th Data Driven Control and Learning Systems Conference (DDCLS), Chongqing, China, 26–27 May 2017; pp. 754–759. [Google Scholar]
- Trivedi, A.; Singh, A. A hybrid multi-objective decision model for emergency shelterlocation-relocation projects using fuzzy analytic hierarchy process and goal programming approach. Int. J. Proj. Manag. 2017, 35, 827–840. [Google Scholar] [CrossRef]
- Zhu, G.-N.; Hu, J.; Ren, H. A fuzzy rough number-based AHP-TOPSIS fordesign concept evaluation under uncertain environments. Appl. Soft Comput. J. 2020, 91, 106228. [Google Scholar] [CrossRef]
- Lv, L.; Deng, Z.; Meng, H.; Liu, T.; Wan, L. A multi-objective decision-making method for machining process plan and an application. J. Clean. Prod. 2020, 260, 121072. [Google Scholar] [CrossRef]
- Lehai, L.; Fengrong, B.; Yangyang, Y.; Junhong, Z.; Xiangde, M.; Xueling, Z. Influence of Packed Densities of Nonmetallic Spherical Spacers on Propane Explosion Suppression. Chin. J. Energetic Mater. 2021, 29, 840–847. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. JT/T 1046-2016 Technical Requirements for Explosion-Proof Safety of Road Transport Vehicle Fuel Tanks and Liquid Fuel Transportation Tanks; People’s Communications Press: Beijing, China, 2016.

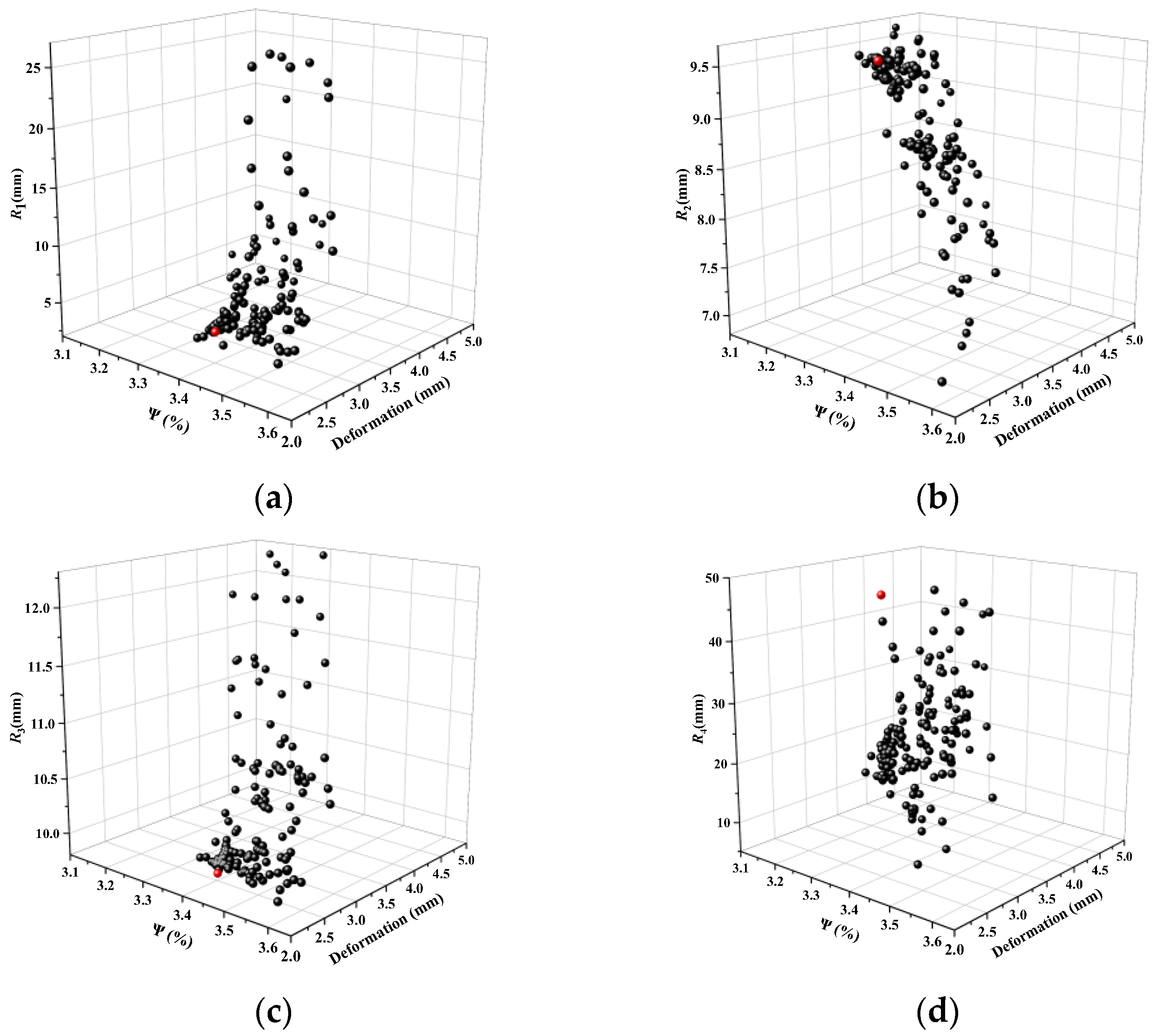

| Parameters | R1 (mm) | R2 (mm) | R3 (mm) | R4 (mm) |
|---|---|---|---|---|
| Variable scope | 2–30 | 6.8–9.7 | 9.9–12.5 | 6–50 |
| No. | R1 (mm) | R2 (mm) | R3 (mm) | R4 (mm) | Deformation (mm) | Displacement Rate (%) |
|---|---|---|---|---|---|---|
| 1 | 21.16 | 7.56 | 10.58 | 50.00 | 2.93 | 3.62 |
| 2 | 16.74 | 8.17 | 11.13 | 29.16 | 3.54 | 3.49 |
| 3 | 25.58 | 7.72 | 12.23 | 43.05 | 4.48 | 3.38 |
| 4 | 9.37 | 7.11 | 10.99 | 10.63 | 3.29 | 3.51 |
| 5 | 4.95 | 8.33 | 11.54 | 47.68 | 4.00 | 3.33 |
| 6 | 24.11 | 9.39 | 11.27 | 45.37 | 3.37 | 3.37 |
| 7 | 13.79 | 8.94 | 11.95 | 8.32 | 4.70 | 3.26 |
| 8 | 28.53 | 6.95 | 10.86 | 24.53 | 3.08 | 3.61 |
| 9 | 27.05 | 8.48 | 9.90 | 31.47 | 2.41 | 3.64 |
| 10 | 12.32 | 9.24 | 10.17 | 40.74 | 2.70 | 3.50 |
| 11 | 22.63 | 8.02 | 10.45 | 6.00 | 2.95 | 3.57 |
| 12 | 3.47 | 9.55 | 11.41 | 26.84 | 4.02 | 3.19 |
| 13 | 2.00 | 7.87 | 12.09 | 22.21 | 4.50 | 3.18 |
| 14 | 6.42 | 8.63 | 10.31 | 12.95 | 2.86 | 3.48 |
| 15 | 30.00 | 8.78 | 11.82 | 19.89 | 4.00 | 3.42 |
| 16 | 7.89 | 7.41 | 10.04 | 33.79 | 2.50 | 3.63 |
| 17 | 19.68 | 9.70 | 10.72 | 17.58 | 3.26 | 3.38 |
| 18 | 10.84 | 6.80 | 11.68 | 38.42 | 3.71 | 3.45 |
| 19 | 18.21 | 7.26 | 12.36 | 15.26 | 4.52 | 3.35 |
| 20 | 15.26 | 9.09 | 12.50 | 36.11 | 5.27 | 3.19 |
| No. | R1 (mm) | R2 (mm) | R3 (mm) | R4 (mm) | Deformation (mm) | Displacement Rate (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
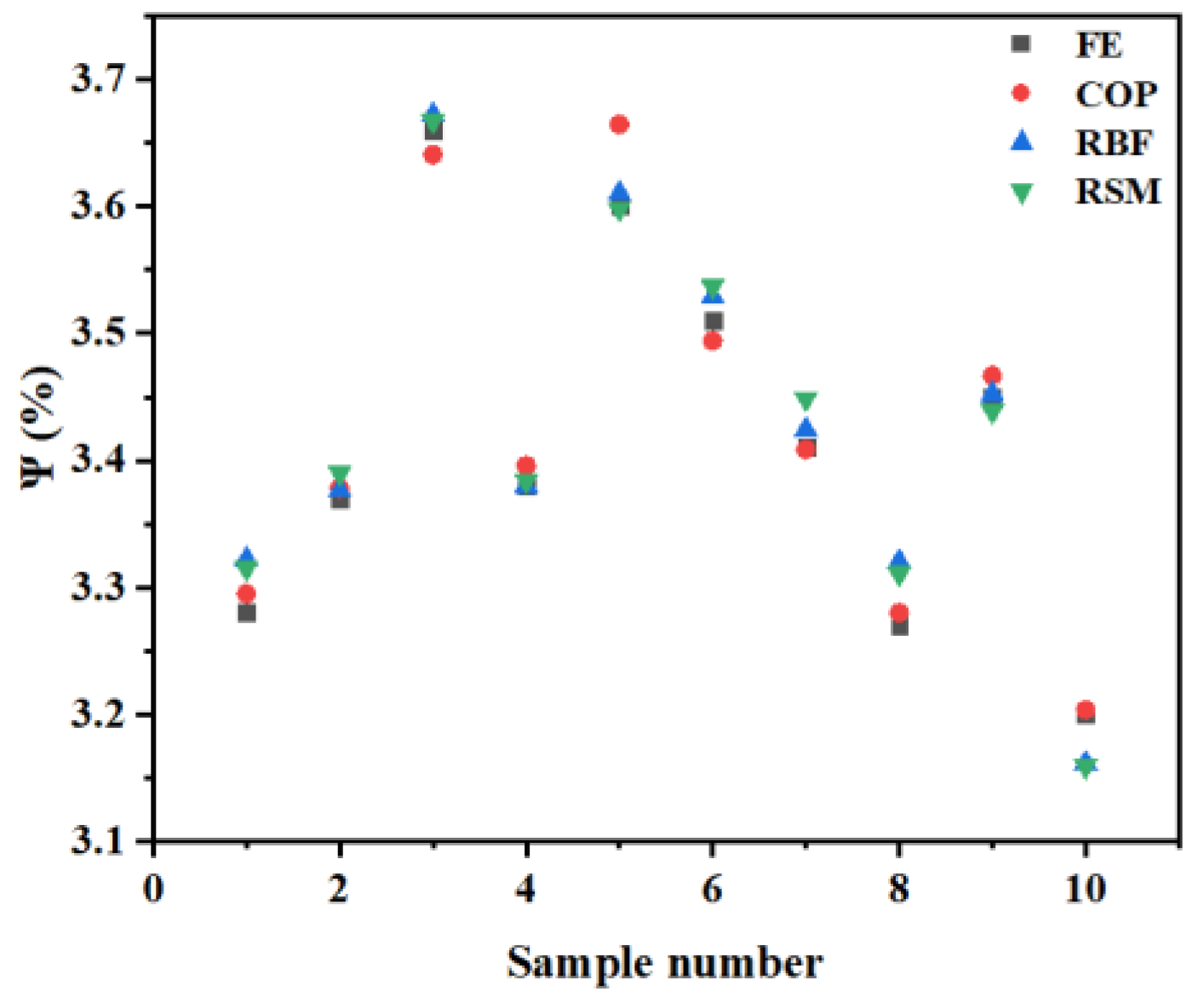
| FE | COP | RBF | RMS | FE | COP | RBF | RMS | |||||
| 1 | 26.89 | 8.41 | 12.5 | 40.22 | 5.05 | 5.004 | 4.799 | 4.794 | 3.28 | 3.295 | 3.322 | 3.315 |
| 2 | 20.67 | 9.7 | 10.77 | 15.78 | 3.31 | 3.253 | 3.280 | 3.242 | 3.37 | 3.378 | 3.376 | 3.390 |
| 3 | 14.44 | 6.8 | 10.19 | 20.67 | 2.53 | 2.400 | 2.566 | 2.634 | 3.66 | 3.641 | 3.672 | 3.667 |
| 4 | 17.56 | 9.38 | 11.06 | 50 | 3.57 | 3.417 | 3.437 | 3.366 | 3.38 | 3.396 | 3.380 | 3.384 |
| 5 | 30 | 8.09 | 10.48 | 35.33 | 2.90 | 2.874 | 2.793 | 2.747 | 3.60 | 3.664 | 3.610 | 3.598 |
| 6 | 5.11 | 8.73 | 9.9 | 30.44 | 2.48 | 2.537 | 2.433 | 2.468 | 3.51 | 3.494 | 3.529 | 3.537 |
| 7 | 23.78 | 7.44 | 11.92 | 10.89 | 4.19 | 4.117 | 4.172 | 4.105 | 3.41 | 3.408 | 3.424 | 3.448 |
| 8 | 2 | 7.77 | 11.34 | 6 | 4.05 | 3.864 | 3.764 | 3.615 | 3.27 | 3.28 | 3.320 | 3.311 |
| 9 | 11.33 | 7.12 | 11.63 | 45.11 | 3.75 | 3.778 | 3.744 | 3.826 | 3.45 | 3.467 | 3.452 | 3.439 |
| 10 | 8.22 | 9.06 | 12.21 | 25.56 | 4.91 | 4.786 | 4.968 | 5.013 | 3.20 | 3.204 | 3.161 | 3.159 |
| R1 (mm) | R2 (mm) | R3 (mm) | R4 (mm) | Deformation (mm) | Displacement Rate (%) | ||
|---|---|---|---|---|---|---|---|
| Optimal | Verification | Optimal | Verification | ||||
| 7.89 | 9.09 | 10.17 | 38.42 | 2.75 | 2.72 | 3.48 | 3.48 |
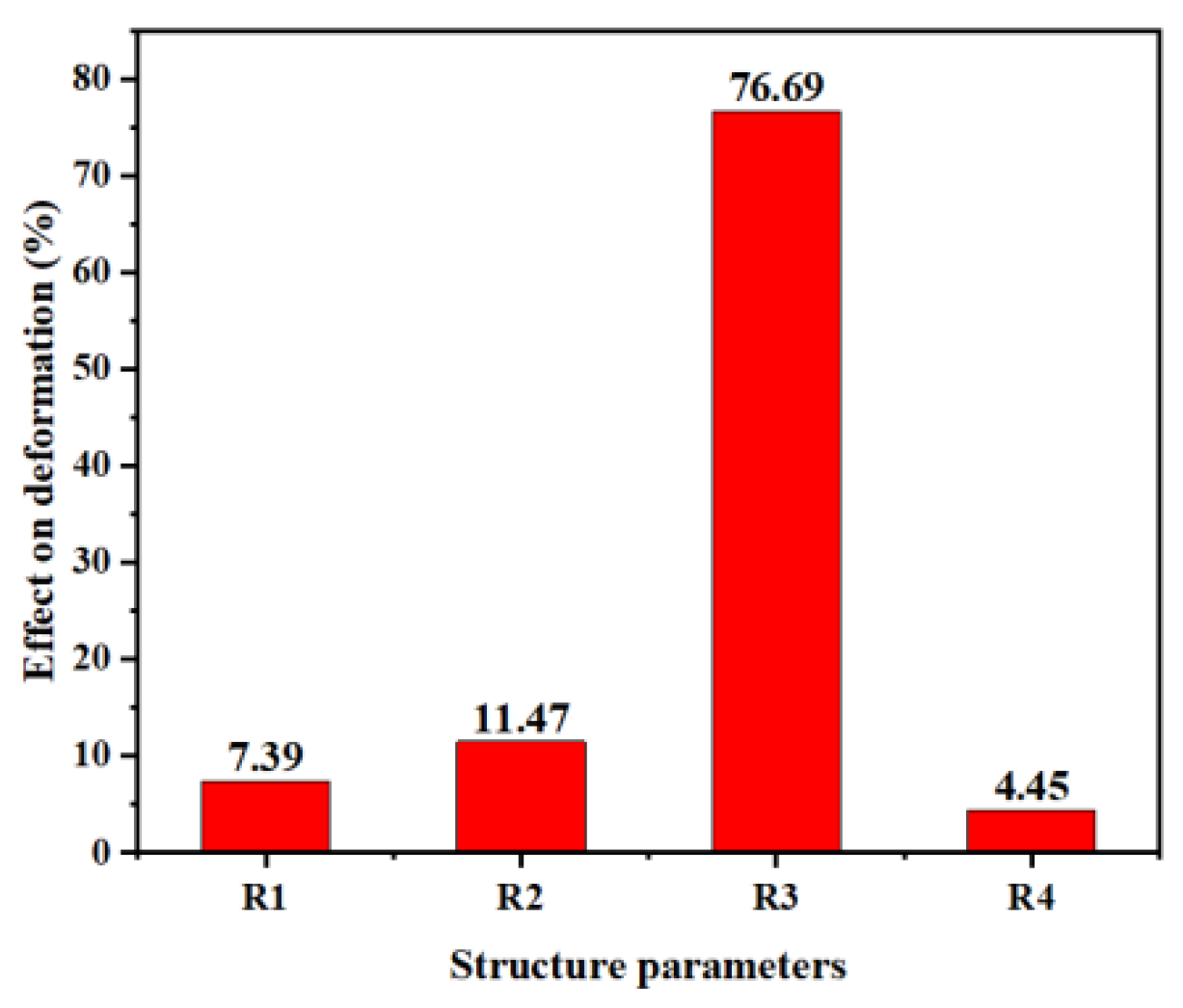
| Parameters | R1/mm | R2/mm | R3/mm | R4/mm |
|---|---|---|---|---|
| weight | 0.08 | 0.15 | 0.70 | 0.07 |
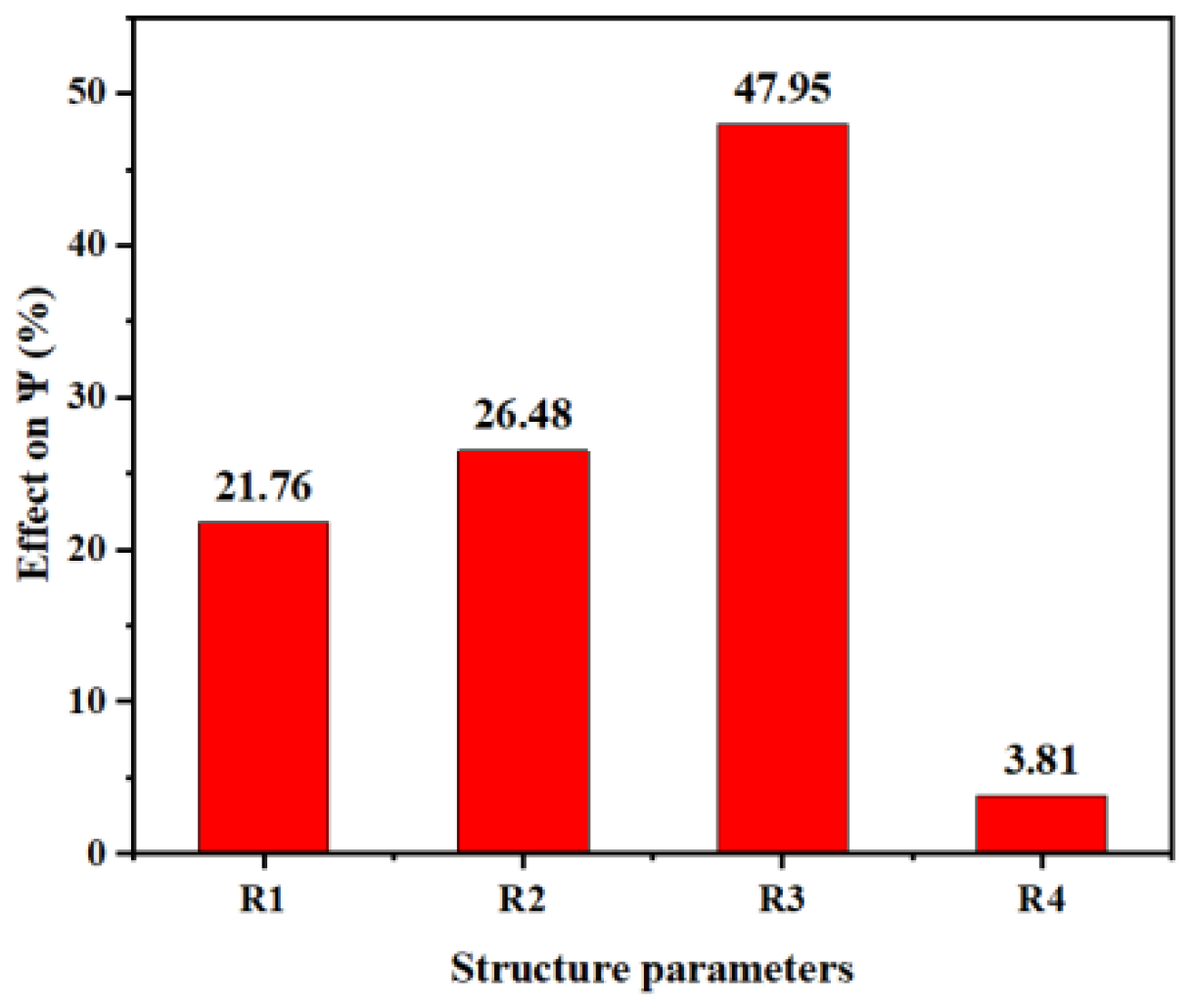
| Parameters | R1/mm | R2/mm | R3/mm | R4/mm |
|---|---|---|---|---|
| weight | 0.12 | 0.21 | 0.56 | 0.11 |
| R1 (mm) | R2 (mm) | R3 (mm) | R4 (mm) | Deformation (mm) | Displacement Rate (%) | ||
|---|---|---|---|---|---|---|---|
| Optimal | Verification | Optimal | Verification | ||||
| 5.02 | 9.70 | 9.90 | 49.51 | 2.43 | 2.48 | 3.41 | 3.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Yu, Y.; Zhang, J.; Wang, D.; Zhang, X.; Yan, M. Research on Multi-Objective Optimization on Explosion-Suppression Structure-Nonmetallic Spherical Spacers. Fire 2024, 7, 28. https://doi.org/10.3390/fire7010028
Liu M, Yu Y, Zhang J, Wang D, Zhang X, Yan M. Research on Multi-Objective Optimization on Explosion-Suppression Structure-Nonmetallic Spherical Spacers. Fire. 2024; 7(1):28. https://doi.org/10.3390/fire7010028
Chicago/Turabian StyleLiu, Minjie, Yangyang Yu, Junhong Zhang, Dan Wang, Xueling Zhang, and Meng Yan. 2024. "Research on Multi-Objective Optimization on Explosion-Suppression Structure-Nonmetallic Spherical Spacers" Fire 7, no. 1: 28. https://doi.org/10.3390/fire7010028
APA StyleLiu, M., Yu, Y., Zhang, J., Wang, D., Zhang, X., & Yan, M. (2024). Research on Multi-Objective Optimization on Explosion-Suppression Structure-Nonmetallic Spherical Spacers. Fire, 7(1), 28. https://doi.org/10.3390/fire7010028





