Combustion of Liquid Fuels in the Presence of CO2 Hydrate Powder
Abstract
1. Introduction
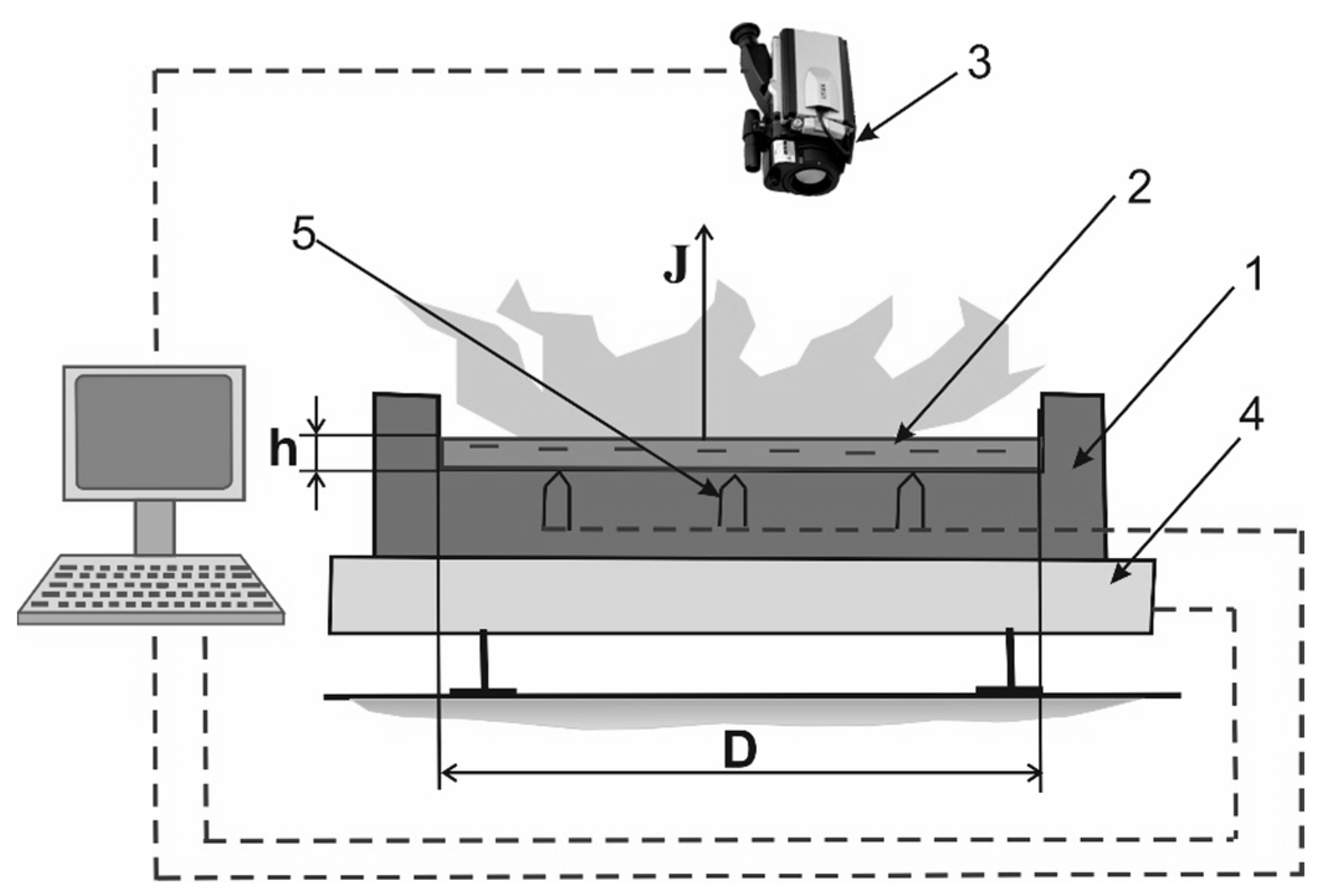
2. Experimental Technique
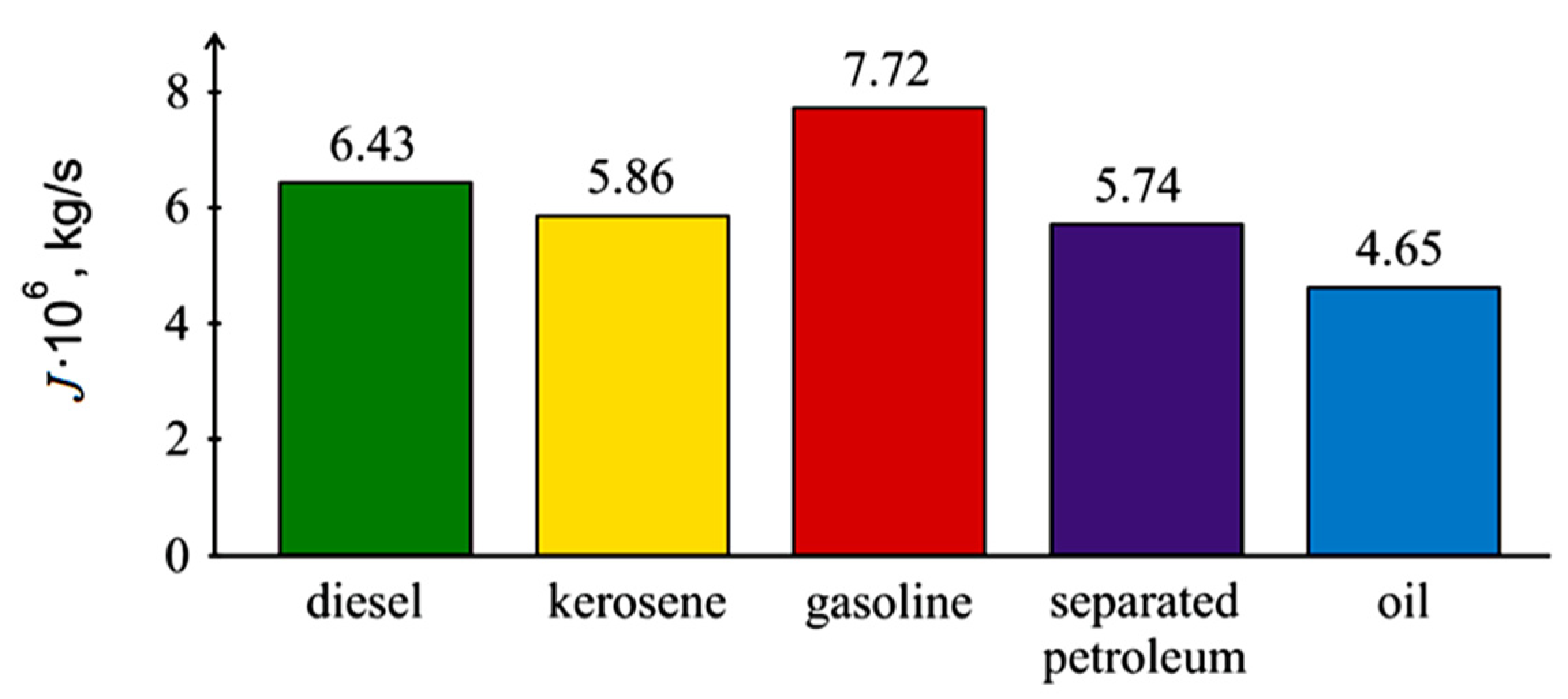
3. Experimental Results and Discussion
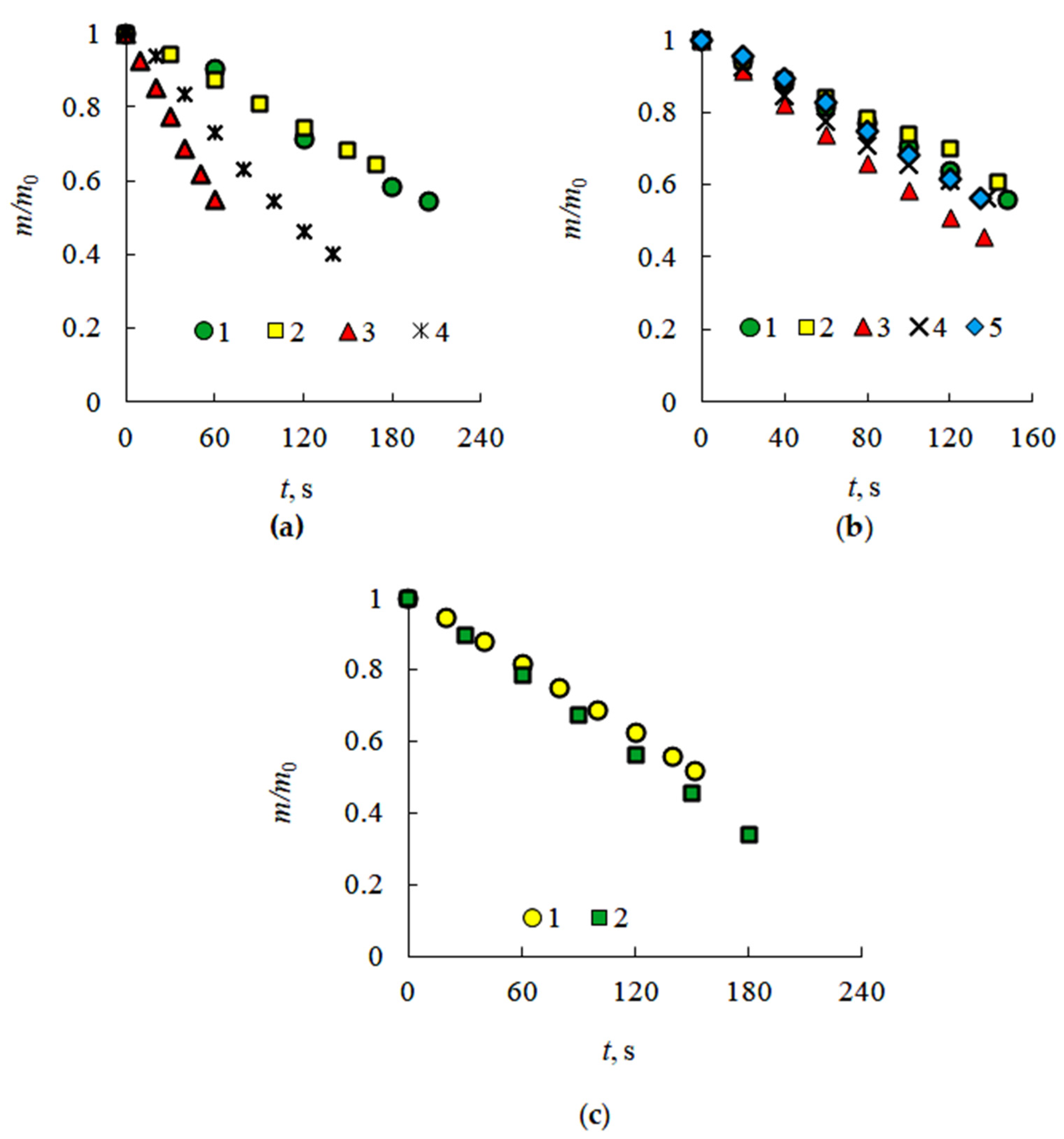
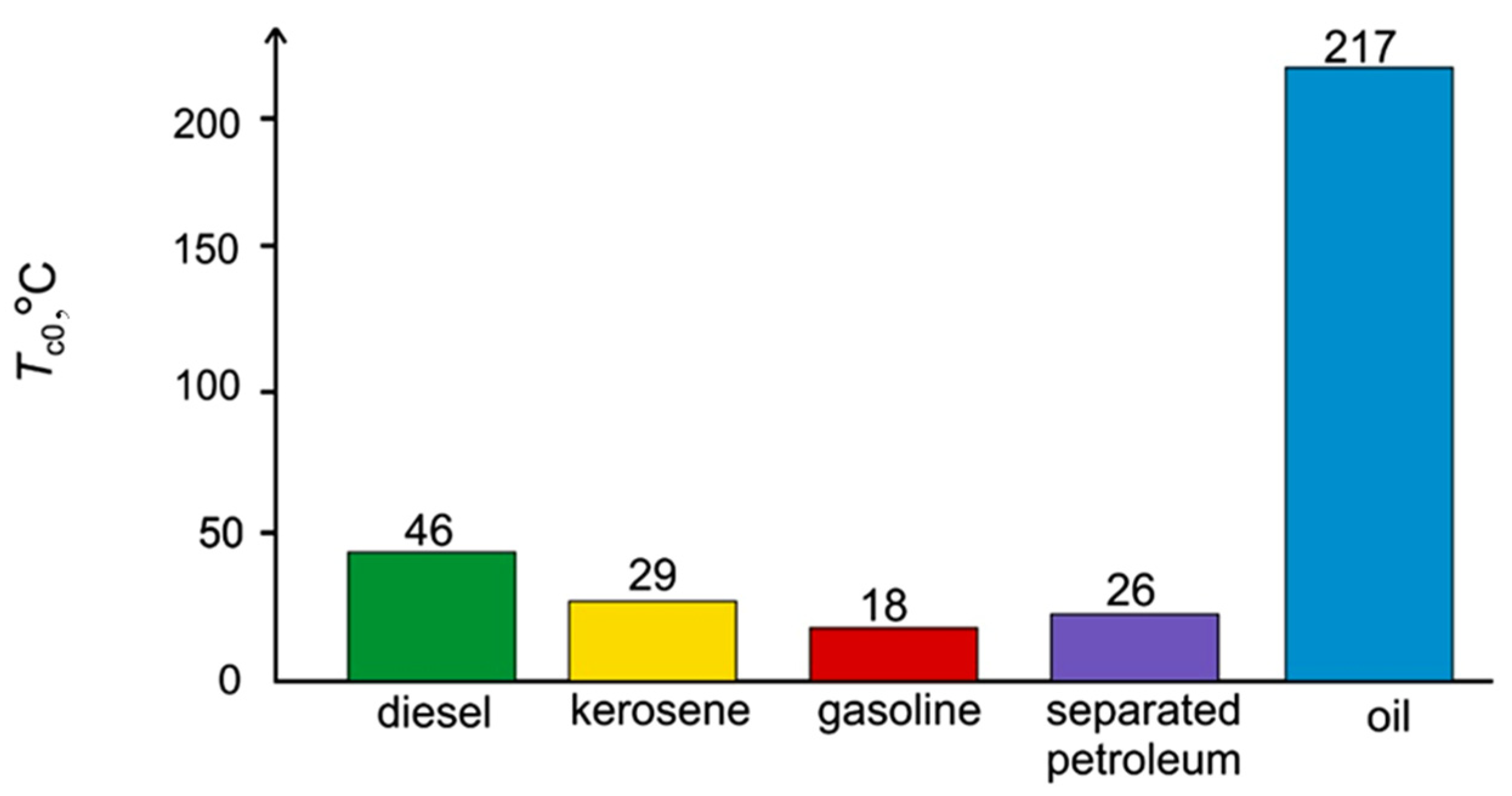
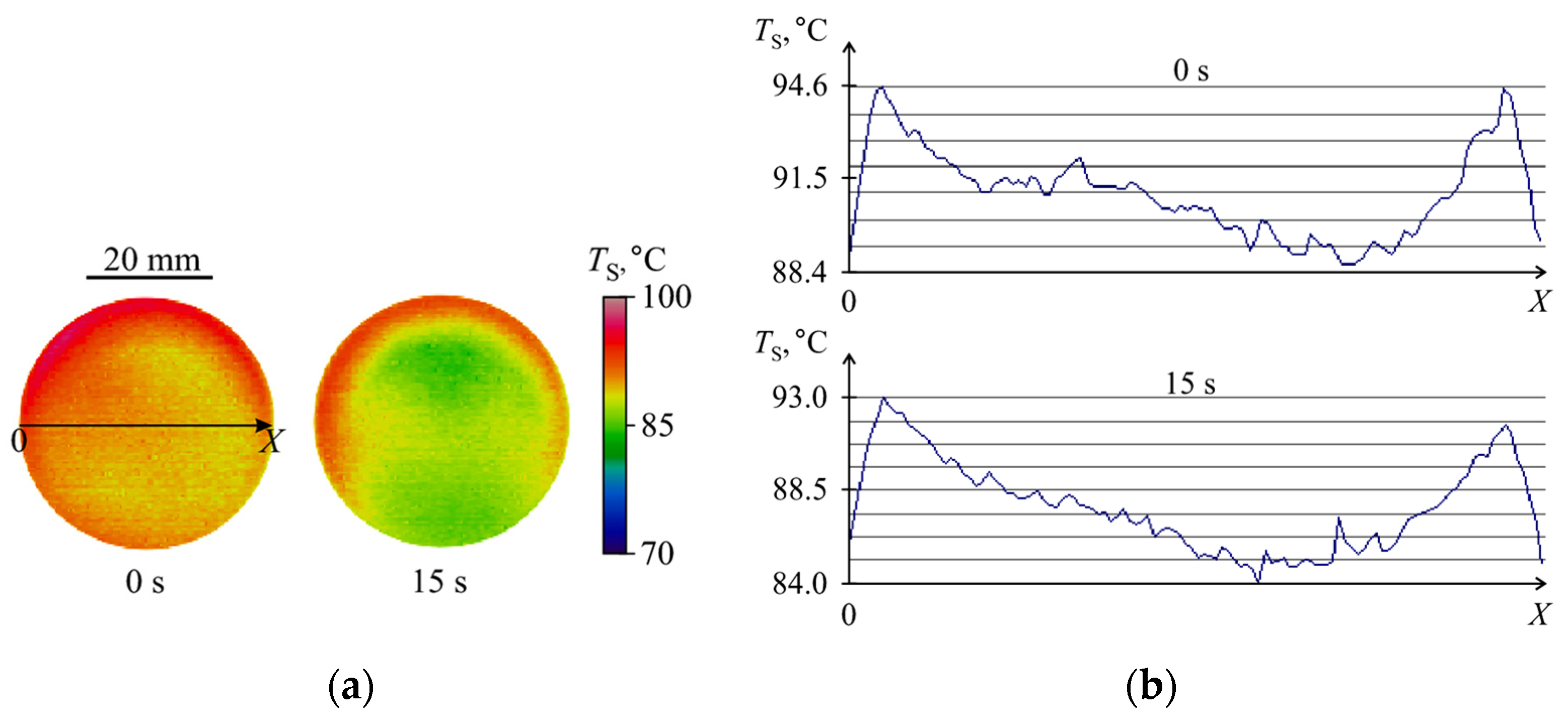
3.1. Evaporation of the Liquid Fuel Layer during Combustion
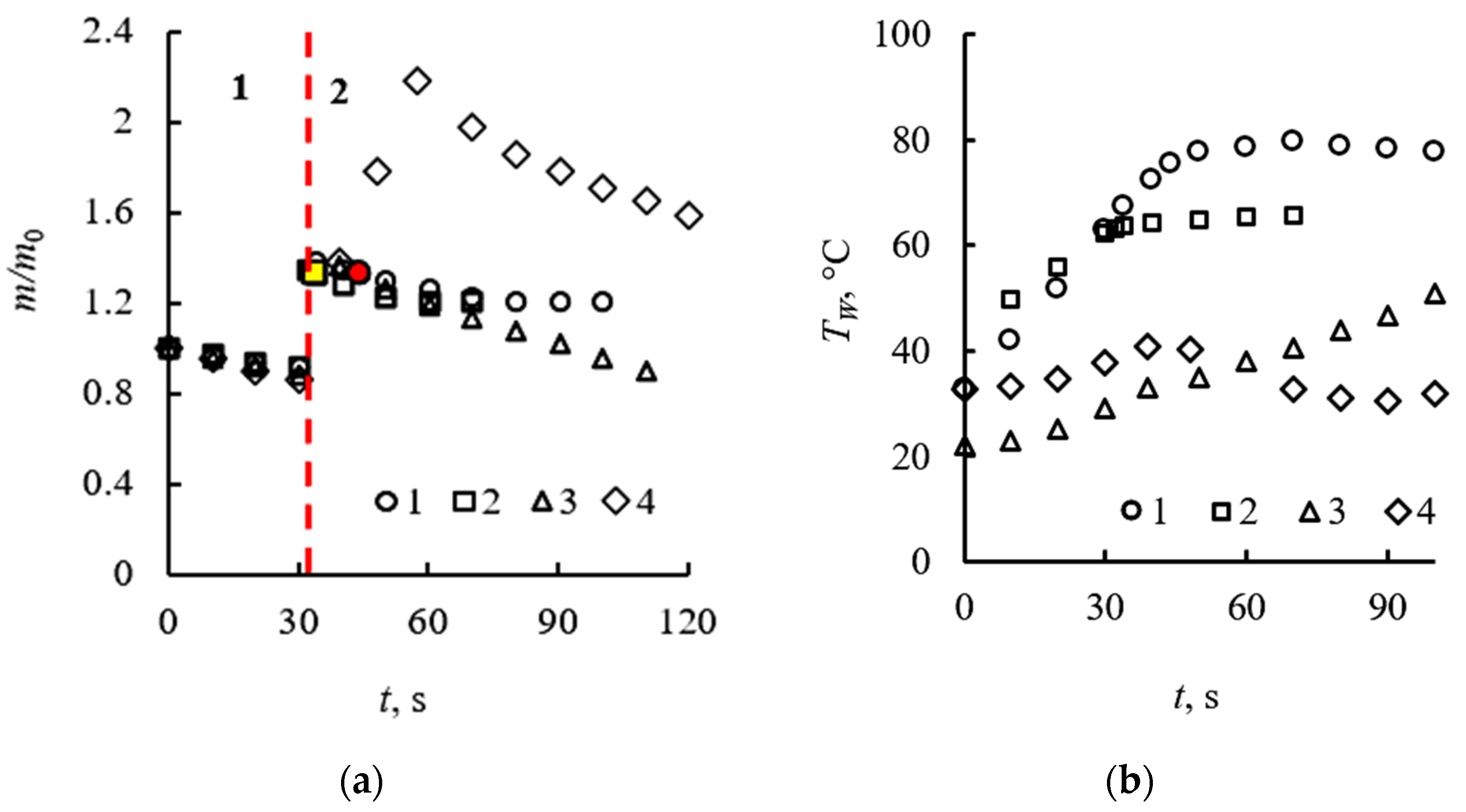
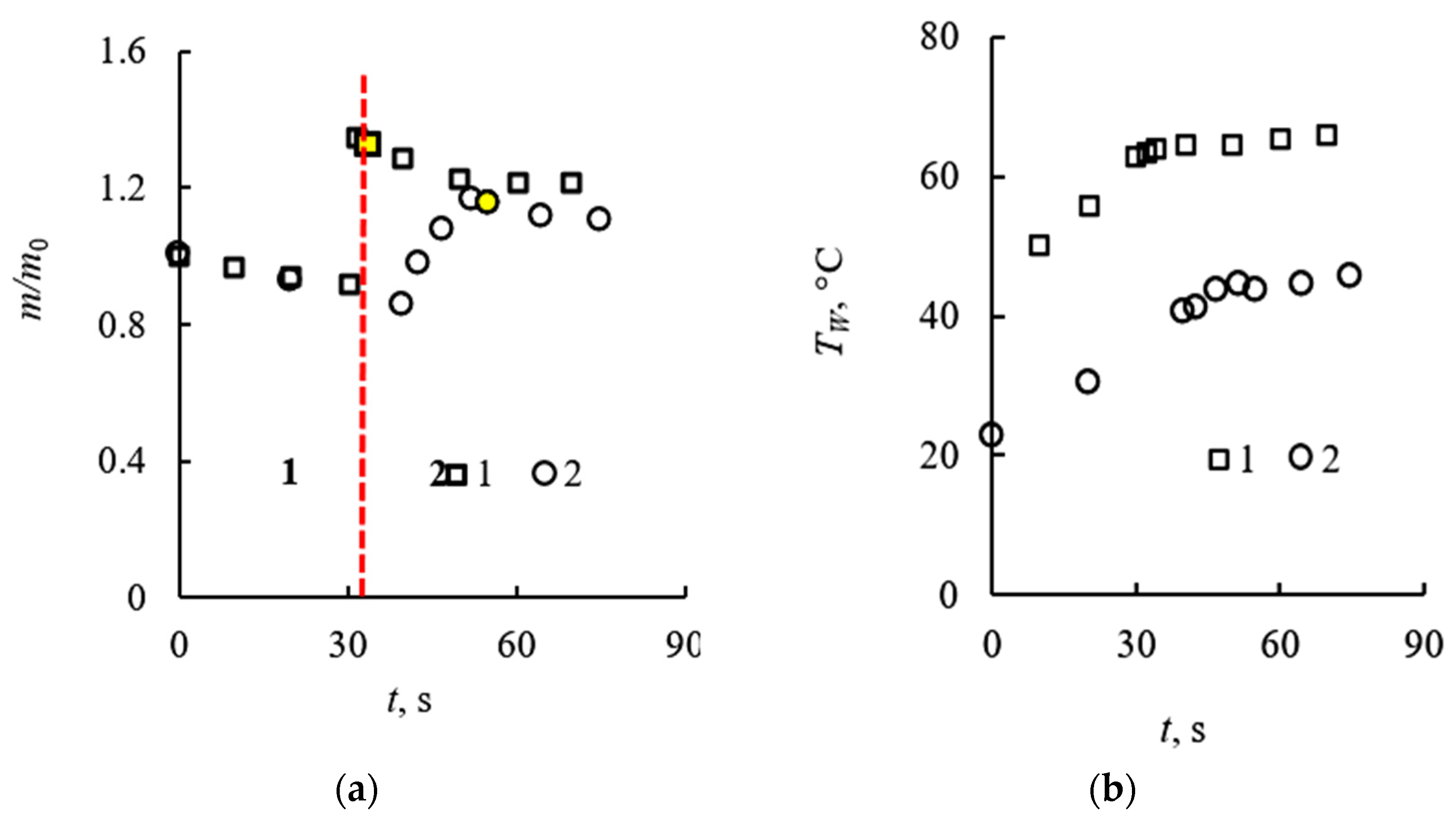
3.2. Evaporation of the Fuel Layer during Dissociation of the Carbon Dioxide Hydrate Tablet
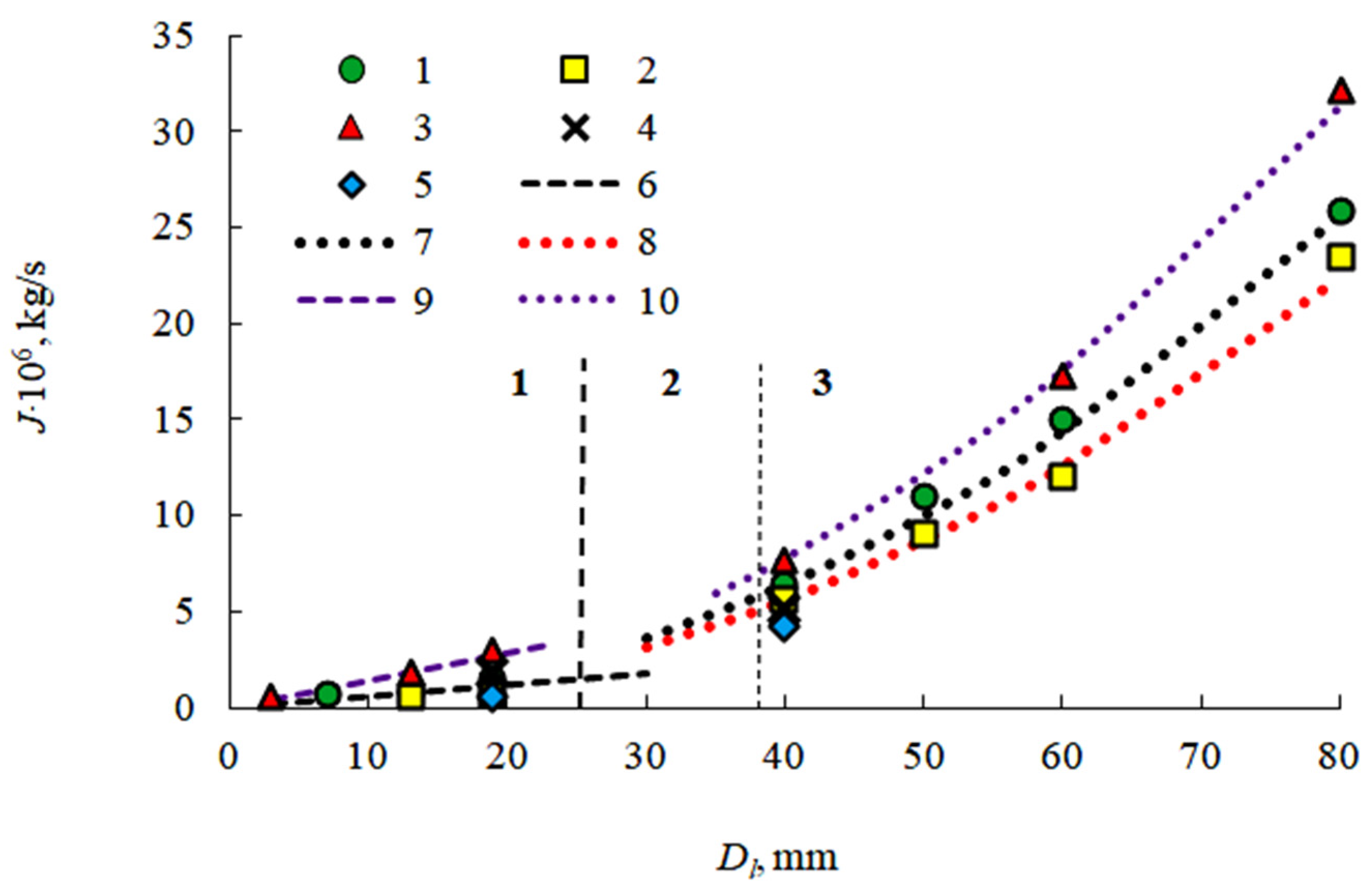
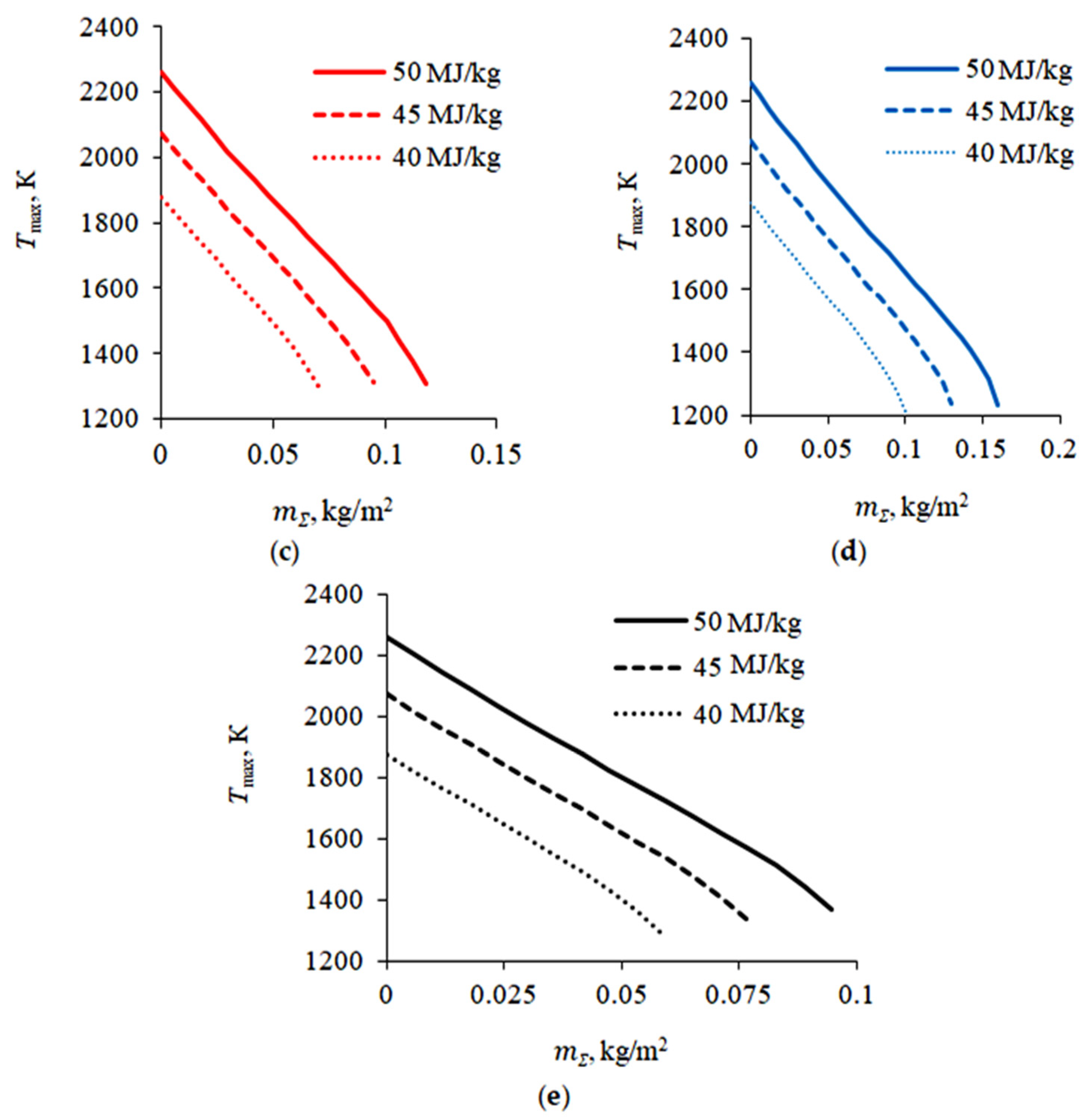
4. Calculation of the Gas Hydrate Dissociation and Flame Extinguishing during Liquid Fuel Combustion
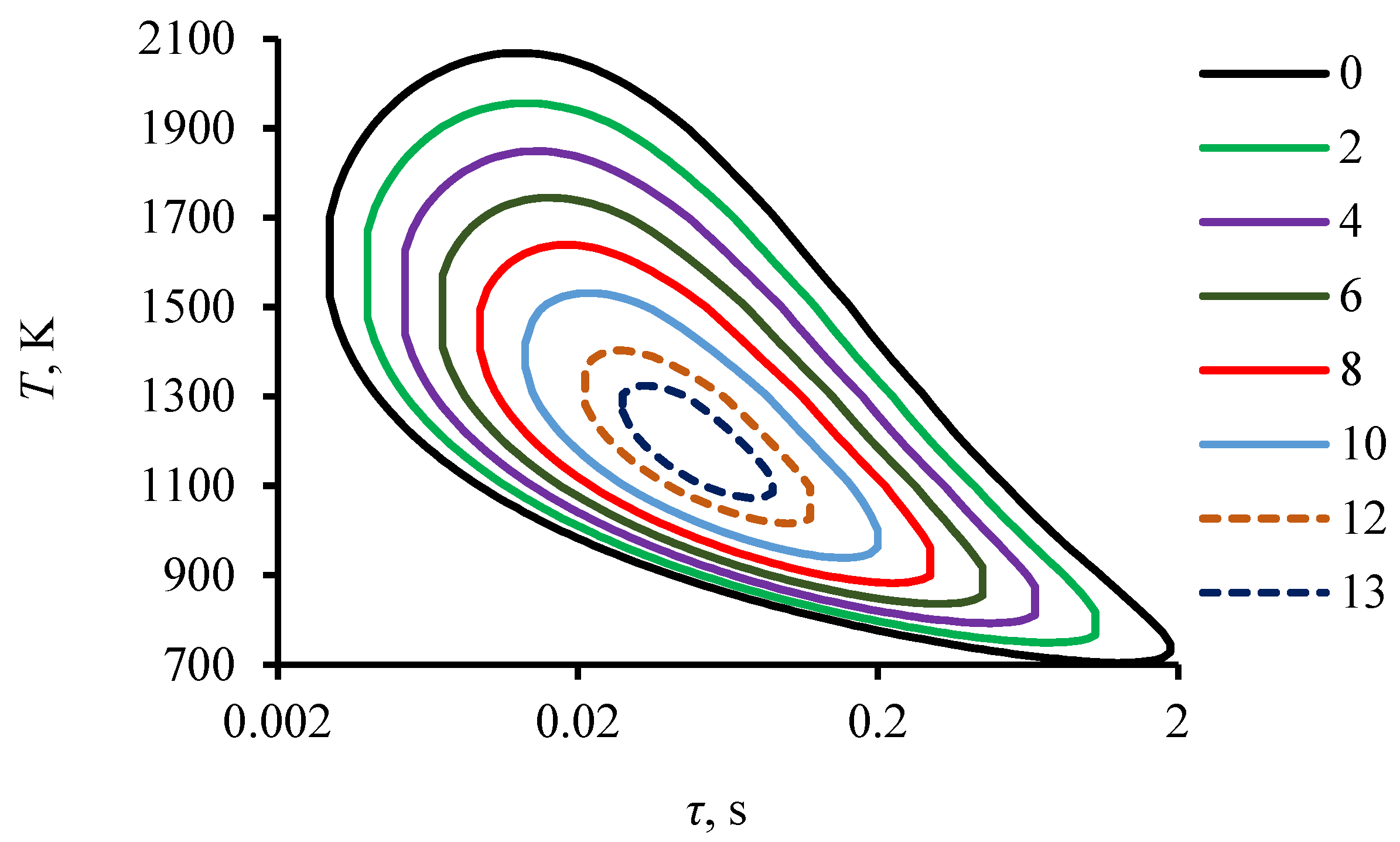
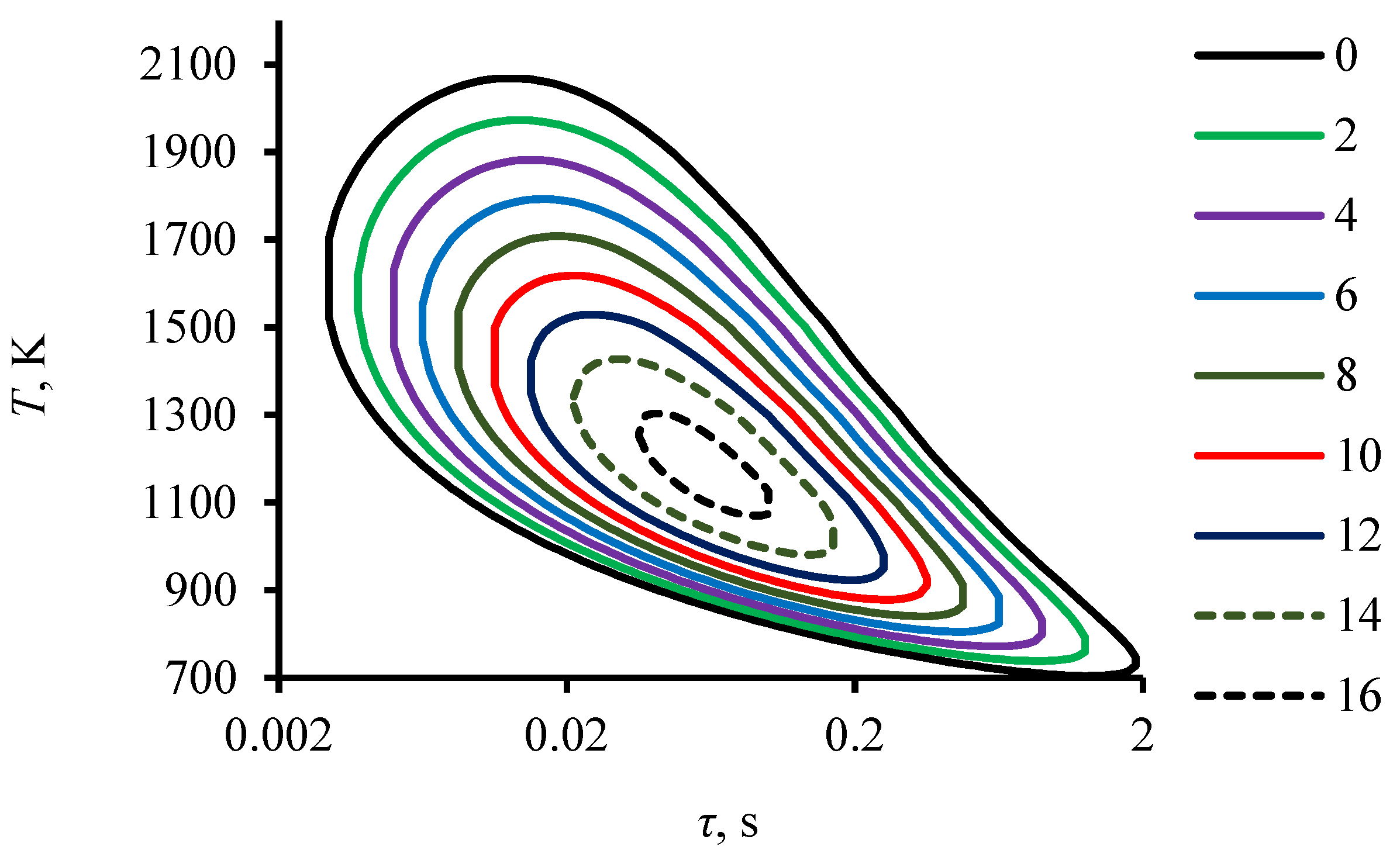
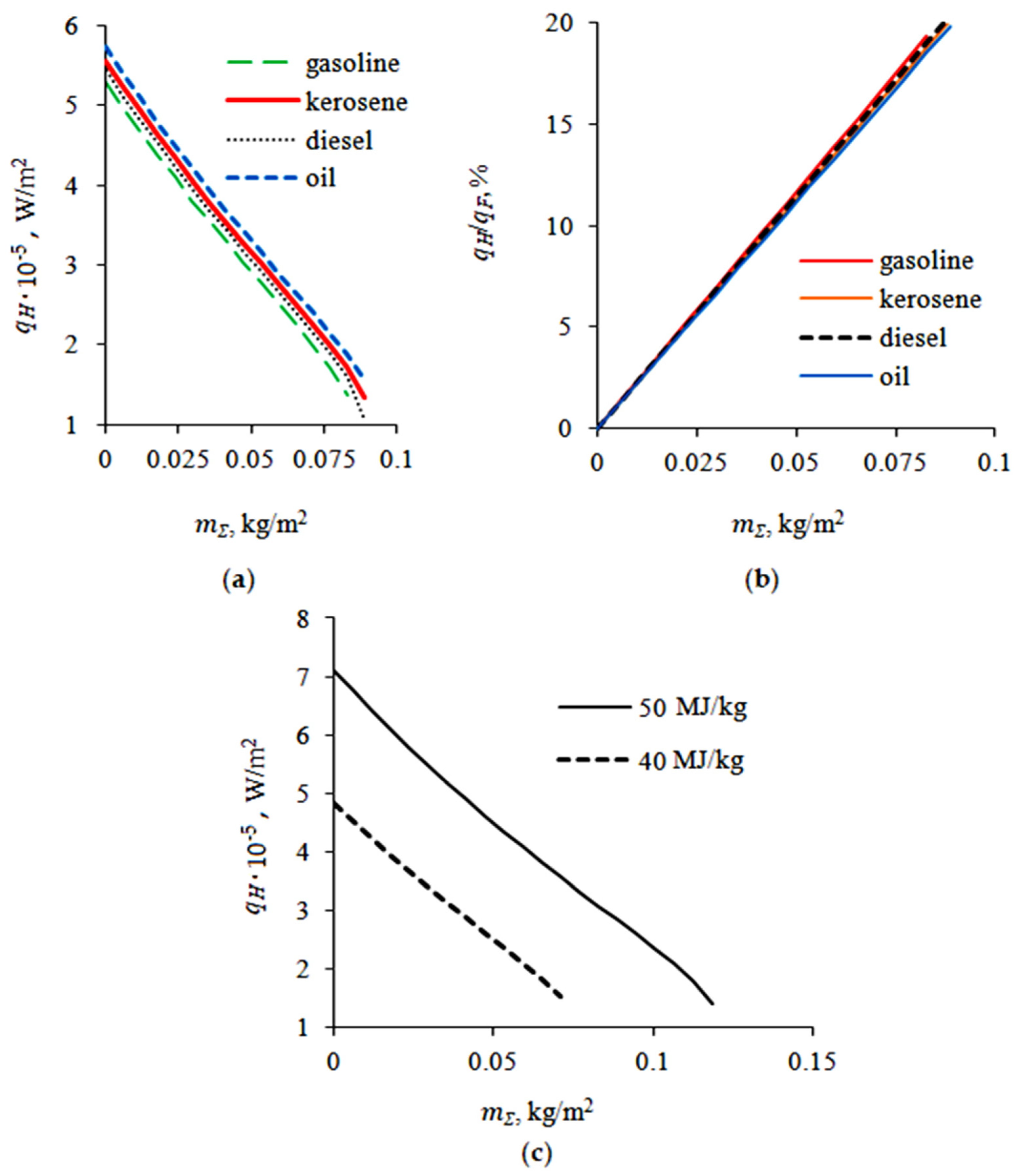
4.1. Dissociation of Carbon Dioxide Hydrate during Combustion
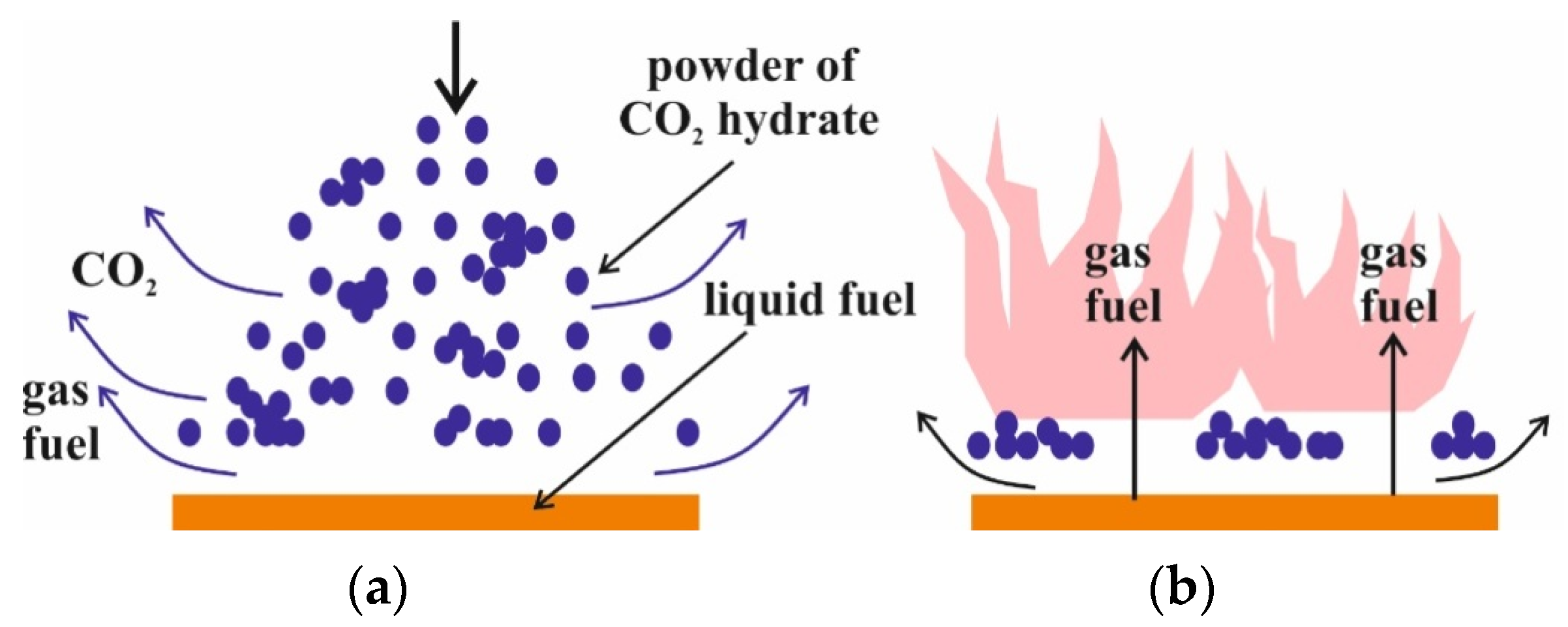
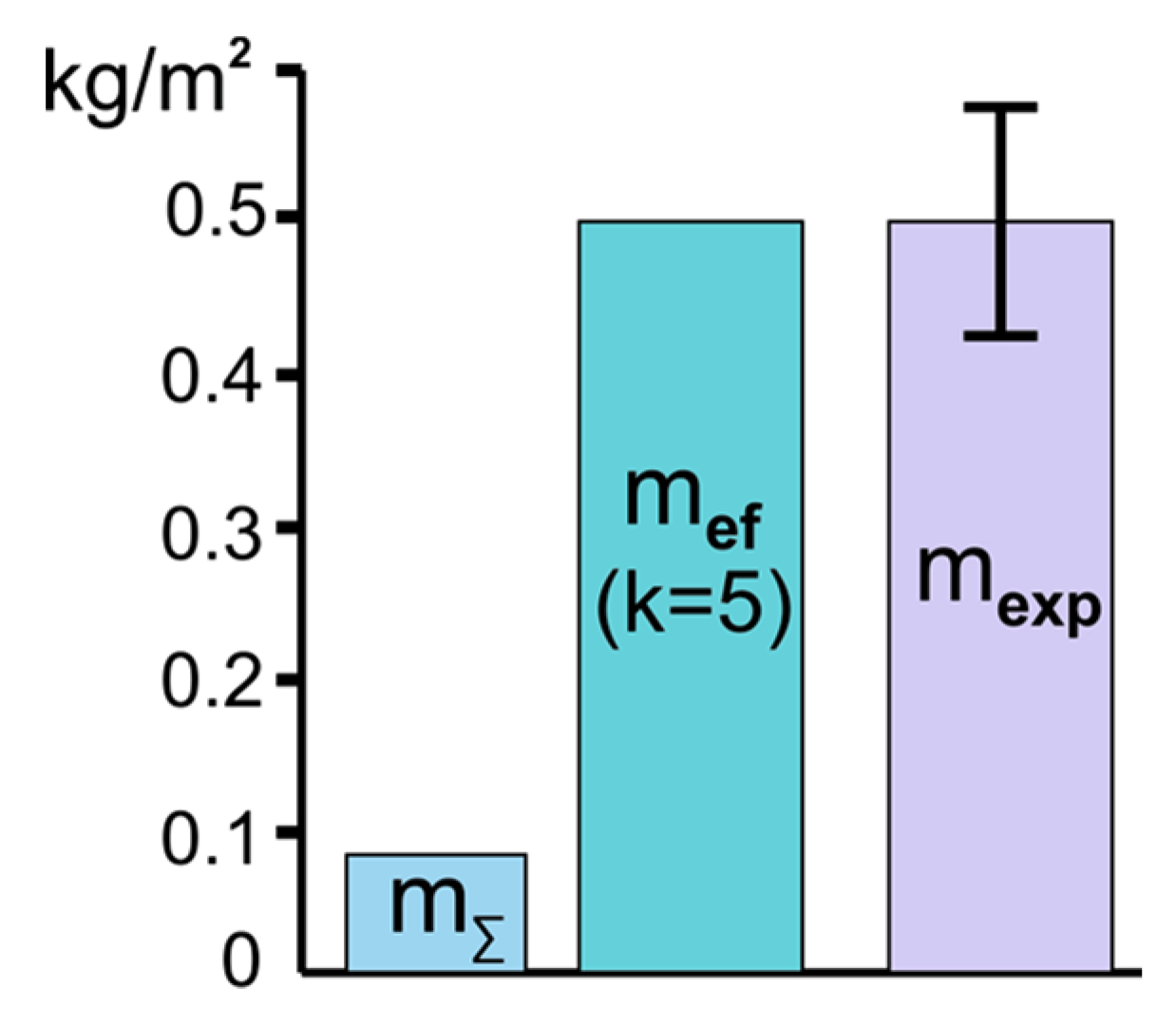
4.2. Flame Extinguishing by CO2 Hydrate Powder
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| AI-92 gasoline | Octane number | 91 |
| Lead content, g/dm3 | 0.01 | |
| Manganese content, mg/dm3 | 18 | |
| Oxidation stability of gasoline, min | 360 | |
| Existent gum content, mg/100 cm3 | 5 | |
| Mass fraction of sulfur, % | 0.05 | |
| TS-1 kerosene | Density at 20 °C, g/cm3 | 0.780 |
| Kinematic viscosity, mm2/s at 20 °C | 1.3 | |
| Lower heating value, kJ/kg | 43,120 | |
| Mass fraction of total sulfur, % | 0.2 | |
| Diesel | Cetane number | 45 |
| Kinematic viscosity, mm2/s at 20 °C | 4 | |
| Ash content, % | 0.01 | |
| Concentration of actual resins, mg per 100 cm3 of fuel | 30 | |
| Oil (Lukoil Genesis Armortech 5W30) | Density at 15 °C, kg/m3 | 844.8 |
| Kinematic viscosity at 100 °C, mm2/s | 9.7 | |
| Viscosity index | 173 | |
| Sulphate ash content, % | 1.05 | |
| Flash point in an open crucible, °C | 223 | |
| Oil separated | Mass fraction of water, wt.% | Absent |
| Density at 15 °C, kg/m3 | 797.5 | |
| Density at 20 °C, kg/m3 | 792.5 | |
| Kinematic viscosity at 15 °C, mm2/s | 4.391 | |
| Kinematic viscosity at 20 °C, mm2/s | 1.741 |
| Fuel | Velocity, m/s |
|---|---|
| AI-92 gasoline | 1.4 |
| TS-1 kerosene | 0.93 |
| Separated oil | 1.3 |
| oil | 0.8 |
| Diesel | 0.1 |
References
- Lu, Y.; Fan, X.; Zhao, Z.; Jiang, X. Dynamic Fire Risk Classification Prediction of Stadiums: Multi-Dimensional Machine Learning Analysis Based On Intelligent Perception. Appl. Sci. 2022, 12, 6607. [Google Scholar] [CrossRef]
- Surya, L. Risk Analysis Model That Uses Machine Learning to Predict the Likelihood of a Fire Occurring at A Given Property. Int. J. Creat. Res. Thoughts (IJCRT) 2017, 5, 2320–2882. [Google Scholar]
- Lo, S.M.; Liu, M.; Zhang, P.H.; Yuen, K.K.R. An Artificial Neural-network Base Predictive Model for Pre-evacuation Human Response in Domestic Building Fire. Fire Technol. 2008, 45, 431–449. [Google Scholar] [CrossRef]
- Argyropoulos, C.D.; Christolis, M.N.; Nivolianitou, Z.; Markatos, N.C. A hazards assessment methodology for large liquid hydrocarbon fuel tanks. J. Loss Prev. Process Ind. 2012, 25, 329–335. [Google Scholar] [CrossRef]
- Kwon, K.; Kim, Y.; Kwon, Y.; Koseki, H. Study on accidental fire at a large-scale floating-roof gasoline storage tank. J. Loss Prev. Process Ind. 2021, 73, 104613. [Google Scholar] [CrossRef]
- Zhou, R.; Dou, X.; Lang, X.; He, L.; Liu, J.; Mu, S. Foaming ability and stability of silica nanoparticle-based triple-phase foam for oil fire extinguishing: Experimental. Soft Mater. 2018, 16, 327–338. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, X.; Wu, Z.; Ju, X.; Peng, Y.; Yang, L. Ignition and burning behaviors of automobile oil in engine compartment. J. Therm. Anal. Calorim. 2018, 132, 305–316. [Google Scholar] [CrossRef]
- Tianwei, Z.; Cunwei, Z.; Hao, L.; Zhiyue, H. Experimental investigation of novel dry liquids with aqueous potassium Solution@Nano-SiO2 for the suppression of liquid fuel fires: Preparation, application, and stability. Fire Saf. J. 2020, 115, 103144. [Google Scholar] [CrossRef]
- von Blottnitz, H.; Curran, M.A. A review of assessments conducted on bio-ethanol as a transportation fuel from a net energy, greenhouse gas, and environmental life cycle perspective. J. Clean. Prod. 2007, 15, 607–619. [Google Scholar] [CrossRef]
- Kim, D.; Sakimoto, K.K.; Hong, D.; Yang, P. Artificial Photosynthesis for Sustainable Fuel and Chemical Production. Angew. Chem. Int. Ed. 2015, 54, 3259–3266. [Google Scholar] [CrossRef]
- Shinoda, K.; Nomura, T. Miscibility of fluorocarbon and hydrocarbon surfactants in micelles and liquid mixtures. Basic studies of oil repellent and fire extinguishing agents. J. Phys. Chem. 1980, 84, 365–369. [Google Scholar] [CrossRef]
- Khoat, H.T.; Kim, J.T.; Quoc, T.D.; Kwark, J.H.; Ryou, H.S. A numerical analysis of the fire characteristics after sprinkler activation in the compartment fire. Energies 2020, 13, 3099. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lee, M.; Hwang, I.J.; Kim, Y.J. Noise reduction of an extinguishing nozzle using the response surface method. Energies 2019, 12, 4346. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, X.; Yan, L.; Kang, W. Fire-extinguishing performance and mechanism of aqueous film-forming foam in diesel pool fire. Case Stud. Therm. Eng. 2020, 17, 100578. [Google Scholar] [CrossRef]
- Wang, H.; Du, Z.; Zhang, T.; Wang, Q.; Li, Y.; Kang, Q. Performance of Foam Agents on Pool Fires at High Altitudes. Fire Technol. 2022, 58, 1285–1304. [Google Scholar] [CrossRef]
- Rie, D.H.; Lee, J.W.; Kim, S. Class B fire-extinguishing performance evaluation of a compressed air foam system at different air-to-aqueous foam solution mixing ratios. Appl. Sci. 2016, 6, 191. [Google Scholar] [CrossRef]
- Lv, D.; Tan, W.; Zhu, G.; Liu, L. Gasoline fire extinguishing by 0.7 MPa water mist with multicomponent additives driven by CO2. Process Saf. Environ. Prot. 2019, 129, 168–175. [Google Scholar] [CrossRef]
- Harding, B.; Zhang, B.; Liu, Y.; Chen, H.; Mannan, M.S. Improved research-scale foam generator design and performance characterization. J. Loss Prev. Process Ind. 2016, 39, 173–180. [Google Scholar] [CrossRef]
- Koshiba, Y.; Okazaki, S.; Ohtani, H. Experimental investigation of the fire extinguishing capability of ferrocene-containing water mist. Fire Saf. J. 2016, 83, 90–98. [Google Scholar] [CrossRef]
- Rumminger, M.D.; Linteris, G.T. Inhibition of premixed carbon monoxide–hydrogen–oxygen–nitrogen flames by iron pentacarbonyl. Combust. Flame 2000, 120, 451–464. [Google Scholar] [CrossRef]
- Liu, C. Fire fighting of wind extinguisher with CO2 gas assisted. Appl. Mech. Mater. 2012, 130–134, 1054–1057. [Google Scholar] [CrossRef]
- Sloan, E.D., Jr.; Koh, C.A. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Misyura, S.; Strizhak, P.; Meleshkin, A.; Morozov, V.; Gaidukova, O.; Shlegel, N.; Shkola, M. A Review of Gas Capture and Liquid Separation Technologies by CO2 Gas Hydrate. Energies 2023, 16, 3318. [Google Scholar] [CrossRef]
- Misyura, S.Y. Dissociation of various gas hydrates (methane hydrate, double gas hydrates of methane-propane and methane-isopropanol) during combustion: Assessing the combustion efficiency. Energy 2020, 206, 118120. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Wang, Y.; Qin, C.; Li, B.; Luo, Y.; Feng, J. Investigating the interaction effects between reservoir deformation and hydrate dissociation in hydrate-bearing sediment by depressurization method. Energies 2021, 14, 548. [Google Scholar] [CrossRef]
- Sahith, S.J.K.; Pedapati, S.R.; Lal, B. Investigation on gas hydrates formation and dissociation in multiphase gas dominant transmission pipelines. Appl. Sci. 2020, 10, 5052. [Google Scholar] [CrossRef]
- Misyura, S.Y. Evaporation of water droplet on heated textured wall at various contact angles. J. Eng. Thermophys. 2022, 31, 414–419. [Google Scholar] [CrossRef]
- Rossi, F.; Gambelli, A.M.; Sharma, D.K.; Castellani, B.; Nicolini, A.; Castaldi, M.J. Experiments on methane hydrates formation in seabed deposits and gas recovery adopting carbon dioxide replacement strategies. Appl. Therm. Eng. 2019, 148, 371–381. [Google Scholar] [CrossRef]
- Kang, K.C.; Linga, P.; Park, K.N.; Choi, S.J.; Lee, J.D. Seawater desalination by gas hydrate process and removal characteristics of dissolved ions (Na+, K+, Mg2+, Ca2+, B3+, Cl−, SO42−). Desalination 2014, 353, 84–90. [Google Scholar] [CrossRef]
- Liu, N.; Meng, F.; Chen, L.; Yang, L.; Liu, D. Investigating the effects of MWCNT-HB on gas storage performance of CO2 hydrate. Fuel 2022, 316, 123289. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Yang, H.; Li, J.; Li, Y.; Wu, Q. Formation and storage characteristics of CO2 hydrate in porous media: Effect of liquefaction amount on the formation rate, accumulation amount. Appl. Therm. Eng. 2022, 214, 118747. [Google Scholar] [CrossRef]
- Prah, B.; Yun, R. CO2 hydrate slurry transportation in carbon capture and storage. Appl. Therm. Eng. 2018, 128, 653–661. [Google Scholar] [CrossRef]
- Sato, T.; Takeya, S.; Nagashima, H.D.; Ohmura, R. Preservation of carbon dioxide clathrate hydrate coexisting with sucrose under domestic freezer conditions. J. Food Eng. 2014, 120, 69–74. [Google Scholar] [CrossRef]
- Choi, J.W.; Kim, S.; Kang, Y.T. CO2 hydrate cooling system and LCC analysis for energy transportation application. Appl. Therm. Eng. 2015, 91, 11–18. [Google Scholar] [CrossRef]
- Liu, R.; Gao, F.; Liang, K.; Yuan, Z.; Ruan, C.; Wang, L.; Yang, S. Experimental study on the correlation between rapid formation of gas hydrate and diffusion of guest molecules. Appl. Therm. Eng. 2019, 154, 393–399. [Google Scholar] [CrossRef]
- Wei, J.; Cheng, Y.; Yan, C.; Li, Q.; Han, S.; Ansari, U. Decomposition prevention through thermal sensitivity of hydrate formations around wellbore. Appl. Therm. Eng. 2019, 159, 113921. [Google Scholar] [CrossRef]
- Hatakeyama, T.; Aida, E.; Yokomori, T.; Ohmura, R.; Ueda, T. Fire extinction using carbon dioxide hydrate. Ind. Eng. Chem. Res. 2009, 48, 4083–4087. [Google Scholar] [CrossRef]
- Sugahara, A.; Nakano, H.; Yokomori, T.; Ohmura, R.; Ueda, T. Effect of fuel boiling point of pool flame for the flame extinction by CO2 hydrate. In Proceedings of the 10th Asia-Pacific Conference on Combustion, ASPACC 2015, Beijing, China, 19–22 July 2015. [Google Scholar]
- GOST 32513-2013; Automotive Fuels. Unleaded Petrol. GOST: Glasgow, UK, 2015.
- GOST 10227-86; Jetfuels. GOST: Glasgow, UK, 1987.
- GOST 305-82; Diesel Fuel. GOST: Glasgow, UK, 1982.
- GOST 5962-2013; Rectified Ethyl Alcohol from Edible Raw Material. GOST: Glasgow, UK, 2013.
- Tupsakhare, S.S.; Castaldi, M.J. Efficiency enhancements in methane recovery from natural gas hydrates using injection of CO2/N2 gas mixture simulating in-situ combustion. Appl. Energy 2019, 236, 825–836. [Google Scholar] [CrossRef]
- Misyura, S.Y.; Manakov, A.Y.; Morozov, V.S.; Nyashina, G.S.; Gaidukova, O.S.; Skiba, S.S.; Volkov, R.S.; Voytkov, I.S. The influence of key parameters on combustion of double gas hydrate. J. Nat. Gas Sci. Eng. 2020, 80, 103396. [Google Scholar] [CrossRef]
- Gaidukova, O.; Donskoy, I.; Misyura, S.; Morozov, V.; Volkov, R. The interaction between a liquid combustion front and a fire barrier made of CO2 hydrate. Fire 2023, 6, 124. [Google Scholar]
- Gaidukova, O.; Morozov, V.; Volkov, R.; Strizhak, P. Containment and suppression of class A fires using CO2 hydrate. Fire 2023, 6, 82. [Google Scholar] [CrossRef]
- Dunn, G.J.; Wilson, S.K.; Duffy, B.R.; David, S.; Sefiane, K. The strong influence of substrate conductivity on droplet evaporation. J. Fluid Mech. 2009, 623, 329–351. [Google Scholar] [CrossRef]
- Carle, F.; Semenov, S.; Medale, M.; Brutin, D. Contribution of convective transport to evaporation of sessile droplets: Empirical model. Int. J. Therm. Sci. 2016, 101, 35–47. [Google Scholar] [CrossRef]
- Misyura, S.Y.; Egorov, R.I.; Morozov, V.S.; Zaitsev, A.S. The influence of the liquid layer height on the velocity field and evaporation during local heating. Exper. Heat Transf. 2023. [Google Scholar] [CrossRef]
- Kutateladze, S.S.; Leontiev, A.I. Heat Transfer, Mass Transfer and Friction in Turbulent Boundary Layer; Hemisphere: New York, NY, USA, 1990. [Google Scholar]
- Kim, H.C.; Bishnoi, P.R.; Heidemann, R.A.; Rizvi, S.S.H. Kinetics of methane hydrate decomposition. Chem. Eng. Sci. 1987, 42, 1645–1653. [Google Scholar] [CrossRef]
- Gaidukova, O.; Misyura, S.; Morozov, V.; Strizhak, P. Gas Hydrates: Applications and Advantages. Energies 2023, 16, 2866. [Google Scholar] [CrossRef]
- Misyura, S.Y.; Donskoy, I.G. Dissociation of gas hydrate for a single particle and for a thick layer of particles: The effect of self-preservation on the dissociation kinetics of the gas hydrate layer. Fuel 2022, 314, 122759. [Google Scholar] [CrossRef]
- Aerov, M.E.; Todes, O.M.; Narinsky, D.A. Apparatuses with the Steady Grain Layer: Hydraulic and Thermal Fundamentals of Operation; Khimiya: Saint Petersburg, Russia, 1979. [Google Scholar]
- Misyura, S.Y.; Donskoy, I.G.; Manakov, A.Y.; Morozov, V.S.; Strizhak, P.A.; Skiba, S.S.; Sagidullin, A.K. Combustion of a powder layer of methane hydrate: The influence of layer height and air velocity above the layer. Flow Turbul. Combust 2022, 109, 175–191. [Google Scholar] [CrossRef]
- Misyura, S.Y.; Donskoy, I.G. Dissociation kinetics of methane hydrate and CO2 hydrate for different granular composition. Fuel 2020, 262, 116614. [Google Scholar] [CrossRef]
- Misyura, S.Y.; Donskoy, I.G. Co-modeling of methane hydrate dissociation and combustion in a boundary layer. Combust. Flame 2022, 238, 111912. [Google Scholar] [CrossRef]
- Gaydukova, O.S.; Misyura, S.Y.; Strizhak, P.A. Investigating regularities of gas hydrate ignition on a heated surface: Experiments and modeling. Combust. Flame 2021, 228, 78–88. [Google Scholar] [CrossRef]
- Misyura, S.Y.; Donskoy, I.G.; Manakov, A.Y.; Morozov, V.S.; Strizhak, P.A.; Skiba, S.S.; Sagidullin, A.K. Studying the influence of key parameters on the methane hydrate dissociation in order to improve the storage efficiency. J. Energy Storage 2021, 44, 103288. [Google Scholar] [CrossRef]
- Misyura, S.Y. Dissociation and combustion of gas hydrates. J. Eng. Thermophys. 2022, 31, 573–579. [Google Scholar] [CrossRef]
- McBride, B.J.; Zehe, M.J.; Gordon, S. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species; National Aeronautics and Space Administration, John H. Glenn Research Center: Cleveland, MD, USA, 2002.
- Ju, Y.; Guo, H.; Liu, F.; Maruta, K. Effects of the Lewis number and radiative heat loss on the bifurcation and extinction of CH4/O2-N2-He flames. J. Fluid Mech. 1999, 379, 165–190. [Google Scholar] [CrossRef]
- Balakotaiah, V.; Luss, D. Global analysis of the multiplicity features of multi-reaction lumped-parameter systems. Chem. Eng. Sci. 1984, 39, 865–881. [Google Scholar] [CrossRef]
- Cui, G.; Dong, Z.; Wang, S.; Xing, X.; Shan, T.; Li, Z. Effect of the water on the flame characteristics of methane hydrate combustion. Appl. Energy 2020, 259, 114205. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Misyura, S.; Morozov, V.; Donskoy, I.; Shlegel, N.; Dorokhov, V. Combustion of Liquid Fuels in the Presence of CO2 Hydrate Powder. Fire 2023, 6, 318. https://doi.org/10.3390/fire6080318
Misyura S, Morozov V, Donskoy I, Shlegel N, Dorokhov V. Combustion of Liquid Fuels in the Presence of CO2 Hydrate Powder. Fire. 2023; 6(8):318. https://doi.org/10.3390/fire6080318
Chicago/Turabian StyleMisyura, Sergey, Vladimir Morozov, Igor Donskoy, Nikita Shlegel, and Vadim Dorokhov. 2023. "Combustion of Liquid Fuels in the Presence of CO2 Hydrate Powder" Fire 6, no. 8: 318. https://doi.org/10.3390/fire6080318
APA StyleMisyura, S., Morozov, V., Donskoy, I., Shlegel, N., & Dorokhov, V. (2023). Combustion of Liquid Fuels in the Presence of CO2 Hydrate Powder. Fire, 6(8), 318. https://doi.org/10.3390/fire6080318









