A Dijkstra-Based Approach to Fuelbreak Planning
Abstract
1. Introduction
2. Materials and Methods
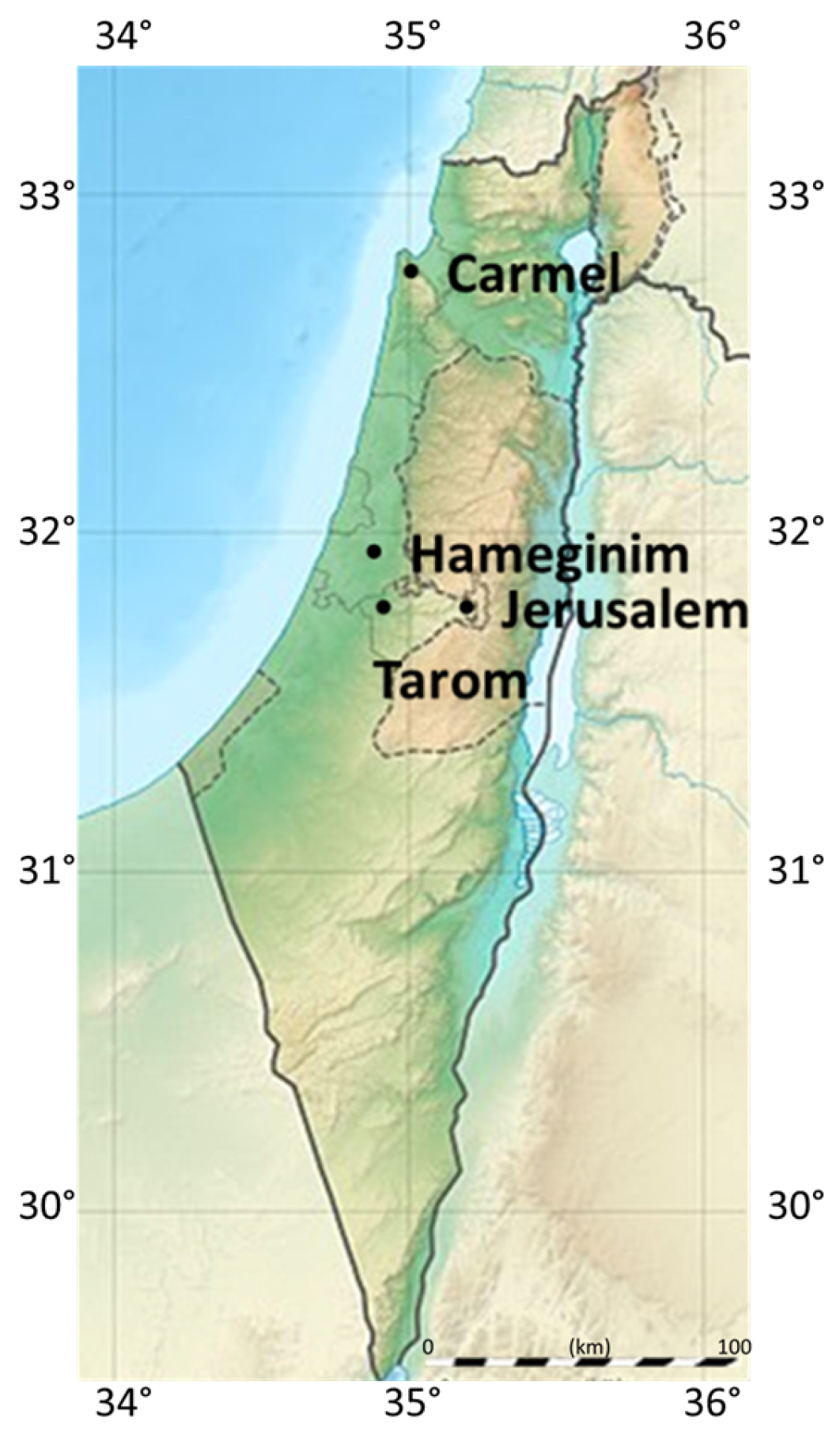
2.1. Study Area
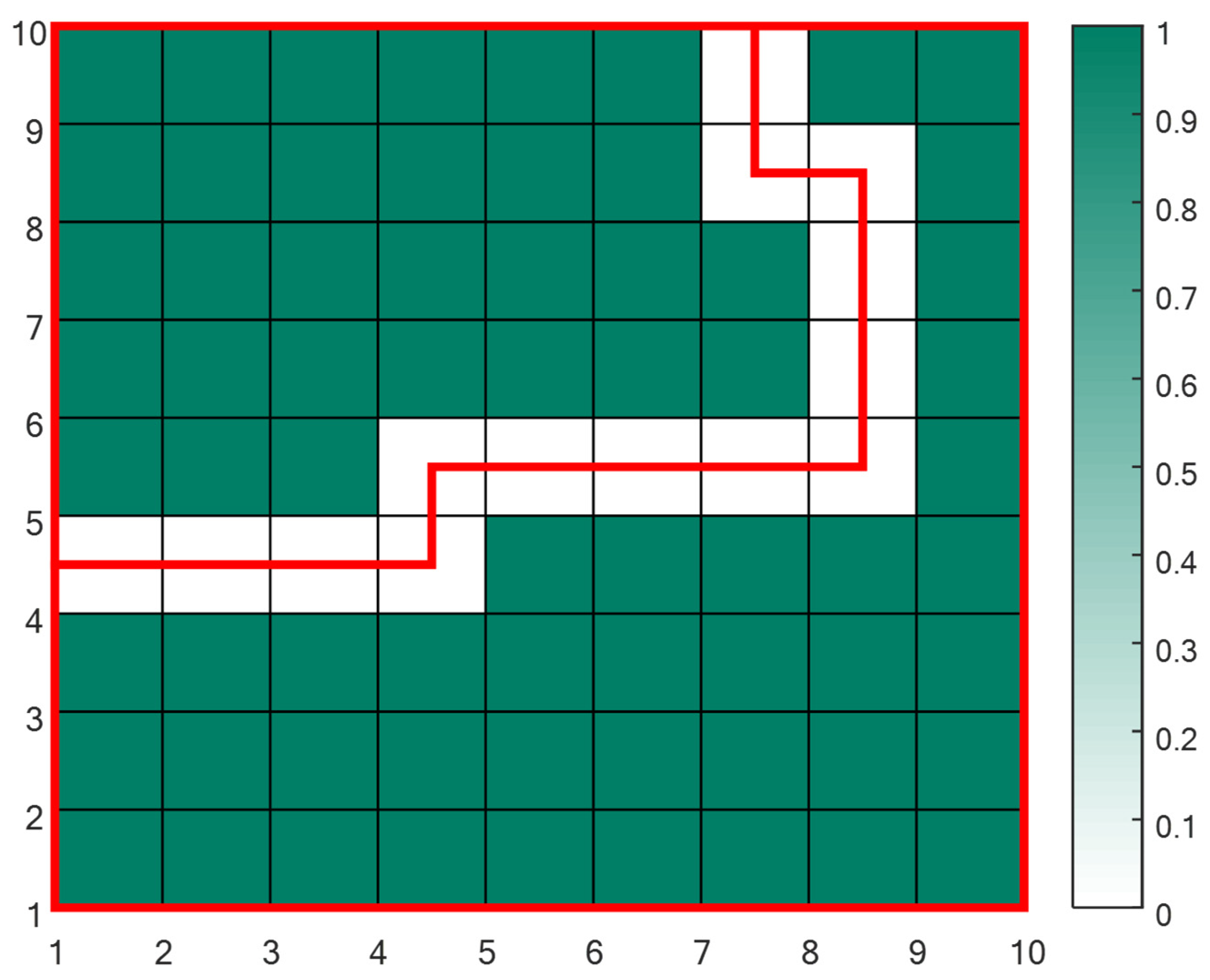
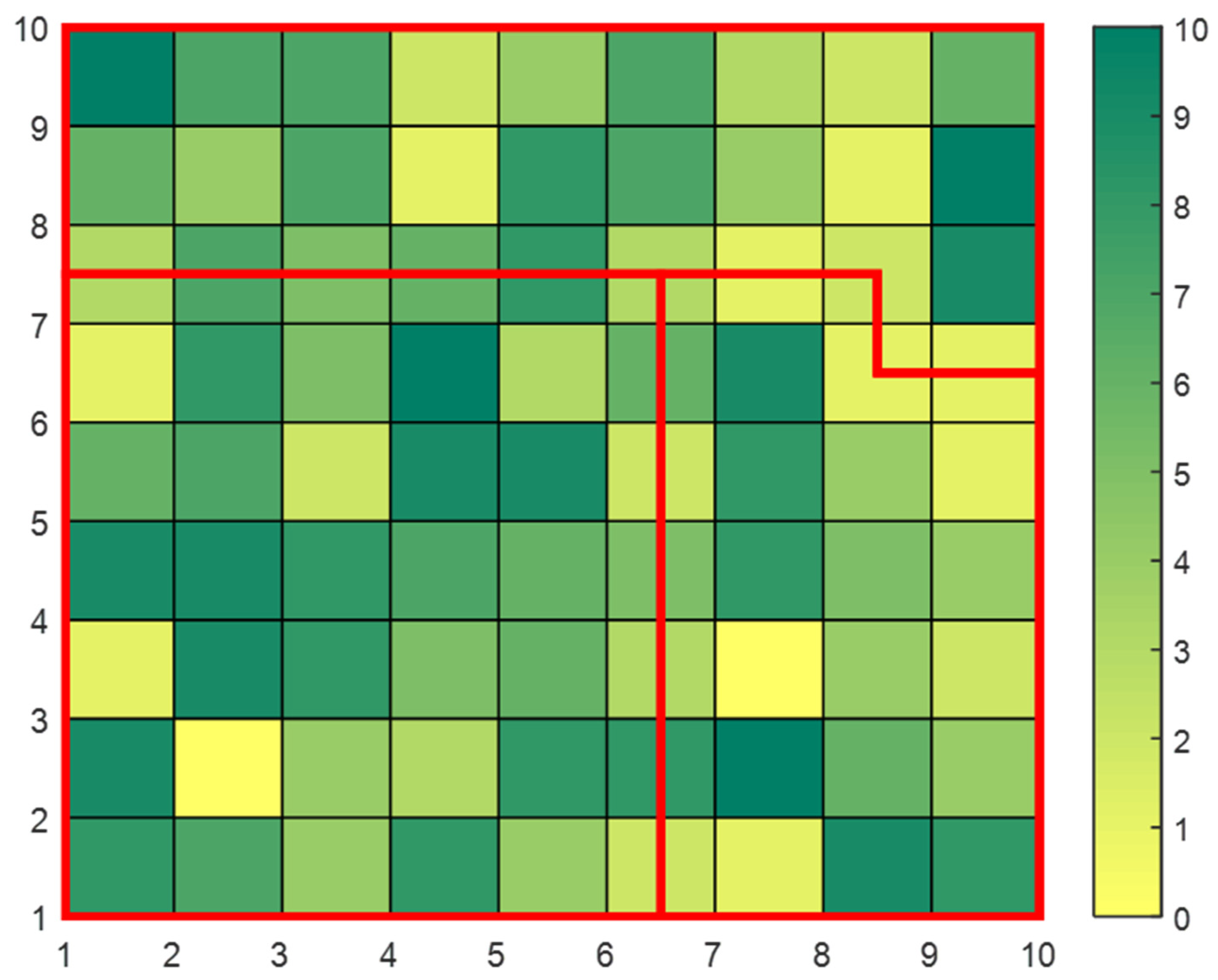
2.2. Fuelbreak Planning Algorithm
- The simulation finds all possible pairs of two nonadjacent pixels in the forest boundary.
- For each pair, the simulation runs the Dijkstra [33] algorithm whose output is the ‘shortest path’ between the two pixels—in the meaning of minimal forestry area that the line passes through (i.e., the minimal sum of forestry cells in each path).
- The algorithm then chooses the shortest path from all the valid paths; a path is defined valid if it divides the forest into two sections where at least one of the sections contains a lower forestry area than the maximal value permitted in a section. Paths that create extremely small forest sections (sections that contain a significantly lower forestry area than the maximal value) are disregarded.
- Out of all the remaining possible paths between two boundary pixels, the simulation chooses the least costly path.
2.3. Research Design and Data
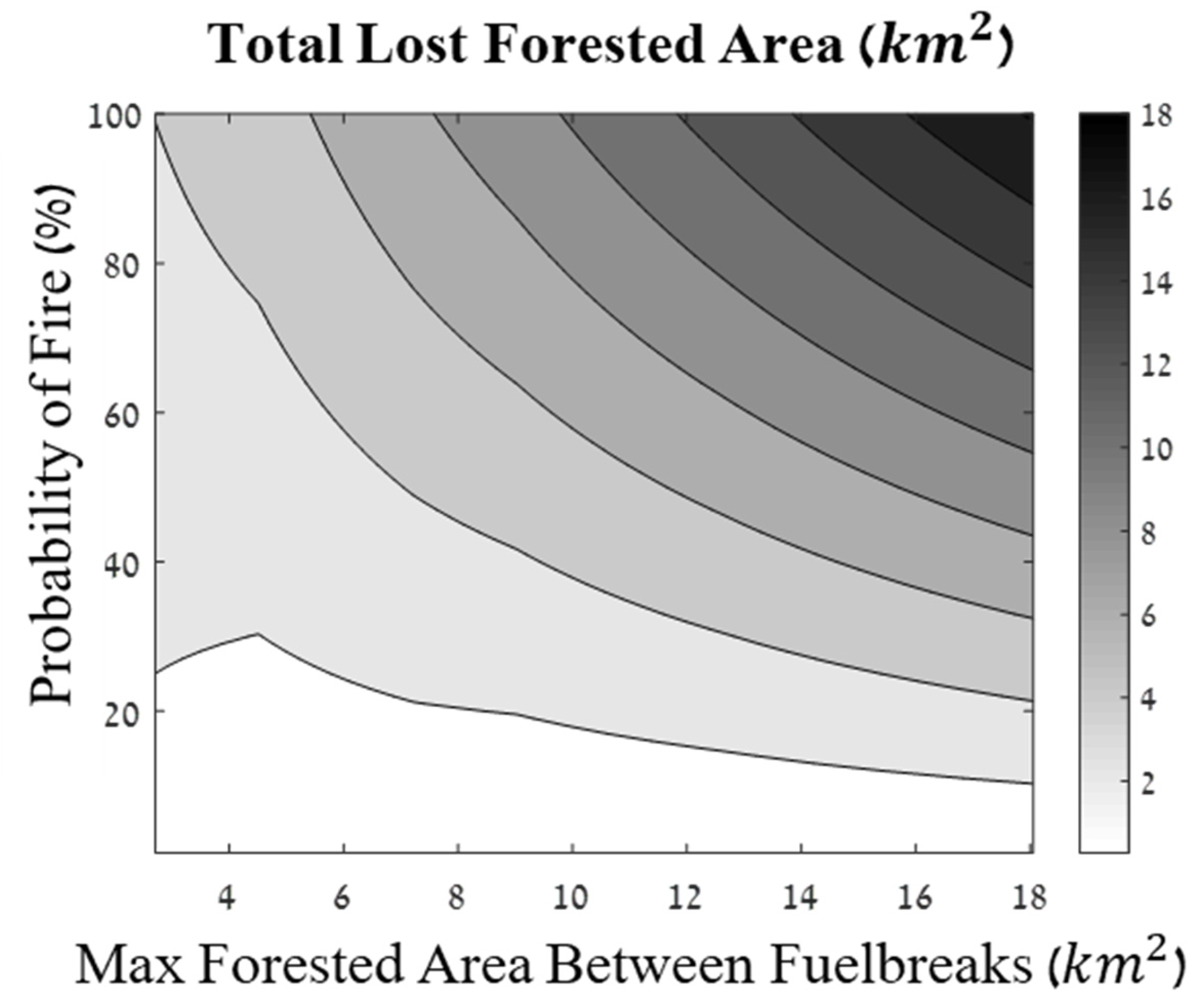
3. Results
3.1. Examples of the Algorithm Run on Artificial Forests
3.2. Actual Forest Run—The Carmel Forest
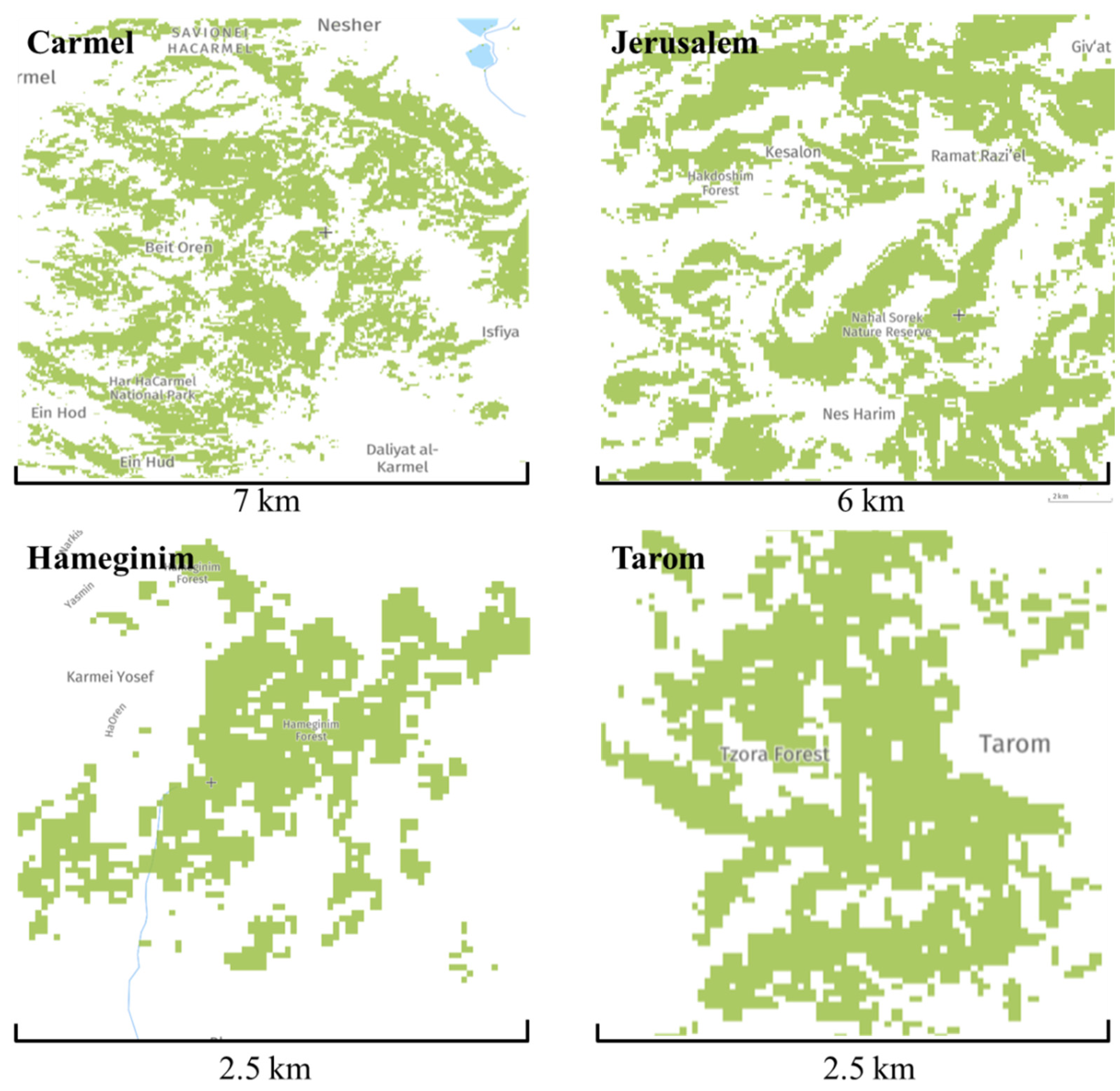
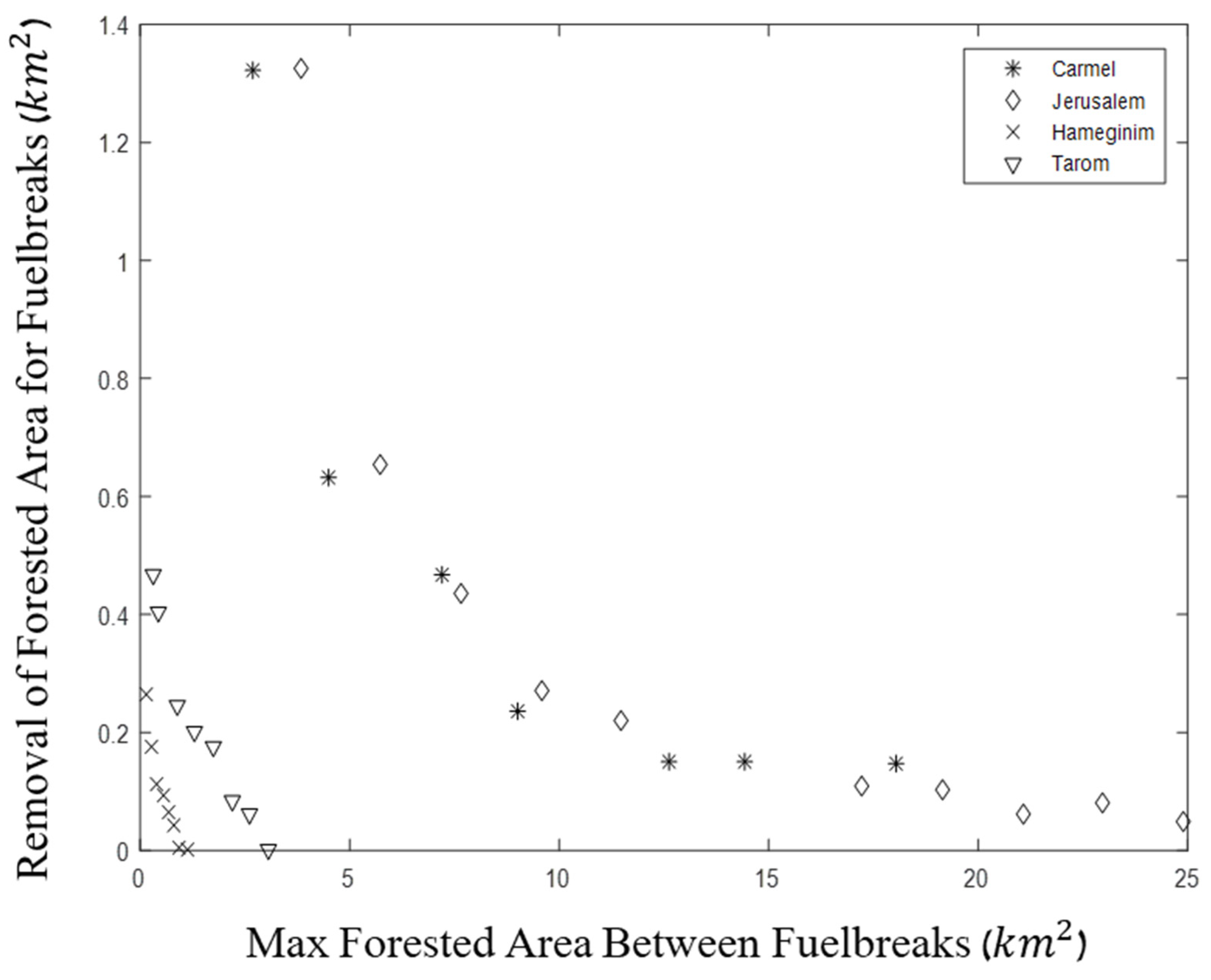
3.3. Additional Forests in Israel
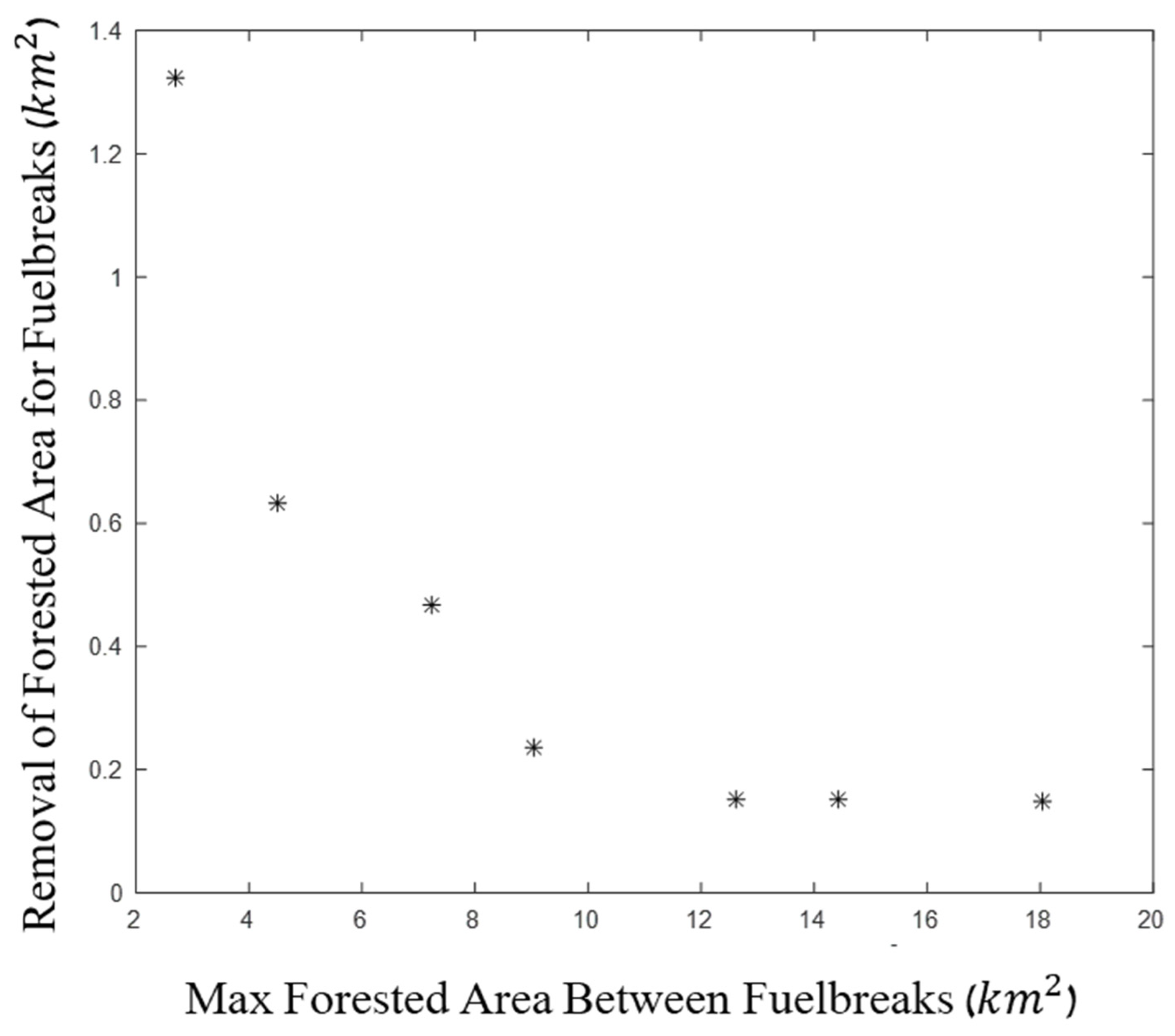
3.4. A Tree-Economy Perspective
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chandrasekaran, R.; Shephard, R.W. Optimal Strategies of Fire Fighting by Firebreaks (No. ORC-66-30); California University Berkley Operations Research Center: Berkeley, CA, USA, 1966. [Google Scholar]
- Strauss, D.; Bednar, L.; Mees, R. Do one percent of the forest fires cause ninety-nine percent of the damage? For. Sci. 1989, 35, 319–328. [Google Scholar]
- Holmes, T.P.; Huggett, R.J.; Westerling, A.L. Statistical analysis of large wildfires. In The Economics of Forest Disturbances; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany, 2008; pp. 59–77. [Google Scholar]
- Mooney, C. Fuelbreak Effectiveness: State of the Knowledge; Wildland Fire Operations Research Group 1176; Switzer Drive: Hinton, AB, Canada, 2007. [Google Scholar]
- Perriez, F.; Bartet, J.H.; Barthélemy, F.; Foin, P.; Battesti, J.P.; David, J.P. Rapport Relatif à la Protection Contre Les Incendies de forêt Après Les Feux de L’éTé 2003 Tome 1: Rapport Général. 2003, p. 126. Available online: https://www.vie-publique.fr/rapport/26676-la-protection-contre-les-incendies-de-foret-apres-les-feux-de-lete-2003 (accessed on 1 July 2023).
- Xanthopoulos, G.; Caballero, D.; Galante, M.; Alexandrian, D.; Rigolot, E.; Marzano, R. Forest fuels management in Europe. In Fuels Management—How to Measure Success: Conference Proceedings; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; Volume 41, pp. 29–46. [Google Scholar]
- Wang, H.H.; Finney, M.A.; Song, Z.L.; Wang, Z.S.; Li, X.C. Ecological techniques for wildfire mitigation: Two distinct fuelbreak approaches and their fusion. For. Ecol. Manag. 2021, 495, 119376. [Google Scholar] [CrossRef]
- Cui, X.; Alam, M.A.; Perry, G.L.; Paterson, A.M.; Wyse, S.V.; Curran, T.J. Green firebreaks as a management tool for wildfires: Lessons from China. J. Environ. Manag. 2019, 233, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Song, H.S.; Lee, S.H. Effects of wind and tree density on forest fire patterns in a mixed-tree species forest. For. Sci. Technol. 2017, 13, 9–16. [Google Scholar] [CrossRef]
- Kim, D.W.; Chung, W.; Lee, B. Exploring tree crown spacing and slope interaction effects on fire behavior with a physics-based fire model. For. Sci. Technol. 2016, 12, 167–175. [Google Scholar] [CrossRef]
- Chung, W. Optimizing fuel treatments to reduce wildland fire risk. Curr. For. Rep. 2015, 1, 44–51. [Google Scholar] [CrossRef]
- Finney, M.A. An overview of FlamMap fire modeling capabilities. In Fuels Management—How to Measure Success: Conference Proceedings; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA; Volume 41, pp. 213–220.
- Mell, W.; Jenkins, M.A.; Gould, J.; Cheney, P. A physics-based approach to modelling grassland fires. Int. J. Wildland Fire 2007, 16, 1–22. [Google Scholar] [CrossRef]
- Mell, W.; Charney, J.; Jenkins, M.A.; Cheney, P.; Gould, J. Numerical simulations of grassland fire behavior from the LANL-FIRETEC and NIST-WFDS models. In Remote Sensing and Modeling Applications to Wildland Fires; Springer: Berlin/Heidelberg, Germany, 2013; pp. 209–225. [Google Scholar]
- Soffer, G. After the Carmel Fire: Ecology of Fire, KKL and Government. Personal Blog. Available online: http://gilisoffer.com/WP/?p=452 (accessed on 19 July 2023).
- Russo, L.; Russo, P.; Siettos, C.I. A complex network theory approach for the spatial distribution of fire breaks in heterogeneous forest landscapes for the control of wildland fires. PLoS ONE 2016, 11, e0163226. [Google Scholar] [CrossRef]
- Ascoli, D.; Russo, L.; Giannino, F.; Siettos, C.; Moreira, F.; Firebreak and Fuelbreak. Encyclopedia of Wildfires and Wildland-Urban Interface (WUI) Fires; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany, 2018; pp. 1–9. [Google Scholar]
- Wei, Y.; Rideout, D.; Kirsch, A. An optimization model for locating fuel treatments across a landscape to reduce expected fire losses. Can. J. For. Res. 2008, 38, 868–877. [Google Scholar] [CrossRef]
- Wei, Y.; Long, Y. Schedule fuel treatments to fragment high fire hazard fuel patches. Math. Comput. For. Nat. Resour. Sci. 2014, 6, 1. [Google Scholar]
- León, J.; Reijnders, V.M.; Hearne, J.W.; Ozlen, M.; Reinke, K.J. A Landscape-scale optimisation model to break the hazardous fuel continuum while maintaining habitat quality. Environ. Model. Assess. 2019, 24, 369–379. [Google Scholar] [CrossRef]
- Hof, J.; Omi, P.N.; Bevers, M.; Laven, R.D. A timing-oriented approach to spatial allocation of fire management effort. For. Sci. 2000, 46, 442–451. [Google Scholar]
- Finney, M.A. A computational method for optimising fuel treatment locations. Int. J. Wildland Fire 2007, 16, 702–711. [Google Scholar] [CrossRef]
- Wei, Y. Optimize landscape fuel treatment locations to create control opportunities for future fires. Can. J. For. Res. 2012, 42, 1002–1014. [Google Scholar] [CrossRef]
- Minas, J.P.; Hearne, J.W. An optimization model for aggregation of prescribed burn units. TOP 2016, 24, 180–195. [Google Scholar] [CrossRef]
- Rachmawati, R.; Ozlen, M.; Reinke, K.J.; Hearne, J.W. An optimisation approach for fuel treatment planning to break the connectivity of high-risk regions. For. Ecol. Manag. 2016, 368, 94–104. [Google Scholar] [CrossRef]
- Minas, J.P.; Hearne, J.W.; Martell, D.L. A spatial optimisation model for multi-period landscape level fuel management to mitigate wildfire impacts. Eur. J. Oper. Res. 2014, 232, 412–422. [Google Scholar] [CrossRef]
- Minas, J.; Hearne, J.; Martell, D. An integrated optimization model for fuel management and fire suppression preparedness planning. Ann. Oper. Res. 2015, 232, 201–215. [Google Scholar] [CrossRef]
- Acuna, M.A.; Palma, C.D.; Cui, W.; Martell, D.L.; Weintraub, A. Integrated spatial fire and forest management planning. Can. J. For. Res. 2010, 40, 2370–2383. [Google Scholar] [CrossRef]
- Palma, C.D.; Cui, W.; Martell, D.L.; Robak, D.; Weintraub, A. Assessing the impact of stand-level harvests on the flammability of forest landscapes. Int. J. Wildland Fire 2007, 16, 584–592. [Google Scholar] [CrossRef]
- Global Forest Watch. Available online: https://www.globalforestwatch.org/ (accessed on 19 July 2023).
- Wittenberg, L.; Malkinson, D.; Beeri, O.; Halutzy, A.; Tesler, N. Spatial and temporal patterns of vegetation recovery following sequences of forest fires in a Mediterranean landscape, Mt. Carmel Israel. Catena 2007, 71, 76–83. [Google Scholar] [CrossRef]
- Gaba, E. Geography of Israel. Available online: https://en.wikipedia.org/wiki/Geography_of_Israel (accessed on 1 July 2023).
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Carlson, J.M.; Doyle, J. Highly optimized tolerance: A mechanism for power laws in designed systems. Phys. Rev. E 1999, 60, 1412. [Google Scholar] [CrossRef] [PubMed]
- Moritz, M.A.; Hessburg, P.F.; Povak, N.A. Native fire regimes and landscape resilience. In The Landscape Ecology of Fire; Springer: Dordrecht, The Netherlands, 2010; pp. 51–86. [Google Scholar]
- Malamud, B.D.; Morein, G.; Turcotte, D.L. Forest fires: An example of self-organized critical behavior. Science 1998, 281, 1840–1842. [Google Scholar] [CrossRef]
- Laschi, A.; Foderi, C.; Fabiano, F.; Neri, F.; Cambi, M.; Mariotti, B.; Marchi, E. Forest road planning, construction and maintenance to improve forest fire fighting: A review. Croat. J. For. Eng. J. Theory Appl. For. Eng. 2019, 40, 207–219. [Google Scholar]
- Thomas, G.; Rosalie, V.; Olivier, C.; Antonio, L.P. Modelling forest fire and firebreak scenarios in a mediterranean mountainous catchment: Impacts on sediment loads. J. Environ. Manag. 2021, 289, 112497. [Google Scholar] [CrossRef]
- Finney, M.A. Design of regular landscape fuel treatment patterns for modifying fire growth and behavior. For. Sci. 2001, 47, 219–228. [Google Scholar]
- Zinck, R.D.; Grimm, V. Unifying wildfire models from ecology and statistical physics. Am. Nat. 2009, 174, E170–E185. [Google Scholar] [CrossRef]
- Thakar, V. A spatial Optimization Approach to Finding Locations for Wildfire Fuel Treatments. Ph.D. Thesis, The University of Texas, Dallas, TX, USA, 2017. [Google Scholar]
- Seto, D.; Jones, C.; Trugman, A.T.; Varga, K.; Plantinga, A.J.; Carvalho, L.M.; Thompson, C.; Gellman, J.; Daum, K. Simulating potential impacts of fuel treatments on fire behavior and evacuation time of the 2018 Camp Fire in northern California. Fire 2022, 5, 37. [Google Scholar] [CrossRef]
- Storey, M.A.; Price, O.F.; Bradstock, R.A.; Sharples, J.J. Analysis of variation in distance, number, and distribution of spotting in Southeast Australian wildfires. Fire 2020, 3, 10. [Google Scholar] [CrossRef]
- Khan, N.; Moinuddin, K. The role of heat flux in an idealised firebreak built in surface and crown fires. Atmosphere 2021, 12, 1395. [Google Scholar] [CrossRef]
- Prior, K.W. The Balmoral Forest Fire. N. Z. J. For. 1958, 7, 35–50. [Google Scholar]
- Marshall, G.; Thompson, D.K.; Anderson, K.; Simpson, B.; Linn, R.; Schroeder, D. The impact of fuel treatments on wildfire behavior in North American boreal fuels: A simulation study using FIRETEC. Fire 2020, 3, 18. [Google Scholar] [CrossRef]
- Shmuel, A.; Heifetz, E. Re-examining the assumption of dominant regional wind and fire spread directions. Int. J. Wildland Fire 2022, 31, 480–491. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Q.; Guo, Y.; Yang, Z.; Zhang, L. An investigation of wind direction and speed in a featured wind farm using joint probability distribution methods. Sustainability 2018, 10, 4338. [Google Scholar] [CrossRef]
- Finney, M.A. FARSITE, Fire Area Simulator—Model Development and Evaluation (No. 4); US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Berkeley, CA, USA, 1998.




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shmuel, A.; Heifetz, E. A Dijkstra-Based Approach to Fuelbreak Planning. Fire 2023, 6, 295. https://doi.org/10.3390/fire6080295
Shmuel A, Heifetz E. A Dijkstra-Based Approach to Fuelbreak Planning. Fire. 2023; 6(8):295. https://doi.org/10.3390/fire6080295
Chicago/Turabian StyleShmuel, Assaf, and Eyal Heifetz. 2023. "A Dijkstra-Based Approach to Fuelbreak Planning" Fire 6, no. 8: 295. https://doi.org/10.3390/fire6080295
APA StyleShmuel, A., & Heifetz, E. (2023). A Dijkstra-Based Approach to Fuelbreak Planning. Fire, 6(8), 295. https://doi.org/10.3390/fire6080295