A Prediction Model for Smoke Spread Path in High Rise Building Fires Based on Graph Theory

Abstract

To satisfy the demand for rapid prediction of smoke transmission paths in high-rise building fires, a graph-based model was developed. The model represents a high-rise building as a Directed Acyclic Graph (DAG) grid model and employs computer simulation to determine the smoke transmission path and generate prediction results. The results were compared with those from similar simulations and were found to be consistent, indicating the feasibility and objective nature of the prediction results. Compared to other methods, this model has a shorter modeling time and can quickly provide prediction results. Furthermore, it can be applied to buildings of any structure, thus serving as a reference for smoke control design in high-rise building fire protection systems, particularly in cases involving complex internal structures.

1. Introduction

The rapid development of urban construction in China, due to the acceleration of the urbanization process, has led to high-rise buildings emerging in large numbers, with the population density continuing to rise. High-rise buildings are more dangerous due to their large size, complex functions, high population density, and the alignment of the upward height and smoke flow direction caused by the chimney effect. Unfavorable situations may occur once a fire occurs in high-rise buildings, such as physical exhaustion of personnel, crowded staircases, or conflicts between personnel evacuation and rescue due to the large number of floors, concentrated personnel, and long vertical evacuation distances [1]. Smoke poses a greater threat to human life safety in high-rise building fires compared to the fire itself due to its flowability, which enables it to quickly reach higher floors. Fire smoke contains SO₂, NH3, carbon particles, N02, SO₂, and HC, which strongly irritate the respiratory system of humans [2,3]. Fire deaths are mainly caused by the CO in smoke. CO, when inhaled into the body, easily combines with hemoglobin (Hb) to form stable COHb, which is difficult to separate and mainly causes tissue hypoxia and suffocation death [4]. To prevent smoke from threatening the lives of personnel inside buildings, highly integrated and complex smoke control systems for high-rise buildings are emerging [5]. The internal algorithms of these systems need to quickly identify the location of the smoke, predict the transmission path, and control smoke near smoke control equipment to limit the spread [6]. To enable the system to predict the transmission path of the smoke, system designers must incorporate the logic for smoke propagation paths into the algorithm. As the internal structures of different high-rise buildings vary greatly, the logic for smoke propagation paths also varies. The logic for smoke propagation paths is more complex in some buildings with a large internal area, a large number of rooms and passages, and interconnected structures [7]. Therefore, it is vital to adopt a reasonable, effective, economical, and fast method to obtain the smoke propagation path in high-rise building fires.

Common methods for predicting smoke propagation paths in buildings include numerical simulations and experimental studies. The full-scale fire simulation is the most accurate method for obtaining the smoke transmission path [8]. However, this requires high site requirements and is time-consuming and costly [9]. The similar simulation is a more commonly used method, which has lower site requirements, experimental costs, and other costs, with high accuracy [10]. Nonetheless, the time and cost of the similar simulation are still high, and one platform can only simulate one building situation at a time. It is more suitable as a supplement to other simulation methods for verification. The numerical simulation is currently the most widely used method [11]. Compared to the previous two methods, a numerical simulation greatly reduces costs, is applicable to any building and situation, and has a high degree of simulation accuracy [12]. However, for large-scale, complex-structured high-rise buildings, a numerical simulation often requires long modeling and calculation time, which can last for hundreds of hours. Moreover, numerical simulations have certain requirements for computer configuration [13]. To solve these problems, graph theory is introduced to obtain smoke transmission paths in high-rise buildings.

Graph theory is a method that uses graphs as research objects. Its rapid and low-cost characteristics have made it widely applicable. For instance, in this study, the modeling and debugging time for the thirteen-story high-rise building was approximately 10 h, while adapting to other building structures takes approximately 1 h, and the simulation time was approximately 1 s. Graph theory has been applied to fight constrained fires in high-rise buildings [14]. This study employs graph theory to address the issue of smoke propagation in high-rise building fires. The proposed model utilizes a network flow-based simulation approach to investigate smoke spread and explores the relevant theories, techniques, and applications associated with this approach. Network flow algorithms are crucial graph theory algorithms primarily employed to solve maximum flow and minimum cut problems based on network structures. Although smoke propagation in high-rise building fires is influenced by various factors such as ventilation conditions and fire power, the fundamental propagation path prediction and the priority of entering different areas during the propagation process are solely related to building structures [15]. The graph theory-based model obtained in this study can efficiently adapt to different building structures, particularly large and complex high-rise buildings, and quickly obtain results. In fire research in high-rise buildings, this model can simulate smoke diffusion and propagation paths, providing support for quick decision making in high-rise building smoke control systems.

2. Materials and Methods

Graph theory is a branch of discrete mathematics that employs graphs as research objects [16]. A graph consists of a set of vertices and edges that connect them. This can be abstractly defined as shown in Equation (1):

Graph = (V, E)

(1)

where V and E represent vertices and edges, respectively. $\mathrm{E}\subseteq \mathrm{V}\times \mathrm{V}$, x is the Cartesian product, V × V, is equivalent to $\{(a,b):a\in \mathrm{V},b\in \mathrm{V}\}$.

The core concepts of graph theory are vertices and edges. Vertices represent different entities under study, such as locations or people, which can be any entity with attributes, while edges represent specific relationships between two vertices [16]. In this model, independent spaces such as rooms, hallways, and stairwells are treated as vertices, and the pathways that allow smoke to directly propagate between two independent spaces are treated as edges.

2.1. Ideal Model

This study uses a typical building as the ideal prototype, with a height of 52 m and 13 floors, each being 4 m high. Each floor consists of six rooms, a corridor, an elevator shaft, and a pair of scissor stairs. Each room is equipped with one operable door and one operable window. The end of the corridor has one operable window. The anteroom has one operable door each leading to the elevator shaft, stairs, and corridor, and one window facing outside. There is also one window on the staircase platform. The overall structure of the ideal model is shown in Figure 1, and its internal structure is depicted in Figure 2. The environmental conditions of the experimental site are set at a temperature of 25 degrees Celsius and atmospheric pressure of 900 pa, without wind. The data for the smoke path prediction model presented in this paper are obtained from the use of this ideal model. The similar simulation platforms used for validation also adopt this ideal model as a prototype.

2.2. Necessary Simplification

High-rise building fires are complex physical events, and this model focuses solely on the path and priority of smoke transmission. Hence, certain assumptions and simplifications are necessary. These include the mechanisms of smoke production from burning fuel, the mixing flow of smoke and air, the exchange of heat and thermal radiation with building materials, and a series of physical processes. To identify the factors that play a determining role, specific studies of these processes require certain assumptions and simplifications.

To simplify the modeling process, several assumptions are made. Firstly, smoke spreading to the outside through holes such as windows is ignored. The model mainly studies the spread of smoke inside high-rise buildings, focusing on the transfer of smoke from rooms to horizontal and vertical passages. Therefore, only adjacent corridor nodes have edges with each room.

Secondly, to simplify the ratio of smoke production and heat release, it is assumed that the ratio is 1:1 per unit time. Although smoke production varies for different materials, it is always proportional to the heat release rate during combustion.

Thirdly, the process of smoke spreading is assumed to follow the permeation law, which means that the smoke capacity of each node is limited, and smoke is easily compressed. Therefore, fire smoke will spread from areas of high concentration to areas of low concentration, from areas of high temperature to areas of low temperature, and from areas of high pressure to areas of low pressure. Although smoke spreading is a complex process involving multiple physical fields and is influenced by factors such as temperature, pressure, and wind speed, and the saturation of smoke concentration varies at different states [2], to establish a network model, each node is assumed to have a certain smoke capacity. When the smoke is saturated, there will only be an increase in temperature, and no change in smoke concentration.

Lastly, the smoke capacity of atmospheric environment nodes is assumed to be infinite.

Overall, these assumptions and simplifications are necessary to establish a network model and identify the factors that play a determining role in the complex physical events of high-rise building fires.

2.3. Representing a High-Rise Building as a DAG Network Model

Directed Acyclic Graphs (DAGs) are widely used data structures in computer science due to their unique topological structure, which allows them to exhibit excellent properties in various algorithmic cases, such as dynamic programming, shortest path searches in navigation, and data compression [17]. In the context of high-rise buildings, rooms, corridors, and vertical passages that may contain smoke in the event of a fire are represented as nodes, and the possible propagation directions between nodes are represented as edges. As a result, a network model schematic of the high-rise building can be constructed, as illustrated in Figure 3, where the gray area represents nodes, and the black area represents edges.

To represent a high-rise building as a Directed Acyclic Graph (DAG), six steps are required. Firstly, each room or area in the building must be identified and allocated a unique identifier or node name using the method described in Equation (2). Secondly, the relationships between each room or area must be determined, including the doors or passages between rooms and the passages such as stairs or elevators. These relationships are represented as directed edges, with arrows pointing from one room or area to another. Thirdly, the dependencies between each room or area must be determined, including some rooms or areas that can only be accessed through others or must be accessed after completion of other rooms or areas. These dependencies are also represented as directed edges. Fourthly, the graph needs to be checked for cycles, and if cycles are present, they should be decomposed into smaller components until each component is a DAG. Fifthly, weights are assigned to each node in the graph based on the area or usage of each room and its fire load. Finally, visualize the DAG. The graph is visualized for better understanding and analysis. The process of representing a room into a DAG model is also the process of flattening the room. Flattening reduces the dimensions of a multidimensional array. A room is a complex three-dimensional space that includes various data such as area, location, height, and internal structure. The flattened room only contains information such as number, node relationship, and smoke saturation.

ID_f = (F − 1) × 10 + R

(2)

where ID_f is numbered unique ID, F represents the floor number, and R represents the room on the F floor. The floor numbering is illustrated in Figure 4.

2.4. Computer Simulation

The spread of fire was modeled using the Networkx and Matplotlib packages in Python [3,18], and was executed in the Thonny IDE development tool environment. The pre-created DAG network model was imported for simulation, and the program was initiated. The simulation program starts with the ignition of the fire source and ends when the heat release from the source ceases and the smoke no longer flows violently, as depicted in Figure 5. Each edge in this network model is assigned a weight representing the volume of smoke flowing from tail to head per unit time. All nodes satisfy Kirchhoff’s law, i.e., the inflow of smoke at each node equals the outflow, as shown in Equation (3) [19]. The size of each room corresponds to the smoke saturation level at the corresponding node. Coefficients were established to simulate the effect of room doors and smoke prevention facilities during smoke transmission between nodes, as well as smoke and exhaust equipment during smoke transmission between the room and the outside. Since this prediction model is a purely mathematical computation model, the simulation results are only based on the attributes of the nodes and the relationships and coefficients between the nodes. Therefore, it is not possible to set boundary or initial conditions directly. In subsequent research, the influence of boundary and initial conditions will be reflected through the coefficients of the edges. If a node has not reached the saturation state, the weight of the smoke stored in the node can be expressed as Equation (4). Smoke transmission between nodes can be obstructed, or a node can have ventilation equipment, in which case the inflow or outflow of smoke is equal to the original inflow or outflow value multiplied by a coefficient. When the outflow of smoke from a node is obstructed, the outflow of smoke in the next time unit is represented by Equation (5).

$${\displaystyle \sum _{\mathrm{k}=1}^n{i}_k=0}$$

(3)

where i_k represents the smoke flow at the ith node.

$$w_t=1-\frac{C_t}{C_a}$$

(4)

where, C_t represents the current smoke volume, C_a represents the smoke capacity of the node, and w_t denotes the weight of the smoke when the node has not reached saturation.

s_n = w_t + s_n+1 × (1 − α),

(5)

where, S_n denotes the actual outflow of smoke from a node in the nth time unit, w_t denotes the weight of the smoke when the node has not reached saturation, s_n+1 denotes the actual outflow of smoke from the same node in the n+1th time unit, and α is a coefficient.

Only the first five floors, each with six room nodes, are displayed for convenience. Room (1, 4) is designated as the ignition point in the simulation program, with the initial heat release set to cease at the end condition. The heat release process is shown in Figure 5. The smoke capacity of each node is recorded, and the time when the smoke content at each node reaches 10 is recorded as the time when smoke reaches that node. This study assumes a 1:1 ratio of smoke generation to heat release, and the formula for smoke generation is replaced by the heat release rate formula (Equation (6)). The smoke generation rate and total smoke generation can be controlled by setting the type and mass of combustibles. If no node reaches its saturation limit, the smoke propagation path is determined based on the smoke content of each node. For saturated nodes, the time taken to reach saturation is used to determine the smoke spread path. Smoke prediction is based on three cases. In Case 1, all doors and windows are open. In Case 2, all doors and windows except the one between the stairwell and corridor on the third floor are closed or partially closed. In Case 3, all doors and windows except the one between the stairwell and corridor on the third floor are closed.

$$Q=m\times \Delta H$$

(6)

where, Q is the heat release rate, m is the mass burning rate of combustibles (kg/s), and $\Delta H$ is the heating value of the combustible.

2.5. Similar Simulation as Validation

A small-scale experimental platform was used to conduct a similar simulation. The experimental platform was constructed based on the Froude similarity principle at a 1/10 scale of a high-rise building, and its physical parameters were measured. The experimental platform consists of 13 floors, with each floor being 0.4 m high and consisting of 6 rooms, a corridor, an elevator shaft, and a pair of scissors stairs. Figure 6 and Figure 7 show the interior and overall diagrams of the experimental platform.

Table 1. Froude’s similarity criterion relationship.

Physical Parameters	Proportional Relationship	Formula Number
Heat release rate (Kw)	$Q_P=Q_M{\left(L_P/L_M\right)}^{5/2}$	(7)
Volume flow rate (m3/s)	$V_P=V_M{\left(L_P/L_M\right)}^{5/2}$	(8)
Time (s)	$t_P=t_M{\left(L_P/L_M\right)}^{1/2}$	(9)
Speed (m/s)	$v_P=v_M{\left(L_P/L_M\right)}^{1/2}$	(10)
Quality (Kg)	$m_P=m_M{\left(L_P/L_M\right)}^3$	(11)
Temperature (K)	$T_P=T_M$	(12)
Fire Load (MJ)	$q_p=q_m{\left(L_P/L_M\right)}^4$	(13)

summarizes the relationships between some physical parameters and the prototype [20].

Next, set similar simulation parameters. Similar simulation parameters were set by using gasoline in a pan as the heat source in the middle of Room 4 and tires as the smoke-generating materials, as shown in Figure 6. To prevent rapid temperature rise due to heat conduction, asbestos mesh was wrapped around the vicinity of the fire source in the experimental platform. The rooms, corridors, and staircases of each floor were flattened, and a carbon monoxide concentration probe was installed in the middle of each node to record the carbon monoxide concentration in that area. The time when the carbon monoxide concentration reached, and stayed above, 50 ppm was recorded as the standard for the smoke reaching that position [21]. According to the Froude similarity principle, the recorded time was converted to the time in the original building. The mobility of doors and windows was used to simulate three different cases, consistent with the prediction model. Case 1 had all doors and windows open, Case 2 had all doors and windows except the one between the stairwell and corridor on the 3rd floor partially closed, and Case 3 had all doors and windows except the one between the stairwell and corridor on the 3rd floor closed. The experiment was conducted at approximately 25 degrees Celsius temperature with no wind and an air pressure of approximately 900 hPa.

3. Results

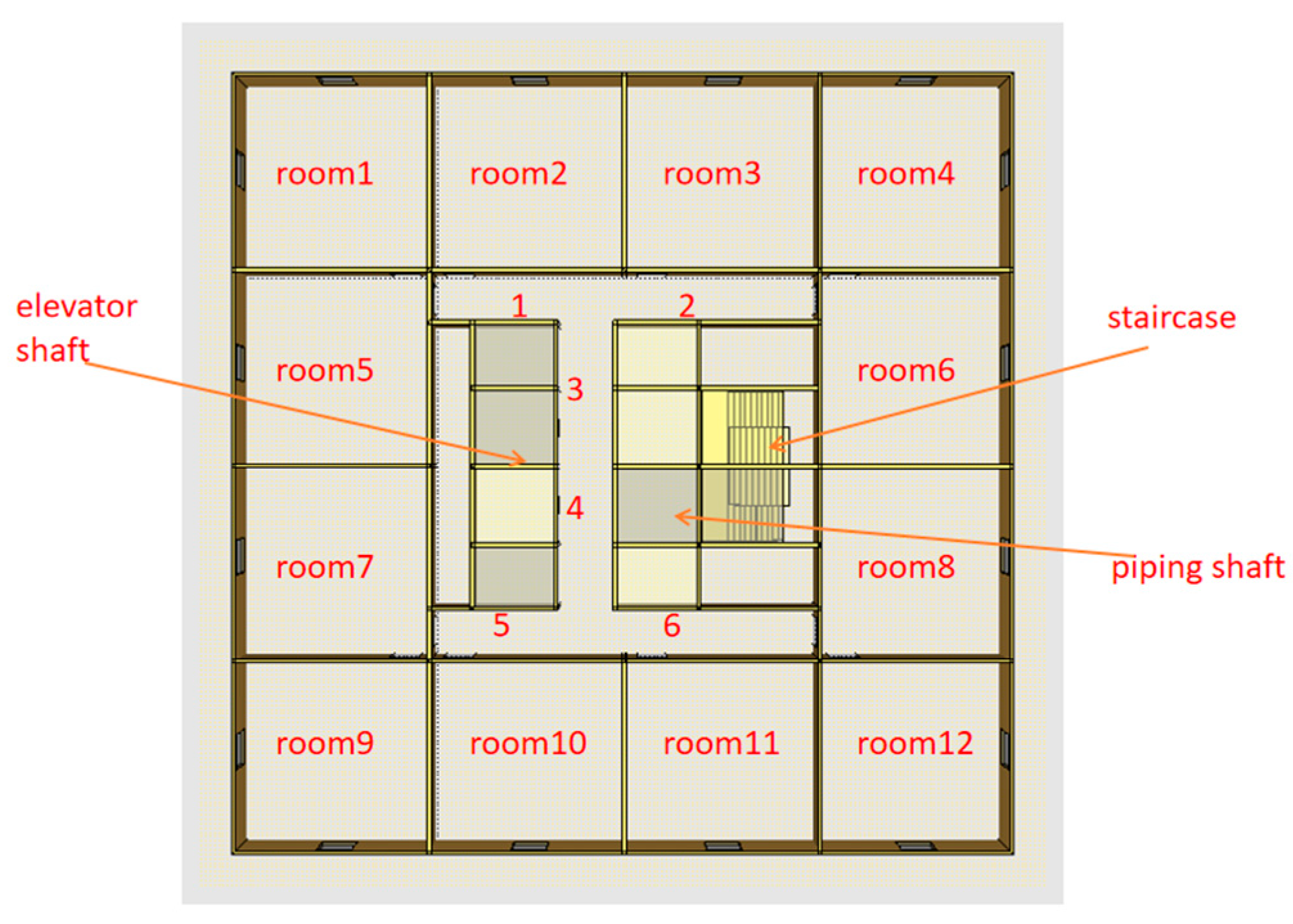
3.1. Comparison of Long Channel Single Node and Multiple Nodes

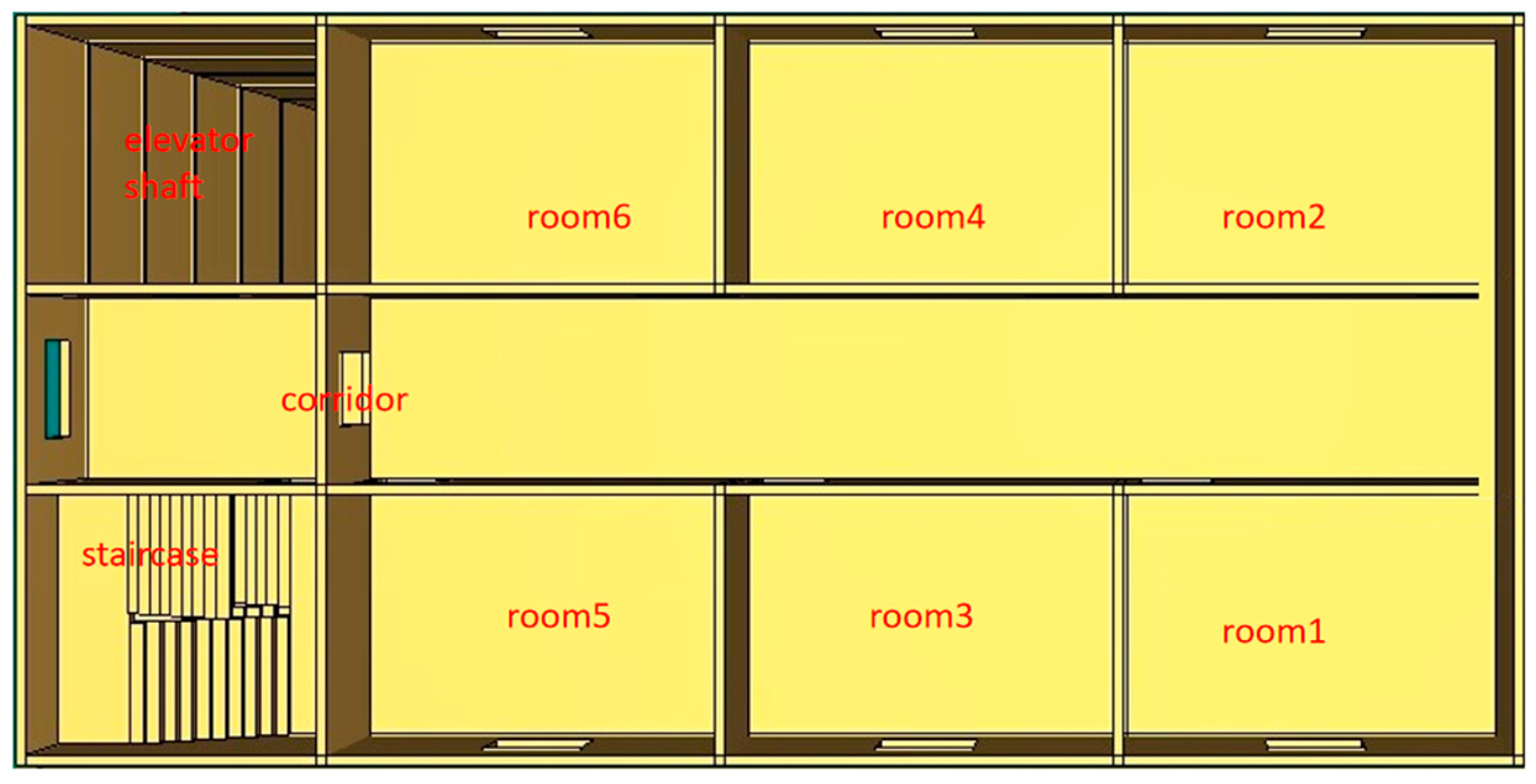
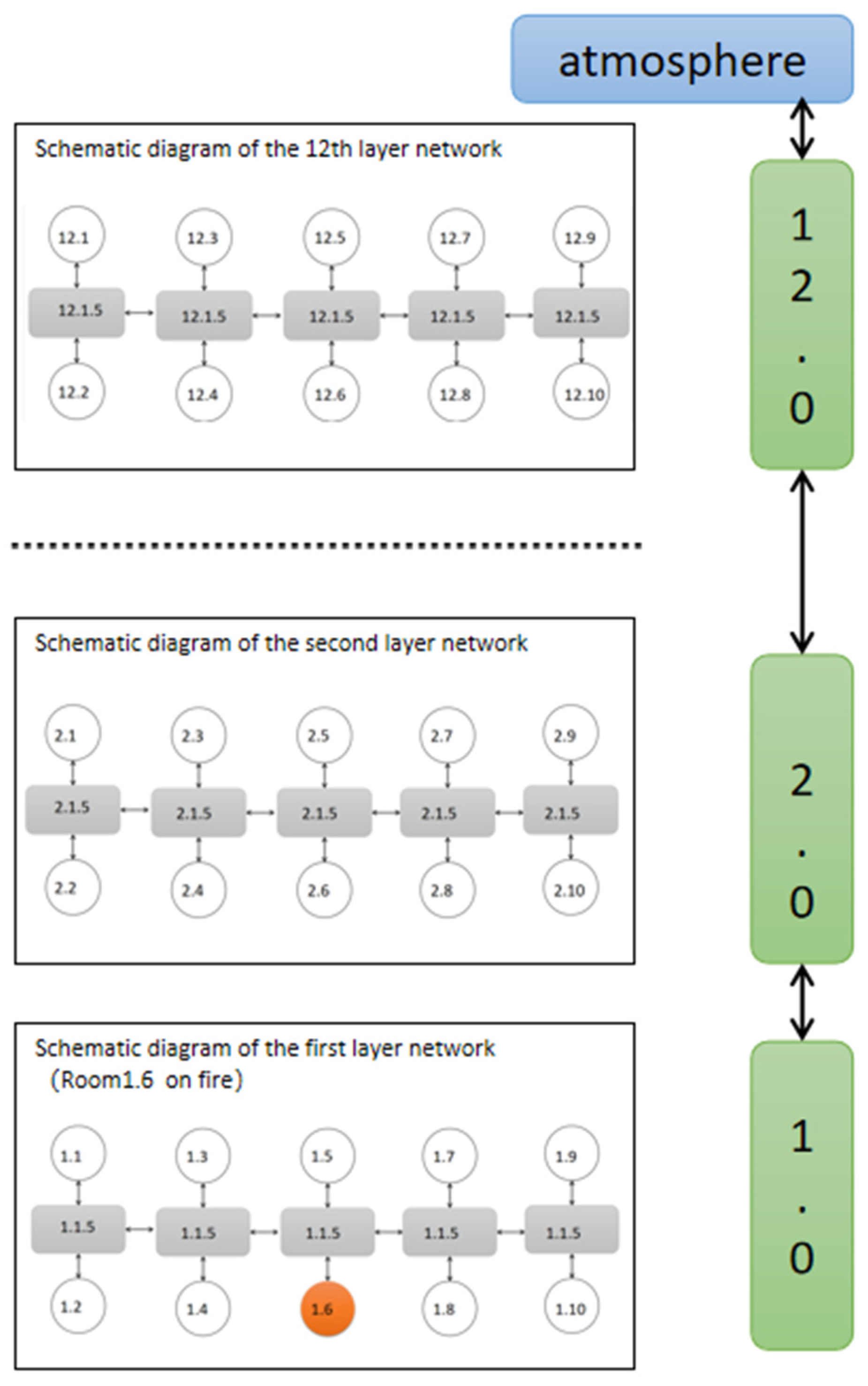
Channels can be represented as either a single node or a combination of multiple nodes. However, to simplify the process, save computation and modeling time, and homogeneously share the attributes of each node, previous research has generally represented horizontally connected passages such as corridors and vertically connected passages such as elevators and stairs as a single node, as shown in Figure 8. Nonetheless, the attributes of horizontally and vertically connected passages are not homogeneous during the development of a fire. 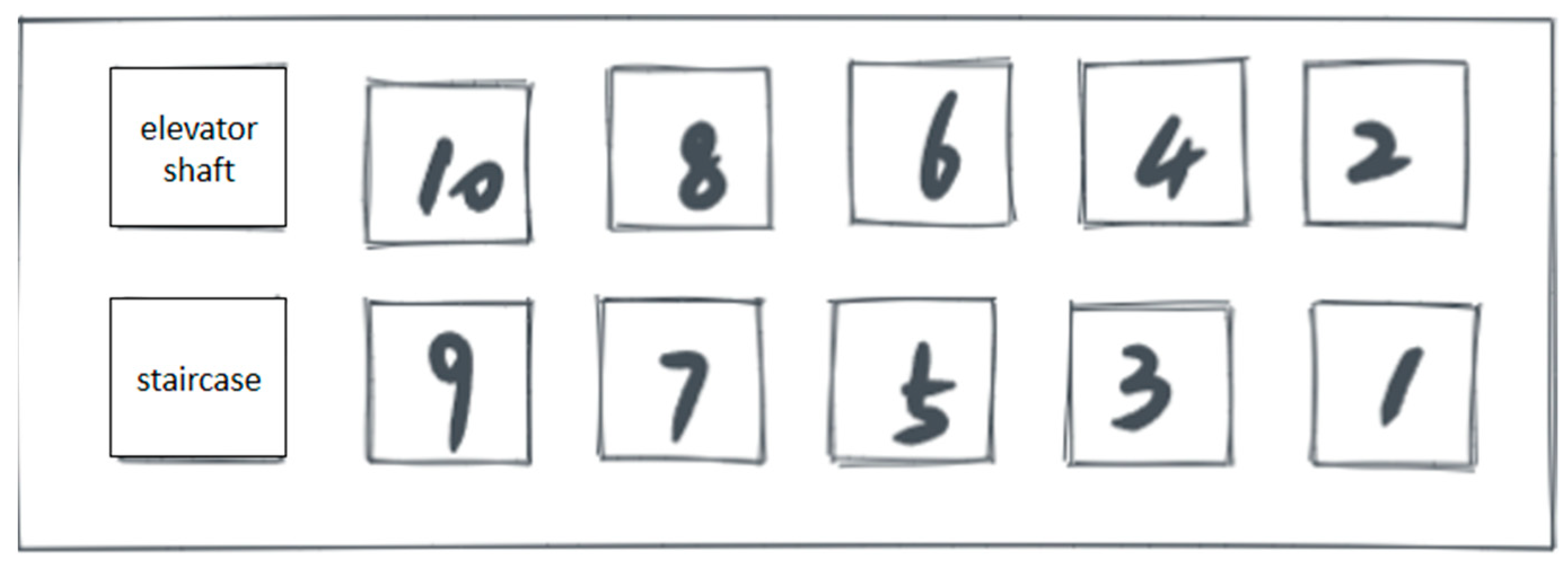As the distribution of physical parameters, such as density and temperature of smoke, in the passages may be inconsistent [22], further verification is necessary to describe this non-homogeneous physical state process using a single node. Non-homogeneous physical state processes can cause confusion and inaccurate results in graph-based simulations. Therefore, this study carefully represents horizontally and vertically connected passages into single and multiple nodes for comparison. In the case of multiple nodes, passages are divided into several small nodes based on the geometric dimensions of the rooms and floors, with the number of nodes depending on the passage length. These nodes generally have different physical state attribute values in actual physical processes, as shown in Figure 9. White nodes represent rooms, gray nodes represent corridors, red nodes represent the room on fire, green nodes represent staircases, and blue nodes represent the atmosphere. For ease of display, only the first five layers are shown.

To analyze the difference between single node and multi-node methods, compare the data in

Table 2. Long channels are considered a single node with different node smoke arrival schedules.

Node	Smoke Arrival Time (s)	Node	Smoke Arrival Time (s)
(1, 1)	0.2	(2, 5)	3.7
(1, 0.5)	0.5	(2, 6)	3.7
(1, 3)	1	(3, 1)	3.7
(1, 2)	1	(3, 2)	3.7
(1, 4)	1	(3, 5)	3.7
(1, 5)	1	(4, 4)	3.7
(1, 6)	1	(3, 6)	3.7
(1, 0)	1	(4, 1)	3.7
(2, 1.0)	2.3	(4, 2)	3.7
(3, 1.0)	2.3	(4, 3)	3.7
(4, 1.0)	2.3	(5, 4)	3.7
(5, 1.0)	2.3	(4, 5)	3.7
(3, 4)	3.7	(4, 6)	3.7
(2, 3)	3.7	(5, 1)	3.7
(3, 3)	3.7	(5, 2)	3.7
(2, 1)	3.7	(5, 3)	3.7
(2, 2)	3.7	(5, 5)	3.7
(2, 4)	3.7	(5, 6)	3.7

and

Table 3. Long channels are considered multiple nodes with different smoke arrival schedules.

Node	Smoke Arrival Time (s)	Node	Smoke Arrival Time (s)
(1, 4)	0.2	(2, 1)	6.1
(1, 3.5)	0.5	(3, 3)	6.1
(1, 3)	1	(3, 4)	6.1
(1, 1.5)	1	(3, 1.5)	6.1
(1, 5.5)	1	(2, 2)	6.1
(1, 1)	2.3	(4, 5)	6.1
(1, 2)	2.3	(4, 6)	6.1
(1, 5)	2.3	(4, 3.5)	6.1
(1, 6)	2.3	(5, 5.5)	6.1
(1, 0)	2.3	(0, 0)	6.1
(2, 0)	3.7	(3, 1)	6.5
(2, 5.5)	4	(3, 2)	6.5
(3, 0)	4	(4, 3)	6.5
(2, 3.5)	4.5	(4, 4)	6.5
(3, 5.5)	4.5	(4, 1.5)	6.5
(4, 0)	4.5	(5, 5)	6.5
(2, 5)	4.9	(5, 6)	6.5
(2, 6)	4.9	(5, 3.5)	6.5
(2, 1.5)	5	(4, 1)	7.2
(2, 3)	5.2	(4, 2)	7.2
(2, 4)	5.2	(5, 3)	7.2
(4, 5.5)	5.2	(5, 4)	7.2
(3, 5)	5.2	(5, 1.5)	7.2
(3, 6)	5.2	(5, 1)	8
(3, 3.5)	5.2	(5, 2)	8
(5, 0)	5.2

. In Table 2 and subsequent tables, the darker the color, the earlier the smoke arrives. According to the simulation results in Table 2, when treating the long passage as a single node, the smoke arrival time at different nodes is almost the same except for the first floor, which is significantly different from the conventional understanding. This indicates that using the single node method in non-homogeneous physical state processes will lead to inaccurate simulation results. Conversely, Table 3 uses the multi-node method to simulate the long passage, and the results show that the smoke arrival time at different nodes is closer to the actual situation. Therefore, in subsequent research, the long passage will be treated as multiple nodes for study.

3.2. Simulation Results

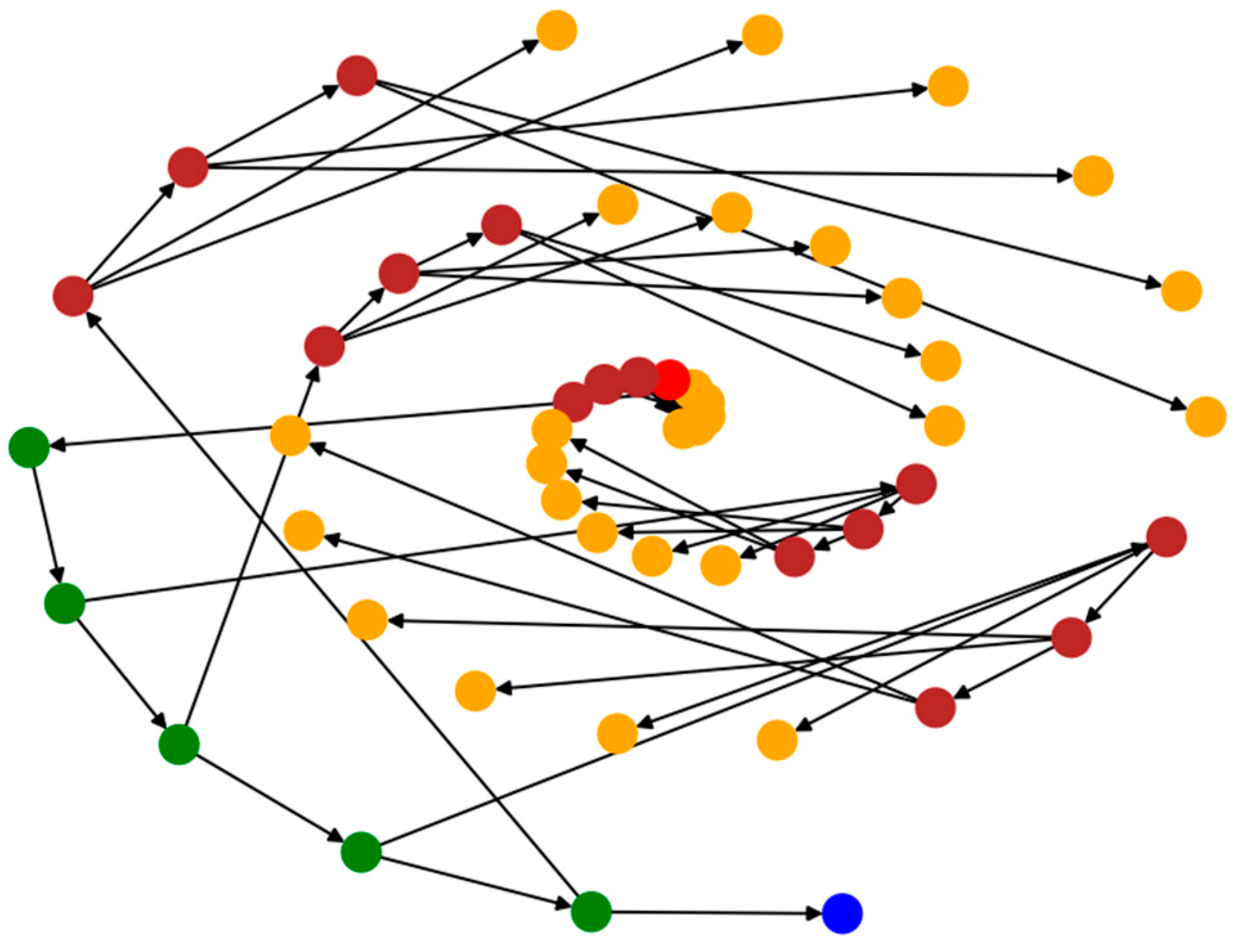
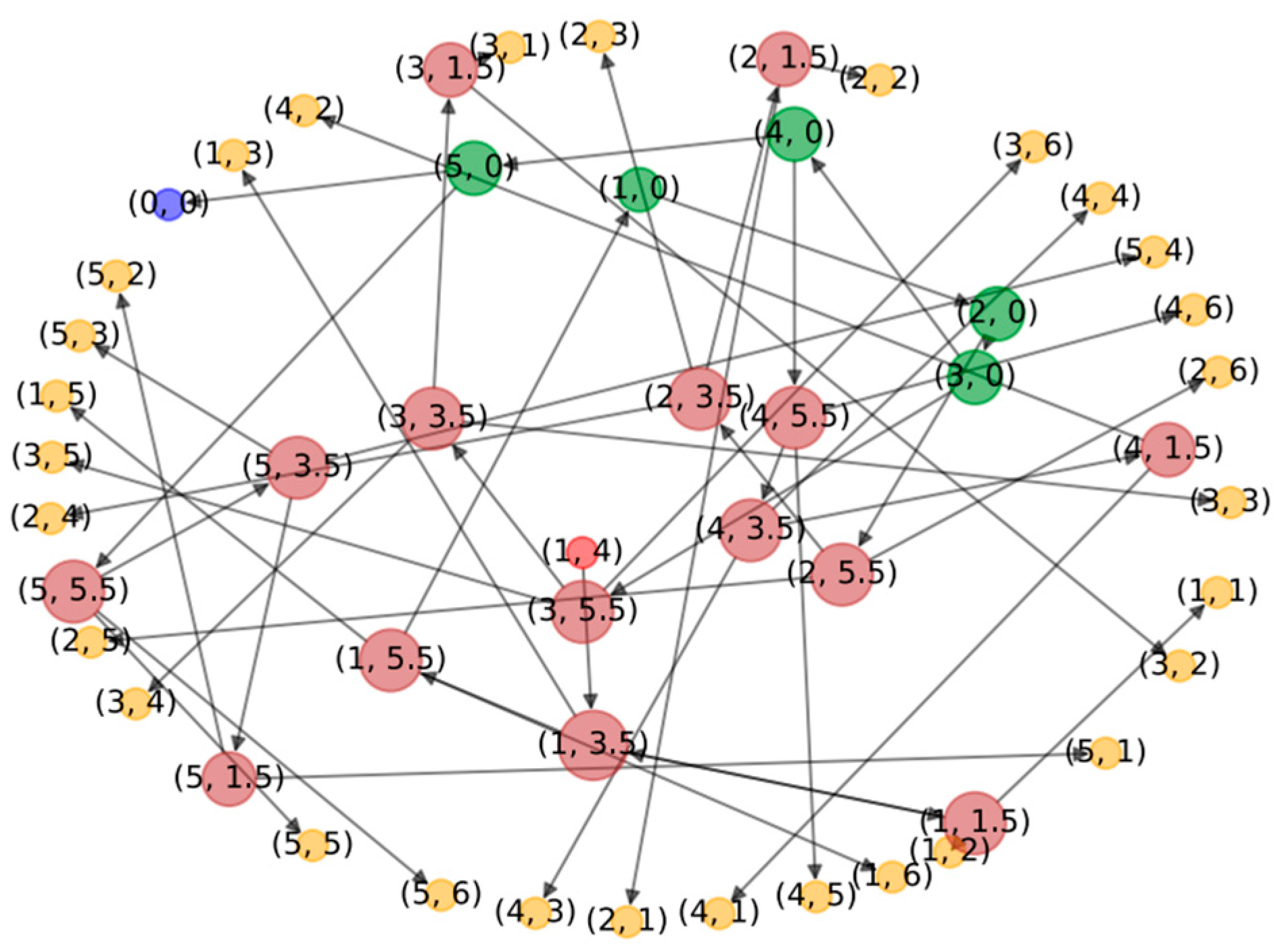
To visualize the results of the DAG model, we utilized the Networkx and Matplotlib packages to implement the overall framework and corresponding logic of the code, as demonstrated in the example visualization shown in Figure 10 [23]. In the figure, red nodes represent ignition nodes, dark red nodes represent horizontal passage nodes, mainly used for corridors, blue nodes represent atmospheric environment nodes, green nodes represent vertical passage nodes, and yellow nodes represent conventional room nodes. In actual high-rise buildings, there may be an extensive network of nodes, which can make the visualization results challenging to distinguish. Therefore, only the first five layers are displayed for ease of presentation. To simulate the fire scenario, we selected Room (1, 4) as the ignition room, with only six room nodes per floor. The simulation results are presented in Figure 11.

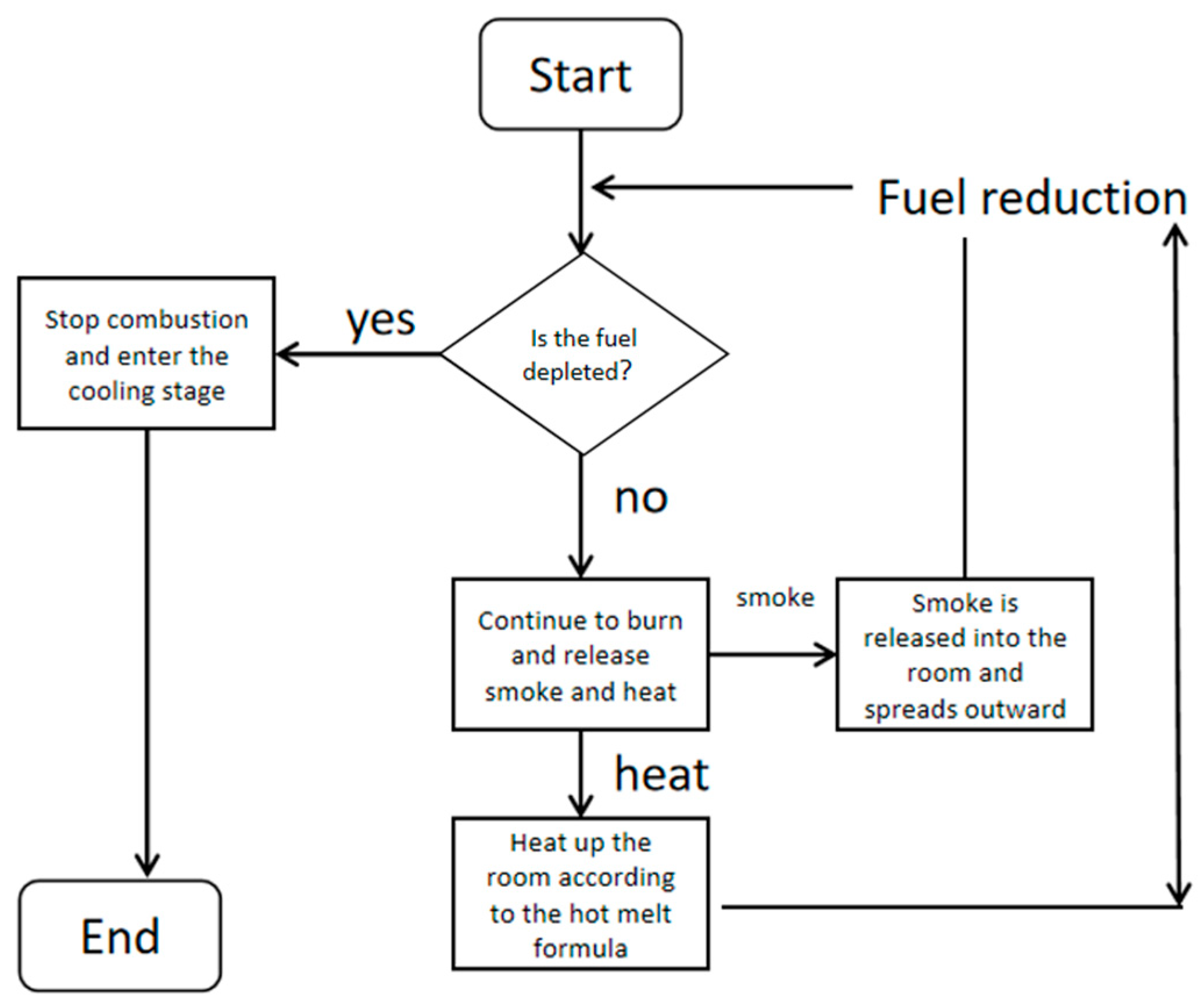
After conducting the simulation, the flue gas content data for each node was analyzed. The fire smoke conditions of case 1, case 2, and case 3 are presented in

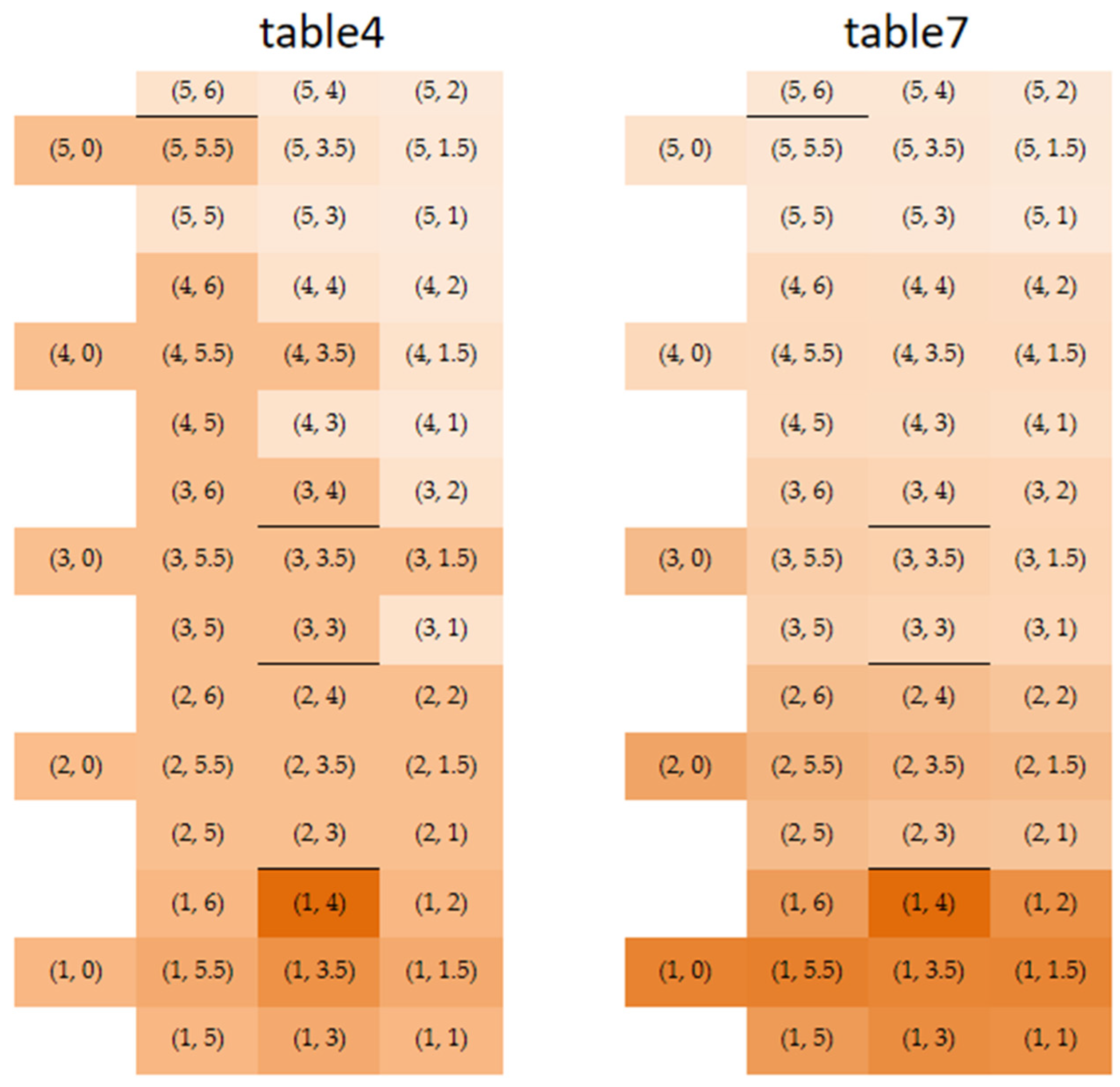
Table 4. Computer simulation results of node smoke content case1.

Node	Smoke Content	Node	Smoke Content
(1, 4)	1,196,204.44	(2, 1)	159.35
(1, 3.5)	652,390.65	(2, 2)	159.35
(1, 3)	299,361.92	(3, 3)	159.35
(1, 1.5)	299,361.92	(3, 4)	159.35
(1, 5.5)	299,361.92	(3, 1.5)	159.35
(1, 1)	116,443.78	(4, 5)	159.35
(1, 2)	116,443.78	(4, 6)	159.35
(1, 5)	116,443.78	(4, 3.5)	159.35
(1, 6)	116,443.78	(5, 5.5)	159.35
(1, 0)	116,443.78	(0, 0)	159.35
(2, 0)	38,893.92	(3, 1)	48.37
(2, 5.5)	11,320.71	(3, 2)	48.37
(3, 0)	11,320.71	(4, 3)	48.37
(2, 5)	2918.91	(4, 4)	48.37
(2, 6)	2918.91	(4, 1.5)	48.37
(2, 3.5)	2918.91	(5, 5)	48.37
(3, 5.5)	2918.91	(5, 6)	48.37
(4, 0)	2918.91	(5, 3.5)	48.37
(2, 3)	685.19	(4, 1)	27.12
(2, 4)	685.19	(4, 2)	27.12
(2, 1.5)	685.19	(5, 3)	27.12
(3, 5)	685.19	(5, 4)	27.12
(3, 6)	685.19	(5, 1.5)	27.12
(3, 3.5)	685.19	(5, 1)	23.36
(4, 5.5)	685.19	(5, 2)	23.36
(5, 0)	685.19

,

Table 5. Computer simulation results of node smoke content case2.

Node	Smoke Content	Node	Smoke Content
(1, 4)	1,196,204.44	(4, 5)	242.58
(1, 3.5)	652,390.65	(4, 6)	242.58
(1, 3)	299,361.92	(4, 3.5)	242.58
(1, 1.5)	299,361.92	(5, 5.5)	242.58
(1, 5.5)	299,361.92	(2, 1)	159.35
(1, 1)	116,443.78	(2, 2)	159.35
(1, 2)	116,443.78	(0, 0)	159.35
(1, 5)	116,443.78	(3, 3)	79.78
(1, 6)	116,443.78	(3, 4)	79.78
(1, 0)	116,443.78	(3, 1.5)	79.68
(2, 0)	38,893.92	(4, 3)	73.63
(2, 5.5)	11,320.71	(4, 4)	73.63
(3, 0)	11,320.71	(4, 1.5)	73.63
(4, 0)	4443.45	(5, 5)	73.63
(2, 5)	2918.91	(5, 6)	73.63
(2, 6)	2918.91	(5, 3.5)	73.63
(2, 3.5)	2918.91	(4, 1)	41.28
(3, 5.5)	1459.46	(4, 2)	41.28
(4, 5.5)	1043.06	(5, 3)	41.28
(5, 0)	1043.06	(5, 4)	41.28
(2, 3)	685.19	(5, 1.5)	41.28
(2, 4)	685.19	(5, 1)	35.56
(2, 1.5)	685.19	(5, 2)	35.56
(3, 5)	342.6	(3, 1)	24.19
(3, 6)	342.6	(3, 2)	24.19
(3, 3.5)	342.6

and

Table 6. Computer simulation results of node smoke content case3.

Node	Smoke Content	Node	Smoke Content
(1, 4)	1,196,204.44	(2, 1)	159.35
(1, 3.5)	652,390.65	(2, 2)	159.35
(1, 3)	299,361.92	(0, 0)	159.35
(1, 1.5)	299,361.92	(4, 3)	98.9
(1, 5.5)	299,361.92	(4, 4)	98.9
(1, 1)	116,443.78	(4, 1.5)	98.9
(1, 2)	116,443.78	(5, 5)	98.9
(1, 5)	116,443.78	(5, 6)	98.9
(1, 6)	116,443.78	(5, 3.5)	98.9
(1, 0)	116,443.78	(4, 1)	55.45
(2, 0)	38,893.92	(4, 2)	55.45
(2, 5.5)	11,320.71	(5, 3)	55.45
(3, 0)	11,320.71	(5, 4)	55.45
(4, 0)	5967.98	(5, 1.5)	55.45
(2, 5)	2918.91	(5, 1)	47.76
(2, 6)	2918.91	(5, 2)	47.76
(2, 3.5)	2918.91	(3, 1)	0
(4, 5.5)	1400.93	(3, 2)	0
(5, 0)	1400.93	(3, 3)	0
(2, 3)	685.19	(3, 4)	0
(2, 4)	685.19	(3, 5)	0
(2, 1.5)	685.19	(3, 6)	0
(4, 5)	325.81	(3, 1.5)	0
(4, 6)	325.81	(3, 3.5)	0
(4, 3.5)	325.81	(3, 5.5)	0
(5, 5.5)	325.81

, respectively. Since the smoke content at each node did not reach its maximum value during the simulation process, the smoke entry speed into each node was roughly the same. The size of the smoke content at each node in Table 4, Table 5 and Table 6 reflects the degree of susceptibility to smoke propagation between nodes. Therefore, the smoke content can be regarded as an indicator of smoke flow rate, where higher smoke content indicates faster smoke flow rate at that node, indicating that smoke is more likely to reach that node first.

The smoke content on the first floor can be ranked in descending order from the data of the three tables as follows: room (1, 4), room (1, 3.5), room (1, 3), room (1, 1.5), room (1, 5.5), room (1, 1), room (1, 2), room (1, 5), room (1, 6), and (1, 0). The room on fire has the highest smoke content, followed by the adjacent corridor, then adjacent rooms and corridors, other rooms, and finally the stairwell. However, the second floor has a different pattern, where the smoke content decreases in order from (2, 0) to (2, 1), with the stairwell having the highest smoke content, followed by the rooms near the stairwell, the rooms in the middle of the corridor and near the stairwell, the rooms far from the stairwell in the middle of the corridor, and finally the rooms far from the stairwell. The smoke distribution on other floors is similar, with the smoke content arranged in order from high to low for the stairwell, rooms near the stairwell, rooms in the middle of the corridor and near the stairwell, rooms far from the stairwell in the middle of the corridor, and finally the rooms far from the stairwell.

The conditions on the fourth and fifth floors were similar in all three cases. In Case 2, a coefficient of 0.5 was set for smoke to travel from (3.0) to (3.3.5), while in Case 1, smoke could directly enter the third-floor corridor from the stairwell, reaching the third-floor rooms the fastest. However, smoke was obstructed when it reached the third-floor corridor from the stairwell in Case 2, and its entry into the third-floor rooms was significantly slower. Furthermore, the smoke reached the fourth and fifth floors faster in Case 2 than in Case 1, while it reached the fourth and fifth floors even faster in Case 3 than in Case 2 because, in Case 3, the coefficient for smoke to travel from the stairwell to the third-floor corridor was set to 0.

This study found that the smoke content at different nodes can help determine the path of smoke propagation. On the fire floor, smoke enters the corridor from the ignition room and then spreads to other rooms and vertical passages from the corridor, mainly discharging outdoors or spreading to other floors via vertical passages. On non-fire floors, smoke enters the corridor from the vertical passage and then enters different rooms based on their distance from the vertical passage. Based on the degree of fire spreading, it is possible to analyze the areas most susceptible to fire propagation in high-rise buildings, which are the nodes that should be given priority consideration in pre-response control strategies.

3.3. Result Validation

In this study, we validated the simulation results of the graph theory method using a small-scale simulating platform. Through this experiment, we obtained data on the arrival time of smoke at each node. The results for all three cases are presented in

Table 7. Similar simulation experiments with different node smoke arrival schedules case1.

Node	Smoke Arrival Time (s)	Node	Smoke Arrival Time (s)
(1, 4)	7.9	(3, 1.5)	189
(1, 5.5)	44.3	(3, 3)	191
(1, 0)	50.3	(3, 4)	191.3
(1, 1.5)	53.5	(3, 2)	199
(1, 3.5)	55.7	(3, 1)	201
(1, 3)	67.2	(4, 0)	221.7
(1, 1)	71.4	(4, 5.5)	230.2
(1, 2)	71.7	(4, 3.5)	235.7
(1, 5)	90.3	(4, 6)	236.3
(1, 6)	92.4	(4, 5)	237.5
(2, 0)	107.7	(4, 1.5)	241.4
(2, 5.5)	133	(4, 4)	244.8
(2, 3.5)	140.4	(4, 3)	244.9
(2, 1.5)	144.6	(4, 2)	255.5
(3, 0)	145	(4, 1)	257.6
(2, 5)	145.4	(5, 0)	285.2
(2, 6)	147	(5, 5.5)	317
(2, 4)	150	(5, 3.5)	319
(2, 3)	158.1	(5, 6)	322
(2, 1)	160.9	(5, 5)	323
(2, 2)	162.5	(5, 4)	328
(3, 5.5)	178.2	(5, 3)	329
(3, 3.5)	181.6	(5, 1.5)	334.1
(3, 5)	185.1	(5, 2)	339
(3, 6)	185.5	(5, 1)	340.7

,

Table 8. Similar simulation experiments with different node smoke arrival schedules case2.

Node	Smoke Arrival Time (s)	Node	Smoke Arrival Time (s)
(1, 4)	7.9	(4, 5)	213.75
(1, 5.5)	44.3	(4, 1.5)	217.26
(1, 0)	50.3	(4, 4)	220.32
(1, 1.5)	53.5	(4, 3)	220.41
(1, 3.5)	55.7	(4, 2)	229.95
(1, 3)	67.2	(4, 1)	231.84
(1, 1)	71.4	(5, 0)	256.68
(1, 2)	71.7	(5, 5.5)	285.3
(1, 5)	90.3	(5, 3.5)	287.1
(1, 6)	92.4	(5, 6)	289.8
(2, 0)	107.7	(5, 5)	290.7
(2, 5.5)	133	(5, 4)	295.2
(2, 3.5)	140.4	(5, 3)	296.1
(2, 1.5)	144.6	(5, 1.5)	300.69
(3, 0)	145	(5, 2)	305.1
(2, 5)	145.4	(5, 1)	306.63
(2, 6)	147	(3, 5.5)	356.4
(2, 4)	150	(3, 3.5)	363.2
(2, 3)	158.1	(3, 5)	370.2
(2, 1)	160.9	(3, 6)	371
(2, 2)	162.5	(3, 1.5)	378
(4, 0)	199.53	(3, 3)	382
(4, 5.5)	207.18	(3, 4)	382.6
(4, 3.5)	212.13	(3, 2)	398
(4, 6)	212.67	(3, 1)	402

and

Table 9. Similar simulation experiments with different node smoke arrival schedules case3.

Node	Smoke Arrival Time (s)	Node	Smoke Arrival Time (s)
(1, 4)	7.9	(4, 0)	177.36
(1, 5.5)	44.3	(4, 5.5)	184.16
(1, 0)	50.3	(4, 3.5)	188.56
(1, 1.5)	53.5	(4, 6)	189.04
(1, 3.5)	55.7	(4, 5)	190
(1, 3)	67.2	(4, 1.5)	193.12
(1, 1)	71.4	(4, 4)	195.84
(1, 2)	71.7	(4, 3)	195.92
(1, 5)	90.3	(4, 2)	204.4
(1, 6)	92.4	(4, 1)	206.08
(2, 0)	107.7	(5, 0)	228.16
(2, 5.5)	133	(5, 5.5)	253.6
(2, 3.5)	140.4	(5, 3.5)	255.2
(2, 1.5)	144.6	(5, 6)	257.6
(3, 0)	145	(5, 5)	258.4
(2, 5)	145.4	(5, 4)	262.4
(2, 6)	147	(5, 3)	263.2
(2, 4)	150	(5, 1.5)	267.28
(2, 3)	158.1	(5, 2)	271.2
(2, 1)	160.9	(5, 1)	272.56
(2, 2)	162.5

. Table 4 and Table 7 were compared, and the results are shown in Figure 12. The spatial arrangement of the rooms is also illustrated in the figure. The darker color of the rooms or corridors in the figure indicates an earlier arrival time of the smoke. From Figure 12, it can be seen that the predicted smoke path of this model under the same conditions is largely consistent with the experimental smoke path. However, since this model can only predict the transmission path of smoke and cannot provide specific time information, there are some differences in the color differentiation. The comparison between Table 5 and Table 8, as well as between Table 6 and Table 9, shows a similar situation. The table and figure show that smoke from the fire room flowed into other rooms on the fire floor through corridors, and smoke from the corridor entered the stairwell and then entered rooms on other floors after rising. These results were consistent with those obtained from the graph theory simulation, even when the flue gas flow channel was closed or restricted. However, the experiment revealed that the speed at which smoke from the fire floor entered the stairwell through the corridor was faster than the speed at which it entered the room. In addition, the speed at which smoke from non-fire floors entered the room through the corridor was slower than the speed at which it entered other positions in the corridor. Moreover, the speed of smoke propagation in the vertical channel was slower in the experiment than in the simulation. Although the speed difference was small, it was inconsistent with the results of the graph theory simulation. Upon analysis, we found that this was because the experiment involved doors as an obstacle, which did not impede the spread of smoke in the horizontal channels such as the corridor. In contrast, the vertical propagation of smoke in the stairwell was affected by the chimney effect. In the simulation, the nodes were considered uniform and identical, without considering the influence of the chimney effect. Although the graph theory simulation cannot fully simulate the spread of smoke, it is close to the actual situation and can be used as a tool to analyze the path of smoke spread, especially in complex calculations.

4. Comparison with FDS Calculation: Application of Prediction Model in Complex Scenarios

4.1. Introduction to Complex Scenarios

A complex building was modeled based on a specific office building, which comprises 30 floors. Each floor has a height of 3 m, resulting in a total height of 90 m, and a total area of 1600 square meters. The overall structure of the building is illustrated in Figure 13, while the internal structure is depicted in Figure 14. Each floor contains 12 identically sized rooms, each with an area of 100 square meters. Rooms 1 and 5, 4 and 6, 7 and 9, and 8 and 10 are interconnected. Additionally, each floor has four elevator shafts, four pipe shafts, and two stairwells, each of which has a lobby. The ignition rooms on the first floor are designated as Rooms 1 and 10, having a heat release rate ratio of 2:1. The ambient temperature is set at 20 degrees Celsius, with standard atmospheric pressure and no wind. All doors and windows in the building are open, except for those in the elevator and pipe shafts. The H-shaped corridor in the middle, as depicted in the figure, is divided into six sections, utilizing a multi-node analysis method for smoke path prediction modeling.

4.2. FDS Simulation

The Fire Dynamics Simulator (FDS) is a CFD software utilized for fire and smoke transport modeling, which adopts the large eddy simulation method to simulate turbulence. In this study, the FDS model was established using the scenario described in Section 4.1 [24]. The mesh area was slightly larger than the building area, and the mesh boundaries were opened. This study simulated a single-room residential fire scenario with an average unit area heat release rate of 0.290 MW/m². To facilitate the experiment, three ideal constant heat sources with a heat release rate of 2500 kW/m² were set up using rubber as fuel. Room 1 had two heat sources and Room 10 had one. The ratio of the fire simulation characteristic dimension D* to the mesh size α was reasonable and within the range of 4–16 [25]. After calculation, a mesh size of 0.25 m was deemed appropriate. The ambient temperature was set to 0 °C, standard atmospheric pressure, and no wind. The model’s layers of rooms, corridors, and stairwells were flattened, and a carbon monoxide concentration probe was placed in the middle of each room to record the carbon monoxide concentration in that area. As people staying in an environment with a carbon monoxide concentration of 50 ppm for a long period of time will exhibit significant symptoms of poisoning, the time when the smoke reaches this level and remains above it was recorded as the standard [22]. All doors and windows in the building were open. The fire simulation characteristic diameter D* can be given by the following Equation (14):

$$D^{*}={(\frac{Q}{p_{00}{c}_p{T}_{00}\sqrt{g}})}^{2/5}$$

(14)

where Q is the heat release rate of the fire source in kW, p₀₀ is the air density and is taken as 1.204 kg/m³, T is the ambient temperature and is taken as 273.15 K, and g is the acceleration due to gravity and is taken as 9.81 m/s² [22].

4.3. Comparison Results

Due to the large number of nodes in the scene, only the situation of the first three levels of rooms is presented. Node (3.1) represents room 1 on the third floor. The arrival times of smoke on the first three levels of rooms obtained from FDS simulation are shown in

Table 10. FDS prediction results under complex conditions.

Node	Smoke Arrival Time (s)	Node	Smoke Arrival Time (s)
1.1	4.5	3.8	27.6
1.10	7.6	3.3	27.8
1.5	8	2.12	28.1
1.2	9.3	3.4	29
1.7	10.1	2.2	30
1.3	15.6	3.11	30
1.9	16	2,10	31.5
1.11	18.8	3.12	31.9
1.8	19	3.2	33.1
1.4	20.3	2.5	35
1.6	21	3.10	35
1.12	23	2.1	35.1
2.6	23	2.7	37.3
2.8	24.1	2.9	37.9
2.3	25.1	3.5	38.5
2.4	25.5	3.1	38.6
2.11	27	3.7	41.1
3.6	27	3.9	41.2

, while the smoke concentrations obtained using the proposed model are shown in

Table 11. Model prediction results under complex conditions.

Node	Smoke Content	Node	Smoke Content
1.1	497,840.6767	3.8	25,270.87091
1.10	367,915.8078	3.3	21,103.26071
1.5	308,110.1704	2.12	19,842.82335
1.2	271,855.896	3.4	18,841.6
1.7	253,551.3143	3.11	14,821.56838
1.3	139,120.9479	2.2	13,071.31879
1.9	131,338.7845	2.10	9039.994989
1.11	105,864.9898	3.12	8215.356354
1.8	103,063.422	3.2	6591.57382
1.4	86,126.57496	2.1	3595.182807
1.6	77,882.01627	3.10	3238.172324
2.6	57,435.07906	2.5	3118.005773
1.12	49,244.33735	2.7	1266.827663
2.8	49,148.44688	2.9	953.6833939
2.3	35,154.89195	3.5	700.159117
2.4	32,743.20143	3.1	679.0939566
3.6	29,137.45159	3.7	117.1456387
2.11	28,454.54256	3.9	105.4677068

. To compare the two tables, the smoke arrival times are sorted from the smallest to the largest, while the smoke concentrations are sorted from the largest to the smallest. Table 10 and Table 11 were compared, and the results are shown in Figure 15. The spatial arrangement of the rooms is also illustrated in the figure. The darker color of the rooms or corridors in the figure indicates an earlier arrival time of the smoke. It can be observed that the smoke path prediction results obtained by the two methods are basically consistent, indicating that the proposed model can be applied to predict smoke paths in complex scenes. During the simulation process, due to the large building area, the number of grids in the FDS model reached an astonishing 90 million, and even simulating only the first three levels of rooms took more than 24 h with millions of grids. In contrast, the proposed model can still predict the results within 10 s when the number of nodes exceeds 500.

5. Discussion

This study presents a smoke path prediction model based on graph theory, which has been validated with similar simulation results. However, smoke transmission is a complex process that is influenced not only by building structure but also by ambient temperature, opening status, ventilation systems, and environmental wind. Although changing the weight of edges in the model and adding a coefficient can reflect changes in these factors to some extent, determining the coefficient is a complex task. In future use of the model, a big data method based on artificial neural networks will be utilized to calculate the coefficient using a large amount of data, and this feedback calculation model can verify the accuracy of the coefficient. However, this method requires substantial data support. Moreover, the model exhibits higher accuracy in the horizontal direction than in the vertical direction, and slight deviations were observed in the predicted results for positions far from the fire source. These issues can be addressed by adjusting the weight of edges and coefficients.

6. Conclusions

This article presents a smoke spread prediction model for high-rise building fires based on graph theory. The building was modeled as a DAG network by representing different areas of the building as nodes and smoke transmission channels as edges. After adding weight, coefficient, and smoke release models to the edges, the DAG network model was imported into a computer simulation to obtain predicted results. The predicted results were compared with similar simulation results and compared to simulations treating long channels as a single node and multiple nodes. The main conclusions are as follows:

(1)

Innovatively, this study divides long channels into multiple nodes in detail. Compared to using a single node, the use of multiple nodes is more realistic and appropriate to the actual situation.

(2)

The predicted results of the two simulations are basically consistent, and changing the state of some smoke transmission channels does not affect accuracy.

(3)

Compared with other simulation methods such as FDS, this model has a shorter modeling time and only takes a few seconds to simulate, without requiring high computer configuration. When only the fire smoke transmission path is needed and rapid predicted results are required, this model can replace other simulation methods such as FDS.

(4)

Changes in the weight of edges and the addition of coefficients can simulate the status of openings and ventilation facilities. However, determining coefficients and weights requires a significant amount of time. Currently, this model can serve as an ideal prediction tool for smoke spread in high-rise building fires.