Experimental and Numerical Behavior of Encased Pultruded GFRP Beams under Elevated and Ambient Temperatures
Abstract
1. Introduction
2. Experimental Program
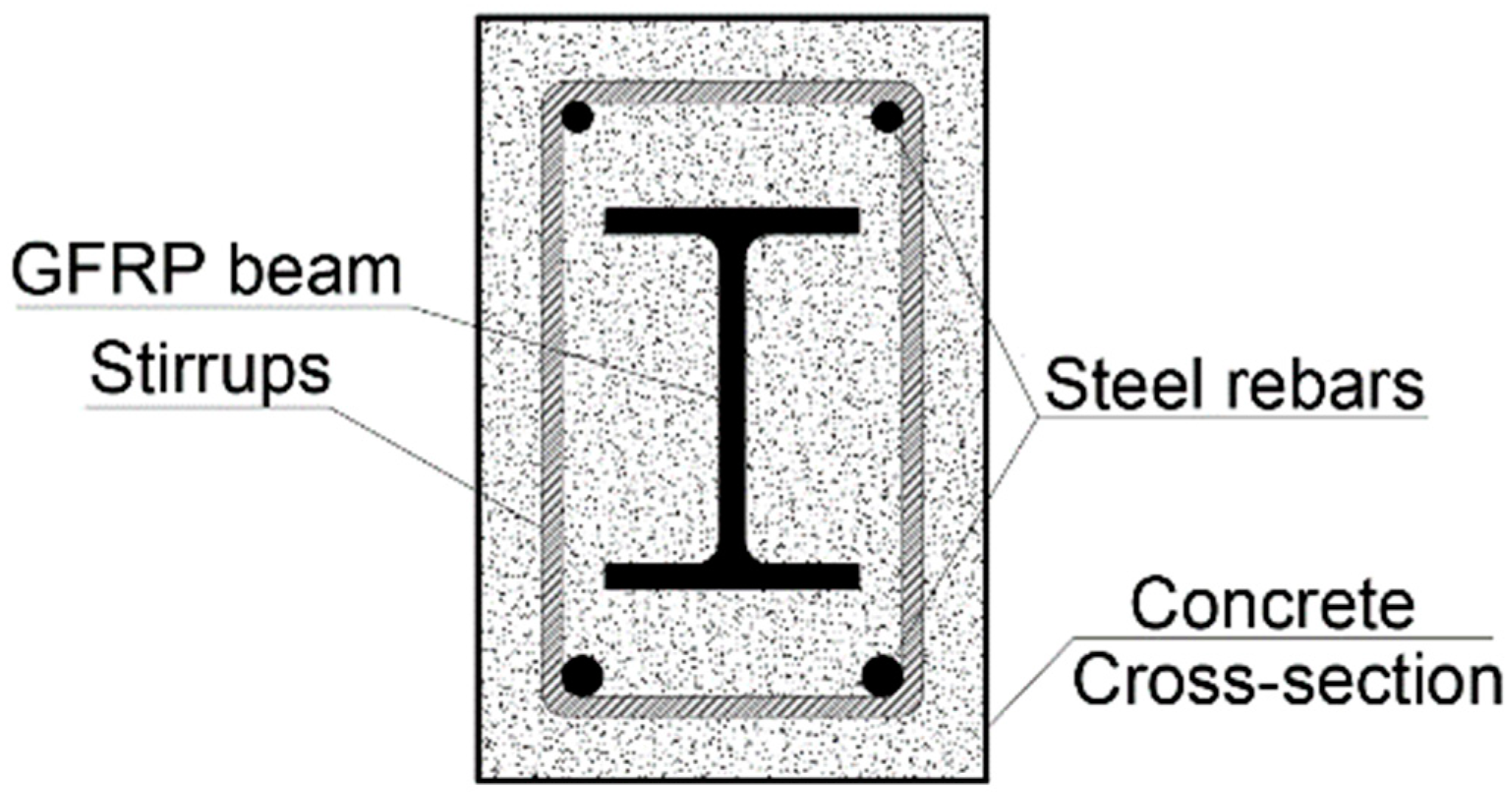
2.1. Details of the Tested Beams
2.2. Material Properties
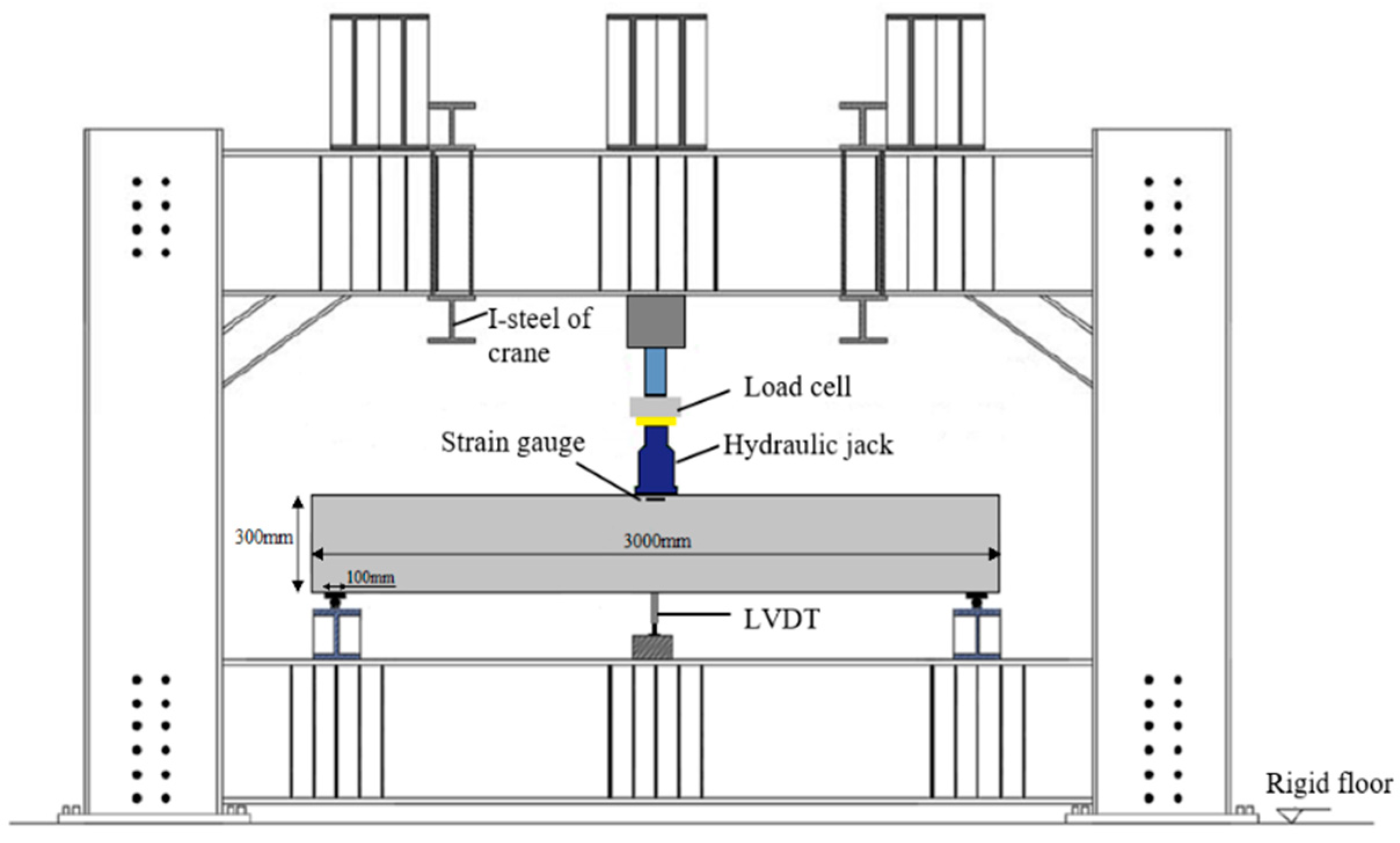
2.3. Static Tests
2.4. Fire Test Setup and Procedures
- The rising temperature stage: the furnace was heated up to 700 °C following the standard fire curve according to ASTM E119-20 [23].
- The constant temperature stage: this stage occurred after the furnace reached the predetermined temperature (700 °C), and the specimen was exposed to this temperature for one hour.
- Cooling stage: the furnace stopped working, and the specimens were left to cool to the ambient temperature.
3. Experimental Results and Discussion
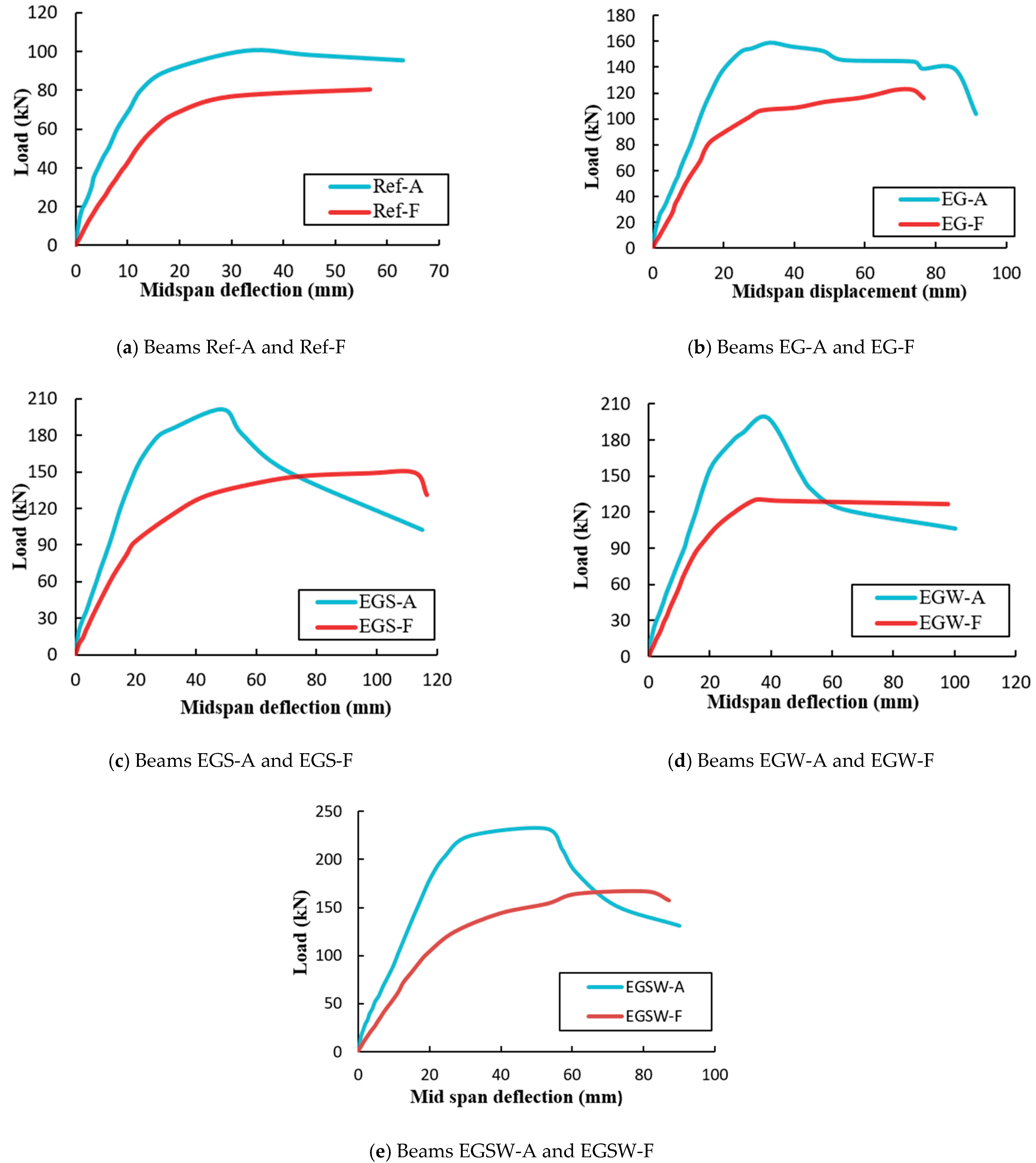
3.1. Static Test Results
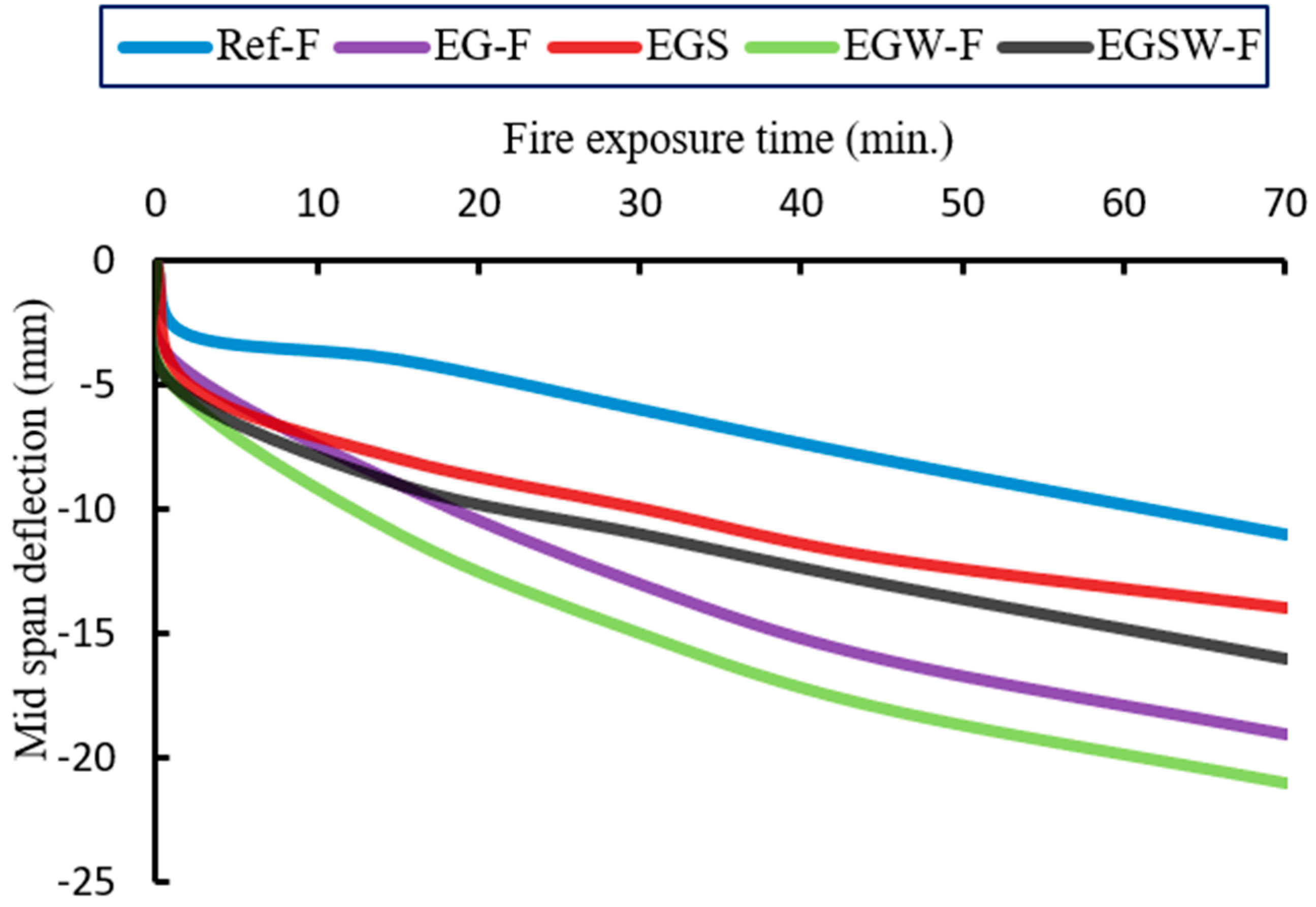
3.2. Fire Test Results
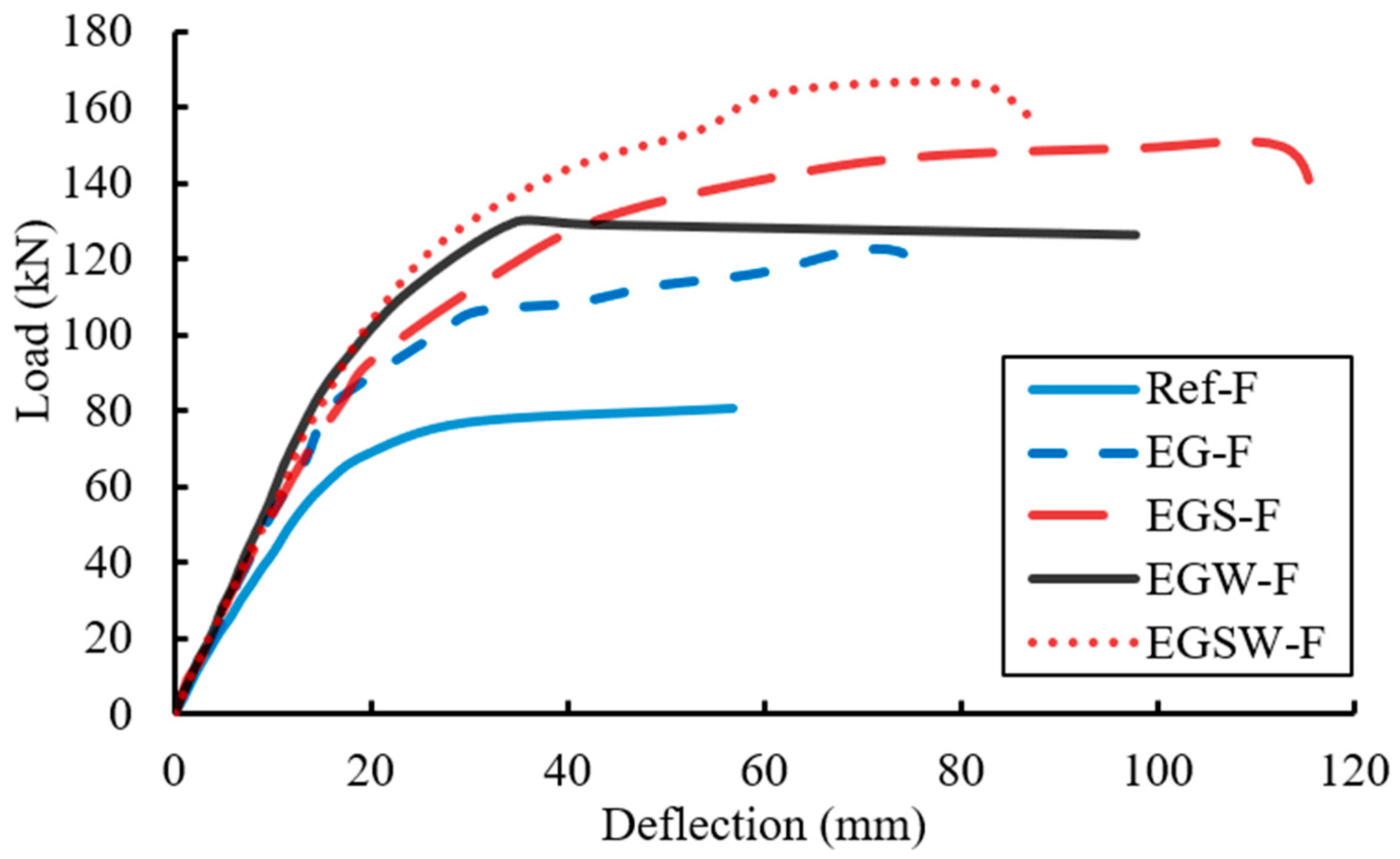
3.3. Residual Static Capacity of the Burned Beams
3.4. Crack Patterns and Failure Modes of the Burned Beams
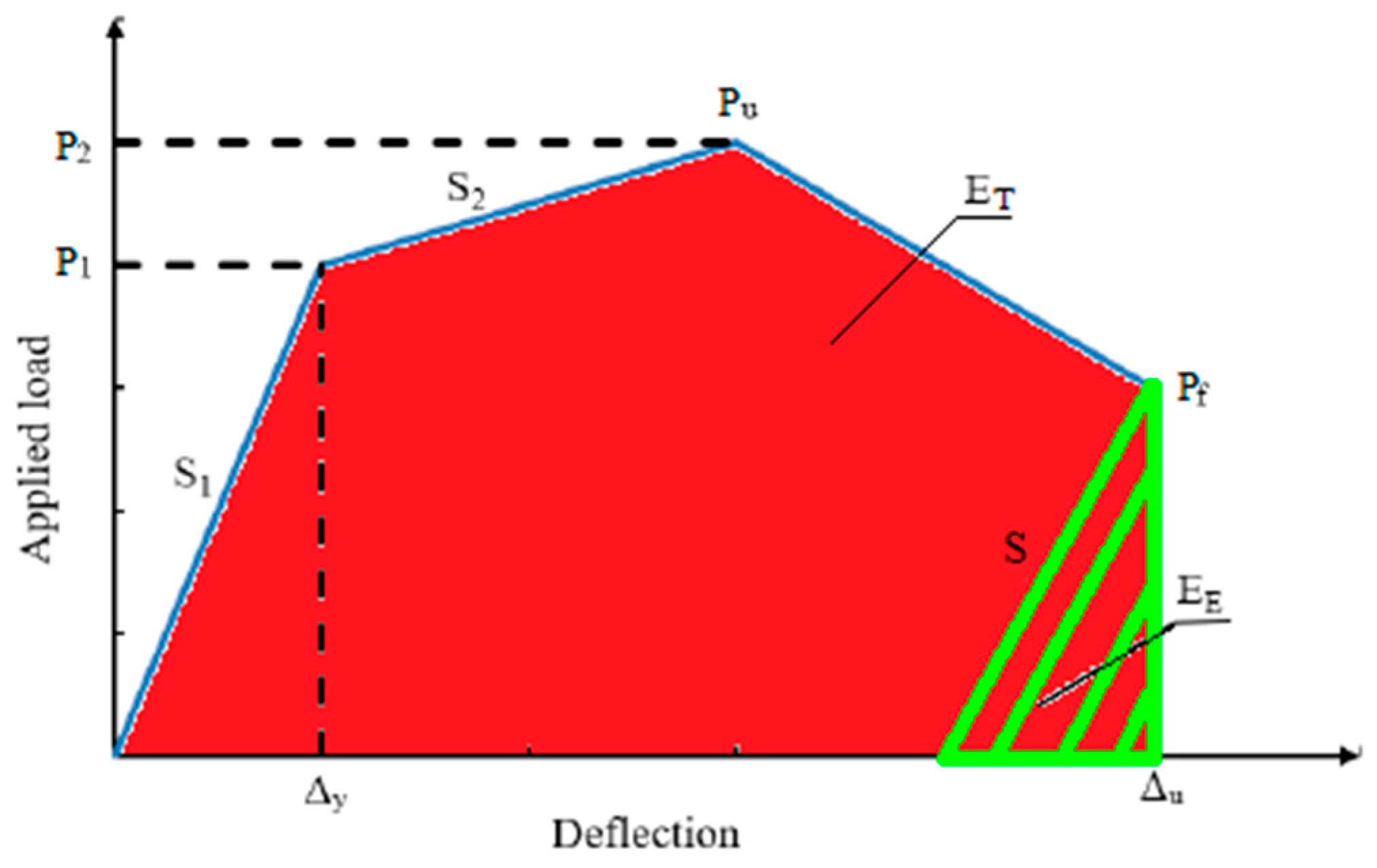
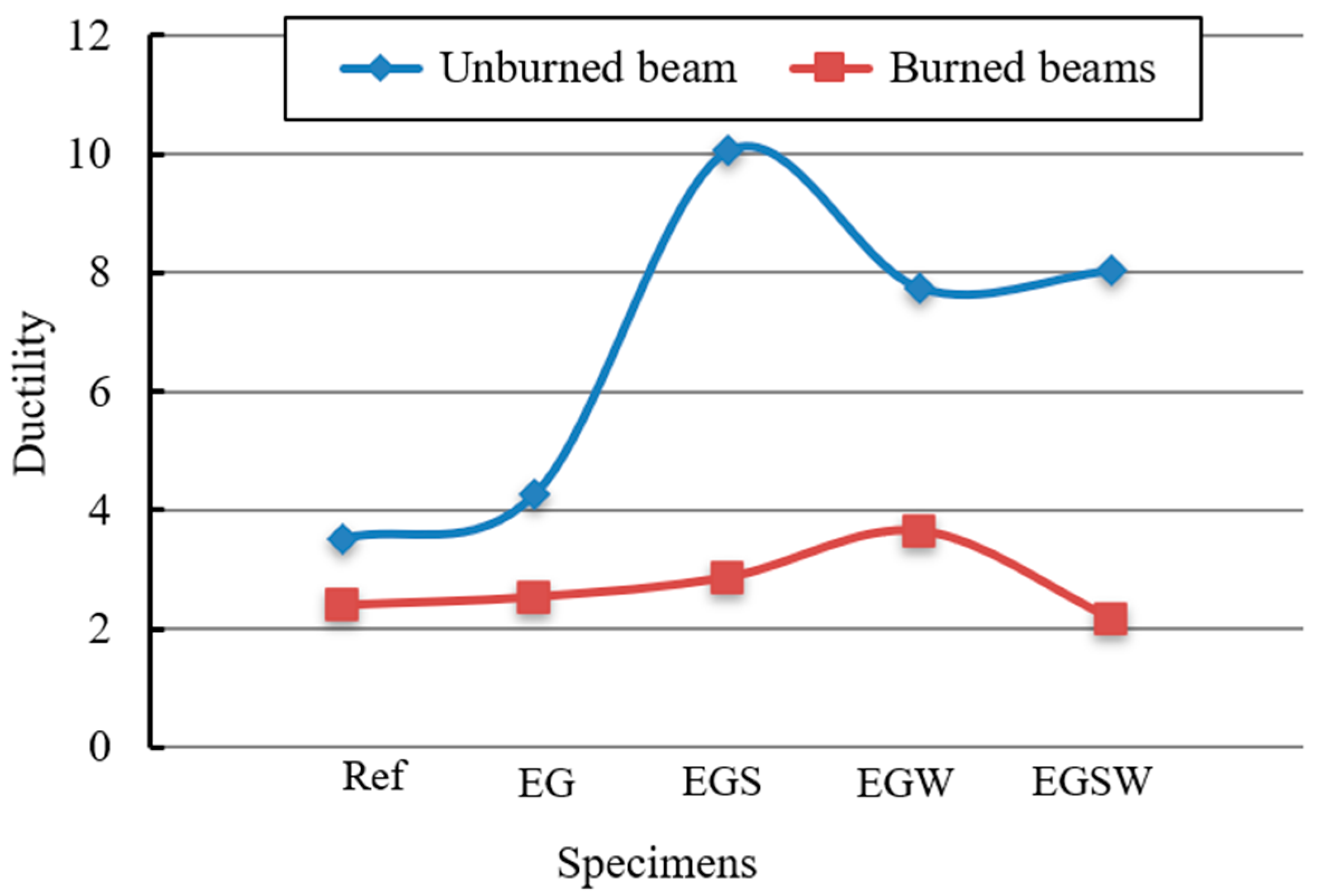
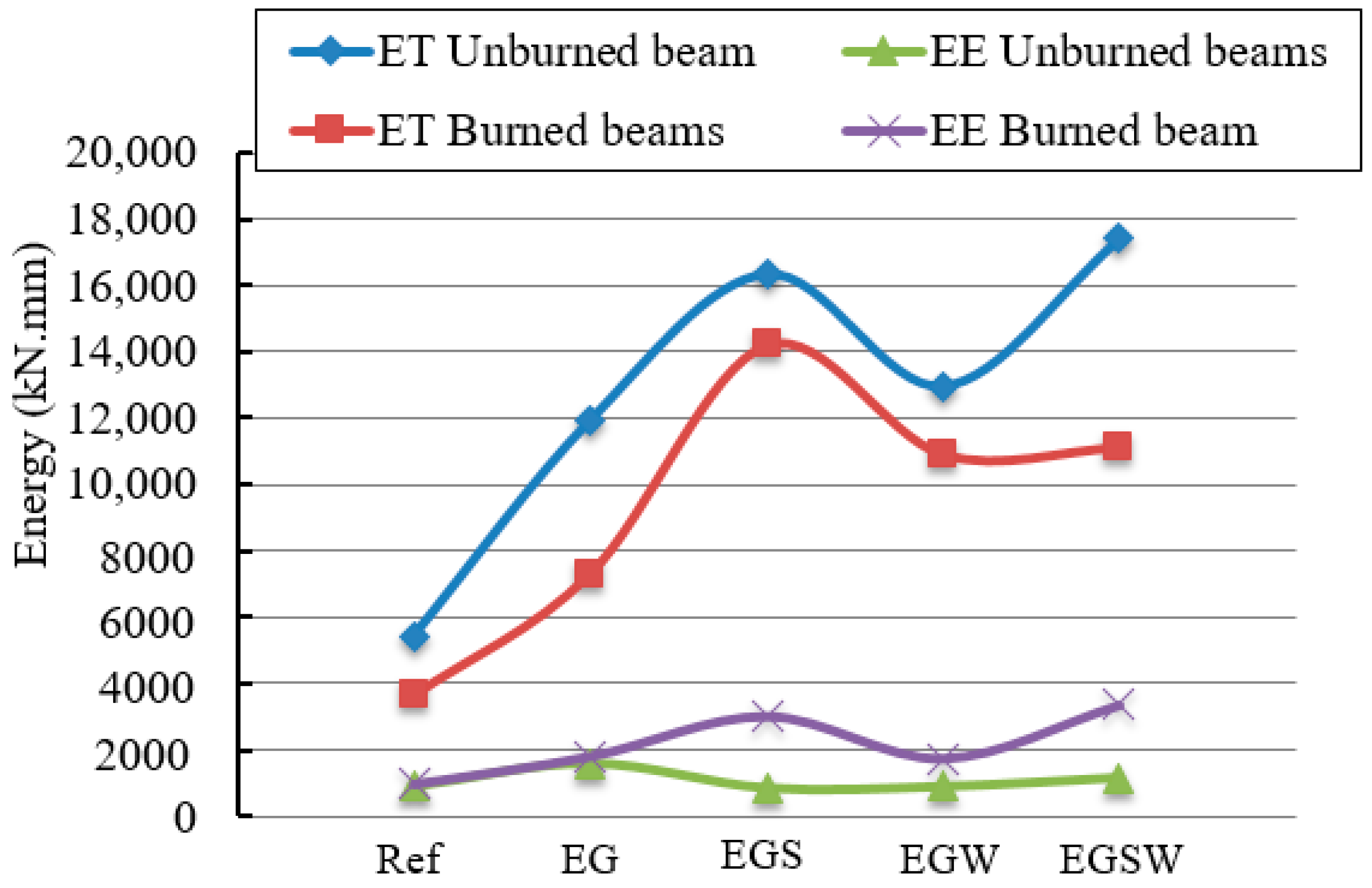
3.5. Ductility
4. Finite Element Analysis
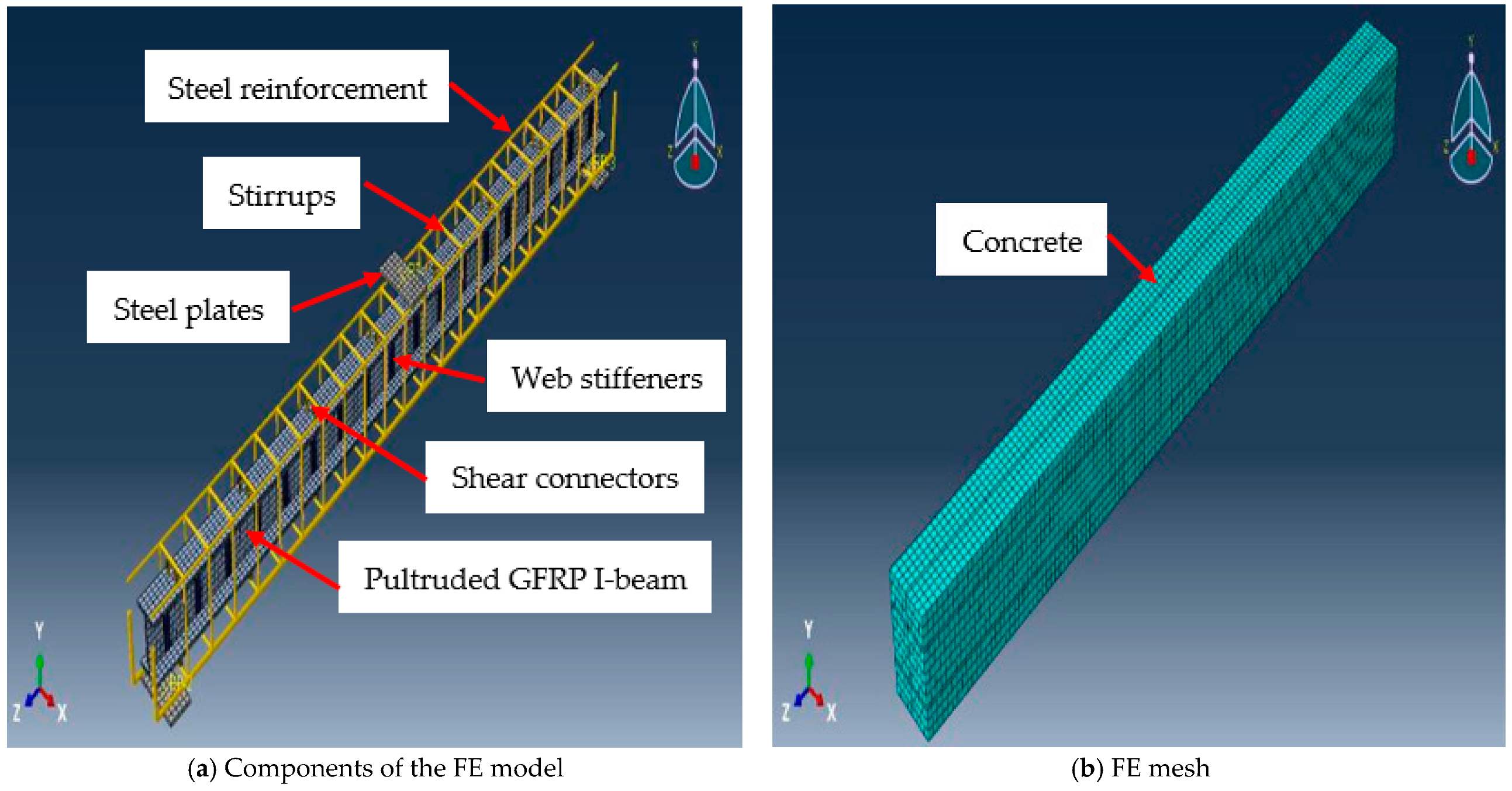
4.1. Element Selection
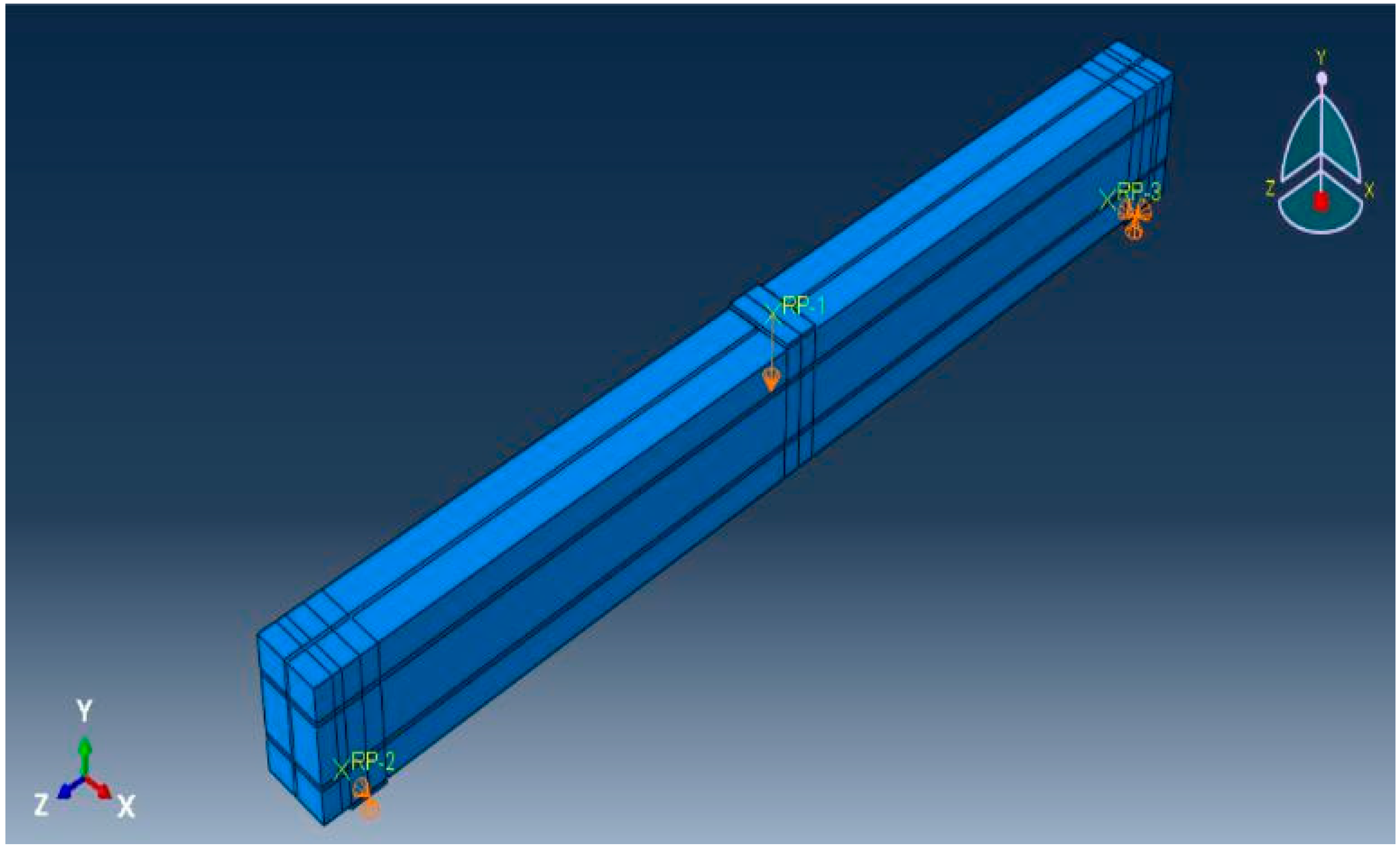
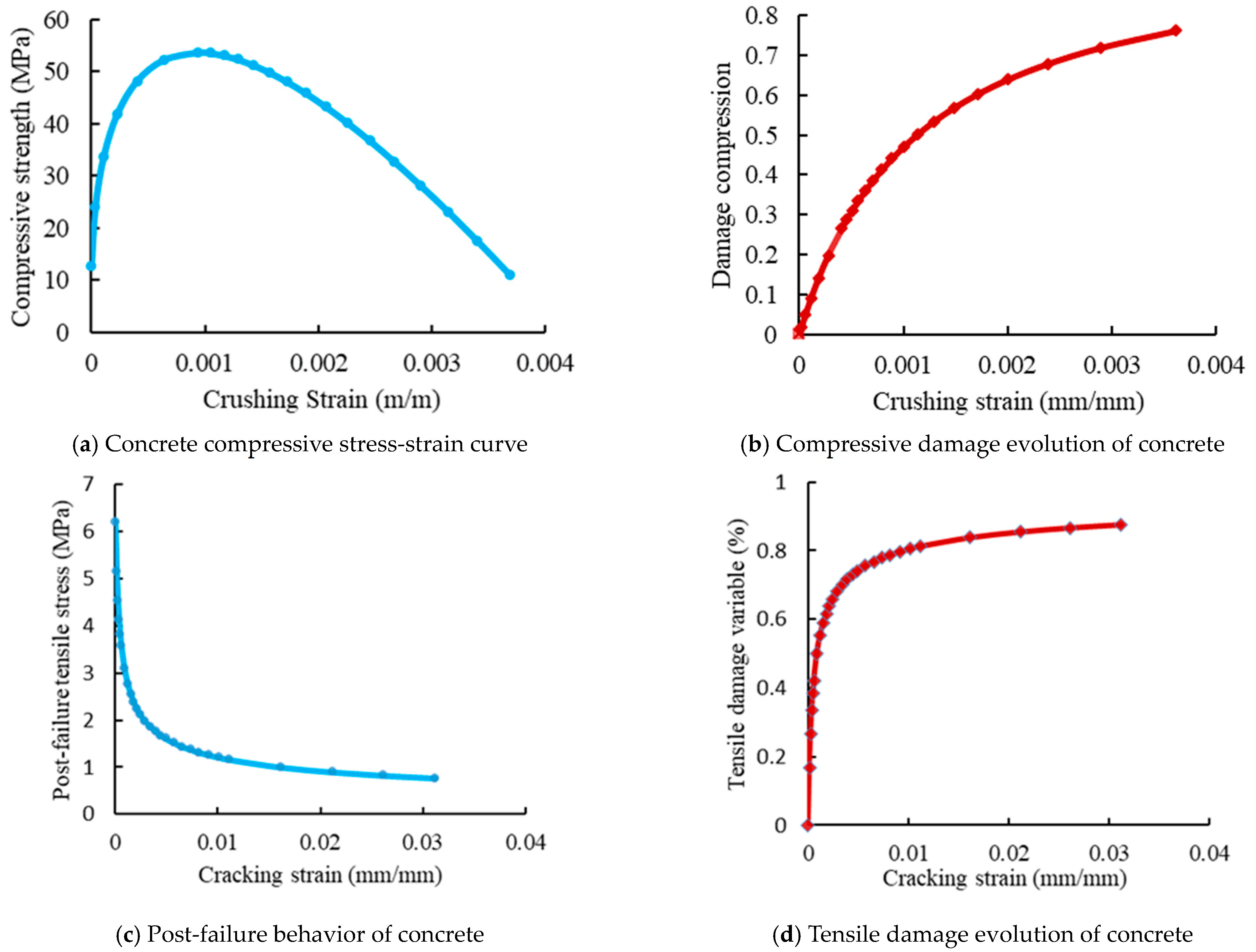
4.2. Material Properties and Boundary Conditions
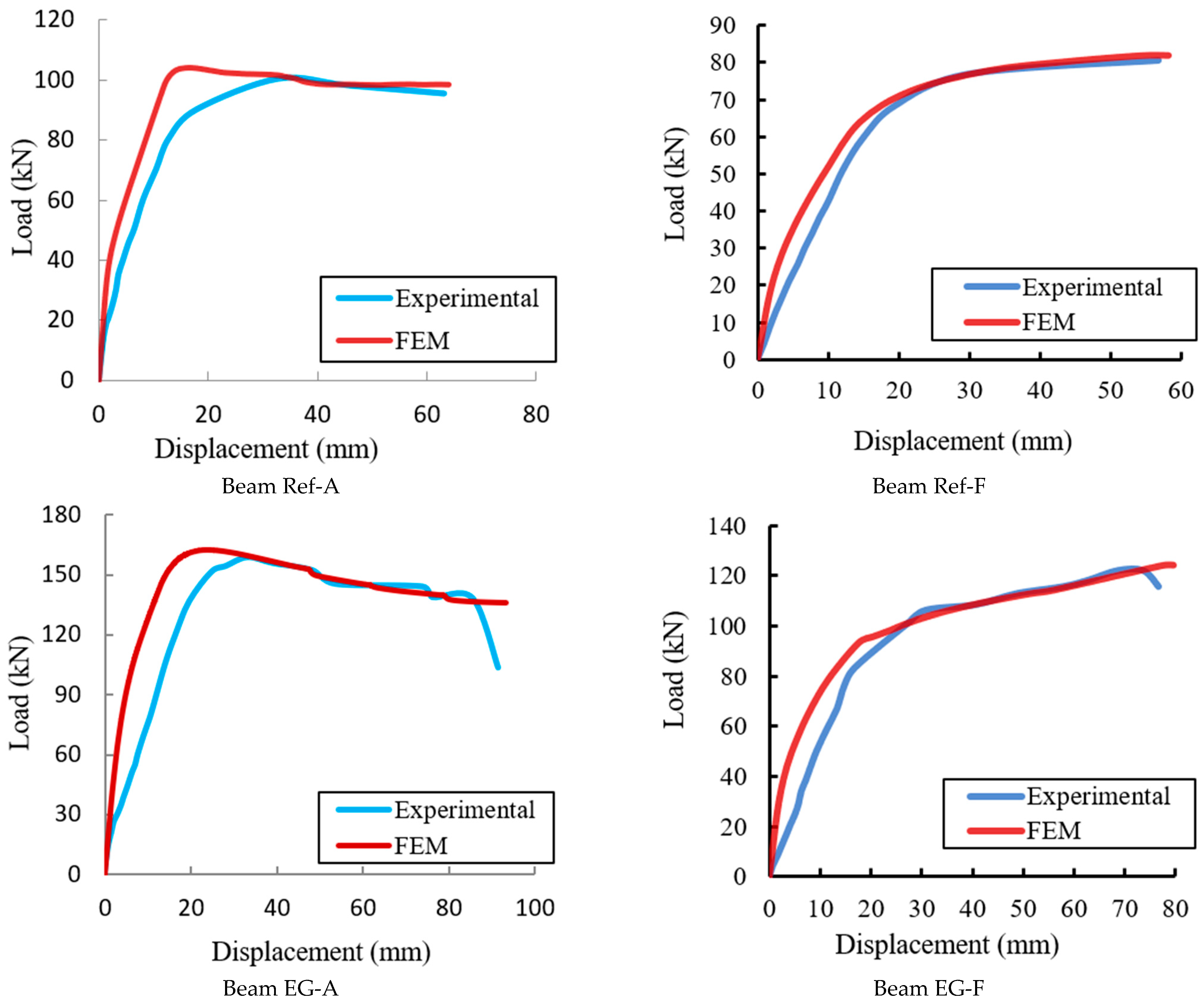
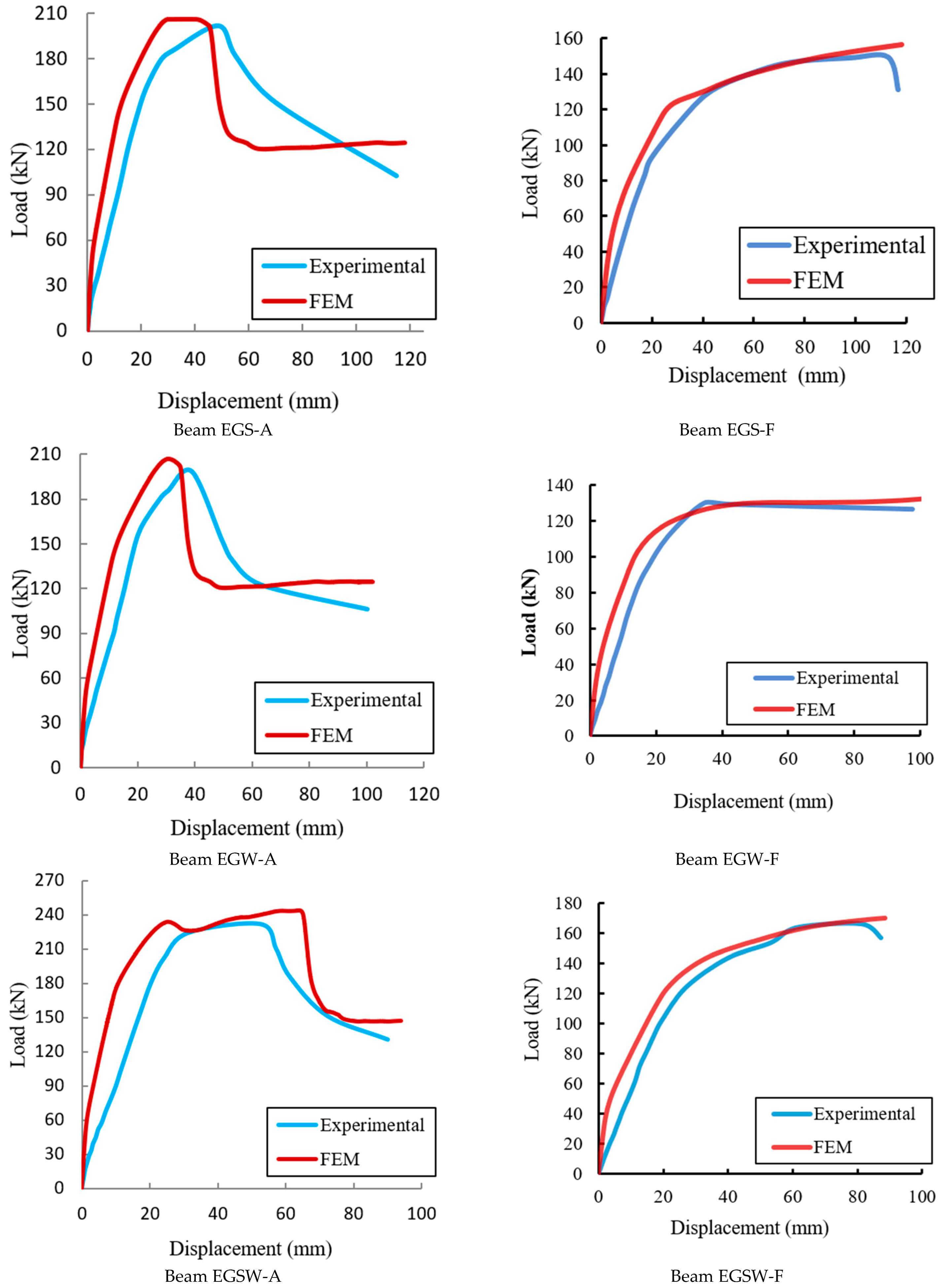
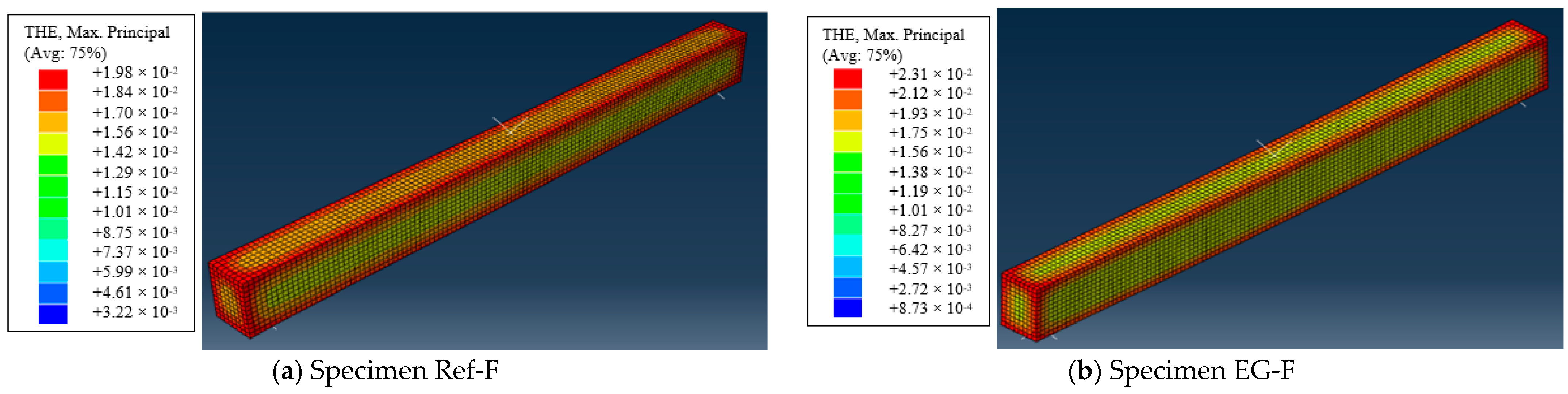
4.3. Verification of the FE Results
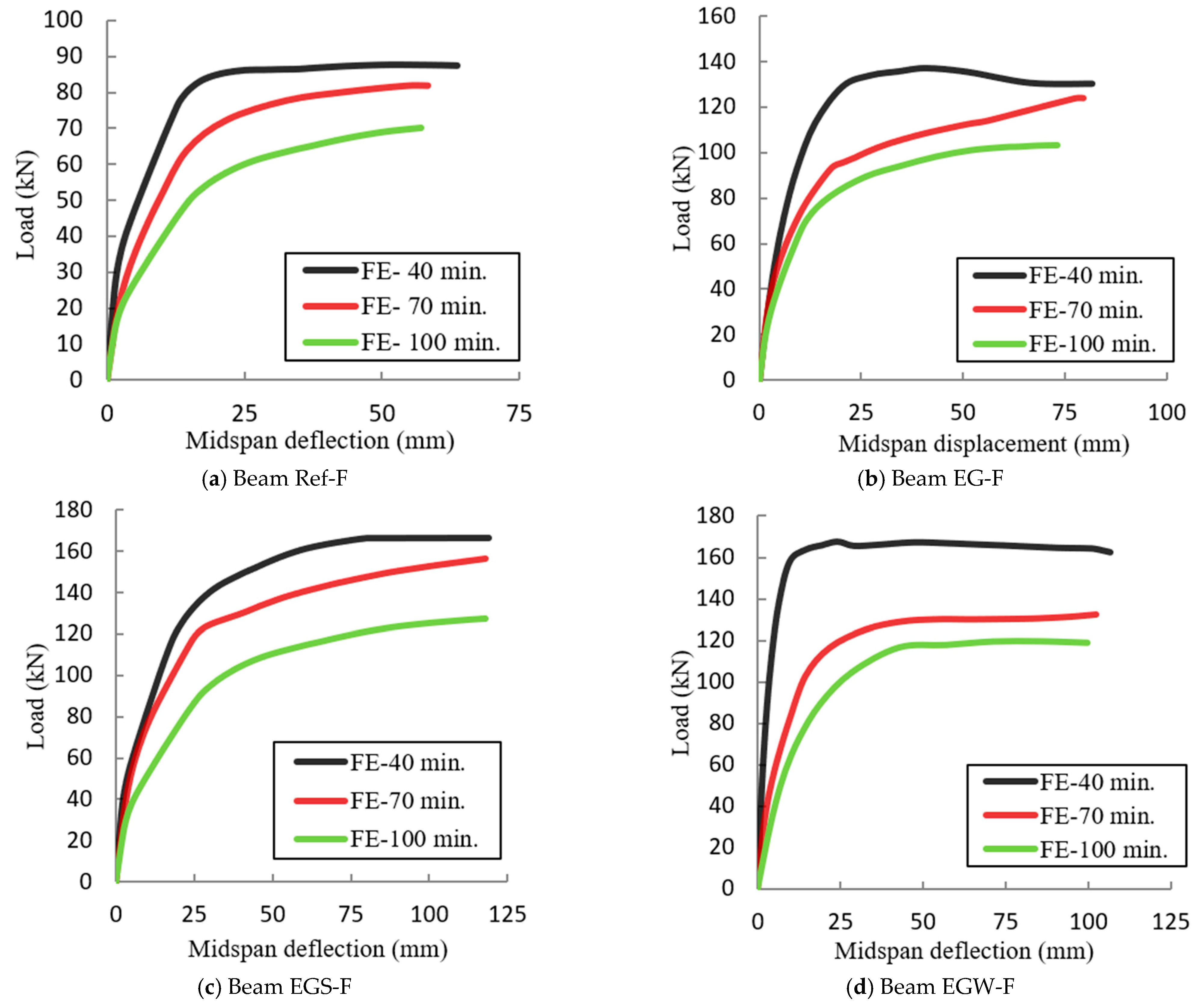
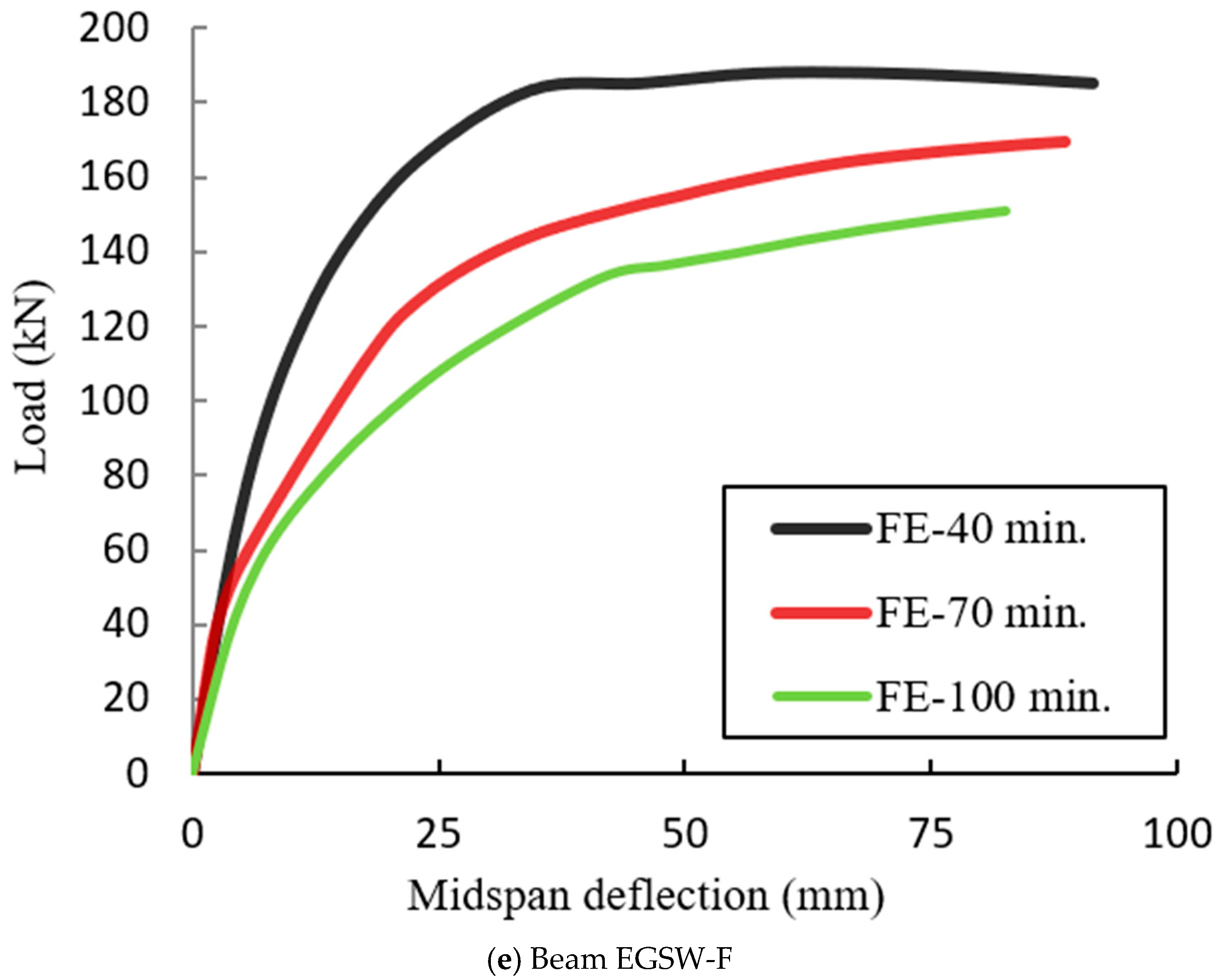
4.4. Effect of the Fire Exposure Duration
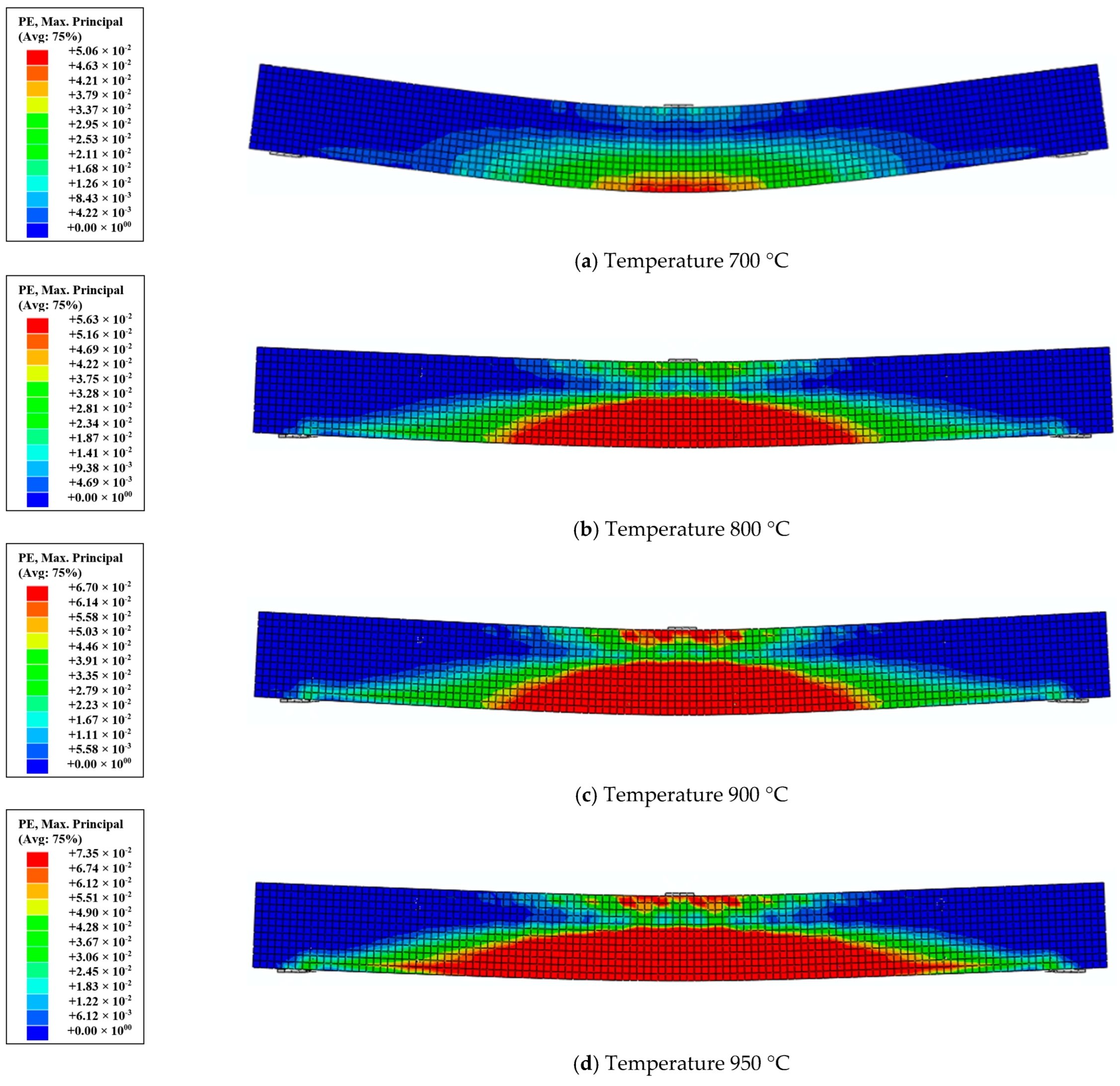
4.5. Effect of Temperature
5. Conclusions
- The load capacities of the fire-damaged encased CFRP beams were less than their peers with the same configurations at ambient temperature. The load capacities dropped by 23–34%, and this drop was the highest in the cases of shear connectors and web stiffeners. However, the shear connectors and web stiffeners enhanced the load-bearing capacity of the tested beams (burned or unburned) relative to their reference beams.
- The ductility of fire-damaged beams was lower than that of the unburned peer beams by 40.9–73%. The reduction was the highest when using shear connectors and web stiffeners. Providing shear connectors and web stiffeners at the same time caused more damage in the burned beam EGSW-F and subsequently a reduction in ductility.
- Additional reductions were observed in the residual capacities of the fire-damaged beams due to exposure to longer fire durations. The improvement in the beam capacity due to using shear connectors and web stiffeners relative to the reference beam under the same exposure time decreased as the exposure duration increased.
- Increasing the temperature to 700 °C, 800 °C, 900 °C, and 950 °C caused reductions in the residual capacities by about 25%, 45%, 70%, and 80% for the encased beams in comparison to their peers at ambient temperature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, E.G.; Shin, Y.S. The structural behavior and simplified thermal analysis of normal-strength and high-strength concrete beams under fire. Eng. Struct. 2011, 33, 1123–1132. [Google Scholar] [CrossRef]
- Mahmood, E.M.; Allawi, A.A.; El-Zohairy, A. Analysis and Residual Behavior of Encased Pultruded GFRP I-Beam under Fire Loading. Sustainability 2022, 14, 13337. [Google Scholar] [CrossRef]
- Allawi, A.A.; Ali, S.I. Flexural behavior of composite GFRP pultruded i-section beams under static and impact loading. Civ. Eng. J. 2020, 6, 143–2158. [Google Scholar] [CrossRef]
- Ibrahim, T.H.; Allawi, A.A.; El-Zohairy, A. Experimental and FE Analysis of Composite RC Beams with Encased Pultruded GFRP I-Beam under Static Loads. Adv. Struct. Eng. 2022, 26, 516–532. [Google Scholar] [CrossRef]
- Mahmood, E.M.; Allawi, A.A.; El-Zohairy, A. Flexural Performance of Encased Pultruded GFRP I-Beam with High Strength Concrete under Static Loading. Materials 2022, 15, 4519. [Google Scholar] [CrossRef]
- Ali, S.I.; Allawi, A.A. Effect of Web Stiffeners on the Flexural Behavior of Composite GFRP Concrete Beam Under Impact Load. J. Eng. 2021, 27, 76–92. [Google Scholar] [CrossRef]
- Ibrahim, T.H.; Allawi, A.A. The Response of Reinforced Concrete Composite Beams Reinforced with Pultruded GFRP to Repeated Loads. J. Eng. 2022, 29, 158–174. [Google Scholar] [CrossRef]
- Zhou, K.; Han, L.-H. Fire Performance of Concrete-Encased CFST Columns and Beam-Column Joints. In Proceedings of the 12th International Conference on Advances in Steel-Concrete Composite Structures, Valencia, Spain, 27–29 June 2018; pp. 779–786. [Google Scholar] [CrossRef]
- Morgado, T.; Correia, J.R.; Silvestre, N.; Branco, F.A. Experimental study on the fire resistance of GFRP pultruded tubular beams. Compos. Part B Eng. 2018, 139, 106–116. [Google Scholar] [CrossRef]
- Parthasarathi, N.; Satyanarayanan, K.S.; Thamilarasu, V. Thermal behavior of reinforced concrete beam with static loading condition. Int. J. Recent Technol. Eng. 2019, 8, 1484–1488. [Google Scholar] [CrossRef]
- Gao, W.Y.; Dai, J.G.; Teng, J.G.; Chen, G.M. Finite element modeling of reinforced concrete beams exposed to fire. Eng. Struct. 2013, 52, 488–501. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Agrawal, A. A numerical approach for evaluating the residual capacity of fire-damaged concrete members. Rev. ALCONPAT 2020, 10, 230–242. [Google Scholar] [CrossRef]
- Ahmed, A. The behavior of FRP-Strengthened Reinforced Concrete Beams under Fire Conditions. Ph.D. Thesis, Civil Engineering Michigan State University, East Lansing, MI, USA, 2010. [Google Scholar]
- Duan, D.; Ouyang, L.; Gao, W.; Xu, Q.; Liu, W.; Yang, J. Fire Performance of FRP-RC Flexural Members: A Numerical Study. Polymers 2022, 14, 346. [Google Scholar] [CrossRef] [PubMed]
- Cai, B.; Li, B.; Fu, F. Finite Element Analysis and Calculation Method of Residual Flexural Capacity of Post-fire RC Beams. Int. J. Concr. Struct. Mater. 2020, 14, 58. [Google Scholar] [CrossRef]
- Serȩga, S.; Wosatko, A. Numerical Prediction of Fire Resistance of RC Beams. AIP Conf. Proc. 2018, 1922, 130001. [Google Scholar] [CrossRef]
- ACI 318; Building Code Requirements for Structural Concrete (ACI 318-19) Commentary on Building Code Requirements for Structural Concrete (ACI 318R-19) an ACI Standard and Report from HIS. ACI: Farmington Hills, MI, USA, 2019.
- ASTM Designation C39-39M; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens Annual Book of ASTM Standards. ASTM: West Conshohocken, PA, USA, 2001.
- ASTM Designation C469-469M; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression ASTM International. ASTM: West Conshohocken, PA, USA, 2001.
- ASTM Designation A615-615M; Standard Test Method for Deformed and Plain Carbon-Steel Bars for Concrete Reinforcement Annual Book of ASTM Standards, American Association State Highway and Transportation Officials Standard AASHTO No.: M 31. ASTM: West Conshohocken, PA, USA, 2009.
- ASTM Designation D695-15; Standard Test Method for Compressive Properties of Rigid Plastics Annual Book of ASTM Standards, American International. ASTM: West Conshohocken, PA, USA, 2015.
- European Standard EN ISO 527-4; Determination of Tensile Properties of Plastics Part 4: Test Conditions for Isotropic and Orthotropic Fiber-Reinforced Plastic Composites, No. 1109a. ISO: Geneva, Switzerland, 1997.
- ASTM E119-00a; Standard Test Methods for Fire Tests of Building Construction and Materials. American Society for Testing and Materials. The United States of America legally binding document. ASTM: Washington, DC, USA, 2000.
- Rafi, M.M.; Nadjai, A. Experimental Behaviour of Carbon FRP Reinforced Concrete Beams at Ambient and Elevated Temperatures. J. Adv. Concr. Technol. 2008, 6, 431–441. [Google Scholar] [CrossRef]
- Ellis, D.S.; Tabatabai, H.; Nabizadeh, A. Residual Tensile Strength and Bond Properties of GFRP Bars after Exposure to Elevated Temperatures. Material 2018, 11, 346. [Google Scholar] [CrossRef]
- Yuan, J. Flexural Behavior of Composite Beams Reinforced with GFRP I-Section. Ph.D. Thesis, School of Civil, Mining, and Environmental Engineering, University of Wollongong, Wollongong, NSW, Australia, 2017. Available online: https://ro.uow.edu.au/theses1 (accessed on 18 May 2023).
- ABAQUS User Manual. Computer Software for Finite Element Analysis Dassault Systems; Simulia: Johnston, RI, USA, 2017. [Google Scholar]
- Earij, A.; Alfano, G.; Cashell, K.; Zhou, X. Nonlinear three–dimensional finite–element modeling of reinforced–concrete beams: Computational challenges and experimental validation. Eng. Fail. Anal. 2017, 82, 92–115. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Chern, J.G.; You, C.M. Deformation of Progressively Cracking Partially Prestressed Concrete Beams. PCI J. 1992, 37, 74–85. [Google Scholar] [CrossRef]
- EN 1992-1-2; Eurocode 2: Design of Concrete Structures—Part 1–2: General Rules—Structural Fire Design. European Committee for Standardization: Brusseles, Belgium, 2004.
- Dwaikat, M.B.; Kodur, V.K.R. Hydrothermal model for predicting fire-induced spalling in concrete structural systems. Fire Safety J. 2009, 44, 425–434. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. Trans. ASME 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Yu, B.; Kodur, V.K.R. Factors governing the fire response of concrete beams reinforced with FRP rebars. Compos. Struct. 2013, 100, 257–269. [Google Scholar] [CrossRef]
- Hadi, M.N.S.; Yuan, J.S. Experimental investigation of composite beams reinforced with GFRP I-beam and steel bars. Constr. Build. Mater. 2017, 144, 462–474. [Google Scholar] [CrossRef]












| Group | Specimens | Encased | Addition * | Temperature | Type of Test |
|---|---|---|---|---|---|
| I | Ref-A | - | - | Ambient | Static |
| EG-A | GFRP | - | Ambient | Static | |
| EGS-A | GFRP | S | Ambient | Static | |
| EGW-A | GFRP | W | Ambient | Static | |
| EGSW-A | GFRP | S and W | Ambient | Static | |
| II | Ref-F | - | - | 700 °C | Fire and residual static |
| EG-F | GFRP | - | 700 °C | Fire and residual static | |
| EGS-F | GFRP | S | 700 °C | Fire and residual static | |
| EGW-F | GFRP | W | 700 °C | Fire and residual static | |
| EGSW-F | GFRP | S and W | 700 °C | Fire and residual static |
| Cement (kg/m3) | Fine Aggregate (kg/m3) | Coarse Aggregate (kg/m3) | Water (kg/m3) | Admixture (kg/m3) |
| 475 | 880 | 910 | 165 | 15.25 |
| Diameter (mm) | As (mm2) | Yield Stress, ƒy (MPa) | Ultimate Strength, ƒu (MPa) | Elongation (%) | Grade | |||
|---|---|---|---|---|---|---|---|---|
| Test | ASTM-A615 (min.) | Test | ASTM-A615 (min.) | Test | ASTM-A615 (min.) | |||
| 16 | 203.58 | 520.73 | 420 | 687.07 | 550 | 23 | 9 | 60 |
| 10 | 76.82 | 407.7 | 280 | 465.63 | 420 | 21 | 11 | 40 |
| Mechanical Properties | Value |
|---|---|
| Transverse Compressive Strength (MPa) | 118.3 |
| Longitudinal Compressive Strength (MPa) | 326.14 |
| Longitudinal Tensile Strength (MPa) | 347.5 |
| Longitudinal Modulus of Elasticity (MPa) | 27,100 |
| Transverse Modulus of Elasticity (MPa) | 6800 |
| Longitudinal Compressive Strain (%) | 0.225 |
| Transverse Compressive Strain (%) | 0.93 |
| Longitudinal Tensile Strain (%) | 2.735 |
| Longitudinal Compressive Strength (MPa) | 354.17 |
| Longitudinal Modulus of Elasticity (MPa) | 26.64 |
| Longitudinal Compressive Strain (%) | 0.322 |
| Geometrical properties * | |
| Area (mm2) | 3300 |
| Perimeter (mm) | 680 |
| Moment of inertia (mm4) | 11,647,500 |
| Mass (kg/m) | 5.94 |
| Web and Flange thickness (mm) | 10 |
| Physical properties * | |
| Relative density | 1.8 |
| Water absorption (%) | 0.5 |
| Specific Heat (KJ) | 1.5 |
| Thermal Conductivity (W/mk) | 0.37 |
| Coefficient of thermal expansion (1/k) | 1.3 × 10−5 |
| Specimen | Initial Crack Load (kN) | Yield Load (kN) | Peak Load (kN) | Change (%) | Yield Displacement (mm) * | Change (%) | Failure Mode |
|---|---|---|---|---|---|---|---|
| Ref-A | 19.93 | 90.22 | 100.46 | – | 32.80 | – | Yielding of reinforcement and crushing in concrete |
| EG-A | 20.24 | 151.81 | 159.04 | +58.3 | 33.07 | +0.8 | Yielding of reinforcement, crushing of concrete, and fracture in GFRP |
| EGS-A | 19.73 | 148.26 | 201.54 | +100.6 | 48.68 | +48.4 | Yielding of reinforcement, crushing of concrete, and fracture in GFRP |
| EGW-A | 20.12 | 175.20 | 198.24 | +97.3 | 38.96 | +18.8 | Yielding of reinforcement, crushing of concrete, and fracture in GFRP |
| EGSW-A | 22.26 | 224.43 | 231.88 | +130.8 | 52.56 | +60.2 | Yielding of reinforcement, crushing of concrete, and fracture in GFRP |
| Specimen | Initial Deflection (mm) | Initial Stiffness (kN/mm) | First Period ASTM-E119 @ 10 min | Second Period Exposure 700 °C @70 min | Third Period Cooling | |||
|---|---|---|---|---|---|---|---|---|
| Deflection (mm) | Stiffness (kN/mm) | Deflection (mm) | Stiffness (kN/mm) | Ultimate Deflection (mm) | Residual Deflection (mm) | |||
| Ref-F | 3 | 8.33 | 4 | 6.25 | 11 | 2.27 | 16 | 1 |
| EG-F | 4 | 10 | 7 | 5.71 | 19 | 2.10 | 25 | 3 |
| EGS-F | 5 | 10 | 7 | 7.14 | 14 | 3.57 | 23 | 1 |
| EGW-F | 5 | 10 | 9 | 5.55 | 21 | 2.38 | 32 | 3 |
| EGSW-F | 5 | 13 | 8 | 8.13 | 16 | 4.06 | 27 | 2 |
| Specimen | Yielding Load (kN) | Change (%) | Peak Load (kN) | Change (%) | Ultimate Deflection (mm) | Strain in Concrete | Change in Strain (%) |
|---|---|---|---|---|---|---|---|
| Ref-F | 59.8 | – | 80.6 | – | 56.7 | 0.0029 | – |
| EG-F | 83.6 | +39.7 | 122.1 | +51.5 | 68.6 | 0.0032 | +10 |
| EGS-F | 92.5 | +54.4 | 149.6 | +85.6 | 112.5 | 0.004 | +38 |
| EGW-F | 93.1 | +55.4 | 130.1 | +61.3 | 34.7 | 0.0033 | +14 |
| EGSW-F | 107.1 | +78.7 | 166.2 | +106.2 | 81.1 | 0.0033 | +14 |
| Specimen | Unburned | Burned | Change (%) | |||
|---|---|---|---|---|---|---|
| Peak Load (kN) | Displacement at Peak Load (mm) | Peak Load (kN) | Displacement at Peak Load (mm) | Peak Load | Disp. | |
| Ref | 100.4 | 32.8 | 80.6 | 56.7 | −19.7 | +72.9 |
| EG | 159.1 | 33.1 | 122.1 | 68.6 | −23.1 | +107.7 |
| EGS | 201.5 | 48.6 | 149.6 | 112.5 | −25.7 | +131.2 |
| EGW | 198.2 | 38.9 | 130.1 | 34.7 | −34.3 | −10.8 |
| EGSW | 231.8 | 52.5 | 166.2 | 81.1 | −28.3 | +54.4 |
| Group | Specimen | Slope S1 | Slope S2 | Slope S | Total Energy ET (kN·mm) | Elastic Energy EE (kN·mm) | Ductility μE | Change (%) |
|---|---|---|---|---|---|---|---|---|
| I | Ref-A | 6.1 | 0.9 | 5.1 | 5443 | 900 | 3.52 | – |
| EG-A | 6.3 | 0.9 | 6.1 | 11,933 | 1576 | 4.28 | +21.6 | |
| EGS-A | 6.8 | 1 | 6.1 | 16,344 | 852 | 10.05 | +185.5 | |
| EGW-A | 6.7 | 1.6 | 6.3 | 12,962 | 895 | 7.74 | +119.8 | |
| EGSW-A | 7.6 | 0.4 | 7.4 | 17,397 | 1154 | 8.04 | +128.4 | |
| II | Ref-F | 4.0 | 1.1 | 3.4 | 3645 | 962 | 2.39 | – |
| EG-F | 5.1 | 1.1 | 4.1 | 7312 | 1802 | 2.53 | +5.86 | |
| EGS-F | 4.7 | 1.8 | 3.7 | 14,217 | 3014 | 2.86 | +19.67 | |
| EGW-F | 5.6 | 2.1 | 4.6 | 10,926 | 1739 | 3.64 | +52.3 | |
| EGSW-F | 5.5 | 1.5 | 4.1 | 11,133 | 3352 | 2.16 | −9.6 |
| Specimen | Ductility of Group I | Ductility of Group II | Change (%) | Total Energy ET of Group I (kN·mm) | Total Energy ET of Group II (kN·mm) | Change (%) |
|---|---|---|---|---|---|---|
| Ref | 3.52 | 2.39 | 32.10 | 5443 | 3645 | 33.03 |
| EG | 4.28 | 2.53 | 40.9 | 11,933 | 7312 | 38.72 |
| EGS | 10.05 | 2.86 | 71.54 | 16,344 | 14,217 | 13.01 |
| EGW | 7.74 | 3.64 | 52.97 | 12,962 | 10,926 | 15.71 |
| EGSW | 8.04 | 2.16 | 73.13 | 17,397 | 11,133 | 36.00 |
| Definition | Value | ||
|---|---|---|---|
| Engineering Elastic Constants | Longitudinal Modulus of Elasticity (Ez) | 27.1 GPa | |
| Transverse Modulus of Elasticity (Ex = Ey) | 6.8 GPa | ||
| Transverse Shear Modulus of Elasticity (Gxy) | 17.5 GPa | ||
| In-Plane Shear Modulus of Elasticity (Gzx = Gzy) | 2.7 GPa | ||
| Major Poisson Ratio (υzx= υzy) | 0.23 | ||
| Minor Poisson Ratio (υxy) | 0.1 | ||
| Strength Values | Tensile Strength | Longitudinal | 347.5 MPa |
| Transverse | 50 MPa | ||
| Compressive Strength | Longitudinal | 326.14 MPa | |
| Transverse | 118.3 MPa | ||
| Shear Strength | Transverse | 8.04 MPa | |
| In-Plane | 104.23 MPa | ||
| Damage Evolution | Tensile Fracture Energy | Longitudinal | 18.3 |
| Transverse | 5 | ||
| Compressive Fracture Energy | Longitudinal | 5.8 | |
| Transverse | 5.5 | ||
| Beam No. | Exp. Results | FEM Results | Change (%) | |||
|---|---|---|---|---|---|---|
| Ultimate Load (kN) | Max. Disp. (mm) | Ultimate Load (kN) | Max. Disp. (mm) | Ultimate Load | Max. Disp. | |
| Ref-A | 100.46 | 63 | 104.24 | 64.11 | 3.7 | 1.76 |
| EG-A | 159.04 | 91 | 162.51 | 93.19 | 2.18 | 2.4 |
| EGS-A | 201.55 | 115 | 206.02 | 120.12 | 2.22 | 4.45 |
| EGW-A | 198.24 | 100 | 206.67 | 102.24 | 4.25 | 2.24 |
| EGSW-A | 231.88 | 90 | 233.96 | 94.07 | 0.90 | 4.52 |
| Ref-F | 80.62 | 56 | 81.85 | 58 | 1.53 | 3.57 |
| EG-F | 122.15 | 77 | 124.14 | 80 | 1.63 | 3.90 |
| EGS-F | 149.64 | 116 | 156.41 | 118 | 4.52 | 1.72 |
| EGW-F | 130.12 | 98 | 132.64 | 102 | 1.94 | 4.08 |
| EGSW-F | 166.24 | 87 | 169.75 | 89 | 2.11 | 2.30 |
| Beam No. | Ultimate Load (kN) | |||
|---|---|---|---|---|
| Ambient Temperature | Exposure to Temperature of 700 °C | |||
| 30 min | 60 min | 90 min | ||
| Ref-F | 104.24 | 87.77 | 81.85 | 67.55 |
| EG-F | 162.51 | 137.35 | 124.14 | 103.19 |
| EGS-F | 206.02 | 166.46 | 156.41 | 127.36 |
| EGW-F | 206.67 | 167.72 | 132.64 | 119.72 |
| EGSW-F | 233.96 | 188.06 | 169.75 | 151.14 |
| Beam No. | Comparison of the results with a reference beam (%) | |||
| Ambient temperature | Exposure to the temperature of 700 °C | |||
| 30 min | 60 min | 90 min | ||
| Ref-F | – | – | – | – |
| EG-F | 55.90 | 56.49 | 51.67 | 52.76 |
| EGS-F | 97.64 | 89.65 | 91.09 | 88.54 |
| EGW-F | 98.26 | 91.09 | 62.05 | 77.23 |
| EGSW-F | 124.44 | 114.26 | 107.39 | 123.74 |
| Beam No. | Comparison of the results with ambient temperature (%) | |||
| Ambient temperature | Exposure to the temperature of 700 °C | |||
| 30 min | 60 min | 90 min | ||
| Ref-F | – | 15.80 | 21.48 | 35.20 |
| EG-F | – | 15.48 | 23.61 | 36.50 |
| EGS-F | – | 19.20 | 24.08 | 38.18 |
| EGW-F | – | 18.82 | 35.82 | 42.07 |
| EGSW-F | – | 19.62 | 27.44 | 35.40 |
| Beam No. | Ultimate Load (kN) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ambient Temp. | Exposure to Elevated Temperature | ||||||||
| 700 °C | Change % | 800 °C | Change % | 900 °C | Change % | 950 °C | Change % | ||
| Ref-F | 104.24 | 81.85 | 21.48 | 61.49 | 41.01 | 38.22 | 63.33 | 24.07 | 76.91 |
| EG-F | 162.51 | 124.14 | 23.61 | 93.85 | 42.25 | 52.69 | 67.58 | 32.33 | 80.12 |
| EGS-F | 206.02 | 156.41 | 24.08 | 121.39 | 41.07 | 60.86 | 70.46 | 38.34 | 81.39 |
| EGW-F | 206.67 | 132.64 | 35.82 | 104.62 | 49.38 | 50.71 | 75.46 | 33.56 | 83.76 |
| EGSW-F | 233.96 | 169.75 | 27.44 | 124.24 | 46.90 | 45.88 | 80.39 | 33.67 | 85.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, E.M.; Ibrahim, T.H.; Allawi, A.A.; El-Zohairy, A. Experimental and Numerical Behavior of Encased Pultruded GFRP Beams under Elevated and Ambient Temperatures. Fire 2023, 6, 212. https://doi.org/10.3390/fire6050212
Mahmood EM, Ibrahim TH, Allawi AA, El-Zohairy A. Experimental and Numerical Behavior of Encased Pultruded GFRP Beams under Elevated and Ambient Temperatures. Fire. 2023; 6(5):212. https://doi.org/10.3390/fire6050212
Chicago/Turabian StyleMahmood, Enas M., Teghreed H. Ibrahim, Abbas A. Allawi, and Ayman El-Zohairy. 2023. "Experimental and Numerical Behavior of Encased Pultruded GFRP Beams under Elevated and Ambient Temperatures" Fire 6, no. 5: 212. https://doi.org/10.3390/fire6050212
APA StyleMahmood, E. M., Ibrahim, T. H., Allawi, A. A., & El-Zohairy, A. (2023). Experimental and Numerical Behavior of Encased Pultruded GFRP Beams under Elevated and Ambient Temperatures. Fire, 6(5), 212. https://doi.org/10.3390/fire6050212








