Post-Fire Seismic Property of Reinforced Concrete Frame Joints with Carbon Fiber-Reinforced Polymer Using Numerical Analysis
Abstract
1. Introduction
2. Specimen Design
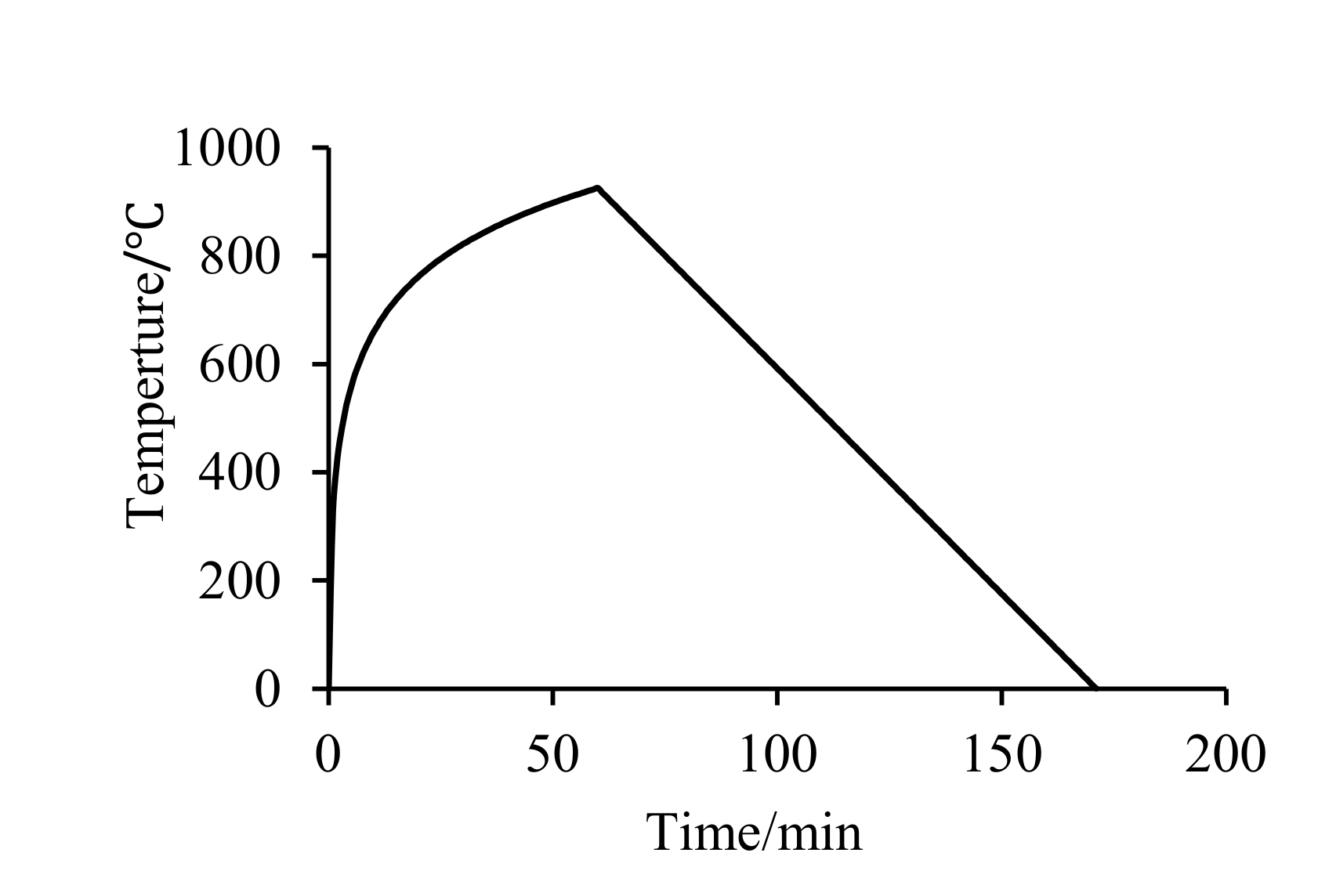
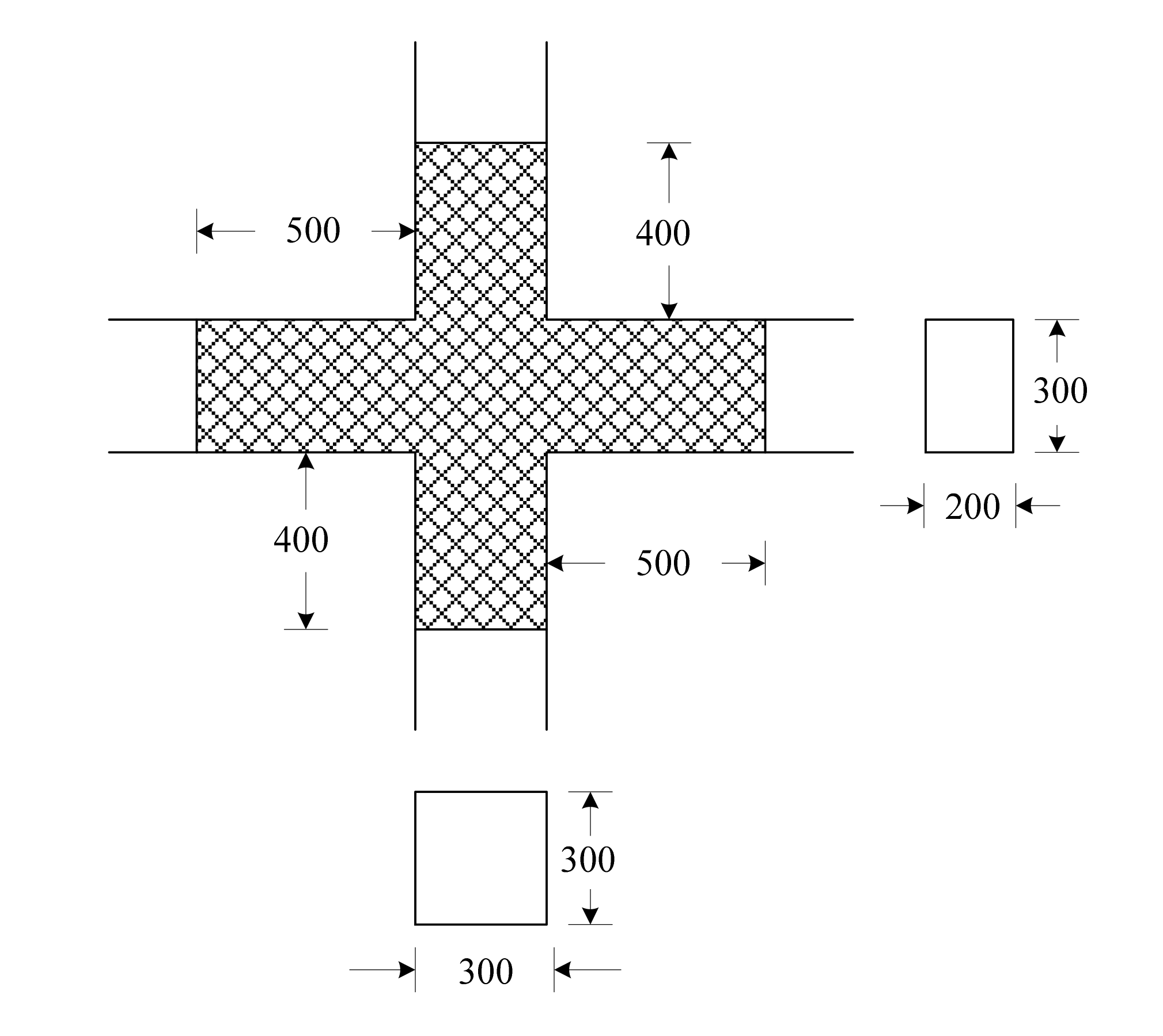
3. Simulation of Temperature Field
4. Joint Reinforcement after Fire
5. Post-Fire Seismic Calculation of Reinforced Joints
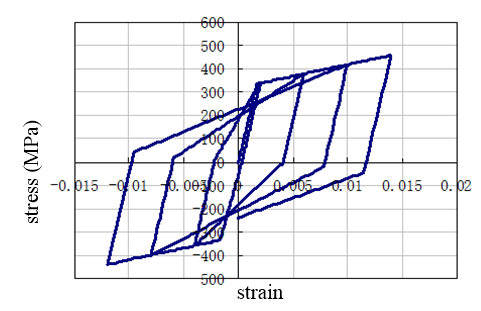
5.1. Post-Fire Material’s Constitutive Relationship
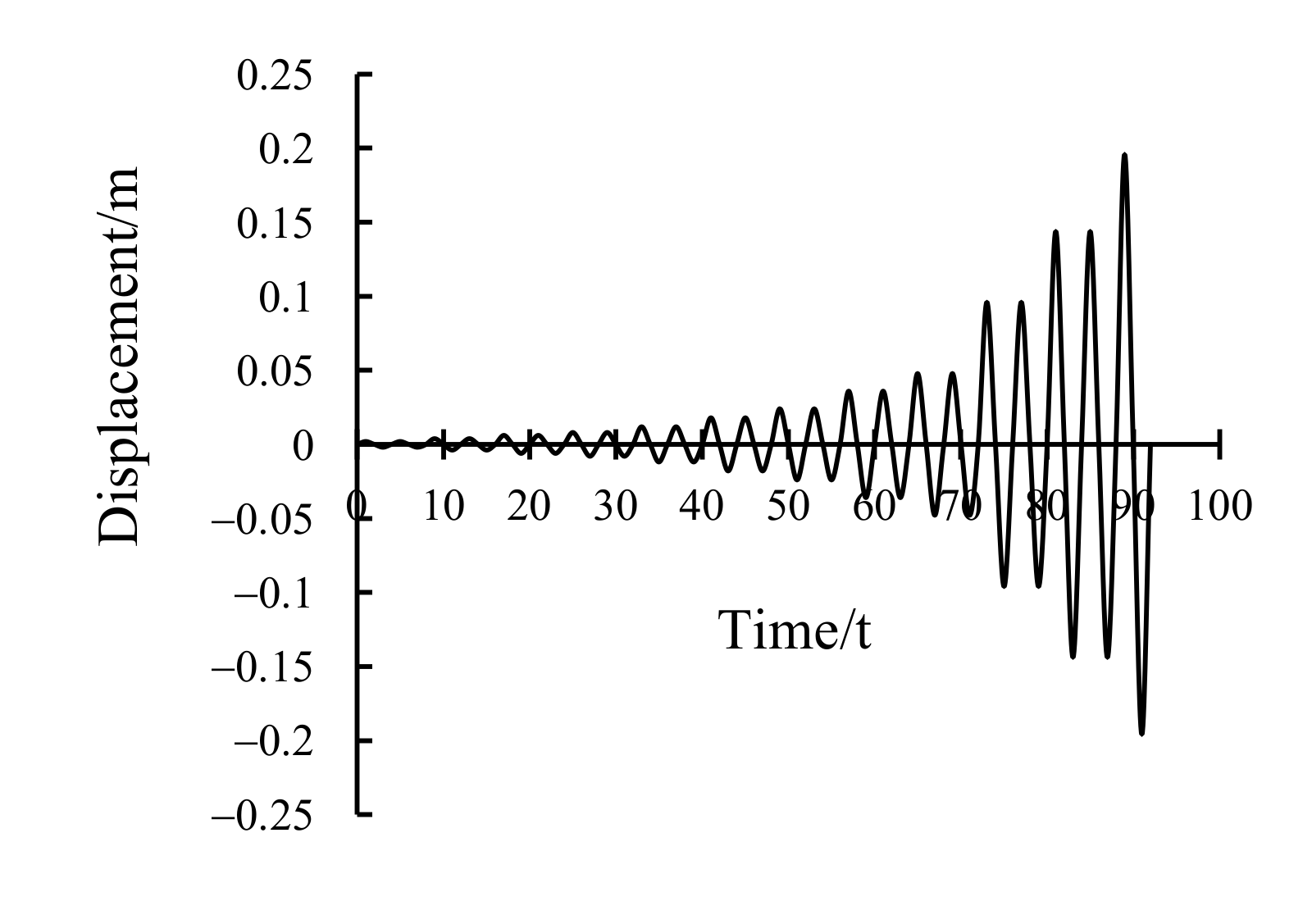
5.2. Boundary Condition and Loading Pattern
5.3. Calculation Results and Analysis
5.3.1. Hysteretic Curves
5.3.2. Skeleton Curves
5.3.3. Joint Bearing Capacity of Joints
5.3.4. Energy Dissipation
5.3.5. Ductility Analysis
5.3.6. Stress Distribution
6. Conclusions
- When the specimen is subjected to fire on all four sides, the temperature field of the beam and column sections displays symmetry with respect to the longitudinal and transverse axes of the corresponding cross-sections. The heat is transferred layer by layer from the outermost reinforced concrete layer inward, resulting in a delayed rise of the internal temperature compared to the outer interface. After exposure to fire, the maximum temperature of the beam and column cross-sections decreases non-linearly from the surface towards the interior.
- In the elastic phase post-fire, the bearing capacity of the reinforced joint remains largely comparable to that of the unreinforced joints. However, the ductility, energy dissipation capacity, and ultimate bearing capacity of the reinforced joint demonstrate significant improvements, though this enhancement does not continue with an increasing number of reinforcement layers. The use of two reinforcement layers results in an energy dissipation capacity and ultimate bearing capacity increase of 26.5% and 30.3%, respectively, showcasing an excellent reinforcement effect. These results suggest that the repaired joints effectively regain their original strength and stiffness.
- Analysis of the joint’s stress distribution reveals that as the axial compression ratio increases, the high-stress zones at the joint expand. The failure mode also transitions from plastic damage at the joint’s beam end under low axial compression ratios to the column’s crushing failure under high axial compression ratios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.-H.; Chang, Y.-F.; Yao, G.C.; Sheu, M.-S. Experimental research on post-fire behaviour of reinforced concrete columns. Fire Saf. J. 2009, 44, 741–748. [Google Scholar] [CrossRef]
- Molkens, T.; Van Coile, R.; Gernay, T. Assessment of damage and residual load bearing capacity of a concrete slab after fire: Applied reliability-based methodology. Eng. Struct. 2017, 150, 969–985. [Google Scholar] [CrossRef]
- Kamath, P.; Sharma, U.K.; Kumar, V.; Bhargava, P.; Usmani, A.; Singh, B.; Singh, Y.; Torero, J.; Gillie, M.; Pankaj, P. Full-scale fire test on an earthquake-damaged reinforced concrete frame. Fire Saf. J. 2015, 73, 1–19. [Google Scholar] [CrossRef]
- Benmarce, A.; Guenfoud, M. Experimental behaviour of high-strength concrete columns in fire. Mag. Concr. Res. 2005, 57, 283–287. [Google Scholar] [CrossRef]
- Kodur, V.K.R. Guidelines for Fire Resistance Design of High-strength Concrete Columns. J. Fire Prot. Eng. 2005, 15, 93–106. [Google Scholar] [CrossRef]
- Franssen, J.-M.; Dotreppe, J.-C. Fire Tests and Calculation Methods for Circular Concrete Columns. Fire Technol. 2003, 39, 89–97. [Google Scholar] [CrossRef]
- Junhua, L.; Xingqiang, Z.; Chunheng, Z.; Huazong, W.; Ru, C.J. Experimental study on seismic performance of steel reinforced concrete column reinforced concrete beam joints after fire. J. Build. Struct. 2021, 42, 143–151. [Google Scholar] [CrossRef]
- Junhua, L.; Zihua, Z.; Yuyu, C. Experimental study on seismic performance of steel reinforced concrete beam column joints after fire. Eng. Mech. 2017, 34, 156–165. [Google Scholar]
- Jian, Q.; Xin, C.; Weigen, Y.; Tao, L.; Yong, S.; Yanqing, Z. Vulnerability analysis of existing RC frame shear wall structures subjected to seismic strengthening in high intensity regions. Build. Struct. 2021, 51, 84–91. [Google Scholar] [CrossRef]
- Siqing, W.; Yu, C.; Huijun, A.; Xuewu, T.; Lei, S.; Tuming, M. Performance-based seismic strengthening design of existing buildings with buckling-resistant braces. J. Build. Sci. Eng. 2021, 38, 38–46. [Google Scholar] [CrossRef]
- Mai, W.; Zheng, L.; Jiqiang, Y.; Xin, Z. Application of viscous dampers in seismic strengthening of existing buildings. Eng. Seism. Resist. Reinf. Transform. 2020, 42, 90–95. [Google Scholar] [CrossRef]
- Mazza, F. Residual seismic load capacity of fire-damaged rubber bearings of r.c. base-isolated buildings. Eng. Fail. Anal. 2017, 79, 951–970. [Google Scholar] [CrossRef]
- Xiaolei, X. Experimental Research on Seismic Behavior of Joints in a Reinforced Concrete Frame after Fire. Master’s Thesis, Shandong Jianzhu University, Jinan, China, 2010. [Google Scholar]
- Zhi-Wu, Y.; Fa-Xing, D.; Jian-Ping, L. Experimental research on mechanical properties of different type of concrete after high temperature. J. Saf. Environ. 2005, 5, 1–6. [Google Scholar]
- Guirong, L. Experimental Study on Fire-Resistance and Post-Fire Seismic Behavior of Concrete Shear Walls. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2010. [Google Scholar]
- Guowei, N. Experimental and Numerical Simulation Research on Repairment and Reinforcement for Seismic Damage Reinforced Concrete Members. Ph.D. Thesis, Tianjin University, Tianjin, China, 2014. [Google Scholar]
- Bo, T. The Finite Element Analysis of Carbon Fiber Reinforced High Strength Concrete Beams. Master’s Thesis, Dalian University of Technology, Dalian, China, 2014. [Google Scholar]
- Dexin, L. Experimental Study and Finite Element Analysis of Wedge-bond Anchorage for CFRP Tendons. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2013. [Google Scholar]
- Zhang, Z. Experimental Study on Flexural Behavior and Finite Element Analysis of Damaged RC Beams Strengthened with CFRP. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2013. [Google Scholar]
- Xin, Y. Research on Strengthening Methods and Finite Element Analysis of Beam-Column Joints in Frame Structure. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2015. [Google Scholar]
- Chen, J.F.; Teng, J.G. Anchorage Strength Models for FRP and Steel Plates Bonded to Concrete. J. Struct. Eng. 2001, 127, 784–791. [Google Scholar] [CrossRef]
- Nakaba, K.; Kanakubo, T.; Furuta, T.; Yoshizawa, H. Bond Behavior between Fiber-Reinforced Polymer Laminates and Concrete. Struct. J. 2001, 98, 359–367. [Google Scholar]
- Zhang, B.; Benmokrane, B. Design and evaluation of a new bond-type anchorage system for fiber reinforced polymer tendons. Can. J. Civ. Eng. 2004, 31, 14–26. [Google Scholar] [CrossRef]
- Hollaway, L.C. A review of the present and future utilisation of FRP composites in the civil infrastructure with reference to their important in-service properties. Constr. Build. Mater. 2010, 24, 2419–2445. [Google Scholar] [CrossRef]
- Braimah, A.; Green, M.; Campbell, T.I. Fatigue behaviour of concrete beams post-tensioned with unbonded carbon fibre reinforced polymer tendons. Can. J. Civ. Eng. 2006, 33, 1140–1155. [Google Scholar] [CrossRef]
- Xudong, S.; Zhenhai, G. Analysis of the temperature field of reinforced concrete structure. Eng. Mech. 1996, 13, 35–43. [Google Scholar]
- Jiangtao, Y.; Min, X.; Zhoudao, L. Stochastic Damage Constitutive Law for Fire damaged Concrete. J. Tongji Univ. (Nat. Sci.) 2011, 39, 158–165. [Google Scholar]
- Yu, X.; Zhisheng, X. Experiment Investigation of Strength of Concrete after High Temperature. Concrete 2000, 2, 44-45 + 53. [Google Scholar]
- IS. EN 1993-1-2:2005; Eurocode 3: Design of Steel Structures-Part 1-2: General Rules-Structural Fire Design. European Committee for Standardisation. European Committee for Standardisation: London, UK, 2007.
- ISO 834-1:1999; Fire Resistance Tests-Elements of Building Construction. International Organization for Standardization: Geneva, Switzerland, 1999.
- Wang, J.Y.; Yue, X.C.; Sun, Y.Z. Numerical simulation on the seismic performance of post-fire steel concrete frame joint bonded with steel. IOP Conf. Ser. Mater. Sci. Eng. 2019, 531, 012091. [Google Scholar] [CrossRef]
- Huazong, W. Research on Seismic Performance and Reinforcement Repair of Steel Reinforced Concrete Column Reinforced Concrete Joints after Fire. Master’s Thesis, Ningbo University, Ningbo, China, 2015. [Google Scholar]
- Zhejun, Q.; Junhua, L.; Yuyu, C.; Bin, S. Experimental study on reinforcement of steel reinforced concrete beam column joints at room temperature and after fire. Build. Struct. 2017, 47, 33–39. [Google Scholar] [CrossRef]
- Melo, J.; Triantafyllidis, Z.; Rush, D.; Bisby, L.; Rossetto, T.; Arede, A.; Varum, H.; Ioannou, I. Experimental assessment of post-fire retrofitted RC columns tested under cyclic loading. In Proceedings of the Third European Conference on Earthquake Engineering and Seismology-3ECEES, Bucharest, Romania, 4–9 September 2022. [Google Scholar]
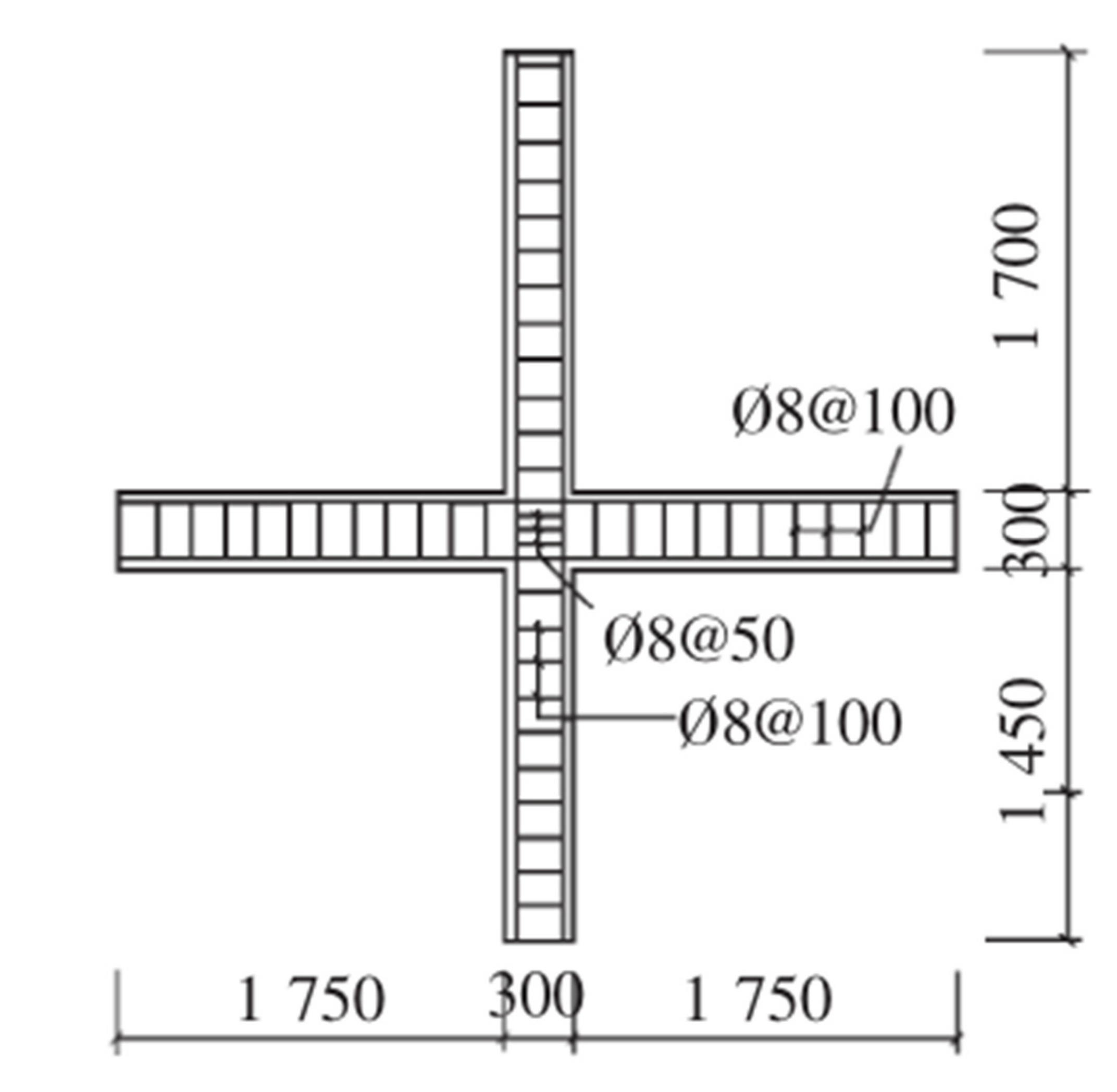






| Joint | |
|---|---|
| Concrete strength grade | C30 |
| Longitudinal reinforcement of the beam | 6ϕ16 |
| Longitudinal reinforcement of the column | 6ϕ20 |
| Stirrups of the beam | ϕ8@100 |
| Stirrups of the column | ϕ8@100 |
| Stirrups of the core area | ϕ8@50 |
| Beam sectional size (mm·mm) | 200 × 300 |
| Column sectional size (mm·mm) | 300 × 300 |
| Protective layer thickness (mm) | 30 |
| Axial compression ratio | 0.3 |
| Reinforcement Diameter/mm | Elastic Modulus/MPa | Yield Strength/MPa |
|---|---|---|
| 20 | 1.99 × 105 | 484 |
| 16 | 2.05 × 105 | 452.5 |
| Model Specification/(g/m2) | Design Thickness/mm | Standard Tensile Strength/MPa | Elastic Modulus/MPa | Elongation/% |
|---|---|---|---|---|
| 300 | 0.167 | 3027 | 2.16 × 105 | 1.51 |
| Number of Reinforcement Layers | Yield Load/kN | Ultimate Load/kN | Failure Load/kN | Growth Rate of the Ultimate Load |
|---|---|---|---|---|
| 0 | 35,011.8 | 46,682.4 | 35,011.8 | - |
| 1 | 38,468.4 | 51,291.2 | 43,597.52 | 9.8% |
| 2 | 45,633.375 | 60,844.5 | 51,717.825 | 30.3% |
| 3 | 45,986.325 | 61,315.1 | 52,117.835 | 31.3% |
| 4 | 46,362.3 | 61,816.4 | 52,543.94 | 32.4% |
| Number of Reinforcement Layers | he | Growth Rate |
|---|---|---|
| 0 | 0.2106 | - |
| 1 | 0.2542 | 20.7% |
| 2 | 0.2664 | 26.5% |
| 3 | 0.2521 | 19.6% |
| 4 | 0.2351 | 11.7% |
| Number of Reinforcement Layers | Yield Displacement/mm | Failure Displacement/mm | Ductility Coefficient | Growth Rate of the Ductility |
|---|---|---|---|---|
| 0 | 33 | 137 | 4.15 | - |
| 1 | 53 | 261 | 4.92 | 18.5% |
| 2 | 59 | 268 | 4.55 | 9.4% |
| 3 | 66 | 285 | 4.31 | 3.8% |
| 4 | 67 | 237 | 3.53 | −14.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Yue, X.; Li, F.; Sun, Y.; Li, Z. Post-Fire Seismic Property of Reinforced Concrete Frame Joints with Carbon Fiber-Reinforced Polymer Using Numerical Analysis. Fire 2023, 6, 205. https://doi.org/10.3390/fire6050205
Wang J, Yue X, Li F, Sun Y, Li Z. Post-Fire Seismic Property of Reinforced Concrete Frame Joints with Carbon Fiber-Reinforced Polymer Using Numerical Analysis. Fire. 2023; 6(5):205. https://doi.org/10.3390/fire6050205
Chicago/Turabian StyleWang, Jinyan, Xingchao Yue, Fuli Li, Yuzhou Sun, and Ziqi Li. 2023. "Post-Fire Seismic Property of Reinforced Concrete Frame Joints with Carbon Fiber-Reinforced Polymer Using Numerical Analysis" Fire 6, no. 5: 205. https://doi.org/10.3390/fire6050205
APA StyleWang, J., Yue, X., Li, F., Sun, Y., & Li, Z. (2023). Post-Fire Seismic Property of Reinforced Concrete Frame Joints with Carbon Fiber-Reinforced Polymer Using Numerical Analysis. Fire, 6(5), 205. https://doi.org/10.3390/fire6050205






