Effect of Socioeconomic Variables in Predicting Global Fire Ignition Occurrence
Abstract
1. Introduction
2. Materials and Methods
2.1. Ignition Density
2.2. Landcover
2.3. Climate
2.4. Soil Moisture
2.5. Vegetation State
2.6. Socio-Economic Variables
2.6.1. Population Density
2.6.2. Gross Domestic Product
2.6.3. Road Density
2.6.4. Gridded Livestock
2.6.5. Grazed Lands
2.7. Data Preparation
2.8. Random Forest Model Setup
2.9. Variable Selection
2.10. Model Training Iterations
2.11. Data Sampling
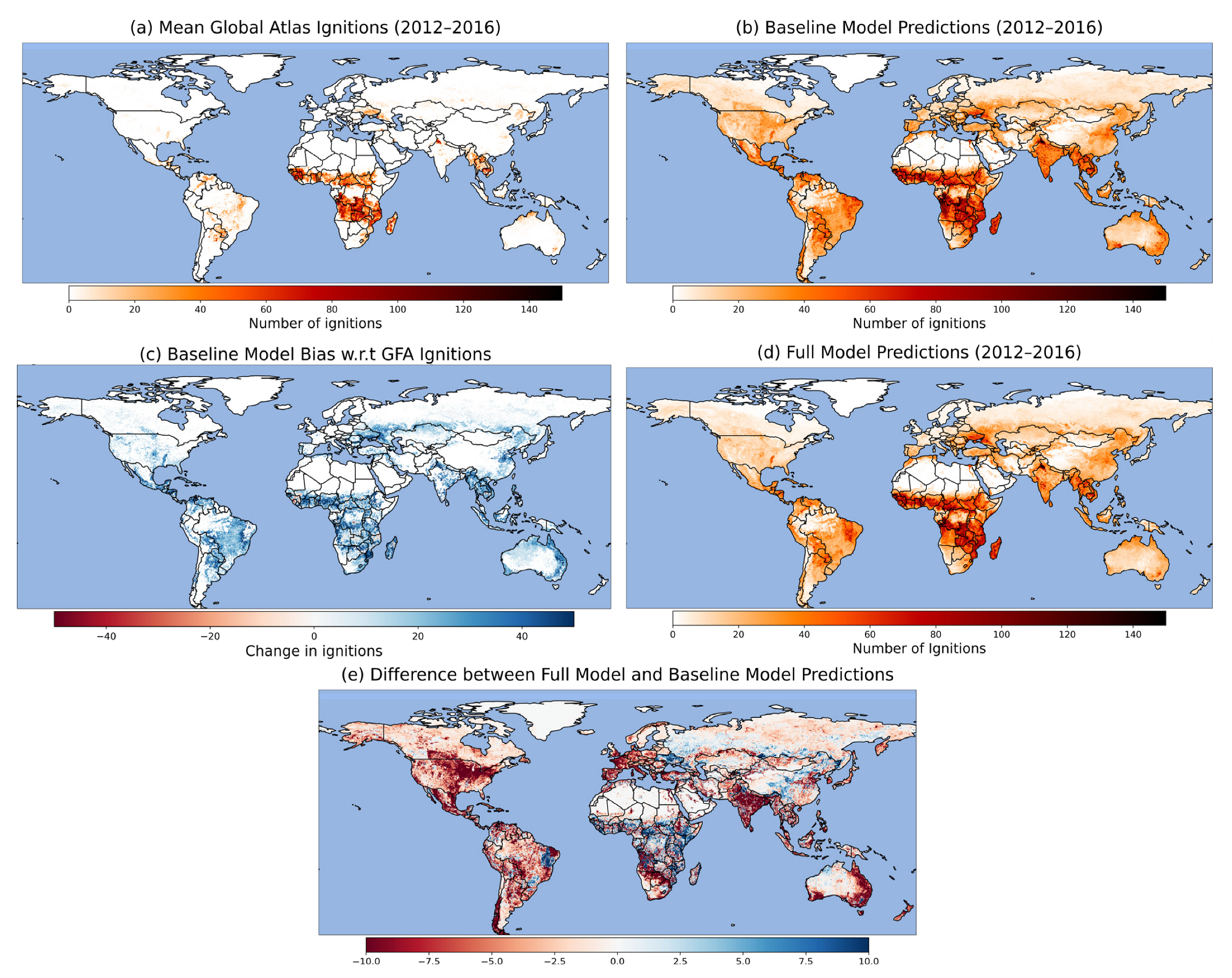
3. Results
3.1. Performance of the Climate/Vegetation Baseline Model
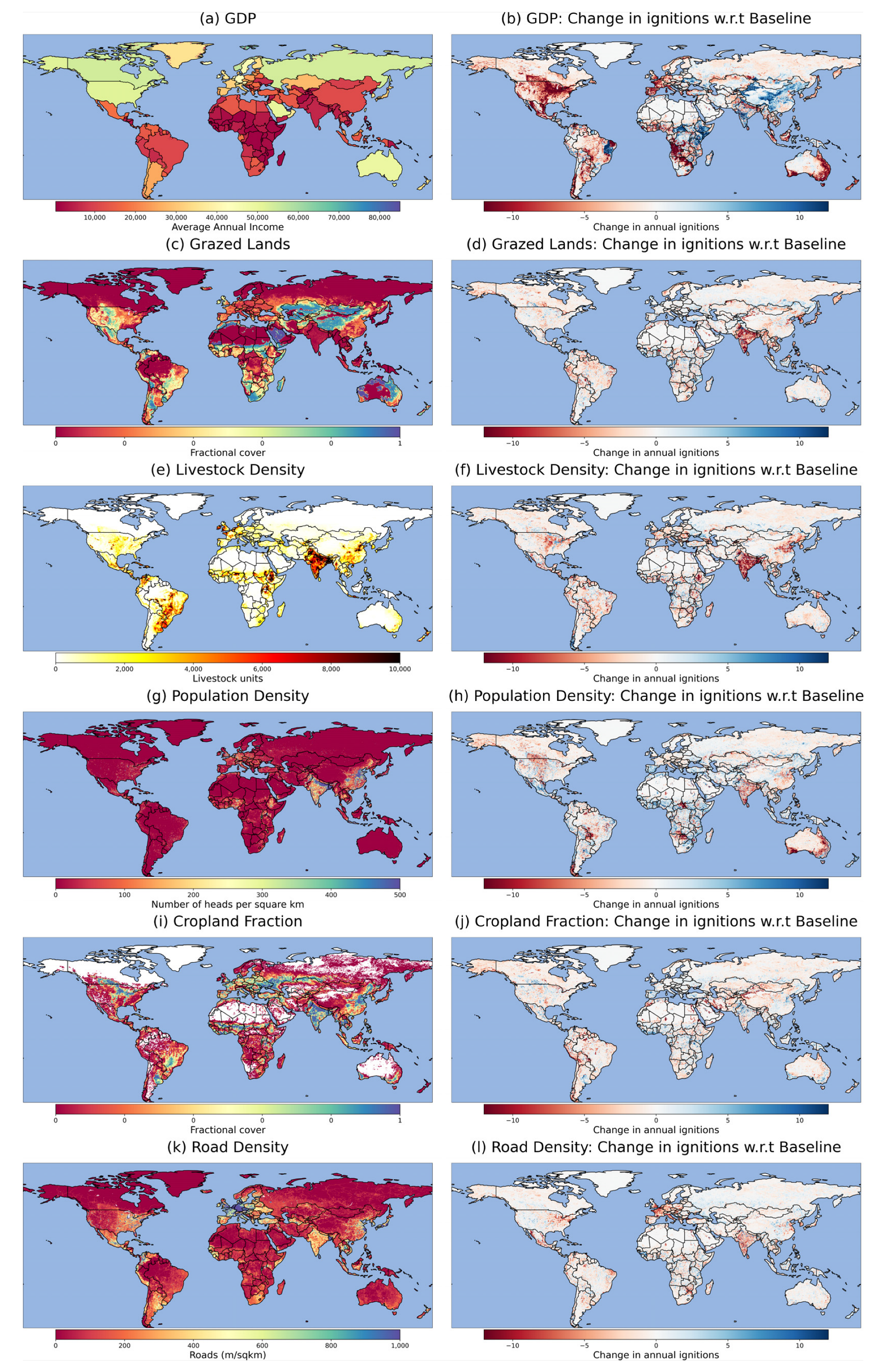
3.2. Effect of GDP
3.3. Effect of Grazed Land Fraction (GLF) and Livestock Density (LD)
3.4. Effect of Population Density (PD)
3.5. Effect of Cropland Fraction (CF)
3.6. Effect of Road Density (RD)
3.7. Combined Effect of All Human Variables
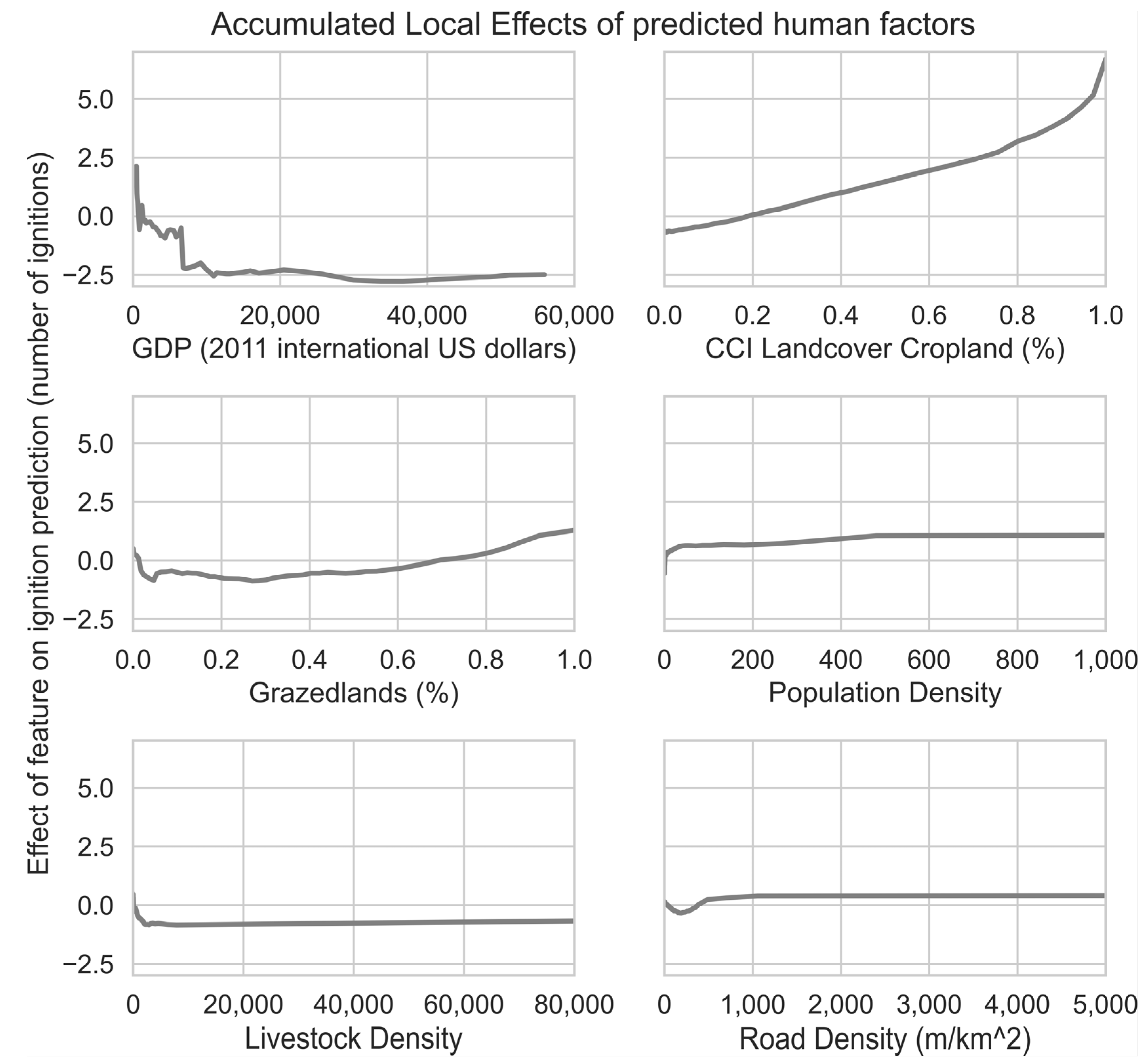
3.8. Accumulated Local Effect Analysis
4. Discussion
4.1. Overall Performance
4.2. GDP
4.3. Grazed Lands and Livestock
4.4. Cropland
4.5. Road and Population Density
4.6. Full Model
4.7. Data and Model Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lasslop, G.; Coppola, A.I.; Voulgarakis, A.; Yue, C.; Veraverbeke, S. Influence of Fire on the Carbon Cycle and Climate. Curr. Clim. Chang. Rep. 2019, 5, 112–123. [Google Scholar] [CrossRef]
- Li, Y.; Mickley, L.J.; Liu, P.; Kaplan, J.O. Trends and spatial shifts in lightning fires and smoke concentrations in response to 21st century climate over the national forests and parks of the western United States. Atmos. Chem. Phys. 2020, 20, 8827–8838. [Google Scholar] [CrossRef]
- Burrows, N.D.; Burbidge, A.A.; Fuller, P.J.; Behn, G. Evidence of altered fire regimes in the Western Desert region of Australia. Conserv. Sci. West. Aust. 2006, 5, 14–26. [Google Scholar]
- Cawley, K.M.; Hohner, A.K.; McKee, G.A.; Borch, T.; Omur-Ozbek, P.; Oropeza, J.; Rosario-Ortiz, F.L. Characterization and spatial distribution of particulate and soluble carbon and nitrogen from wildfire-impacted sediments. J. Soils Sediments 2018, 18, 1314–1326. [Google Scholar] [CrossRef]
- Dietze, E.; Theuerkauf, M.; Bloom, K.; Brauer, A.; Dörfler, W.; Feeser, I.; Feurdean, A.; Gedminienė, L.; Giesecke, T.; Jahns, S.; et al. Holocene fire activity during low-natural flammability periods reveals scale-dependent cultural human-fire relationships in Europe. Quat. Sci. Rev. 2018, 201, 44–56. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Kolden, C.A.; Abatzoglou, J.T.; Johnston, F.H.; van der Werf, G.R.; Flannigan, M. Vegetation fires in the Anthropocene. Nat. Rev. Earth Environ. 2020, 1, 500–515. [Google Scholar] [CrossRef]
- Chuvieco, E.; Giglio, L.; Justice, C. Global characterization of fire activity: Toward defining fire regimes from Earth observation data. Glob. Chang. Biol. 2008, 14, 1488–1502. [Google Scholar] [CrossRef]
- Balch, J.K.; Bradley, B.A.; Abatzoglou, J.T.; Chelsea Nagy, R.; Fusco, E.J.; Mahood, A.L. Human-started wildfires expand the fire niche across the United States. Proc. Natl. Acad. Sci. USA 2017, 114, 2946–2951. [Google Scholar] [CrossRef]
- Cattau, M.E.; Wessman, C.; Mahood, A.; Balch, J.K. Anthropogenic and lightning-started fires are becoming larger and more frequent over a longer season length in the U.S.A. Glob. Ecol. Biogeogr. 2020, 29, 668–681. [Google Scholar] [CrossRef]
- Hantson, S.; Arneth, A.; Harrison, S.P.; Kelley, D.I.; Colin Prentice, I.; Rabin, S.S.; Archibald, S.; Mouillot, F.; Arnold, S.R.; Artaxo, P.; et al. The status and challenge of global fire modelling. Biogeosciences 2016, 13, 3359–3375. [Google Scholar] [CrossRef]
- Head, L. Transformative change requires resisting a new normal. Nat. Clim. Chang. 2020, 10, 173–174. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.P.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M.D. A review of machine learning applications in wildfire science and management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Kim, S.J.; Lim, C.H.; Kim, G.S.; Lee, J.; Geiger, T.; Rahmati, O.; Son, Y.; Lee, W.K. Multi-temporal analysis of forest fire probability using socio-economic and environmental variables. Remote Sens. 2019, 11, 86. [Google Scholar] [CrossRef]
- Lee, S.W.; Davidson, R.A. Physics-based simulation model of post-earthquake fire spread. J. Earthq. Eng. 2010, 14, 670–687. [Google Scholar] [CrossRef]
- Hoffman, C.M.; Canfield, J.; Linn, R.R.; Mell, W.; Sieg, C.H.; Pimont, F.; Ziegler, J. Evaluating Crown Fire Rate of Spread Predictions from Physics-Based Models. Fire Technol. 2016, 52, 221–237. [Google Scholar] [CrossRef]
- Haines, D.A. Relation between the National Fire Danger Spread Component and Fire Activity in the Lake States; North Central Forest Experiment Station, Forest Service, U.S. Department of Agriculture: St. Paul, MN, USA, 1970.
- Martell, D.L.; Stocks, B.J. A logistic model for predicting daily people-caused forest fire occurrence in Ontario. Can. J. For. Res. 1987, 17, 394–401. [Google Scholar] [CrossRef]
- Levi, M.R.; Bestelmeyer, B.T. Biophysical influences on the spatial distribution of fire in the desert grassland region of the southwestern USA. Landsc. Ecol. 2016, 31, 2079–2095. [Google Scholar] [CrossRef]
- Mohajane, M.; Costache, R.; Karimi, F.; Bao Pham, Q.; Essahlaoui, A.; Nguyen, H.; Laneve, G.; Oudija, F. Application of remote sensing and machine learning algorithms for forest fire mapping in a Mediterranean area. Ecol. Indic. 2021, 129, 107869. [Google Scholar] [CrossRef]
- Archibald, S.; Roy, D.P.; van Wilgen, B.W.; Scholes, R.J. What limits fire? An examination of drivers of burnt area in Southern Africa. Glob. Chang. Biol. 2009, 15, 613–630. [Google Scholar] [CrossRef]
- Forkel, M.; Dorigo, W.; Lasslop, G.; Teubner, I.; Chuvieco, E.; Thonicke, K. A data-driven approach to identify controls on global fire activity from satellite and climate observations (SOFIA V1). Geosci. Model Dev. 2017, 10, 4443–4476. [Google Scholar] [CrossRef]
- Forkel, M.; Andela, N.; P Harrison, S.; Lasslop, G.; Van Marle, M.; Chuvieco, E.; Dorigo, W.; Forrest, M.; Hantson, S.; Heil, A.; et al. Emergent relationships with respect to burned area in global satellite observations and fire-enabled vegetation models. Biogeosciences 2019, 16, 57–76. [Google Scholar] [CrossRef]
- Kuhn-Régnier, A.; Voulgarakis, A.; Nowack, P.; Forkel, M.; Prentice, I.C.; Harrison, S. Quantifying the Importance of Antecedent Fuel-Related Vegetation Properties for Burnt Area using Random Forests. Biogeosciences 2020, 1–24. [Google Scholar] [CrossRef]
- Maingi, J.K.; Henry, M.C. Factors influencing wildfire occurrence and distribution in eastern Kentucky, USA. Int. J. Wildl. Fire 2007, 16, 23. [Google Scholar] [CrossRef]
- Andela, N.; Morton, D.C.; Giglio, L.; Paugam, R.; Chen, Y.; Hantson, S.; van der Werf, G.R.; Randerson, J.T. The Global Fire Atlas of individual fire size, duration, speed, and direction. Earth Syst. Sci. Data 2019, 11, 529–552. [Google Scholar] [CrossRef]
- Defourny, P. ESA Land Cover Climate Change Initiative (Land_Cover_cci): Land Cover Maps, v2.0.7. Centre for Environmental Data Analysis. 2019. Available online: https://catalogue.ceda.ac.uk/uuid/b382ebe6679d44b8b0e68ea4ef4b701c (accessed on 15 May 2021).
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Rudolf, B.; Beck, C.; Grieser, J.; Schneider, U. Global Precipitation Analysis Products of the GPCC; Global Precipitation Climatology Centre (GPCC): Offenbach, Germany, 2015. [Google Scholar]
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500m SIN Grid V006. 2015. NASA EOSDIS Land Process. DAAC 2015. [Google Scholar] [CrossRef]
- Moesinger, L.; Dorigo, W.; De Jeu, R.; Van Der Schalie, R.; Scanlon, T.; Teubner, I.; Forkel, M. The global long-term microwave Vegetation Optical Depth Climate Archive (VODCA). Earth Syst. Sci. Data 2020, 12, 177–196. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O. ESA Biomass Climate Change Initiative (Biomass_cci): Global datasets of forest above-ground biomass for the year 2017, v1. Cent. Environ. Data Anal. 2019. [Google Scholar] [CrossRef]
- Goldewijk, K.K.; Beusen, A.; Doelman, J.; Stehfest, E. Anthropogenic land use estimates for the Holocene—HYDE 3.2. Earth Syst. Sci. Data 2017, 9, 927–953. [Google Scholar] [CrossRef]
- Meijer, J.R.; Huijbregts, M.A.J.; Schotten, K.C.G.J.; Schipper, A.M. Global patterns of current and future road infrastructure. Environ. Res. Lett. 2018, 13, 064006. [Google Scholar] [CrossRef]
- Kummu, M.; Taka, M.; Guillaume, J.H.A. Gridded global datasets for Gross Domestic Product and Human Development Index over 1990-2015. Sci. Data 2018, 5, 10–13. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, M.; Nicolas, G.; Cinardi, G.; Van Boeckel, T.P.; Vanwambeke, S.O.; Wint, G.R.W.; Robinson, T.P. Global distribution data for cattle, buffaloes, horses, sheep, goats, pigs, chickens and ducks in 2010. Sci. Data 2018, 5, 180227. [Google Scholar] [CrossRef] [PubMed]
- Popp, A.; Calvin, K.; Fujimori, S.; Havlik, P.; Humpenöder, F.; Stehfest, E.; Bodirsky, B.L.; Dietrich, J.P.; Doelmann, J.C.; Gusti, M.; et al. Land-use futures in the shared socio-economic pathways. Glob. Environ. Chang. 2017, 42, 331–345. [Google Scholar] [CrossRef]
- Schroeder, W.; Giglio, L. NASA VIIRS Land Science Investigator Processing System (SIPS) Visible Infrared Imaging Radiometer Suite (VIIRS) 375 m & 750 m Active Fire Products: Product User’s Guide Version 1.4. Nasa 2018, 1, 23. [Google Scholar]
- Poulter, B.; Ciais, P.; Hodson, E.; Lischke, H.; Maignan, F.; Plummer, S.; Zimmermann, N.E. Plant functional type mapping for earth system models. Geosci. Model Dev. 2011, 4, 993–1010. [Google Scholar] [CrossRef]
- Venevsky, S.; Thonicke, K.; Sitch, S.; Cramer, W. Simulating fire regimes in human-dominated ecosystems: Iberian Peninsula case study. Glob. Chang. Biol. 2002, 8, 984–998. [Google Scholar] [CrossRef]
- Bistinas, I.; Harrison, S.P.; Prentice, I.C.; Pereira, J.M.C. Causal relationships versus emergent patterns in the global controls of fire frequency. Biogeosciences 2014, 11, 5087–5101. [Google Scholar] [CrossRef]
- Gruber, A.; Scanlon, T.; Van Der Schalie, R.; Wagner, W.; Dorigo, W. Evolution of the ESA CCI Soil Moisture climate data records and their underlying merging methodology. Earth Syst. Sci. Data 2019, 11, 717–739. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Jiang, C.; Ryu, Y.; Fang, H.; Myneni, R.; Claverie, M.; Zhu, Z. Inconsistencies of interannual variability and trends in long-term satellite leaf area index products. Glob. Chang. Biol. 2017, 23, 4133–4146. [Google Scholar] [CrossRef]
- Van Der Schalie, R.; Kerr, Y.H.; Wigneron, J.P.; Rodríguez-Fernández, N.J.; Al-Yaari, A.; Jeu, R.A.M.d. Global SMOS Soil Moisture Retrievals from The Land Parameter Retrieval Model. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 125–134. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Carvalhais, N.; Rozendaal, D.M.A.; Avitabile, V.; Araza, A.; De Bruin, S.; Herold, M.; Quegan, S.; Rodríguez-Veiga, P.; et al. The global forest above-ground biomass pool for 2010 estimated from high-resolution satellite observations. Earth Syst. Sci. Data 2021, 13, 3927–3950. [Google Scholar] [CrossRef]
- Pesaresi, M.; Ehrlich, D.; Florczyk, A.J.; Freire, S.; Julea, A.; Kemper, T.; Soille, P.; Syrris, V. Operating Procedure for the Production of the Global Human Settlement Layer from Landsat Data of the Epochs; Publications Office of the European Union: Luxembourg, Luxembourg, 2016; ISBN 9789279550126. [Google Scholar]
- Valcke, S.; Piacentini, A.; Jonville, G. Benchmarking Regridding Libraries Used in Earth System Modelling. Math. Comput. Appl. 2022, 27, 31. [Google Scholar] [CrossRef]
- Pavlov, Y.L. Random forests. In Text Mining with Machine Learning; CRC Press: Boca Raton, FL, USA, 2019; pp. 1–122. [Google Scholar] [CrossRef]
- Ghojogh, B.; Crowley, M. The Theory Behind Overfitting, Cross Validation, Regularization, Bagging, and Boosting: Tutorial. arXiv 2019, arXiv:1905.12787. [Google Scholar]
- Bisong, E. Introduction to Scikit-learn. In Building Machine Learning and Deep Learning Models on Google Cloud Platform; Apress: Berkeley, CA, USA, 2019; pp. 215–229. [Google Scholar]
- García, C.B.; García, J.; López Martín, M.M.; Salmerón, R. Collinearity: Revisiting the variance inflation factor in ridge regression. J. Appl. Stat. 2015, 42, 648–661. [Google Scholar] [CrossRef]
- Salmerón, R.; García, C.B.; García, J. Variance Inflation Factor and Condition Number in multiple linear regression. J. Stat. Comput. Simul. 2018, 88, 2365–2384. [Google Scholar] [CrossRef]
- Apley, D.W.; Zhu, J. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Shearman, T.M.; Varner, J.M.; Hood, S.M.; Cansler, C.A.; Hiers, J.K. Modelling post-fire tree mortality: Can random forest improve discrimination of imbalanced data? Ecol. Modell. 2019, 414, 108855. [Google Scholar] [CrossRef]
- Barker, J.S.; Gray, A.N.; Fried, J.S. The Effects of Crown Scorch on Post-fire Delayed Mortality Are Modified by Drought Exposure in California (USA). Fire 2022, 5, 21. [Google Scholar] [CrossRef]
- Almunia, J. Measuring progress, true wealth, and the well-being of nations. Brussels 2007, 4, 551–594. [Google Scholar]
- Asefa, M.; Cao, M.; He, Y.; Mekonnen, E.; Song, X.; Yang, J. Ethiopian vegetation types, climate and topography. Plant Divers. 2020, 42, 302–311. [Google Scholar] [CrossRef] [PubMed]
- Gil-Romera, G.; Adolf, C.; Benito, B.M.; Bittner, L.; Johansson, M.U.; Grady, D.A.; Lamb, H.F.; Lemma, B.; Fekadu, M.; Glaser, B.; et al. Long-term fire resilience of the Ericaceous Belt, Bale Mountains, Ethiopia. Biol. Lett. 2019, 15, 20190357. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Zhang, L.; Jin, S.; Tigabu, M.; Su, Z.; Wang, W. Modeling anthropogenic fire occurrence in the boreal forest of China using logistic regression and random forests. Forests 2016, 7, 250. [Google Scholar] [CrossRef]
- Starns, H.D.; Fuhlendorf, S.D.; Elmore, R.D.; Twidwell, D.; Thacker, E.T.; Hovick, T.J.; Luttbeg, B. Recoupling fire and grazing reduces wildland fuel loads on rangelands. Ecosphere 2019, 10, e02578. [Google Scholar] [CrossRef]
- Priya, R.; Ramesh, D.; Khosla, E. Naïve Bayes MapReduce Precision Agricultural Model. In Proceedings of the 2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Bangalore, India, 19–22 September 2018; pp. 99–104. [Google Scholar]
- Ying, H.; Yin, Y.; Zheng, H.; Wang, Y.; Zhang, Q.; Xue, Y.; Stefanovski, D.; Cui, Z.; Dou, Z. Newer and select maize, wheat, and rice varieties can help mitigate N footprint while producing more grain. Glob. Chang. Biol. 2019, 25, 4273–4281. [Google Scholar] [CrossRef]
- Di Mauro, G.; Cipriotti, P.A.; Gallo, S.; Rotundo, J.L. Environmental and management variables explain soybean yield gap variability in Central Argentina. Eur. J. Agron. 2018, 99, 186–194. [Google Scholar] [CrossRef]
- Alvarado, S.T.; Silva, T.S.F.; Archibald, S. Management impacts on fire occurrence: A comparison of fire regimes of African and South American tropical savannas in different protected areas. J. Environ. Manag. 2018, 218, 79–87. [Google Scholar] [CrossRef]
| Dataset | Derived Variables | Description | Native Spatial Resolution | Period | Temporal Resolution |
|---|---|---|---|---|---|
| Global Fire Atlas | [25] | ||||
| Ignition occurrence | Fire ignition occurrences per pixel and month | 500 m | January 2003–December 2016 | monthly | |
| Predictor variables | |||||
| Land cover | ESA land cover_cci version 2.0.7, http://maps.elie.ucl.ac.be/CCI/viewer/index.php (accessed on 5 August 2020) Land cover classes were translated to fractional coverages of plant functional types (PFTs) in 0.25° grid cells [26] | 300 m | January 1992–December 2015 | annual | |
| Climate and soil moisture | |||||
| CRU | CRU TS4.04 climate data [27] | ||||
| Tmx (degrees Celsius) | Max temperature (degrees Celsius) | 0.50° | January 1901–December 2019 | monthly | |
| Dtr | Diurnal temperature range (degrees Celsius) | 0.50° | January 1901–December 2019 | monthly | |
| Wet (days) | Number of wet days | 0.50° | January 1901–December 2019 | monthly | |
| Pet (mm) | Potential evapotranspiration (millimeters) | 0.50° | January 1901–December 2019 | monthly | |
| GPCC | Global Precipitation Climatology Centre (GPCC) [28] | ||||
| Precip (mm/month) | Daily precipitation (mm/month) | 0.25° | January 1891–December 2019 | monthly | |
| Soil Moisture | ESA soil moisture_cci version 6.1, http://cci.esa.int/data (accessed on 18 July 2022) | ||||
| sm (m3 m−3) | Mean monthly soil moisture | 0.25° | January 1978–December 2020 | monthly | |
| Vegetation state | |||||
| FAPAR/LAI | [29] | ||||
| FPAR (unitless) | Fraction of absorbed Photosynthetic Active Radiation | 500 m | January 2000–December 2019 | 8-day average | |
| LAI (m3 m−3) | Leaf Area Index | 0.25° | January 2000–December 2019 | 8-day average | |
| VOD | The global long-term microwave Vegetation Optical Depth Climate Archive (VODCA) [30] | ||||
| VOD_K lag (unitless) | Ku-band anomalies in Vegetation Optical Depth | 0.25° | July 1987–July 2017 | monthly | |
| Biomass | ESA Biomass Climate Change Initiative: Global datasets of forest above-ground biomass for the year 2017, v1 [31] | ||||
| agb (Mg ha−1) | Above Ground Biomass | 0.25° | 2017–2017 | static | |
| Socioeconomics | |||||
| Population density | Anthropogenic land-use estimates for the Holocene–HYDE 3.2 [32] | ||||
| Popdens | Number of heads per square km | 0.083333° | 2000–2017 | annual | |
| Road density | Global Roads Inventory Project (GRIP) [33] | ||||
| road_density (m/km2) | Global patterns of current and future road infrastructure | n/a | static | static | |
| GDP | [34] Gridded global datasets for Gross Domestic Product and Human Development Index over 1990–2015 | ||||
| GDP_PPP (constant 2011 international US dollar) | Gross Domestic Product Purchasing Power Parity | Country level | 1990–2015 | annual | |
| Livestock density | Global Livestock distribution | Livestock distribution per pixel; [35] | 5 min | 2010 | static |
| Grazed land fraction | Pasture fraction | Area fraction of managed pasture; [36] | 0.83333° | 850–2015 | annual |
| Variable | Pre-VIF | Post-VIF |
|---|---|---|
| agb | 1.38 | 1.31 |
| sm | 5.01 | 4.85 |
| pftTreeBE | 81.69 | 2.44 |
| pftHerb | 102.36 | 4.05 |
| pftShrubBD | 48.86 | 3.43 |
| pftShrubNE | 15.59 | 3.25 |
| pftTreeBD | 57.88 | 2.12 |
| pftTreeNE | 15.17 | 1.46 |
| fAPAR | 212.55 | 9.03 |
| vod_K_anomalies | 8.92 | 1.03 |
| pet | 22.66 | 5.45 |
| wet | 4.10 | 3.90 |
| precip | 2.68 | 2.54 |
| pftTreeND | 6.47 | 1.13 |
| tmx | 27.90 | - |
| dtr | 16.14 | - |
| LAI | 4052.46 | - |
| Predictor Variables | R2 | MAE | NMSE |
|---|---|---|---|
| Baseline model (BL): WET + Precip + PET + SM + fPAR + VOD_K′ + Herb + TreeBD + ShrubBD + TreeBE + ShrubBE + TreeNE + ShrubNE + TreeND | 0.53 | 0.33 | 0.04 |
| BL + pftCrop (CF) | 0.54 | 0.28 | 0.04 |
| BL + Livestock density (LD) | 0.56 | 0.32 | 0.03 |
| BL + Grazed lands fraction (GLF) | 0.55 | 0.30 | 0.04 |
| BL +GDP | 0.52 | 0.32 | 0.05 |
| BL + Road density (RD) | 0.53 | 0.33 | 0.04 |
| BL + Population density (PD) | 0.57 | 0.31 | 0.03 |
| Full model: (FM): BL + pftCrop + GDP + grazed lands fraction + livestock density + road density | 0.63 | 0.81 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukunga, T.; Forkel, M.; Forrest, M.; Zotta, R.-M.; Pande, N.; Schlaffer, S.; Dorigo, W. Effect of Socioeconomic Variables in Predicting Global Fire Ignition Occurrence. Fire 2023, 6, 197. https://doi.org/10.3390/fire6050197
Mukunga T, Forkel M, Forrest M, Zotta R-M, Pande N, Schlaffer S, Dorigo W. Effect of Socioeconomic Variables in Predicting Global Fire Ignition Occurrence. Fire. 2023; 6(5):197. https://doi.org/10.3390/fire6050197
Chicago/Turabian StyleMukunga, Tichaona, Matthias Forkel, Matthew Forrest, Ruxandra-Maria Zotta, Nirlipta Pande, Stefan Schlaffer, and Wouter Dorigo. 2023. "Effect of Socioeconomic Variables in Predicting Global Fire Ignition Occurrence" Fire 6, no. 5: 197. https://doi.org/10.3390/fire6050197
APA StyleMukunga, T., Forkel, M., Forrest, M., Zotta, R.-M., Pande, N., Schlaffer, S., & Dorigo, W. (2023). Effect of Socioeconomic Variables in Predicting Global Fire Ignition Occurrence. Fire, 6(5), 197. https://doi.org/10.3390/fire6050197






