Influence of Gradually Inflated Obstructions on Flame Propagation in a Tube Closed at One End

Abstract

Rapid suppression is a must in the mitigation of ventilation air methane (VAM) explosions. Flame suppression proves to be much more challenging than prevention of flame initiation due to the small physics timescale (~1 s). This study numerically investigates the effect of spherical obstructions on flame propagation dynamics in a tube closed at one end. Obstructions with an inflating geometry, installed at different locations, were examined. Noticeably, in the presence of a single or multiple obstructions that partially block the tube, flame and pressure waves propagate faster upstream than in an empty tube; this phenomenon is more pronounced when the obstruction is located further away from the ignition point. In scenarios of a full blockage of the tube, the high pressure builds up inside the blocked region, e.g., surging up to 7.5 bar in less than 0.1 s at a location 10 m away from the ignition point (tube diameter: 0.456 m). Obstructions located closer to the ignition point experience more tearing in terms of duration and strength.

1. Introduction

Abatement of ventilation air methane (VAM) is one of the effective approaches for the coal industry to reduce the emission of the sector’s fugitive methane [1,2]. In the short to medium term, this can be achieved in some mines using a fleet of high temperature (800–1100 °C) thermo-chemical oxidisers connected to the mine ventilation system by a capture duct. However, such settings will inherently increase the risk of VAM explosions and, thereby, flashback to the mine via the capture duct [3].

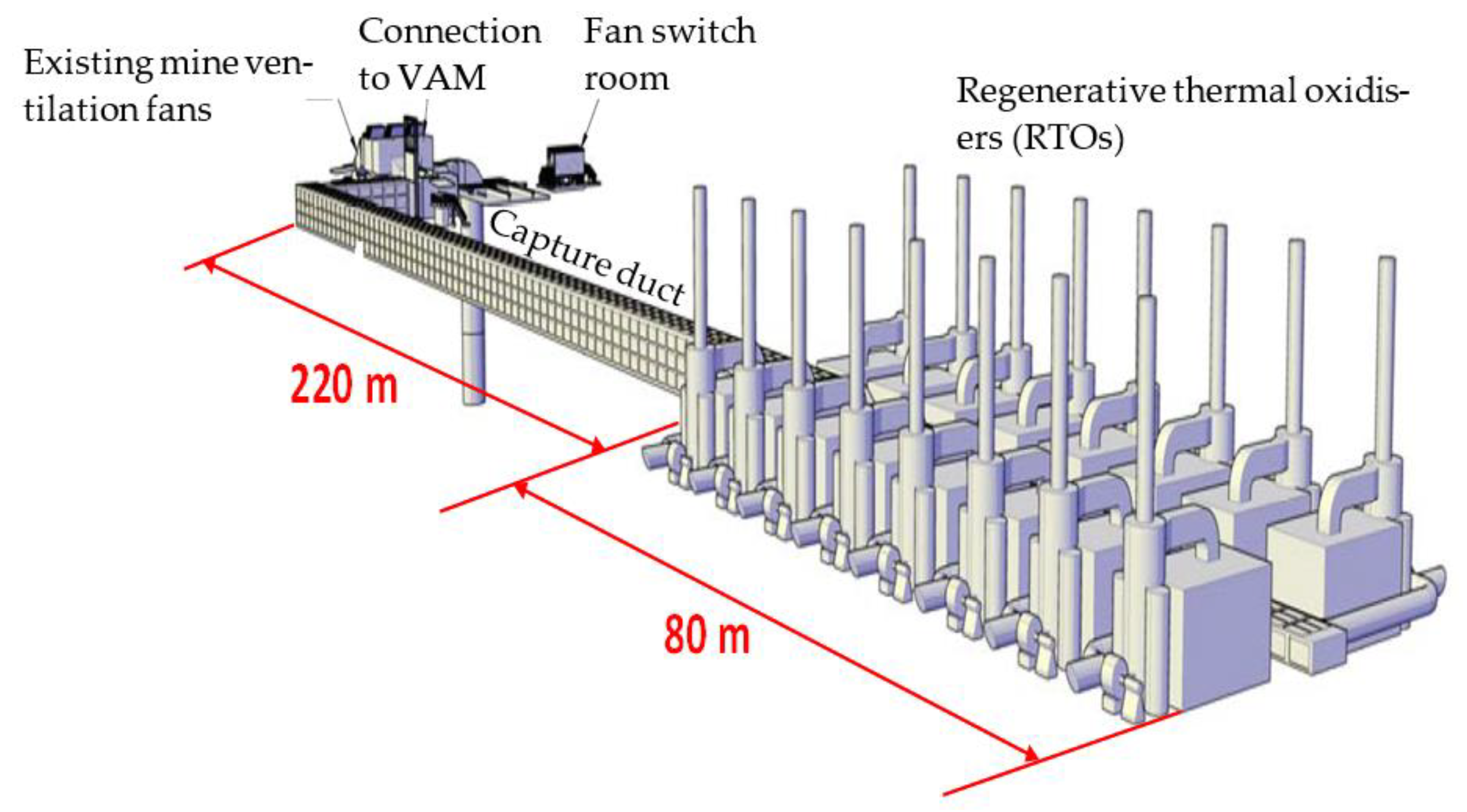
As shown in Figure 1, a typical VAM abatement plant based on thermo-chemical oxidisers consists of three essential sets of components namely: (i) VAM abatement units, e.g., regenerative thermal oxidisers (RTOs), (ii) a capture duct connecting RTOs to the mine ventilation system, and (iii) a suite of prevention and mitigation countermeasures to provide the plant with several layers of protection.

The main role of preventive measures is to stop the initiation/formation of any flame or explosion. However, if preventive measures fail for any reason, the mitigation countermeasures are expected to suppress the out-of-control explosion front and stop it from reaching the mine ventilation system (flashback phenomenon). By default, the task of mitigating an explosion is more difficult than preventing the explosion to form in the first place. This is primarily because the time scale for prevention is typically between 10 s and 15 s—assuming a plug of VAM with a methane concentration above the allowable safe level (~1 vol%) is travelling through the capture duct (~200 m of the straight section) and towards the RTOs at a speed of 15 m/s. This time scale is well within the capabilities of current prevention technologies that largely employ strategies such as venting, bypassing, inerting, ignition source avoidance and dust removal.

In contrast, the time scale for mitigation is approximately 1 s because the explosion front, comprising of a pressure front followed by a flame front, is travelling at a very high speed from the RTOs to the mine. This short time scale makes mitigation techniques, such as active isolation valves and water/chemical suppression systems, ineffective as they require seconds to respond. Similarly, burst panels alone cannot provide an adequate level of protection as they only decelerate the explosion front and delay the inevitable. The use of flame arrestors is also doubtful in the context of VAM abatement given the operational (e.g., pressure drop, flow blockage, etc.) and maintenance issues. Clearly, there is a technology gap in the area of rapid suppression of gas explosion (under 1 s).

Inspired by automotive airbags, this study proposes a novel method to rapidly suppress the explosion once its ignition is detected. Specifically, on-line identification of upstream explosion nearly instantaneously triggers the inflation of air bags installed along the pathway which, in turn, block and suppress the further propagation of flame and pressure waves. To sustain the destruction originating from the high pressure and high temperature of gases generated in the explosion, the airbags, henceforth referred to as instructions in general, are composed of material that has the required physical properties (e.g., sufficiently high tensile strength, not in the scope of the present study). These spherical obstructions offer not only the uniform distribution of internal pressure (hence the high controllability of the system), but the large surface area (of the dome) exposed to the impinging flame and pressure waves, thereby attenuating the destructive power (as opposed to those with a planar surface). The method combines countermeasure principles, such as isolation, flow obstruction, impact energy absorption, cooling and inerting, into a unified platform for suppressing the explosion. Prior to the implementation of this method in practical systems, a good understanding of how flame and pressure waves respond to the gradually inflated obstructions installed downstream is the prerequisite.

Laudable effort has been directed in the past with obstructions present to hinder the propagations of flame and pressure waves. Nie and colleagues [4,5] conducted experiments to examine the flame propagation characteristics in an empty pipe and in the presence of Al₂O₃ and SiC foam ceramics; from comparisons they found a significant hinderance effect of the obstructions on the propagation of flame. In particular, Na’inna [6] investigated the relation between the separation distance between obstructions and the explosion severity, and reported that high congestion in a given layout does not necessarily imply higher explosion severity, heavily depending on the separation distance between the obstructions. Dong et al. [7] found that the mean maximum explosion overpressure increased with the number of obstructions installed in the pipe, but noticed that the pressure fluctuation amplitude was reduced when coal dust was deposited at the bottom of the pipe. Relevant studies were also reported by Ciccarelli and colleagues (see e.g., [8,9]) who, however, specifically placed the focus on the deflagration-to-detonation transition (DDT) in the presence of obstructions. In the VAM explosion scenarios, the flame propagation dynamics may be more associated with the regime of deflagration due to the low flame speeds with relatively modest overpressures. We are not aware of any previous study that has dealt with flame propagation dynamics in the presence of gradually inflated obstructions. Compared to experimental investigations that are expensive, highly risky and very limited in accessible data in the context of gas explosion, the approach of numerical modelling [10] offers advantages such as flexibility in altering variables, safety, and cost-effectiveness.

This work numerically examines the propagation dynamics of flame and pressure waves in the presence of obstructions that are installed along the pathway in a tube closed at one end. The study aims to provide data that (i) aid in the understanding of the propagation dynamics of flame and pressure waves in the presence of gradually inflated obstructions, and (ii) inform the design and development of novel flame mitigation technologies. The Flamelet Generated Manifold (FGM) model in which the source terms for the unnormalized reaction progress variable are tabulated using the detailed chemistry [11], is deployed to simulate the deflagration of methane–air mixtures in the tube. Single or multiple obstructions are gradually inflated to partially or fully block the path of flame propagation. Special attention is paid to the propagation speeds of flame and pressure waves, overpressure inside the tube, and the stress exerted on the surface of obstructions by the high-speed gas flow.

2. Mathematical Model

2.1. Governing Equations

Generally, the main factor that affects the prediction of flame propagation is the accuracy of the specified or calculated flame speed. In this study, a partially premixed combustion model that does not require the input of flame speeds was developed based on the FGM model [11,12,13] to simulate the explosion and flame propagation dynamics.

In the FGM model, a probability distribution function (PDF) look-up table with respect to the progress variable $\left(c\right)$ and the mixture fraction $\left(f\right)$ is generated [11,12,13]. The reaction progress variable $\left(c\right)$ is defined as the normalised sum of the mass fractions of product species as,

$$c=\frac{\sum _i{a}_i\left(Y_i-Y_i^u\right)}{\sum _i{a}_i{Y}_i^{eq}}=\frac{Y_c}{Y_c^{eq}}$$

(1)

The 1D adiabatic premixed flame equations can be transformed from physical space to reaction-progress space, as given in Equations (2) and (3) for the species mass fraction and temperature, respectively.

$$\rho \frac{\partial Y_i}{\partial t}+\frac{\partial Y_i}{\partial c}{\dot{\omega }}_c=\rho {\chi }_c\frac{{\partial }^2{Y}_i}{\partial c^2}+{\dot{\omega }}_i$$

(2)

$$\rho \frac{\partial T}{\partial t}+\frac{\partial T}{\partial c}{\dot{\omega }}_c=\rho {\chi }_c\frac{{\partial }^{2}T}{\partial c^2}-\frac{1}{c_p}\sum _i{h}_i{\dot{\omega }}_i+\frac{\rho {\chi }_c}{c_p}\left(\frac{\partial c_p}{\partial c}+\sum _i{c_p}_i\frac{\partial Y_i}{\partial c}\right)\frac{\partial T}{\partial c}$$

(3)

where $c_p={\sum }_{i=1}^N{c_p}_i{Y}_i$ is the mixture-averaged heat capacity at constant pressure per unit of mass. Differential-diffusion is neglected in these equations. The scalar dissipation rate $\left({\chi }_c\right)$ is given by,

$${\chi }_c=\frac{\lambda }{\rho c_p}{\left|\nabla c\right|}^2$$

(4)

It can be noted that the scalar dissipation varies with progress variable $\left(c\right)$, is an input to the set of equations and is modelled using [14],

$${\chi }_c\left(c\right)={\chi }_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-2{\left({\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}}^{-1}\left(2c\right)\right)}^2\right]$$

(5)

A 1D premixed flamelet is calculated at a single equivalence ratio, which can be directly related to a corresponding mixture fraction. For partially premixed combustion, premixed laminar flamelets are generated over a range of mixture fractions. Premixed flamelets at different mixture fractions have different maximum scalar dissipations, ${\chi }_{\mathrm{m}\mathrm{a}\mathrm{x}}$. The scalar dissipation ${\chi }_c(f,c)$ at any given mixture fraction is modelled by

$${\chi }_c\left(f,c\right)={\chi }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{sto}\mathrm{e}\mathrm{x}\mathrm{p}\left[-2{\left({\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}}^{-1}\left(\frac{f}{f_{sto}}\right)\right)}^2\right]\mathrm{e}\mathrm{x}\mathrm{p}\left[-2{\left({\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}}^{-1}\left(2c\right)\right)}^2\right]$$

(6)

The only input required to the premixed flamelet generator is the scalar dissipation at stoichiometric mixture fraction, ${\chi }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{sto}$. A value of 1000 s^–1, which matches the solutions of unstrained physical-space flamelets for rich, lean and stoichiometric hydrocarbon and hydrogen flames at standard pressure and temperature conditions, is used.

The transport equation for the Reynolds averaged un-normalized progress variable, ${\tilde{Y}}_c$ reads,

$$\frac{\partial \left(\overline{\rho }{\tilde{Y}}_c\right)}{\partial t}+\nabla ·\left(\overline{\rho }\tilde{\mathrm{u}}{\tilde{Y}}_c\right)=\nabla ·\left(\overline{\rho }{D}_{\mathrm{e}\mathrm{f}\mathrm{f}}{\widetilde{\nabla Y}}_c\right)+{\overline{S}}_c$$

(7)

where $D_{\mathrm{e}\mathrm{f}\mathrm{f}}$ is the effective diffusivity coefficient calculated by

$$\overline{\rho }{D}_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{\lambda }{c_p}+\frac{{\mu }_t}{{Sc}_t}$$

(8)

where ${Sc}_t$ is the turbulent Schmidt number and ${Sc}_t={\mu }_t/\left(\rho D_t\right)$. ${\mu }_t$ is the turbulent viscosity and $D_t$ is the turbulent diffusivity. The mean source term, ${\overline{S}}_c$ is modelled from the finite-rate obtained from the premixed flamelet as given by

$${\overline{S}}_c=\overline{\rho }\iint S_{FR}\left(c,f\right) P\left(c,f\right)dc df={\overline{S}}_{FR}$$

(9)

Specifically, ${\overline{S}}_c$ determines the turbulent flame position. The finite rate source term which is tabulated from the detailed chemistry is used in the present work (i.e., Equation (9)) which does not involve any empirical constants. It is important to stress that this model contains no adjustable parameters, as would be the case for existing models in which a correlation is used for the turbulent flame speed.

2.2. Numerical Modelling

A transient, 2D, axisymmetric model proved capable of capturing the most important properties of a 3D flow [15] and a model of the experimental tube was developed using ANSYS Fluent 2020 R2. The transient pressure field variation, along with flame propagation is modelled using the unsteady RANS (URANS) approach, which represents the computationally cheapest model, but proves capable of providing reasonable accuracy. The standard k-ε turbulence model with standard log-law wall functions is used in this study.

In the combustion simulations, GRI-Mech 3.0 is used for flamelet generation and 64 × 64 grid point resolution is applied in table construction for mixture fraction and progress variable space. Flamelets are generated for a pressure of 1 atm and the effect of changes in pressure on different quantities is considered. The progress variable equation source term is modelled using the Finite Rate option as described in Equation (9); the variance of the progress variable is calculated using the progress variable variance transport equation.

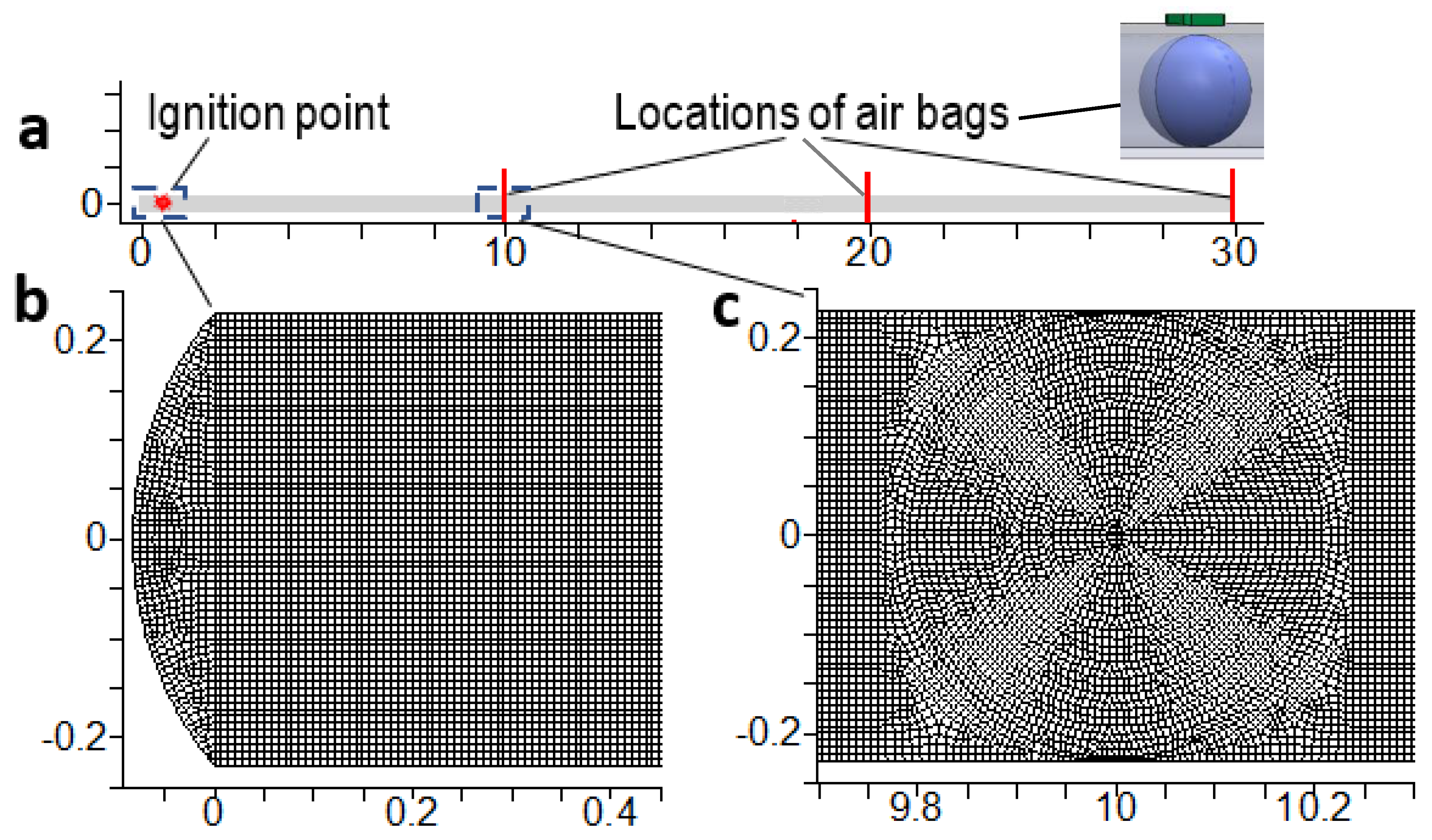
Figure 2 shows the computational domain and mesh. Based on sensitivity studies, a mesh with a size of 7.125 mm was drawn, yielding an element count of 134,561. Obstructions are installed at locations of 10 m, 20 m and 30 m. Considering the spherical balloon shape, a quadrilateral mesh (Figure 2c) was deployed in the region of obstructions. A time step of 10 µs were used, resulting in a convective Courant number below 0.1, and these were able to fully resolve the rapid explosion process. Pressure–Velocity coupling is enforced using the SIMPLE algorithm. Gradients are modelled using the Least Squared Cell-Based Method and all convective terms are represented using the bounded Second Order Upwind (SOU) scheme. The transient terms are modelled using the Bounded Second Order Implicit scheme.

The species concentrations and temperatures are set in the various sections of the tube to the measured experimental values. Specifically, the mole fraction of water vapor in the humid air is calculated by

$$x_{{\mathrm{H}}_2\mathrm{O}}=\frac{\varphi p_{{\mathrm{H}}_2\mathrm{O}}^{*}}{p}$$

(10)

where $\varphi$ denotes the relative humidity. The saturated humid air pressure, $p_{{\mathrm{H}}_2\mathrm{O}}^{*}$, is expressed as a function of temperature by

$$p_{{\mathrm{H}}_2\mathrm{O}}^{*}=f\left(T\right)=610.78\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{17.2694T}{T+238.3}\right)$$

(11)

where T is the temperature in Celsius. The initial mixture fraction (i.e., methane mass fraction) in each reactive section is calculated by

$$Y_{{\mathrm{C}\mathrm{H}}_4}=\frac{x_{{\mathrm{C}\mathrm{H}}_4}{W}_{{\mathrm{C}\mathrm{H}}_4}}{x_{{\mathrm{C}\mathrm{H}}_4}{W}_{{\mathrm{C}\mathrm{H}}_4}+x_{\mathrm{a}\mathrm{h}}{W}_{\mathrm{a}\mathrm{h}}}$$

(12)

where W_ah is the molar mass of humid air.

In the simulation, the entire tube is set as the explosive zone with the stoichiometric methane concentration (9.5% mole fraction); at time zero, the progress variable is set to 1 in two computational cells around the ignition point to start the reaction.

The growth of obstructions is simulated by the change of boundary conditions, implemented by modifying the built-in models using Scheme Macros. All walls are treated as no slip and adiabatic. The latter is justified due to the very short time available for heat loss. At the exit the absolute pressure is set to 1 bar and a reflecting boundary condition is used to consider the finite length of the tube (with properties different from those in the atmosphere).

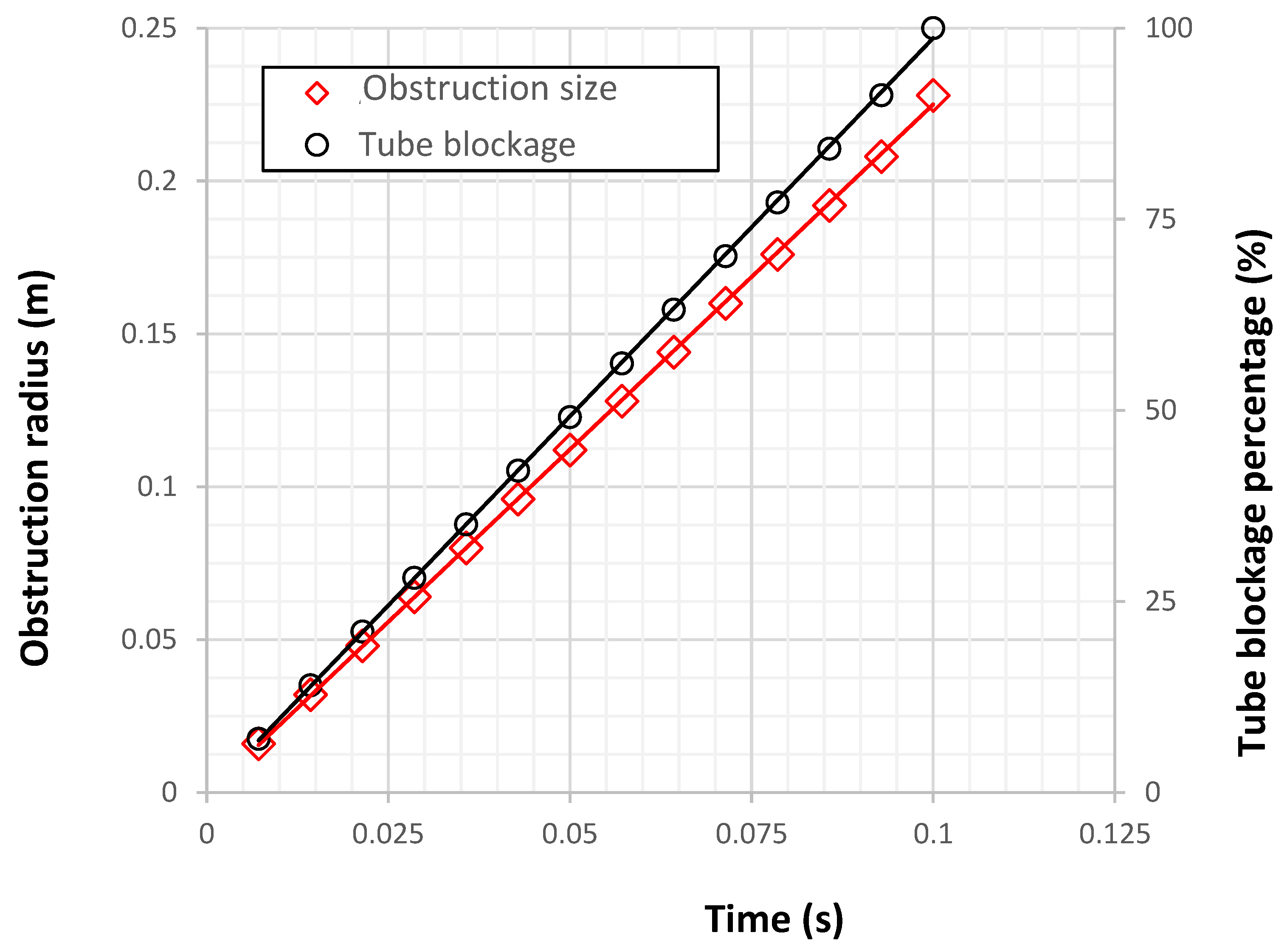
The obstruction is inflated once explosion is detected. The growth rate of obstruction is shown in Figure 3, and is constant at 2.24 m/s. It takes approximately 0.05 s for the obstruction to half block the tube, and 0.1 s to fully block the tube with a radius 0.228 m. This numerical setting allows for a more realistic simulation of practical systems where the size of obstructions is adjustable. A variety of scenarios, as detailed in

Table 1. Scenarios of obstruction number, installation location, and inflation degree at each location.

	Location (m)	10	20	30
Number (-)
1		0	−	−
		50%	−	−
		100%	−	−
2		0	50%	−
		50%	50%	−
		50%	100%	−
3		0	0	50%
		0	50%	50%
		50%	50%	100%

, were examined. In Table 1, the inflation degree at each installation location (i.e., at 10 m, 20 m, and 30 m away from the tip of the dome) represents the percentage by which the tube is blocked by the obstruction. For the case with one obstruction installed, the bag is installed at the location 10 m away from the dome tip; for the case with two obstructions installed, the bags are installed at the locations 10 m and 20 m away from the dome tip, respectively; for the case with three obstructions installed, the bags are installed at the locations 10 m, 20 m, and 30 m away from the dome tip, respectively. The results from CFD modelling for each case (with different numbers of obstruction installed) are presented and discussed as follows.

2.3. Model Validation

This work is part of our research on the VAM abatement. The numerical model developed for the research, namely the FGM-based model, applies to problems pertinent to the VAM abatement featuring the deflagration of methane−air mixtures (with different initial/operating and boundary conditions). Several relevant works conducted in our group have been published (see e.g., [3,16]), where extensive validation of the developed FGM-based combustion model was presented using our own experimental data from different perspectives, including transient evolution of local absolute pressure, local maximum pressure, pressure wave propagation speed, and flame front propagation speed. In these works, the FGM-based model was applied to solve problems encountered in the operation of real VAM abatement systems, such as the explosion propagation dynamics in large-scale tubes and through fixed beds of RTO devices. 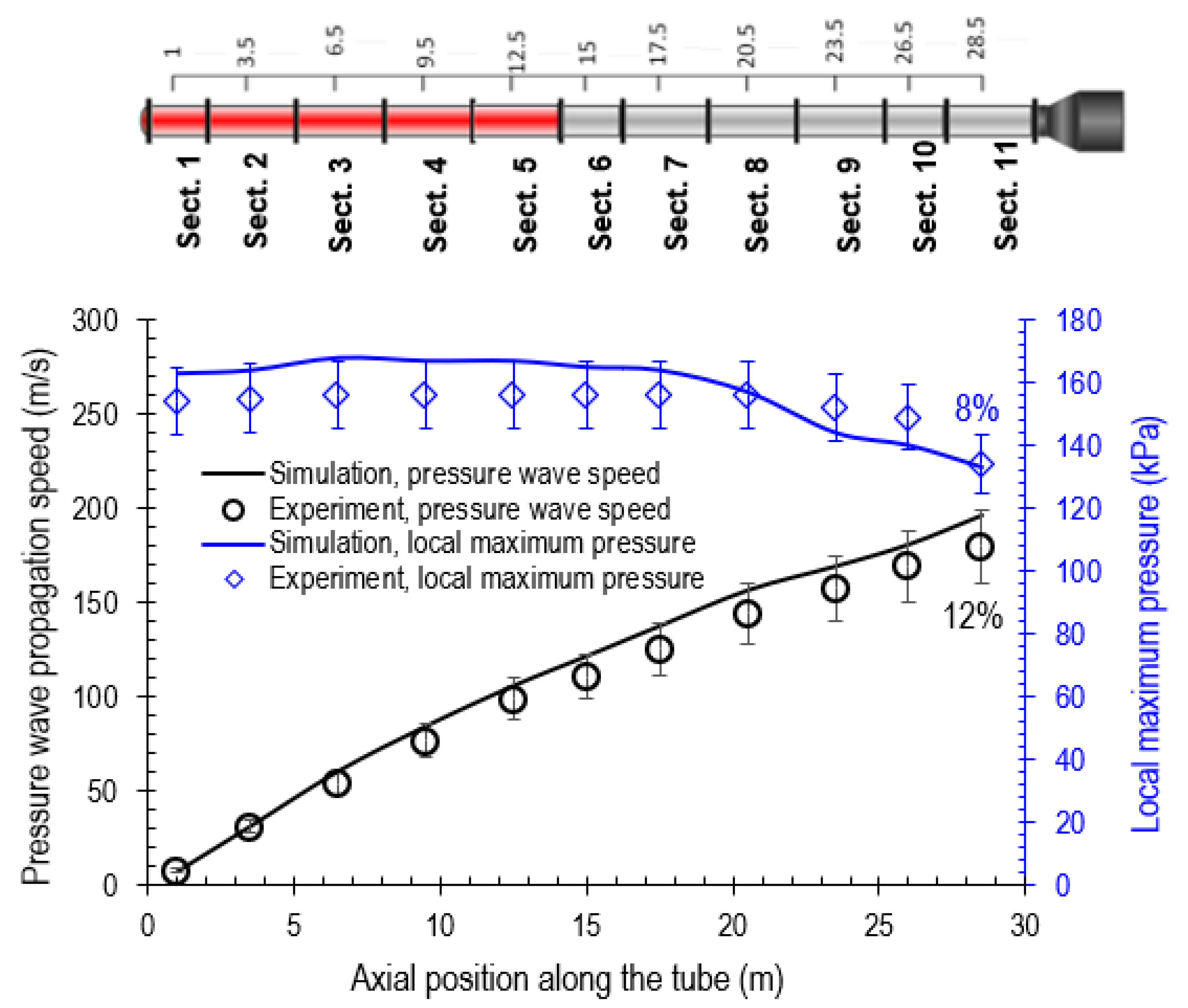Figure 4 shows the comparisons between predicted results and measured values of propagation speeds of flame and pressure waves. The sketch of the experimental tube is also inserted indicating the locations where the data are monitored and predicted. Details of the experimental set-up and operating procedures can be found in our previous work such as [17]. Evidently, the predicted results reasonably agree with the measured values with a maximum deviation of 12% for predicting the propagation speed of pressure waves and 8% for predicting the local maximum pressure, which are within the limits of the experimental error [18]. These agreements corroborate the capabilities of the model in capturing the main features of methane–air deflagrations, given the propagation dynamics of pressure waves and the local maximum pressure are generated based on the thermodynamics of methane–air combustion throughout the tube.

3. Results and Discussion

3.1. Flame and Pressure Wave Propagation in an Empty Tube

Explosion in an empty tube was simulated and the results used as a baseline to reflect the effect of obstruction installation on the propagation dynamics of flame and pressure waves.

Figure 5 shows the evolution of temperature, pressure, and velocity fields immediately after ignition (within 2 ms) in the empty tube. Clearly, despite the flame’s subtle growth in 2 ms (left column of Figure 3), the expansion of hot gases generated from the combustion of methane results in the rapid and intense propagation of pressure waves. Specifically, the temperature of combustion products rises to 2200 K and heats the surrounding unburnt gases to ignite the adjacent methane (at the boundary of the tiny circle region of combusted methane). The rapid expansion of hot gases induces the compression of unburnt gases and leads to subsequent alternate rarefactions and compressions of unburnt gases, generating pressure waves. The energy liberated from methane combustion is transmitted mainly through the pressure waves. Moreover, the pressure waves initially propagate outward spherically (before t = 0.5 ms). After hitting the wall, the reflections of pressure waves from tube walls can be seen from the pressure contours at t = 1 ms. The pressure waves after t = 1 ms are rather chaotic as a result of their reflections. However, the propagation of pressure waves towards the tube open end is evident after t = 1 ms. The velocity field corresponds to the pressure field, with alternate high and low speed regions.

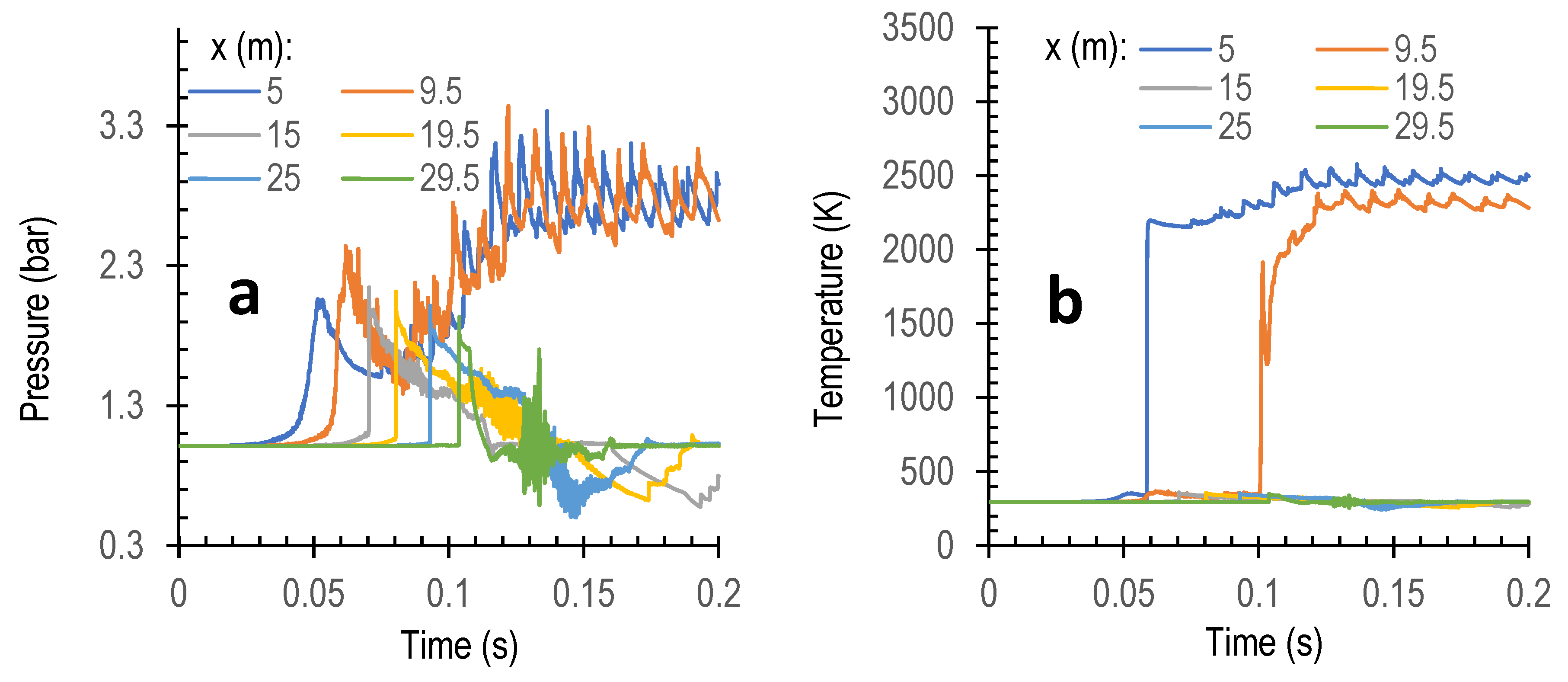
The local temperature and pressure monitored at different locations are shown in Figure 6 as a function of time. It can be seen at each location that the temperature profile (Figure 6a) has an abrupt rise, which indicates the arrival of the flame front. Over the same distance between two consecutive locations (i.e., 4.5 m), the time taken by the flame becomes shorter as the flame propagates towards the tube open end, as can be seen from the increasingly smaller gap between the temperature profiles. The smaller time interval indicates the faster flame propagation speed. The results are in line with those we previously reported and results of other researchers in the literature (e.g., [16,19,20]). There are peaks on the pressure profiles (Figure 6b) which indicate the arrival of pressure waves. The pressure peaks occur rather smoothly, not as abruptly as the temperature rises shown on the temperature profiles. The second peaks observed at the late stage (after t > 0.13 s) result from reflections from the tube open end, as discussed further. In addition, the time to reach the pressure peaks at each monitored location is also much shorter, particularly at the downstream locations, which indicates that the propagation speed of pressure waves also becomes increasingly faster as it propagates towards the tube open end. It takes less than 0.11 s for the pressure wave to reach the open end of the tube, i.e., at the location of 29.5 m, whereas it takes 0.185 s for the flame to reach the tube open end. The much faster propagation speed of pressure waves than those of flame is due to the rapid expansion of hot gases pushing the unburnt gases towards the tube open end. The results are in in line with the deflagration theory presented in our earlier studies [3,16,19].

After t = 0.11 s, that is, when the pressure wave front reaches the tube end, the pressure profile at each monitored location becomes non-monotonic and fluctuating. This is due to the reflections from the tube open end. To consider the inconsistency in the physical properties of gases between the tube internal space and the atmosphere, the boundary condition at the tube open end is set as reflecting boundary. It can be seen that the local pressure peak generally increases due to reflections, particularly at the locations in the middle of the tube, which might be attributed to the resonance of reflections from both the tube closed and open ends. The pressure peak at the location close to the tube open end (x = 29.5 m) is the lowest due to the release of gases from the tube into the atmosphere.

3.2. Single Obstruction

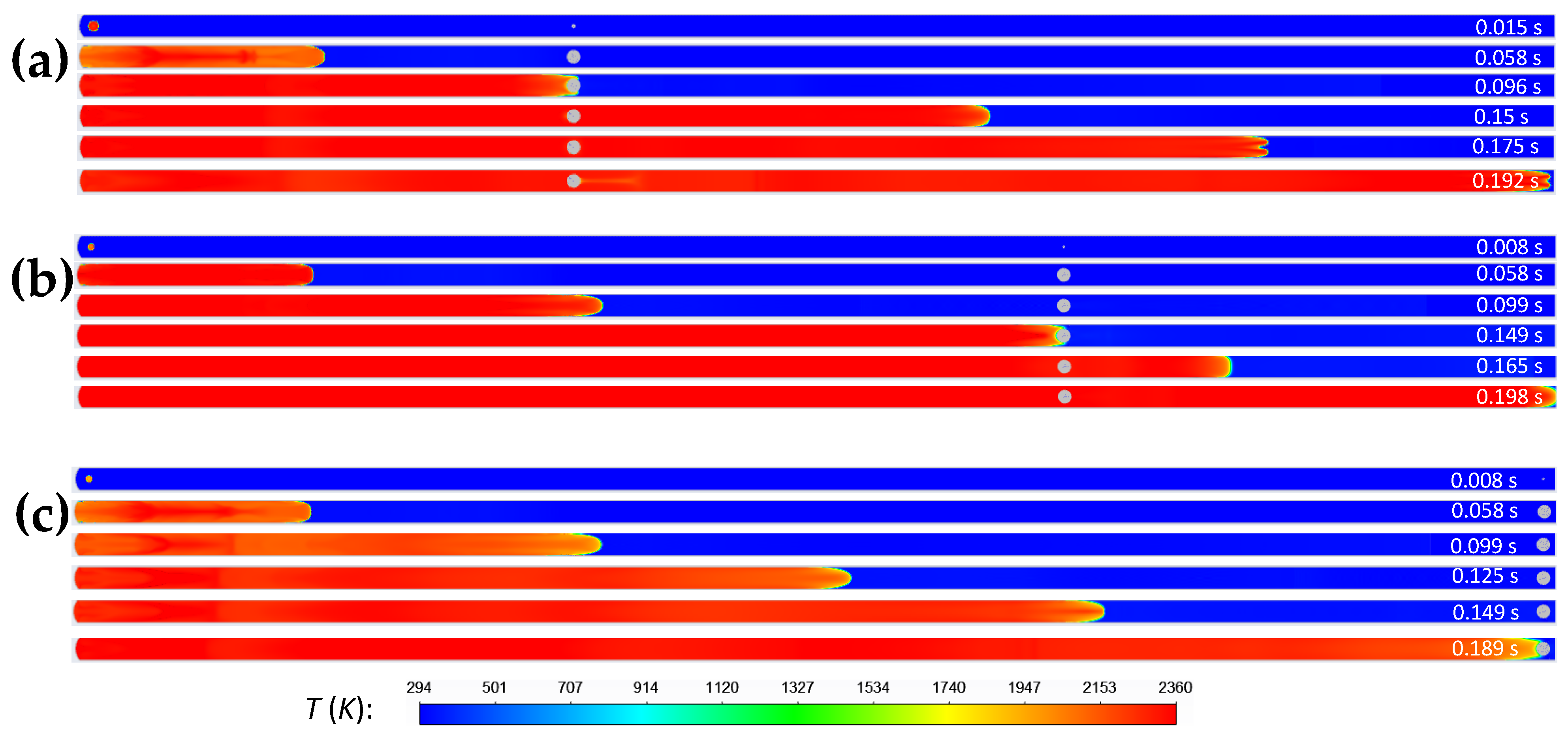
The single obstruction is installed at different axial locations, namely at x = 10 m, x = 20 m and x = 30 m, all with the bag inflated by 50%, corresponding to half blockage of the tube. At the location x = 10 m, the bag is also 100% inflated, corresponding to complete blockage of the tube.

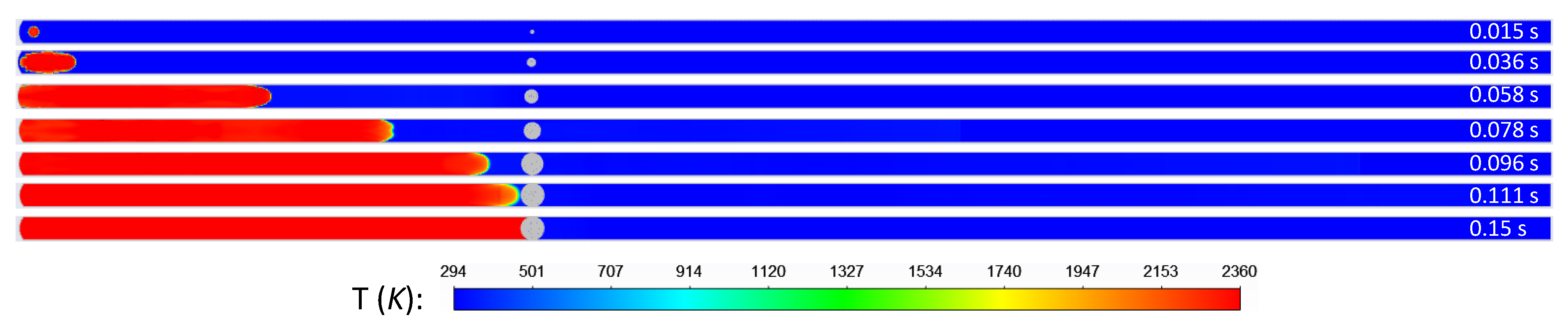
Figure 7 shows the flame propagation through the tube. At t = 0.058 s, the obstruction is inflated by 50% and the tube is half blocked. The flame front profile maintains the bullet shape and does not change much as it propagates through the tube until it approaches the obstruction. In the vicinity of the obstruction, the flame front profile appears to differ from those far away from the obstruction. The hindered flame propagation by the obstruction can be seen by comparing the flame front location. In Figure 7a, at t = 0.15 s, the flame front does not reach x = 20 m, but in Figure 7b, it can be seen it does, even at t = 0.149 s, whereas in Figure 7c, it passes x = 20 m at t = 0.149 s. The results indicate that the presence of obstruction hinders the flame propagation downstream.

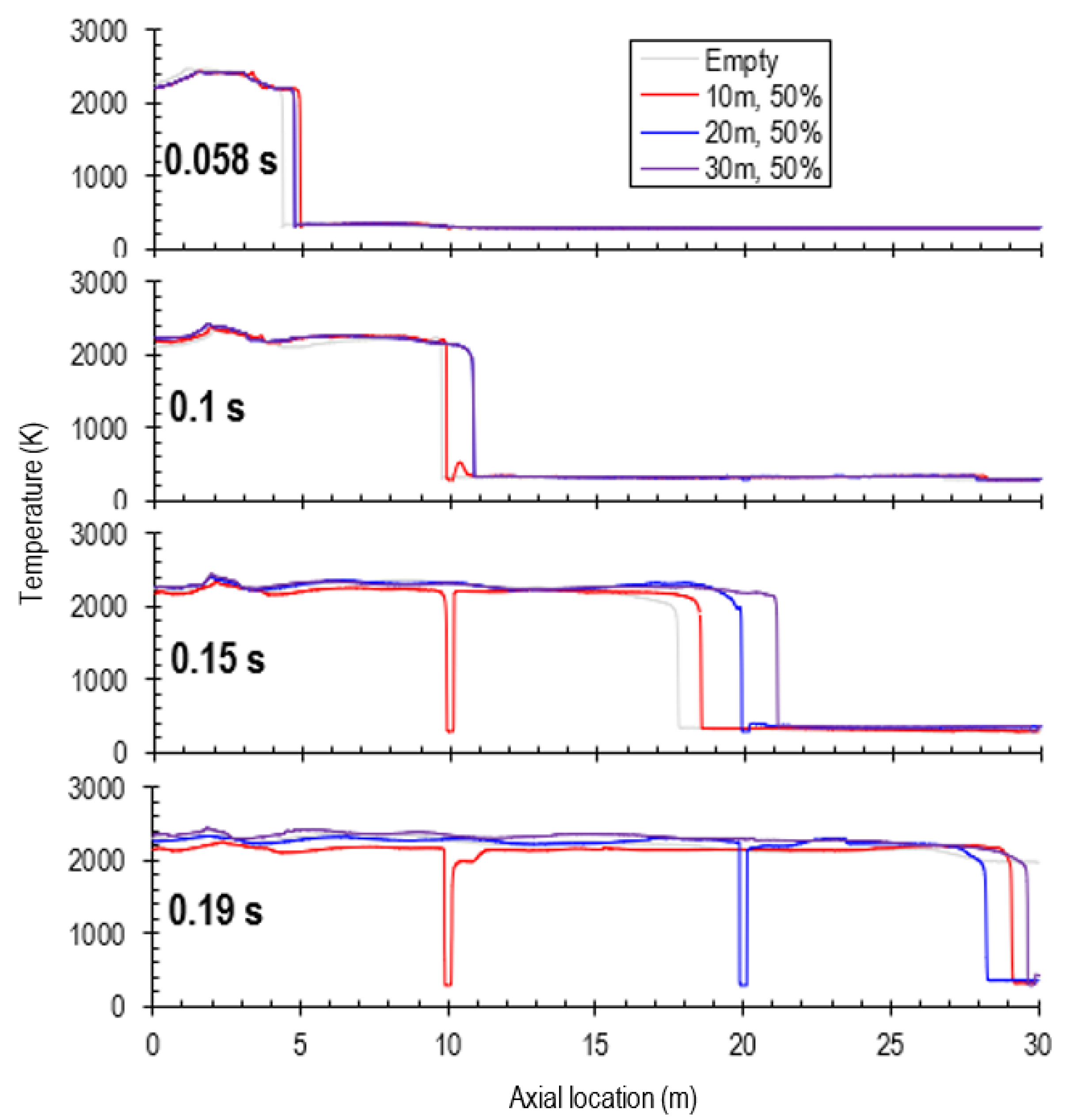
Figure 8 shows the temperature profiles along the tube centreline at different times. As indicated above, the location where temperature abruptly drops indicates where the flame front is. Before the flame propagates out of the tube, compared to the empty tube, quite surprisingly, the flame propagates faster in tubes with a partially inflated obstruction. This can probably be attributed to the low pressure generated between the obstruction and the tube wall due to the smaller cross-sectional area (based on mass and energy conservations). This local pressure also acts as the driving force (a large pressure difference compared to the high upstream pressure) to accelerate the flow of upstream gases or flame propagation, particularly when the upstream pressure increases due to reflections from the obstruction (leading to an even greater pressure difference).

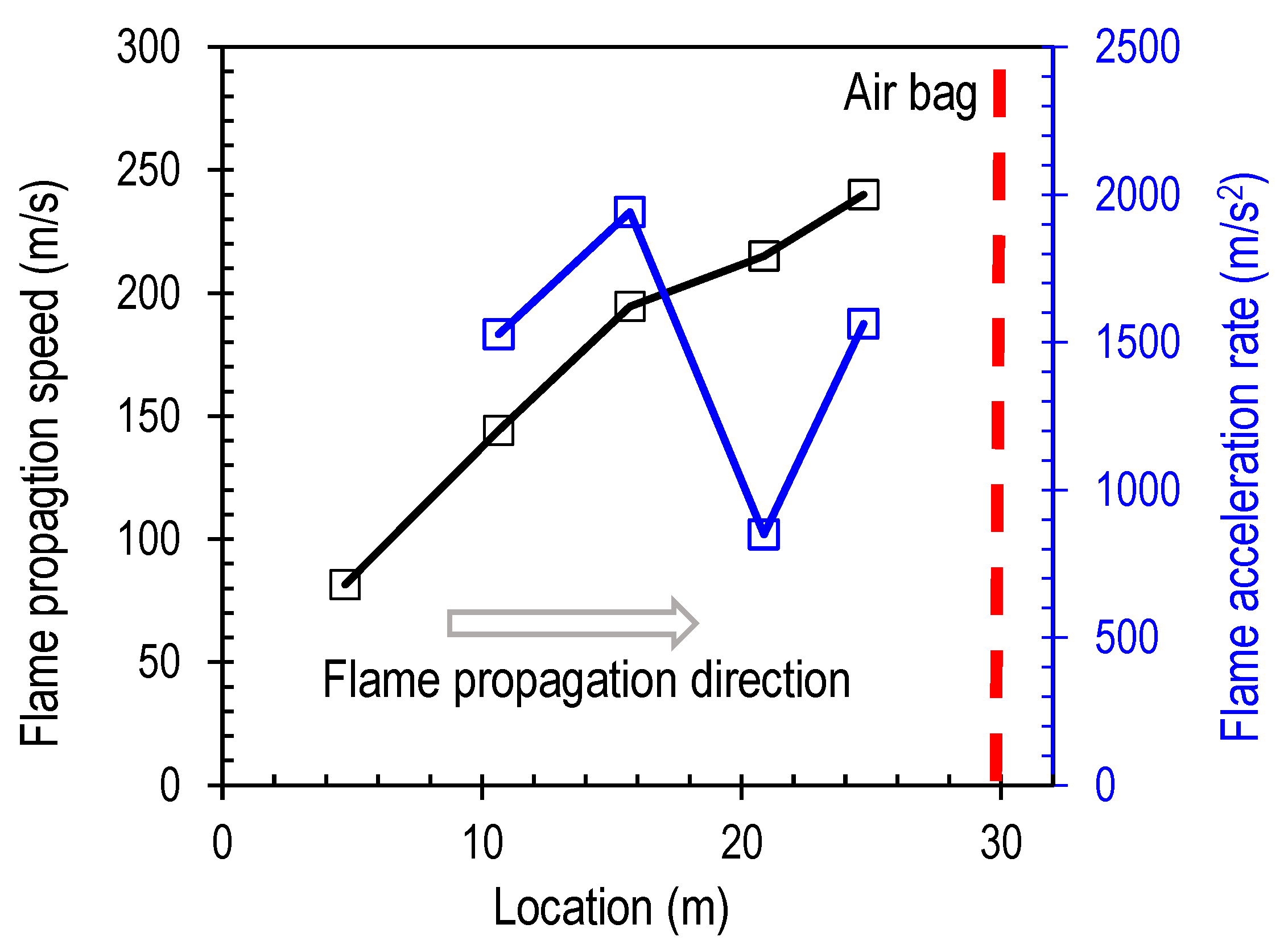
Therefore, the presence of a partially inflated obstruction, on the one hand, increases the flame propagation speed in the upstream region due to the increased pressure difference; on the other hand, the obstruction by the blockage of pathway (high pressure at the stagnation point in front of the obstruction) slows down the propagation of flame in the downstream region after the flame has passed the obstruction. The above two counteracting factors leads to the overall fastest flame propagation speed when the obstruction is installed at x = 30 m, particularly when the flame has passed the obstruction that is installed at x = 10 m and x = 20 m, but is far away from the obstruction installed at x = 30 m, i.e., at t = 0.15 s. The flame propagation speed and acceleration rate for the scenario where a single obstruction is installed at x = 30 m is shown in Figure 9. This is a very good example showing that the flame acceleration rate increases at the beginning, then decreases and increases again in the upstream region before the obstruction, justifying the above observations.

Overall, it takes at least 0.189 s for the flame to propagate out of the tube in the presence of the obstruction, but takes 0.185 s in the empty tube. This is attributed to the obstruction effect of the obstruction installed at the tube open end on flame propagation. Discontinuities in temperature profiles are observed at the locations of obstruction: at the location where the obstruction is installed, there is an abrupt temperature drop (to room temperature) as the time is too short for heat transfer between the hot gases and the wall of obstruction.

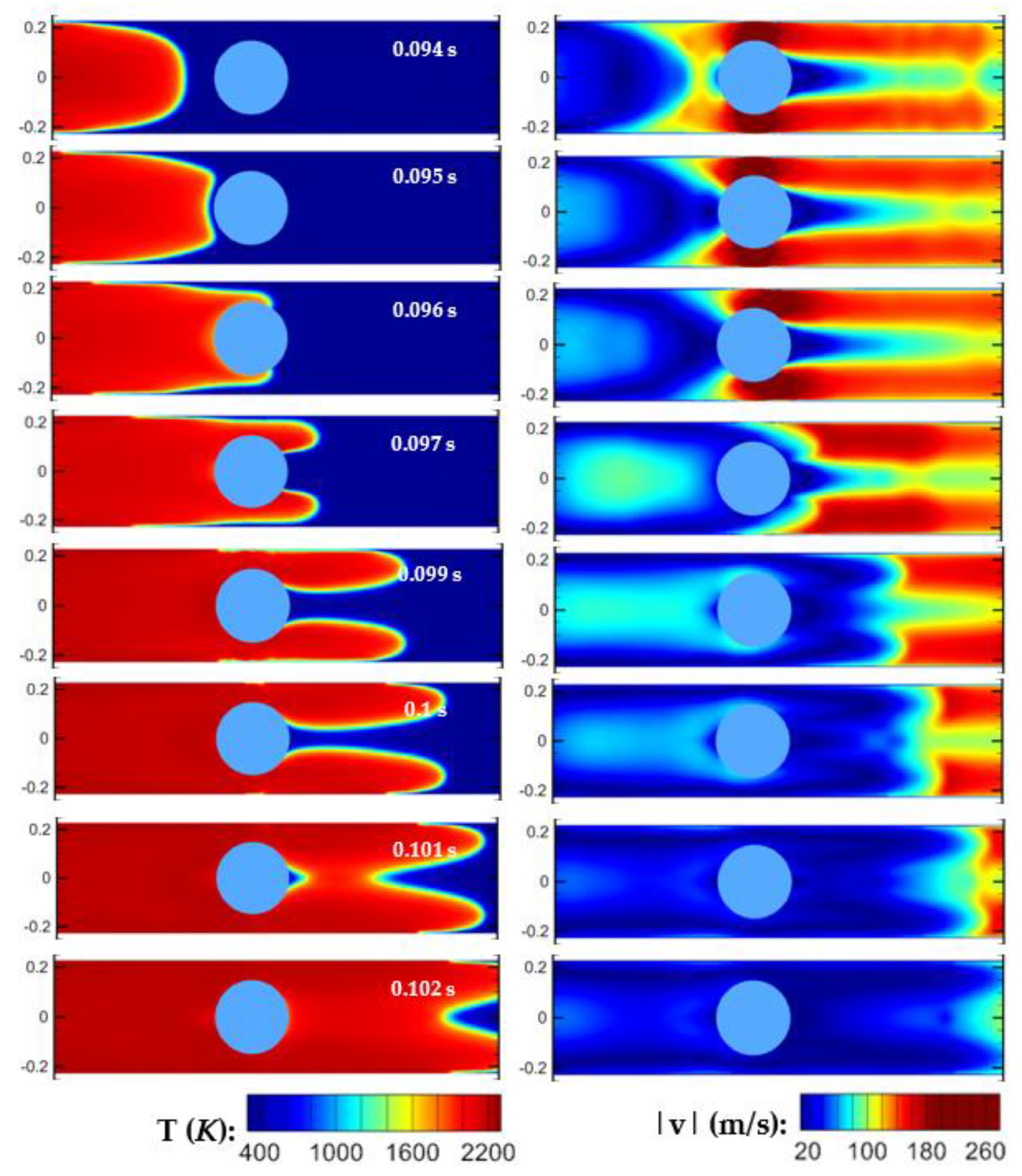
Figure 10 shows the moment when the flame propagates across the half-inflated obstruction in terms of flame profile and the contour of velocity magnitude. The obstruction splits the flame into two high speed streams, which radially expand and merge soon. The presence of the half-inflated obstruction leads to the local low pressure and high air flow through the space between the obstruction and tube wall, which accelerates the upstream flow, but decelerates the downstream flow. It is also worth reiterating that the flame propagation falls within the regime of deflagration. Due to the large size increment by which the obstruction is inflated (Figure 3), the space between the obstruction and the tube wall is so large that flame speeds reaching detonation are not covered in the present study, which, albeit challenging, would be a valuable next step.

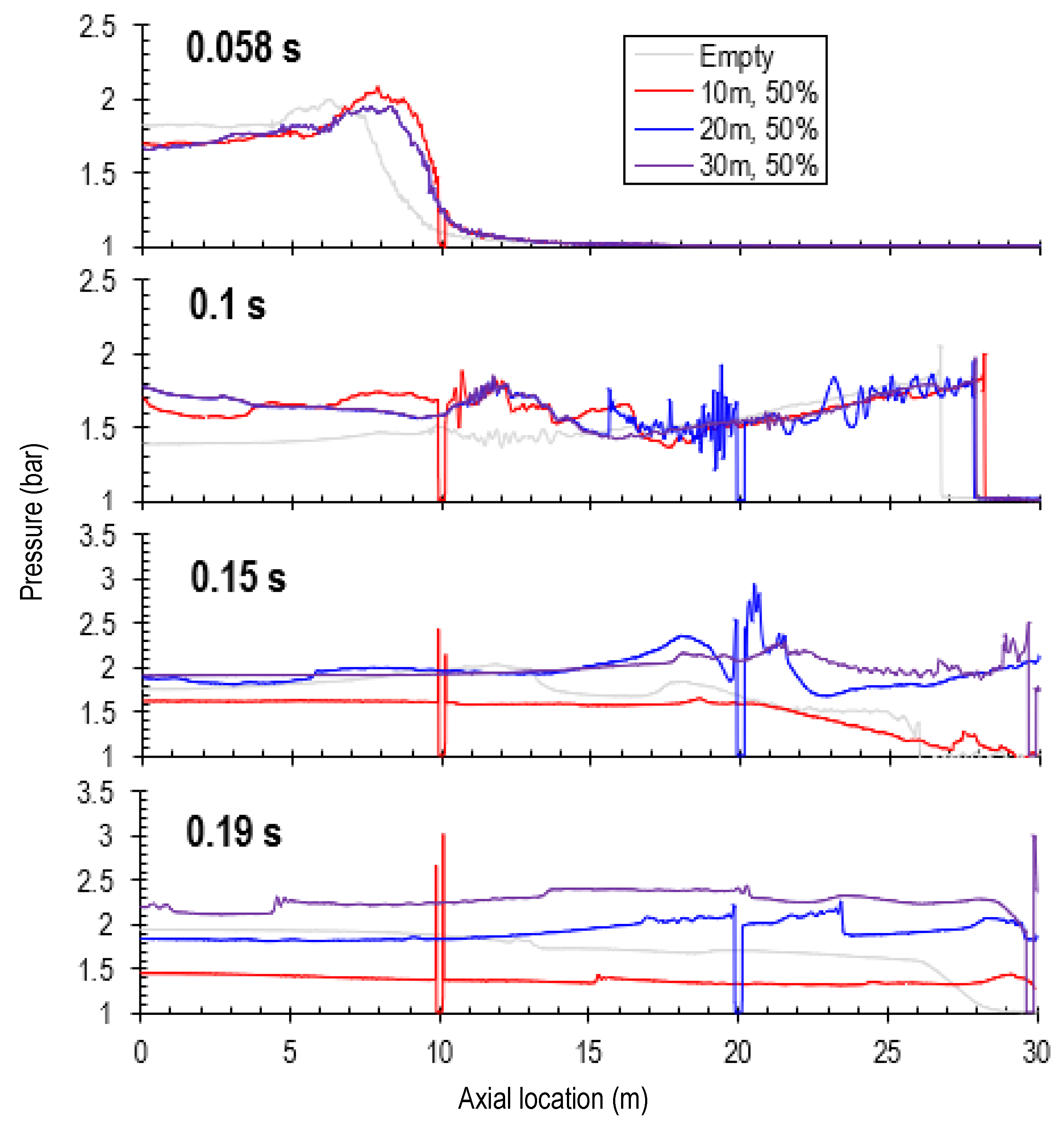
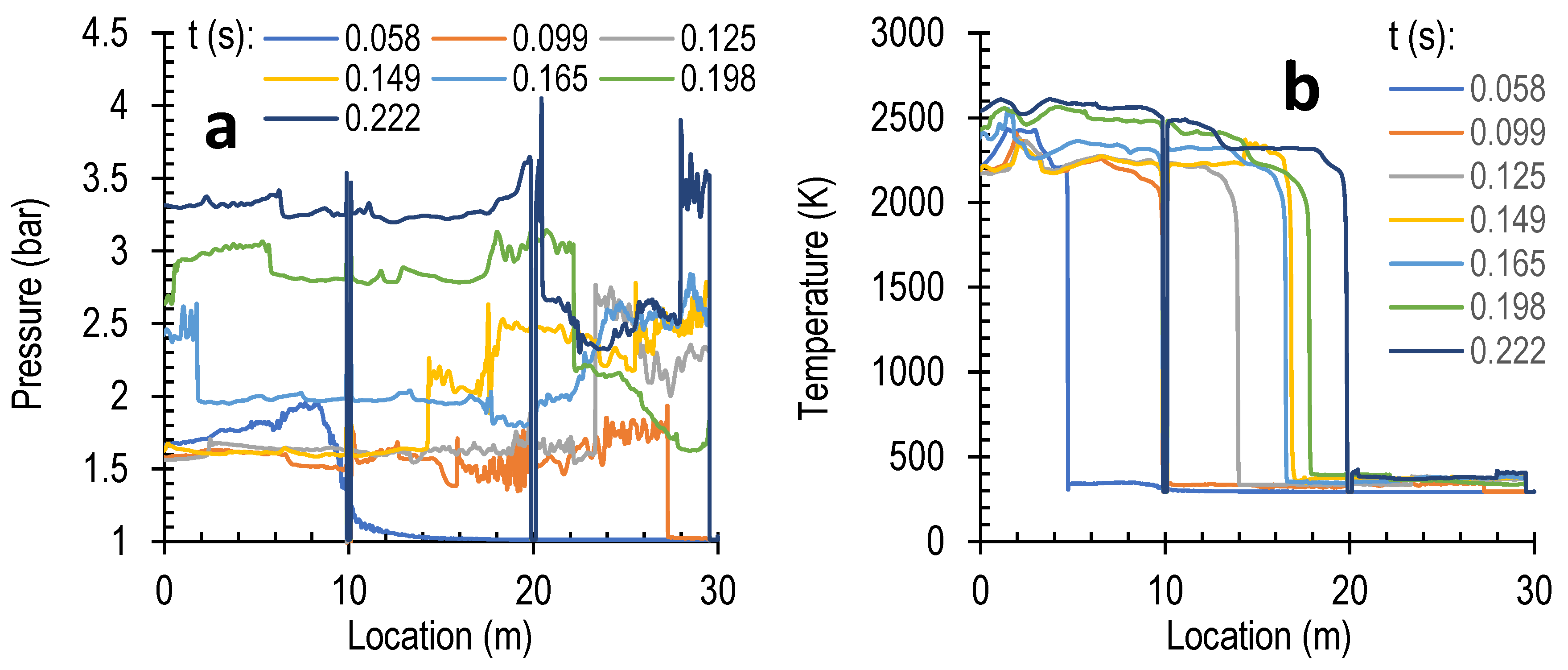
Figure 11 shows the corresponding pressure profiles along the tube centreline. Similarly, the location where the pressure abruptly drops indicates where the pressure wave front is. Generally, as also discussed above, the pressure waves propagate much faster than the flame front (see profiles at t = 0.058 s) and reach the tube end just over 0.1 s. In contrast to the flame propagation, the pressure waves propagate at the fastest speed when the obstruction is installed at x = 10 m. The presence of obstruction that half blocks the tube significantly accelerates the propagation of pressure waves; this effect occurs earlier when the obstruction is installed closer to the ignition point. As the pressure waves propagate out of the tube, the high pressure drops due to the release of gases into the atmosphere. However, when the obstruction is installed further away from the ignition point (or closer to the tube open end), the high pressure in the tube accumulates more. As shown in Figure 11, at t = 0.19 s, the pressure in the tube stays the highest when the obstruction is installed at x = 30 m, whereas for the case with the obstruction is installed at x = 10 m, the pressure drops even below that in the empty tube.

Figure 12 shows the flame propagation with the obstruction gradually inflated by 100% at x = 10 m, i.e., the tube is completely blocked. The flame propagation dynamics is the same as those shown in Figure 7a before the obstruction is half inflated. As the obstruction continuously grows, the tube is more blocked and the high pressure in the upstream slows down the flame propagation. For example, at t = 0.096 s the flame has not yet reached the obstruction, whereas when the bag is half inflated the flame has just reached the obstruction (Figure 7a). When the obstruction is 100% inflated to completely block the tube, not surprisingly, the flame stops propagating.

Figure 13 shows the local pressure and temperature monitored at different locations for the scenario where the obstruction is 100% inflated at x =10 m (the tube is fully blocked). The evolution of pressure at different locations is completely different when the obstruction is fully inflated. Before the obstruction is fully inflated at t = 0.1 s, or before the tube is blocked, the pressure wave propagates through the tube and accordingly, each location experiences the peak pressure. The pressure at the location just before the obstruction is the highest due to the presence of the obstruction, reaching approximately 7.5 bar at the location the obstruction is installed (not shown in Figure 13). However, after the obstruction is fully inflated, at locations before the obstruction (i.e., x ≤ 10 m) the pressure rises significantly due to the choked flow, whereas at locations after the obstruction (i.e., x > 10 m) the pressure drops to the atmospheric pressure as the flame has been restrained in the upstream by the obstruction. The temperature in the region before the location of obstruction (x < 10 m) increases due to the continuous combustion of methane; in the region after the obstruction (x > 10 m), the temperature remains at the room temperature as there is no combustion occurring in this region, suggesting the flame propagation is completely stopped by the obstruction.

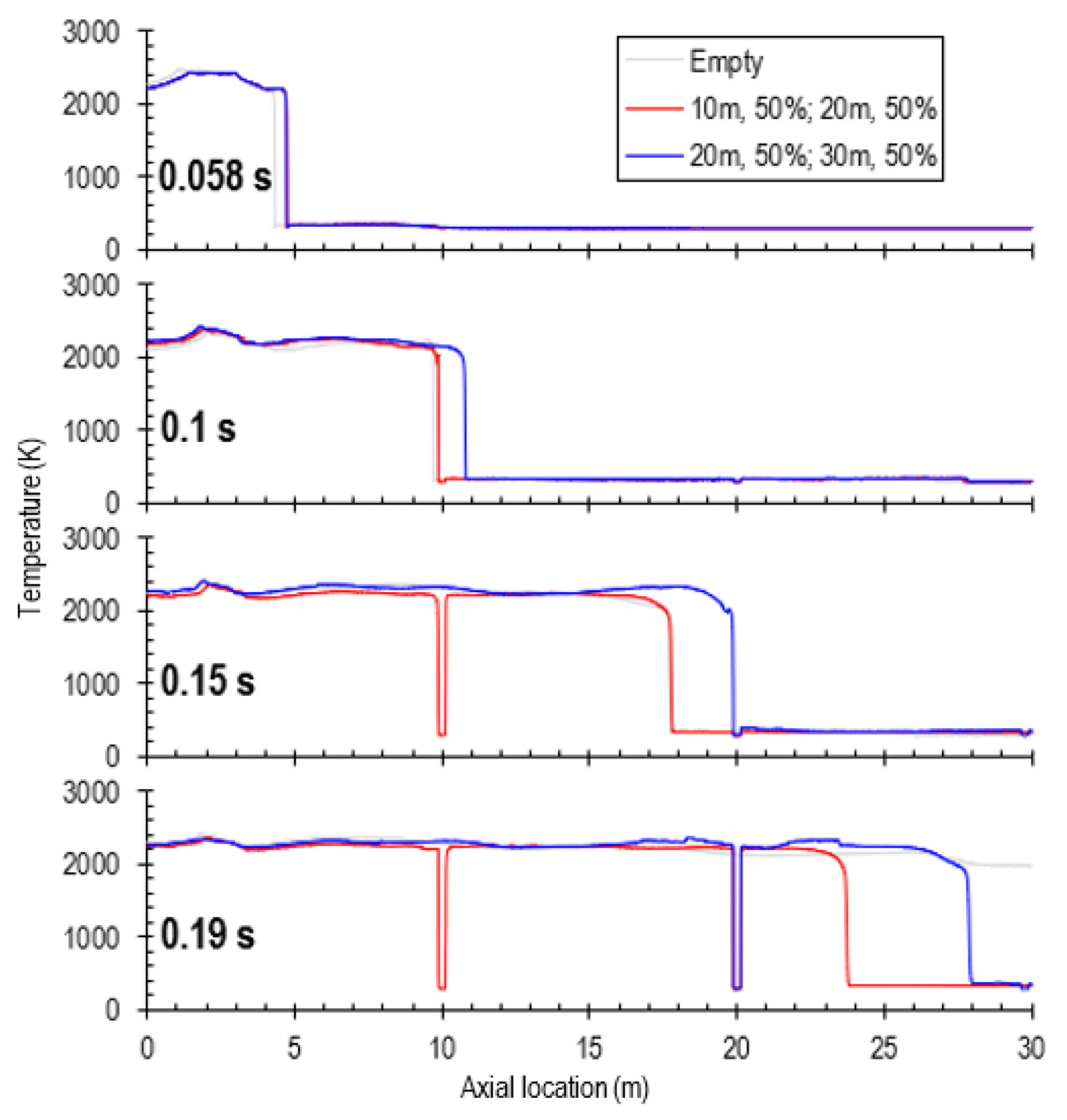
3.3. Double Obstructions

In the case of double obstructions, two obstructions have been installed, at locations x = 10 m and x = 20 m, and at locations x = 20 m and x = 30 m, with an obstruction inflation of 50%. For the installation locations x = 10 m and x = 20 m, the obstruction at x = 20 m is also 100% inflated. For clarity, we refer to the first and second obstructions along the flame propagation direction as Obstruction 1 and Obstruction 2, respectively.

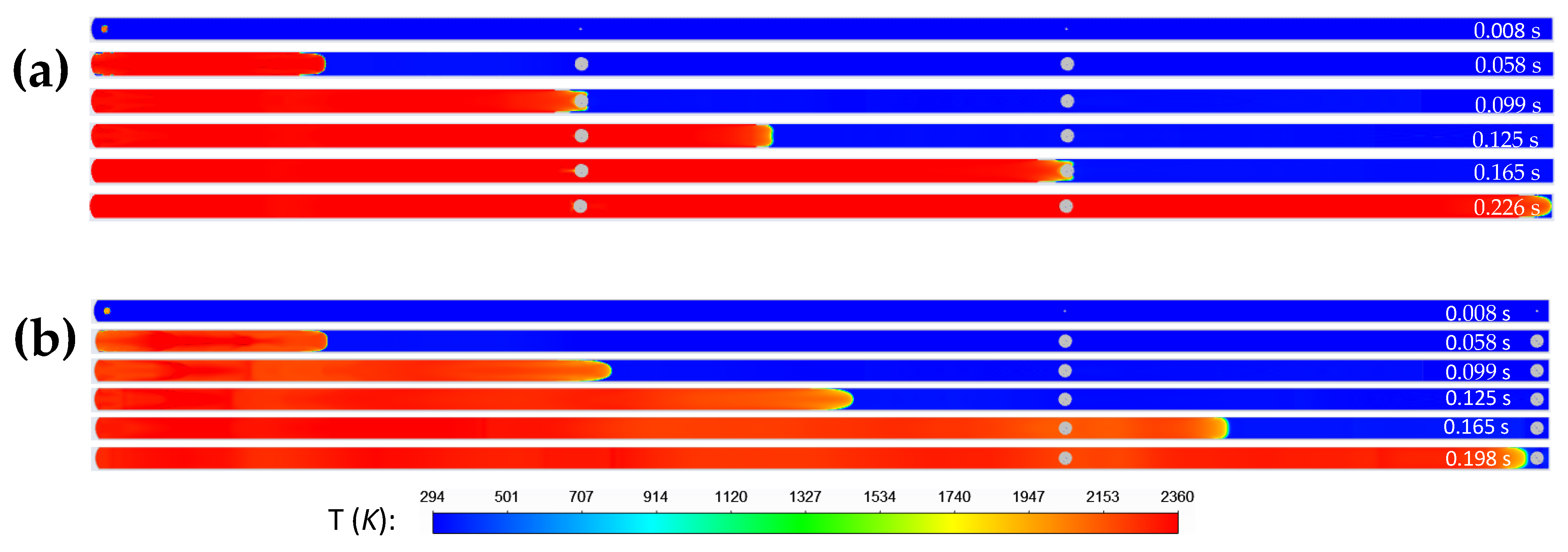
Figure 14 shows the flame propagation through the tube. For the case where the obstructions are installed at x = 10 m and x = 20 m (Figure 14a), it takes approximately 0.099 s for the flame to propagate to the location where Obstruction 1 is installed (at x = 10 m). As Obstruction 1 is only half inflated, the flame continues propagating through the space between the obstruction and tube walls. At t = 0.165 s, the flame reaches the location where Obstruction 2 is installed. Likewise, the flame continues propagating through the space between Obstruction 2 and the tube walls. At approximately t = 0.226 s, the flame reaches the end of the tube. Clearly, the total time required for the flame to reach the tube end is much longer than in the cases of empty tube or one obstruction installed at x = 10 m (Figure 7). In the case where the obstructions are installed at x = 20 m and x = 30 m (Figure 14b), the flame front profile does not change much until reaching Obstruction 2; after propagating over Obstruction 2. The flame front is then split into two streams (the top and bottom) as shown in Figure 10. Subsequently, the flame front becomes less sharp in the region between Obstruction 1 and Obstruction 2. The flame reaches Obstruction 2 at t = 0.198 s.

In both cases, the time required for the flame to reach the tube end is longer than that in the cases where a single obstruction is installed (Figure 7) due to the obstruction effect.

Figure 15 shows the temperature profiles for the two scenarios where two obstructions are installed at two different locations. It is evident that the flame propagates faster in the scenario where two obstructions are installed towards the tube open end, i.e., at locations x =20 m and x = 30 m; this is more pronounced in the late stage when the flame propagates further way from the ignition point. As discussed above, the presence obstruction accelerates the upstream flow, but decelerates the downstream flow. Therefore, the flame propagation speed is higher when the obstructions are installed closer to the tube open end, as it leads to more time for the acceleration. However, the flame takes the shortest time to propagate out of the empty tube (as seen at t = 0.19 s) due to the presence of the obstruction at the tube open end.

Figure 16 shows the corresponding pressure profiles along the tube centreline. Clearly, the pressure in the scenario where the two obstructions are installed closer to the tube open end (at x = 20 m and x = 30 m) is much higher than in the scenario where the obstructions are installed closer to the ignition point (at x = 10 m and x = 20 m) due to the longer time for pressure accumulation. In the scenario where the obstructions are installed further away from the tube open end (at x = 10 m and x = 20 m), due to the vent of gases into the atmosphere, the pressure in the tube drops and becomes close to that in the empty tube. Noticeably, the temperature remains relatively constant in the tube in this scenario up to t = 0.19 s.

3.4. Triple Obstructions

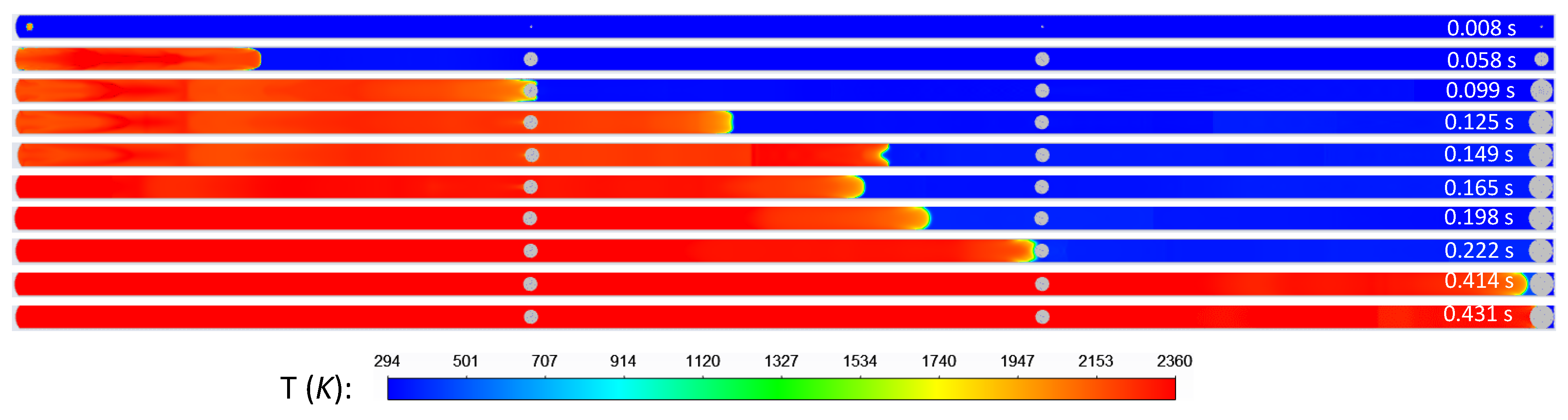
In the case of triple obstructions, three obstructions are installed at locations of 10 m, 20 m, and 30 m, referred to as Obstruction 1, Obstruction 2, and Obstruction 3, respectively. Obstructions 1 and 2 are half inflated, whereas Obstruction 3 is fully inflated. Figure 17 shows the flame propagation through the tube. It can be seen at t = 0.099 s that Obstruction 3 is fully inflated, and the tube is completely blocked. Accordingly, the flame propagation slows down, and the flame front becomes flat at t = 0.125 s. Noticeably, at t = 0.149 s, the centre of the flame front propagates slower than the flame sides, leading to a spear-like flame front. Subsequently, at t = 0.165 s the flame front propagates backwards, as a result of the choked flow due to the complete blockage of Obstruction 3. However, the combustion of methane continues, despite the choked flow, which makes the flame propagate towards the tube end again, but at a much slower speed. For instance, at t = 0.198 s, the flame has not reached Obstruction 2 (i.e., at x = 20 m), whereas in other scenarios the flame has reached the tube end (Figure 7 and Figure 14).

The quantitative pressure, temperature and velocity profiles along the tube centreline at different times are shown in Figure 18. For t ≥ 0.149 s, pressure accumulates in the region between Obstruction 2 and Obstruction 3. For t ≥ 0.198 s, the pressure in the entire tube is high, particularly in the region before Obstruction 3 due to the choked flow and the continuous combustion of methane. When the tube is completely blocked by Obstruction 3, the flame has not reached the tube end even at t = 0.222 s, indicating the flame propagation has been largely suppressed, as discussed further on. Noticeably, the temperature inside the tube is higher than those in the other scenarios where the tube is empty (Figure 6a) or partially blocked by the obstructions (Figure 8 and Figure 15) as the space is confined leading to less heat loss. Despite the tube being completely blocked by Obstruction 3, there is still gas flow throughout the tube, indicated by the velocity peaks that shift from left to right with time. This is due to reflections of pressure waves which act as the driving force for the gas flow, though in a confined space. It is also noticeable that the flow inside the tube is rather chaotic with discontinuous regions of high-speed gas flows after the tube is fully blocked (after t > 0.1 s); the majority of the velocity magnitudes sit under 200 m/s.

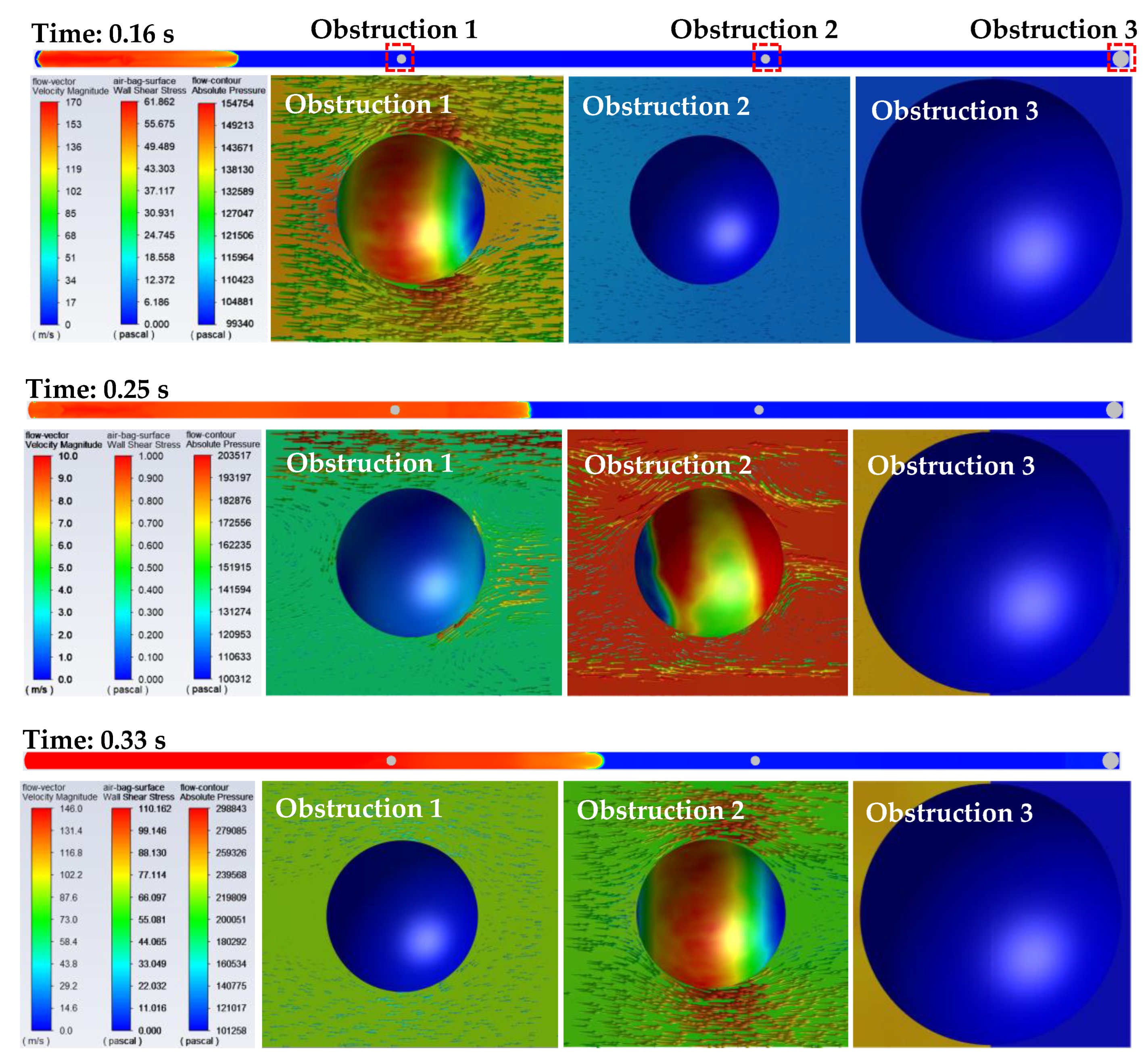
Figure 19 shows the flow field characterised by flow vector (3D arrows) and the contour of pressure and wall shear stress on the surface of obstructions around the obstructions when the flame is propagating through the tube. The wall shear stress expresses the force per unit area exerted by the fluid on the wall in a direction on the local tangent plane, calculated by

$${\tau }_w=\mu ·{\dot{\gamma }}_w$$

(13)

where $\mu$ is the dynamic viscosity (Pa · s) of the fluid and ${\dot{\gamma }}_w$ is the wall shear rate (s⁻¹).

For this scenario, Obstruction 3 is fully inflated at t = 0.1 s. At t = 0.16 s, the strong air flow and pressure waves still do not yet reach Obstruction 3. Rapid expansion caused by the heat generated from methane combustion forces the air to flow towards the obstructions. It can be seen that strong air flow reaches Obstruction 1, but has not reached Obstruction 2 and Obstruction 3. Wall shear stress up to 62 Pa is observed on the surface of Obstruction 1. The velocity magnitude through the gap between Obstruction 1 and tube wall reaches 170 m/s and the pressure right in front of Obstruction 1 reaches 1.55 atm. At t = 0.25 s, the strong air flow and pressure waves have reached Obstruction 3 and due to the blockage, air flow and the propagation of pressure waves switch directions, i.e., from towards the tube open end to towards the tube closed end. The back flow meets the original air flow and weakens its momentum, and accordingly, the maximum velocity magnitude drops to approximately 10 m/s. The weakened air flow accordingly generates a low shear stress on the surface of the obstructions with the maximum wall shear stress being approximately 1 Pa. However, the pressure increases rapidly (to approximately 2 atm) due to the blockage. As the combustion of methane is still going on, more heat energy is liberated, and the air flow becomes chaotic and strong as a result of the conversion from heat energy to kinetic energy. At t = 0.33 s, the air flow velocity increases to 146 m/s, and accordingly, the local maximum wall shear stress increases up to 110 Pa.

At the early stage before the strong air flow and pressure wave reach Obstruction 3, the high wall shear stress is constantly imposed on the surface region of obstruction close to the tube wall. After the air flow and pressure waves reach Obstruction 3 and change the propagation direction, high wall shear stress is imposed almost everywhere on the obstruction surface. The strong air flow reduces its speed when approaching Obstruction 3, leading to a near zero flow velocity on the obstruction surface (non-slip boundary conditions). As a result, the wall shear stress on the surface of Obstruction 3 is extremely low. However, the pressure adjacent to the surface of Obstruction 3 is high. Therefore, obstructions installed closer to the ignition point suffer more tearing forces; this requires more attention.

4. Conclusions

CFD modelling was conducted to examine the propagation dynamics of flame and pressure waves through a tube (30 m long) in which one or more spherical obstructions were present. Different numbers of obstructions were installed at different locations with different inflation degrees. Local and transient data were analysed and discussed. The main findings of the study are listed below.

1. The presence of a half-inflated obstruction led to the local low pressure, which in turn, generated a large pressure difference (compared to the high upstream pressure). This large pressure difference acted as the driving force that accelerated the flow of gases upstream. However, the presence of obstruction also hindered the flame propagation due to the blockage of the pathway (a high pressure at the stagnation point in front of the obstruction).

2. Before reaching the single obstruction, the flame propagated faster when the obstruction was installed at a location further away from the ignition point.

3. When the obstruction was fully inflated, the flame front upstream initially propagated backwards. However, the combustion of methane continued, which drove the flame to propagate towards the tube end again, but at a much slower speed.

4. The temperature inside a blocked tube was much higher than those in scenarios where the tube was empty or partially blocked. In addition, the flow inside the tube was rather chaotic with discontinuous regions of high-speed gases after the tube was fully blocked.

5. At the instant just prior to the obstruction’s complete inflation at x = 10 m, the local pressure at the location of the obstruction reached approximately 7.5 bar.

6. Obstructions installed closer to the ignition point experienced more tearing forces.