Cyclic Trends of Wildfires over Sub-Saharan Africa
Abstract
1. Introduction
2. Materials and Methods
2.1. Proportion of Burnt Area
2.2. Regression and Spectral Analysis
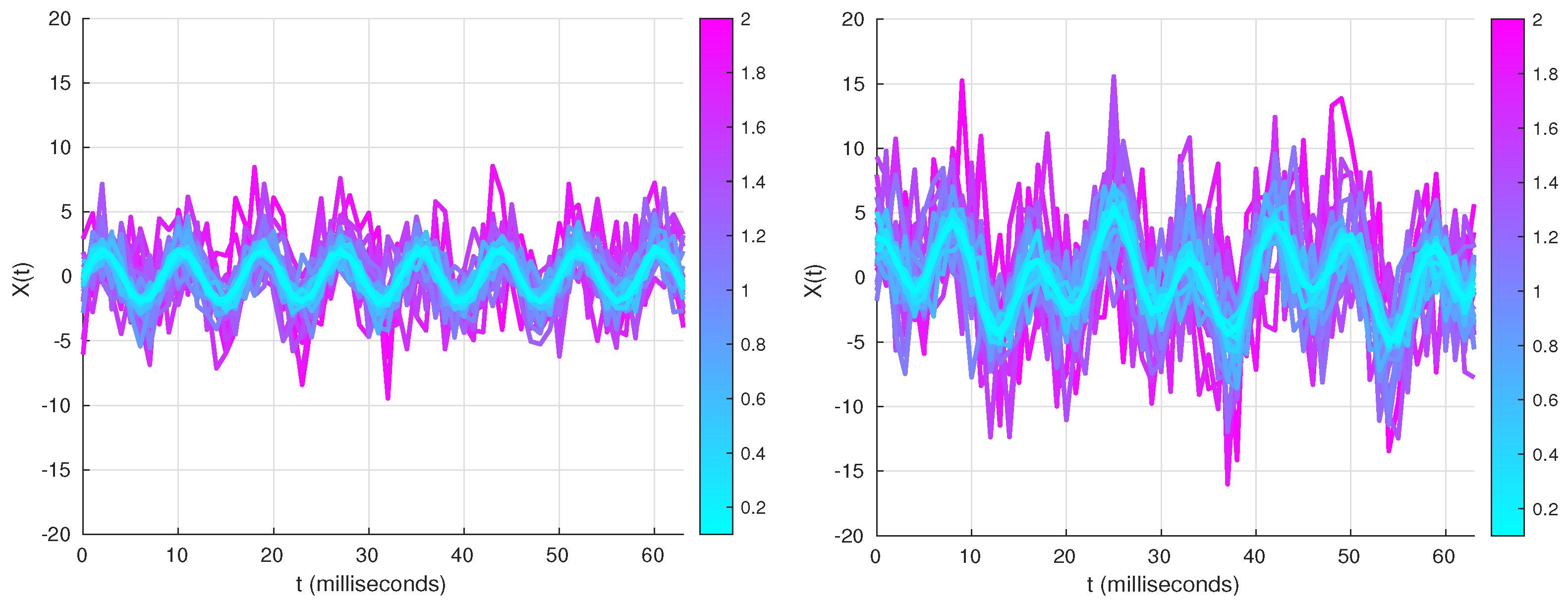
2.3. Simulation Example
3. Numerical Results
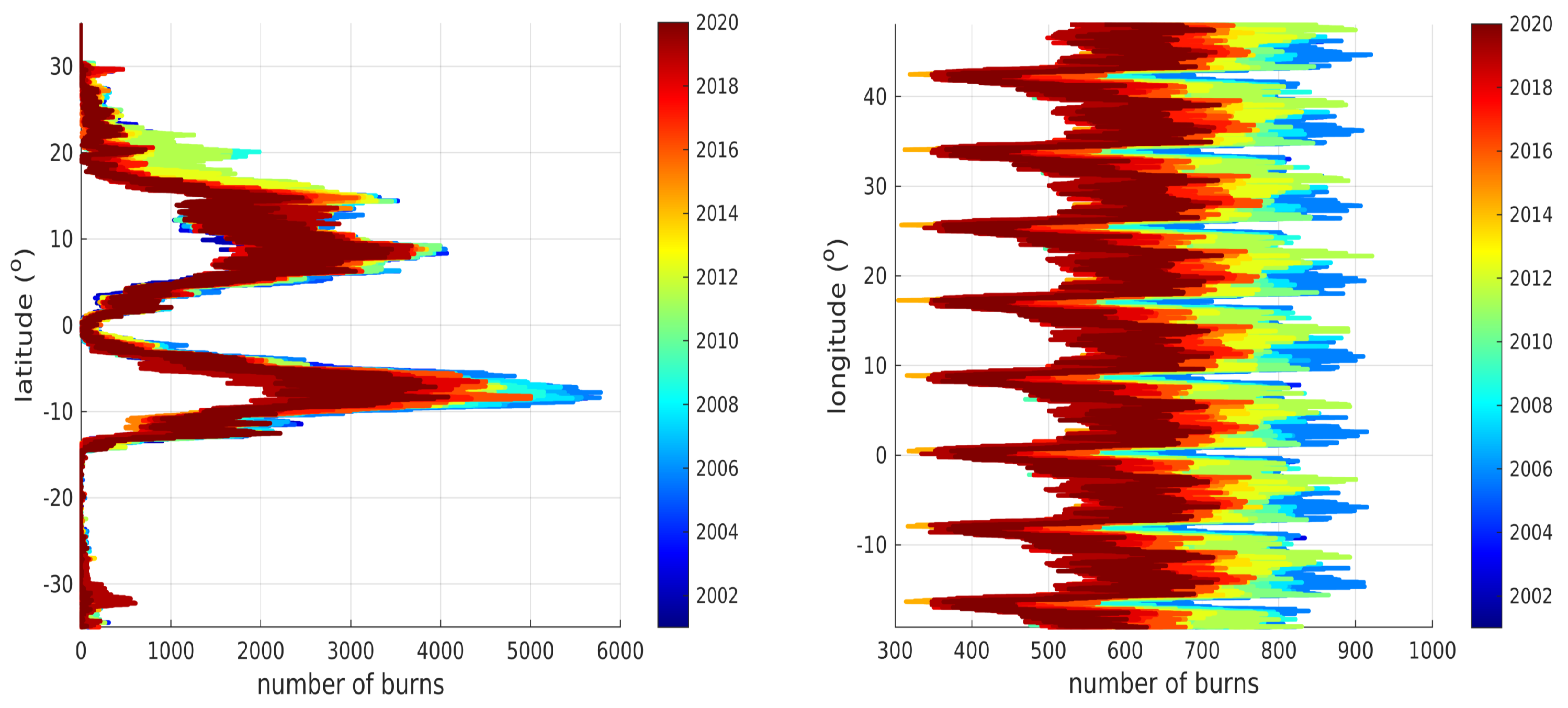
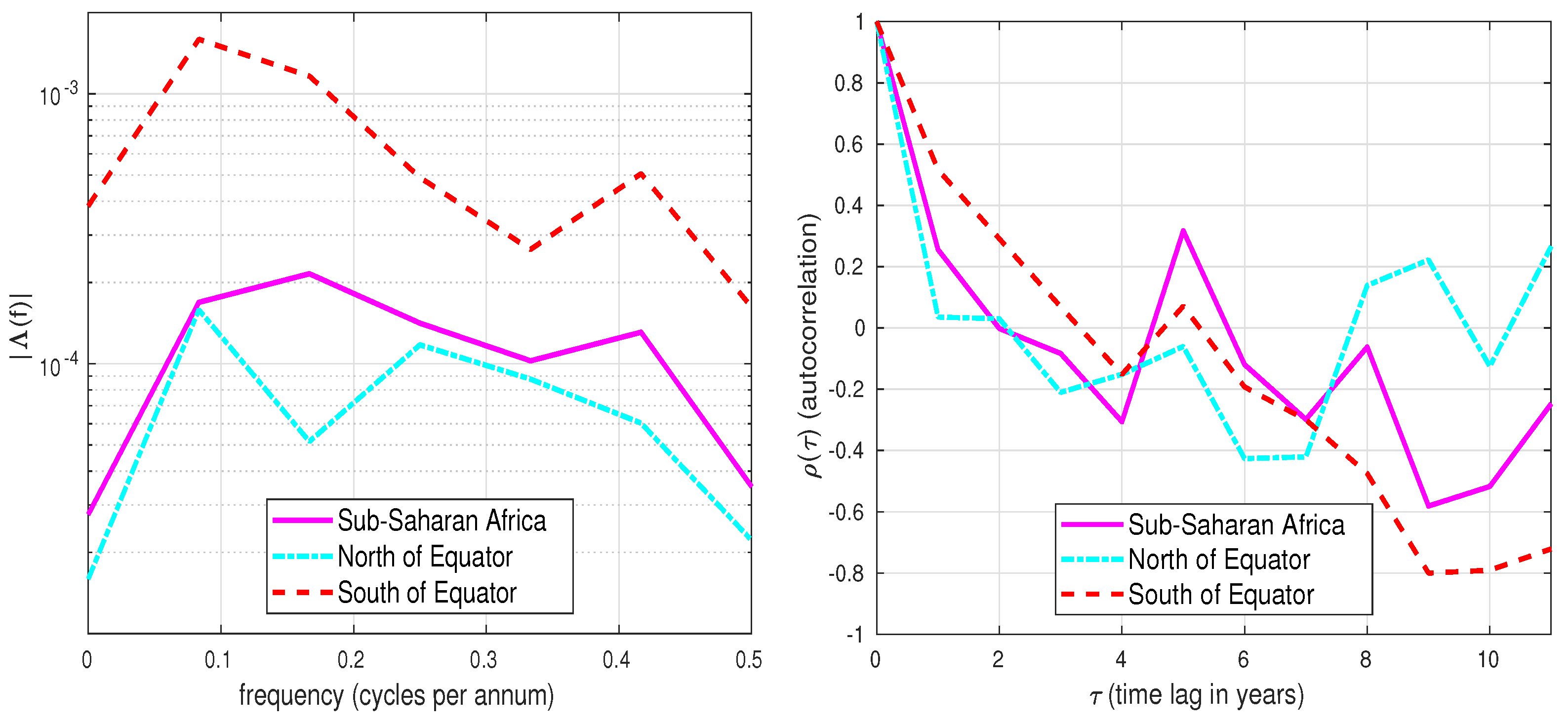
3.1. Sub-Saharan Africa: All Vegetation
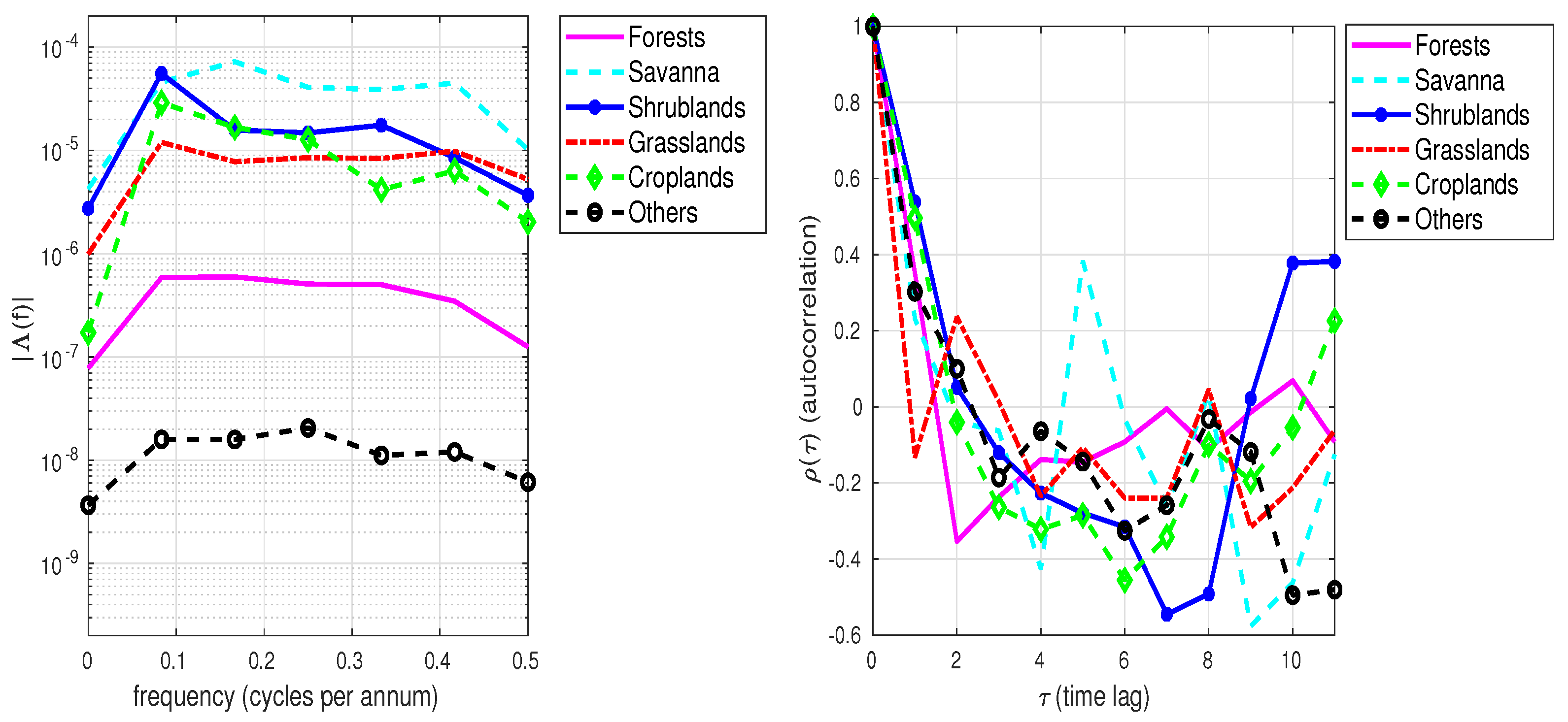
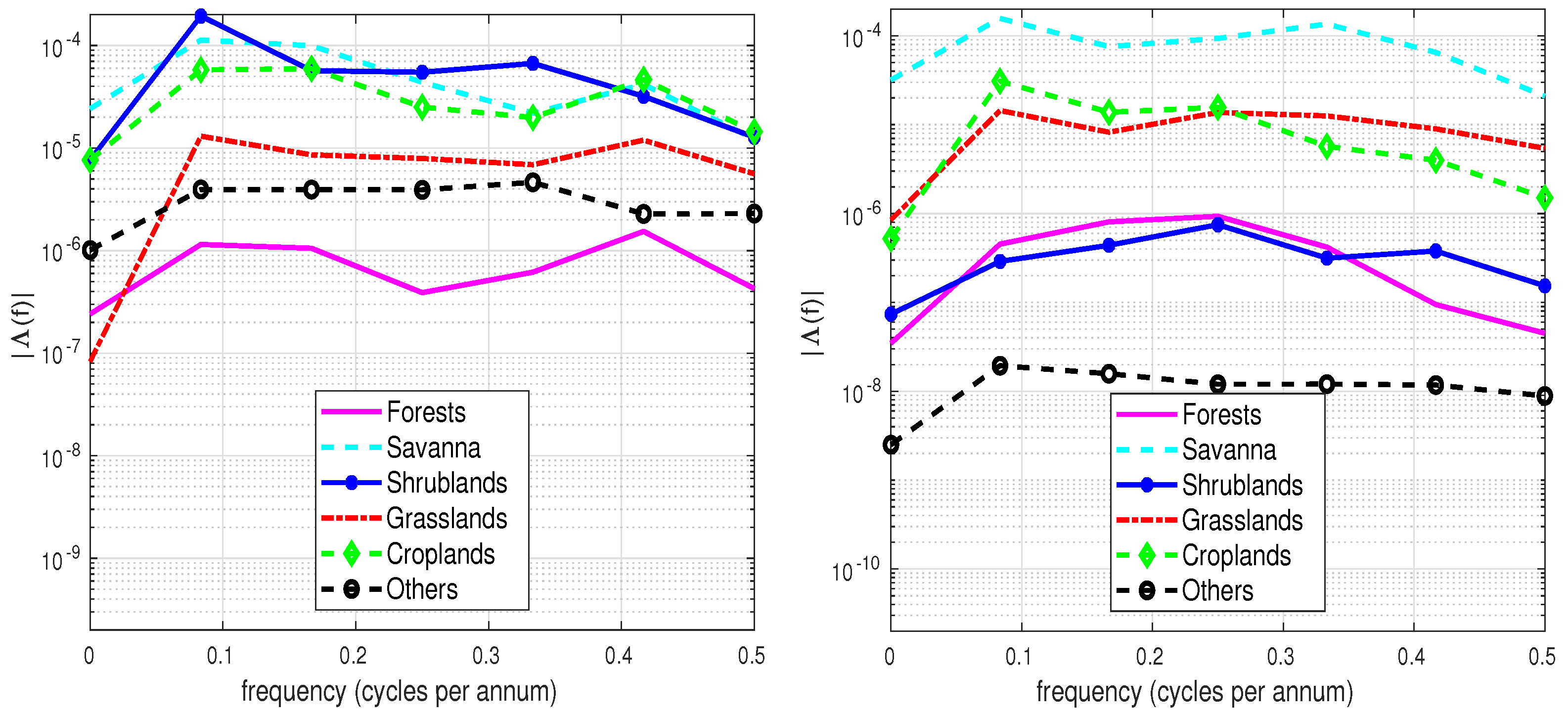
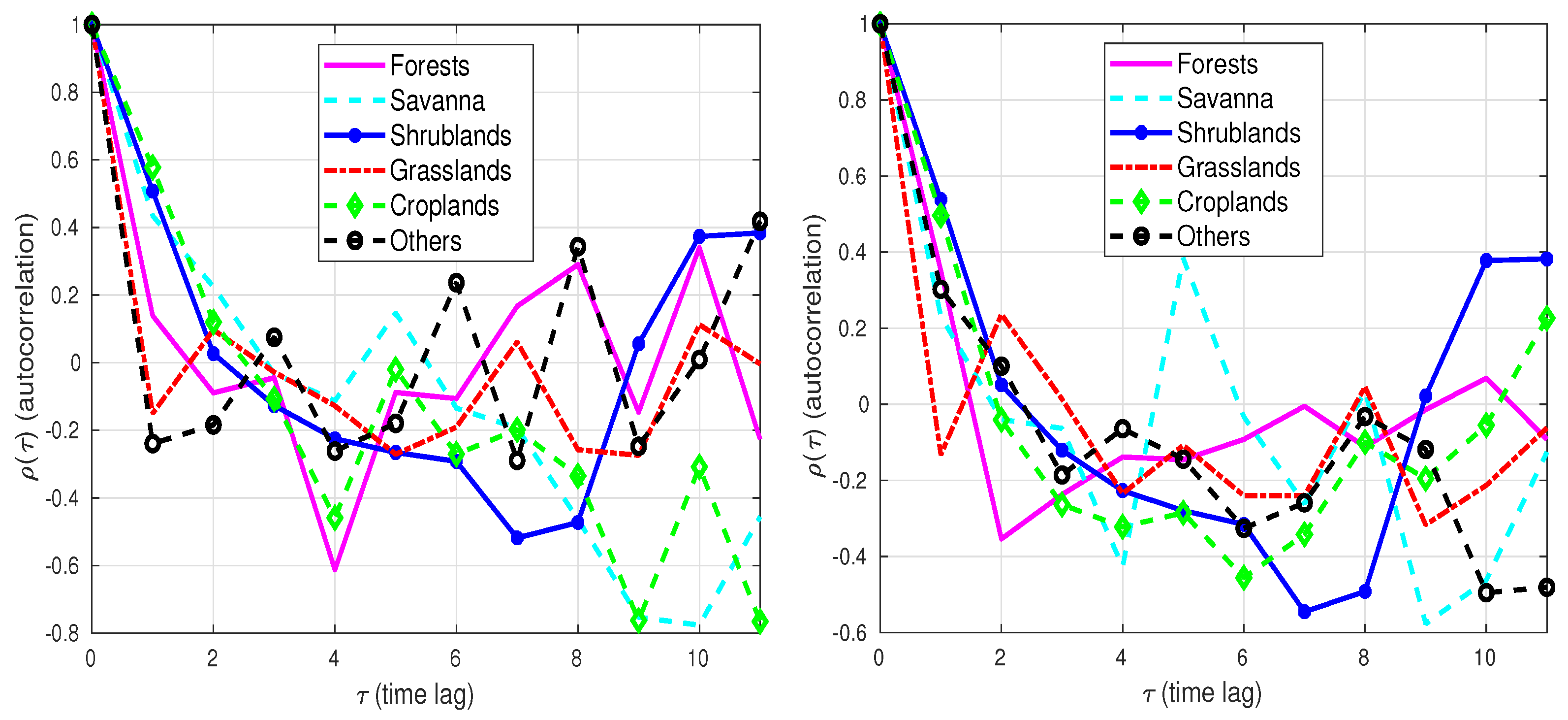
3.2. All Sub-Saharan Africa: Vegetation-Specific
3.3. Northern Sub-Saharan Africa: Vegetation-Specific
3.4. Southern Hemisphere Africa: Vegetation-Specific
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Glasspool, I.; Edwards, D.; Axe, L. Charcoal in the Silurian as evidence for the earliest wildfire. Geology 2004, 32, 381–383. [Google Scholar] [CrossRef]
- Hao, W.; Liu, M.H. Spatial and temporal distribution of tropical biomass burning. Glob. Biogeochem. Cycles 1994, 8, 495–503. [Google Scholar] [CrossRef]
- Tansey, K.; Grégoire, J.M.; Binaghi, E.; Boschetti, L.; Ershov, D.; Flasse, S.; Fraser, R.; Graetz, D.; Maggi, M.; Peduzzi, P.; et al. A Global Inventory of Burned Areas at 1 Km Resolution for the Year 2000 Derived from Spot Vegetation Data. Clim. Chang. 2004, 67, 345–377. [Google Scholar] [CrossRef]
- Lipsett-Moore, G.J.; Wolff, N.H.; Game, E.T. Emissions mitigation opportunities for savanna countries from early dry season fire management. Nat. Commun. 2018, 9, 2247. [Google Scholar] [CrossRef] [PubMed]
- Grunow, J.O.; Groenveld, H.T.; Du Troit, S.H.C. Above-Ground Dry Matter Dynamics of the Grass Layer of a South African Tree Savanna. J. Ecol. 1980, 68, 877–889. [Google Scholar] [CrossRef]
- Ramankutty, N.; Foley, J.A. Estimating Historical Changes in Global Land Cover: Croplands from 1700 to 1992. Glob. Biogeochem. Cycles 1999, 13, 997–1027. [Google Scholar] [CrossRef]
- Smit, G. An approach to tree thinning to structure southern African savannas for long-term restoration from bush encroachment. J. Environ. Manag. 2004, 71, 179–191. [Google Scholar] [CrossRef]
- Kgope, B.S.; Bond, W.J.; Mingley, G.F. Growth Responses of African Savanna Trees Implicate Atmospheric [CO2] as a Driver of Past and Current Changes in Savanna Tree Cover. Austral Ecol. 2010, 35, 451–463. [Google Scholar] [CrossRef]
- Shackleton, C.M.; Scholes, R.J. Above Ground Woody Community Attributes, Biomass and Carbon Stocks along a Rainfall Gradient in the Savannas of the Central Lowveld, South Africa. S. Afr. J. Bot. 2011, 77, 184–192. [Google Scholar] [CrossRef]
- Fuller, G.D. The Geobotany and Soils of Africa. Ecology 1924, 5, 205–207. [Google Scholar] [CrossRef]
- Scholes, R.J.; Archer, S.R. Tree-Grass interactions in savannas. Annu. Rev. Ecol. Syst. 1997, 28, 517–544. [Google Scholar] [CrossRef]
- Grace, J.; Jose, J.S.; Meir, P.; Miranda, H.S.; Montes, R.A. Productivity and carbon fluxes of tropical savannas. J. Biogeogr. 2006, 33, 387–400. [Google Scholar] [CrossRef]
- Ingvar, B. Distribution and Vegetation Dynamics of Humid Savannas in Africa and Asia. J. Veg. Sci. 1992, 3, 345–356. [Google Scholar]
- Chen, X.; Hutley, L.B.; Eamus, D. Carbon Balance of a Tropical Savanna of Northern Australia. Oecologia 2003, 137, 405–416. [Google Scholar] [CrossRef] [PubMed]
- Blydenstein, J. Tropical Savanna Vegetation of Llanos of Colombia. Ecology 1967, 48, 1–15. [Google Scholar] [CrossRef]
- Goodland, R.; Pollard, R. The Brazilian Cerrado Vegetation: A Fertility Gradient. J. Ecol. 1973, 61, 219–224. [Google Scholar] [CrossRef]
- Medina, E.; Silva, J.F. Savannas of Northern South America: A Steady State Regulated by Water-Fire Interactions on a Background of Low Nutrient Availability. J. Biogeogr. 1990, 17, 403–413. [Google Scholar] [CrossRef]
- Romero-Ruiz, M.; Etter, A.; Sarmiento, A.; Tansey, K. Spatial and temporal variability of fires in relation to ecosystems, land tenure and rainfall in savannas of northern South America. Glob. Chang. Biol. 2010, 16, 2013–2023. [Google Scholar] [CrossRef]
- Hartmann, D.; Klein Tank, A.M.G.; Rusticucci, M.; Alexander, L.V.; Bronnimann, S.; Charabi, Y.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and Surface. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Knapp, A.; Beier, C.; Briske, D.; Classen, A.; Luo, Y.; Reichstein, M.; Smith, M.; Smith, S.; Bell, J.; Fay, P.; et al. Consequences of More Extreme Precipitation Regimes for Terrestrial Ecosystems. BioScience 2008, 58, 811–821. [Google Scholar] [CrossRef]
- Shongwe, M.; van Oldenborgh, G.; van den Hurk, B.; de Boer, B.; Coelho, C.; van Aalst, M. Projected Changes in Mean and Extreme Precipitation in Africa under Global Warming. Part I: Southern Africa. J. Clim. 2009, 22, 3819–3837. [Google Scholar] [CrossRef]
- Cao, M.; Zang, Q.; Shuggart, H.H. Dynamic Response of African ecosystem carbon cycling to climate change. Clim. Res. 2001, 17, 183–193. [Google Scholar] [CrossRef]
- Dintwe, K.; Okin, G.S.; D’Odorico, P.; Hrast, T.; Mladenov, N.; Handorean, A.; Battachan, A.; Caylor, K.K. Soil organic C and total N pools in the Kalahari: Potential impacts on C sequenstration in Savanna. Plant Soil 2014, 396, 27–44. [Google Scholar] [CrossRef]
- Hoffmann, W.; Schroeder, W.; Jackson, R. Positive feedbacks of fire, climate, and vegetation and the conversion of tropical savanna. Geophys. Res. Lett. 2002, 29, 9/1–9/4. [Google Scholar] [CrossRef]
- Liu, Y.; Stanturf, J.; Goodrick, S. Trends in global wildfire potential in a changing climate. For. Ecol. Manag. 2010, 259. [Google Scholar] [CrossRef]
- Shongwe, M.; van Oldenborgh, G.; van den Hurk, B.; van Aalst, M. Projected Changes in Mean and Extreme Precipitation in Africa under Global Warming. Part II: East Africa. J. Clim. 2011, 24, 3718–3733. [Google Scholar] [CrossRef]
- Biasutti, M. Rainfall trends in the African Sahel: Characteristics, processes and causes. WIREs Clim. Chang. 2019, 10, e591. [Google Scholar] [CrossRef]
- Tyson, P.D.; Crimp, S.J. The Climate of the Kalahari Transect. Trans. R. Soc. S. Afr. 1998, 53, 93–112. [Google Scholar] [CrossRef]
- Caylor, K.K.; Shugart, H.H.; Dowty, P.R.; Smith, T.M. Tree Spacing along the Kalahari Transect in Southern Africa. J. Arid Environ. 2003, 54, 281–296. [Google Scholar] [CrossRef]
- Cahoon, D.R.J.; Stocks, B.J.; Levine, J.S.; Cofer, W.R., III; O’Neill, K.P. Seasonal Distribution of African Savanna Fires. Nature 1992, 359, 812–815. [Google Scholar] [CrossRef]
- Cooke, W.F.; Koffi, B.; Gregoire, J.M. Seasonality of vegetation fires in Africa from remote sensing data and application to a global chemistry model. J. Geophys. Res. Atmos. 1992, 101, 21051–21065. [Google Scholar] [CrossRef]
- D’Odorico, P.; Caylof, K.; Okin, G.S.; Scanlon, T.M. On soil moisture-vegetation feedbacks and their possible effects on the dynamics of dryland ecosystems. J. Geophys. Res. Biogeosci. 2004, 112, G04010. [Google Scholar] [CrossRef]
- Flanagan, L.B.; Wever, L.A.; Carlson, P.J. Seasonal and interannual variation in carbon dioxide exchange and carbon balance in a northern temperate grassland. Glob. Chang. Biol. 2002, 8, 599–615. [Google Scholar] [CrossRef]
- Scholes, R.J. Greenhouse gas emissions from vegetation fires in southern Africa: Environ. Monit. Assess. 1995, 38/2–3 (169–179). Summ. in Engl. Environ. Pollut. 1996, 94, 169–179. [Google Scholar] [CrossRef]
- van der Werf, G.; Randerson, J.; Giglio, L.; Collatz, G.; Kasibhatla, P.; Arellano, A., Jr. Interannual variability in global biomass burning emissions from 1997 to 2004. Atmos. Chem. Phys. 2006, 6, 3423–3441. [Google Scholar] [CrossRef]
- Archer, S.; Boutton, T.W.; Hibbard, K.A. Trees in Grasslands: Biogeochemical Consequences of Woody Plant Expansion. In Global Biogeochemical Cycles in the Climate System; Schulze, E.D., Heimann, M., Harrison, S., Holland, E., Loyd, J., Prentice, I.C., Schimel, D., Eds.; Academic Press: San Diego, CA, USA, 2001; pp. 115–137. [Google Scholar]
- Dintwe, K.; Okin, G.S.; Hue, Y. Fire-induced albedo change and surface radiative forcing in sub-Saharan Africa savanna ecosystems: Implications for the energy balance. J. Geophys. Res. Atmos. 2017, 122, 6186–6201. [Google Scholar] [CrossRef]
- Roy, D.P.; Boschetti, L.; Justice, C.O.; Ju, J. The collection 5 MODIS burned area product—Global evaluation by comparison with the MODIS active fire product. Remote Sens. Eviron. 2008, 112, 3690–3707. [Google Scholar] [CrossRef]
- Nelder, J.; Wedderburn, R. Generalised Linear Models. J. R. Stat. Soc. Ser. A 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Barth, J.R.; Bennett, J.T. Cyclic behavior, seasonality and trends in economic time series. Neb. J. Econ. Bus. 1974, 13, 48–69. [Google Scholar]
- Roger, J.H. A significance test for cyclic trends in incidence data. Biometrika 1977, 64, 152–155. [Google Scholar] [CrossRef]
- Son, R.; Wang, S.-Y.S.; Kim, S.H.; Kim, H.; Jeong, J.H. Recurrent pattern of extreme fire weather in California. Environ. Res. Lett. 2021, 16, 094031. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing: Principles, Algorithms and Applications, 3rd ed.; Prentice-Hall International: Hoboken, NJ, USA, 1996. [Google Scholar]
- Dirac, P. Principles of Quantum Mechanics, 1st ed.; Oxford University Press: Oxford, UK, 1930. [Google Scholar]
- Podschwit, H.; Guttorp, P.; Larkin, H.; Steel, E.A. Estimating wildfire growth from noisy and incomplete incident data using a state space model. Environ. Ecol. Stat. 2018, 25, 325–340. [Google Scholar] [CrossRef]
- Thayjes, S. Wildfire Spread Prediction and Assimilation for FARSITE Using Ensemble Kalman Filtering. Ph.D. Thesis, University of California, San Diego, CA, USA, 2016. [Google Scholar]
- Andela, N.; Morton, D.C.; Giglio, L.; Chen, Y.; van der Werf, G.R.; Kasibhatla, P.S.; Defrie, R.S.; Collatz, G.J.; Hantso, S.; Kloster, S.; et al. A human-driven decline in global burned area. Science 2017, 356, 1356–1362. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Zhou, L.; Raghavenda, A. Observed changes in patterns and possible drivers over Central Africa. Environ. Res. Lett. 2020, 15, 0940b8. [Google Scholar] [CrossRef]
- Farkondehmaal, F.; Ghaffarzadegan, N. A cyclical wildfire pattern as the outcome of a coupled human natural system. Sci. Rep. 2022, 12, 5280. [Google Scholar] [CrossRef]
- Yocom, L.L.; Fule, P.Z.; Brown, P.M.; Cerano, J.; Villanueza-Diaz, J.; Falk, D.A.; Cornejo-Oviedo, E. El Nino-southern oscillation effect on fire regime in northeastern Mexico has changed over time. Ecology 2010, 91, 1660–1671. [Google Scholar] [CrossRef] [PubMed]
- Van Wilgen, B.W.; Govender, N.; Biggs, H.C.; Ntsala, D.; Funda, X.N. Response of savanna fire regimes to changing fire-management policies in a large African national park. Conserv. Biol. 2004, 18, 1533–1540. [Google Scholar] [CrossRef]
- Le, T.; Kim, S.H.; Bae, D.H. Decreasing causal impacts of El Nino Southern Oscillation on future fire activities. Sci. Total Environ. 2022, 826, 154031. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machete, R.L.; Dintwe, K. Cyclic Trends of Wildfires over Sub-Saharan Africa. Fire 2023, 6, 71. https://doi.org/10.3390/fire6020071
Machete RL, Dintwe K. Cyclic Trends of Wildfires over Sub-Saharan Africa. Fire. 2023; 6(2):71. https://doi.org/10.3390/fire6020071
Chicago/Turabian StyleMachete, Reason L., and Kebonyethata Dintwe. 2023. "Cyclic Trends of Wildfires over Sub-Saharan Africa" Fire 6, no. 2: 71. https://doi.org/10.3390/fire6020071
APA StyleMachete, R. L., & Dintwe, K. (2023). Cyclic Trends of Wildfires over Sub-Saharan Africa. Fire, 6(2), 71. https://doi.org/10.3390/fire6020071






