Experimental and Numerical Study of the Trench Fire Spread Rule over a Sloped Uniform Fuel Bed: Rate of Fire Spread, Flame Morphology, and Heat Flux
Abstract
:1. Introduction
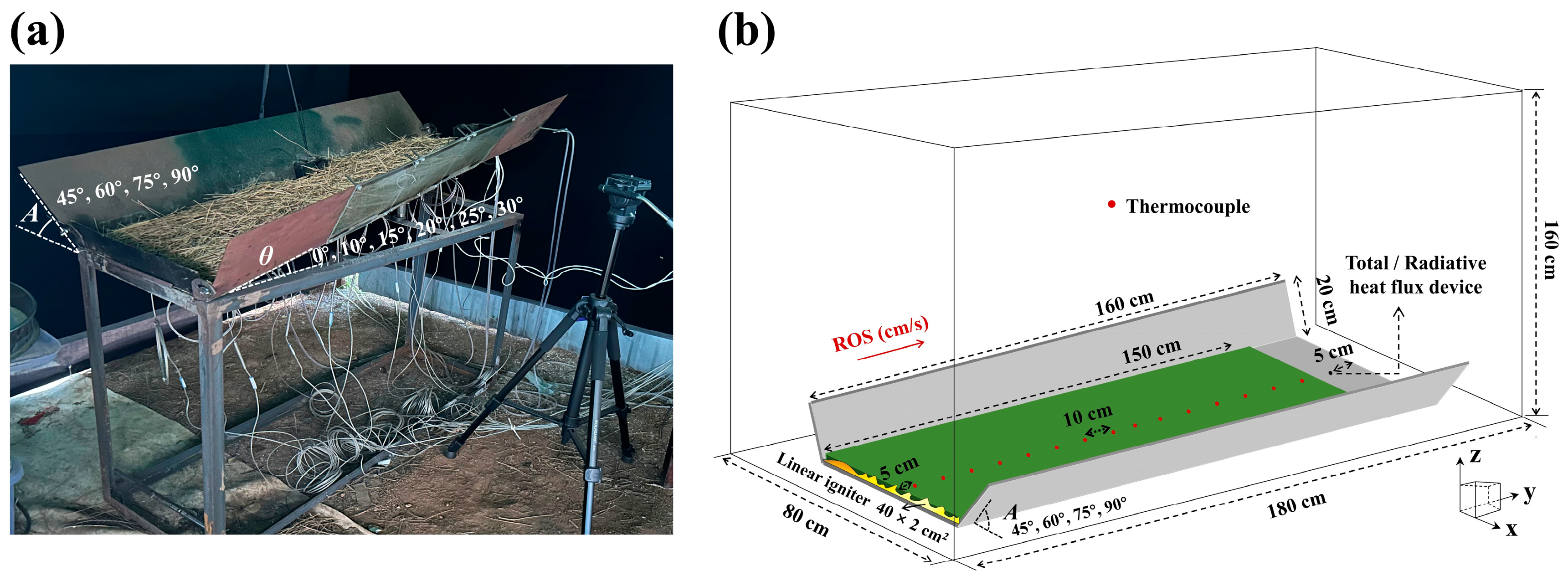
2. Experimental Methodology
3. Numerical Simulation
3.1. Lagrangian Particle Model and Boundary Fuel Model
3.2. Thermal Degradation Model for Vegetation
3.3. Numerical Set Up
4. Results and Discussion
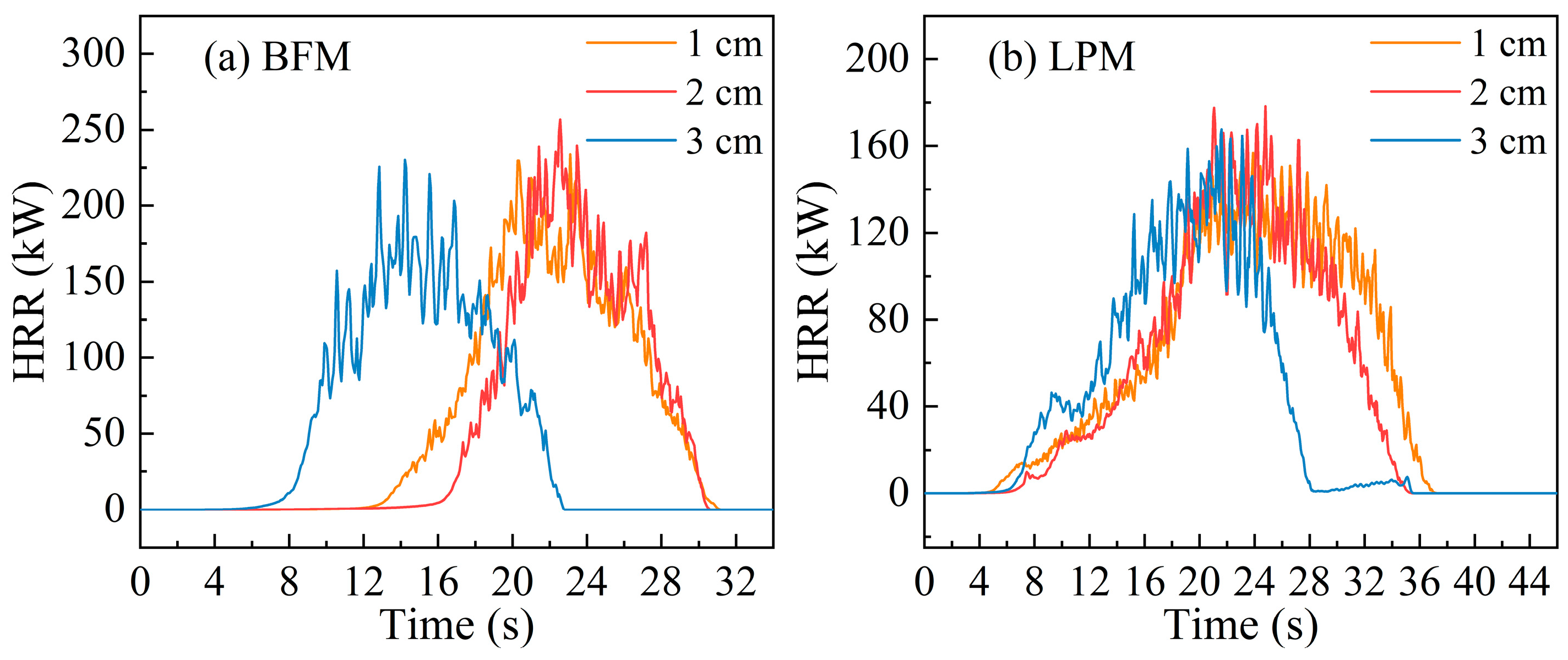
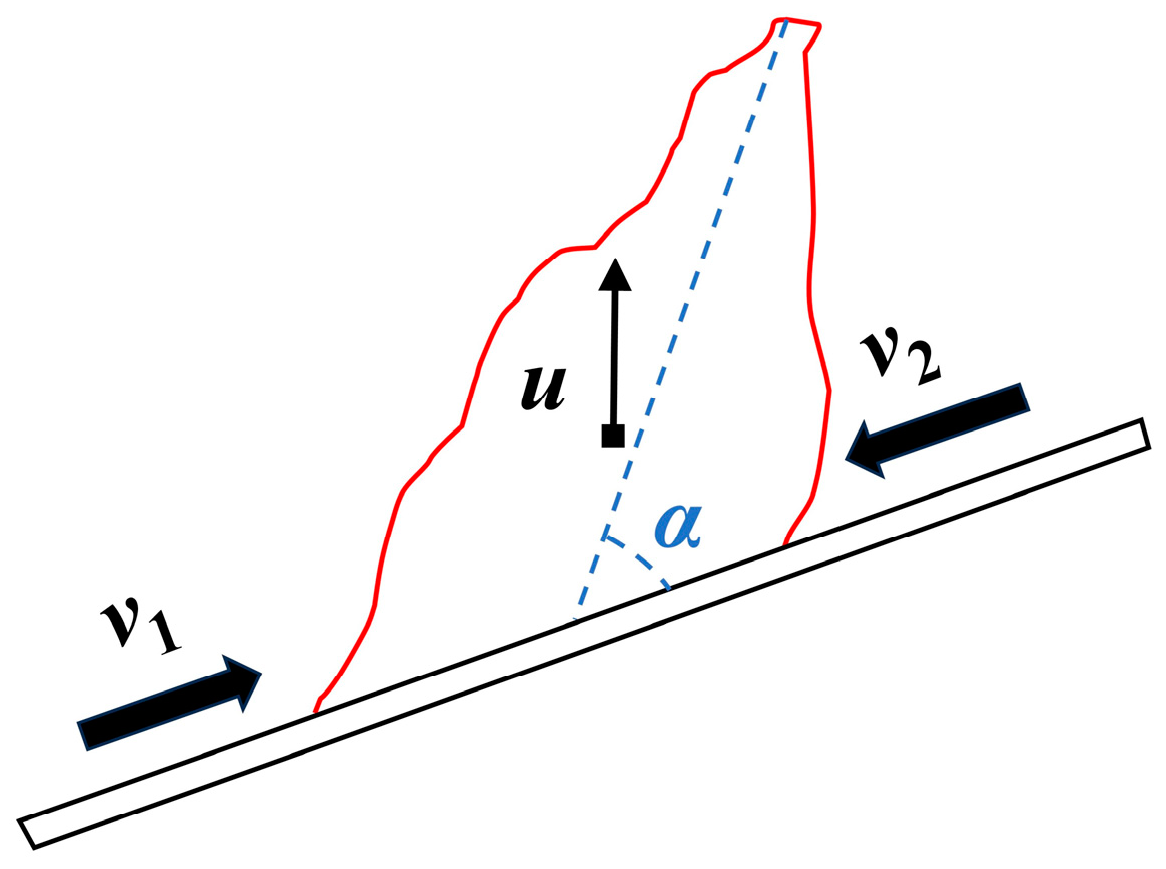
4.1. Rate of Fire Spread
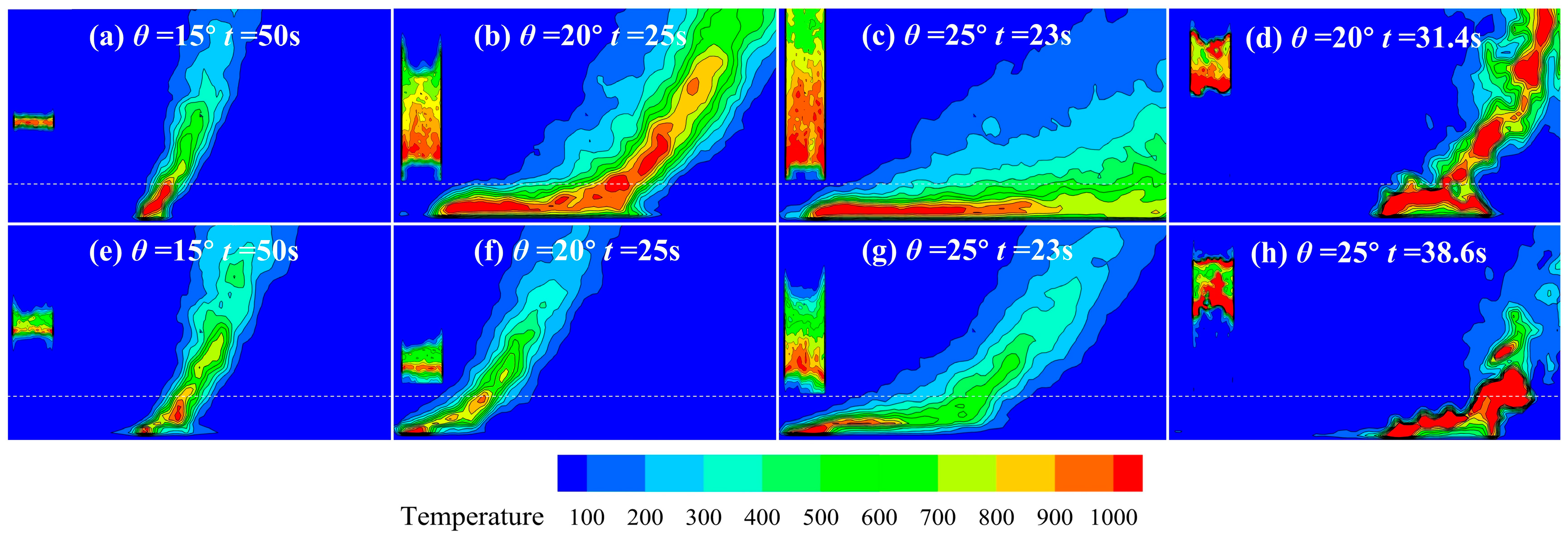
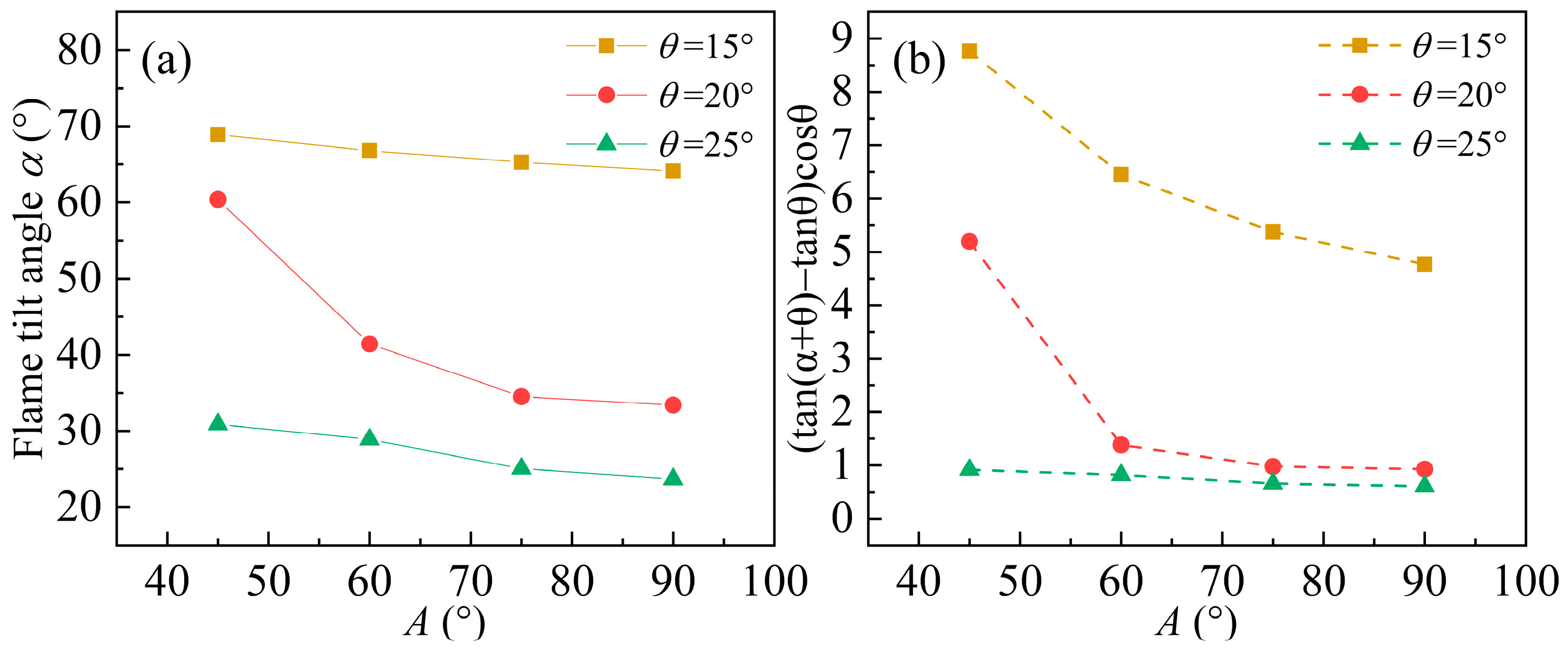
4.2. Flame Morphology Characteristics
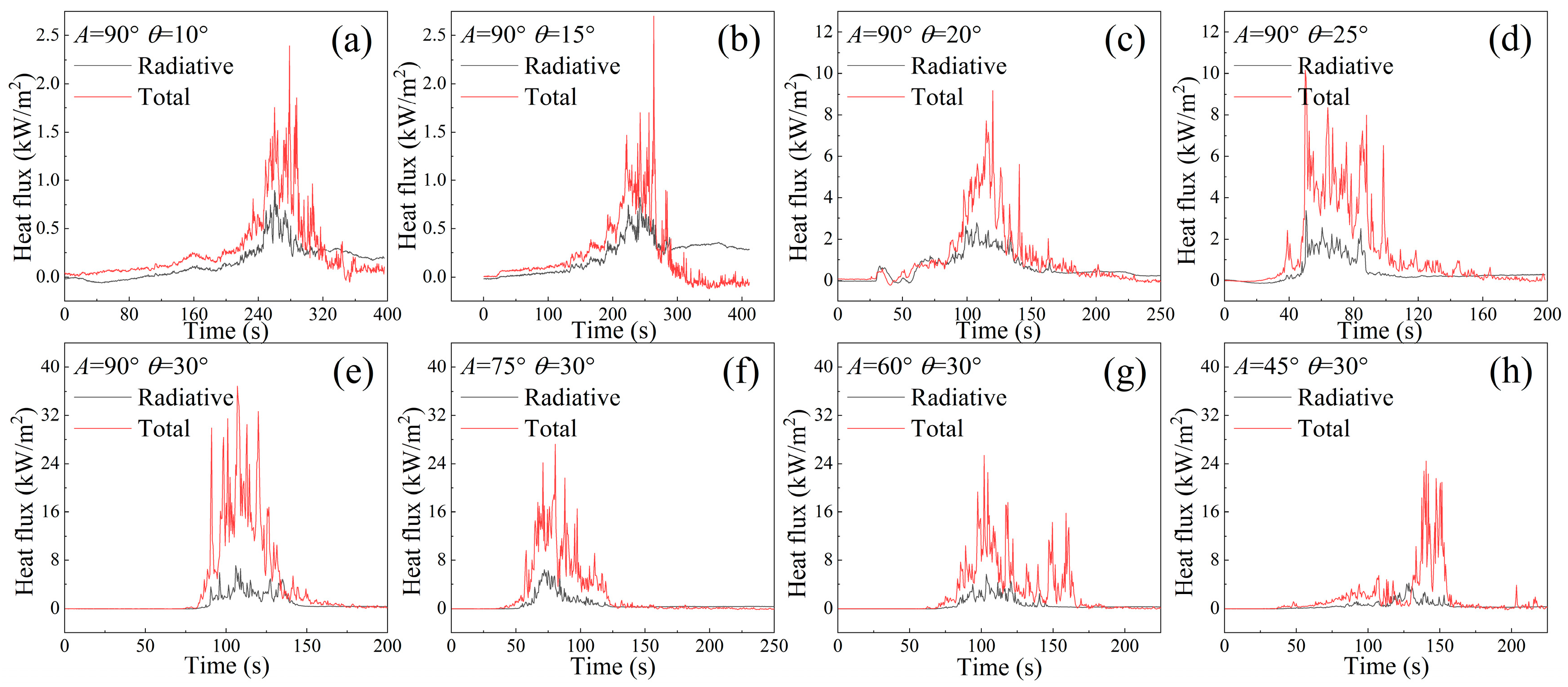
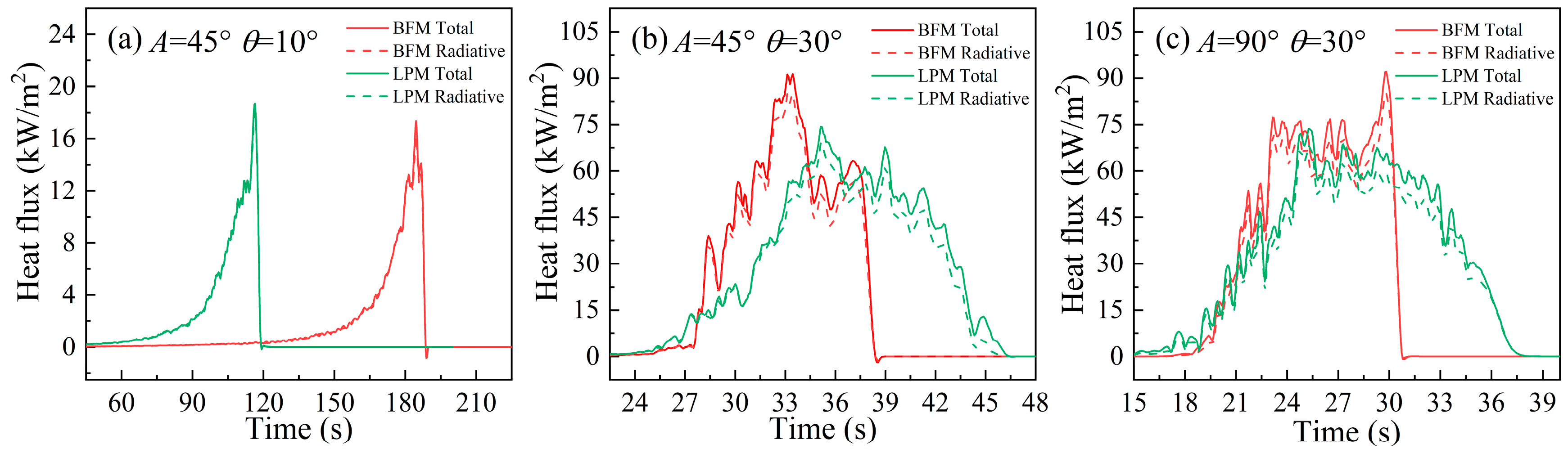
4.3. Fuel Preheating Mechanism
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, N.; Lei, J.; Gao, W.; Chen, H.; Xie, X. Combustion Dynamics of Large-Scale Wildfires. Proc. Combust. Inst. 2021, 38, 157–198. [Google Scholar] [CrossRef]
- Bufacchi, P.; Krieger, G.C.; Mell, W.; Alvarado, E.; Santos, J.C.; Carvalho, J.A. Numerical Simulation of Surface Forest Fire in Brazilian Amazon. Fire Saf. J. 2016, 79, 44–56. [Google Scholar] [CrossRef]
- Frangieh, N.; Accary, G.; Rossi, J.-L.; Morvan, D.; Meradji, S.; Marcelli, T.; Chatelon, F.-J. Fuelbreak Effectiveness against Wind-Driven and Plume-Dominated Fires: A 3D Numerical Study. Fire Saf. J. 2021, 124, 103383. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland Surface Fire Spread Modelling, 1990–2007. 1: Physical and Quasi-Physical Models. Int. J. Wildland Fire 2009, 18, 349. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland Surface Fire Spread Modelling, 1990–2007. 2: Empirical and Quasi-Empirical Models. Int. J. Wildland Fire 2009, 18, 369. [Google Scholar] [CrossRef]
- Li, H.; Liu, N.; Xie, X.; Zhang, L.; Yuan, X.; He, Q.; Viegas, D.X. Effect of Fuel Bed Width on Upslope Fire Spread: An Experimental Study. Fire Technol. 2021, 57, 1063–1076. [Google Scholar] [CrossRef]
- Xie, X.; Liu, N.; Lei, J.; Shan, Y.; Zhang, L.; Chen, H.; Yuan, X.; Li, H. Upslope Fire Spread over a Pine Needle Fuel Bed in a Trench Associated with Eruptive Fire. Proc. Combust. Inst. 2017, 36, 3037–3044. [Google Scholar] [CrossRef]
- Sánchez-Monroy, X.; Mell, W.; Torres-Arenas, J.; Butler, B.W. Fire Spread Upslope: Numerical Simulation of Laboratory Experiments. Fire Saf. J. 2019, 108, 102844. [Google Scholar] [CrossRef]
- Viegas, D.X. Parametric Study of an Eruptive Fire Behaviour Model. Int. J. Wildland Fire 2006, 15, 169. [Google Scholar] [CrossRef]
- Viegas, D.X.; Simeoni, A. Eruptive Behaviour of Forest Fires. Fire Technol. 2011, 47, 303–320. [Google Scholar] [CrossRef]
- Viegas, D.X.; Rodrigues, A.; Abouali, A.; Almeida, M.; Raposo, J. Fire Downwind a Flat Surface Entering a Canyon by Lateral Spread. Fire Saf. J. 2021, 122, 103349. [Google Scholar] [CrossRef]
- Dold, J. Flow Attachment in Eruptive Fire Growth. In Proceedings of the VI International Conference on Forest Fire Research, Coimbra, Portugal, 18–19 November 2010. [Google Scholar]
- Dupuy, J.-L.; Marechal, J.; Portier, D.; Valette, J.-C. The Effects of Slope and Fuel Bed Width on Laboratory Fire Behaviour. Int. J. Wildland Fire 2011, 20, 272–288. [Google Scholar] [CrossRef]
- Chen, C.; Nie, Y.; Zhang, Y.; Lei, P.; Jiao, W.; Wang, X. Experimental Study on Flame Spread over Poplar Plywood in Inclined Trench: Phenomenon of Flame Injection. J. Therm. Anal. Calorim. 2021, 146, 253–263. [Google Scholar] [CrossRef]
- Xu, T.; Zhao, D.; Tao, H.; Lei, P. Extended CFD Models for Numerical Simulation of Tunnel Fire under Natural Ventilation: Comparative Analysis and Experimental Verification. Case Stud. Therm. Eng. 2022, 31, 101815. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland Surface Fire Spread Modelling, 1990–2007. 3: Simulation and Mathematical Analogue Models. Int. J. Wildland Fire 2009, 18, 387. [Google Scholar] [CrossRef]
- Woodburn, P.J.; Drysdale, D.D. Fires in Inclined Trenches: The Dependence of the Critical Angle on the Trench and Burner Geometry. Fire Saf. J. 1998, 31, 143–164. [Google Scholar] [CrossRef]
- Mell, W.; Maranghides, A.; McDermott, R.; Manzello, S.L. Numerical Simulation and Experiments of Burning Douglas Fir Trees. Combust. Flame 2009, 156, 2023–2041. [Google Scholar] [CrossRef]
- Mell, W.; Jenkins, M.A.; Gould, J.; Cheney, P. A Physics-Based Approach to Modelling Grassland Fires. Int. J. Wildland Fire 2007, 16, 1–22. [Google Scholar] [CrossRef]
- Innocent, J.; Sutherland, D.; Khan, N.; Moinuddin, K. Physics-Based Simulations of Grassfire Propagation on Sloped Terrain at Field Scale: Motivations, Model Reliability, Rate of Spread and Fire Intensity. Int. J. Wildland Fire 2023, 32, 496–512. [Google Scholar] [CrossRef]
- Innocent, J.; Sutherland, D.; Khan, N.; Moinuddin, K. Physics-Based Simulations of Grassfire Propagation on Sloped Terrain at Field Scale: Flame Dynamics, Mode of Fire Propagation and Heat Fluxes. Int. J. Wildland Fire 2023, 32, 513–530. [Google Scholar] [CrossRef]
- Fiorini, C.; Craveiro, H.D.; Santiago, A.; Laím, L.; Simões Da Silva, L. Parametric Evaluation of Heat Transfer Mechanisms in a WUI Fire Scenario. Int. J. Wildland Fire 2023, 32, 1600–1618. [Google Scholar] [CrossRef]
- Valero, M.M.; Jofre, L.; Torres, R. Multifidelity Prediction in Wildfire Spread Simulation: Modeling, Uncertainty Quantification and Sensitivity Analysis. Environ. Model. Softw. 2021, 141, 105050. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; Floyd, J.; McDermott, R.; Vanella, M.; Mueller, E. Sixth Edition Fire Dynamics Simulator User’s Guide (FDS); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023; Volume 6.
- Meerpoel-Pietri, K.; Tihay-Felicelli, V.; Graziani, A.; Santoni, P.-A.; Morandini, F.; Perez-Ramirez, Y.; Bosseur, F.; Barboni, T.; Sánchez-Monroy, X.; Mell, W. Modeling with WFDS Combustion Dynamics of Ornamental Vegetation Structures at WUI: Focus on the Burning of a Hedge at Laboratory Scale. Combust. Sci. Technol. 2022, 195, 3181–3211. [Google Scholar] [CrossRef]
- Perez-Ramirez, Y.; Mell, W.E.; Santoni, P.A.; Tramoni, J.B.; Bosseur, F. Examination of WFDS in Modeling Spreading Fires in a Furniture Calorimeter. Fire Technol. 2017, 53, 1795–1832. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Radiative fraction | 0.27 [8] | Moisture fraction M | 0.1 |
| Soot yield (kg/kg) | 0.02 [22] | Char fraction | 0.2 [24] |
| Drag coefficient Cd | 2.8 [24] | Density ρ (kg/m3) | 500 [24] |
| Shape factor Cs | 0.25 [24] | Conductivity c (W/(m·K)) | 0.1 [24] |
| Fuel height h (m) | 0.04 | Specific heat (kJ/(kg·K)) | 1.0 [24] |
| Fuel packing ratio β | 0.03 | Reference temperature (°C) | 300 [24] |
| Fuel load ω (kg/m2) | 0.625 | Heat of pyrolysis | 711 [8] |
| Ignition area s (m2) | 0.4 × 0.02 | Fuel gas | C6H10O5 [24] |
| Ignition temperature (°C) | 1000 | Combustion heat of fuel gas Q () | 17,260 [24] |
| Environment temperature Tg (°C) | 20 | Surface area-to-volume ratio σ (m−1) | 2010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Huang, R. Experimental and Numerical Study of the Trench Fire Spread Rule over a Sloped Uniform Fuel Bed: Rate of Fire Spread, Flame Morphology, and Heat Flux. Fire 2023, 6, 469. https://doi.org/10.3390/fire6120469
Wang Y, Huang R. Experimental and Numerical Study of the Trench Fire Spread Rule over a Sloped Uniform Fuel Bed: Rate of Fire Spread, Flame Morphology, and Heat Flux. Fire. 2023; 6(12):469. https://doi.org/10.3390/fire6120469
Chicago/Turabian StyleWang, Yi, and Rui Huang. 2023. "Experimental and Numerical Study of the Trench Fire Spread Rule over a Sloped Uniform Fuel Bed: Rate of Fire Spread, Flame Morphology, and Heat Flux" Fire 6, no. 12: 469. https://doi.org/10.3390/fire6120469
APA StyleWang, Y., & Huang, R. (2023). Experimental and Numerical Study of the Trench Fire Spread Rule over a Sloped Uniform Fuel Bed: Rate of Fire Spread, Flame Morphology, and Heat Flux. Fire, 6(12), 469. https://doi.org/10.3390/fire6120469




