Abstract
The increasing frequency of wildfires has posed significant challenges to communities worldwide. The effectiveness of all aspects of disaster management depends on a credible estimation of the prevailing risk. Risk, the product of a hazard’s likelihood and its potential consequences, encompasses the probability of hazard occurrence, the exposure of assets to these hazards, existing vulnerabilities that amplify the consequences, and the capacity to manage, mitigate, and recover from their consequences. This paper employs the multiple criteria decision-making (MCDM) framework, which produces reliable results and allows for the customization of the relative importance of factors based on expert opinions. Utilizing the AROMAN algorithm, the study ranks counties in the state of Arizona according to their wildfire risk, drawing upon 25 factors categorized into expected annual loss, community resilience, and social vulnerability. A sensitivity analysis demonstrates the stability of the results when model parameters are altered, reinforcing the robustness of this approach in disaster risk assessment. While the paper primarily focuses on enhancing the safety of human communities in the context of wildfires, it highlights the versatility of the methodology, which can be applied to other natural hazards and accommodate more subjective risk and safety assessments.
1. Introduction
The Wildland-Urban Interface (WUI), defined as the transitional zone between unoccupied wildland and human development, emerges as the primary hotspot for escalating wildfire threats. In the year 2022 alone, the United States witnessed nearly 69,000 wildfires, which consumed 7.5 million acres, roughly equivalent to 30,000 square kilometers [1]. A substantial portion of the contiguous United States, ranging from 5.6% to 18.8%, falls under the WUI classification [2], rendering over 46 million homes in approximately 700,000 communities susceptible to wildfire risks [3]. A larger population residing in WUI communities amplifies wildfire risk in two ways: it exposes more people to the potential for wildfires and increases the likelihood of human-caused fires. It is worth noting that in 2022, over 89% of the wildfires in the United States were caused by human activities [1].
Estimating natural hazards risk proves to be an invaluable tool across all phases of disaster management, encompassing policy-making, prevention and mitigation, planning and preparedness, response, and recovery [4]. In essence, risk is defined as the product of the likelihood of hazard occurrence and its potential consequences [5]. However, conducting a comprehensive risk assessment for natural hazards is challenging, as none of the aforementioned risk components are easy to evaluate. Such assessments typically require the thorough integration of various factors and a deep understanding of their intricate relationships.
For example, in the case of wildfires, the likelihood of occurrence depends on several parameters, including but not limited to land cover and land use, vegetation characteristics, weather conditions, precipitation, and topography [6]. Furthermore, modeling wildfire dynamics [7], spread patterns [8], intensity, and flame length [9] introduce a layer of complexity when estimating the exposure of WUI communities to fire. On the other hand, population distribution and demographic profiles [10], infrastructure extent and quality [11], and the extent of existing mitigation projects [12] all play pivotal roles in assessing potential consequences. Therefore, there is no single approach to wildfire risk assessment; it is highly subjective and relies on expert judgment and the perspective of risk evaluators. In the literature, researchers have proposed diverse wildfire risk evaluations by addressing the following questions differently [5]:
What highly valued resources and assets are considered (e.g., people, forests, protected areas, infrastructure, agricultural lands, wildlife ecosystem)? What are risk’s most critical driving factors, and how do their relative importance vary? How should the selected factors be combined to yield a reasonable risk assessment?
As a result, in quantitative risk assessment, the relative risk scores and rankings, rather than the absolute value of risk, provide more meaningful insights for disaster planning, budget allocation, and prioritization. This paper addresses the existing gap in employing a systematic MCDM approach to rank various communities based on their wildfire risk. The primary outcome of this research is the development of a structured approach, firmly grounded in MCDM literature, that empowers well-informed, risk-based decision-making processes before, during, and after wildfire incidents. This approach equips stakeholders with the tools they need to proactively plan for, respond to, and recover from wildfires.
The primary objective of this paper is to introduce a wildfire risk scoring methodology focused on enhancing community safety. In pursuit of this goal, this methodology centers its attention on communities, specifically targeting the assessment of the risk for buildings, agriculture, and the population, collectively identified as Highly Valued Resources and Assets (HVRAs). While acknowledging the importance of natural resources, wildlife, and landscapes, this evaluation excludes these assets from consideration in assessing potential consequences. Taking inspiration from the National Risk Index (NRI) introduced by the U.S. Federal Emergency Management Agency (FEMA) [13], which integrates factors derived from extensive expert judgments across various entities and federal agencies, this paper adopts the same set of factors for wildfire risk scoring. These factors encompass the FEMA’s Expected Annual Loss (EAL) for buildings, agriculture, and population [13], the U.S. Centers for Disease Control and Prevention (CDC) Social Vulnerability Index (SVI) [14,15], and the University of South Carolina’s Baseline Resilience Indicators for Communities (BRIC) [16]. This alignment with NRI-established criteria ensures a comprehensive and expert-informed approach to wildfire risk assessment within the context of community safety. The proposed methodology is used to compute the risk score and ranking for all counties in the state of Arizona.
Utilizing MCDM methodologies in the context of natural hazard risk scoring offers a robust foundation for effective disaster management and informed policy-making. MCDM plays a crucial role in simplifying the complex task of handling conflicting objectives within risk scoring. For instance, factors related to social vulnerability and community resilience often exert opposing influences on risk. MCDM provides a structured framework for identifying a reasonable balance between these conflicting criteria. Furthermore, MCDM introduces a systematic approach for incorporating subjective preferences and expert judgments into scoring, leading to more context-sensitive risk assessments. The same community may exhibit different risk scores in distinct contexts (e.g., evacuation, recovery, etc.), highlighting the flexibility and adaptability of MCDM in tailoring risk scoring to specific conditions and needs.
The MCDM methodology applied to the concept mentioned above is the alternative ranking order method accounting for two-step normalization (AROMAN), that is developed by Bošković et al. [17] and further extended by Bošković et al. [18]. The method combines linear and vector normalization techniques and creates a precise data structure for further calculation steps to obtain trustable ranking alternatives. In addition to its application, sensitivity analyses are performed, and the results prove high stability.
Considering the fact that the AROMAN method is relatively new, so far it has been applied in solving several types of problems: Intuitionistic fuzzy model for EcoPorts performance evaluation [19], interval type 2 decision-making method Fuzzy AROMAN for improving the sustainability of the postal network in rural areas [20], decision-making model for the selection of professional drivers [21], evaluation of sustainable human resource management in manufacturing firms [22].
The rest of the paper is organized as follows: Section 1 is the introduction. Section 2 is the literature review in the field. Section 3 is a mathematical description of the AROMAN methodology. Section 4 reveals the results and its discussion. Section 5 concludes and gives future research directions for the manuscript.
2. Literature Review
In this section, we performed an extensive literature survey to collect the previous studies on wildfire risk assessment. The authors’ primary purpose is to identify these papers’ contributions and managerial implications aside from the research gaps these works have not filled. Hence, we collected forest fire risk estimation and mitigation studies using MCDM approaches.
For this purpose, well-known and popular scientific databases such as Web of Science, Scopus, Mendeley, and Google Scholar were investigated using some keywords such as forest fires risk assessment and analysis, wildfire risk assessment, and MCDM. In the first investigation, using the wildfire risk assessment keyword, we found a total of 1210 papers. However, most of these studies discuss risk assessment and mitigation methods with the help of various qualitative techniques, and no mathematical model or methodological framework proposal has been found in these studies. In conclusion, when keywords such as multiple criteria decision making and MCDM were added to these keywords, thirty studies were identified. However, in twenty of these studies, a decision-making or mathematical model for evaluating forest fires has been proposed. Table 1 presents the relevant studies in the literature and their details.
When the methodological frameworks preferred by the authors in the previous studies to compute the criteria weights are evaluated, the analytic hierarchy process (AHP) is the most used approach by the authors. This weighting technique was used 13 times in 22 methodological frameworks used in 20 related studies. Next, while ANP was used three times, modified AHP, SAW, DEMATEL, and TOPSIS were applied once in the relevant literature. In addition, when ranking procedures are used in the literature to estimate forest fire risks, geographical information systems (GIS) is the most preferred technique. It was used nine times in 20 studies (41%). While the AHP was employed four times, PROMETHEE was preferred in only one study. Additionally, in six papers, there were no mathematical tools to assess the preference ratings of the alternatives, as these works investigated only the influential criteria affecting wildfire risk assessment. In addition, the classical fuzzy set [23] was used in only five works to handle uncertainties influencing the decision-making processes. In the remaining studies, subjective decision-making techniques were preferred by the authors.

Table 1.
The previous works in the relevant literature and their details.
Table 1.
The previous works in the relevant literature and their details.
| Approach | The Number of | The Most Important: | ||||||
|---|---|---|---|---|---|---|---|---|
| Author(s) | Weighting | Ranking | Fuzzy Sets | Country | Criteria | Options | The Criteria | Alternative |
| Dolui (2023) [24] | AHP and DEMATEL | - | - | India | 14 | - | Forest fire susceptibility | - |
| Thakur and Singh (2014) [25] | AHP | AHP | - | India | 6 | 4 | Existing road | Area-3 |
| Marques et al. (2017) [26] | Multi-MCDM | - | - | Spain | 4 | 5 | Fuel treatments | Pine forests |
| Goleiji et al. (2017) [27] | ANP | - | C.FS | Iran | 16 | - | Distance from tourism site | - |
| Lamat et al. (2021) [28] | AHP | AHP | - | India | 12 | 4 | Population density | Meghalaya |
| Ghorbanzadeh et al. (2019) [29] | AHP | GIS | - | Iran | 16 | 5 | Livestock and farms | Mazandaran |
| Duodu et al. (2017) [30] | GAIA | PROMETHEE | - | Australia | 9 | 15 | Using benzo(a)pyrene | Commercial field |
| Varela et al. (2005) [31] | AHP | AHP | - | Spain | 7 | 5 | Proximity to aircraft point | Spread Index |
| Nuthammachot and Stratoulias (2021) [32] | AHP | GIS | - | Thailand | 7 | - | Precipitation | - |
| Sinha et al. (2023) [33] | AHP | AHP | C.FS | India | 10 | - | Land Surface Temperature | Kedarnath |
| Ghanbari Motlagh et al. (2022) [34] | ANP | GIS | - | Iran | 11 | - | Distance from farmlands | - |
| Abedi Gheshlaghi (2019) [35] | ANP | GIS | - | Iran | 10 | - | Annual rainfall | - |
| Abedi (2022) [36] | SAW and TOPSIS | - | - | Iran | 29 | Cooperation of institutions | - | |
| Eskandari (2017) [37] | AHP | GIS | C.FS | Iran | 17 | - | Distance from road | - |
| Pourghasemi et al. (2016) [38] | M-AHP | - | - | Iran | 7 | - | Annual temperature | - |
| Gigović et al. (2018) [39] | AHP | GIS | - | Bosnia | 8 | Distance from roads | - | |
| Güngöroğlu (2017) [40] | AHP | GIS | C.FS | Turkey | 15 | - | Socioeconomic properties | - |
| Suryabhagavan et al. (2016) [41] | AHP | - | Ethiopia | 5 | - | Vegetation type | - | |
| Vadrevu et al. (2010) [42] | AHP | GIS | India | 7 | - | forest fire protection | - | |
| Gonzalez-Olabarria et al. (2019) [43] | AHP | GIS | - | Spain | 17 | 7 | Patch proportion | - |
| Our work | AROMAN | - | USA | 25 | 15 | EALB | Greenlee | |
When the criteria influencing the wildfire risk assessment are evaluated, in almost all papers, the most influential criterion is different. In three studies [25,37,39], risk degree was associated with the criteria of distance to the road or existence of the road in the region. Additionally, the distance to farms criterion is determined as the most critical factor in the two studies.
2.1. Research Gaps
As understood from Table 1, most authors focusing on wildfire risk assessment with the help of decision-making tools mainly employed the AHP method. The AHP method is the most criticized approach in the literature due to its structural problems and disadvantages [44]. It has a complicated and time-consuming basic algorithm, and computations and comparisons become more challenging based on the number of criteria. Additionally, it is not sufficiently resistant to the rank reversal problem [45,46], as adding or removing a criterion can dramatically change the overall results. Hence, it may not provide satisfactory and reliable outcomes for decision-makers. Further, it requires additional computations to identify the consistency ratio.
Additionally, the number of papers dealing with wildfire risk assessment using MCDM frameworks is incredibly scarce. Despite our team’s ceaseless effort, we could find only twenty papers investigating this current subject in the literature. However, thousands of studies are related to forest fires in the literature. Consequently, examination of this issue with the aid of MCDM tools has considerably been neglected by the members of the research society.
2.2. Objectives and Motivations of the Work
The current study’s main aim is to fill the research gaps. For this purpose, it proposes a novel and has not been used to evaluate wildfire risk assessment problems in the relevant literature. This approach, namely AROMAN, is an efficient and robust decision-making procedure, and it can be applied to address many intricate decision-making problems. Further, it does not require many comparisons and can achieve reliable and reasonable results. Also, it can be employed to compute the criteria weights and identify the preference ratings of the alternatives together. Hence, it does not need additional weighting approaches to calculate the criteria weights.
Decision-makers in the field of forest protection can consider the proposed model as a guideline to produce efficient solutions for mitigating fire risks. In addition, policy-makers can create new regulations and procedures to improve the existing ecological system and forest conditions to manage the existing natural assets of the societies.
3. Methodology
As elucidated in the Introduction, this paper employs three datasets for MCDM-based wildfire risk assessment. Prior to delving into the methodology explanation, it is beneficial to gain an overview of the factors utilized in this study. The 25 factors in this study are categorized into 3 main groups.
The first three factors are derived from the National Risk Index and encompass the annual expected loss (AEL) of buildings, agriculture, and populations. These factors provide the potential consequences of a wildfire for a given community. It is noteworthy to mention that all AEL values are provided in US dollars to facilitate comparability. It is also necessary to emphasize that the process of estimating loss values for each asset type is a topic beyond the scope of this paper, as it entails extensive expert judgment alongside a comprehensive multidisciplinary evaluation of the losses. FEMA has leveraged the expert judgment of professionals from various federal agencies in this process.
The next six factors are derived from the Baseline Resilience Indicators for Communities (BRIC) dataset. This dataset employs 49 variables, primarily sourced from open-source federal government databases, which significantly impact community resilience. The dataset generates six major factors encompassing social, economic, community capital, institutional, infrastructural, and environmental dimensions. All of these factors are presented at the county level for the entire United States. Each set of these six factors encompasses a broad array of community attributes and features capable of mitigating the consequences of hazards during emergency situations.
The final 16 factors are derived from the Social Vulnerability Index (SVI) dataset. These factors elucidate community features that may amplify hazard consequences by highlighting vulnerabilities in emergency preparedness, risk mitigation capacity, emergency management, or disaster recovery. Encompassing a wide range of variables, these factors cover different aspects of vulnerabilities against natural hazards including socioeconomic status, household characteristics, racial and ethnic minority status, as well as housing type and transportation.
This paper utilizes an alternative ranking order method accounting two-step normalization (AROMAN). This method was originally developed by Bošković et al. [17]. The method can be described through the six steps:
- Step 1. Define the initial input data decision-making matrix.
Formulating the initial input data decision-making matrix is essential. The input data regarding the alternatives and criteria are mostly collected in advance. In that sense, let us suppose we have a decision matrix Xmxn with the input data ,…, , Equation (1):
- Step 2. Normalize the input data.
The second step of the AROMAN method is to normalize the input data.
In other words, the input data should be restructured in intervals between 0 and 1. Two types of normalization techniques are used and further combined Equations (2) and (3):
Step 2.1. Linear Normalization:
Step 2.2. Vector Normalization:
When it comes to normalization, the criteria type is not considered. The criteria are treated equally.
Step 2.3. Aggregated averaged normalization.
The aggregated averaged normalization is calculated by utilizing Equation (4):
where denotes the aggregated averaged normalization. β is a weighting factor varying from 0 to 1. In our case, we suggest β to be 0.5. According to Bošković et al. [17], coupling two normalization techniques is more effective than using the only one.
- Step 3. Multiply the Aggregated Averaged Normalized decision-making matrix with the criteria weights to obtain a weighted DM matrix.
In this step, it is necessary to obtain the normalized weighted decision-making matrix. It can be calculated by applying Equation (5):
- Step 4. Summarize the normalized weighted values of the criteria type min () and the normalized weighted values of the max type ().
In this step, we summarize the normalized weighted values of the criteria type min and the normalized weighted values of the max type.
This can be calculated by applying Equations (6) and (7):
- Step 5. Raise the obtained sum of and values to the degree of .
λ denotes the coefficient degree of the criterion type. In our case, λ is 0.5. However, variations of the parameter λ when considering the criteria type are used in the sensitivity analysis.
- Step 6. Calculate the difference between the values and and finally, rank alternatives ( (Equation (10)).
The steps of the AROMAN method are depicted in Figure 1.
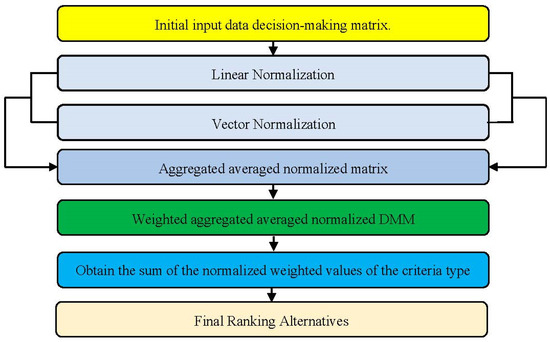
Figure 1.
Description of the AROMAN method.
4. Results and Discussion
This section reveals the results obtained by the AROMAN method. The input data matrix is formulated and presented in Table 2.

Table 2.
Input Data Matrix.
The second step of the AROMAN method is to formulate a normalized input data matrix. After two-step normalization techniques (linear and vector) and their combination, the aggregated normalized matrix is obtained and presented in Table 3. β represents a weighting factor ranging from 0 to 1 in the aggregated normalization. In the context of the risk assessment, the input data were coupled into the aggregated structure, considering β as 0.5. However, the decision-maker can make variations of the parameter β between the intervals 0 to 1. In this paper, we utilized this variation in the sensitivity analysis.

Table 3.
Aggregated Normalization.
By applying the Step 3, we calculate the weighted-aggregated normalized matrix. This means that each value of the normalized matrix multiplies the criteria weight. This is presented in Table 4.

Table 4.
Weighted-Aggregated Normalized Matrix.
The next step summarizes the normalized weighted values of the criteria type min () and the normalized weighted values of the max type (). In addition, the distinction between the and values is calculated as well. Moreover, the final rank () is calculated, and all of those values are presented in Table 5.

Table 5.
values with the final rank .
The AROMAN method, based on Figure 2, ranked Greenlee as the best, followed by Coconino, etc.
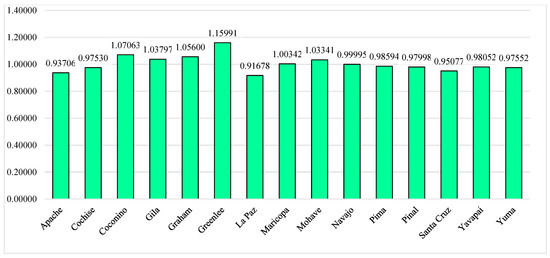
Figure 2.
Final ranking alternatives.
As the results clearly indicate, the proposed methodology excels more in risk scoring rather than risk quantification. This implies that the MCDM-based risk assessment is primarily employed to rank a set of communities based on their risk levels. This ranking directly furnishes valuable information for decision-makers and policy-makers in various managerial aspects, such as resource allocations and prioritization for preparedness and risk mitigation programs.
4.1. Sensitivity Analyses
In this paper, sensitivity analyses are performed to check the stability of the AROMAN method. The first sensitivity analysis is based on a variation of parameter β, while the second one refers to a variation of parameter λ.
4.1.1. Sensitivity Analysis Based on a Variation of Parameter β
As mentioned above, β represents a weighting factor ranging from 0 to 1 in the aggregated normalization. In the context of the risk assessment, the input data were coupled into the aggregated structure, considering β as 0.5. However, we tested different cases when β was ranged from 0 to 1 with a step 0.1. The results of the first analysis are presented in Table 6 and Figure 3, respectively.

Table 6.
Sensitivity Analysis based on a variation of parameter β.
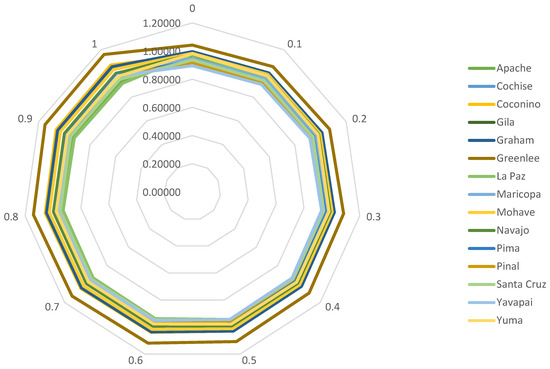
Figure 3.
Sensitivity Analysis on Parameter β.
The results of the first sensitivity analysis reveal that the final ranking alternatives remain the same regardless of changing the parameter β.
4.1.2. Sensitivity Analysis Based on a Variation of Parameter λ
The second sensitivity analysis is based on a variation of parameter λ. As mentioned above, λ represents a coefficient degree of each criterion type and can vary between the intervals 0 and 1. We obtained different ranks for each parameter λ (0.1–0.9) by applying Equations (8)–(10), respectively. We made variations with a step of 0.1 and the obtained results were depicted in Figure 4. In addition, the results were also presented in Table 7.
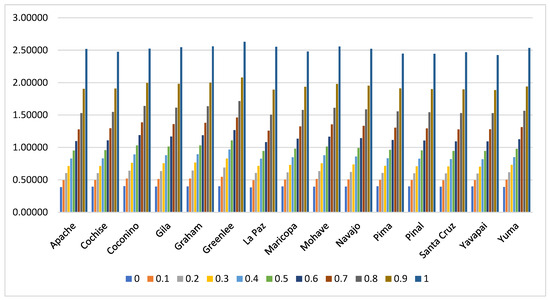
Figure 4.
Sensitivity Analysis on parameter λ.

Table 7.
Sensitivity Analysis based on a variation of parameter λ.
In the second sensitivity analysis, we revealed that the ranking order remains stable, except when λ = 0, where Coconino holds the first position, and Greenlee is the second best. In conclusion, both sensitivity analyses indicate a high stability level of the AROMAN method.
4.2. Comparative Analysis
Comparative Analysis (CA) is performed to check the reliability of the results. In addition to the AROMAN method, the same problem is solved by applying the MARCOS method. The results of the MARCOS method are presented in Figure 5.
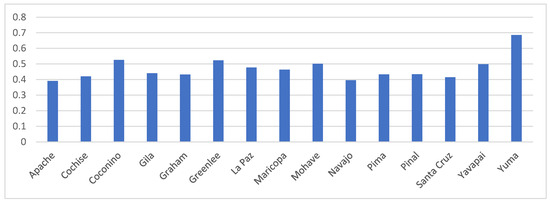
Figure 5.
MARCOS ranking method.
As can be noticed, the MARCOS method ranks Yuma as the highest, followed by Coconino, Greenlee, etc. The comparison results of both methods are presented in Figure 6.
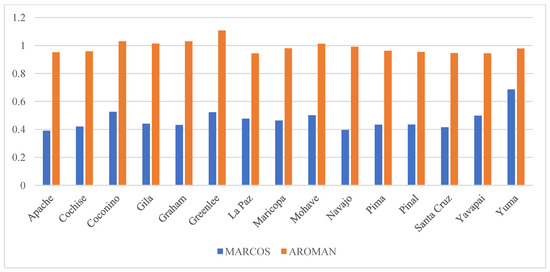
Figure 6.
Comparative Analysis with the MARCOS method.
In case of the AROMAN, Greenlee has the highest-ranking value, followed by Coconino and Graham. The ranking order between two methods is slightly different. However, we accept the ranking order obtained by the AROMAN. The AROMAN method has a high level of sensitivity in terms of criteria type. In our case, most of the criteria are minimized and that significantly affected the decision.
5. Managerial Implications
The results indicate that the AROMAN methodology leads to a stable wildfire risk ranking of communities. While this paper focuses on a detailed explanation of the method using 15 counties in the state of Arizona, the true potential of this methodology becomes evident in larger-scale studies. At higher managerial levels, understanding the distribution of risk among communities plays a crucial role in appropriate resource allocation and prioritizing actions. Specifically, this risk ranking methodology can serve as a valuable tool for policy-makers, aiding them in understanding different combinations of geographical and social characteristics that result in similar wildfire risks. This understanding will assist them in formulating more unbiased and equitable policies that encompass a broader spectrum of communities.
Another crucial aspect of wildfire risk planning and management is the ability to assess the effectiveness of the plans during the planning phase. The AROMAN-based wildfire risk ranking allows us to compare the overall risk distribution before and after each scenario. Consequently, planners have the opportunity to compare several plans, which may involve various wildfire mitigation actions and vulnerability reductions, among other factors, and determine the optimum scenario with the greatest overall risk reduction. In this manner, MCDM provides an ideal tool for planners to establish optimal goals.
Last but not least, disaster planners and managers must always take into account the potential combination of multiple natural hazards affecting communities. This is particularly crucial since numerous planning components influence the risk of various natural disasters. For instance, enhancing community resilience across multiple facets would reduce the risk of wildfires and mitigate the risk of numerous other potential disasters. Consequently, the AROMAN risk analysis methodology, which incorporates more factors for various types of disasters, can be applied to large-scale general disaster planning efforts.
In addition to the discussed benefits of the proposed methodology, presenting a list of its limitations can be highly informative. Similar to any other MCDM-based methodology, the proposed approach necessitates specific input data of a certain quality. Although all of the requisite datasets for this study are available for the entire United States, comparable datasets with the same set of factors are not available for all other regions or countries. This limitation constrains the direct applicability of our methodology beyond the United States. However, it is essential to note that the primary focus of the paper is on the MCDM methodology rather than the specific criteria applied. Consequently, the same methodology can be adapted for other countries
Another limitation of the proposed methodology is its scale of application. This paper seeks to furnish a wildfire risk scoring system suitable for large-scale studies, encompassing the scale of states or regional assessments. While this objective brings numerous advantages for regional and federal management, especially in cases where data quality remains relatively consistent across all communities (as is the case in our study), it introduces challenges when applied to smaller communities. The required data is not always readily available for such communities, and disparate datasets may not share the same resolution, posing difficulties in integrating these incompatible datasets.
For example, the BRIC dataset provides all six factors at the county level for the entire United States. In contrast, the NRI and SVI datasets offer data at both the county and census tracts (official sub-county divisions) levels. Consequently, generating risk scores for communities at scales smaller than the county level will introduce new challenges based on the availability of relevant datasets.
6. Conclusions
Estimating risk is typically a complex task, given the numerous uncertainties involved across all aspects of the assessment. This complexity is amplified when addressing natural disasters and their impact on human communities. A comprehensive risk assessment methodology must encompass a vast array of pertinent factors. However, the analysis of numerous factors necessitates a systematic analytical approach. AROMAN, a method extensively employed across various disciplines, offers an ideal framework for ranking the risk and safety of human communities in the context of natural hazards.
- This paper utilizes the AROMAN method for wildfire risk assessment. The methodology is tested at the county level in the state of Arizona to evaluate and rank counties according to their wildfire safety. This study incorporates the factors utilized by the National Risk Index [13], encompassing a total of 25 factors divided into three main categories. Each of these categories is regarded as equally significant, and within each category, the factors are assigned identical weights. The conducted sensitivity analysis demonstrates that the obtained results remain highly stable even when the model’s parameters are adjusted.
- The results reveal that Greenlee County received the highest safety ranking among all of the counties in Arizona. This conclusion appears to be well-founded upon closer examination of the risk factors. Within the EAL group, both the expected annual loss for buildings and agriculture are over 98% lower than the state-wide average for Arizona. Furthermore, Greenlee’s EAL for its population is more than 90% lower than the average value. In terms of resilience, all six factors for Greenlee County hover around the state average. However, in the context of social vulnerability, seven factors exhibit values between 50% and 74% lower than the state averages, while only three factors have values approximately 20% higher than the average.
- Conversely, La Paz County has received the highest risk rating (indicating the lowest level of safety) in Arizona. A detailed analysis of the factors in this scenario provides valuable insights. While this county exhibits lower EAL to wildfires compared to Greenlee County, its resilience and vulnerability factors differ significantly. It is essential to bear in mind that EAL assesses the exposure of community assets to wildfires, but exposure alone does not solely determine the risk level.
- In the case of La Paz County, five out of six factors in the resilience group fall below the state averages. Additionally, 10 out of 16 social vulnerability factors indicate that La Paz County is considerably more vulnerable than the state average. Specifically, this county demonstrates vulnerability levels exceeding 87%, 61%, and 162% more than the state average concerning elderly residents, disabilities, and mobile homes.
- In this research, the factors in each group (EAL, resilience, and vulnerability) are given equal weight. Concerning EAL, all three factors (buildings, agriculture, and population losses) are specifically calculated for wildfire and converted into US dollars. This conversion inherently incorporates expert judgment, making assigning equal weights to these factors in general risk calculations reasonable. However, the corresponding factors are assumed to carry equal weight for resilience and vulnerability due to the original methodologies underlying the BRIC [16] and SVI [14,15] indices. Nonetheless, additional expert opinions can alter the relative importance of factors within each group, leading to more insightful ranking results. Future work may focus on gathering surveys from experts in the field of disaster management, specifically in wildfire scenarios, to establish a more realistic set of weights within each group. The relative importance may vary based on different objectives; for example, factors may hold different relative importance for wildfire evacuation compared to economic or environmental considerations.
Author Contributions
Conceptualization, M.P. and S.H.Z.; methodology, S.J. and V.S.; validation, M.P. and S.H.Z.; formal analysis, S.H.Z. and V.S.; investigation, M.P. and Ö.F.G.; writing—original draft preparation, M.P. and S.H.Z.; writing—review and editing, M.P. and S.H.Z.; supervision, S.H.Z.; project administration, M.P. and S.H.Z.; funding acquisition, M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- National Interagency Fire Center. Fire Information|Statistics; National Interagency Fire Center: Boise, ID, USA, 2023. Available online: https://www.nifc.gov/fire-information/statistics (accessed on 15 September 2023).
- Carlson, A.R.; Helmers, D.P.; Hawbaker, T.J.; Mockrin, M.H.; Radeloff, V.C. The wildland–urban interface in the United States based on 125 million building locations. Ecol. Appl. 2022, 32, e2597. [Google Scholar] [CrossRef]
- Butler, K.; Butry, D.; Forney, G.P.; Johnsson, E.L.; Link, E.; Maranghides, A.; Prasad, K. Wildland-Urban Interface (WUI) Fire Data Collection on Parcel Vulnerabilities; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2021. Available online: https://www.nist.gov/programs-projects/wildland-urban-interface-wui-fire-data-collection-parcel-vulnerabilities (accessed on 15 September 2023).
- Xi, D.D.; Taylor, S.W.; Woolford, D.G.; Dean, C. Statistical Models of Key Components of Wildfire Risk. Annu. Rev. Stat. Its Appl. 2019, 6, 197–222. [Google Scholar] [CrossRef]
- Oliveira, S.; Rocha, J.; Sá, A. Wildfire risk modeling. Curr. Opin. Environ. Sci. Health 2021, 23, 100274. [Google Scholar] [CrossRef]
- Mhawej, M.; Faour, G.; Adjizian-Gerard, J. A novel method to identify likely causes of wildfire. Clim. Risk Manag. 2017, 16, 120–132. [Google Scholar] [CrossRef]
- Hilton, J.E.; Sullivan, A.L.; Swedosh, W.; Sharples, J.; Thomas, C. Incorporating convective feedback in wildfire simulations using pyrogenic potential. Environ. Model. Softw. 2018, 107, 12–24. [Google Scholar] [CrossRef]
- Masoudvaziri, N.; Szasdi Bardales, F.; Keskin, O.K.; Sarreshtehdari, A.; Sun, K.; Elhami-Khorasani, N. Streamlined wildland-urban interface fire tracing (SWUIFT): Modeling wildfire spread in communities. Environ. Model. Softw. 2021, 143, 105097. [Google Scholar] [CrossRef]
- Jahdi, R.; Del Giudice, L.; Melis, M.; Lovreglio, R.; Salis, M.; Arca, B.; Duce, P. Assessing the effects of alternative fuel treatments to reduce wildfire exposure. J. For. Res. 2023, 34, 373–386. [Google Scholar] [CrossRef]
- Lambrou, N.; Kolden, C.; Loukaitou-Sideris, A.; Anjum, E.; Acey, C. Social drivers of vulnerability to wildfire disasters: A review of the literature. Landsc. Urban Plan. 2023, 237, 104797. [Google Scholar] [CrossRef]
- Fraser, A.M.; Chester, M.V.; Underwood, B.S. Wildfire risk, post-fire debris flows, and transportation infrastructure vulnerability. Sustain. Resilient Infrastruct. 2022, 7, 188–200. [Google Scholar] [CrossRef]
- Molina, A.; Little, J.; Drury, S.; Jandt, R. Homeowner Preferences for Wildfire Risk Mitigation in the Alaskan Wildland Urban Interface. Sustainability 2021, 13, 11754. [Google Scholar] [CrossRef]
- Zuzak, C.; Mowrer, M.; Goodenough, E.; Burns, J.; Ranalli, N.; Rozelle, J. The national risk index: Establishing a nationwide baseline for natural hazard risk in the US. Nat. Hazards 2022, 114, 2331–2355. [Google Scholar] [CrossRef]
- Flanagan, B.E.; Gregory, E.W.; Hallisey, E.J.; Heitgerd, J.L.; Lewis, B. A Social Vulnerability Index for Disaster Management. J. Homel. Secur. Emerg. Manag. 2011, 8, 3. [Google Scholar] [CrossRef]
- Flanagan, B.E.; Hallisey, E.J.; Adams, E.; Lavery, A. Measuring Community Vulnerability to Natural and Anthropogenic Hazards: The Centers for Disease Control and Prevention’s Social Vulnerability Index. J. Environ. Health 2018, 80, 34–36. [Google Scholar] [PubMed]
- Cutter, S.L.; Ash, K.D.; Emrich, C.T. The geographies of community disaster resilience. Glob. Environ. Chang. 2014, 29, 65–77. [Google Scholar] [CrossRef]
- Bošković, S.; Švadlenka, L.; Jovčić, S.; Dobrodolac, M.; Simić, V.; Bacanin, N. An Alternative Ranking Order Method Accounting for Two-Step Normalization (AROMAN)—A Case Study of the Electric Vehicle Selection Problem. IEEE Access 2023, 11, 39496–39507. [Google Scholar] [CrossRef]
- Bošković, S.; Švadlenka, L.; Dobrodolac, M.; Jovčić, S.; Zanne, M. An Extended AROMAN Method for Cargo Bike Delivery Concept Selection. Decis. Mak. Adv. 2023, 1, 1–9. [Google Scholar] [CrossRef]
- Yalçın, G.C.; Kara, K.; Toygar, A.; Simic, V.; Pamucar, D.; Köleoğlu, N. An intuitionistic fuzzy-based model for performance evaluation of EcoPorts. Eng. Appl. Artif. Intell. 2023, 126, 107192. [Google Scholar] [CrossRef]
- Nikolić, I.; Milutinović, J.; Božanić, D.; Dobrodolac, M. Using an Interval Type-2 Fuzzy AROMAN Decision-Making Method to Improve the Sustainability of the Postal Network in Rural Areas. Mathematics 2023, 11, 3105. [Google Scholar] [CrossRef]
- Čubranić-Dobrodolac, M.; Jovčić, S.; Bošković, S.; Babić, D. A Decision-Making Model for Professional Drivers Selection: A Hybridized Fuzzy–AROMAN–Fuller Approach. Mathematics 2023, 11, 2831. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Alrasheedi, A.F.; Xie, B.; Dwivedi, R. Evaluating the Sustainable Human Resource Management in Manufacturing Firms Using Single-Valued Neutrosophic Distance Measure-Based RANCOM-AROMAN Model. Preprints 2023, 2023, 2023091698. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Dolui, S. Forest fire susceptibility mapping and risk assessment using integrated AHP and DEMATEL method for Purulia District, West Bengal (India). In Water, Land, and Forest Susceptibility and Sustainability: Geospatial Approaches and Modeling; Elsevier: Amsterdam, The Netherlands, 2023; Volume 1, pp. 401–5452. [Google Scholar] [CrossRef]
- Thakur, A.K.; Singh, D. Forest Fire Risk Zonation Using Geospatial Techniques and Analytic Hierarchy Process in Dehradun District, Uttarakhand, India. Univers. J. Environ. Res. Technol. 2014, 4, 82–89. [Google Scholar]
- Marques, S.; Marto, M.; Bushenkov, V.; McDill, M.; Borges, J.G. Addressing wildfire risk in forest management planning with multiple criteria decision making methods. Sustainability 2017, 9, 298. [Google Scholar] [CrossRef]
- Goleiji, E.; Hosseini, S.M.; Khorasani, N.; Monavari, S.M. Forest fire risk assessment-an integrated approach based on multicriteria evaluation. Environ. Monit. Assess. 2017, 189, 612. [Google Scholar] [CrossRef] [PubMed]
- Lamat, R.; Kumar, M.; Kundu, A.; Lal, D. Forest fire risk mapping using analytical hierarchy process (AHP) and earth observation datasets: A case study in the mountainous terrain of Northeast India. SN Appl. Sci. 2021, 3, 425. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Aryal, J. Forest fire susceptibility and risk mapping using social/infrastructural vulnerability and environmental variables. Fire 2019, 2, 50. [Google Scholar] [CrossRef]
- Duodu, G.O.; Ogogo, K.N.; Mummullage, S.; Harden, F.; Goonetilleke, A.; Ayoko, G.A. Source apportionment and risk assessment of PAHs in Brisbane River sediment, Australia. Ecol. Indic. 2017, 73, 784–799. [Google Scholar] [CrossRef]
- Varela, J.; Arias, J.E.; Sordo, I.; Tarela, A. Multicriteria Decision Analysis for Forest Fire Risk Assessment in Galicia, Spain. In Proceedings of the 4th International Workshop on Remote Sensing and GIS applications to Forest Fire Management, Ghent, Belgium, 5–7 June 2005; pp. 1–233. [Google Scholar]
- Nuthammachot, N.; Stratoulias, D. Multi-criteria decision analysis for forest fire risk assessment by coupling AHP and GIS: Method and case study. Environ. Dev. Sustain. 2021, 23, 17443–17458. [Google Scholar] [CrossRef]
- Sinha, A.; Nikhil, S.; Ajin, R.S.; Danumah, J.H.; Saha, S.; Costache, R.; Rajaneesh, A.; Sajinkumar, K.S.; Amrutha, K.; Johny, A.; et al. Wildfire Risk Zone Mapping in Contrasting Climatic Conditions: An Approach Employing AHP and F-AHP Models. Fire 2023, 6, 44. [Google Scholar] [CrossRef]
- Ghanbari Motlagh, M.; Abbasnezhad Alchin, A.; Daghestani, M. Detection of high fire risk areas in Zagros Oak forests using geospatial methods with GIS techniques. Arab. J. Geosci. 2022, 15, 835. [Google Scholar] [CrossRef]
- Abedi Gheshlaghi, H. Using GIS to Develop a Model for Forest Fire Risk Mapping. J. Indian Soc. Remote Sens. 2019, 47, 1173–1185. [Google Scholar] [CrossRef]
- Abedi, R. Application of multi-criteria decision making models to forest fire management. Int. J. Geoheritage Parks 2022, 10, 84–96. [Google Scholar] [CrossRef]
- Eskandari, S. A new approach for forest fire risk modeling using fuzzy AHP and GIS in Hyrcanian forests of Iran. Arab. J. Geosci. 2017, 10, 190. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Beheshtirad, M.; Pradhan, B. A comparative assessment of prediction capabilities of modified analytical hierarchy process (M-AHP) and Mamdani fuzzy logic models using Netcad-GIS for forest fire susceptibility mapping. Geomat. Nat. Hazards Risk 2016, 7, 861–885. [Google Scholar] [CrossRef]
- Gigović, L.; Jakovljević, G.; Sekulović, D.; Regodić, M. GIS multi-criteria analysis for identifying and mapping forest fire hazard: Nevesinje, Bosnia and Herzegovina. Teh. Vjesn. 2018, 25, 891–897. [Google Scholar] [CrossRef]
- Güngöroğlu, C. Determination of forest fire risk with fuzzy analytic hierarchy process and its mapping with the application of GIS: The case of Turkey/Çakırlar. Hum. Ecol. Risk Assess. 2017, 23, 388–406. [Google Scholar] [CrossRef]
- Suryabhagavan, K.V.; Alemu, M.; Balakrishnan, M. Gis-based multi-criteria decision analysis for forest fire susceptibility mapping: A case study in Harenna forest, southwestern Ethiopia. Trop. Ecol. 2016, 57, 33–43. [Google Scholar]
- Vadrevu, K.P.; Eaturu, A.; Badarinath, K.V.S. Fire risk evaluation using multicriteria analysis—A case study. Environ. Monit. Assess. 2010, 166, 223–239. [Google Scholar] [CrossRef]
- Gonzalez-Olabarria, J.R.; Reynolds, K.M.; Larrañaga, A.; Garcia-Gonzalo, J.; Busquets, E.; Pique, M. Strategic and tactical planning to improve suppression efforts against large forest fires in the Catalonia region of Spain. For. Ecol. Manag. 2019, 432, 612–622. [Google Scholar] [CrossRef]
- Sabaei, D.; Erkoyuncu, J.; Roy, R. A review of multi-criteria decision making methods for enhanced maintenance delivery. Procedia CIRP 2015, 37, 30–35. [Google Scholar] [CrossRef]
- Barzilai, J.; Golany, B. AHP rank reversal, normalization and aggregation rules. INFOR Inf. Syst. Oper. Res. 1994, 32, 57–63. [Google Scholar] [CrossRef]
- Wang, Y.M.; Luo, Y. On rank reversal in decision analysis. Math. Comput. Model. 2009, 49, 1221–1229. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).