The Demographic Response of Grass Species to Fire Treatments in a Guinean Savanna
Abstract
1. Introduction
2. Material and Methods
2.1. Study Site
2.2. Study Plots
2.3. Data Collection
2.4. Matrix Models
2.5. Demographic Analyses
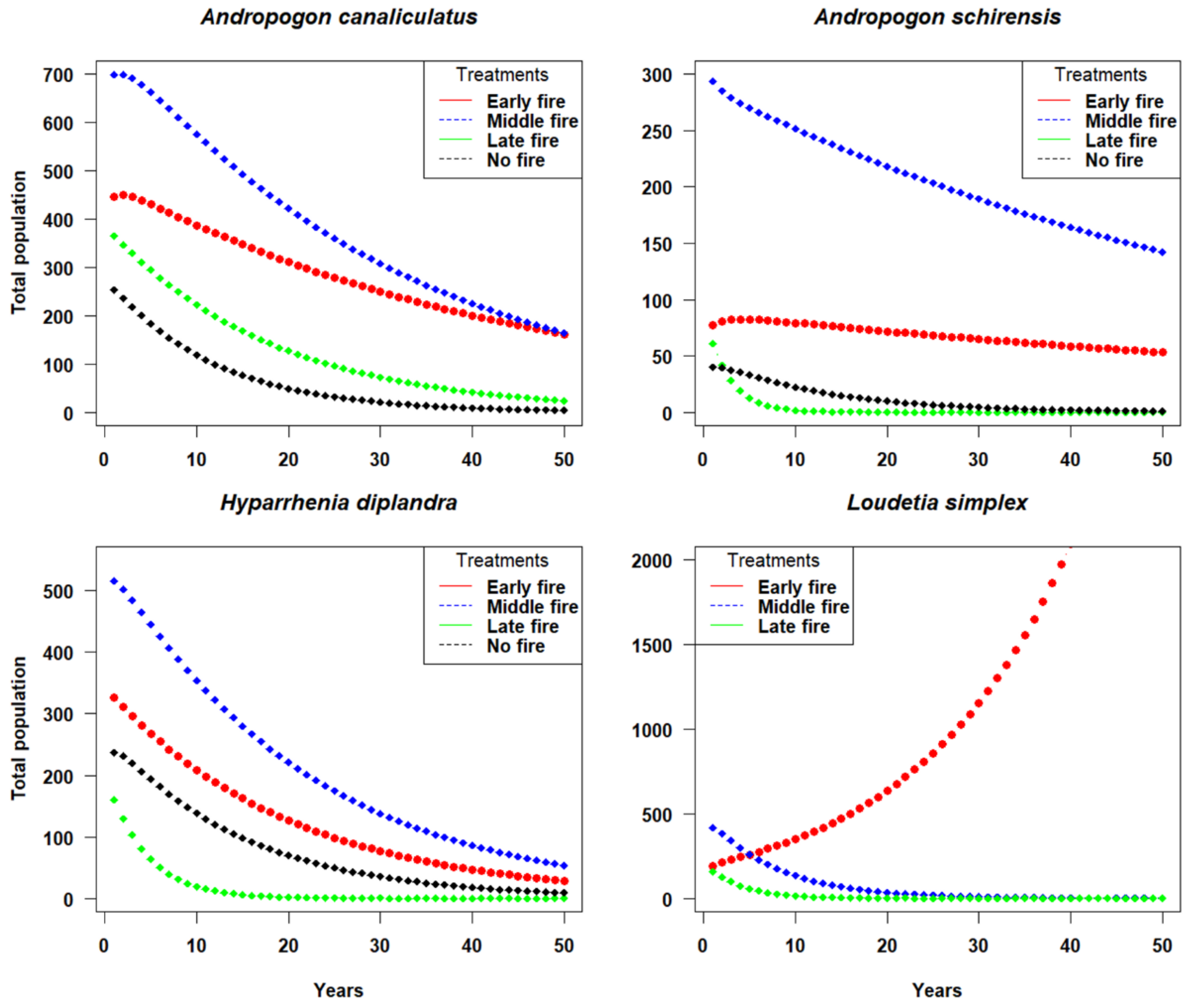
3. Results
3.1. Average Matrix of Species in the Fire Treatments
3.2. Asymptotic Growth Rate (Λ) of Grass Species under the Fire Treatments
3.3. Loglinear Analysis
3.4. Elasticity Analysis
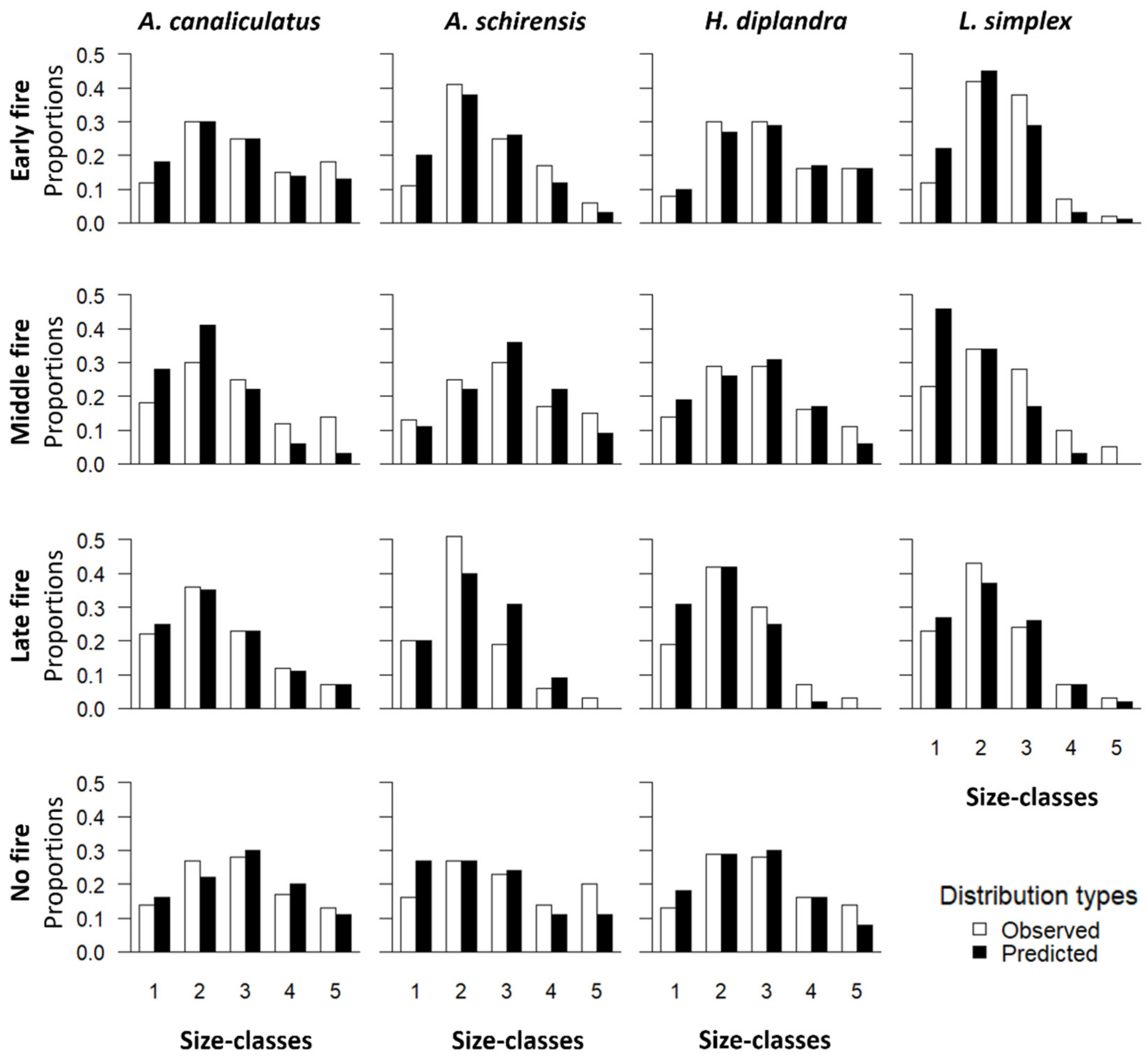
3.5. Stable Size Distribution Analysis
3.6. LTRE Analysis
3.7. Age-Based Life-History Parameters
4. Discussion
4.1. General Effect of the Fire Treatments on the Demography of the Grass Species
4.2. Responses of the Grass Species to Fire Treatments
4.2.1. Similarities in the Response of Species to the Fire Treatments
4.2.2. Contrasting Responses of the Grass Species to the Fire Treatments
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sankaran, M.; Hanan, N.P.; Scholes, R.J.; Ratnam, J.; Augustine, D.J.; Cade, B.S.; Gignoux, J.; Higgins, S.I.; Le Roux, X.; Ludwig, F.; et al. Determinants of Woody Cover in African Savannas. Nature 2005, 438, 846–849. [Google Scholar] [CrossRef] [PubMed]
- Menaut, J.-C.; Abbadie, L. Vegetation. In Lamto; Abbadie, L., Gignoux, J., Le Roux, X., Lepage, M., Eds.; Ecological Studies; Springer: New York, NY, USA, 2006; Volume 179, pp. 63–74. [Google Scholar]
- Williams, R.J.; Müller, W.J.; Wahren, C.-H.; Setterfield, S.A.; Cusack, J. Vegetation. In Fire in Tropical Savannas; Andersen, A.N., Cook, G.D., Williams, R.J., Eds.; Ecological Studies; Springer: New York, NY, USA, 2003; pp. 79–106. [Google Scholar]
- Savadogo, P.; Zida, D.; Sawadogo, L.; Tiveau, D.; Tigabu, M.; Oden, P.C. Fuel and Fire Characteristics in Savanna-Woodland of West Africa in Relation to Grazing and Dominant Grass Type. Int. J. Wildland Fire 2007, 16, 531–539. [Google Scholar] [CrossRef]
- Gignoux, J.; Lahoreau, G.; Julliard, R.; Barot, S. Establishment and Early Persistence of Tree Seedlings in an Annually Burned Savanna. J. Ecol. 2009, 97, 484–495. [Google Scholar] [CrossRef]
- Smit, I.P.J.; Asner, G.P.; Govender, N.; Vaughn, N.R.; van Wilgen, B.W. An Examination of the Potential Efficacy of High-Intensity Fires for Reversing Woody Encroachment in Savannas. J. Appl. Ecol. 2016, 53, 1623–1633. [Google Scholar] [CrossRef]
- Stevens, N.; Lehmann, C.E.R.; Murphy, B.P.; Durigan, G. Savanna Woody Encroachment Is Widespread across Three Continents. Glob. Chang. Biol. 2017, 23, 235–244. [Google Scholar] [CrossRef]
- Barot, S.; Gignoux, J.; Legendre, S.; Vuattoux, R. Demography of a Savanna Palm Tree in Ivory Coast (Lamto): Population Persistence, and Life History. J. Trop. Ecol. 2000, 16, 637–655. [Google Scholar] [CrossRef]
- Jurisch, K.; Hahn, K.; Wittig, R.; Bernhardt-Römermann, M. Population Structure of Woody Plants in Relation to Land Use in a Semi-Arid Savanna, West Africa. Biotropica 2012, 44, 744–751. [Google Scholar] [CrossRef]
- O’Connor, T.G. Demography of Woody Species in a Semi-Arid African Savanna Reserve Following the Re-Introduction of Elephants. Acta Oecologica 2017, 78, 61–70. [Google Scholar] [CrossRef]
- Garnier, L.K.M.; Dajoz, I. The Influence of Fire on the Demography of a Dominant Grass Species of West African Savannas, Hyparrhenia diplandra. J. Ecol. 2001, 89, 200–208. [Google Scholar] [CrossRef]
- Keeley, J.E.; Pausas, J.G.; Rundel, P.W.; Bond, W.J.; Bradstock, R.A. Fire as an Evolutionary Pressure Shaping Plant Traits. Trends Plant Sci. 2011, 16, 406–411. [Google Scholar] [CrossRef]
- Pilon, N.A.L.; Hoffmann, W.A.; Abreu, R.C.R.; Durigan, G. Quantifying the Short-Term Flowering after Fire in Some Plant Communities of a Cerrado Grassland. Plant Ecol. Divers. 2018, 11, 259–266. [Google Scholar] [CrossRef]
- Gignoux, J.; Clobert, J.; Menaut, J.-C. Alternative Fire Resistance Strategies in Savanna Trees. Oecologia 1997, 110, 576–583. [Google Scholar] [CrossRef] [PubMed]
- Bond, W.J. What Limits Trees in C4 Grasslands and Savannas? Annu. Rev. Ecol. Evol. Syst. 2008, 39, 641–659. [Google Scholar] [CrossRef]
- Accatino, F.; Wiegand, K.; Ward, D.; De Michele, C. Trees, Grass, and Fire in Humid Savannas: The Importance of Life History Traits and Spatial Processes. Ecol. Model. 2016, 320, 135–144. [Google Scholar] [CrossRef]
- Ott, J.P.; Klimešová, J.; Hartnett, D.C. The Ecology and Significance of Below-Ground Bud Banks in Plants. Ann. Bot. 2019, 123, 1099–1118. [Google Scholar] [CrossRef]
- Bond, W.J.; Wilgen, B.W. Fire and Plants; Chapman & Hall: London, UK; Springer: London, UK, 1996; pp. 1–263. [Google Scholar]
- Simpson, K.J.; Ripley, B.S.; Christin, P.-A.; Belcher, C.M.; Lehmann, C.E.R.; Thomas, G.H.; Osborne, C.P. Determinants of Flammability in Savanna Grass Species. J. Ecol. 2016, 104, 138–148. [Google Scholar] [CrossRef]
- N’Dri, A.B.; Fongbe, M.; Soro, T.D.; Gignoux, J.; Kone, M.; Dosso, K.; N’dri, J.K.; Kone, N.A.; Barot, S. Principaux Indices de l’intensité Du Feu Dans Une Savane Guinéenne d’Afrique de l’ouest. Int. J. Biol. Chem. Sci. 2018, 12, 266–274. [Google Scholar] [CrossRef]
- Werner, P.A.; Prior, L.D. Demography and Growth of Subadult Savanna Trees: Interactions of Life History, Size, Fire Season, and Grassy Understory. Ecol. Monogr. 2013, 83, 67–93. [Google Scholar] [CrossRef]
- N’Dri, A.B.; Kpangba, K.P.; Werner, P.A.; Koffi, K.F.; Bakayoko, A. The Response of Sub-Adult Savanna Trees to Six Successive Annual Fires: An Experimental Field Study on the Role of Fire Season. J. Appl. Ecol. 2022, 59, 1347–1361. [Google Scholar] [CrossRef]
- Flory, S.L.; Bauer, J.; Phillips, R.P.; Clay, K. Effects of a Non-Native Grass Invasion Decline over Time. J. Ecol. 2017, 105, 1475–1484. [Google Scholar] [CrossRef]
- Koffi, K.F.; N’Dri, A.B.; Lata, J.-C.; Konaté, S.; Srikanthasamy, T.; Konaré, S.; Konan, M.; Barot, S. Effect of Fire Regimes on the Demographic Parameters of the Perennial Tussock Grasses of a Humid Savanna. J. Veg. Sci. 2019, 30, 950–962. [Google Scholar] [CrossRef]
- Amoako, E.; Misana, S.; Kranjac-Berisavljevic, G.; Zizinga, A.; Duwieja, B.A. Effect of the Seasonal Burning on Tree Species in the Guinea Savanna Woodland, Ghana: Implications for Climate Change Mitigation. Appl. Ecol. Environ. Res. 2018, 16, 1935–1949. [Google Scholar] [CrossRef]
- Oliveira, S.L.J.; Maier, S.W.; Pereira, J.M.C.; Russell-Smith, J. Seasonal Differences in Fire Activity and Intensity in Tropical Savannas of Northern Australia Using Satellite Measurements of Fire Radiative Power. Int. J. Wildland Fire 2015, 24, 249. [Google Scholar] [CrossRef]
- N’Dri, A.B.; Kpré, A.J.-N.; Kpangba, K.P.; Soro, T.D.; Kouassi, K.V.; Koffi, K.F.; Kouamé, Y.A.G.; Koffi, A.B.; Konan, L.N. Experimental Study of Fire Behavior in Annually Burned Humid Savanna of West Africa in the Context of Bush Encroachment. In Sustainable Development in Africa; Leal Filho, W., Pretorius, R., de Sousa, L.O., Eds.; World Sustainability Series; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 491–505. [Google Scholar]
- Moleele, N.M.; Ringrose, S.; Matheson, W.; Vanderpost, C. More Woody Plants? The Status of Bush Encroachment in Botswana’s Grazing Areas. J. Environ. Manag. 2002, 64, 3–11. [Google Scholar] [CrossRef]
- Koffi, K.F.; N’Dri, A.B.; Konaré, S.; Srikanthasamy, T.; Lata, J.-C.; Konaté, S.; Konan, M.; Barot, S. Demography of the Dominant Perennial Grass Species of a Humid African Savanna. Acta Oecologica 2022, 114, 103816. [Google Scholar] [CrossRef]
- Koffi, K.F.; N’Dri, A.B.; Lata, J.-C.; Konaté, S.; Srikanthasamy, T.; Konan, M.; Barot, S. Effect of Fire Regime on the Grass Community of the Humid Savanna of Lamto, Ivory Coast. J. Trop. Ecol. 2019, 35, 1–7. [Google Scholar] [CrossRef]
- Lamotte, M.; Tireford, J.-L. Le Climat de la Savane de Lamto (Côte d’Ivoire) et sa Place Dans les Climats de l’Ouest Africain; Université d’Abidjan, Station d’Ecologie Tropicale de Lamto: N’douci, Côte d’Ivoire, 1988; pp. 1–146. [Google Scholar]
- Abbadie, L.; Gignoux, J.; Lepage, M.; Le Roux, X. Environmental Constraints on Living Organisms. In Lamto; Abbadie, L., Gignoux, J., Le Roux, X., Lepage, M., Eds.; Ecological Studies; Springer: New York, NY, USA, 2006; Volume 179, pp. 45–61. [Google Scholar]
- Harvell, C.D.; Caswell, H.; Simpson, P. Density Effects in a Colonial Monoculture: Experimental Studies with a Marine Bryozoan (Membranipora membranacea L.). Oecologia 1990, 82, 227–237. [Google Scholar] [CrossRef]
- Caswell, H. Matrix Population Models: Construction, Analysis, and Interpretation; Sinauer Associates Inc.: Sunderland, UK, 2001; pp. 1–770. [Google Scholar]
- Crouse, D.T.; Crowder, L.B.; Caswell, H. A Stage-Based Population Model for Loggerhead Sea Turtles and Implications for Conservation. Ecology 1987, 68, 1412–1423. [Google Scholar] [CrossRef]
- Huenneke, L.F.; Marks, P.L. Stem Dynamics of the Shrub Alnus incana ssp. rugosa: Transition Matrix Models. Ecology 1987, 68, 1234–1242. [Google Scholar]
- Caswell, H. Matrix Population Models; Sinauer Associates Inc.: Sunderland, UK, 1989; pp. 1–328. [Google Scholar]
- De Kroon, H.; Plaisier, A.; Van Groenendael, J.; Caswell, H. Elasticity: The Relative Contribution of Demographic Parameters to Population Growth Rate. Ecology 1986, 67, 1427–1431. [Google Scholar] [CrossRef]
- Van Groenendael, J.; De Kroon, H.; Caswell, H. Projection Matrices in Population Biology. Trends Ecol. Evol. 1988, 3, 264–269. [Google Scholar] [CrossRef]
- Fingleton, B. Models of Category Counts; Cambridge University Press: Cambridge, UK, 1984; pp. 1–204. [Google Scholar]
- Cochran, M.E.; Ellner, S. Simple Methods for Calculating Age-Based Life History Parameters for Stage-Structured Populations. Ecol. Monogr. 1992, 62, 345–364. [Google Scholar] [CrossRef]
- Barot, S.; Gignoux, J.; Legendre, S. Stage-Structured Matrix Models and Age Estimates. Oikos 2002, 96, 56–61. [Google Scholar] [CrossRef]
- Keyfitz, N. Introduction to the Mathematics of Populations; Addison-Wesley Educational Publishers Inc: Boston, MA, USA, 1968; pp. 1–450. [Google Scholar]
- Stubben, C.J.; Milligan, B.G. Estimating and Analyzing Demographic Models Using the Popbio Package in R. J. Stat. Softw. 2007, 22, 1–23. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2021. [Google Scholar]
- Liu, H.; Menges, E.S.; Quintana-Ascencio, P.F. Population Viability Analyses of Chamaecrista keyensis: Effects of Fire Season and Frequency. Ecol. Appl. 2005, 15, 210–221. [Google Scholar] [CrossRef]
- Lowe, S.; Browne, M.; Boudjelas, M.; De Poorter, M. 100 of the World’s Worst Invasive Alien Species: A Selection from the Global Invasive Species Database; IUCN: Gland, Switzerland; Hollands Printing Ltd: Auckland, New Zealand, 2000; pp. 1–12. [Google Scholar]
- D’Antonio, C.M.; Vitousek, P.M. Biological Invasions by Exotic Grasses, the Grass/Fire Cycle, and Global Change. Annu. Rev. Ecol. Syst. 1992, 2, 63–87. [Google Scholar] [CrossRef]
- Raventós, J.; Silva, J.F. Competition Effects and Responses to Variable Numbers of Neighbours in Two Tropical Savanna Grasses in Venezuela. J. Trop. Ecol. 1995, 11, 39–52. [Google Scholar] [CrossRef]
- Hiers, J.K.; Wyatt, R.; Mitchell, R.J. The Effects of Fire Regime on Legume Reproduction in Longleaf Pine Savannas: Is a Season Selective? Oecologia 2000, 125, 521–530. [Google Scholar] [CrossRef]
- Zimmermann, J.; Higgins, S.I.; Grimm, V.; Hoffmann, J.; Linstädter, A. Grass Mortality in Semi-Arid Savanna: The Role of Fire, Competition and Self-Shading. Perspect. Plant Ecol. Evol. Syst. 2010, 12, 1–8. [Google Scholar] [CrossRef]
- Kaye, T.N.; Pendergrass, K.L.; Finley, K.; Kauffman, J.B. The Effect of Fire on the Population Viability of an Endangered Prairie Plant. Ecol. Appl. 2001, 11, 15. [Google Scholar] [CrossRef]
- Silva, J.F.; Raventos, J.; Caswell, H.; Trevisan, M.C. Population Responses to Fire in a Tropical Savanna Grass, Andropogon semiberbis: A Matrix Model Approach. J. Ecol. 1991, 79, 345–355. [Google Scholar] [CrossRef]
- Garnier, L.K.; Durand, J.; Dajoz, I. Limited Seed Dispersal and Microspatial Population Structure of an Agamospermous Grass of West African Savannahs, Hyparrhenia diplandra (Poaceae). Am. J. Bot. 2002, 89, 1785–1791. [Google Scholar] [CrossRef] [PubMed]
- Hulbert, L.C. Causes of Fire Effects in Tallgrass Prairie. Ecology 1988, 69, 46–58. [Google Scholar] [CrossRef]
- Srikanthasamy, T.; Barot, S.; Koffi, F.K.; Tambosco, K.; Marcangeli, Y.; Carmignac, D.; N’Dri, A.B.; Gervaix, J.; Roux, X.L.; Lata, J.-C. Short-Term Impact of Fire on the Total Soil Microbial and Nitrifier Communities in a Wet Savanna. Ecol. Evol. 2021, 11, 9958–9969. [Google Scholar] [CrossRef] [PubMed]
- Baruch, Z.; Bilbao, B. Effects of Fire and Defoliation on the Life History of Native and Invader C4 Grasses in a Neotropical Savanna. Oecologia 1999, 119, 510–520. [Google Scholar] [CrossRef]
- Lesica, P. Effects of Fire on the Demography of the Endangered, Geophytic Herb Silene spaldingii (Caryophyllaceae). Am. J. Bot. 1999, 86, 996–1002. [Google Scholar] [CrossRef]
- Jiménez-Sierra, C.; Mandujano, M.C.; Eguiarte, L.E. Are Populations of the Candy Barrel Cactus (Echinocactus platyacanthus) in the Desert of Tehuacán, Mexico at Risk? Population Projection Matrix and Life Table Response Analysis. Biol. Conserv. 2007, 135, 278–292. [Google Scholar] [CrossRef]
- Jiménez-Valdés, M.; Godínez-Alvarez, H.; Caballero, J.; Lira, R. Population Dynamics of Agave marmorata Roezl. under Two Contrasting Management Systems in Central Mexico. Econ. Bot. 2010, 64, 149–160. [Google Scholar] [CrossRef]
- Morris, W.F.; Tuljapurkar, S.; Haridas, C.V.; Menges, E.S.; Horvitz, C.C.; Pfister, C.A. Sensitivity of the Population Growth Rate to Demographic Variability within and between Phases of the Disturbance Cycle. Ecol. Lett. 2006, 9, 1331–1341. [Google Scholar] [CrossRef]
- Williams, J.L.; Ellis, M.M.; Bricker, M.C.; Brodie, J.F.; Parsons, E.W. Distance to Stable Stage Distribution in Plant Populations and Implications for Near-Term Population Projections: Distance to Stable Stage Distribution. J. Ecol. 2011, 99, 1171–1178. [Google Scholar] [CrossRef]
- Clutton–Brock, T.H.; Coulson, T. Comparative Ungulate Dynamics: The Devil Is in the Detail. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2002, 357, 1285–1298. [Google Scholar] [CrossRef] [PubMed]
- Ujvari, B.; Andersson, S.; Brown, G.; Shine, R.; Madsen, T. Climate-Driven Impacts of Prey Abundance on the Population Structure of a Tropical Aquatic Predator. Oikos 2010, 119, 188–196. [Google Scholar] [CrossRef]
- Liu, H.; Menges, E.S. Winter Fires Promote Greater Vital Rates in the Florida Keys than Summer Fires. Ecology 2005, 86, 1483–1495. [Google Scholar] [CrossRef]
- Violle, C.; Richarte, J.; Navas, M.-L. Effects of Litter and Standing Biomass on Growth and Reproduction of Two Annual Species in a Mediterranean Old-Field. J. Ecol. 2006, 94, 196–205. [Google Scholar] [CrossRef]
- Wang, P.; Stieglitz, T.; Zhou, D.W.; Cahill, J.F., Jr. Are Competitive Effect and Response Two Sides of the Same Coin, or Fundamentally Different? Funct. Ecol. 2010, 24, 196–207. [Google Scholar] [CrossRef]
- Miller, R.G.; Tangney, R.; Enright, N.J.; Fontaine, J.B.; Merritt, D.J.; Ooi, M.K.J.; Ruthrof, K.X.; Miller, B.P. Mechanisms of Fire Seasonality Effects on Plant Populations. Trends Ecol. Evol. 2019, 34, 1104–1117. [Google Scholar] [CrossRef] [PubMed]
- Schemske, D.W.; Husband, B.C.; Ruckelshaus, M.H.; Goodwillie, C.; Parker, I.M.; Bishop, J.G. Evaluating Approaches to the Conservation of Rare and Endangered Plants. Ecology 1994, 75, 584–606. [Google Scholar] [CrossRef]
- Kesler, H.C.; Trusty, J.L.; Hermann, S.M.; Guyer, C. Demographic Responses of Pinguicula ionantha to Prescribed Fire: A Regression-Design LTRE Approach. Oecologia 2008, 156, 545–557. [Google Scholar] [CrossRef]
- Douffi, K.G.-C.; Yao, A.C.; Koffi, K.J.; Traore, A.S.; Kone, M. Afforestation in Response to Thermal Change in the Forest-Savannah Transition of the Lamto Scientific Reserve, Côte d’Ivoire. Eur. J. For. Eng. 2021, 7, 45–56. [Google Scholar]
- Van Wilgen, B.W.; Govender, N.; Biggs, H.C.; Ntsala, D.; Funda, X.N. Response of Savanna Fire Regimes to Changing Fire Management Policies in a Large African National Park. Conserv. Biol. 2004, 18, 1533–1540. [Google Scholar] [CrossRef]
- Srikanthasamy, T.; Leloup, J.; N’Dri, A.B.; Barot, S.; Gervaix, J.; Koné, A.W.; Koffi, K.F.; Le Roux, X.; Raynaud, X.; Lata, J.-C. Contrasting Effects of Grasses and Trees on Microbial N-Cycling in an African Humid Savanna. Soil Biol. Biochem. 2018, 117, 153–163. [Google Scholar] [CrossRef]

| Species | Fire Treatments | λs | SE | 95% Confidence Interval |
|---|---|---|---|---|
| Andropogon canaliculatus | early fire | 0.978 | 0.040 | [0.899, 1.057] |
| middle fire | 0.969 | 0.031 | [0.907, 1.030] | |
| late fire | 0.945 | 0.047 | [0.853, 1.037] | |
| no fire | 0.915 | 0.055 | [0.807, 1.024] | |
| Andropogon schirensis | early fire | 0.989 | 0.099 | [0.794, 1.185] |
| middle fire | 0.985 | 0.047 | [0.893, 1.078] | |
| late fire | 0.670 | 0.103 | [0.467, 0.872] | |
| no fire | 0.920 | 0.123 | [0.677, 1.162] | |
| Hyparrhenia diplandra | early fire | 0.951 | 0.043 | [0.865, 1.036] |
| middle fire | 0.953 | 0.036 | [0.881, 1.025] | |
| late fire | 0.783 | 0.065 | [0.655, 0.912] | |
| no fire | 0.933 | 0.054 | [0.826, 1.040] | |
| Loudetia simplex | early fire | 1.061 | 0.060 | [0.943, 1.179] |
| middle fire | 0.872 | 0.042 | [0.788, 0.955] | |
| late fire | 0.758 | 0.064 | [0.632, 0.885] | |
| no fire | - | - | - |
| Model | Effects | G2 | ΔG2 | df | Δdf | p-Value |
|---|---|---|---|---|---|---|
| DS,SET | 1573.7 | 375 | <0.001 | |||
| DSE,SET | 1176.1 | 300 | <0.001 | |||
| DE,DSE | Species | 397.6 | 75 | <0.001 | ||
| DST,SET | 900.9 | 300 | <0.001 | |||
| DT,DST | Treatment | 672.8 | 75 | <0.001 | ||
| DSE,DST,SET | 515.0 | 225 | <0.001 | |||
| DT,DST | Treatment | 661.1 | 75 | <0.001 | ||
| DE,DSE | Species | 385.9 | 75 | <0.001 | ||
| DSET | 0.0 | 0.0 | 1.000 | |||
| DET,DSET | Species × Treatment | 515.0 | 225 | <0.001 |
| Species | Treatments | Fate | |||||
|---|---|---|---|---|---|---|---|
| Dead | Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | ||
| Andropogon canaliculatus | early fire | 11.2 | 11.4 | 24.7 | 23.6 | 14.6 | 14.6 |
| middle fire | 7.0 | 15.2 | 29.5 | 25.1 | 11.0 | 12.2 | |
| late fire | 14.7 | 16.4 | 30.8 | 21.9 | 10.1 | 6.1 | |
| no fire | 16.3 | 9.1 | 20.8 | 25.8 | 16.9 | 11.2 | |
| Andropogon schirensis | early fire | 11.9 | 9.9 | 33.8 | 24.8 | 14.6 | 5.0 |
| middle fire | 5.3 | 7.2 | 23.3 | 31.4 | 19.3 | 13.5 | |
| late fire | 36.8 | 10.1 | 32.0 | 14.5 | 4.8 | 1.8 | |
| no fire | 17.3 | 12.8 | 19.6 | 20.7 | 12.3 | 17.3 | |
| Hyparrhenia diplandra | early fire | 8.6 | 7.2 | 25.1 | 28.3 | 16.3 | 14.6 |
| middle fire | 7.2 | 9.7 | 25.6 | 29.9 | 17.1 | 10.5 | |
| late fire | 33.7 | 12.8 | 29.0 | 18.7 | 4.7 | 1.1 | |
| no fire | 13.2 | 8.4 | 24.0 | 27.4 | 16.3 | 10.7 | |
| Loudetia simplex | early fire | 5.1 | 14.0 | 40.9 | 33.4 | 5.4 | 1.3 |
| middle fire | 10.3 | 24.3 | 30.2 | 22.5 | 8.1 | 4.6 | |
| late fire | 27.3 | 14.7 | 30.0 | 23.1 | 4.0 | 1.0 | |
| no fire | - | - | - | - | - | - | |
| Species | Treatments | Matrix Entry Categories | |||
|---|---|---|---|---|---|
| Fecundity | Stasis | Retrogression | Growth | ||
| Andropogon canaliculatus | early fire | 7.5 | 46.4 | 19.0 | 26.8 |
| middle fire | 9.4 | 55.9 | 12.0 | 22.5 | |
| late fire | 8.2 | 49.3 | 13.4 | 28.9 | |
| no fire | 4.4 | 51.3 | 17.4 | 26.7 | |
| Andropogon schirensis | early fire | 6.9 | 50.2 | 15.6 | 27.1 |
| middle fire | 3.1 | 59.3 | 16.4 | 21.0 | |
| late fire | 10.5 | 33.0 | 20.7 | 35.6 | |
| no fire | 12.1 | 42.5 | 12.6 | 32.5 | |
| Hyparrheniadiplandra | early fire | 4.9 | 55.1 | 16.2 | 23.5 |
| middle fire | 5.5 | 52.2 | 16.5 | 25.7 | |
| late fire | 15.0 | 34.9 | 13.0 | 36.9 | |
| no fire | 8.1 | 41.0 | 17.6 | 33.0 | |
| Loudetiasimplex | early fire | 13.3 | 44.7 | 13.0 | 28.8 |
| middle fire | 16.8 | 48.9 | 9.0 | 25.0 | |
| late fire | 16.2 | 39.9 | 11.3 | 32.3 | |
| no fire | - | - | - | - | |
| Species | Treatment 1 × Treatment 2 | ∆𝜆 | C-Value | Demographic Parameters | |||
|---|---|---|---|---|---|---|---|
| Fec. | Sta. | Ret. | Gro. | ||||
| Andropogon canaliculatus | middle fire × early fire middle fire × late fire middle fire × no fire early fire × late fire early fire × no fire late fire × no fire | 0.0091 −0.0238 −0.0531 −0.0329 −0.0623 −0.0293 | 0.0108 −0.0249 −0.0545 −0.0312 −0.0631 −0.0290 | −0.016 0.006 −0.019 0.028 −0.003 −0.026 | −0.095 −0.086 −0.085 0.020 0.008 −0.012 | 0.008 −0.013 −0.037 −0.015 −0.038 −0.014 | 0.114 0.069 0.088 −0.064 −0.029 0.024 |
| Andropogonschirensis | middle fire × early fire middle fire × late fire middle fire × no fire early fire × late fire early fire × no fire late fire × no fire | 0.0041 −0.3157 −0.0656 −0.3198 −0.0697 0.2500 | 0.0036 −0.3150 −0.0630 −0.3172 −0.0681 0.2484 | 0.035 0.020 0.076 −0.013 0.035 0.066 | −0.069 −0.361 −0.180 −0.281 −0.113 0.155 | 0.072 0.059 −0.017 −0.006 −0.084 −0.055 | −0.034 −0.033 0.058 −0.015 0.094 0.082 |
| Hyparrhenia diplandra | middle fire × early fire middle × late fire middle fire × no fire early fire × late fire early fire × no fire late fire × no fire | −0.0026 −0.1698 −0.0199 −0.1672 −0.0173 0.1499 | −0.0028 −0.1681 −0.0198 −0.1744 −0.0171 0.1519 | −0.026 0.047 0.003 0.092 0.033 −0.053 | 0.011 −0.208 −0.108 −0.223 −0.122 0.108 | −0.036 0.014 0.001 0.047 0.041 −0.017 | 0.048 −0.022 0.084 −0.091 0.029 0.113 |
| Loudetia simplex | middle fire × early fire middle fire × late fire middle fire × no fire early fire × late fire early fire × no fire late fire × no fire | 0.1890 −0.1138 - −0.3028 - - | 0.1862 −0.1142 - −0.3012 - - | −0.051 −0.037 - 0.010 - - | 0.043 −0.120 - −0.166 - - | 0.020 −0.010 - −0.034 - - | 0.173 0.054 - −0.110 - - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koffi, K.F.; N’Dri, A.B.; Srikanthasamy, T.; Lata, J.-C.; Konaté, S.; Konan, M.; Barot, S. The Demographic Response of Grass Species to Fire Treatments in a Guinean Savanna. Fire 2022, 5, 193. https://doi.org/10.3390/fire5060193
Koffi KF, N’Dri AB, Srikanthasamy T, Lata J-C, Konaté S, Konan M, Barot S. The Demographic Response of Grass Species to Fire Treatments in a Guinean Savanna. Fire. 2022; 5(6):193. https://doi.org/10.3390/fire5060193
Chicago/Turabian StyleKoffi, Kouamé Fulgence, Aya Brigitte N’Dri, Tharaniya Srikanthasamy, Jean-Christophe Lata, Souleymane Konaté, Marcel Konan, and Sébastien Barot. 2022. "The Demographic Response of Grass Species to Fire Treatments in a Guinean Savanna" Fire 5, no. 6: 193. https://doi.org/10.3390/fire5060193
APA StyleKoffi, K. F., N’Dri, A. B., Srikanthasamy, T., Lata, J.-C., Konaté, S., Konan, M., & Barot, S. (2022). The Demographic Response of Grass Species to Fire Treatments in a Guinean Savanna. Fire, 5(6), 193. https://doi.org/10.3390/fire5060193







