1. Introduction
The prevalence of wildland fires in recent years in the western United States illustrates the need for improved understanding and management of fire behavior. Fires in grasslands have been studied in detail both with empirical models [
1] and detailed simulations involving computational fluid dynamics [
2,
3]. Fires in tree crowns have also been studied, although perhaps in less detail [
4]. Less research has been performed on fire behavior in shrubs, where the “fuel bed” is heterogenous in both the horizontal and vertical dimensions. One of the aspects of shrub combustion is the spread of fire through a spatially sparse fuel. Combustion experiments have been performed on individual leaves [
5,
6,
7,
8], and on shrubs [
9,
10,
11,
12]. Simulations of the combustion of shrubs have been performed using computational fluid dynamics [
13] where the shrub volume is represented by a uniform fuel bed with a specified porosity and permeability. Attempts to model shrub combustion that utilize more informed geometries of shrubs, but without the complicated computational fluid dynamics, have also been performed [
11,
12]. Such reduced order shrub combustion models use empirical descriptions of flame geometry to describe leaf-to-leaf flame propagation, and have attempted to use flame merging behavior equations developed from horizontally spaced pool fires or wood cribs. One of the main needs for accurate shrub combustion modeling is the complicated flame growth pattern caused by the merging of flames from multiple leaves and small branches in three dimensions. Such descriptions of flame merging behavior will also be useful in detailed descriptions of fires in other fuels, including trees.
The interactions of neighboring flames have only been studied using regularly spaced fuel sources located on a horizontal plane [
13,
14,
15,
16,
17,
18]. Flames in a burning shrub or tree merge or coalesce to form large flames from fuel arrangements which are not described by horizontal plane geometries. A careful study of flame interactions from fuels in three-dimensional arrangements is a necessary step in strengthening our understanding of flames in complex fuel structures.
This paper describes a set of experiments where flames interactions were studied by changing both the horizontal and vertical spacing between flame sources. In order to provide a semi-stable flame, zirconia felt pads soaked in n-heptane were used to provide the flames. Computerized image analysis permitted frame-by-frame characterization of flame behavior, including merging probability and flame shape. Correlations of these measures of flame behavior were developed for this system, with the eventual goal that a generalized model of flame merging behavior can be developed.
2. Background
The merging behavior of fires from individual fuel or shrub elements involves the interaction of turbulent flaming fronts, formation of intervening regions which may be starved of oxygen, and changes in conditions, under which any intervening unburned fuel element is ignited. Merging behavior is complicated, involving changes in convective and radiative heat transfer and mass transfer. Although our motivation is on wildland fuels, the underlying physics are relevant to many situations, such as wildland urban interface fires involving adjacent structures, warehouse fires from stacked containers, industrial flare spacing, and ground-to-shrub-to-crown progression of fires (i.e., ladder fuels). Flame merging also takes place at larger scales. For instance, flame merging occurs when a main fire meets a spot fire, or when multiple spot fires grow and interact with each other [
19,
20]. Other examples include flame merging in back fires and fire complexes.
Finney and McAllister [
20] discussed the mechanisms at work in various merging regimes, and reviewed the literature on fire merging, but found no unifying method to describe flame merging behavior or the conditions needed to produce a fire with mass fire characteristics. Flame merging in two-dimensional horizontal arrays has been studied somewhat in jets [
21,
22], pool fires [
14,
17,
18,
23,
24,
25,
26,
27], burners [
16,
27,
28,
29,
30], and wood cribs [
16,
31].
Not much fundamental research has been performed on vertically spaced fuel elements. Arrays of vertically oriented match sticks in horizontal arrays or arrays on slopes have been studied [
32,
33,
34]. These studies have focused on critical spacing for flame merging as well as flame merging effects on flame height. Several correlations have been developed for flame height and merging probability as a function of normalized flame spacing. Pickett et al. [
35] studied flame interactions and burning characteristics of two live leaves suspended above a flat-flame burner. These leaves were positioned horizontally, one above the other. Gollner et al. [
36] studied flame propagation in arrays of vertically placed matchsticks. Convective heating was determined to be the dominant physical process in upward flame propagation in this experiment. Vasanth et al. [
37] made computational fluid dynamics (CFD) calculations of two pool fires at different vertical heights and compared these with measurements by Fukuda et al. [
38]. The burning rate of the upper pool fire was higher than for the lower pool fire, but had a lower flame height. Experimental results were explained based on air flow patterns as well as radiative and convective heat feedback. The containers for the upper pool fires in this situation were likely involved in the heat transfer system. Flame merging in 3-D arrangements requires further study in order to describe fire behavior in complex fuel structures, such as trees or shrubs.
The purpose of this research was to investigate the merging behavior of small-scale buoyant flames that might be representative of a leaf in a shrub. The eventual idea is to try to understand how a 5 to 40 cm flame from a single leaf merges with flames from neighboring leaves to form large flames (2–3 m high) when a shrub burns. Since leaves in a shrub occur in a 3-D geometry, flame merging in both vertical and horizontal spacing arrangements were studied.
3. Materials and Methods
3.1. Two-Pad Arrangement
A repeatable, bench-top buoyant flame with a sufficient duration was desired for this project. Several systems were explored, including natural gas jets, cardboard, balled-up excelsior (shredded poplar strips), paper, and match sticks. None of these systems gave us repeatable buoyant flames of a sufficient enough duration to explore flame merging behavior, due to curling of the solid or interactions with the tube (for the case of the gas flame jet).
Finally, a system was developed to soak porous zirconia felt pads in n-heptane, suspending the pad on a ceramic rod. The zirconia felt pads were 3 mm thick and cut into 3.8 × 3.8 cm squares. Flames from these n-heptane-soaked pads were about 40 cm high, lasted approximately 55 s, and were fairly repeatable. Care was taken to avoid air currents in the lab as much as possible. The distance between the flame and the lab ceiling was 3.5 m.
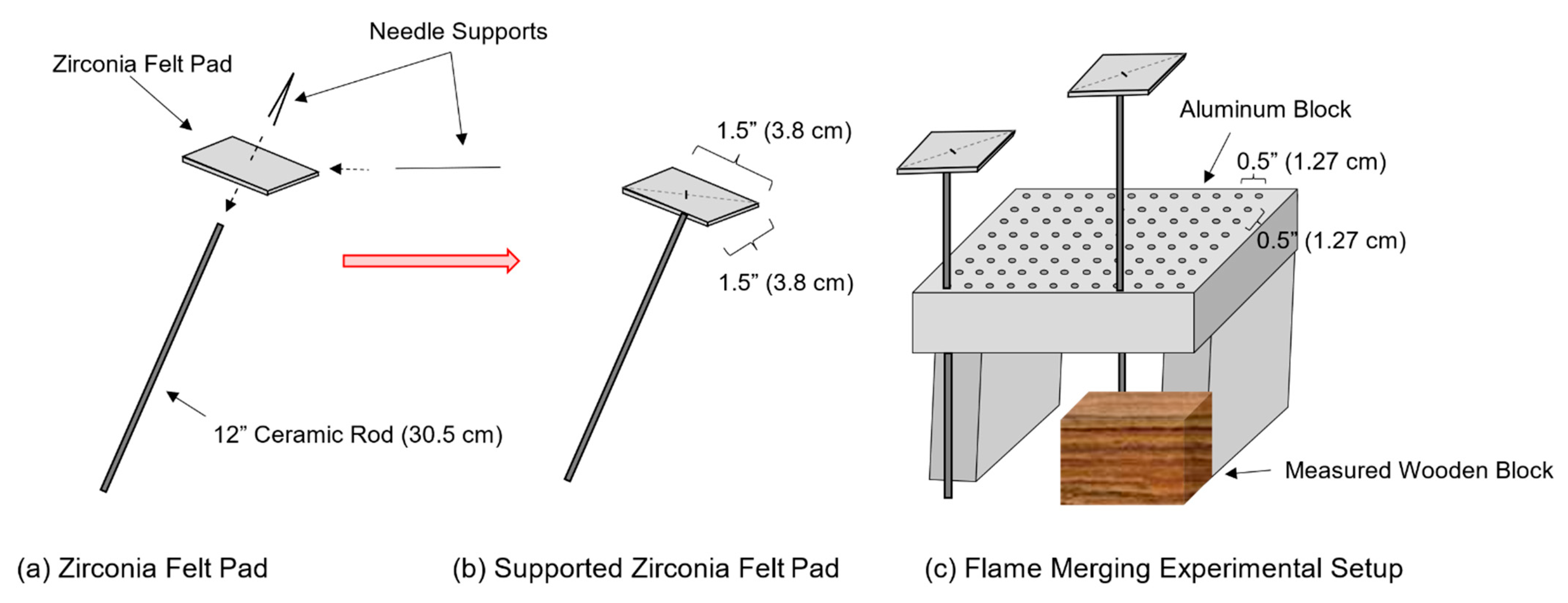
Two zirconia felt pads were individually placed on 30.5 cm long ceramic rods (32 mm diameter with two longitudinal holes) and pinned in place using thin U-shaped needles (see
Figure 1a). An additional straight needle was then placed horizontally through each zirconia felt pad to prevent the felt from tipping during the combustion process and to provide additional stability. These felt pads were soaked in n-heptane for three minutes to allow for absorption of the fuel into the felt. After three minutes, the pads were immediately removed from the n-heptane, attached to the ceramic rods, and placed into a pre-drilled aluminum block (see
Figure 1b) to provide structural support and accurate measurements of the distance between the pads. An additional three minutes were allotted to set up the block before ignition of the pads, during which time the pads drip-dried concurrently with a small amount of evaporation.
Holes were drilled through the black anodized aluminum block every 0.5 inches (1.27 cm) to hold the ceramic rods in place. This array of holes provided an accurate way to set the horizontal distance between the pads that could be easily repeated. Additionally, this block was elevated from the table so that the rods slid through it. The distance from the benchtop to the top of the aluminum plate was 18.6 cm, leaving a minimum vertical space of 11.9 cm between the aluminum block and the pad. Wooden spacers were placed underneath the aluminum block to add a vertical separation dimension to the grid system. A ruler was placed next to the aluminum block within the same plane as the ceramic rods to provide an appropriate scale for flame image analysis.
Once the felt pads were set in place (and after the 3 min equilibration period since their being removed from the n-heptane container), the two pads were ignited simultaneously using two household lighters. Flame images were recorded using a Samsung HMX-F90 camera at 30 frames per second.
3.2. Three-Pad Arrangement
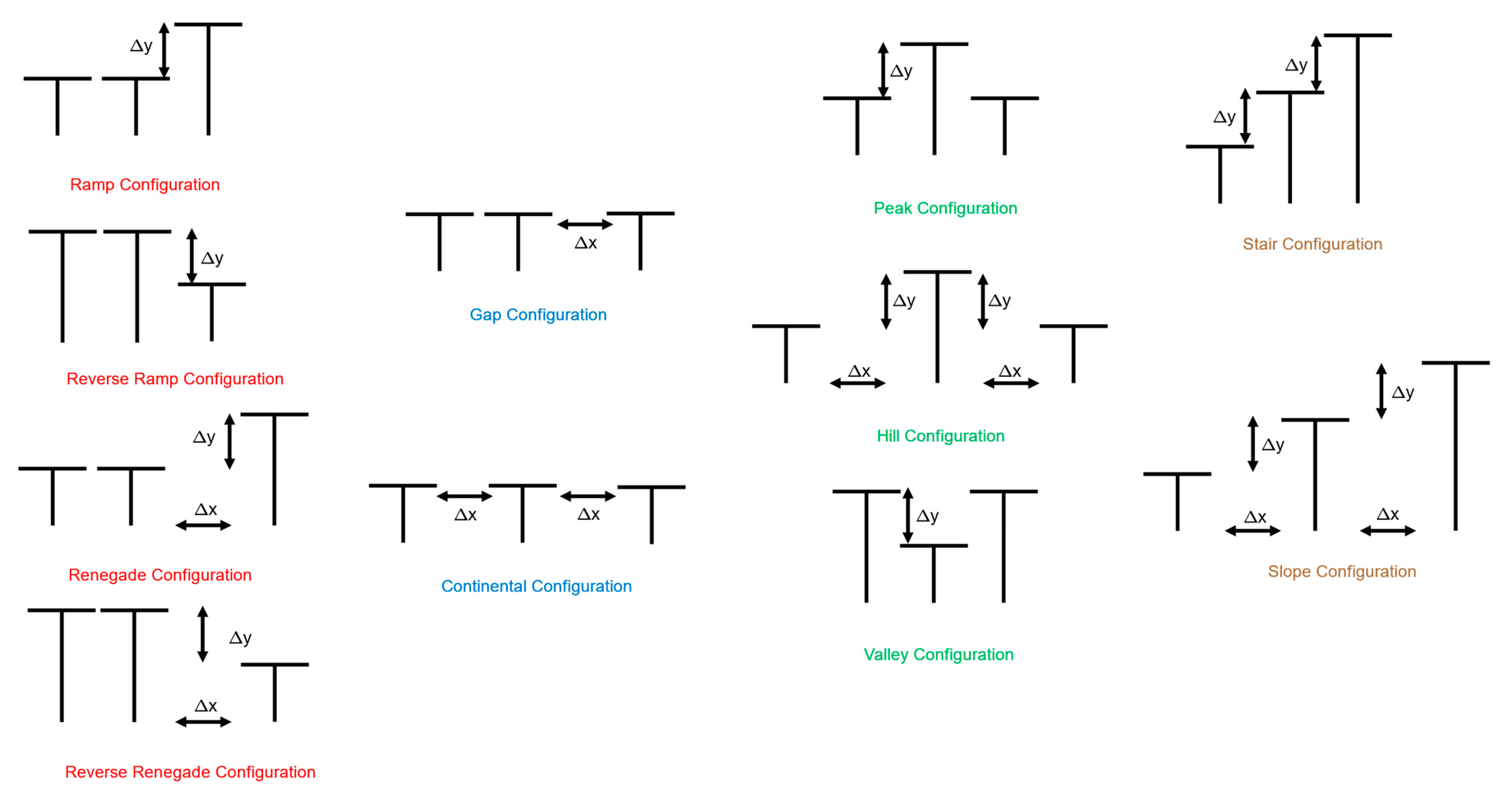
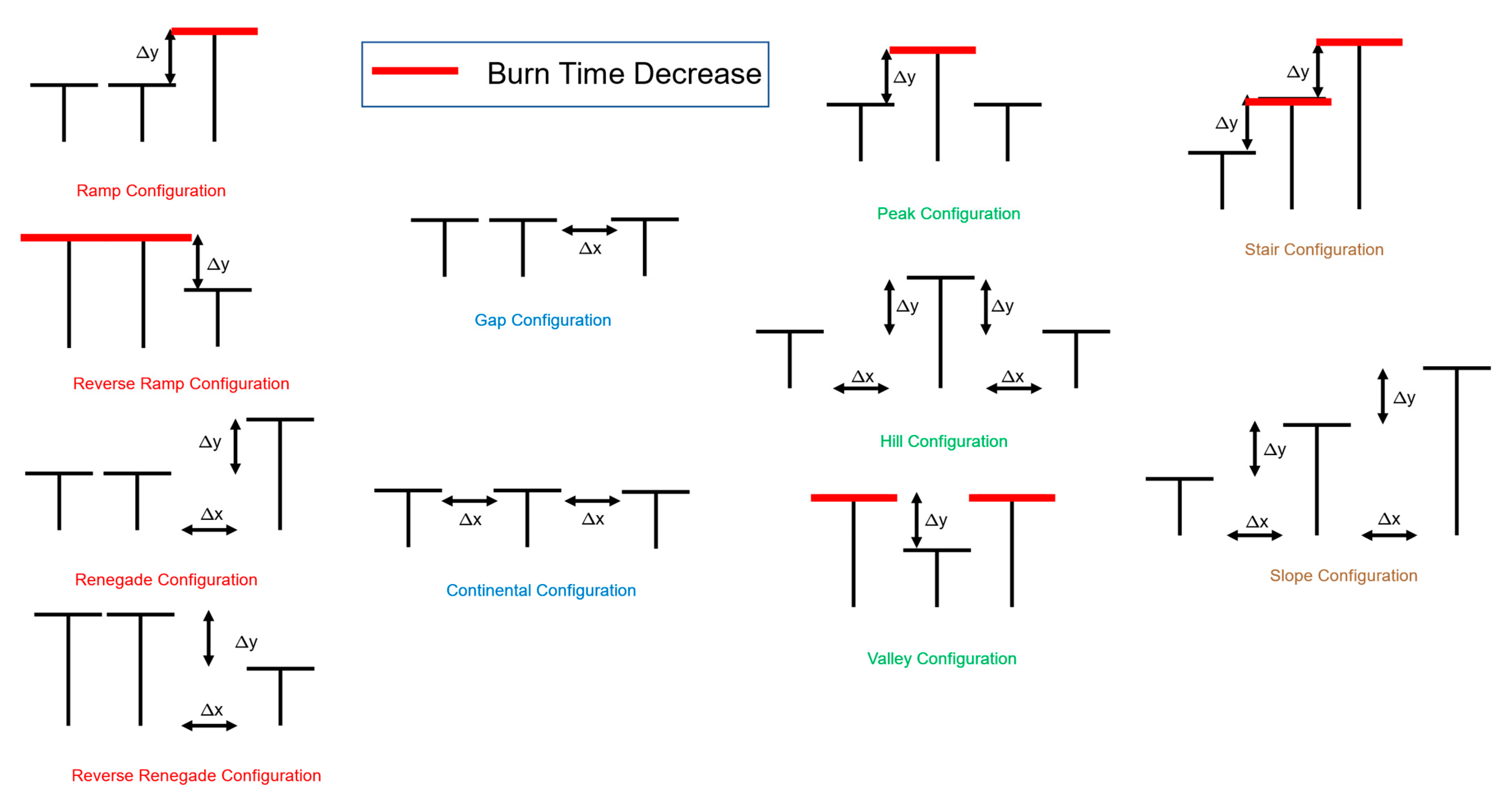
The same zirconia felt pads, support rods, and aluminum and wood blocks that were used for two-pad configurations were used for three-pad configurations. In the three-pad configuration, three zirconia felt pads, all in the same vertical plane, were arranged using the drilled aluminum block and wood spacers to achieve specific horizontal and vertical spacing between the pads. Four general configurations for three pads were devised to change the general shape of the configuration, as shown in the columns in
Figure 2. The labels for each configuration are colored by similarity. The horizontal and vertical spacing between the pads (∆x and ∆y, measured from pad edge to pad edge) were varied, as indicated in
Figure 2. The names for each configuration in
Figure 2 are used for convenience.
3.3. Data Collection and Analysis
Frame-by-frame image analysis of each video was conducted using a MATLAB code to determine the time-dependent flame height, width, and area. The MATLAB analysis procedure first rendered the color image to a gray-scale image (see
Figure 3a,b), and then to a black and white image (see
Figure 3c). The number of white pixels were counted, thereby determining the total flame area. Flame height and width were calculated according to
Figure 3c, again counting white pixels, but in these cases only determining a one-dimensional length and width. The ruler in the image is used to change the flame height, width, and area from the number of pixels into centimeters.
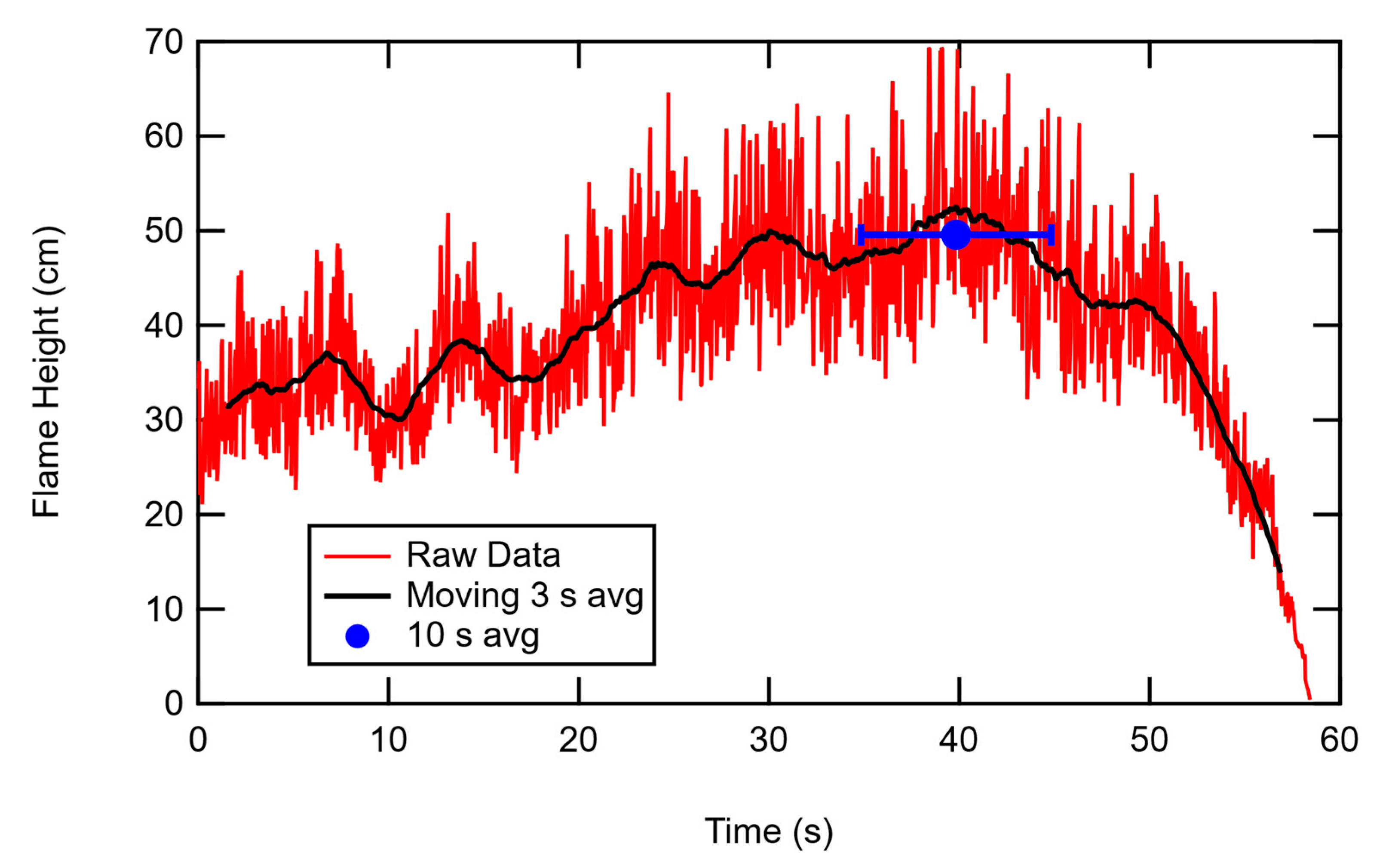
The time-dependent flame characteristics were noisy due to the turbulence, as shown in
Figure 4 for flame height. Due to effects of flame ignition and extinction, the flame heights, areas, and widths were first filtered using a 3 s moving average (heavy black line in
Figure 4). The time of the maximum filtered flame height was determined, and average flame characteristics (height, width, and area) were taken from a time window of 10 s centered on the time when the filtered flame height was maximum. The blue dot in
Figure 4 is located at the time and average flame height determined for this set of data. The horizontal “error bars” represent the 10 s averaging time at this location.
The flame image in each frame was analyzed to determine if the flames were touching. Percent merging was defined in this study as the percentage of frames that showed a connection or overlap between the flame images.
Each configuration of pad spacing for the two-pad and three-pad experiments was repeated between 3 and 18 times in order to reduce the confidence intervals of the mean flame characteristics. Time-averaged (i.e., frame-averaged) flame characteristics were obtained for each individual experiment. Mean flame characteristics were obtained for each configuration by averaging the data from the repeat experiments, and the 95% confidence interval on each measured flame characteristic was determined for each configuration.
3.4. Flame Characteristics and Normalization
The flame parameters and separation distances were normalized by the average flame properties of a single pad, as summarized in
Table 1. Flame heights (
L) were divided by the average height of a single flame (
L1), which was found to be 38.7 cm. Flame widths (
W) were divided by the average width of a single pad flame (
W1), which was found to be 12.4 cm. Flame areas (
A) were divided by the average area of a flame from a single pad (
A1), which was found to be 232.7 cm
2. The flame height is often normalized by the characteristic dimension of the flame source, and is termed
L/
D, where
D in this case is the pad width (3.81 cm). The normalized heat release rate (
Q*), which was calculated using the formulation described in Drysdale [
39] (Equation (1)), was 10.9, indicating a buoyant flame regime.
Separation distance normalization was a bit more involved; horizontal (Δ
x) and vertical (Δ
y) separation distances were divided by the width of a single pad (
Wp). However, because some configurations have both horizontal and vertical separations and some configurations only have one or the other, it was necessary to make a total separation distance parameter (
Stot). This parameter was determined by taking the square root of the sum of the squares of the normalized horizontal and vertical separations, as shown in Equation (2):
where Δ
x is the horizontal separation distance, Δ
y is the vertical separation, and
Wp is the width of a single pad (where
D =
Wp). With three pads, the separation distances for both gaps were added together.
3.5. Definition of Flame Merging
Flame merging can be defined in different ways. For example, Baldwin [
14] defined flame merging based on the change in flame height from a single flame. In this investigation, merging was defined based on the video image recognition software used to analyze the physical experiments. In the frame-by-frame video analysis, any frames in which the flames were at least “touching” at any vertical location were considered merged flame frames. The total number of frames in which merging was observed was divided by the total number of frames in which the flames were burning. The fraction of frames in which flame merging occurred was defined as the probability of merging (
PM). A
PM value of one means that merging occurred the entire time, and a
PM value of zero means that merging did not occur at all.
3.6. Corrections for Pad Spacing
3.6.1. Corrected Flame Heights
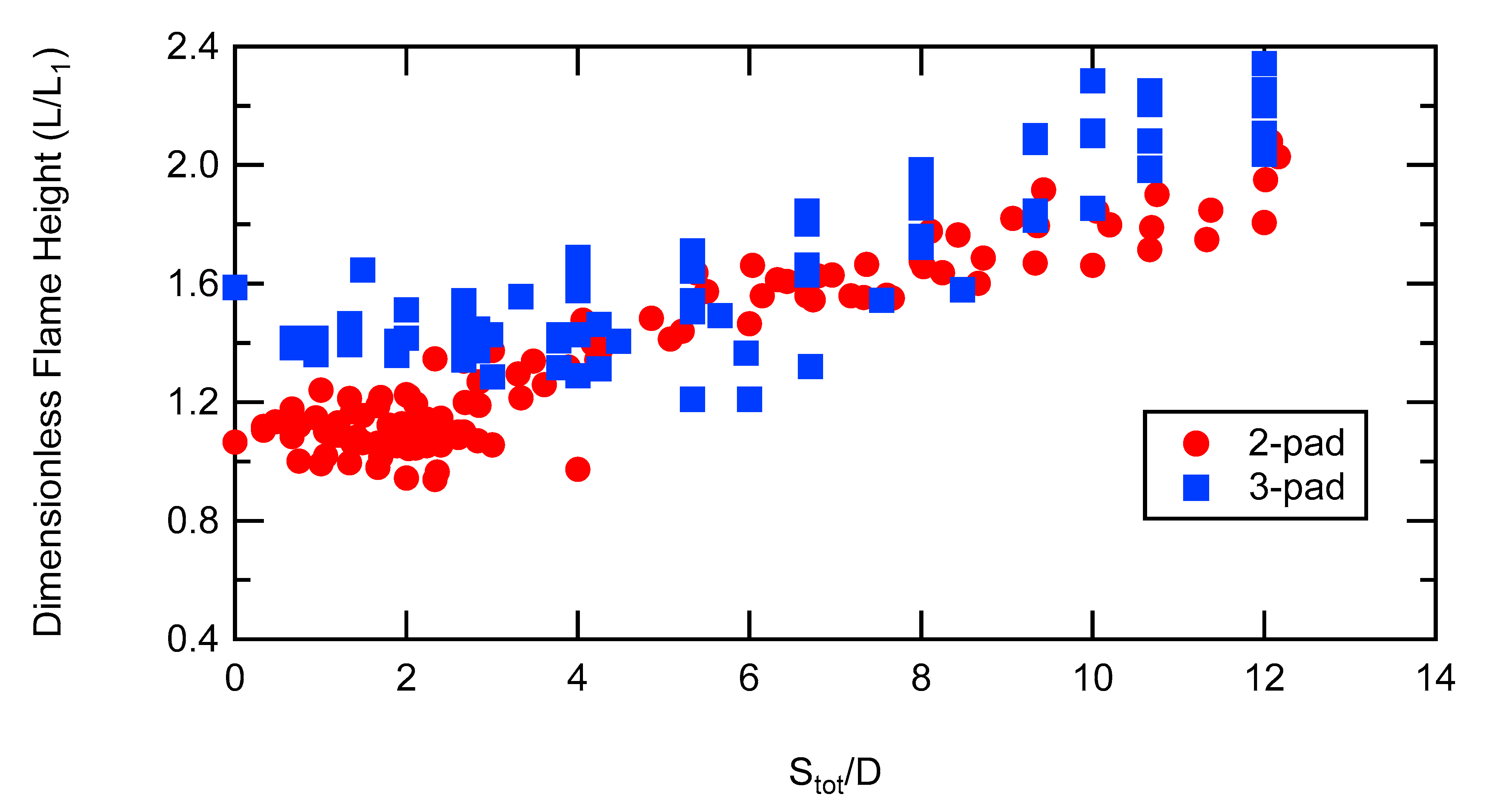
The uncorrected flame heights are shown in
Figure 5 for both the two-pad and three-pad experiments, and a general increase in flame height is seen as total separation increases. However, there are two effects for vertically-separated flames: (1) flames from the lower source filling the space between the two sources, and (2) actual flame interaction causing increased flame height. Flame heights were corrected by subtracting the vertical separation from the flame height, as follows:
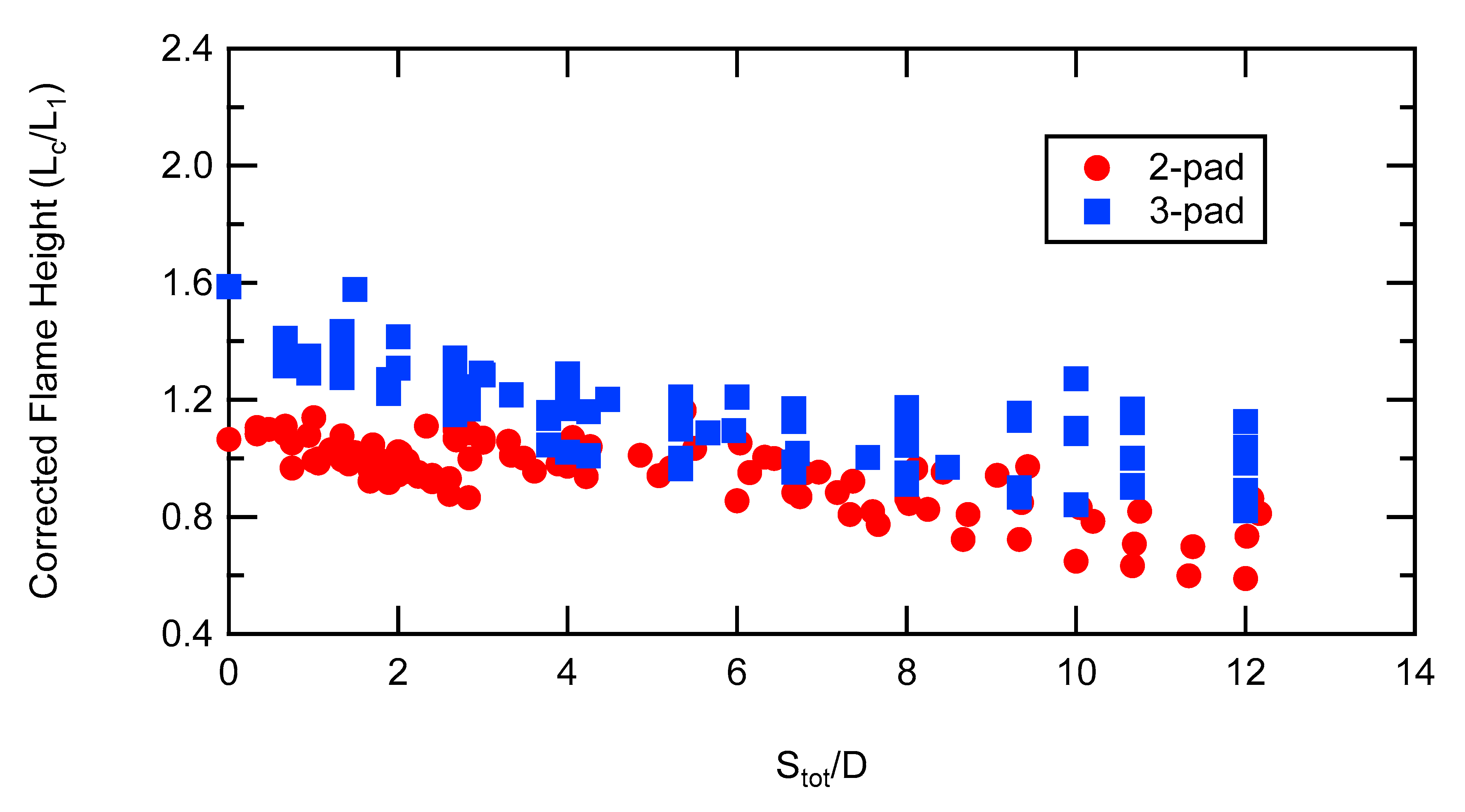
With three pads, the total vertical separation distance between the lowest and highest pads was used in Equation (3). Corrected flame heights reveal the actual impact of flame interaction on flame height, as shown in
Figure 6. The corrected flame height data for both two-pad and three-pad experiments show that increases in separation distance (
Stot/D) result in decreased corrected flame heights, indicating decreased flame interactions.
3.6.2. Corrected Flame Widths
Similar to how flame heights were corrected, the measured widths of flames from the experiments were corrected for the horizontal separation distance between pads (Equation (4)). For the three-pad data, both the left and right horizontal separation distances were subtracted. In this way, different horizontal separation distance configurations can be compared using actual flame width, rather than using flame width measurements inflated by the distance between the pads. This correction is necessary because of the way that flame properties were measured; the MATLAB code used the furthest points of fire from left to right to measure flame width. The correction was made before normalization by the width of the pads involved.
4. Results
Experimental measurements included merging probability and flame heights, widths, and areas. Burn times of each pad were also measured. These data were compared between different configurations and between experiments with different numbers of pads (two or three). As mentioned above, all of the data were normalized, and corrections to the normalized flame heights and widths were made as described.
4.1. Flame Merging
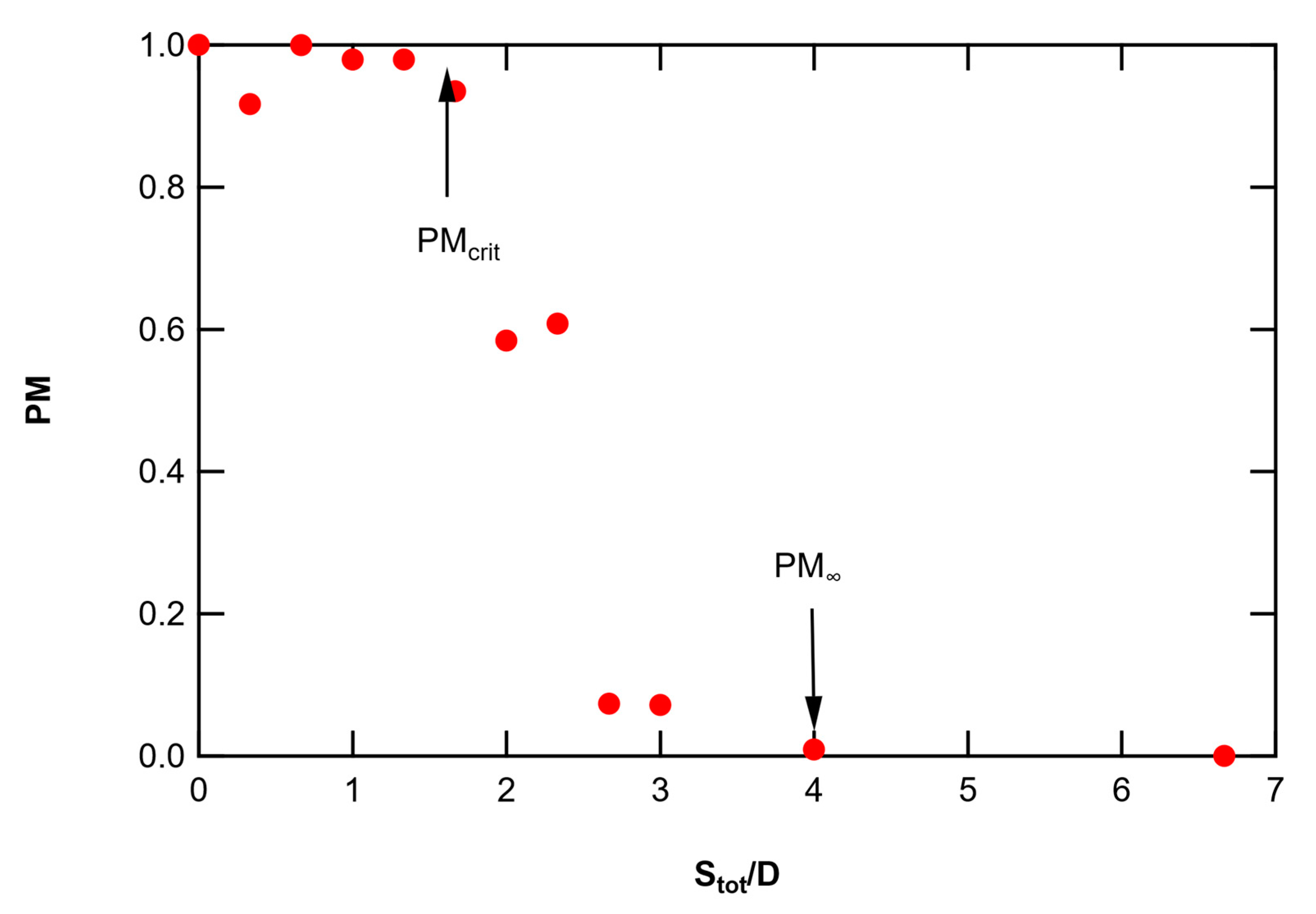
4.1.1. Two-Pad PM Data
The merging probability for the two-pad experiments was first plotted vs. the normalized separation distance (
Stot/D), showing complete merging as
Stot/D approached zero and eventually no merging as
Stot/D increased. The two-pad
PM data with no vertical separation are shown vs.
Stot/D in
Figure 7. Values of
PM begin to deviate from 1.0 when
Stot/D is about 1.5, and
PM approaches 0.0 when
Stot/D is between 3 and 4. The point at which
PM starts to deviate from 1.0 is called the critical flame merging distance, and was correlated by Baldwin [
14] as follows:
The value of
Stot/D calculated from Equation (5) for the critical
PM is 1.6 (called
PMcrit), which is consistent with the data in
Figure 7. Sugawa and Takahashi [
18] reported that no flame merging would occur when S/D was greater than 4 (called
PM∞), which is also consistent with these horizontally-spaced
PM data. The agreement between the horizontally-spaced
PM data and these correlations gives us confidence that the experiment and optical analysis of flame merging were performed correctly.
A correlation was developed to include the effects of both horizontal and vertical spacing on
PM. The correlation had to start at 1.0 and end at 0.0 with increased spacing. Correlating vs.
Stot did not work well, since the vertical spacing configurations were affected by the buoyant nature of the flames. The following correlation seemed to fit the two-pad
PM data quite well:
Note that as
Sx and
Sy grow large, the denominator becomes very large, and
PM approaches zero if the coefficients are positive. When
Sx and
Sy are zero,
PM can approach 1 depending on the value of coefficient
D. The resulting curve fit with the form of Equation (6) is shown in
Figure 8, with the constants given in
Table 2. A parity plot of the model fit vs. the data is shown in
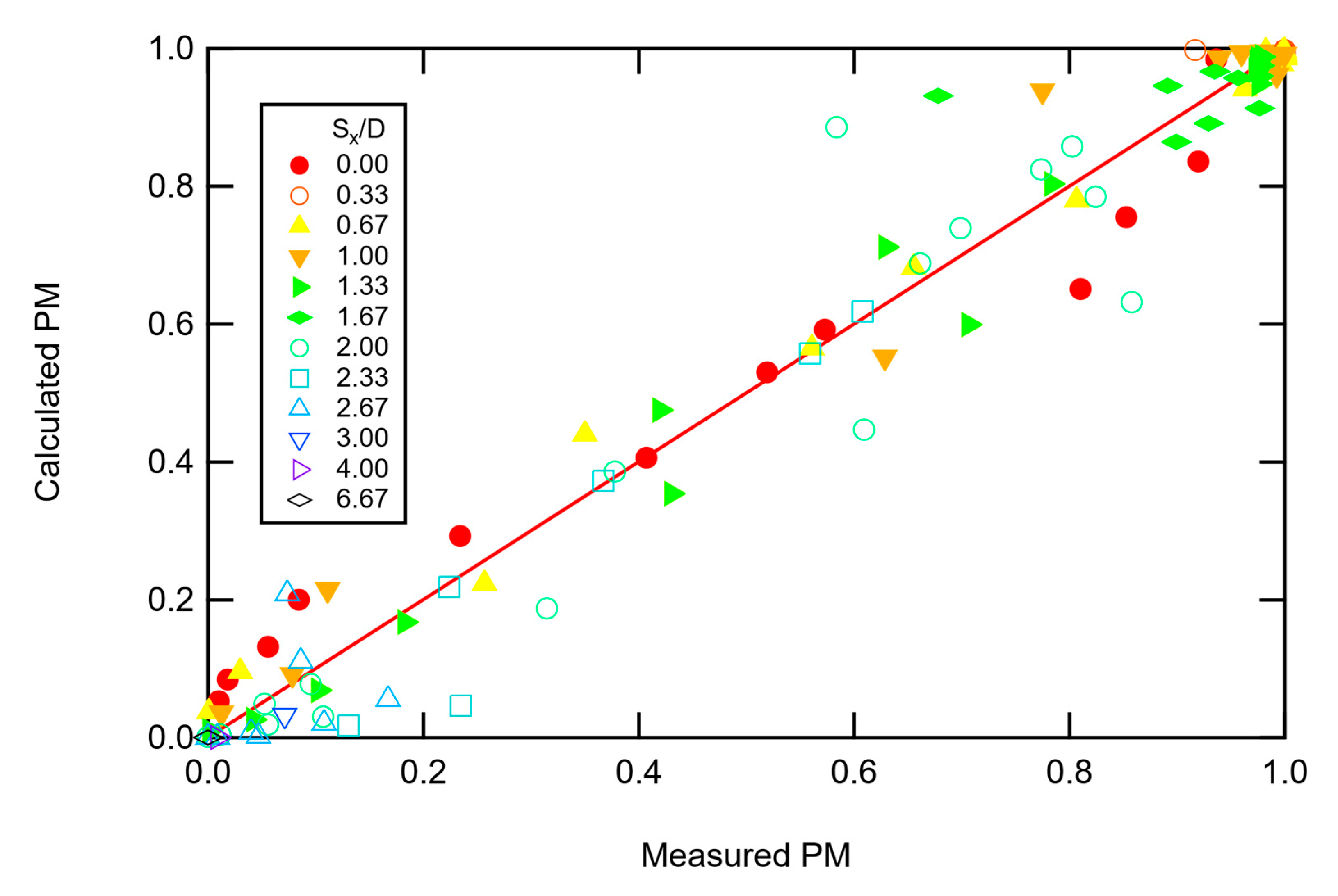
Figure 9. The curve fit matches both the trend and magnitude of the data. Note that the exponential part of Equation (6) is quadratic in
Sx. The quadratic form gave a smaller sum-square error than a linear form by an order of magnitude. Using a quadratic in
Sy, or in both
Sx and
Sy, gave similar results.
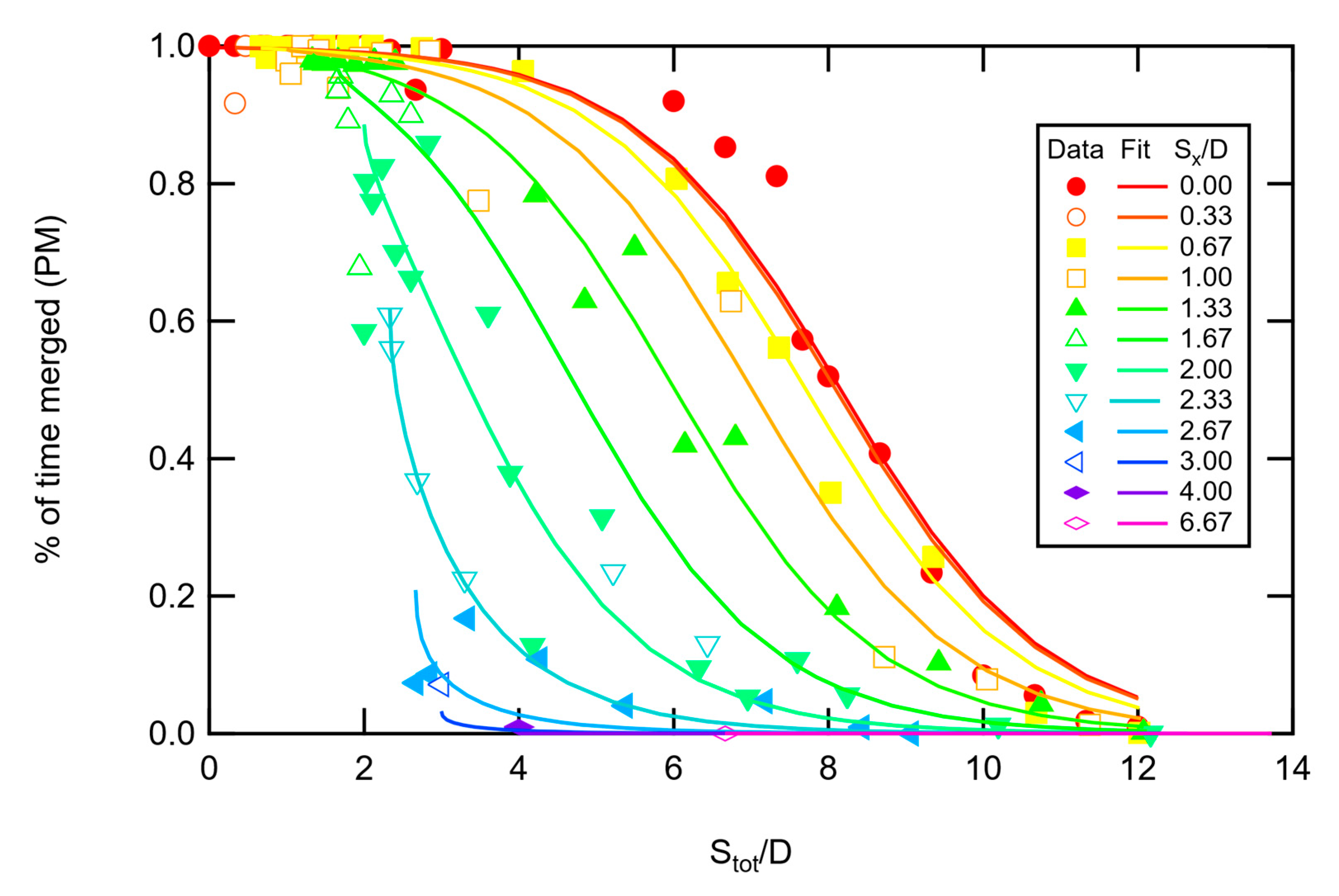
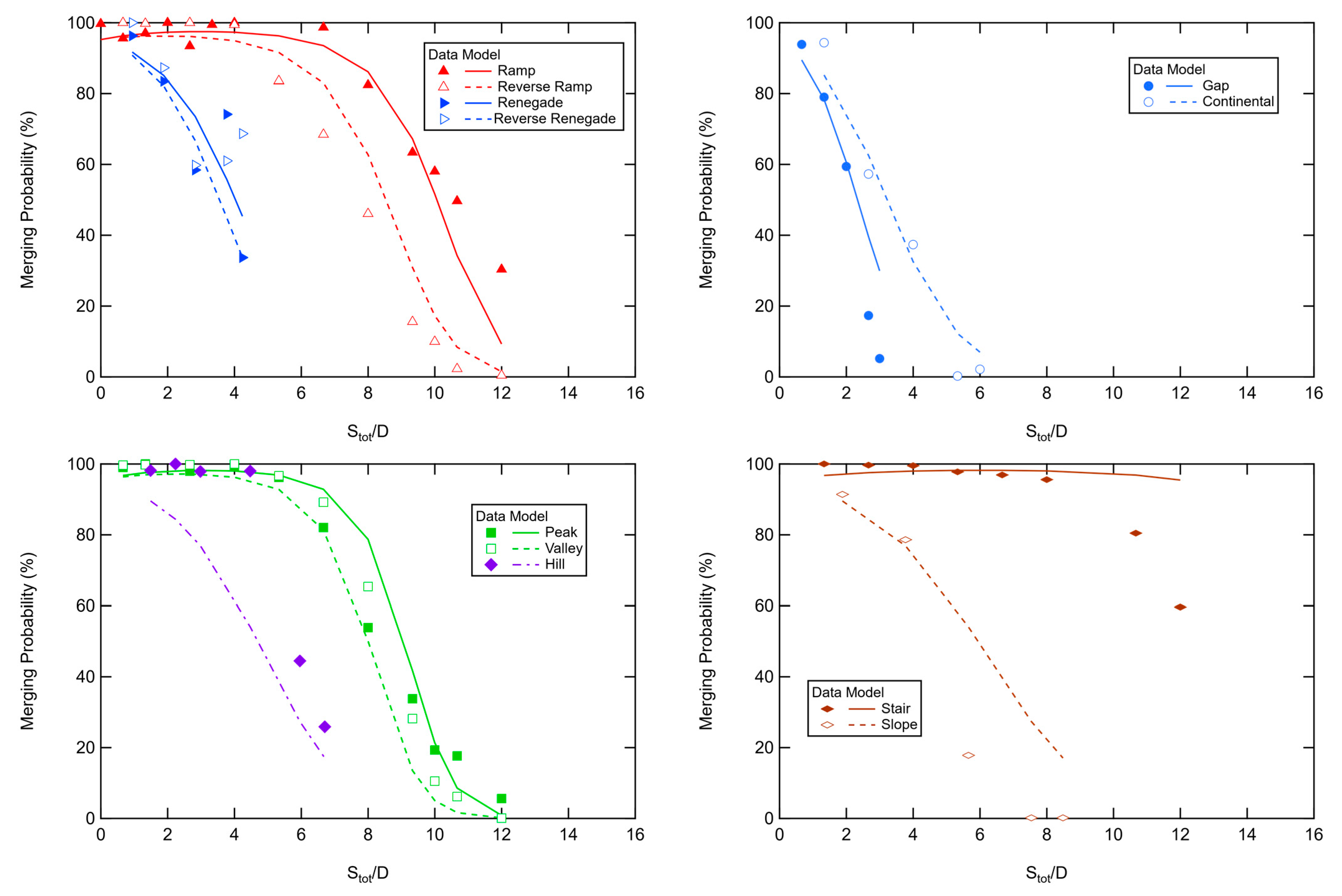
4.1.2. Three-Pad PM Data
In the two-pad data, it did not matter if the left or the right-hand pad was higher, so
Sy was always a positive value. However, the sign on
Sy is important in some of the three-pad configurations. For example, the Peak, Hill and Valley configurations can have the same
Sy while having different flame characteristics. The same issue arises with the Ramp vs. Reverse Ramp and the Renegade vs. Reverse Renegade configurations. Therefore, a factor (
Yfac) was introduced into Equation (7) to account for the configuration. This factor was set to 1.0 for the peak, hill, ramp, and renegade configurations, and to −1.0 for the valley, reverse ramp, and reverse renegade configurations. In addition, some of the configurations had no horizontal spacing on the left-hand side but did include spacing on the right-hand side. It was therefore necessary to include a correlating factor for spacing in the horizontal and vertical dimensions (i.e., S
x1,
Sx2, S
y1, and S
y2). While a correlation for each configuration could be developed, a single correlation was sought in order to correlate the data from all configurations. The form of the equation used to correlate the three-pad
PM data was:
Note that a quadratic form of
Sy was used inside the exponential, which gave much better results for the three-pad data than forms with quadratic expressions in
Sx. The results of the curve fit using Equation (7) are shown in
Figure 10 with multiple panels, since there are so many data points. Each panel is a family of curves, as denoted by a column of configurations in
Figure 2. Constants are given in
Table 3.
While all configurations experienced the same trend, namely a decrease in merge probability with increasing separation distance, not all configurations experienced this trend in the same way. For example, in configurations with horizontal-only separation, like the Gap or Continental configurations, the merge probability drops more dramatically as separation increases than in configurations with vertical-only separation, like the Peak or Ramp configurations. This indicates that the type of separation (vertical or horizontal) impacts flame merging in different ways. It is also an indication that the geometry of fuel sources has an impact on overall merged flame behavior.
4.2. Flame Height
Flame height (FH) is defined in this study as the length of flame in the vertical direction from its lowest point to its highest point, as seen from the perspective of the camera that recorded the experiments. Because of this definition, and to make the results more comparable to other studies, flame heights have been normalized and corrected, as described above.
4.2.1. Two-Pad FH Data
The corrected flame heights are shown as a function of the separation distance in
Figure 11. The corrected flame height of 1.0 is the average flame height of a single pad experiment. All corrected flame heights for the two-pad experiments were less than 1.3, with an average 95% confidence interval for the mean corrected flame height of 0.07. Flame heights approached the single flame height as the horizontal separation distance increased. The shaded region in
Figure 11 represents the 95% confidence interval for the mean corrected flame height of a single flame. All flame heights for
Sx/D > 1.67 fell within the shaded region, and for clarity are not shown here. The two-pad flame height data are somewhat scattered, and do not seem to follow a clear trend. However, there seems to be an initial rise in corrected flame height in the region
Stot/D <1, followed by a decrease in corrected flame height in the region 1 <
Stot/D <2, followed by increased flame height in the region 2 <
Stot/D <3. Flame heights generally decrease for
Stot/
D > 3. This trend of an initial increase is seen in several sets of data (
Sx/D < 1.5), but it is not clear that the trend is greater than the scatter in the data.
The corrected flame height data (
Lc) were correlated using Equation (8), and the results of this correlation are shown by the solid lines in
Figure 11.
Table 4 shows the best-fit coefficients using this correlation. The correlation did not try to account for the faint trend described in the paragraph above. The correlation shows that the flame height resorts to the single-pad flame height at large separation distances. However, this fit is not as good as the fits for
PM shown earlier due to the large scatter in the data.
Looking at the constants in
Table 4, the fact that the best-fit correlation had a value of
B that was close to 0 indicates that vertical separation had very little effect on the corrected flame height.
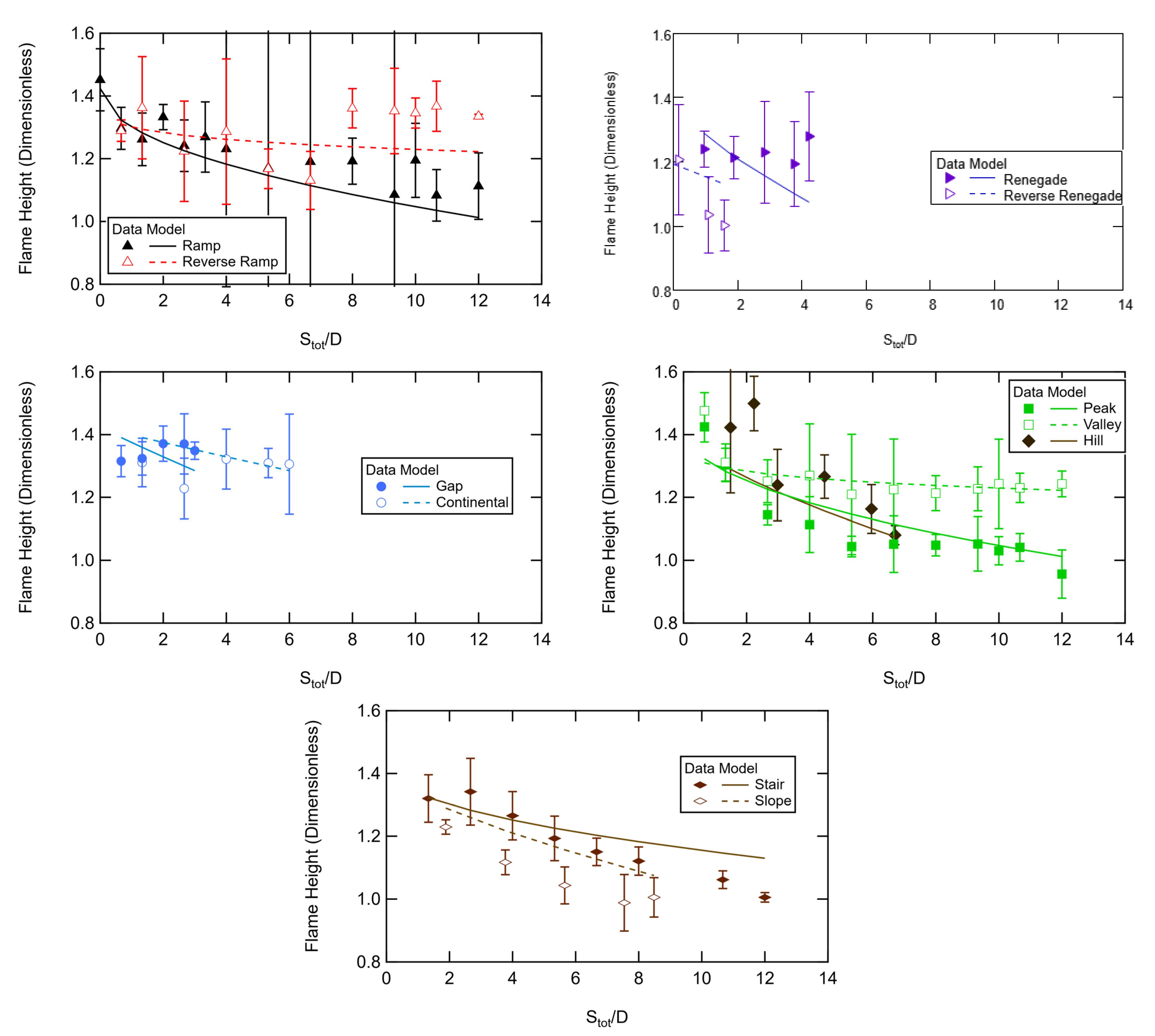
4.2.2. Three-Pad FH Data
The three-pad corrected flame height (
Lc) data are shown in
Figure 12 for the different configurations shown in
Figure 2. All values of
Lc were less than 1.5. The highest values of
Lc were at low separation distances. The positive vs. negative displacement of the middle or end pads (Peak vs. Valley, Ramp vs. Reverse Ramp, Renegade vs. Reverse Renegade) indicates the need for
Yfac as used in the
PM correlation. The best-fit correlation for the
Lc data is given in Equation (9), with coefficients shown in
Table 5. The exponential form gave a much better fit to the data than a linear form, and gave more asymptotic behavior. The curve fit seems reasonable for most configurations. However, it is not clear why the
Lc data seem to rise at high separation distances (
Stot/D > 8) for the Reverse Ramp configuration.
It is clear that different configurations produce different flame heights, even at similar separation distances, indicating that the geometries of the fuel sources impact flame merging and other parameters in a way not captured by the separation distance alone. The geometries tested in this study did not include vertically overlapped fuel sources, which is a realistic geometry of fuel sources (leaves) in bushes, trees, and other vegetation. Because the heat transfer of flames is most dominant in the vertical direction, it is likely that vertically overlapped fuel sources would experience a greater amount of direct heat transfer from lower fuel sources, and flame merging would be much more likely. If the results of these experiments can be extrapolated to vertically overlapped fuel sources, then some general flame properties could be predicted. The flame height of vertically overlapped merged flames would be largest at small separation distances, and would decrease with increasing separation distance, until it levels off and is basically not dependent on separation distance.
4.3. Flame Area
As described in detail in the experimental setup section, flame area is a measure of the cross-sectional area of a flame that is viewed by the camera during an experiment. It is not a perfect representation of total flame area, because some flame enlargements may have happened in the direction of the camera or have been blocked from view of the camera. Nonetheless, it is a good parameter to use in comparisons between experiments.
4.3.1. Two-Pad Experiments
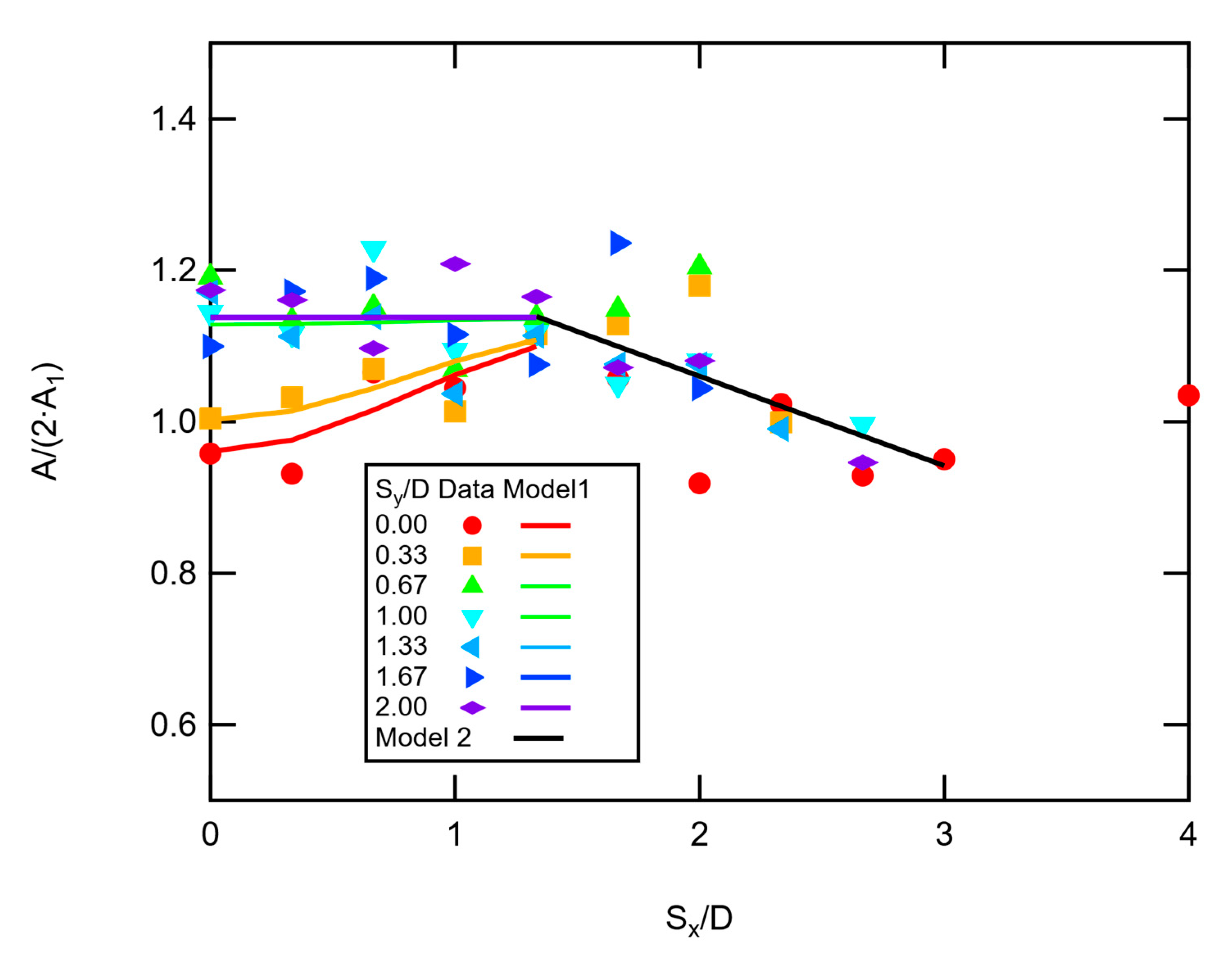
The combined two-pad flame areas were normalized by twice the flame area of a single flame, hence a value of 1.0 would mean no change. The normalized flame areas for the two-pad experiments are shown in
Figure 13. The combined flame area increased by a maximum of 23%. The general trend was an increase in flame area for low values of
Sy when
Sx/D < 1.5. At higher values of
Sy, the normalized flame area was near 1.15 on average, although the individual data sets for each vertical separation distance exhibited slightly different features. When
Sx/D > 1.5, the normalized flame area decreased linearly with
Sx/D to a value of 1.0 (with scatter). A two-part model was used to correlate these data, as shown in Equations (10) and (11).
Figure 13 shows the two models compared to the data, with coefficients listed in
Table 6.
4.3.2. Three-Pad Experiments
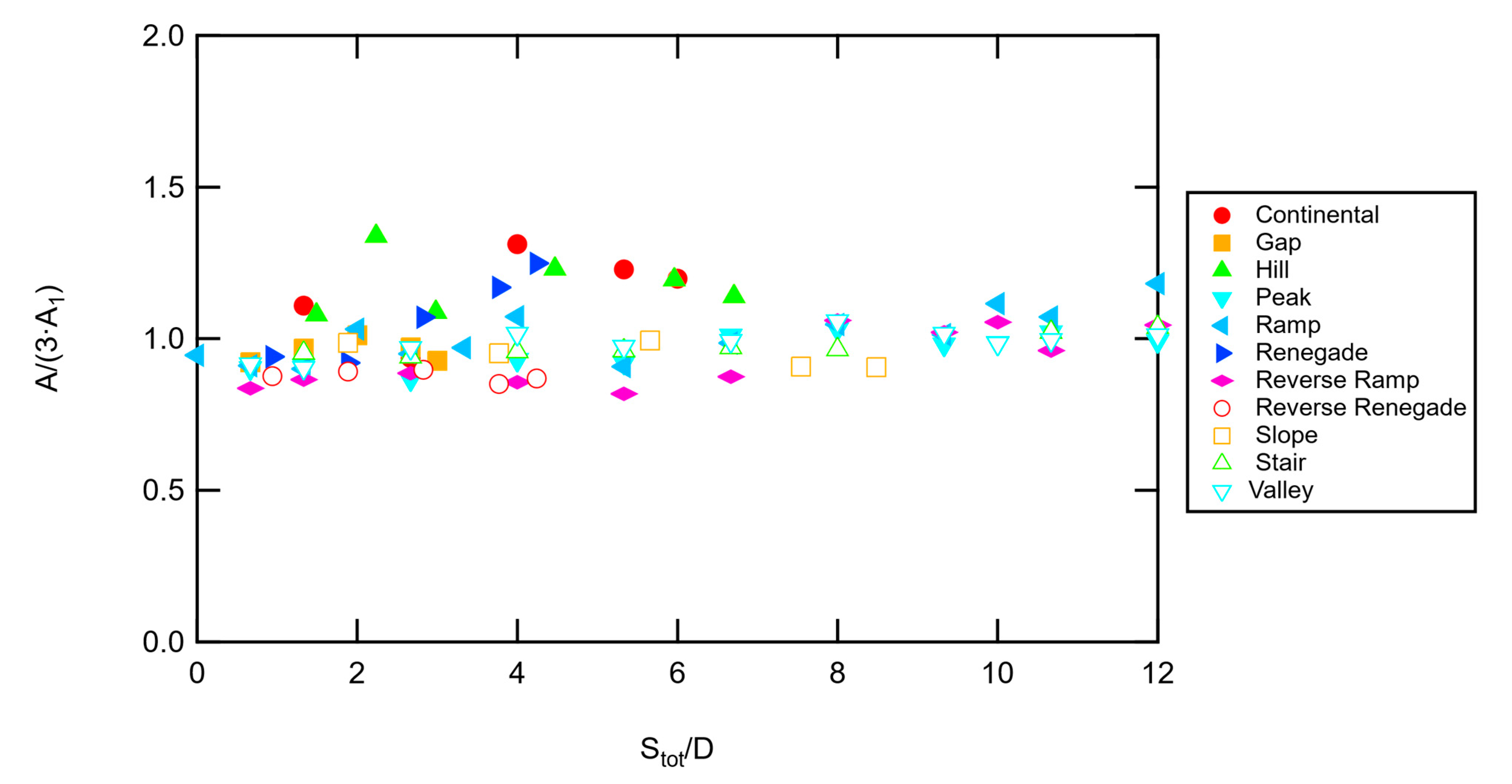
The three-pad flame area data are shown in
Figure 14, normalized by three times the average flame area of a single flame. The 95% confidence intervals averaged ±0.08, except for the ramp configuration, which for some reason were ±0.45 to 0.83 for 4 <
Stot/D < 9. Most of the data show a relatively constant trend at three times the area of a single-pad flame (1.0 on the plot). The maximum combined flame area reaches four times the area of a single pad flame (corrected to 1.3 on the plot), occurring at 2 <
Stot/D < 6 for the continental and hill configurations. In general, the flame area appears to stay relatively constant in these experiments.
4.4. Flame Width
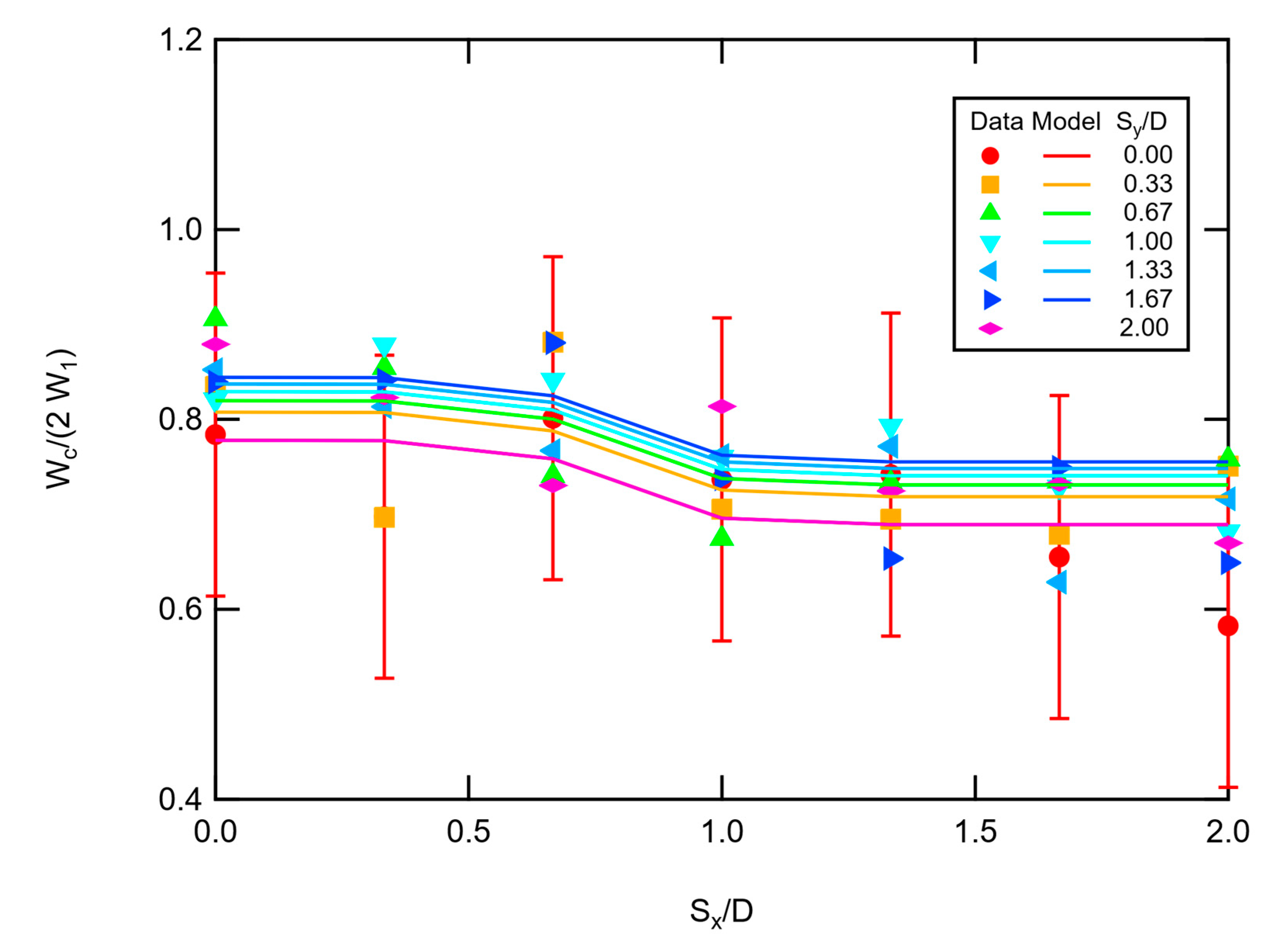
Flame widths (W) were measured as the distance between the leftmost and rightmost points of an observed flame, and were corrected (Wc) by subtracting the horizontal distance between fuel sources (as described above). Corrected flame widths were normalized by the average width of the flame from a single pad. The optical analysis method placed a rectangle to enclose the flame image for each frame, and determined the width of the rectangle. However, in the two-pad experiments, at large vertical spacing configurations (Sy/D > 2), the flames tended to tilt occasionally to the right or left in spite of best efforts to maintain a quiescent room atmosphere. This flame tilting caused the “measured” flame width numbers to increase substantially, even though the visible width at any vertical location did not show the same increase. The flame width data presented here are therefore limited to Sy/D ≤ 2.0.
4.4.1. Two-Pad Flame Width Data
The normalized flame widths are shown in
Figure 15. For convenience, the average 95% confidence interval of the mean (0.17) is plotted on the
Sy/D = 0 data. The flame widths appear to decrease as a function of horizontal separation distance to an asymptotic value for
Sx/D < 2 and
Sy < 2. Maximum corrected flame widths in this region are only 90.5% of two single-pad flame widths, with a minimum of 58% recorded. The best-fit correlation is shown in Equation (12), with coefficients listed in
Table 7. The effect of the vertical separation distance on flame width is small. Note that the change in normalized flame widths of about 0.2 (about 12%) shown here is comparable to the 95% confidence interval of 0.17.
4.4.2. Three-Pad Flame Width Data
For the three-pad experiments, the corrected flame widths of a given configuration are shown in
Figure 16. Error bars were omitted for ease of viewing. The error bars were quite large for the ramp configuration, just as in the flame area data. The maximum corrected flame width was 1.55 (Ramp configuration), while the minimum value was 0.27 (Valley configuration). The average standard deviation of the flame widths for individual configurations across all separation distances was just 0.153 dimensionless units. No consistent correlation for flame width was found for the three-pad data. The ramp configuration reached a peak of 1.55 at
Stot/D = 2, and then gradually decreased to 1.15, meaning that all vertical spacing in the ramp configuration resulted in increased corrected flame widths. In contrast,
Wc/3 for the Slope, Continental and Hill configurations decreased significantly from 1 with increasing
Stot/D, with a minimum value of 0.27 recorded for the slope configuration. Other configurations seemed to have relatively constant values of
Wc/3, such as the peak configuration. Flame diameters for a single pool fire, which are normalized by the pool diameter, would be expected to be less than 1 due to air intake at the base of the flame, so a decrease in
Wc/3 for some of the configurations could be expected. However, the increase in flame width, especially for the ramp configuration, was somewhat unexpected.
4.5. Flame Duration
Flame duration times were measured from the videos of the single-pad, two-pad, and three-pad experiments. In some configurations, the duration of the upper flame decreased, indicating that the lower flame heated the upper pad and increased the burning rate. The lower pad burn time was also influenced to a lesser extent by heat feedback from the second pad.
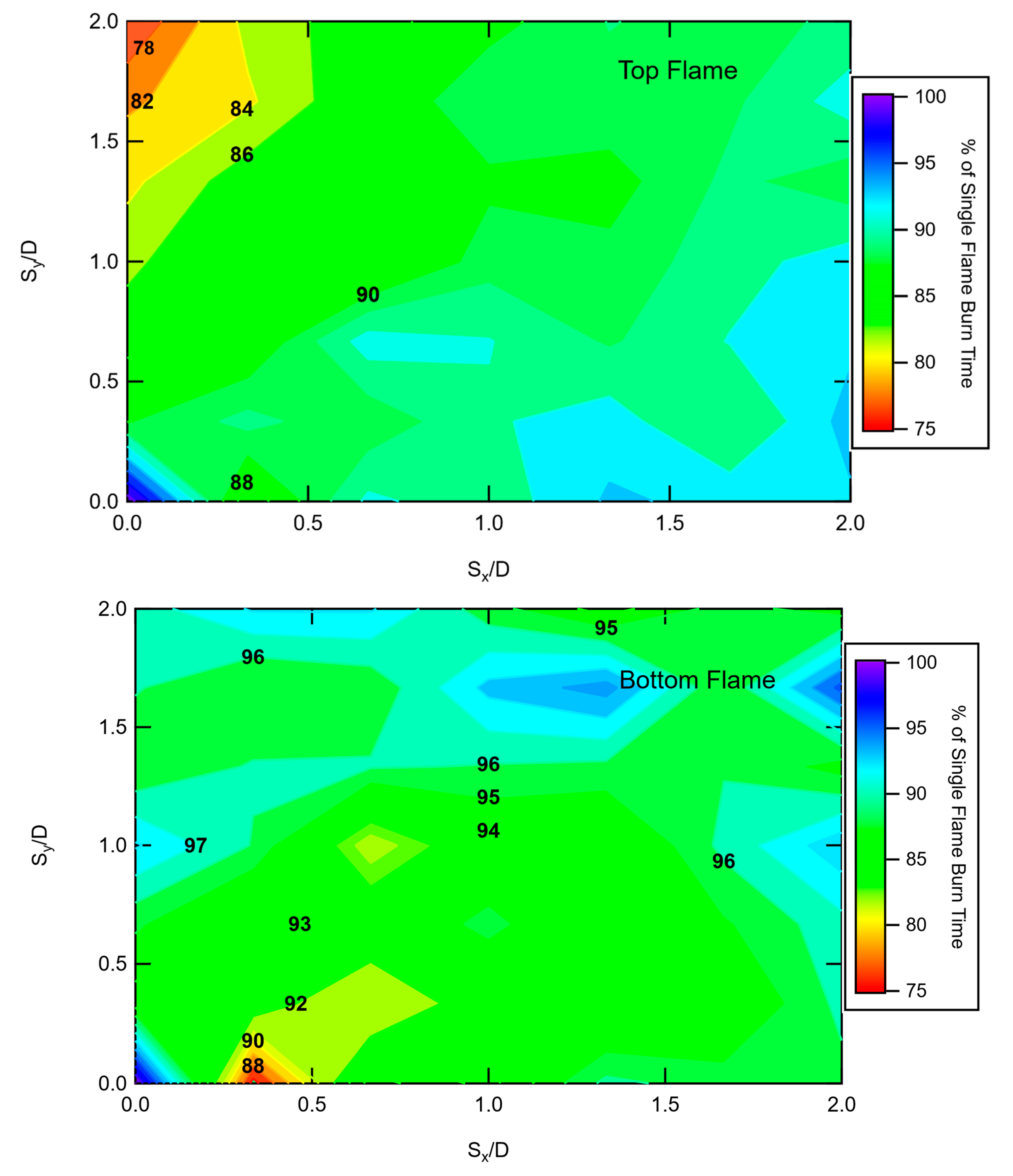
4.5.1. Two-Pad Flame Duration Data
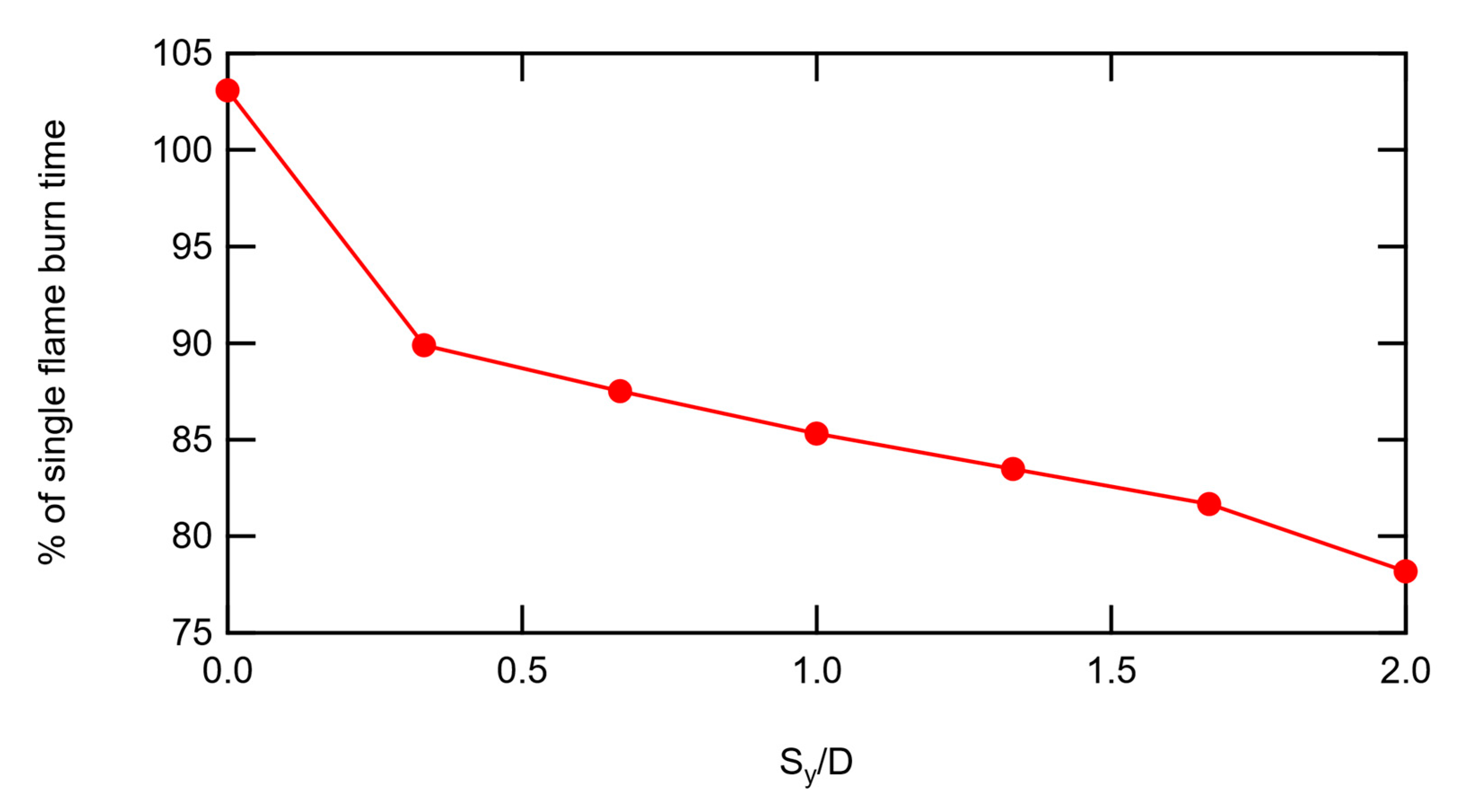
Figure 17 shows contour plots of the burn times for the upper and lower pad flames in the two-pad configuration. For the horizontal-only pad spacing, the “upper pad” was assumed to be the right-hand pad as viewed from the camera. As seen in the image from the top flame, the largest decrease in flame duration was 78% of the single pad flame duration, which occurred at low horizontal separation distances but a vertical separation distance of
Sy/D = 1.5 to 2. A plot showing the decrease in burn time for the top flame at increasing vertical separation distance for
Sx/D = 0 is shown in
Figure 18.
Figure 17 shows a large region of flame duration in the 90% to 95% range for the top flame. In contrast, the bottom flame showed the most influence from the top flame (86% of single pad flame duration) at low horizontal separation distances (
Sx/D = 0.75) and no vertical separation. The bottom flame duration image shows that there was also a large region in the 90% to 95% range.
4.5.2. Three-Pad Flame Duration Data
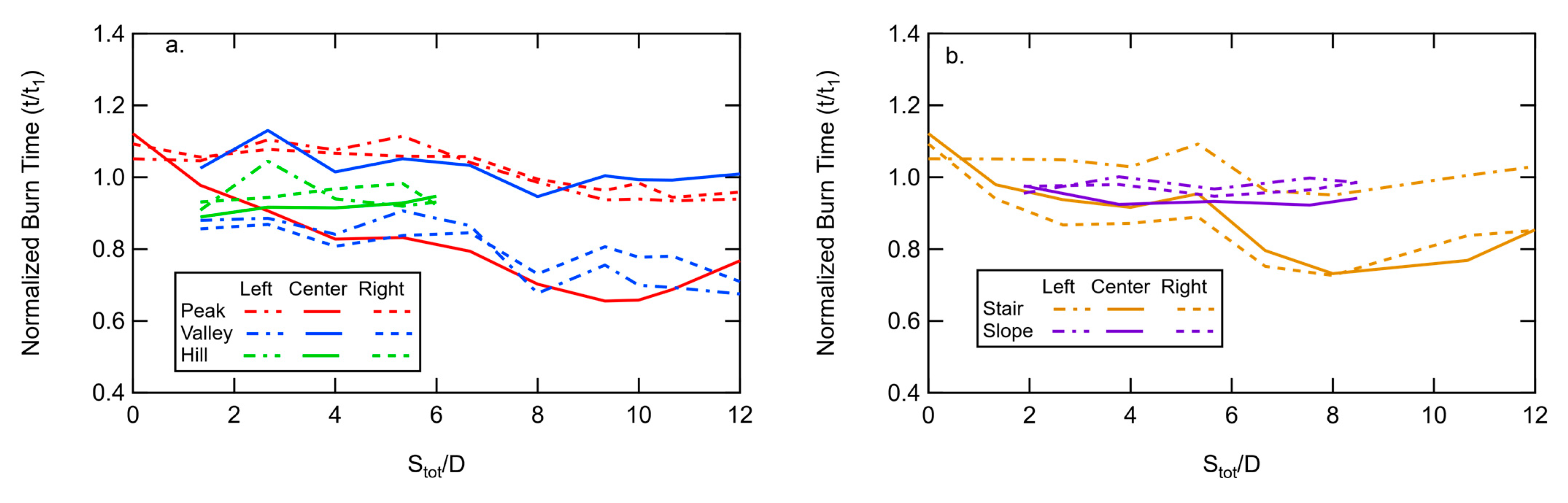
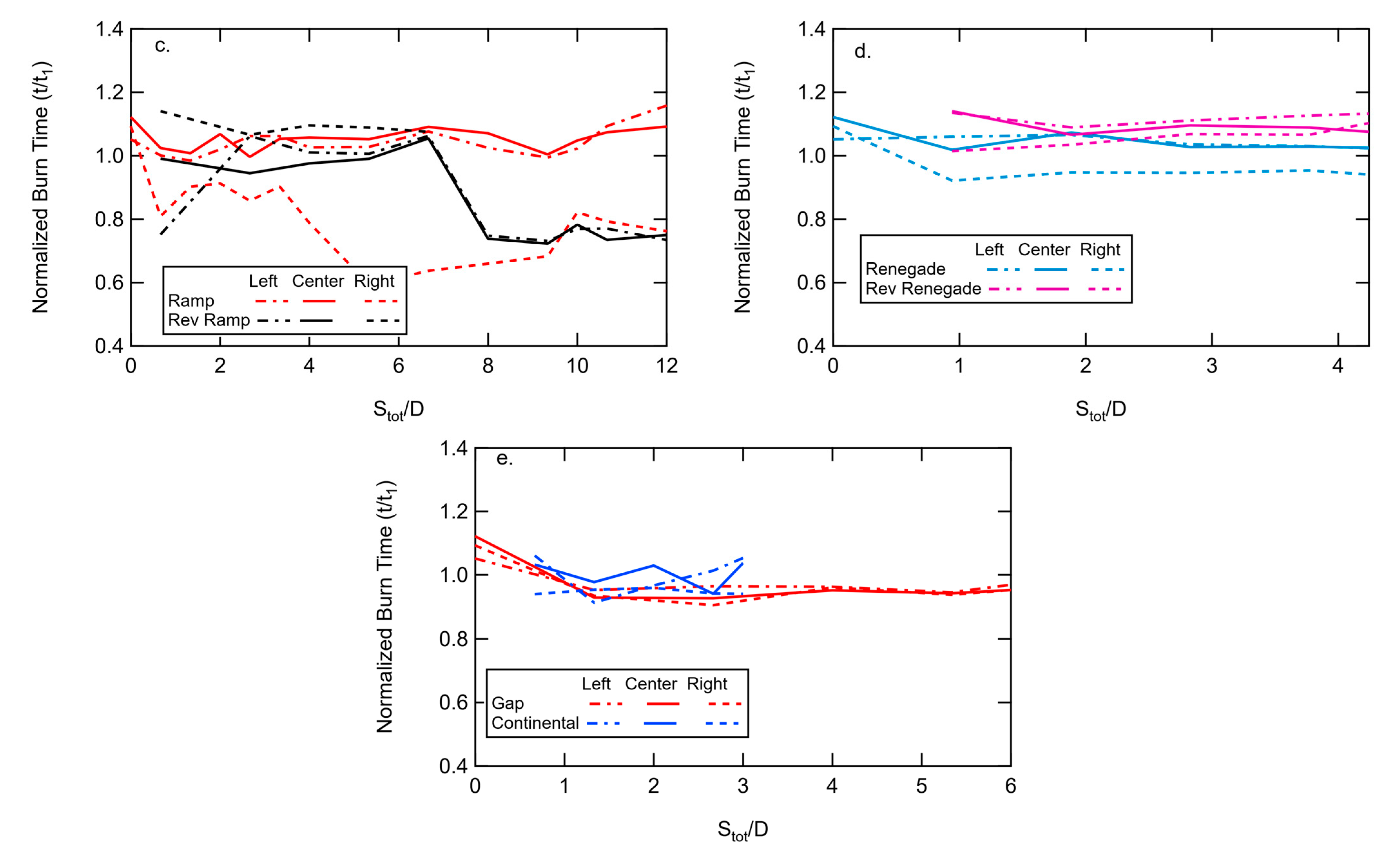
With three pads, it was not possible to show the flame duration data with a 2-D color plot. Therefore, 2-D line plots are shown in
Figure 19 for the three-pad configurations. Burn times for each of the three pads in each configuration are shown. Noticeable deviations from a value of 1.0 represent changes in burn times due to flame merging. Lower burn times represent increased burning rates due to convective and radiative heating from neighboring pads. Decreased burn times, and hence increased burning rates, are observed for the center pad for the peak configuration and for the two end pads for the valley configuration (
Figure 19a) at increasing separation distances. Similar changes were observed for the center and right-hand pads in the stair configuration, the right-hand pad in the ramp configuration, and the center and left-hand pads in the reverse ramp configuration. Most of the other configurations showed small differences in flame duration. To make more sense of the change in burn time data,
Figure 2 is repeated in
Figure 20, with the pads emphasized in red where the burn times decreased. From
Figure 20, it is easy to see that the burn times decreased only for upper pads in configurations where there was no horizontal separation distance. This result would support convection from the lower flame(s) as the mechanism of heat transfer in these experiments, which increased the burning rate of upper flames. Radiation would have affected burn times with horizontal spacing as well as vertical spacing, but no significant change in burn times was observed with horizontal spacing.
5. Discussion
The objective of this work was to provide some insight into flame-merging behavior when flames are spaced both vertically and horizontally, which may help with reduced-order models of flame spread in sparsely populated and non-uniform arrays of fuel elements, such as in shrubs. The choice of zirconia felt pads soaked in n-heptane avoided interactions with the container that would be present for pool fires, and avoided curling and ignition problems that would be present with paper or cardboard. The flames were in the buoyant region, which is applicable to shrub fires with no wind, but the flame heights for these experiments (38 cm) were at the top of the range observed with single leaves (5–40 cm) [
5,
40,
41]. The high heating value of the liquid n-heptane was 48.07 MJ/kg, which is 2.8 times higher than the average heating value of live leaves (18.4 MJ/kg) reported by Matt et al. [
42], suggesting that the heating value should be considered as a correlating parameter in future work. In addition, future work might include the orientation of the flame source, since this work only used horizontally oriented pads (and leaves may be oriented vertically or at angles).
The merging probability data from the current flame-merging experiments were in agreement with correlations of the onset of flame merging and the limit of flame merging for horizontal spacing (see
Figure 7). The probability of flame merging based on horizontal and vertical spacing for both the two-pad and three-pad experiments was correlated with the same model form that consisted of an exponential decay function, which may prove useful for other flame merging configurations.
Flame dimensions are a function of many things, such as the heat release rate, the local air ingress rate, and the radiant heat loss (or gain) from the soot in the flame.
Table 8 shows the maximum and minimum flame characteristics observed in the two-pad and three-pad experiments. The three-pad experiments exhibited the largest maximum corrected flame heights, areas, and widths, as well as burn times. The three-pad experiments exhibited the minimum burn time as well (meaning the fastest burning rate). The second highest maximum flame height occurred for the ramp configuration, which also had the largest flame width and the lowest burning time. The low burning time means a high burning rate and hence a high heat release rate for the ramp configuration, resulting in an increased flame height and area. The average values are somewhat low because the data were taken from a wide range of
Sx and
Sy, including places where no flame merging was observed.
The flame heights did not increase significantly when corrected for the vertical spacing between pads, and therefore do not explain how a 5 to 40 cm high flame from a single leaf can blossom into a 2 to 3 m flame in a fully consumed bush. However, none of the configurations observed in the current experiments had an overlap of flame sources because the zirconia felt pad would have interfered with the combined flame. Experiments with vertical overlaps were conducted on arrays of matchsticks by Gollner et al. [
36], but were not specifically analyzed for flame merging behavior due to the transient nature of their experiment. However, their data indicate increased merged flame heights for flames where the horizontal spacing overlaps with multiple vertical fuel elements. The data presented here present a nice reference for future modeling efforts that would be helpful in understanding the complex processes involved in flame merging, such as oxygen depletion, heat feedback, flame-induced eddies, etc. Additional experiments with horizontally overlapped fuel sources would be helpful, but may need to be performed computationally due to the complexities of finding suitable fuel elements.
6. Conclusions
Flame merging experiments were conducted successfully with zirconia felt pads soaked in n-heptane and suspended on thin ceramic rods. Both two-pad and three-pad experiments were conducted, varying both horizontal and vertical spacing. Video images of the buoyant flames were processed frame-by-frame to determine flame characteristics (i.e., probability of flame merging and flame shape defined by height, width, and area of the combined flame).
The probability of flame merging (PM) was determined based on the percentage of time the pixels in the combined flame image indicated no flame separation. The two-pad PM data showed an exponential decay with separation distance. The best correlation of the two-pad PM data was obtained with an exponential function containing a quadratic function of Sx and/or Sy. The same model form from the correlation of the two-pad data was shown to agree well with most of the PM data from the three-pad data.
Combined flame heights were corrected by subtracting the vertical space between the pads, and normalized by the flame length of a single-pad flame. The normalized and corrected flame heights in the two-pad experiments increased by less than 40% when the separation distances were small, with an average increase of about 20% recorded for normalized separation distances lower than 3. The two-pad flame height data were correlated with an exponential decay function that was linear in both horizontal and vertical pad spacing. The flame height data from the three-pad configurations showed a maximum increase of flame height of 50%, and were correlated with the same model form as the two-pad flame height data.
The maximum flame area observed in the two-pad experiments was only 24% higher than the single-pad flame area. The average increase in flame area in the two-pad spacing configurations where flame merging occurred was only 10%. Based on the fluctuations in flame area which led to a 95% confidence interval of ±8% for the average flame area, it may be assumed that the flame area stayed relatively constant for most of the two-pad experiments. The flame areas for most configurations in the three-pad experiments also remained relatively constant. However, there were two configurations that showed as much as a 34% increase in flame area, while others experienced as much as a 16% decrease in flame area. One of the configurations resulted in large 95% confidence intervals of flame areas that were as high as 40% (ramp configuration), which may indicate flame-enhanced turbulence for that specific configuration.
Flame widths were corrected for the space between pads. The corrected flame widths for the two-pad data in the regions with a high merging probability decreased by as much as 42%. Corrected flame widths from the three-pad experiments in the flame merging region increased by as much as 55% in one configuration and decreased by as much as 73% in other configurations. A two-part model was found to correlate the flame width data. For many configurations (but not all), an assumption of constant corrected flame width seemed appropriate.
Flame duration data were obtained for each pad in each configuration. In the two-pad experiments, the upper pad showed a decreasing burn time with increasing vertical distance when there was no horizontal spacing, with a maximum decrease of 22% recorded. The decreased burn time for the upper pad, and hence the increased burning rate, was caused by convective heating from the bottom flame. This convective heating from the bottom flame seemed to decrease substantially with even small horizontal spacing. The bottom flame burn time was not significantly influenced by the top flame, except for small horizontal spacing with no vertical spacing. The three-pad burn times indicated a similar trend to the two-pad data; configurations with no horizontal spacing and an elevated pad showed decreased burn times for the upper pads. No significant change was observed in burning times for three-pad configurations with even small horizontal spacing.
This work is viewed as an important step in understanding flame merging behavior when flames are spaced both horizontally and vertically. However, more work must be performed to treat effects of wind, fuel type, and vertically overlapping fuel elements to improve wildland fire modeling efforts.
Author Contributions
Conceptualization, T.H.F.; methodology, T.H.F., D.H., S.T.; software, D.O.L.; formal analysis, T.H.F., D.H., S.T., D.O.L.; writing—original draft preparation, T.H.F., D.H.; writing—review and editing, T.H.F., D.H., S.T., D.O.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Science Foundation, grant number NSF-CBET-1603316.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data are available from the principal author due to the large amount and variety of data.
Acknowledgments
We gratefully acknowledge work on this project by Trevor Black, Caleb Harper, Connor Last, Dan Oliveira, Mahmood Rahmati, Dallin Sabin, Chen Shen, and Colton Van Wagoner.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Research Paper INT-115; U.S. Department of Agriculture, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1972; pp. 1–40. [Google Scholar]
- Linn, R.R.; Reisner, J.; Colman, J.J.; Winterkamp, J. Studying Wildfire Behavior using FIRETEC. Int. J. Wildland Fire 2002, 11, 233–246. [Google Scholar] [CrossRef]
- Mell, W.; Jenkins, M.A.; Gould, J.; Cheney, P. A Physics-based Approach to Modelling Grassland Fires. Int. J. Wildland Fire 2007, 16, 1–22. [Google Scholar] [CrossRef]
- Scott, J.H. Comparison of Crown Fire Modeling Systems Used in Three Fire Management Applications; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; p. 25. [Google Scholar] [CrossRef] [Green Version]
- Prince, D.R.; Fletcher, T.H. Differences in Burning Behavior of Live and Dead Leaves, Part 1: Measurements. Combust. Sci. Technol. 2014, 186, 1844–1857. [Google Scholar] [CrossRef]
- Cole, W.J.; Dennis, M.H.; Fletcher, T.H.; Weise, D.R. The effects of wind on the flame characteristics of individual leaves. Int. J. Wildland Fire 2011, 20, 657–667. [Google Scholar] [CrossRef]
- Fletcher, T.H.; Pickett, B.M.; Smith, S.G.; Spittle, G.S.; Woodhouse, M.M.; Haake, E.; Weise, D.R. Effects of Moisture on Ignition Behavior of Moist California Chaparral and Utah Leaves. Combust. Sci. Technol. 2007, 179, 1183–1203. [Google Scholar] [CrossRef] [Green Version]
- Engstrom, J.D.; Butler, J.K.; Smith, S.G.; Baxter, L.L.; Fletcher, T.H.; Weise, D.R. Ignition Behavior of Live California Chaparral Leaves. Combust. Sci. Technol. 2004, 176, 1577–1591. [Google Scholar] [CrossRef]
- Li, J.; Mahalingam, S.; Weise, D.R. Experimental investigation of fire propagation in single live shrubs. Int. J. Wildland Fire 2017, 26, 58–70. [Google Scholar] [CrossRef]
- Zhou, X.; Mahalingam, S.; Weise, D. Experimental study and large eddy simulation of effect of terrain slope on marginal burning in shrub fuel beds. Proc. Combust. Inst. 2007, 31, 2547–2555. [Google Scholar] [CrossRef]
- Prince, D.; Shen, C.; Fletcher, T. Semi-empirical Model for Fire Spread in Shrubs with Spatially-Defined Fuel Elements and Flames. Fire Technol. 2017, 53, 1439–1469. [Google Scholar] [CrossRef]
- Shen, C.; Fletcher, T.H.; Weise, D.R. Semi-empirical fire spread model for chamise and big sagebrush shrubs with spatially-defined fuel elements and flames. In Advances in Forest Fire Research; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2018; pp. 637–642. [Google Scholar] [CrossRef] [Green Version]
- Dahale, A.; Shotorban, B.; Mahalingam, S. Interactions of Fires of Neighboring Shrubs in Two- and Three-shrub Arrangements. Int. J. Wildland Fire 2015, 24, 624–639. [Google Scholar] [CrossRef]
- Baldwin, R. Flame merging in multiple fires. Combust. Flame 1968, 12, 318–324. [Google Scholar] [CrossRef]
- Dahm, W.J.A. Scaling Relations for Flare Interactions, Flame Lengths, and Crosslighting Requirements in Large Flare Fields. In Proceedings of the AFRC-JFRC International Symposium, Marriott Waikoloa, HI, USA, 22–24 October 2007. [Google Scholar]
- Kamikawa, D.; Weng, W.G.; Kagiya, K.; Fukuda, Y.; Mase, R.; Hasemi, Y. Experimental study of merged flames from multifire sources in propane and wood crib burners. Combust. Flame 2005, 142, 17–23. [Google Scholar] [CrossRef]
- Weng, W.G.; Kamikawa, D.; Fukuda, Y.; Hasemi, Y.; Kagiya, K. Study on flame height of merged flame from multiple fire sources. Combust. Sci. Technol. 2004, 176, 2105–2123. [Google Scholar] [CrossRef]
- Sugawa, O.; Takahashi, W. Flame Height Behavior from Multi-fire Sources. Fire Mater. 1993, 17, 111–117. [Google Scholar] [CrossRef]
- Morvan, D.; Hoffman, C.; Rego, F.; Mell, W. Numerical Simulation of the Interaction between Two Fire Fronts in Grassland and Shrubland. Fire Saf. J. 2011, 46, 469–479. [Google Scholar] [CrossRef]
- Finney, M.A.; McAllister, S.S. A Review of Fire Interactions and Mass Fires. J. Combust. 2011, 548328. [Google Scholar] [CrossRef]
- Putnam, A.A.; Speich, C.F. A model study of the interaction of multiple turbulent diffusion flames. Symp. Combust. 1963, 9, 867–877. [Google Scholar] [CrossRef]
- Shen, C.; Lignell, D.O.; Fletcher, T.H. Flame Merging Experiments in Low Speed, Non-Premixed Natural Gas Flames. In Flame Merging Experiments in Low Speed, Non-Premixed Natural Gas Flames, Proceedings of the 9th U.S. National Combustion Institute Meeting, Cincinatti, OH, USA, 17–20 May 2015; Combustion Institute: Pittsburgh, PA, USA, 2015. [Google Scholar]
- Wan, H.; Gao, Z.; Ji, J.; Zhang, Y. Experimental study on flame radiant heat flux from two heptane storage pools and its application to estimating safety distance. Energy 2019, 182, 11–20. [Google Scholar] [CrossRef]
- Jiao, Y.; Gao, W.; Liu, N.; Lei, J.; Xie, X.; Zhang, L.; Tu, R. Interpretation on fire interaction mechanisms of multiple pool fires. Proc. Combust. Inst. 2019, 37, 3967–3974. [Google Scholar] [CrossRef]
- Delichatsios, M.A. A Correlation for the Flame Height in “Group” Fires. Fire Sci. Technol. 2007, 26, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Fukuda, Y.; Kamikawa, D.; Hasemi, Y.; Kagiya, K. Flame characteristics of group fires. Fire Sci. Technol. 2004, 23, 164–169. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Liu, Q.; Lozano, J.S.; Shu, L.; Zhang, L.; Zhu, J.; Deng, Z.; Satoh, K. Global Burning Rate of Square Fire Arrays: Experimental Correlation and Interpretation. Proc. Combust. Inst. 2009, 32, 2519–2526. [Google Scholar] [CrossRef]
- Wan, H.; Gao, Z.; Ji, J.; Wang, L.; Zhang, Y. Experimental study on merging behaviors of two identical buoyant diffusion flames under an unconfined ceiling with varying heights. Proc. Combust. Inst. 2019, 37, 3899–3907. [Google Scholar] [CrossRef]
- Li, B.; Wan, H.; Gao, Z.; Ji, J. Experimental study on the characteristics of flame merging and tilt angle from twin propane burners under cross wind. Energy 2019, 174, 1200–1209. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, S.; Luo, X.; Lei, J.; Chen, H.; Xie, X.; Zhang, L.; Tu, R. Interaction of two parallel rectangular fires. Proc. Combust. Inst. 2019, 37, 3833–3841. [Google Scholar] [CrossRef]
- Weng, W.; Kamikawa, D.; Hasemi, Y. Experimental study on merged flame characteristics from multifire sources with wood cribs. Proc. Combust. Inst. 2015, 35, 2597–2606. [Google Scholar] [CrossRef]
- Beer, T. Fire Propagation in Vertical Stick Arrays—The Effects of Wind. Int. J. Wildland Fire 1995, 5, 43–49. [Google Scholar] [CrossRef]
- Vogel, M.; Williams, F.A. Flame Propagation Along Matchstick Arrays. Combust. Sci. Technol. 1970, 1, 429–436. [Google Scholar] [CrossRef]
- Weber, R.O. A model for fire propagation in arrays. Math. Comput. Model. 1990, 13, 95–102. [Google Scholar] [CrossRef]
- Pickett, B.M.; Isackson, C.; Wunder, R.; Fletcher, T.H.; Butler, B.W.; Weise, D.R. Flame interactions and burning characteristics of two live leaf samples. Int. J. Wildland Fire 2009, 18, 865–874. [Google Scholar] [CrossRef]
- Gollner, M.J.; Xie, Y.; Lee, M.; Nakamura, Y.; Rangwala, A.S. Burning Behavior of Vertical Matchstick Arrays. Combust. Sci. Technol. 2012, 184, 585–607. [Google Scholar] [CrossRef]
- Vasanth, S.; Tauseef, S.M.; Abbasi, T.; Abbasi, S.A. CFD simulation of pool fires situated at differing elevation. Process. Saf. Environ. Prot. 2015, 94, 89–95. [Google Scholar] [CrossRef]
- Fukuda, M.; Kudo, Y.; Ito, A. Fire Characteristics of Subsisting Multiple Fire Sources in Three Dimensions. Bull. Jpn. Assoc. Fire Sci. Eng. 2006, 56, 45–52. [Google Scholar] [CrossRef]
- Drysdale, D. An Introduction to Fire Dynamics, 3rd ed.; John Wiley & Sons, Ltd.: West Sussex, UK, 2011. [Google Scholar]
- Shen, C.; Fletcher, T.H. Fuel Element Combustion Properties for Live Wildland Utah Shrubs. Combust. Sci. Technol. 2015, 187, 428–444. [Google Scholar] [CrossRef]
- Gallacher, J.R. The Influence of Season, Heating Mode and Slope Angle on Wildland Fire Behavior. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 2016. [Google Scholar]
- Matt, F.J.; Dietenberger, M.A.; Weise, D.R. Summative and Ultimate Analysis of Live Leaves from Southern U.S. Forest Plants for Use in Fire Modeling. Energy Fuels 2020, 34, 4703–4720. [Google Scholar] [CrossRef]
Figure 1.
Schematic of the flame merging experimental setup.
Figure 1.
Schematic of the flame merging experimental setup.
Figure 2.
General three-pad configurations, where altering Δx or Δy will change the pad separation for that given configuration. No horizontal spacing was used if there is no Δx shown.
Figure 2.
General three-pad configurations, where altering Δx or Δy will change the pad separation for that given configuration. No horizontal spacing was used if there is no Δx shown.
Figure 3.
Schematic of image analysis. (a) Original colored image, (b) gray-scale image, and (c) black and white image showing the flame height and width measurements.
Figure 3.
Schematic of image analysis. (a) Original colored image, (b) gray-scale image, and (c) black and white image showing the flame height and width measurements.
Figure 4.
Flame height vs. time for two pads with no horizontal or vertical spacing, showing the 3 s moving average as well as the average flame height at the maximum filtered flame height.
Figure 4.
Flame height vs. time for two pads with no horizontal or vertical spacing, showing the 3 s moving average as well as the average flame height at the maximum filtered flame height.
Figure 5.
Comparison of two-pad and three-pad flame heights (uncorrected). Both flame height and total pad separation distance have been normalized, as described above.
Figure 5.
Comparison of two-pad and three-pad flame heights (uncorrected). Both flame height and total pad separation distance have been normalized, as described above.
Figure 6.
Corrected two-pad and three-pad flame heights as a function of total normalized pad separation distance.
Figure 6.
Corrected two-pad and three-pad flame heights as a function of total normalized pad separation distance.
Figure 7.
Probability of merging (PM) for two pads separated only by horizontal distance.
Figure 7.
Probability of merging (PM) for two pads separated only by horizontal distance.
Figure 8.
Merging probability (PM) as a function of normalized distance for the two-pad experiments. Lines are the curve fits using Equation (6). Error bars omitted for ease of viewing.
Figure 8.
Merging probability (PM) as a function of normalized distance for the two-pad experiments. Lines are the curve fits using Equation (6). Error bars omitted for ease of viewing.
Figure 9.
Parity plot of calculated PM vs. measured PM for the two-pad data using Equation (6).
Figure 9.
Parity plot of calculated PM vs. measured PM for the two-pad data using Equation (6).
Figure 10.
Merging probability (
PM) as a function of normalized distance for the three-pad experiments. Lines are the curve fit using Equation (7). Configurations are shown in
Figure 2.
Figure 10.
Merging probability (
PM) as a function of normalized distance for the three-pad experiments. Lines are the curve fit using Equation (7). Configurations are shown in
Figure 2.
Figure 11.
Corrected flame heights of experiments with two pads, plotted against dimensionless separation distance of the fuel sources. Lines are curve fits based on Equation (8).
Figure 11.
Corrected flame heights of experiments with two pads, plotted against dimensionless separation distance of the fuel sources. Lines are curve fits based on Equation (8).
Figure 12.
Corrected flame heights and associated 95% confidence intervals of experiments with three pads. Lines are best overall fit correlations using Equation (9). Configurations are shown in
Figure 2.
Figure 12.
Corrected flame heights and associated 95% confidence intervals of experiments with three pads. Lines are best overall fit correlations using Equation (9). Configurations are shown in
Figure 2.
Figure 13.
Normalized flame areas for the two-pad experiments in the region where flame merging occurred.
Figure 13.
Normalized flame areas for the two-pad experiments in the region where flame merging occurred.
Figure 14.
Flame area (
A) vs. total separation (
Stot/D) from experiments with 3 pads. Total flame area here was normalized by three times the average flame area of single pad experiments. Configurations are shown in
Figure 2.
Figure 14.
Flame area (
A) vs. total separation (
Stot/D) from experiments with 3 pads. Total flame area here was normalized by three times the average flame area of single pad experiments. Configurations are shown in
Figure 2.
Figure 15.
Corrected flame widths for the two-pad experiments. Lines are best overall fit correlations using Equation (12). Average error bars (95% confidence intervals) are only shown on the Sy = 0 data for convenience.
Figure 15.
Corrected flame widths for the two-pad experiments. Lines are best overall fit correlations using Equation (12). Average error bars (95% confidence intervals) are only shown on the Sy = 0 data for convenience.
Figure 16.
Corrected flame width (
Wc) vs. normalized total separation distance (
Stot/D) from experiments with three pads. Flame widths normalized by three times the width of a single pad. Configurations are shown in
Figure 2.
Figure 16.
Corrected flame width (
Wc) vs. normalized total separation distance (
Stot/D) from experiments with three pads. Flame widths normalized by three times the width of a single pad. Configurations are shown in
Figure 2.
Figure 17.
Flame duration times for the top and bottom flames in the two-pad experiments, normalized by the flame duration time for the single-pad experiment.
Figure 17.
Flame duration times for the top and bottom flames in the two-pad experiments, normalized by the flame duration time for the single-pad experiment.
Figure 18.
Normalized flame duration times for the top flame in the two-pad experiments with no horizontal separation (Sx/D = 0).
Figure 18.
Normalized flame duration times for the top flame in the two-pad experiments with no horizontal separation (Sx/D = 0).
Figure 19.
Flame duration times for the three-pad experiments, normalized by the flame duration time for the single-pad experiment (
a–
e). Data were split into subfigures containing only two or three of the configurations shown in
Figure 2 and
Figure 20. Error bars were omitted for ease of viewing.
Figure 19.
Flame duration times for the three-pad experiments, normalized by the flame duration time for the single-pad experiment (
a–
e). Data were split into subfigures containing only two or three of the configurations shown in
Figure 2 and
Figure 20. Error bars were omitted for ease of viewing.
Figure 20.
General three-pad configurations (repeated from
Figure 2) with pads for which the burn times decreased due to flame merging highlighted.
Figure 20.
General three-pad configurations (repeated from
Figure 2) with pads for which the burn times decreased due to flame merging highlighted.
Table 1.
Single-pad flame characteristics.
Table 1.
Single-pad flame characteristics.
| Description | Symbol | Value |
|---|
| Average height of single-pad flame | L1 | 38.7 ± 1.7 * cm |
| Average width of single-pad flame | W1 | 12.4 ± 0.7 cm |
| Average area of single-pad flame | A1 | 232.7 ± 12.6 cm2 |
| Width of a single pad | Wp | 3.81 cm |
| Dimensionless flame height | L/D | 10.2 ± 0.45 |
| Burnout time of a single pad | t1 | 54.6 ± 2 s |
| Average initial mass of n-heptane per pad | m0 | 3.35 ± 0.2 g |
| Heating of combustion of liquid n-heptane | ΔHc | −48.07 MJ/kg |
| Average heat release rate | | 2.95 kJ/s |
| Normalized heat release rate | Q * | 10.9 |
Table 2.
Curve-fit constants for correlation of two-pad PM data (Equation (6)).
Table 2.
Curve-fit constants for correlation of two-pad PM data (Equation (6)).
| Constant | Value |
|---|
| A | 1.132 |
| B | −0.215 |
| C | 0.753 |
| D | −6.145 |
| SSE | 58.7 |
Table 3.
Curve-fit constants for correlation of three-pad PM data (Equation (7)).
Table 3.
Curve-fit constants for correlation of three-pad PM data (Equation (7)).
| Constant | Value |
|---|
| A1 | 0.580 |
| A2 | 1.281 |
| B1 | −0.224 |
| B2 | −0.359 |
| C | −2.994 |
| D | −0.082 |
| E | 0.036 |
| F | 0.073 |
| SSE | 1.43 × 104 |
Table 4.
Curve-fit constants for correlation of two-pad FH data (Equation (8)).
Table 4.
Curve-fit constants for correlation of two-pad FH data (Equation (8)).
| Constant | Value |
|---|
| A | 0.844 |
| n2 | 0.807 |
| B | 1.6 × 10−5 |
| n | 5.20 |
| C | 0.990 |
| D | 0.187 |
| SSE | 0.345 |
Table 5.
Curve-fit constants for correlation of three-pad FH data (Equation (9)).
Table 5.
Curve-fit constants for correlation of three-pad FH data (Equation (9)).
| Constant | Value |
|---|
| A | 4.236 |
| B | 2.775 |
| C | 0.013 |
| n | 1.063 |
| D | 0.050 |
| m | 0.317 |
| E | 0.015 |
| SSE | 0.656 |
Table 6.
Curve-fit constants for correlation of two-pad flame area data (Equations (10) and (11)).
Table 6.
Curve-fit constants for correlation of two-pad flame area data (Equations (10) and (11)).
| Constant | Value | Constant | Value |
|---|
| A1 | 1.138 | A2 | 1.296 |
| B1 | −0.177 | B2 | −0.079 |
| C | 0.370 | SSE2 | 0.096 |
| D | 2.931 | | |
| n | 2.047 | | |
| m | 3.436 | | |
| SSE1 | 0.062 | | |
Table 7.
Curve-fit constants for correlation of two-pad flame width data (Equation (12)).
Table 7.
Curve-fit constants for correlation of two-pad flame width data (Equation (12)).
| Constant | Value |
|---|
| A | 0.052 |
| m | 1.5 |
| B | 0.089 |
| C | 2.56 |
| n | 5.75 |
| D | 0.689 |
| SSE | 0.619 |
Table 8.
Maximum and minimum flame dimensions (corrected) and burning times.
Table 8.
Maximum and minimum flame dimensions (corrected) and burning times.
| | 2-Pad | 3-Pad |
|---|
| | Min | Max | Avg | Min | Max | Avg |
|---|
| Flame Height | 0.90 | 1.27 | 1.06 | 0.96 | 1.5 | 1.22 |
| Area | 0.76 | 1.24 | 1.05 | 0.82 | 1.34 | 1.00 |
| Width | 0.58 | 0.91 | 1.76 | 0.27 | 1.55 | 0.94 |
| Burn time | 0.78 | 1.03 | 1.03 | 0.59 | 1.16 | 0.95 |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).