1. Introduction
Escape routes are some of the most important safety measures available to wildland firefighters, acting as pre-defined pathways for firefighters to access a safety zone or other low-risk area from their current position [
1]. They are an integral component of the Lookouts, Communications, Escape routes, and Safety zones (LCES) safety protocol and are imbedded throughout the 10 Standard Firefighting Orders and the 18 Situations that Shout Watch Out [
2,
3]. The Incident Response Pocket Guide, which is used by all US wildland firefighters, describes some ideal characteristics of escape routes, including having more than one, avoiding steep uphill routes, and timing them considering the slowest crewmember given current levels of fatigue [
4]. In order to be maximally-effective, escape routes should provide fire crews with a positive Margin of Safety (MOS) [
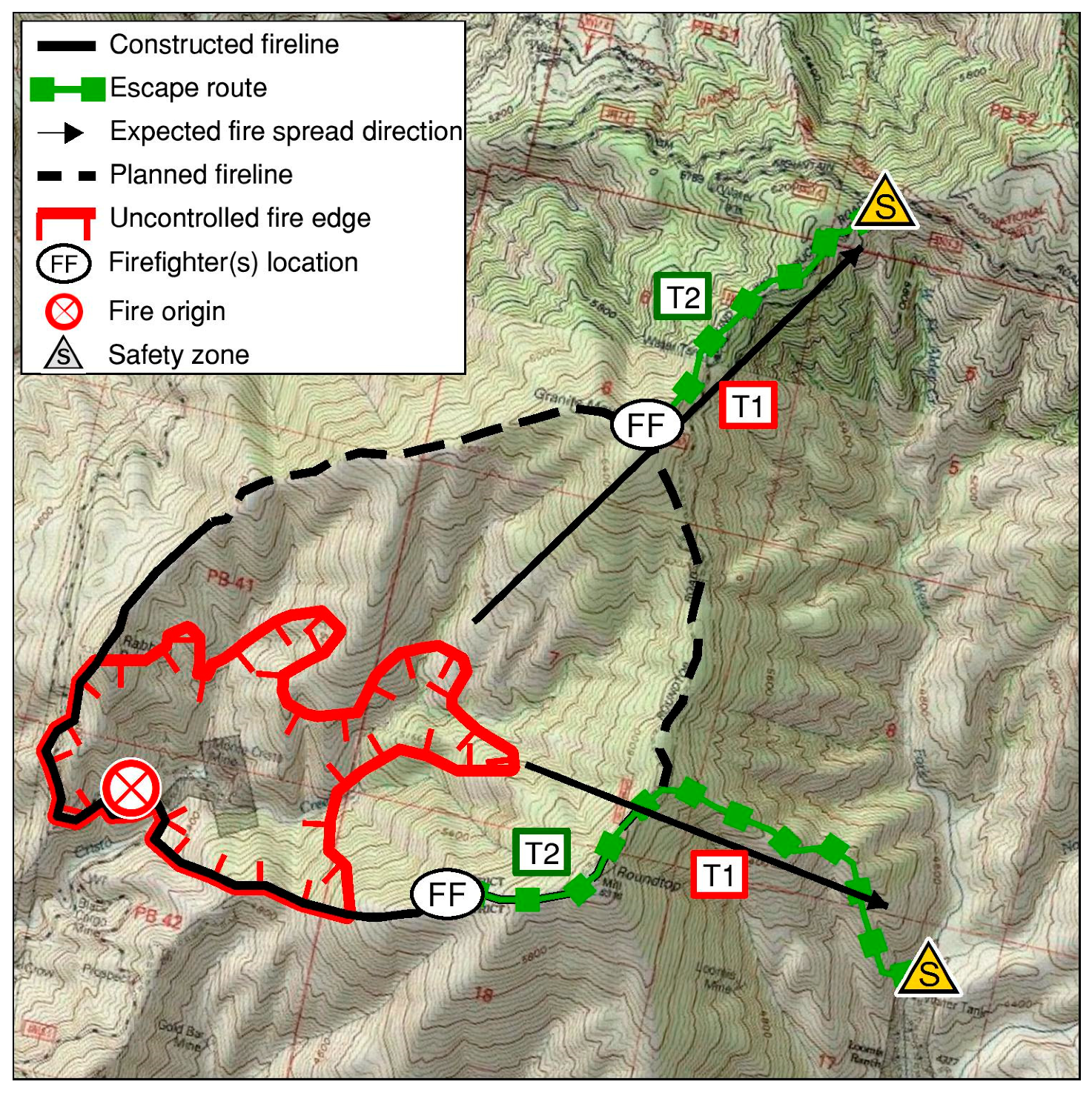
5]. MOS is defined as the difference between the time it takes a fire to reach a given location, such as a safety zone (T1) and the time it takes a fire crew to reach that same location (T2) (
Figure 1). If T1 is greater than T2 (positive MOS), the crew should reach the safety zone without harm; however, if T2 is greater than T1 (negative MOS), the crew is at risk of becoming entrapped and suffering a burnover.
Both T1 and T2 are difficult to predict accurately in the field. T1 is controlled by fire behavior, the drivers of which are fuel, weather, and topography [
6]. Due to both the complexity of modeling fire behavior and the importance of being able to understand how fire moves through and affects a landscape, there is an extensive body of literature and several operational products aimed at predicting fire behavior (for a review of fire behavior modeling systems, please refer to [
7]). Considerably less attention has been devoted to predicting T2, which is controlled by a combination of internal factors (e.g., height, weight, fitness and endurance levels, and load carriage) and external factors (e.g., landscape and environmental conditions). Internal factors are highly variable within a population, but if a fire crew moves as a unit, then they are only as fast as the slowest individual in the group. This makes modeling population-level differences as a function of external factors more important than modeling individual differences. An additional benefit to focusing on external factors is that most external factors can be mapped on a broad spatial scale using a combination of remote sensing and geographic information systems (GIS).
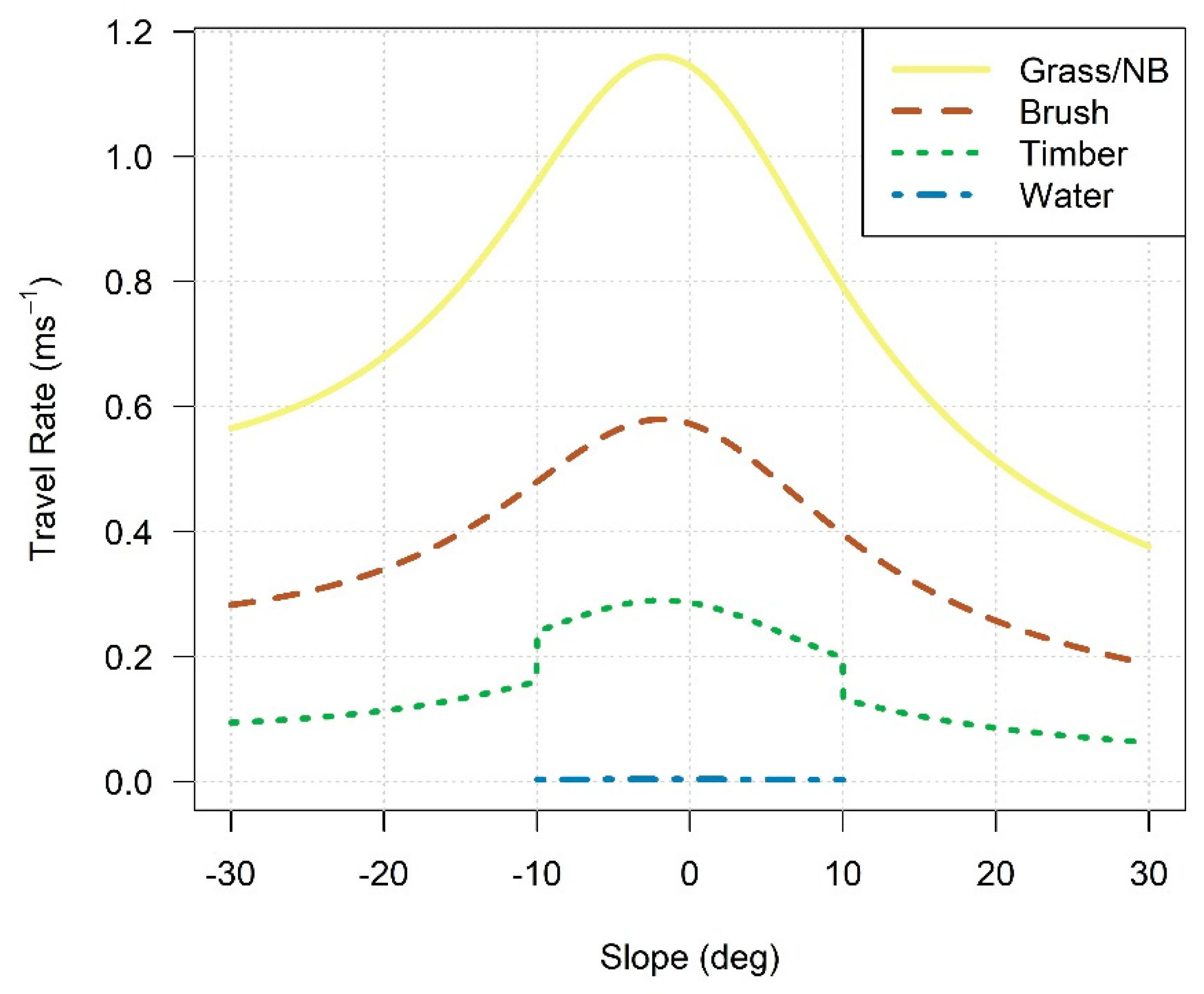
The most important external factors that affect one’s ability to efficiently move through a given landscape include terrain slope, ground surface condition (e.g., roughness, firmness, and stability), and the presence, abundance, and arrangement of vegetation [
8]. The effects of slope on travel rates have been studied since the nineteenth century, and several models for predicting travel rates based on slope have been developed, including the widely-used Naismith’s Rule and Tobler’s Hiking Function [
9,
10]. Though widely-cited, these travel rate functions lack the scientific rigor inherent to large sample sizes, GPS-driven instantaneous travel rates, and modern statistical modeling techniques. A recent study by Campbell et al. [
11] overcame previous limitations, producing an improved slope-travel rate predictive model based on a very large database of GPS tracks harvested from the widely-used mobile fitness tracking application Strava, and light detection and ranging (lidar)-derived terrain slope data. At present, their resulting model represents the most accurate understanding of the relationship between slope and travel rates, and as such, will be used as the basis of simulating slope impedance in this study. Given the fact that digital elevation models (DEM) are available on a nationwide basis in the US as a part of the United States Geological Survey (USGS) 3D Elevation Program (3DEP) [
12], a slope-based, spatially-explicit model for predicting optimal, or “least-cost” escape routes could be realized (e.g., [
8,
13]). However, to more accurately simulate movement in a wildland environment, the effects of land cover on travel rates also need to be taken into account.
The effects of ground surface condition and vegetation are both less well-understood and more difficult to map. In a review of the energetic costs associated with traversing a diversity of landscape conditions, Richmond et al. [
14] identify four parameters that affect the efficiency of pedestrian movement in a wildland environment: (1) sinkage (how deep a foot will sink into the ground surface); (2) slipperiness (the relative friction of the ground surface); (3) roughness (the microtopography that controls foot placement on the ground surface); and (4) vegetation (the presence, abundance, and arrangement of physical impediments on top of the ground surface). The first three parameters can be categorized broadly as ground surface conditions, controlled primarily by a combination of soil type (e.g., clay vs. sand), soil condition (e.g., dry vs. wet), underlying geology (e.g., sedimentary vs. igneous), history of geomorphological activity (e.g., erosion vs. deposition), history of human activity (e.g., paved vs. natural) and presence and depth of snow or ice on the ground surface. The fourth parameter—vegetation—impedes movement in a variety of ways, including obstacle avoidance (avoiding dense patches of vegetation altogether, thus increasing travel distance and decreasing net travel rate), obstacle navigation (stepping over debris, crouching under branches, squeezing through gaps), friction (woody and/or foliar biomass resisting forward movement), and bushwhacking (physical alteration of the desired path requiring additional time and energy). Much of the research aimed at understanding how these different landscape conditions affect pedestrian movement stems from the field of applied physiology, where human experimentation dating back to the 1970s has yielded estimates for the energetic costs associated with traversing diverse landscape conditions. However, due to the complex and interacting nature of the effects of these four parameters, rather than quantifying the effects individually, they are typically described in terms of broadly-defined “terrain coefficients”, which represent the relative energetic costs associated with traversing a variety of general land cover types, as seen in
Table 1 [
15,
16].
Campbell et al. [
8] used airborne lidar remote sensing to derive continuous measures of slope, vegetation density, and ground surface roughness as the basis of travel impedance analysis. Absent direct quantification of ground surface condition and vegetation, land cover or fuel type can serve as a proxy, assuming that land cover classes or fuel types represent typical or average vegetation and ground surface conditions within each class. Alexander et al. [
17] tested the combined effects of load carriage, terrain slope, and fuel type on wildland firefighter travel rates. They did not present specific multiplicative factors, such as those in
Table 1 and travel rates were measured, rather than metabolic costs. The results show that open fuel types, such as grasslands and logging slash tend to promote the fastest travel, whereas lodgepole pine stands with an open understory increase travel time by a factor of about 1.3, and dense spruce and fir forests increased travel time by a factor of about 1.8. The Wildland Fire Decision Support System (WFDSS) uses land cover factors to adjust travel rates for its Ground Medevac Time dataset (
Table 2). This is a US nationwide GIS dataset representing transport time to the nearest hospital [
18].
By combining the slope-travel rate function defined by Campbell et al. [
11], and the land cover-travel rate effects defined by WFDSS [
18], spatially-explicit escape route mapping could become a reality. However, as the National Wildfire Coordinating Group (NWCG) points out, escape routes are “probably the most elusive component of LCES” [
19], as their effectiveness changes continuously throughout a day. Thus, to be useful for wildland firefighters, escape route mapping has to be done in real-time or near-real-time, which requires three things: (1) the location of the crew; (2) the location of the designated safety zone; and (3) the extent and predicted spread of the fire. In the absence of a widely-adopted, GPS-driven, mobile platform to implement such a real-time mapping effort, operational escape route mapping may not be currently feasible. However, even without knowing (1), (2), or (3) described above, one can still use pre-mapped terrain and land cover information to help wildland firefighters determine what areas have generally better or worse egress capacity.
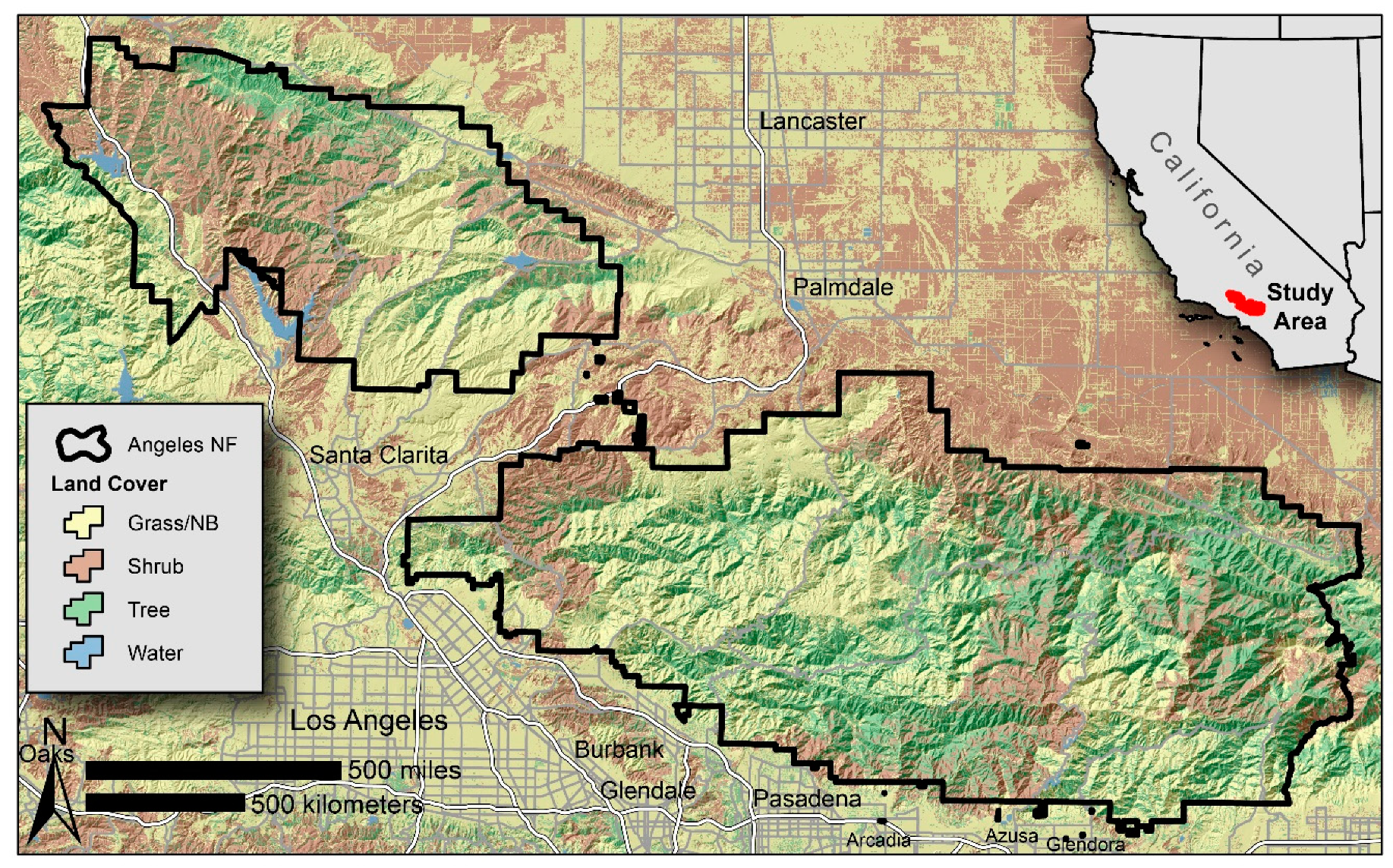
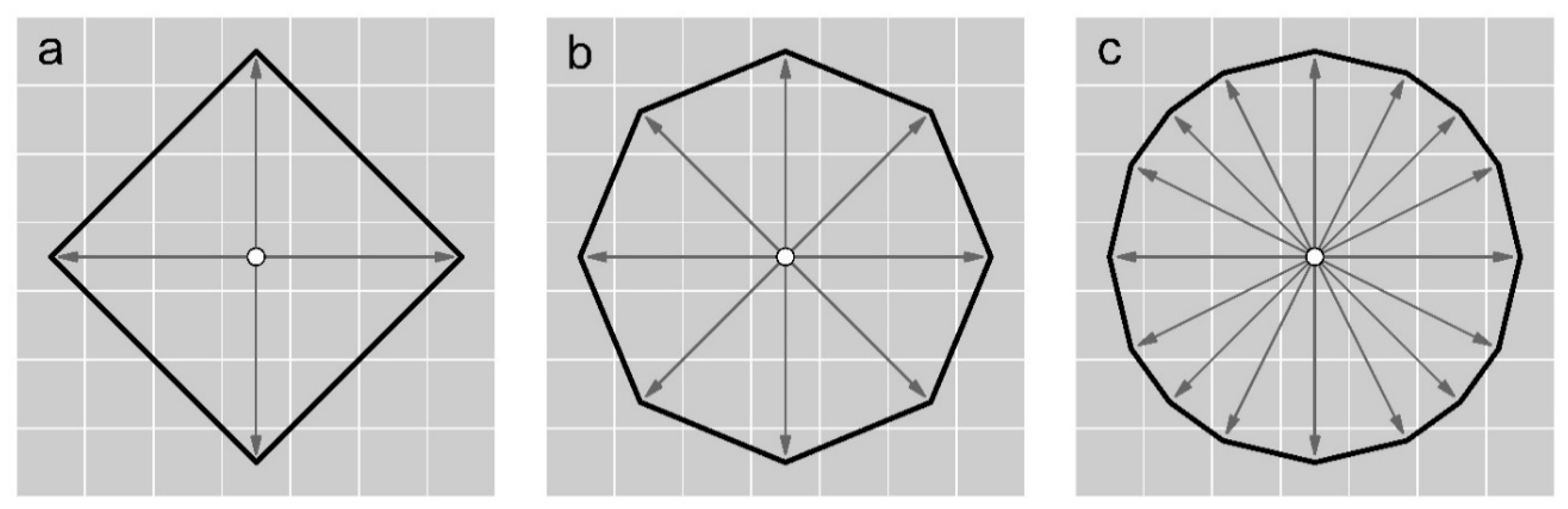
The goal of this paper is to introduce the Escape Route Index (ERI), which is a spatially-explicit measure of relative egress capacity based on the effects of terrain slope and land cover on pedestrian travel rates. ERI is a suite of four spatial metrics aimed at capturing the directionally-specific effects of the landscape on travel rates: (1) ERImean (average ERI in all travel directions from a given starting location); (2) ERImin (ERI in the direction of lowest/worst egress); (3) ERImax (ERI in the direction of highest/best egress); and (4) ERIazimuth (azimuth of the direction of highest/best egress). When mapped in advance of a wildland fire, the ERI can help wildland firefighters identify potential control locations in areas with favorable conditions for evacuation. We first describe the conceptual basis of ERI, followed by a detailed description of how it is implemented in a geospatial environment. To demonstrate utility on a broad spatial scale, ERI is mapped throughout the entire Angeles National Forest (ANF) in southern California. Lastly, ERI is used to look back in time at previous wildland firefighter entrapment events to assess how slope and land cover may have contributed to the events.
3. Results
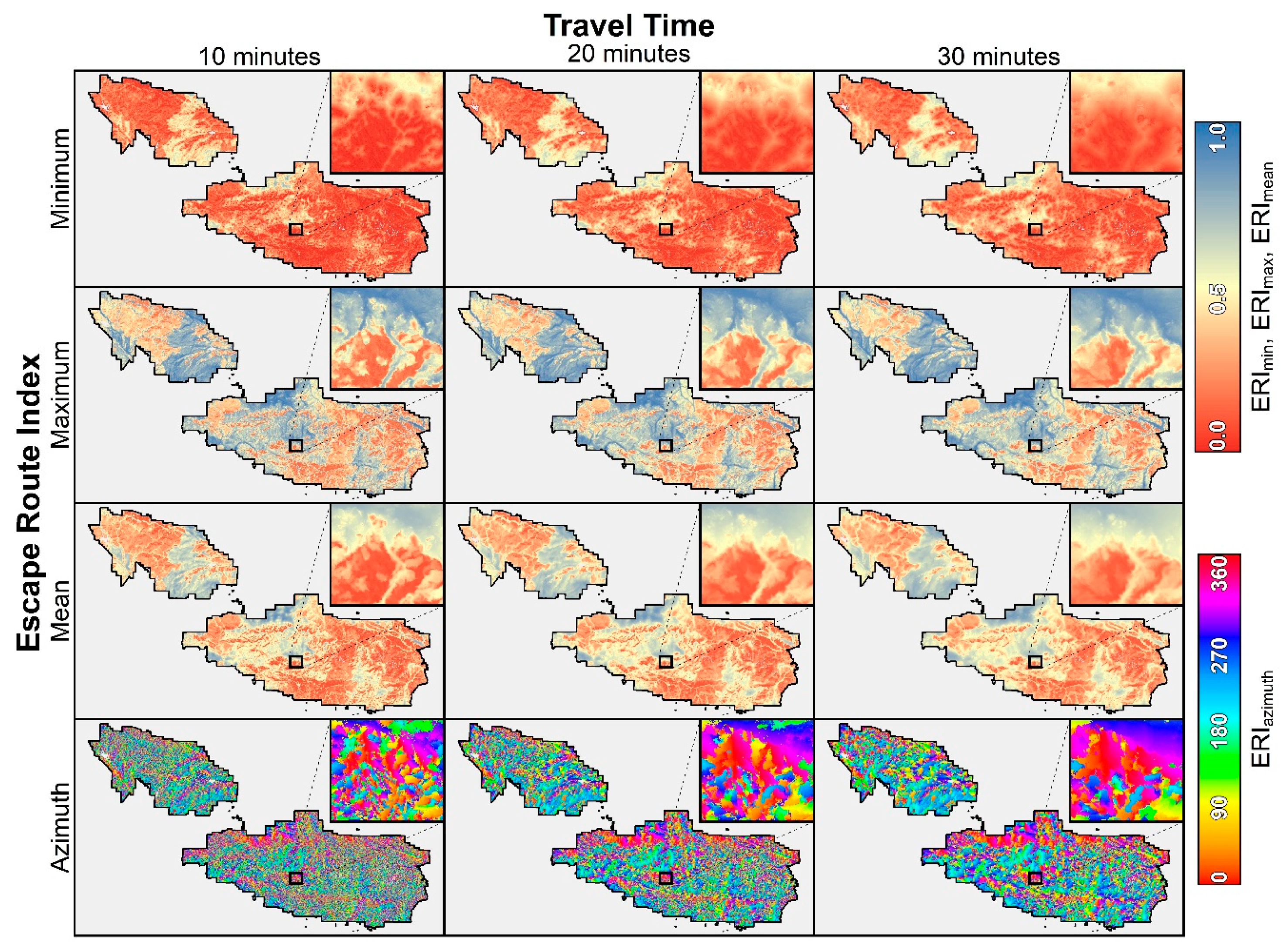
The results of the study area-wide ERI modeling effort can be seen in
Figure 6 and
Figure 7, and
Table 7. By virtue of their formulations, ERI
max values are higher than ERI
mean values which are higher than ERI
min values. Spatially, ERI
min, ERI
max, and ERI
mean all follow similar geographic patterns—areas of high ERI in one metric tended to produce high ERI in another and vice versa. This is because areas that had high travel impedance (e.g., steep slopes, and tree-dominated land cover) tended to reduce the egress capacity, regardless of travel direction. However, the directionality of egress had a definite effect. ERI
max, representing the best-case scenario for evacuation, and ERI
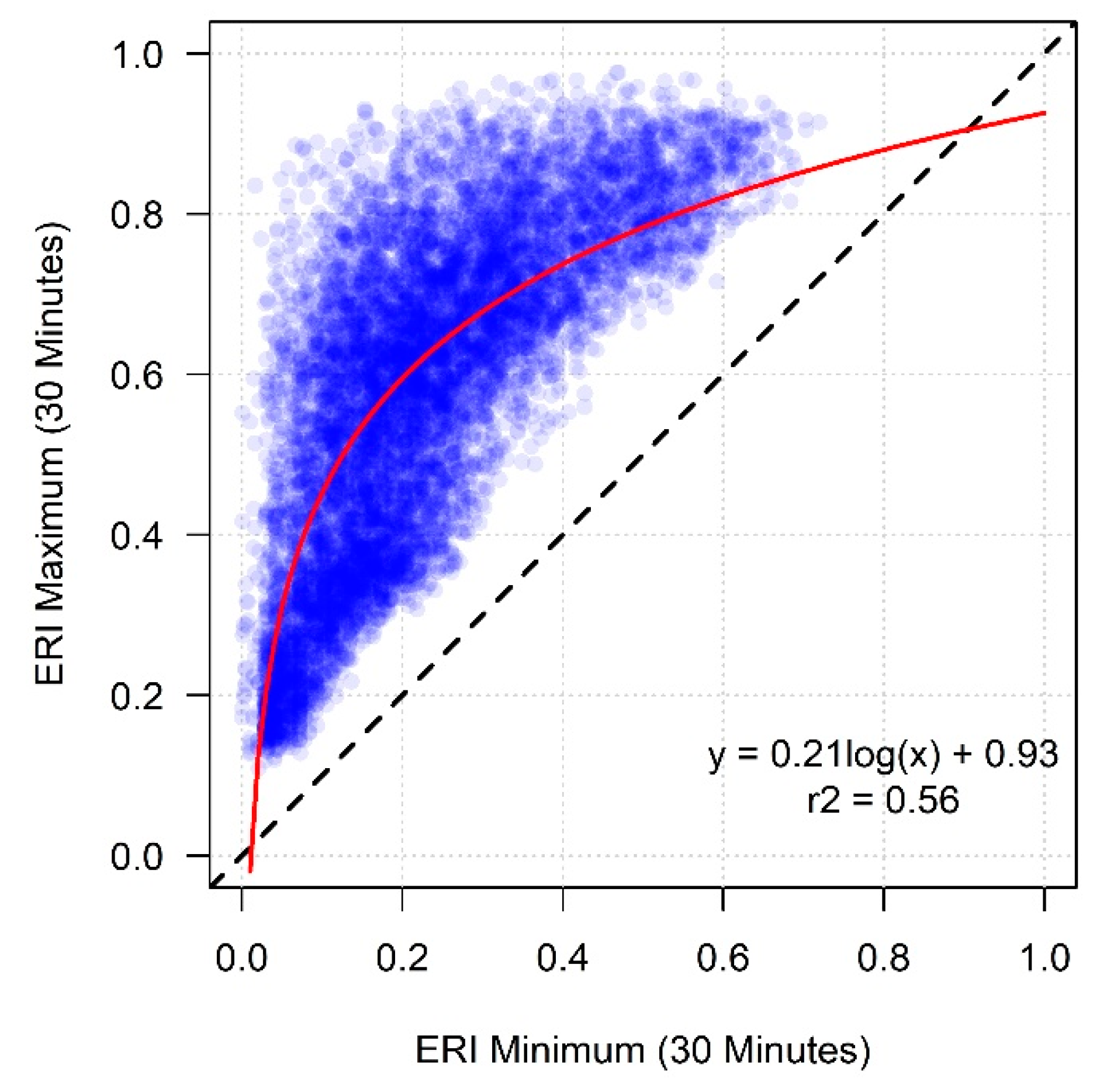
min, representing the worst-case scenario, although correlated, have a high degree of variability between them (
Figure 8). The magnitude of difference between ERI
max and ERI
min can yield valuable information about the spatial characteristics of the egress in a given area. For example, a high ERI
max:ERI
min ratio suggests a high degree of escape route directionality—that is, there is at least one direction by which evacuation would be relatively more efficient and at least one direction where evacuation would be relatively less so. Conversely, an ERI
max:ERI
min ratio that approaches 1 would suggest directional independence of evacuation, as the worst-case and the best-case evacuation direction have similar travel impedance.
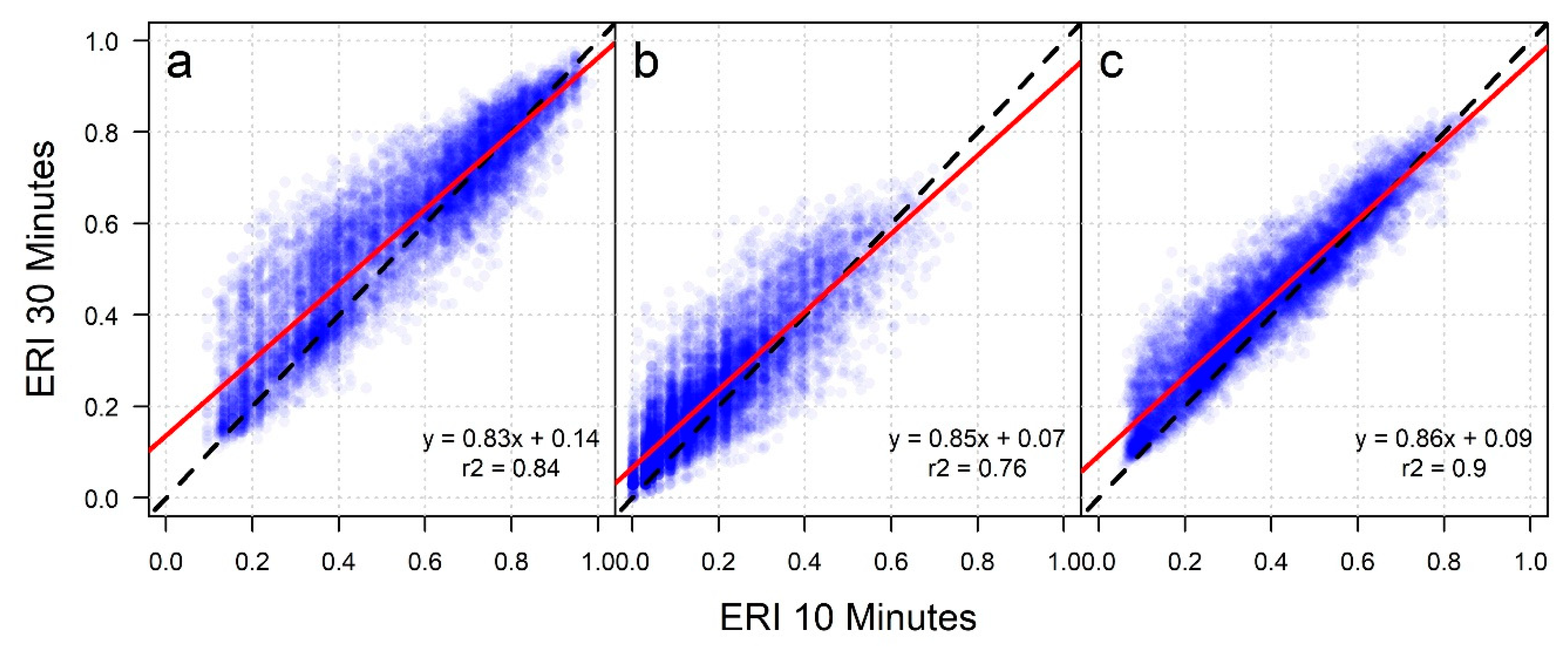
Figure 6 also highlights the effects of evacuation time frame on ERI values, best illustrated in the larger-scale inset maps. Across all ERI metrics, as travel time increases, the ERI values “smooth out” over space. This is because, for a short evacuation (e.g., 10 min), a small, spatially-isolated impeding feature, such as a cliff or a dense patch of forest, can have a large relative effect on the distance one could travel. For longer evacuations, smaller travel impediments do not have as significant of an effect on the relative distance one can travel. This smoothing effect is evident across ERI
max, ERI
min, and ERI
mean in
Figure 9, as the slope of the regression line is less than 1. The smoothing is also particularly clear in the ERI
azimuth values, such that longer travel times tend to produce larger patches of area with similar evacuation direction. From an operational standpoint, having these larger patches may be more useful for escape route planning.
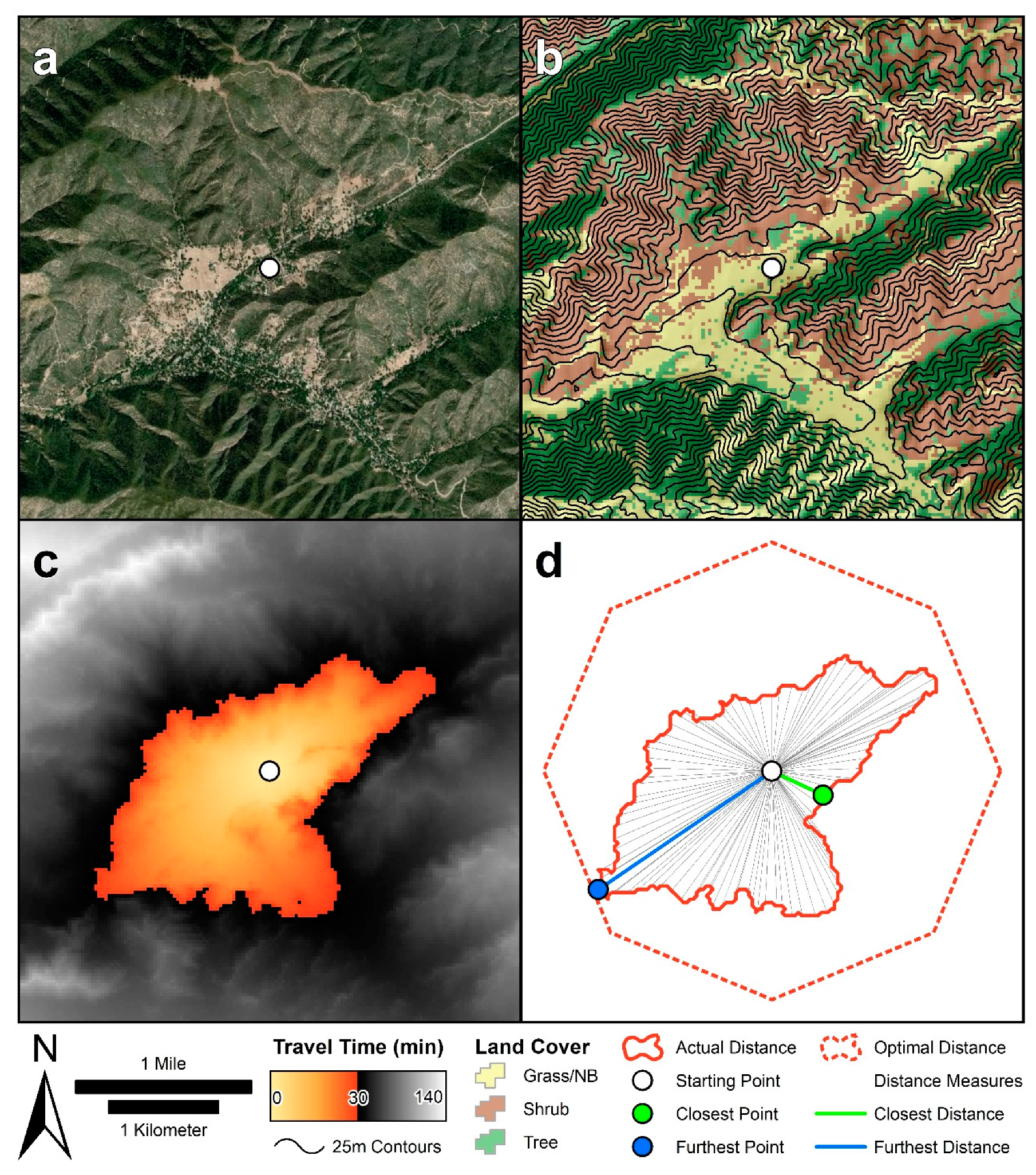
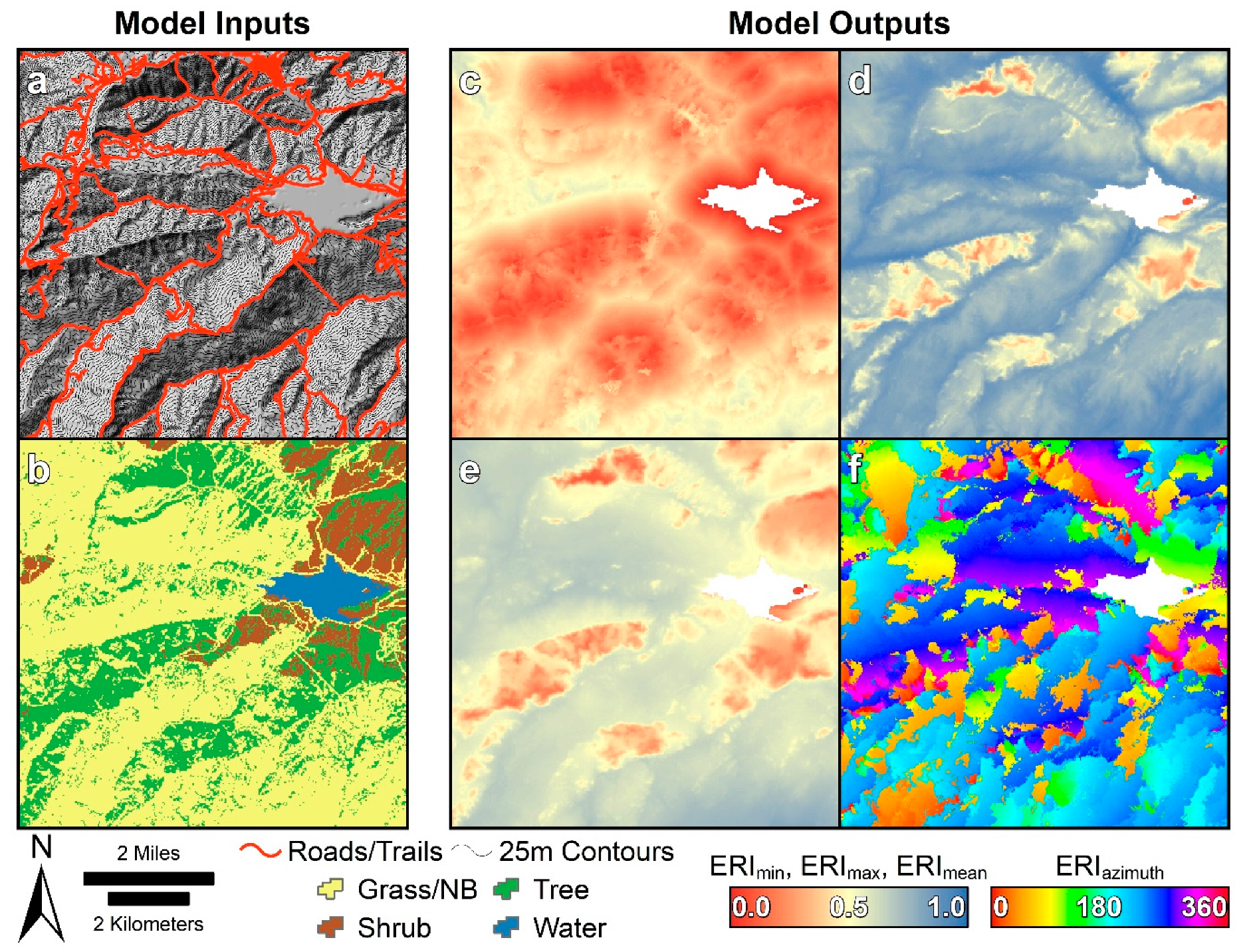
When comparing the spatial characteristics of the input datasets seen in the study area map (
Figure 3) and those of the ERI
max, ERI
min, and ERI
mean results (
Figure 6), it becomes apparent that land cover has a dominant effect on egress capacity.
Figure 10 contains a larger-scale depiction of the model inputs and outputs to highlight this effect. As can be seen, the forested areas demonstrate a strong influence on the ERI model results, particularly ERI
max and ERI
mean (
Figure 10d,e, respectively). Land cover has 3–4x the influence of slope based on multiple regression-based variable importance analysis (
Table 8). This is predictable, given the fact that the maximum relative effects of the input conductance values differ significantly between slope and land cover. However, it is also important to note that, due to the fact that ERI is not simply calculated on a cell-by-cell basis by performing raster map algebra on input cells, the R
2 values for the regression analyses are not very high. ERI values are calculated based not just on local conditions, but broader surrounding conditions. In the case of 30 min travel time simulations, conditions as far away as 2 km can affect ERI values at a given location. Accordingly, as discussed earlier, shorter travel time simulations are more affected by local conditions. This is also evident in the fact that the 10 min ERI values have higher R
2 values than the 20 and 30 min values.
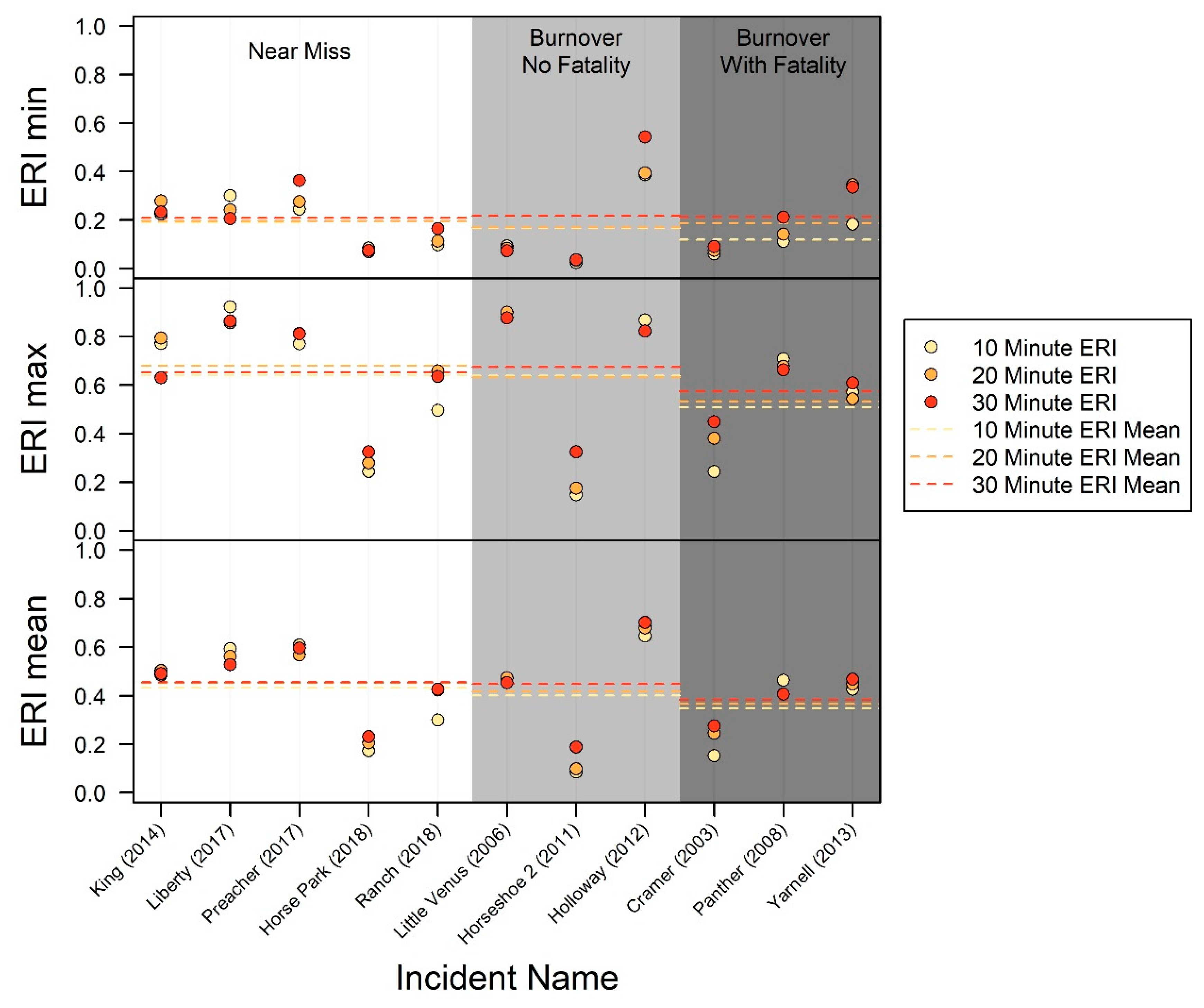
Mapped travel times for wildland firefighter entrapments can be seen in
Figure 11. The results highlight a diversity of landscape conditions faced by firefighters among these events, with some featuring comparably favorable landscape conditions (e.g., Holloway (
Figure 11e), Yarnell (
Figure 11f), King (
Figure 11g), and Preacher (
Figure 11i)), and others featuring comparably unfavorable conditions (e.g., Cramer (
Figure 11a), Little Venus (
Figure 11b), Horseshoe 2 (
Figure 11d), and Horse Park (
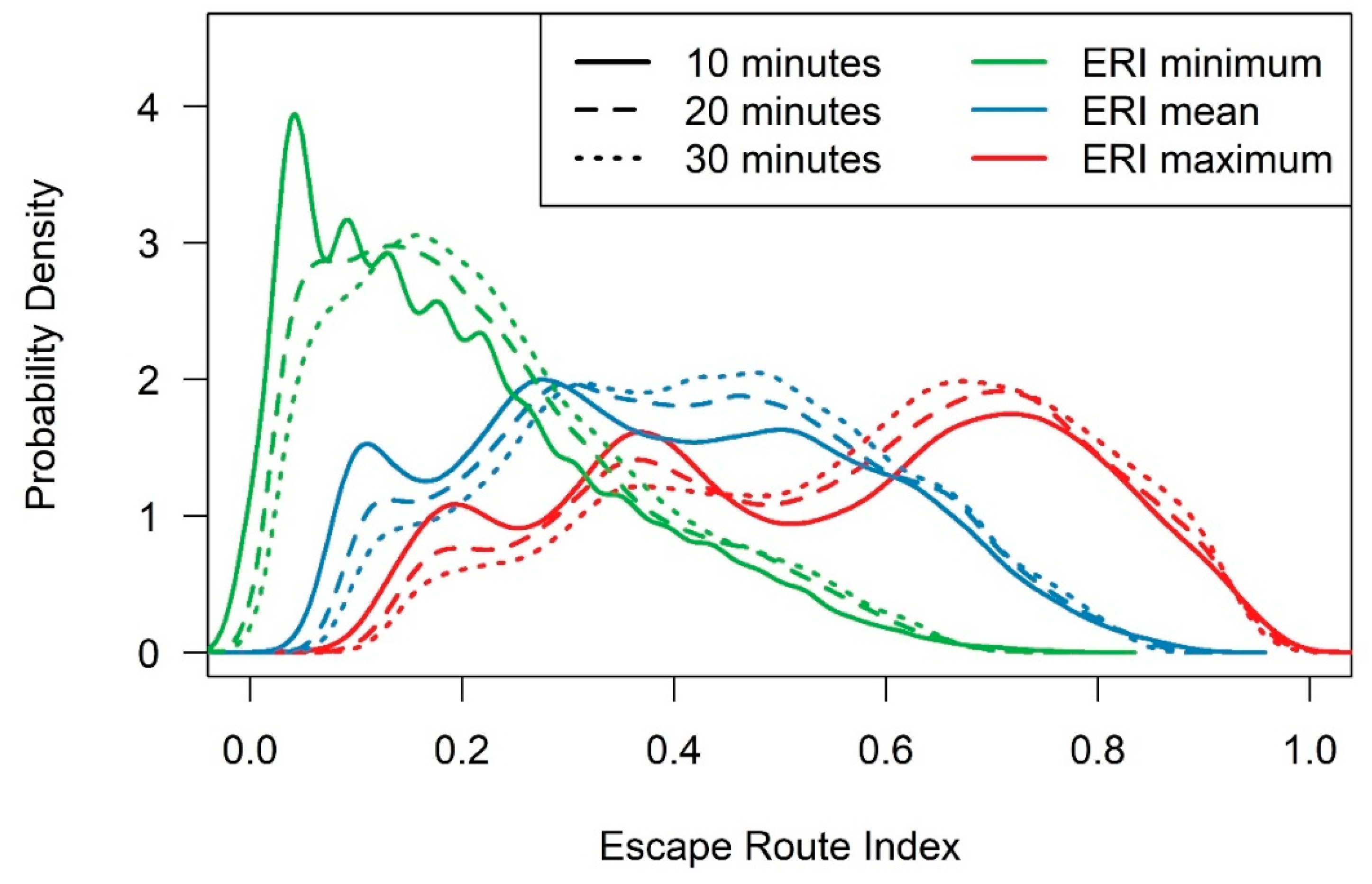
Figure 11j)). However, these results should be interpreted with caution for a few important reasons: (1) the mapped land cover conditions represent pre-fire conditions, and do not reflect the degree to which the fires had altered the cover (i.e., travel in the “black” can be substantially faster); (2) it is impossible to determine on a case-by-case scenario the temporal accuracy of the roads and trails—some may have existed pre-fire, but some may have been developed during or after the fire; (3) the ERI does not include any information on the spatial extent of the fire at the time of evacuation, which has perhaps the most important effect on evacuation direction; and (4) although some of the travel distances mapped are larger than others, and as such suggest greater egress capacity, the ERI values across the board are still quite low (
Figure 12). For example, for the 30-min evacuation simulations, the mean ERI
min across all incidents was 0.21, the mean ERI
max across all incidents was 0.64, and the mean ERI
mean across all incidents was 0.43. The mean ERI values for burnovers with fatalities tended to be lower than the near misses and the burnovers without fatalities.
4. Discussion
ERI is focused on pre-fire terrain and land cover conditions. Accordingly, it does not account for a number of critical variables that can affect a fire crew’s safety planning decision making processes. Perhaps the most important variable not considered by ERI is the fire extent and growth trajectory. ERI makes the naïve assumption that travel is not restricted in any direction by any factors other than slope and land cover. In reality, fire crews may have 50% or more of potential evacuation directions cut off by the fire itself. Thus, ERI is not a real-time product, as it does not reflect real-time conditions making it a pre-fire decision support tool.
Another important consideration not included in the ERI modeling process is the presence of safety zones. LCES is not a sequence of four disparate safety measures, it is an integrated system of four inherently interdependent safety measures. If no suitable safety zone is accessible from the fireline, then no escape route, regardless of how efficient, is going to be of value. This could be remedied in the future by incorporating ERI maps with maps of existing safety zones, such as those mapped using lidar [
26,
27]. However, safety zones are often designated “in the black”—in areas that have already burned [
28]. As in the case of the fire extent, the dynamism of the fire environment and the associated evolving presence of safety zones is not accounted for in ERI.
Other important safety factors not directly incorporated into ERI are: (1) situational awareness; and (2) potential for snag hazard. Regarding the first exclusion, one could potentially model situational awareness, at least in terms of the ability to perceive surrounding conditions through a GIS-driven viewshed analysis. It is likely that ERI and a terrain-driven viewshed analysis would be highly correlated, since, for example a narrow canyon with limited visibility would also have low egress capacity and vice versa. Regarding the second exclusion, snags act as a significant hazard to wildland firefighters, and thus it is suggested that ERI be used in conjunction with a snag hazard map [
29].
Although critical, safety is but one component of the complex, multifaceted wildland fire decision making process [
30]. For example, fire crews should also consider the relative potential for suppression effectiveness, incorporating the suppression difficulty index into control location establishment [
31]. Accordingly, we are suggesting that ERI become integrated into existing decision support systems, such as WFDSS—particularly since WFDSS data play such a critical role in the formulation of ERI [
32]. It is important to distinguish between the existing WFDSS ground evacuation map product and ERI. Although the same land cover travel impedance coefficients are used in both, the end goals of the two products are distinct. WFDSS evacuation maps provide fire managers with a map of the estimated time it would take someone to evacuate to the nearest hospital, and as such, necessarily takes into account the distance to hospitals and automotive travel along a road network. In addition, relatively coarse slope categories are used to model travel impedance. The resulting product is a map of absolute travel time. ERI maps, on the other hand, provide fire managers with a map of relative egress capacity from anywhere in a wildland environment, regardless of proximity to a hospital, and are thusly focused more on evacuation from the fireline to a safety zone than to a health care facility. Additionally, a more precise slope-travel rate function is used as a basis of travel impedance. The output maps either provide a relative safety index, ranging from 0 to 1, or a suggested travel direction.
In its current formulation, based on its current input parameters and datasets, ERI clearly demonstrates a strong influence from land cover—a much greater influence than that of slope. While a previous study has likewise concluded that land cover (in particular, the density of vegetation) can have a stronger effect than slope on travel rates [
8], the magnitude of the relative land cover effects derived from WFDSS in this study are very dominant (
Figure 10;
Table 8). When compared to the few previous studies who have tested the effects of land cover on travel rates, the WFDSS-based effects are the strongest. Given the sparseness of experimental data on the effects of land cover on travel rates, it is unclear which among the few studies, have produced the most reliable results. WFDSS was chosen in this study due to its reliance on existing nationwide data and its wide use in the wildland fire community, but future research may reveal different, more accurate land cover conductance values that should be incorporated into future iterations of ERI.
Another limitation of the WFDSS-driven approach is the fact that, in reality, tree-dominated land cover types are not universally more difficult to traverse than shrub-dominated land cover types. For example, one can move through a mature ponderosa pine parkland environment with a sparse understory, even though it is technically “tree-dominated”, much more readily than one can move through a “shrub-dominated” chaparral environment, such as is present in ANF. This may explain some of the surprising results of the comparison to recent firefighter entrapment events. For example, our evaluation highlighted the fact that the starting point of the escape route that the Granite Mountain Hotshots took possessed a relatively high ERI value, even though their evacuation resulted in one the most significant fatality events in the history of wildland firefighting. This may be due, in part, to the fact that the LANDFIRE EVT data classified the pre-fire land cover for that area as being “shrub-dominated”, thus having a much higher travel conductance than other events. However, according to the Yarnell Hill Serious Accident Investigation Report, “the dominant vegetation type, chaparral brush, ranged in height from one to ten feet and, in some places, was nearly impenetrable” [
33].
To overcome the limitations imposed by using categorical land cover types as the basis of travel conductance, we recommend that future research attempt to refine our understanding of how travel rates are affected by more objective, continuous measures of landscape conditions. Because land cover datasets are predominantly derived from passive remote sensing instruments that record reflected solar radiation from the uppermost portions of the Earth’s surface, such as Landsat, they lack the ability to precisely model vertical structure of the landscape. However, active instruments, such as lidar, are capable of making precise
x,
y, and
z measurements, and exploiting small gaps in a vegetated canopy to make measurements of understory vegetation density, which is thought to be a much better predictor of travel conductance [
8,
34]. With the ever-increasing availability of lidar data in the US, future research should aim to enhance ERI with more precise measures of structurally-based, rather than categorically-based, pedestrian travel conductance.
5. Conclusions
In this paper, we have introduced a new metric for assessing and mapping egress capacity, or the degree to which one can evacuate from a given location, on a broad, spatial scale based on existing landscape conditions. ERI is not a single metric, but a suite of four spatially-explicit metrics that define the relative travel impedance caused by terrain and land cover faced by a fire crew, should that fire crew need to evacuate. The intent is that this modeling technique will be employed to aid in wildland firefighter safety operations prior to engaging a fire, acting as a decision support tool. Given that the metric relies on US nationwide, publicly-available datasets, the goal is that ERI metrics would be mapped in advance of fire suppression and used to direct fire crews toward potential control locations with higher capacity for evacuation, thus reducing the potential for injurious or even fatal entrapments. ERI does not map escape routes, per se, it highlights areas that have a greater or lesser capacity for providing efficient escape routes. Areas with high ERI values will likely have an abundance of open, easily-traversable terrain, through which many potential escape routes may exist requiring little alteration of the land cover. Conversely, areas with low ERI values possess some combination of rugged terrain and dense vegetation, thus making the designation of suitable escape routes difficult or even impossible.
We suggest that the four metrics be used as follows. If a single metric is to be used, then ERImean should be that metric. It is the best representation of the overall egress capacity for a given location. High ERImean values are likely to produce desirable evacuation conditions. However, means are simply a measure of central tendency, and do not reflect the directionally-specific evacuation conditions. Thus, if a more nuanced planning process is feasible, it is advisable to use the remaining three metrics in conjunction with ERImean. ERImin provides fire personnel with a sense of the worst-case evacuation scenario based on existing landscape conditions. For example, even with a relatively high ERImean, if a crew is backed up against a cliff or other impassable feature ERImin will be very low. In wildland firefighting, where risk levels are high and threats abound, conservative safety planning, such as is offered by ERImin may be advisable. ERImean and ERImin being equal, a crew might want to know what areas to target for suppression based on the best-case evacuation scenario. This is where ERImax and ERIazimuth come into play. A high ERImax value tells a fire crew that there is at least one direction by which pedestrian evacuation travel efficiency will be very high. ERIazimuth tells that same fire crew which direction, generally, to take.