Multi-Configuration Calculation of Ionization Potential Depression
Abstract
1. Introduction
2. Analytical Ionization Potential Depression Models
2.1. Debye-Hückel Model
2.2. Stewart-Pyatt Model
2.3. Ecker-Kröll Model
2.4. Modified Ecker-Kröll Model
3. Self-Consistent Calculations—General Case (Screening of Ions)
- (i)
- From to : calculation of by a four-point quadrature formula, the electron density behaving as (the value of is specified in Appendix D) when .
- (ii)
- From to : calculation of the second term of relation (14) by a four-point quadrature formula.
4. Self-Consistent Calculations—Unscreened Case
5. Calculation of Ionization Potential Depression
5.1. Difference between Screened and Unscreened Energies
5.2. First-Order Perturbation Theory
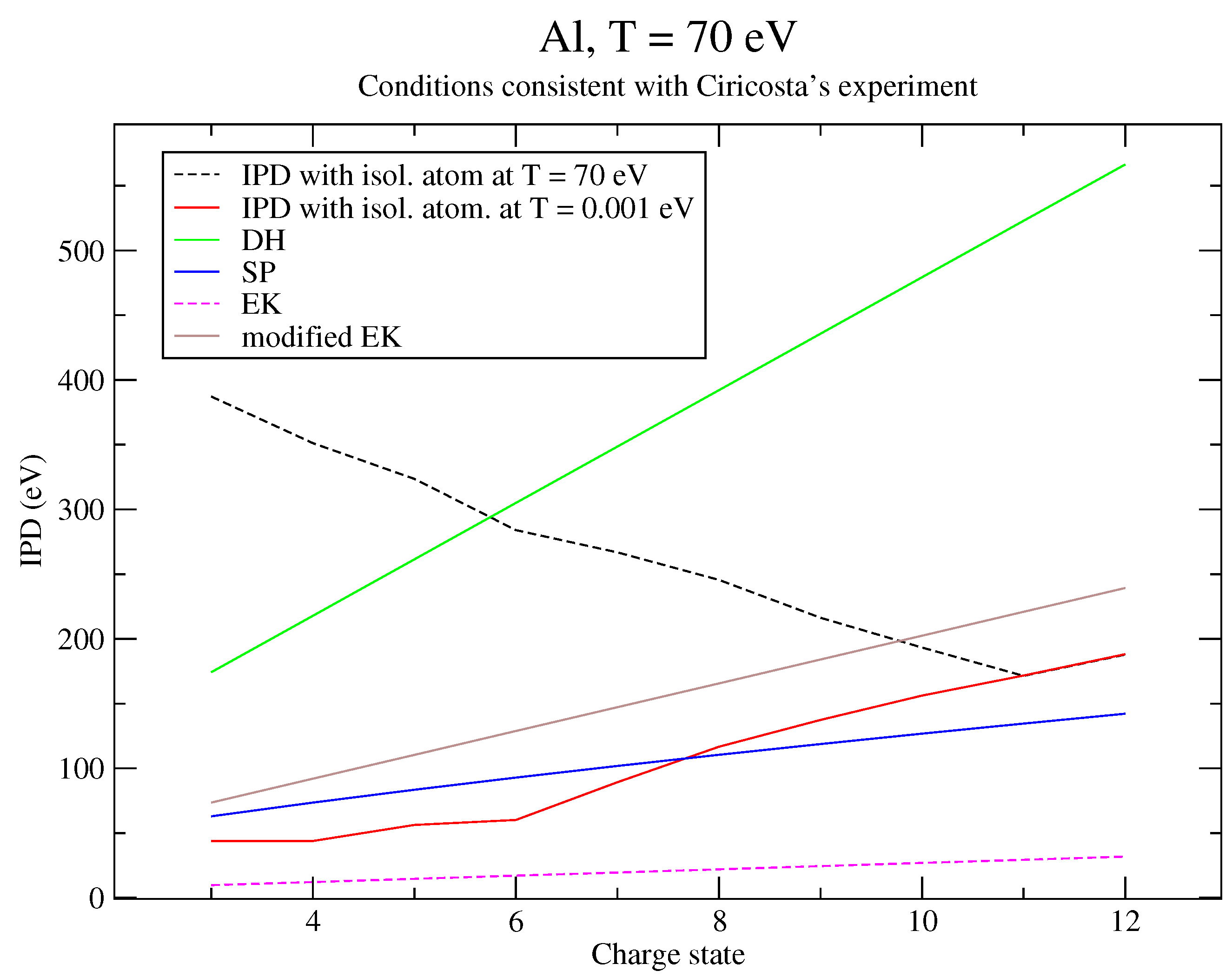
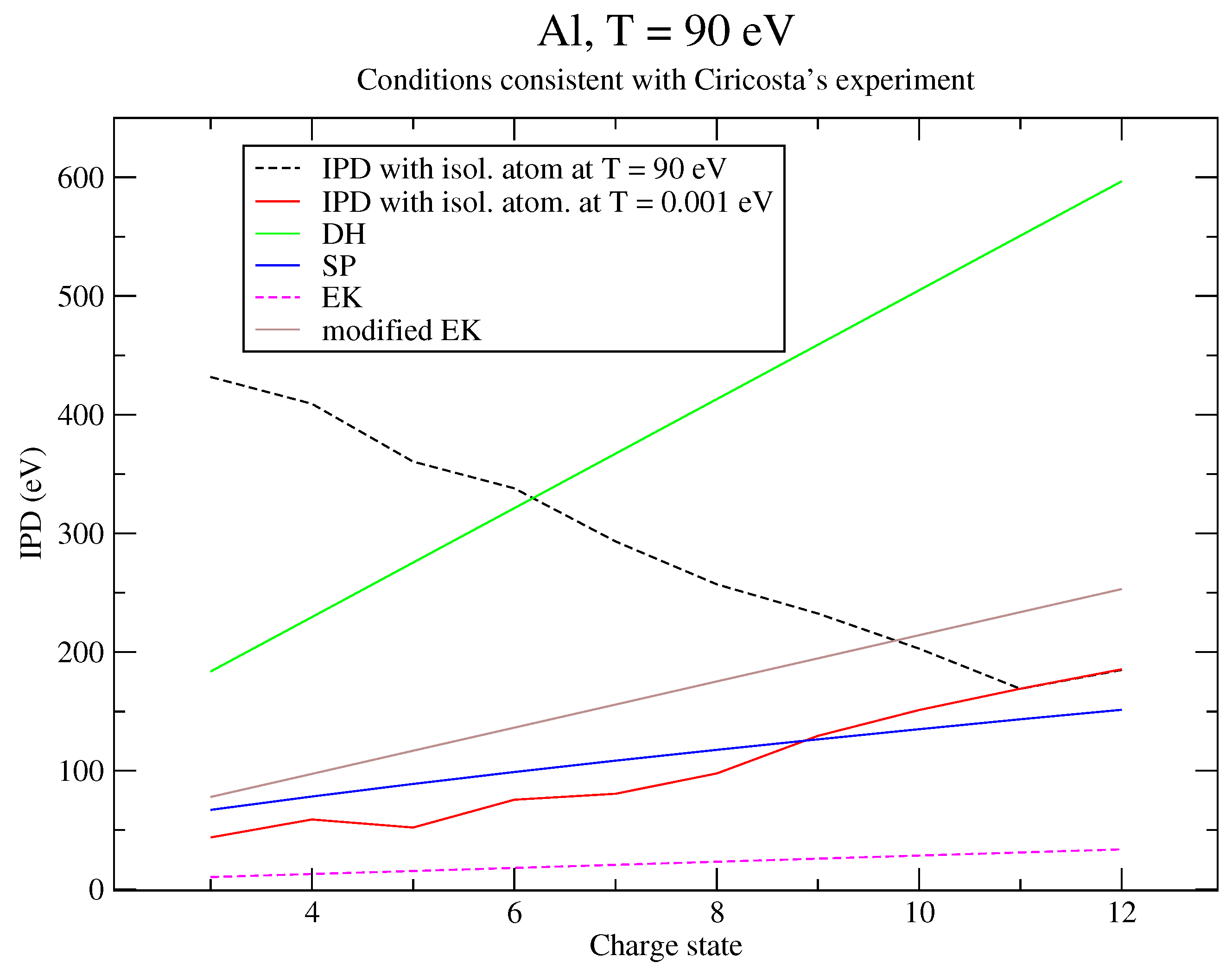
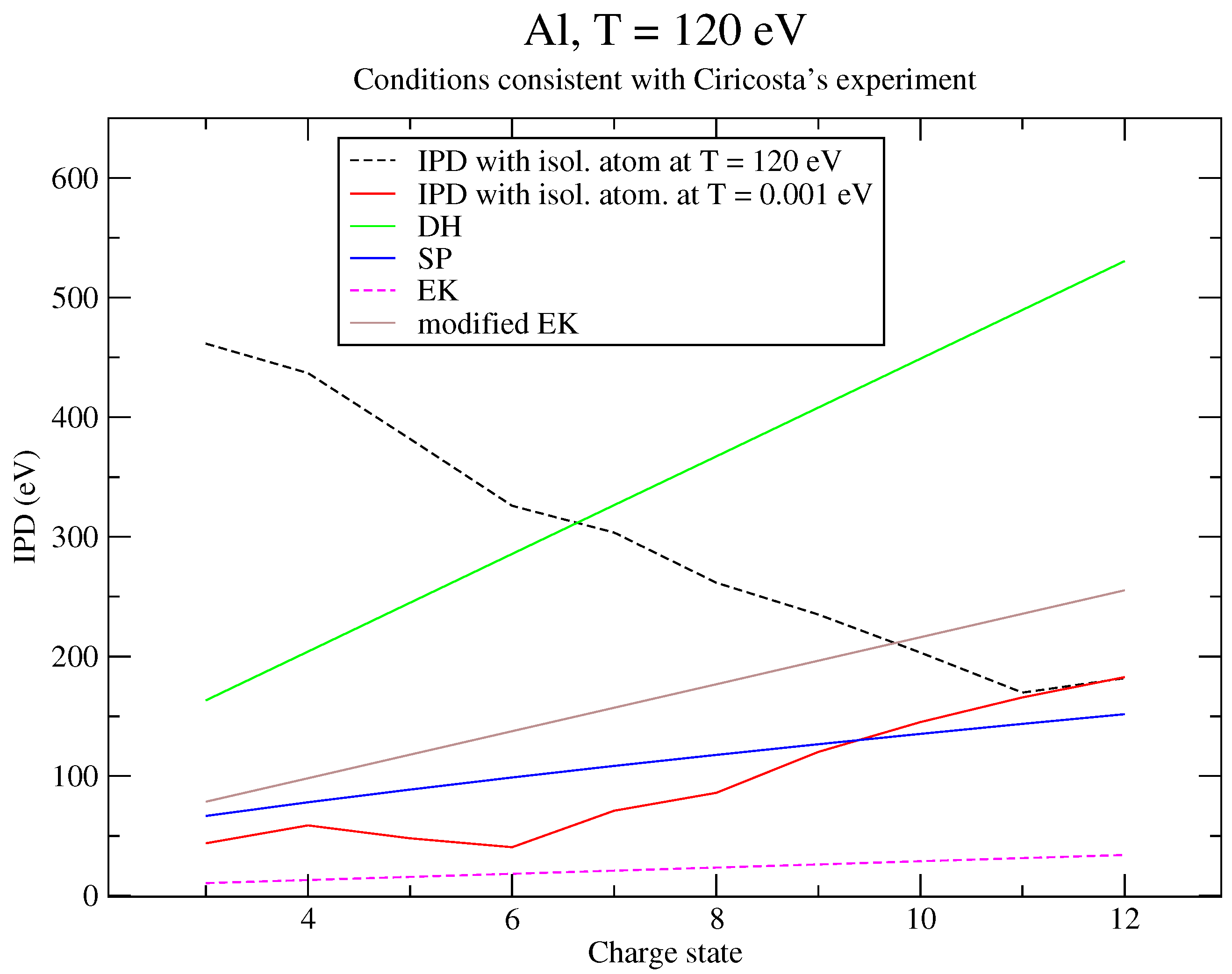
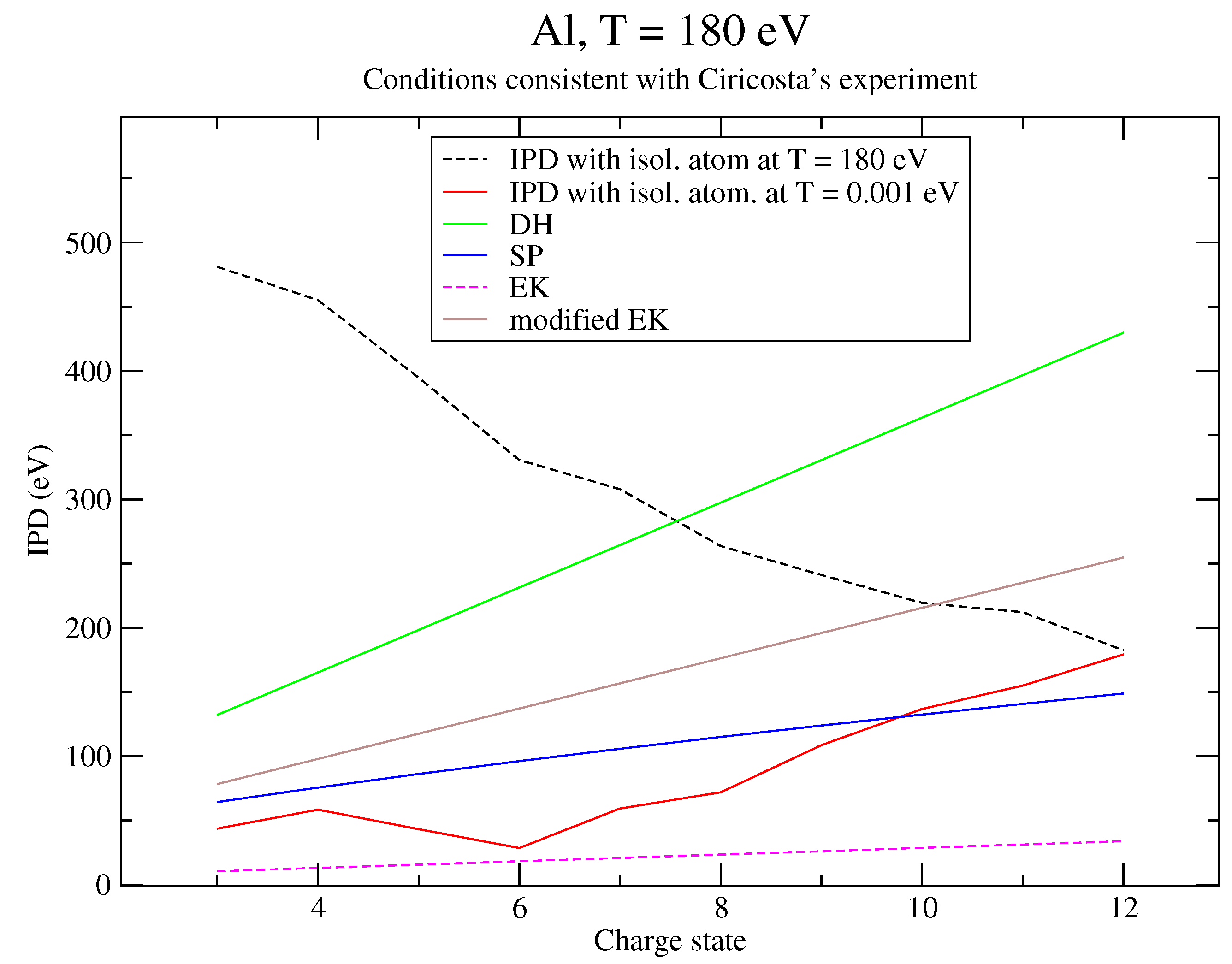
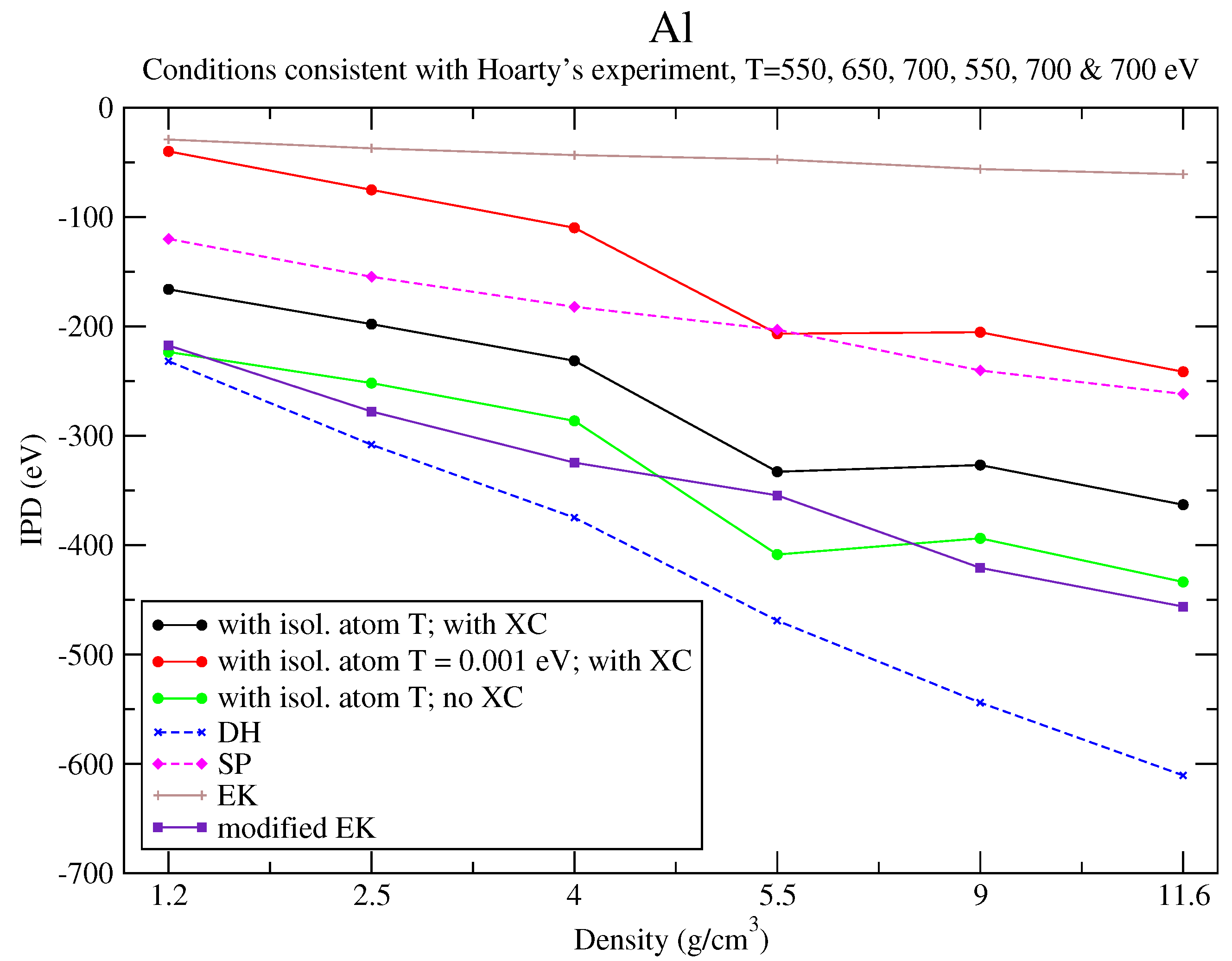
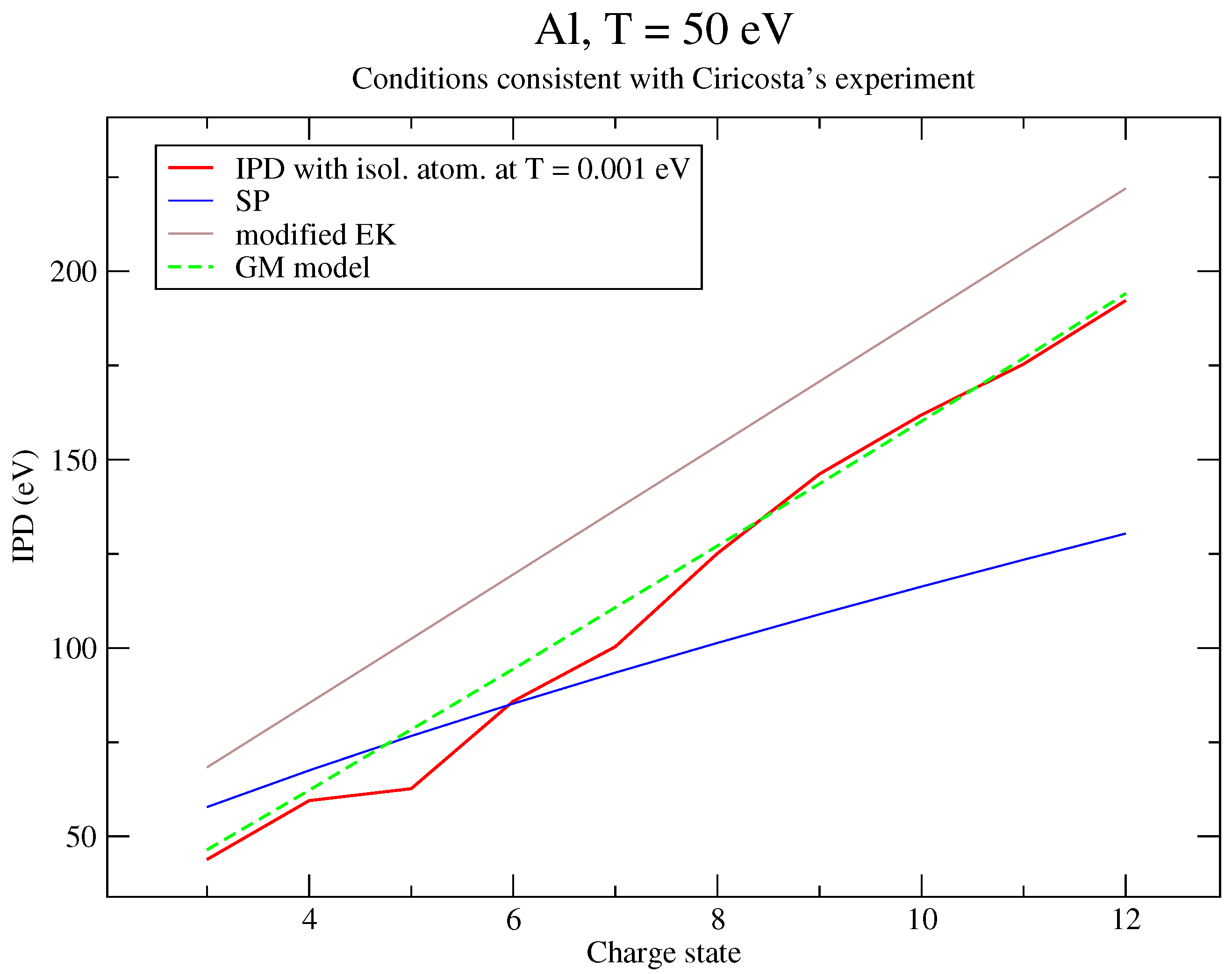
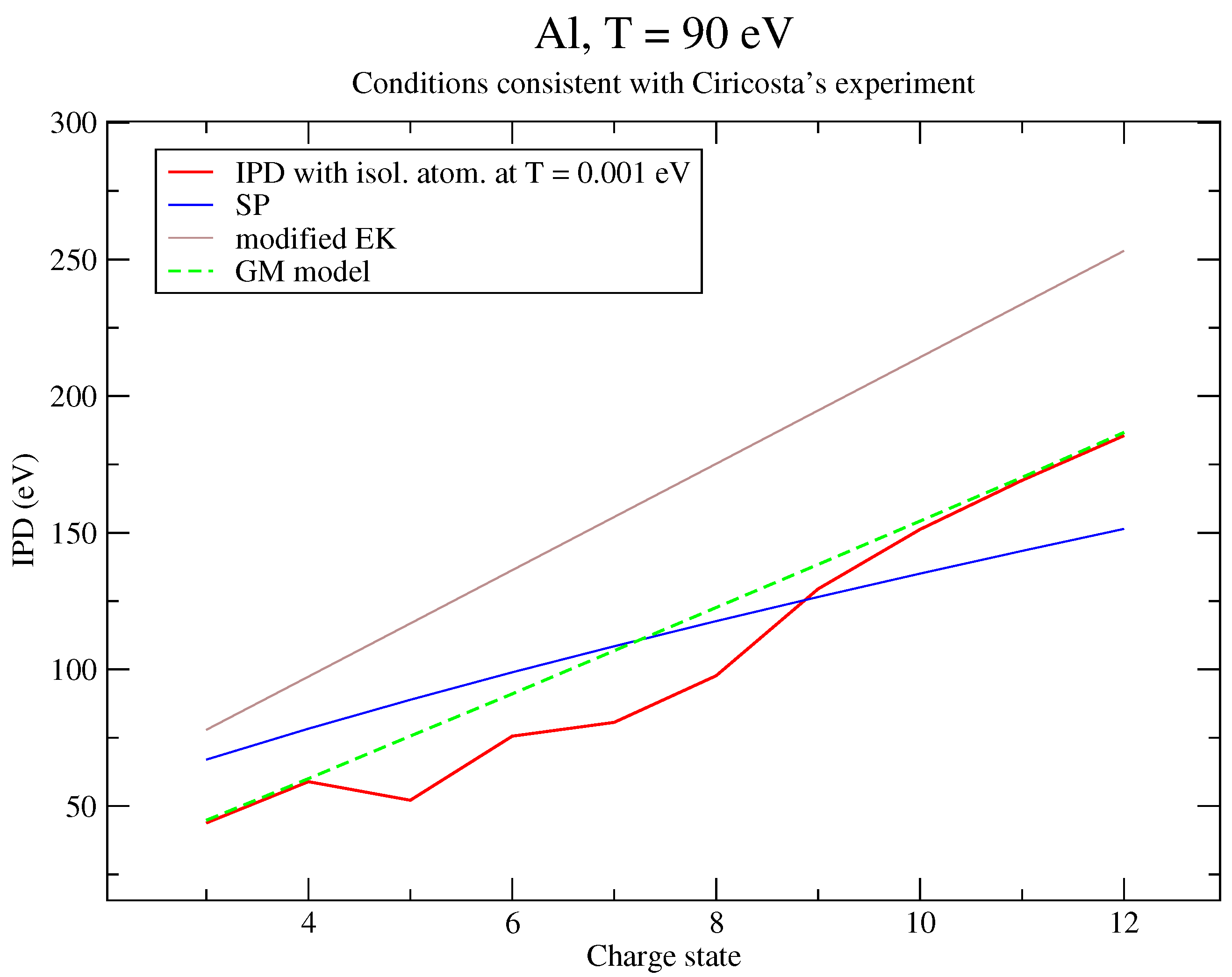
6. Discussion of the Results and Comparison to an Alternative Approach
6.1. Analysis of the Results
6.2. Reformulation of the Potential
6.3. Correction to Recover Perturbation Theory
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| DH | Debye-Hückel |
| EK | Ecker-Kröll |
| IPD | Ionization Potential Depression |
| LCLS | Linear Coherent Light Source |
| LDA | Local Density Approximation |
| LTE | Local Thermodynamic Equilibrium |
| NIF | National Ignition Facility |
| PAW | Projector Augmented-Wave |
| SP | Stewart-Pyatt |
| WS | Wigner-Seitz |
| XC | Exchange-correlation |
Appendix A. Differences between SP Models in the Literature
Appendix B. Value of CEK at Critical Density nc
Appendix C. Solving the Poisson Equation
Appendix D. Numerical Scheme Used for the Determination of the Wave Functions
References
- Brillet, W.-Ü.L.; Artru, M.-C. Extension of the Analysis of Quadruply Ionized Silicon (Si V). Phys. Scr. 1976, 14, 285–289. [Google Scholar] [CrossRef]
- Obadasi, H. Regularities in ionization potentials. Phys. Scr. 1979, 19, 313–317. [Google Scholar]
- Liu, P.; Gao, C.; Hou, Y.; Zeng, J.; Yuan, J. Transient space localization of electrons ejected from continuum atomic processes in hot dense plasma. Commun. Phys. 2018, 1, 95–101. [Google Scholar] [CrossRef]
- Lin, C. Ionization Potential Depression and Ionization Balance in Dense Plasmas. arXiv 2019, arxiv:1904.04456. [Google Scholar]
- Lin, C. Quantum statistical approach for ionization potential depression in multi-component dense plasmas. Phys. Plasmas 2019, 26, 122707. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Y.; Hou, Y.; Gao, C.; Yuan, J. Ionization potential depression and ionization balance in dense carbon plasma under solar and stellar interior conditions. A&A 2020, 644, A92. [Google Scholar]
- Pain, J.-C. A model of dense-plasma atomic structure for equation-of-state calculations. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 1553–1573. [Google Scholar] [CrossRef]
- Pain, J.-C.; Dejonghe, G. Electrical Resistivity in Warm Dense Plasmas Beyond the Average-Atom Model. Contrib. Plasma Phys. 2010, 50, 39–45. [Google Scholar] [CrossRef]
- Wetta, N.; Pain, J.-C. Consistent approach for electrical resistivity within Ziman’s theory from solid state to hot dense plasma: Application to aluminum. Phys. Rev. E 2020, 102, 053209. [Google Scholar] [CrossRef]
- Wetta, N.; Pain, J.-C. Issues in the calculation of dc conductivity of warm dense aluminum. Contrib. Plasma Phys. 2022, e202200003. [Google Scholar] [CrossRef]
- Pain, J.-C.; Dejonghe, G.; Blenski, T. Quantum-mechanical model for the study of pressure ionization in the superconfiguration approach. J. Phys. A Math. Gen. 2006, 39, 4659–4666. [Google Scholar] [CrossRef]
- Pain, J.-C.; Dejonghe, G.; Blenski, T. A self-consistent model for the study of electronic properties of hot dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 451–468. [Google Scholar] [CrossRef]
- Rogers, F.J.; Iglesias, C.A. Astrophysical opacity. Science 1994, 263, 50–55. [Google Scholar] [CrossRef] [PubMed]
- Guillot, T. Interiors of giant planets inside and outside the solar system. Science 1999, 286, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Potekhin, A.Y.; Massacrier, G.; Chabrier, G. Equation of state for partially ionized carbon at high temperatures. Phys. Rev. E 2005, 72, 046402. [Google Scholar] [CrossRef] [PubMed]
- Massacrier, G.; Potekhin, A.Y.; Chabrier, G. Equation of state for partially ionized carbon and oxygen mixtures at high temperatures. Phys. Rev. E 2011, 84, 056406. [Google Scholar] [CrossRef] [PubMed]
- Lindl, J.D.; Amendt, P.; Berger, R.L.; Glendinning, S.G.; Glenzer, S.H.; Haan, S.W.; Kauffman, R.L.; Landen, O.L.; Suter, L.J. The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 2004, 11, 339–491. [Google Scholar] [CrossRef]
- Hu, S.X.; Militzer, B.; Goncharov, V.N.; Skupsky, S. Strong Coupling and Degeneracy Effects in Inertial Confinement Fusion Implosions. Phys. Rev. Lett. 2010, 104, 235003. [Google Scholar] [CrossRef]
- Jarrah, W.; Pain, J.-C.; Benredjem, D. Plasma potential and opacity calculations. High Energy Density Phys. 2019, 32, 8–13. [Google Scholar] [CrossRef]
- Pain, J.-C.; Benredjem, D. Simple electron-impact excitation cross-sections including plasma density effects. High Energy Density Phys. 2021, 38, 100923. [Google Scholar] [CrossRef]
- Bruce, R.E.; Todd, F.C. Lowering of the Ionization Potential in Dense Aluminum Plasmas. Proc. Okla. Acad. Sci. 1963, 95–102. [Google Scholar]
- Zaghloul, M.R. Thermodynamic depression of ionization potentials in nonideal plasmas: Generalized self-consistency criterion and a backward scheme for deriving the excess free energy. Astrophys. J. 2009, 699, 885–891. [Google Scholar] [CrossRef]
- Crowley, B.J.B. Continuum lowering, a new perspective. High Energy Density Phys. 2014, 13, 84–102. [Google Scholar] [CrossRef]
- Massacrier, G.; Böhme, M.; Vorberger, J.; Soubiran, F.; Militzer, B. Reconciling ionization energies and band gaps of warm dense matter derived with ab initio simulations and average atom models. Phys. Rev. Res. 2021, 3, 023026. [Google Scholar] [CrossRef]
- Zan, X.; Lin, C.; Hou, Y.; Yuan, J. Local field correction to ionization potential depression of ions in warm or hot dense matter. Phys. Rev. E 2021, 104, 025203. [Google Scholar] [CrossRef]
- Callow, T.J.; Hansen, S.B.; Kraisler, E.; Cangi, A. First-principles derivation and properties of density-functional average-atom models. Phys. Rev. Res. 2022, 4, 023055. [Google Scholar] [CrossRef]
- Ecker, G.; Kröll, W. Lowering of the Ionization Energy for a Plasma in Thermodynamic Equilibrium. Phys. Fluids 1963, 6, 62–69. [Google Scholar] [CrossRef]
- Stewart, J.C.; Pyatt, K.D., Jr. Lowering of ionization potentials in plasmas. Astrophys. J. 1966, 144, 1203–1211. [Google Scholar] [CrossRef]
- LCLS. Available online: http://lcls.slac.stanford.edu/ (accessed on 14 September 2022).
- Ciricosta, O.; Vinko, S.M.; Chung, H.-K.; Cho, B.-I.; Brown, C.R.D.; Burian, T.; Chapulsky, J.; Engelhorn, K.; Falcone, R.W.; Graves, C.; et al. Direct Measurements of the Ionization Potential Depression in a Dense Plasmas. Phys. Rev. Lett. 2012, 109, 065002. [Google Scholar] [CrossRef]
- Ciricosta, O.; Vinko, S.M.; Barbrel, B.; Rackstraw, D.S.; Preston, T.R.; Burian, T.; Chalupský, J.; Cho, B.I.; Chung, H.-K.; Dakovski, G.L.; et al. Measurements of continuum lowering in solid-density plasmas created from elements and compounds. Nat. Commun. 2016, 7, 11713. [Google Scholar] [CrossRef]
- Hoarty, D.J.; Allan, P.; James, S.F.; Brown, C.R.D.; Hobbs, L.M.R.; Hill, M.P.; Harris, J.W.O.; Morton, J.; Brookes, M.G.; Shepherd, R.; et al. Observations of the Effect of Ionization-Potential Depression in Hot Dense Plasma. Phys. Rev. Lett. 2013, 110, 265003. [Google Scholar] [CrossRef]
- Fletcher, L.B.; Kritcher, A.L.; Pak, A.; Ma, T.; Döppner, T.; Fortmann, C.; Divol, L.; Jones, O.S.; Landen, O.L.; Scott, H.A.; et al. Observations of Continuum Depression in Warm Dense Matter with X-Ray Thomson Scattering. Phys. Rev. Lett. 2014, 112, 145004. [Google Scholar] [CrossRef] [PubMed]
- Kraus, D.; Chapman, D.A.; Kritcher, A.L.; Baggott, R.A.; Bachmann, B.; Collins, G.W.; Glenzer, S.H.; Hawreliak, J.A.; Kalantar, D.H.; Landen, O.L.; et al. X-ray scattering measurements on imploding CH spheres at the National Ignition Facility. Phys. Rev. E 2016, 94, 011202. [Google Scholar] [CrossRef] [PubMed]
- Son, S.-K.; Thiele, R.; Jurek, Z.; Ziaja, B.; Santra, R. Quantum-mechanical calculation of ionization potential lowering in dense plasmas. Phys. Rev. X 2014, 4, 031004. [Google Scholar] [CrossRef]
- Vinko, S.M.; Ciricosta, O.; Wark, J.S. Density functional theory calculations of continuum lowering in strongly coupled plasmas. Nat. Commun. 2014, 5, 3533. [Google Scholar] [CrossRef]
- Hu, S.X. Continuum Lowering and Fermi-Surface Rising in Strongly Coupled and Degenerate Plasmas. Phys. Rev. Lett. 2017, 119, 065001. [Google Scholar] [CrossRef]
- Calisti, A.; Ferri, S.; Talin, B. Ionization Potential Depression in Hot Dense Plasmas Through a Pure Classical Model. Contrib. Plasma Phys. 2015, 55, 360–365. [Google Scholar] [CrossRef]
- Stransky, M. Monte Carlo simulations of ionization potential depression in dense plasmas. Phys. Plasmas 2016, 23, 012708. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Sterne, P.A. Fluctuations and the ionization potential in dense plasmas. High Energy Density Phys. 2013, 9, 103–107. [Google Scholar] [CrossRef]
- Lin, C.; Kraeft, W.-D.; Röpke, G.; Reinholz, H. Ionization-potential depression and dynamical structure factor in dense plasmas. Phys. Rev. E 2017, 96, 013202. [Google Scholar] [CrossRef]
- Rosmej, F.B. Ionization potential depression in an atomic-solid-plasma picture. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 09LT01. [Google Scholar] [CrossRef]
- Alexiou, S.; Stambulchik, E.; Gomez, T.; Koubiti, M. The Fourth Workshop on Lineshape Code Comparison: Line merging. Atoms 2018, 6, 13. [Google Scholar] [CrossRef]
- Stein, J. Line shifts in plasmas: A quantum mechanical approach. J. Quant. Spectrosc. Radiat. Transf. 1995, 54, 395–399. [Google Scholar] [CrossRef]
- Ren, S.; Shi, Y.; van den Berg, Q.Y.; Firmansyah, M.; Chung, H.-K.; Fernandez-Tello, E.V.; Velarde, P.; Wark, J.S.; Vinko, S.M. Non-thermal evolution of dense plasmas driven by intense X-ray fields. arXiv 2022, arXiv:2208.00573v3. [Google Scholar]
- Massacrier, G. Self-consistent schemes for the calculation of ionic structures and populations in dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 1994, 51, 221–228. [Google Scholar] [CrossRef]
- Massacrier, G. Ionization potential depression in warm and hot solid-density plasma. In Proceedings of the HEDLA (High Energy Density Laboratory Astrophysics), Bordeaux, France, 12–16 May 2014. [Google Scholar]
- Massacrier, G. Ionization potential depression in warm dense matter conditions. In Proceedings of the ILP (Fédération Lasers et Plasmas) Forum, Porquerolles, France, 14–19 June 2015. [Google Scholar]
- Debye, P.; Hückel, E. On the theory of electrolytes, I. Freezing point depression and related phenomena. Phys. Z 1923, 24, 185–206. [Google Scholar]
- Preston, T.R.; Vinko, S.M.; Ciricosta, O.; Chung, H.-K.; Lee, R.W.; Wark, J.S. The effects of ionization potential depression on the spectra emitted by hot dense aluminum plasmas. High Energy Density Phys. 2013, 9, 258–263. [Google Scholar] [CrossRef]
- Pain, J.-C. Super Transition Arrays: A Tool for Studying Spectral Properties of Hot Plasmas. Plasma 2021, 4, 42–64. [Google Scholar] [CrossRef]
- Pain, J.-C. Adaptive Algorithm for the Generation of Superconfigurations in Hot-Plasma Opacity Calculations. Plasma 2022, 5, 154–175. [Google Scholar] [CrossRef]
- More, R.M. Pressure Ionization, Resonances, and the Continuity of Bound and Free States. Adv. At. Mol. Phys. 1985, 21, 305–356. [Google Scholar]
- Blenski, T.; Ishikawa, K. Pressure ionization in the spherical ion-cell model of dense plasmas and a pressure formula in the relativistic Pauli approximation. Phys. Rev. E 1995, 51, 4869–4881. [Google Scholar] [CrossRef] [PubMed]
- Froese-Fischer, C. The Hartree-Fock Method for Atoms: A Numerical Approach; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Benredjem, D.; Pain, J.-C.; Calisti, A.; Ferri, S. Ionization by electron impacts and ionization potential depression. J. Phys. B At. Mol. Opt. Phys. 2022, 55, 105001. [Google Scholar] [CrossRef]
- Hartree, D.R. The Calculation of Atomic Structures; John Wiley: New York, NY, USA, 1957. [Google Scholar]
- Nikiforov, A.F.; Novikov, V.G.; Uvarov, V.B. Quantum Statistical Models of Hot Dense Matter; Birkhauser: Basel, Switzerland, 2005. [Google Scholar]
- Pain, J.-C. Résolution de l’équation de Schrödinger à une Dimension par la Méthode de la Fonction Phase. Master’s Thesis, CEA & Ecole Normale Supérieure, Paris, France, 1999. (In French). [Google Scholar]

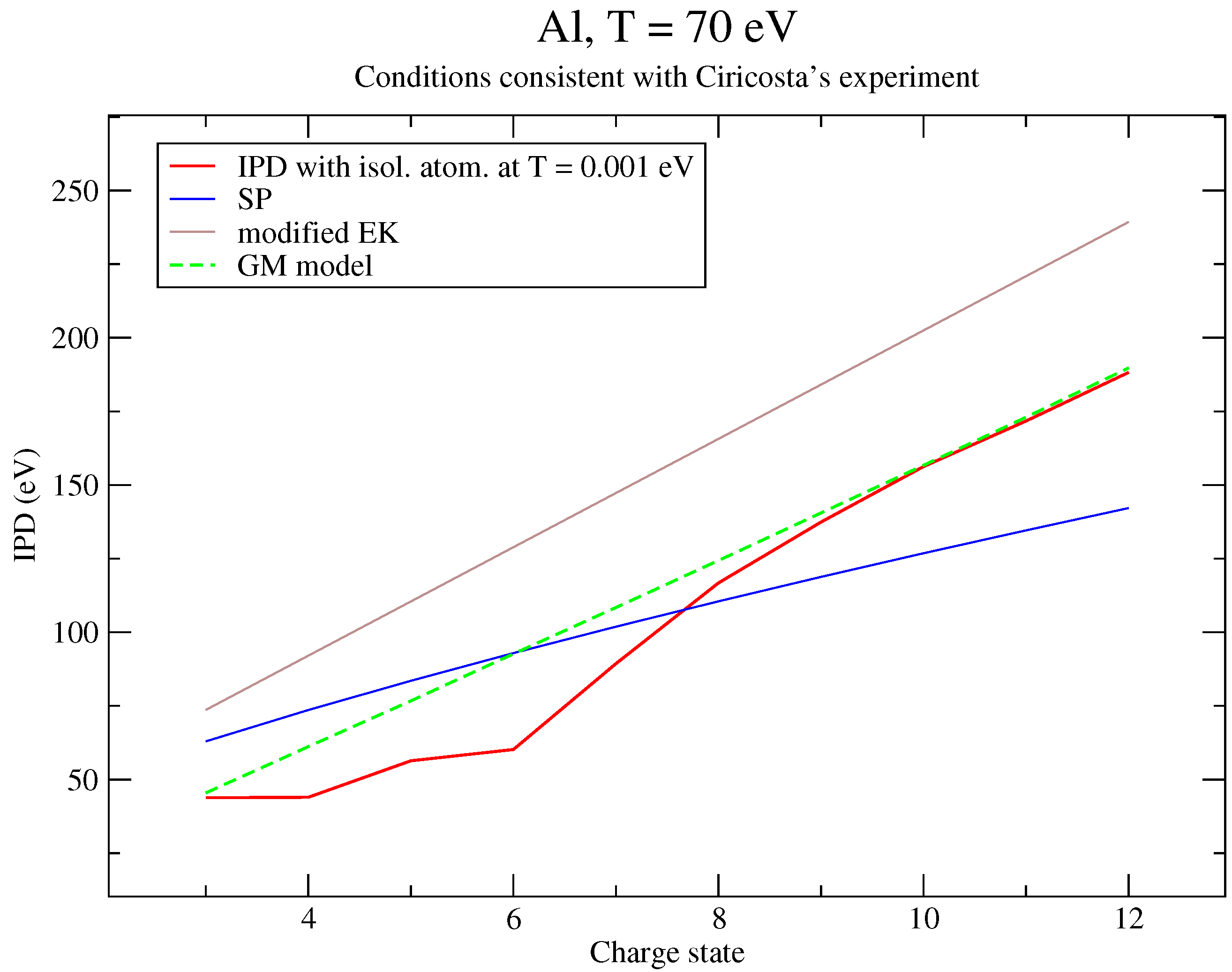
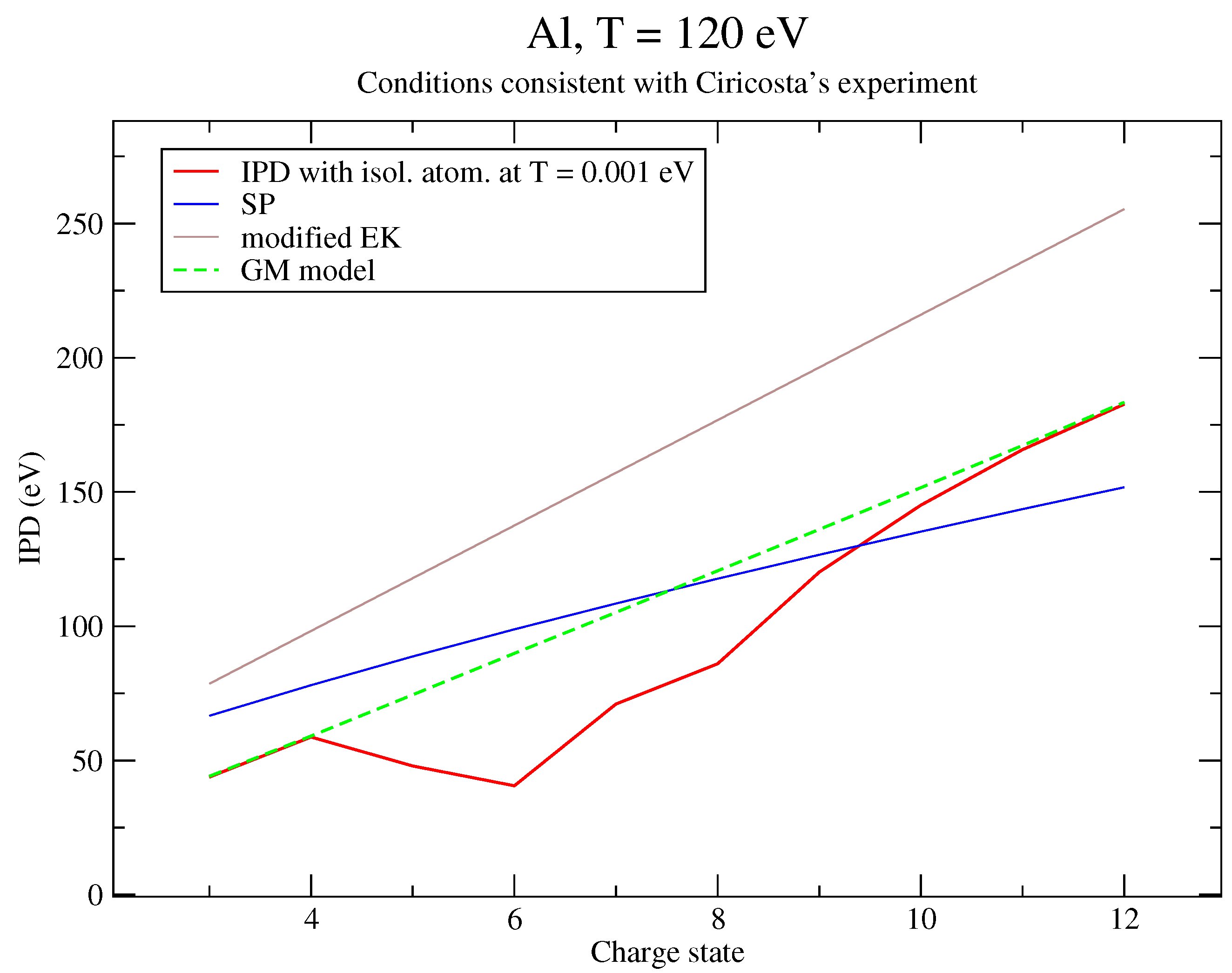
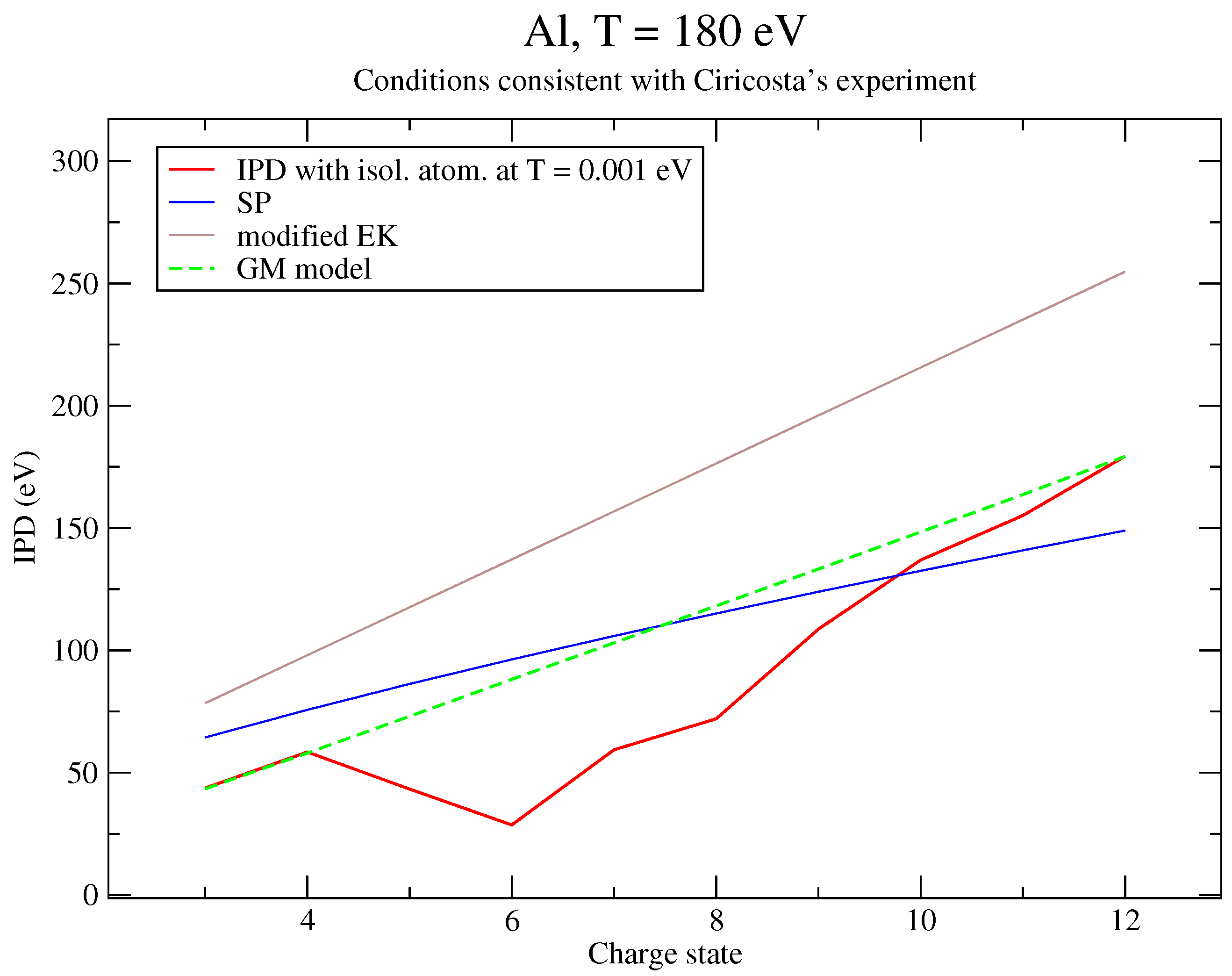
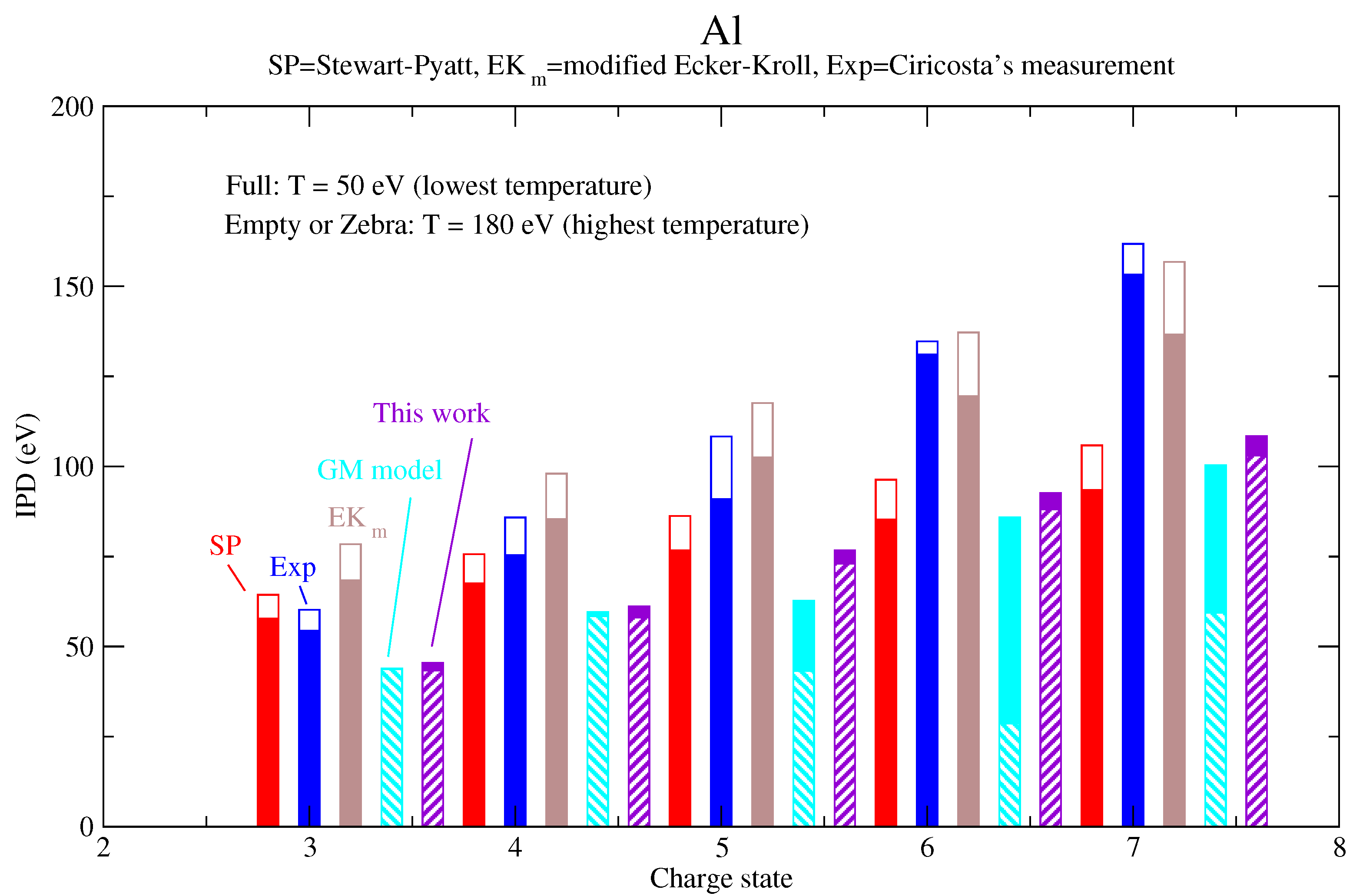
| IPD (eV) | IPD + Corr. (eV) | |
|---|---|---|
| 3 | 45.4514 | 45.2086 |
| 4 | 61.1704 | 60.8535 |
| 5 | 76.731 | 76.338 |
| 6 | 92.6603 | 92.1946 |
| 7 | 108.447 | 107.908 |
| 8 | 124.383 | 123.772 |
| 9 | 140.522 | 139.841 |
| 10 | 156.718 | 155.968 |
| 11 | 173.024 | 172.208 |
| 12 | 189.777 | 188.912 |
| IPD (eV) | IPD + Corr. (eV) | |
|---|---|---|
| 3 | 43.3625 | 43.2009 |
| 4 | 58.0276 | 57.8132 |
| 5 | 73.0231 | 72.7569 |
| 6 | 88.1355 | 87.8175 |
| 7 | 103.047 | 102.678 |
| 8 | 118.151 | 117.730 |
| 9 | 133.214 | 132.742 |
| 10 | 148.368 | 147.846 |
| 11 | 163.623 | 163.052 |
| 12 | 179.232 | 178.624 |
| T (eV) | (g/cm3) | IPD (eV) | IPD + Corr. (eV) | |
|---|---|---|---|---|
| 12.3698 | 550 | 1.2 | 133.661 | 133.484 |
| 12.4739 | 650 | 2.5 | 172.536 | 172.194 |
| 12.3827 | 700 | 4 | 200.787 | 200.264 |
| 11.6673 | 550 | 5.5 | 212.477 | 211.729 |
| 12.0979 | 700 | 9 | 259.155 | 258.022 |
| 12.0762 | 700 | 11.6 | 282.298 | 280.847 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pain, J.-C. Multi-Configuration Calculation of Ionization Potential Depression. Plasma 2022, 5, 384-407. https://doi.org/10.3390/plasma5040029
Pain J-C. Multi-Configuration Calculation of Ionization Potential Depression. Plasma. 2022; 5(4):384-407. https://doi.org/10.3390/plasma5040029
Chicago/Turabian StylePain, Jean-Christophe. 2022. "Multi-Configuration Calculation of Ionization Potential Depression" Plasma 5, no. 4: 384-407. https://doi.org/10.3390/plasma5040029
APA StylePain, J.-C. (2022). Multi-Configuration Calculation of Ionization Potential Depression. Plasma, 5(4), 384-407. https://doi.org/10.3390/plasma5040029






