Abstract
Global modeling of inductively coupled plasma (ICP) reactors is a powerful tool to investigate plasma parameters. In this article, the argon ICP global model is revisited to explore the effect of excited species on collisional energy through the study of different approaches to particle and energy balance equations. The collisional energy loss is much more sensitive to modifications in the balance equations than the electron temperature. According to the simulations, the multistep ionization reduces the collisional energy loss in all investigated reaction sets and the inclusion of heavy species reactions has negligible influence. The plasma parameters obtained, such as total energy loss and electron temperature, were compared with experimental results from the literature. The simulated cases that have more excited species and reactions in the energy balance are in better agreement with the experimental measurements.
1. Introduction
Inductively coupled plasma (ICP) is a low-temperature and high-density plasma used in various fields, such as nanostructure fabrication [1,2,3], space propulsion systems [4,5,6], and energy/environment [1,7,8,9]. Several inert and reactive gases are used in these applications, with argon being the main component in the processing and modeling of plasmas [1].
The plasma-assisted applications are determined by several process parameters, including applied power, gas pressure, flow rate, among others. The plasma environment can be characterized by plasma parameters such as electron temperature and density, heavy species density, gas temperature, energy lost per electron-ion pair created, and other physical/chemical parameters. To study these parameters and the relationship between them, many experimental and/or modeling studies have been carried out. Modeling is a fundamental research tool to complement experimental diagnostics, especially when the target quantities are difficult to obtain or experimentally inaccessible [10].
The interest in plasma modeling has increased in recent decades. Several numerical models such as zero-dimensional (global modeling) [11,12,13,14,15,16,17,18,19,20], kinetic [21,22,23], and hybrid Monte Carlo/fluid [22] models have been used to study plasmas generated with different gases in ICP reactors. The global model is based on fluid equations, neglecting spatial derivatives to improve computational efficiency [10,23]. It comprises a system of differential equations that includes a particle balance equation for each atomic or molecular species and an energy balance equation [23].
In argon plasmas, many excited species are observed. The lowest four excited states of the argon atom are the levels 4s[3/2]2, 4s[3/2]1, 4s’[1/2]0, and 4s’[1/2]1 in Paschen notation they correspond to 1s5, 1s4, 1s3, and 1s2, respectively (see Figure 1). The states 1s5 and 1s3 correspond to the metastable species. Due to their long lifetime, in order of a few seconds, the metastable have a significant contribution in collisional process, diffusion, and deexcitation at the walls [24,25,26]. The states 1s4 and 1s2 are the resonance levels. For them, the main deexcitation process in the plasma is radiative decay. The next ten energy levels in the argon atom correspond to the 4p configuration. In the plasma chemistry studies, these fourteen energy levels are grouped in three species according to their rate constant [24]. The metastable states form one metastable state called Arm, while the resonant state that includes the two resonant levels is termed as Arr. The 4p levels are defined as state Arp [23,24].
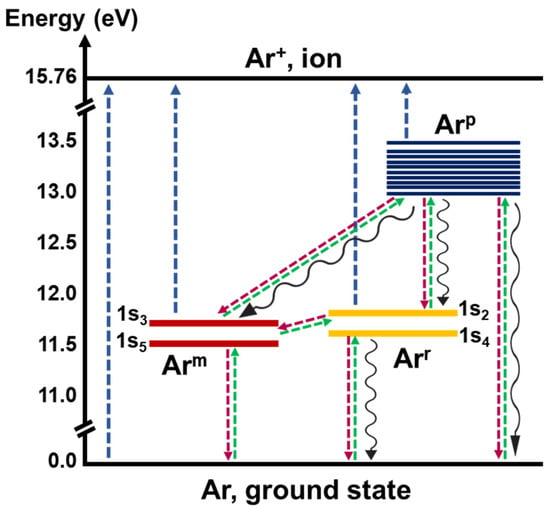
Figure 1.
Diagram of energy levels and transitions of an argon atom. The arrows represent some reactions considered in the model. Blue arrows denote ionization of Ar ground state and excited species (reactions R2–R5), green arrows the excitations (reactions R6–R8, R12–R14), red arrows the deexcitations collisions (reactions R9–R11, R15–R17), and the black wavy arrows the radiative deexcitations (reactions R23–R26).
The ionizations are the main mechanisms for maintaining a gas discharge [23]. The metastable and excited species contribute to ionization rate through stepwise (or multistep) and Penning ionization [25,26,27]. The metastable ionization can obtain a significant fraction of the total ionization and its contribution increases with plasma density [27,28]. The multistep ionization affects the chemical kinetics and the energy balance in the plasma due to the low ionization threshold energy of excited species in comparison to the ground state [13,14,26,29].
In the argon global models presented in the literature, different species and reactions sets are considered, thus altering the particle and/or energy balance. In the energy balance, some models investigated in the literature define differently the collisional energy per electron-ion pair created by the fact that they use different reaction sets. Some models include only the metastable species Arm in the particle balance and the collisional energy assumes only the ionization from the ground state (single-step ionization) [30,31]. Other models developed by Lee et al. [13,14,15] and Magaldi et al. [18], included the Arm, Arr, and Arp species, then rewriting the collisional energy to consider the multistep ionization. Hjartarson et al. [32] included heavy species collisions in the particle balance. Gudmundsson [16] considered distinct species and reactions in the particle and energy balance equations, including Arm in the particle balance, and the other excited species were considered only in the energy balance. These different ways of defining the collisional energy were studied in this work to verify which one gives the best agreement with the experimental results from the literature.
The total energy loss is a sum of the collisional energy loss per electron-ion pair created, the mean kinetic energy of the electrons lost to the walls, the ion energy dissipated due to diffusion to the chamber wall, and the energy gained by the ions when crossing the plasma sheath region [23]. It is the main parameter in the energy balance and describes how the energy supplied to the plasma is dissipated, from which the electron temperature is determined. The total energy loss by electrons can be obtained experimentally and compared with model results. In the literature, some studies have compared the experimental and theoretical total energy loss for argon ICP discharge. Lee et al. [33,34], Ku et al. [35], and Hong et al. [29] reported experimental measurements of total energy loss as a function of absorbed power and gas pressure, and Kim [36] studied the effect of the electron energy distribution on it.
A point to be highlighted in the aforementioned studies and others in literature is the use of different reaction sets, which considerably modifies the collisional energy and, consequently, the results of the plasma parameters. In this work, five different cases considering the effect of excited species Arm, Arr, and Arp were studied for argon ICP discharge varying the species and the reaction set considered in the model. All parameters were simulated as a function of absorbed power and gas pressure. The effects of these variations on the collisional energy, total energy loss, electron density, and electron temperature were analyzed to propose a better reaction set when a Maxwellian electron energy distribution function is considered. The total energy loss and electron temperature were compared with experimental results from the literature.
2. Materials and Methods
For the global model calculations, we assume a cylindrical reactor chamber of radius R = 15 cm and length L = 25 cm, such that the reactor volume is V = πR2L and the total internal area is A = 2πR2 + 2πRL. Neutral gas is introduced at a fixed flow rate Q = 50 sccm. The gas temperature is considered constant at Tg = 300 K. The volume-averaged global model works with a set of differential equations, which includes a particle balance equation for each species and the energy balance equation for electrons and ions. The model was solved using the COMSOL Multiphysics software (version 5.4, COMSOL Inc., Stockholm, Sweden) [37].
2.1. Particle Balance Equation
The global model equations are derived from the moments of the Boltzmann equation [10,23]. The equation of continuity gives the particle balance equation. The balance equation provides the species density as a function of the time and can be expressed for heavy species as
where is the density of specie X, in m−3. In the first term, is the gas flow rate, in s−1, and the second term is the gas pumping rate, in which is the pumping constant in s−1. These first two terms are considered only for ground state argon. represents the sum of all the reaction rates that contributes to the production of the specie X and represents the sum of all the reaction rates that contribute to the loss of the species X. There is one reaction rate for each reaction considered in the model. Reaction rates are calculated from the product of the densities of the species participating in the reaction and the rate constant for that reaction, , according to Equation (2):
The last term in Equation (1) corresponds to the diffusion to the wall, where in , is the particle flux that reaches area . For the ground state argon, diffusion is a positive term and for other species, it is a negative term, as excited (ionized) argon is neutralized in the walls. The density of electrons is obtained through charge neutrality [23]:
where is the electron density, and is the argon-ion density.
The diffusion for neutral species was calculated in COMSOL [37] setting the effective diffusion length :
where is the first zero of the zero-order Bessel function [12].
2.2. Plasma Chemistry
The Ar chemistry model considered in this investigation includes six species: ground state argon (Ar), argon positive ion (Ar+), metastable argon atoms (Arm), resonant argon atoms (Arr), 4p state atoms (Arp), and electrons (e).
Figure 1 shows a diagram of argon states and reactions included in the model. In Table 1, the threshold energy and rate constants are listed. The collisions between electrons and excited Ar atoms (i.e., reactions R12–R17 in Table 1) are considered as they are believed to play a significant role in particles transfer processes in argon discharge. In one case study, collisions between heavy species were considered (reaction R18–R22). The reactions R23–R26 are related to processes of radiative deexcitations. The rate constants are obtained from the literature; the complete reaction set is the same used in the work of Hjartarson et al. [33], one of the models with more reactions for argon (Table 1).

Table 1.
Reactions and corresponding rate constants of the global model. The superscripts r and m denote resonance and metastable levels of the 4s excited state, respectively, and the subscript p denotes the 4p excited state. The electron temperature is given in eV.
The rate constants of electron impact reactions are plotted in Figure 2 as a function of electron temperature and listed in Table 1. Figure 2a shows the rate constants of reactions R1–R8 and Figure 2b of R9–R17 of Table 1.
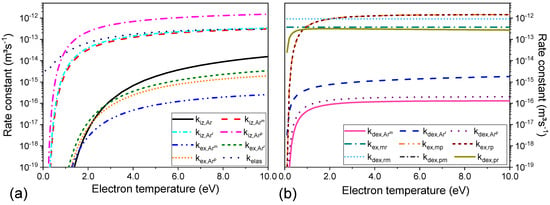
Figure 2.
Rate constants for elastic, excitations, deexcitations, and super-elastic collision, reactions 1–8 (a) and 9-17 (b) of Table 1.
2.3. Power Balance Equation
The power (or energy) balance equation provides how the electron energy changes over time. This equation is used to obtain the electron temperature from a balance between the power absorbed by the electrons, , and the power dissipated, due to the elastic and inelastic collisions, as well as ions and electrons diffusion to the chamber walls.
where is the electron energy density (in J/m3), is the elementary charge, the electron temperature (in eV), and are the power absorbed and lost by the plasma, respectively, and V is the volume of the discharge chamber.
The power lost in its most general form is given by
where is the power lost by the positive ions to the walls, where is the ion density in plasma sheath edge, is the average Bohm velocity and we have assumed Maxwellian electron energy distribution, is the average kinetic energy lost by the ions to the walls, here is the energy gained by the ion in the pre-sheath region and is the potential drop in the sheath formed in the walls of the reactor [23]; is the power lost by electrons in the chamber walls, where is the mean kinetic energy per electron lost to the walls, and is the electron density at the sheath edge [23].
In turn, is the power lost due to electron-heavy particle collisions, . The sum is taken over all neutral species x with positive ion counterparts, having a density , is the ionization rate coefficient, and is the collisional energy lost per electron-ion pair created. Considering only single-step ionization, the collisional energy is given as [23]:
where the superscript (s) denotes single-step ionization, is the ionization energy of ground state argon, and are the excitation energy and rate coefficient for the jth argon excitation, respectively. The indices may denote the species Arm, Arr and Arp produced by excitation from the ground state, it depends on what species are considered in the study. is the elastic scattering rate coefficient of ground state argon, is the electron mass, and is the argon mass.
The power loss due to electron-particle reactions for single-step ionization can be written as
Including the multistep ionization, the collisional energy can be written as [13]:
where the superscript (m) denotes multistep ionization.
The first sum (inside the parentheses) corresponds to argon and metastable species ionizations, the second and third sums are the excitation and de-excitation process from specie, i = Ar, Arm, Arr, and Arp. The deexcitation terms are negative because electrons gain energy in these reactions, so the threshold energy is negative (Table 1). The elastic collision term is considered only for ground state argon atom, due to its much higher density than that of excited states. The collisional energy can be rewritten as a function of the contribution of each specie,
where are the collisional energy of Ar, Arm, Arr, and Arp, respectively. They are the contribution of each neutral species to the total collisional energy. When the multistep ionization is taken into account, the collisional energy depends on the density of the argon species, unlike (Equation (7)).
The power loss due to collisions for multistep ionization is written as
Finally, the total energy loss, , is defined as the sum of collisional energy, , and
2.4. Investigated Cases
The reaction set and how the energy balance equation is calculated will define the energy exchanges in a gas discharge. Over time, excited species and reactions were added in argon global models presented in literature and how energy balance was calculated was modified to include multistep ionization [13,14,15,16,18,30,31,33]. The cases simulated in this work cover these modifications.
The five cases studied are schematized in Table 2. In each of them, the species and reactions included in particle and energy balance equations were modified. Furthermore, the collisional energy was calculated in two different ways, considering in the energy balance only the ionization from Ar ground state (single-step ionization) and including the ionization of excited species (multistep ionization).

Table 2.
Description of the five cases simulated in this study. The second and third columns correspond to the species and reactions rates considered in particle balance, while the fourth and fifth columns are the species and reactions included in energy balance. The reactions are listed in Table 1. The last column is the type of collisional energy equation used in each case.
In all cases, the species Ar, Arm, Ar+, and electrons were considered in particle balance, as well as the reactions R1–R3, R6, and R9 presented in Table 1 that corresponds to elastic collision, neutral and metastable ionization, excitation, and de-excitation of Arm, respectively. The same reaction set was considered for particle balance in cases 1, 2, and 3, and the difference between them is in the energy balance, more specifically, in the calculation of the collisional energy. In the first case, single-step collisional energy, Equation (7), includes only the Arm excitation (reaction R6), while in the second case the Arm, Arr, and Arp excitations from the ground state (reactions R6–R8) are included.
For case 3, the collisional energy was calculated from Equation (10) assuming the multistep ionization and considering only the metastable species Arm, i.e., in Equation (10) it was assumed that and in the sum i = Ar, Arm. In cases 4 and 5, the species Arr and Arp were included in the particle balance using Equation (10) in the complete form. Reactions R1 to R17 corresponds to electron collisions and R23–R26 to the radiative deexcitations. Only for case 5, reactions R18 to R22 referring to collisions between heavy species were included. In both cases, multistep collisional energy was considered.
3. Results and Discussion
Collisional energies obtained for all cases as a function of electron temperature for absorbed powers of 150 W and 300 W, at a gas pressure range of 0.5–100 mTorr, are shown in Figure 3a. When the absorbed power is changed from 150 W to 300 W, the collisional energy dependence on electron temperature is similar for all cases, but the magnitude is different for each one. Collisional energy is unaffected by absorbed power because it also does not affect the electron temperature (Figure 4). On the other hand, for the same absorbed power, the collisional energy decreases with electron temperature (Figure 3a) and increases with gas pressure (Figure 3b). This inverse dependence occurs because the electron temperature decreases with increasing gas pressure (Figure 4). However, even with collisional energy changing for each case, the electron temperatures calculated are close.
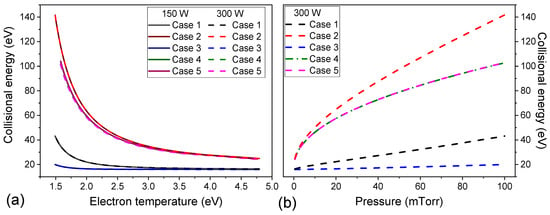
Figure 3.
The collisional energy of all investigated cases as a function of electron temperature at absorbed powers of 150 W and 300 W for a gas pressure of 0.5–100 mTorr (a), and as a function of gas pressure at 300 W (b).
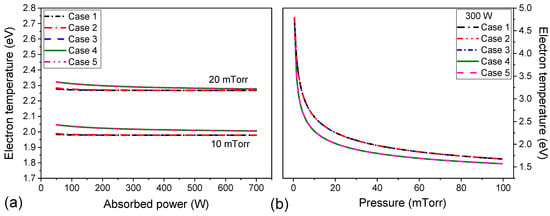
Figure 4.
Electron temperature as a function of absorbed power at 10 mTorr and 20 mTorr (a) and gas pressure at 300 W (b) for the five cases studied.
To understand the collisional energy, it is important to seek relations between the other variables of the model. Single-step collisional energy used in cases 1 and 2, depends on threshold energy () and rate constants considered in the model. Multistep collisional energy of cases 3, 4, and 5, also depends on the densities of the neutral species Ar, Arm, Arr, and Arp (Figure 5). Threshold energies are fixed for all the electron temperatures and plasma parameters. The rate constants are functions of electron temperature (Figure 2), which in turn is affected by gas pressure (Figure 4).
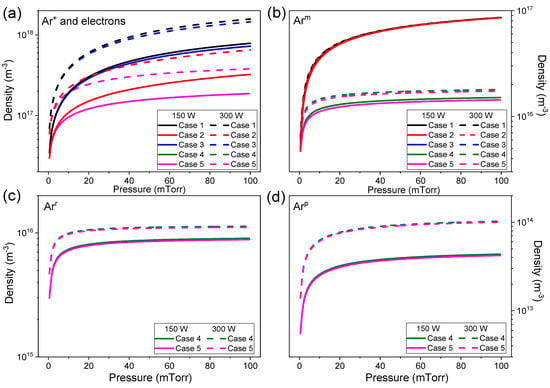
Figure 5.
The electron and Ar+ (a), Arm (b), Arr (c), and Arp (d) species density for all cases as a function of pressure at absorbed power of 300 W. The density of ions and electrons are the same due to the quasi-neutrality. Arr and Arp are not considered in the particle balance in cases 1–3.
Figure 4a,b show the electron temperature as a function of absorbed power and gas pressure for the five cases studied, respectively. It can be observed from Figure 4a that the dependence of the electron temperature with the absorbed power is almost the same for all investigated cases for fixed gas pressure, the values of Te decrease slightly with the increase in the absorbed power. This behavior is in agreement with experimental observations, where the electron temperature is nearly independent of the absorbed power [29,33,34,35,36,48,49]. On the other hand, experimentally, the electron density increases linearly with applied power [48,49,50], which is also corroborated by our simulations for gas pressure above 10 mTorr (Figure 5a). The increase in plasma density is caused by the increase in power dissipated in the plasma. In the steady-state, the power absorbed is equal to power lost. By increasing , the electron temperature remains practically constant (Figure 4a), therefore, the energy dissipated due to the diffusion of electrons and ions to the walls, and by collisions of electrons with neutral species in plasma volume is constant. Although the plasma density increases with the absorbed power. Below 10 mTorr a different behavior is observed because for lower densities experimental observations evidence a non-Maxwellian energy distribution function for argon ICP discharges [23].
Figure 5 shows the electron, Ar+, Arm, Arr, and Arp densities for all investigated cases as a function of gas pressure at absorbed power of 150 W and 300 W. In cases 1–3, the Arm species is produced by ground state excitation (R6) and lost by ionization (R2), de-excitation (R9), and diffusion to the walls. These electron impact reactions depend on electron density that increases with absorbed power (Figure 5). The rate constants are insensitive to the variation of the absorbed power due to the weak dependence of the electron temperature on it (Figure 4). At the same pressure, when the absorbed power is increased from 150 W to 300 W, the reaction rates that produce and reduce Arm equally increase due to the increase in electron density thus, the Arm population is constant with absorbed power (Figure 5b). In cases 4 and 5, the inclusion of Arr and Arp in particle balance reduces the Arm density, which in turn depends on the absorbed power (Figure 5b). In these two cases, Arm also can be lost by excitation to Arr (R12) and Arp (R13) and produced by deexcitation of them (R15 and R16). On increasing absorbed power, the plasma density increases (Figure 5a), and excitation rates are high, as the electron temperature does not vary enough (Figure 4) to reduce significantly the rate constants of these reactions (Figure 2). Thus, the densities of Arr and Arp are guided mainly by electron density (Figure 5c,d). Comparing the species densities of cases 4 and 5 (Figure 5), we see that the heavy species reactions did not change significantly to any particle density.
Experimental results from the literature show that the electron density initially increases abruptly with increasing gas pressure up to 10 mTorr and tends to be monotonic for pressures higher than 10 mTorr [22,31,36,48,49]. For the pressure range simulated, the electron density is found to be in the range of (Figure 5a). All electron densities simulation results are within the range observed in the experiments. The electron temperature is inversely pressure-dependent, decreasing rapidly to 20 mTorr and then varying more smoothly (Figure 4b). This behavior and electron temperature values are in line with experimental measurements [28,29,48,49]. The higher pressure induces more collisions between electrons and heavy particles causing more ionizations, excitations, and elastic collisions [24], consequently, more energy is spent by electrons, decreasing the electron temperature and increasing the collisional energy (see Figure 3 and Figure 4).
Figure 3a shows that the collisional energy abruptly decreases with electron temperature by up to 2.0 eV and then decreases smoothly. Also, it was observed in Figure 3b that it increases with gas pressure for all investigated cases. For cases 1 and 2, in which single-step ionization is considered (Equation (7)), the collisional energy is inverse to the variation of ionization rate constant (Figure 2). The excitation and ionization rate constants increase with temperature, then decrease with pressure (Figure 2a). As far as the raises, the ratios and in Equation (7) decreases since and have a slower increase compared to . Consequently, the collisional energy increases with electron temperature (Figure 3a) and decreases with pressure (Figure 3b).
For case 1, the electrons spend energy to ionize and excite the ground state argon producing Ar+ and Arm, respectively, and in elastic collisions (Table 2). In case 2, electrons also can excite ground state argon atoms to Arr and Arp (Table 2). Thus, more energy is lost between two consecutive ionizations, and the collisional energy increases for the same electron temperature as can be seen in Figure 3 for typical values of ICP temperature between 2.0 eV and 3.0 eV [34,48].
For cases 1 and 2, collisional energy increases with pressure (Figure 3b) and remains constant with absorbed power variation (Figure 3a). The pressure increase reduces the electron temperature (Figure 4) and consequently, collisional energy. But both cases have the same electron temperature at the same pressure (Figure 4b) and the collisional energies are much different, and this gap increases with pressure (Figure 3b). The higher electron density observed for case 1 compared to case 2 (Figure 5a) is a consequence of this difference in collisional energy.
Cases 3, 4, and 5 have a similar dependence on electron temperature and gas pressure (Figure 3) as observed for cases 1 and 2. In , the quotient includes the density of neutral species (Ar and Arm for case 3 and Ar, Arm, Arr and Arp for cases 4 and 5) and their respective ionization rate constants, and the densities also multiply the terms in dividend (Equation (10)). Figure 6 shows the collisional energy for each species Ar, Arm, Arr, and Arp, and the multistep collisional energy for cases 3 and 4 defined in Equation (10). is the major contribution for collisional energy and defines the shape of . Increasing the electron temperature by decreasing the gas pressure the species densities reduce (Figure 5) and ionization rate constants increase (Figure 2), thus the collisional energy decreases (Figure 3).
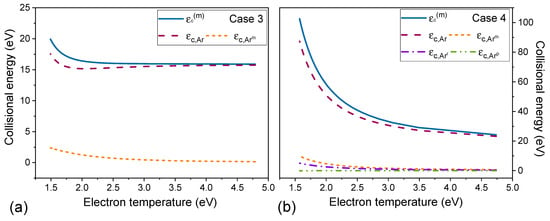
Figure 6.
Collisional energy of each species that contributes to ionization: Ar and Arm for case 3 (a) and Ar, Arm, Arr, and Arp for case 4 (b) as a function of electron temperature for absorbed power of 300 W. In both graphs is the multistep collisional energy.
In Figure 3, comparing cases 1 and 3 that consider only Arm as excited species in particle balance, the use of the multistep ionization in energy balance (including in case 3) reduces the collisional energy for a given electron temperature. In case 3, is the principal contribution in (Figure 6a). Both cases 1 and 3 use the same reactions in particle balance, the difference between them is that the multistep collisional energy depends on Ar and Arm densities and the ionization of Arm (R3) is included in the energy balance of case 3. The metastable argon has lower ionization energy than the neutral one, thus the energy cost to maintain the plasma reduces (Figure 5a). This also explains the difference in collisional energy between cases 2 and 4–5 (Figure 3). When the stepwise ionization of Arr and Arp are taken into account (cases 4 and 5), the energy loss by electron per electron-ion pair created decreases. No significant difference is observed in collisional energy for cases 4 and 5 (Figure 3), showing that the heavy species reactions have no relevant effect on this parameter.
To complement the analysis, Figure 6 presents the collisional energy of each species that contributes to ionization for cases 3 and 4. The collisional energies of excited species are reduced due to reactions that transfer energy to electrons (Figure 6b). All reactions between atoms and electrons cause electrons to lose energy and this loss increases with pressure. For Arm, Arr, and Arp deexcitations result in energy gain by electrons (negative term in Equation (10)) that reduces the collisional energy. For Arm, Arr, and Arp the contribution to the collisional energy decreases with approaching 0 eV for high values of Te (Figure 6). For Arm, electron energy loss in ionization and excitations is greater than the electron energy gain in deexcitations and is positive in this range of Te (Figure 6a,b). For Arr and Arp, their contribution becomes negative with increasing electron temperature but remains close to 0 eV (Figure 6b).
Figure 7a shows the total energy loss as a function of electron temperature, while Figure 7b the electron temperature as a function of the gas pressure. The data points correspond to the experimental data of Hong et al. [29] who obtained at the plasma-sheath edge. The total energy loss is the sum of collisional energy and the energy loss due to the diffusion process of electrons and ions (Equation (12)). and are functions of only [29]. Initially, the collisional energy is greater than and , so decreases such as the collisional energy. As the electron temperature increases, the collisional energy continues to decrease, but the total energy becomes constant and then starts to grow. This fact is caused by the growth of and .
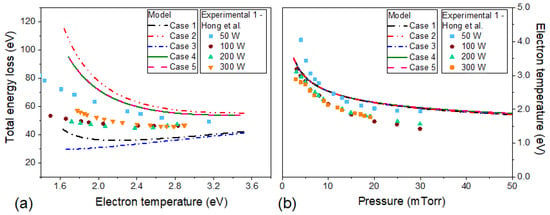
Figure 7.
The total energy loss as a function of electron temperature (a) and electron temperature as a function of gas pressure (b) for the 5 cases studied. The model results are the same for all absorbed power values in the simulated range (50 W a 600 W). The data points are relative to experimental data at different absorbed power of Hong et al. [29]. The simulations (lines) were performed with the input parameters: R = 13 cm, L = 12 cm, Tg = 300 K and .
In Figure 7a, for cases 1, 2, 4, and 5, initially decreases and then increases with electron temperature. This behavior is in agreement with the experimental data. The simulated value for case 1 is less than the experimental results and, for cases 2, 4, and 5, are greater than the experimental data. For case 3, only increases with and is smaller than the experimental results, so this case is the least appropriate for studying argon discharge. Ku et al. [35] reported measurements of total energy loss as a function of electron temperature. They observed that in the temperature range of 1.0 eV to 3.0 eV, decreases and is greater than 100 eV. Cases 2, 4, and 5 (Figure 7) better agree with these results.
Relative to Figure 7b, the electron temperature for all simulations is higher than the experimental measurements, but the maximum difference is around 0.5 eV. Experimentally, the electron temperature does not vary between 100 W and 300 W [29], this fact is supported by the results of our model.
Figure 8a shows the experimental data of Lee et al. for 10 mTorr and the global model results for as a function of absorbed power for cases 2 and 4. For cases 1 and 3, are less than 40 eV and for case 5 it is equal to case 4. Cases 1 and 3 generated results that are very far from the experimental data, so they are not the best options for plasma modeling by Lee et al. [33,34]. Compared with experimental data “2” in Figure 8a, simulated is smaller, but this difference is reduced with the absorbed power. Above 150 W, cases 2, 4, and 5 had a good agreement with experimental data 2. In relation to experimental data 3, the discrepancy was greater for power values lower than 200 W.
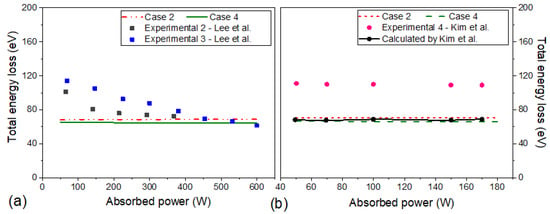
Figure 8.
The total energy loss as a function of absorbed power at 10 mTorr for cases 2 and 4. In (a), the squares are experimental data of Lee et al. [33,34]. The simulations (lines) were performed with the input parameters: R = 19 cm, L = 30 cm, Tg = 300 K and at 10 mTorr. In (b), the circles are experimental data and calculated results of Kim et al. [36]. Here, the simulations (lines) were performed with the input parameters: R = 13 cm, L = 10 cm, Tg = 300 K and at 25 mTorr.
In addition, Figure 8b presents the experimental/simulated data of Kim et al. for 25 mTorr and the global model results for as a function of absorbed power for cases 2 and 4. A constant behavior of with the absorbed power was observed experimentally/numerically by Kim et al. [36] and in our simulations. The experimental values were superior to the total energy loss obtained in cases 2 and 4. Kim et al. also studied the effect of the electron distribution function on the total collision loss. Their results calculated for a Maxwell-Boltzmann distribution were also inferior to the experimental measurements and are close to the results of cases 2 and 4.
There are few experimental works in the literature on total energy loss and there are some disagreements between their results. As can be seen in Figure 8, Lee et al. and Kim et al. experimentally measured the total energy losses as a function of absorbed power [33,34,36], and the trends observed were distinct. The results of Lee et al. showed that collisional energy decreases with increasing absorbed power, but for the case of Kim et al. remained constant for the investigated absorbed power values.
4. Conclusions
The effect of the reaction set on the energy balance of the global model for argon ICP discharge was studied. Five cases were simulated and in each one different argon species and number of reactions were considered. In addition, the contribution of multistep ionization was analyzed in comparison with single-step ionization. This was done by modifying the expression for collisional energy loss per pair electron-ion created. Simulations were made varying gas pressure (0.5–100 mTorr) and absorbed power (150 W and 300 W).
In the energy balance of gas discharge of a global model, the collisional energy loss is much more sensitive to modifications than the electron temperature. The electron temperature is practically equal for all investigated cases. In turn, the collisional energy had the same dependence on pressure, absorbed power, and electron temperature for the five cases, but the magnitude was different.
According to the simulation results, the inclusion of excited species Arr and Arp in the energy balance increases the collisional energy loss by the electrons. This is because more energy is expended by electrons to produce these species by excitation. This was observed by comparing cases 1 and 2 and cases 3 and 4/5.
The consideration of excited species ionization (multistep ionization) reduced the collisional energy loss. Excited species have lower ionization energy than ground state argon, and therefore electrons use less energy to produce an ion. This fact could be observed comparing cases 1 and 3, and cases 2 and 4/5. Case 5 differed from case 4 in that it included heavy species collisions. The contribution of these collisions was negligible.
The total energy loss and electron temperature were compared with experimental results from the literature. The electron temperature was the same for all investigated cases and shows good agreement with the experimental results. The total energy loss of cases 1, 2, 4, and 5 were shown to have a similar dependence on electron temperature. On the other hand, case 3 did not show good agreement.
Finally, we can infer from the analysis performed that cases 2, 4, and 5, which present more species and reactions in the energy balance, were the best option to model argon ICP discharges.
Author Contributions
Conceptualization, J.K. and R.P.; methodology, J.K. and B.M.; software, J.K. and R.P.; writing—original draft preparation, J.K., B.M. and J.S.; writing—review and editing, J.K., B.M., J.S. and R.P.; supervision, R.P.; funding acquisition, R.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
J.K. thank you the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—CAPES for doctorate grant (Finance Code 001).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, H.C. Review of inductively coupled plasmas: Nano-applications and bistable hysteresis physics. Appl. Phys. Rev. 2018, 5, 011108. [Google Scholar] [CrossRef]
- Agati, M.; Amiard, G.; Le Borgne, V.; Castrucci, P.; Dolbec, R.; de Crescenzi, M.; El Khakani, M.A.; Boninelli, S. Growth Mechanisms of Inductively- Coupled Plasma Torch Synthesized Silicon Nanowires and their associated photoluminescence properties. Sci. Rep. 2016, 6, 37598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beaudette, C.A.; Andaraarachchi, H.P.; Wu, C.; Kortshagen, U.R. Inductively coupled nonthermal plasma synthesis of aluminum nanoparticles. Nanotechnology 2021, 32, 395601. [Google Scholar] [CrossRef] [PubMed]
- Mazouffre, S. Electric propulsion for satellites and spacecraft: Established technologies and novel approaches. Plasma Sources Sci. Technol. 2006, 25, 033002. [Google Scholar] [CrossRef]
- Fujino, T.; Yamauchi, M. Numerical study of plasma-fluid characteristics and thrust performance of a low-power argon inductively coupled plasma electrothermal thruster. J. Appl. Phys. 2020, 128, 173302. [Google Scholar] [CrossRef]
- Tsifakis, D.; Charles, C.; Boswell, R. An Inductively-Coupled Plasma Electrothermal Radiofrequency Thruster. Front. Phys. 2020, 8, 34. [Google Scholar] [CrossRef] [Green Version]
- Kamgang-Youbi, G.; Poizot, K.; Lemont, F. Inductively coupled plasma torch efficiency at atmospheric pressure for organo-chlorine liquid waste removal: Chloroform destruction in oxidative conditions. J. Hazard. Mater. 2013, 171, 244–245. [Google Scholar] [CrossRef] [PubMed]
- Bruggeman, P.J.; Kushner, M.J.; Locke, B.R.; Gardeniers, J.G.E.; Graham, W.G.; Graves, D.B.; Hofman-Caris, R.C.H.M.; Maric, D.; Reid, J.P.; Ceriani, E.; et al. Plasma–liquid interactions: A review and roadmap. Plasma Sources Sci. Technol. 2016, 25, 053002. [Google Scholar] [CrossRef]
- Jiang, B.; Zheng, J.; Qiu, S.; Wu, M.; Zhang, Q.; Yan, Z.; Xue, Q. Review on electrical Discharge Plasma Technology for Wastewater Remediation. Chem. Eng. J. 2014, 236, 348–368. [Google Scholar] [CrossRef]
- Alves, L.L.; Bogaerts, A.; Guerra, V.; Turner, M.M. Foundations of modelling of nonequilibrium low- temperature. Plasma Sources Sci. Technol. 2018, 27, 023002. [Google Scholar] [CrossRef]
- Hurlbatt, A.; Gibson, A.R.; Schröter, S.; Bredin, J.; Foote, A.P.S.; Grondein, P.; O’Connell, D.; Gans, T. Concepts, Capabilities, and Limitations of Global Models: A Review. Plasma Process. Polym. 2017, 14, 1600138. [Google Scholar] [CrossRef] [Green Version]
- Ashida, S.; Lee, C.; Lieberman, M.A. Spatially averaged (global) model of time modulated high density argon plasmas. J. Vac. Sci. Technol. A 1995, 13, 2498. [Google Scholar] [CrossRef]
- Lee, M.H.; Chung, C.W. Effect of multistep ionizations on the electron temperature in an argon inductively coupled plasma. Appl. Phys. Lett. 2005, 87, 131502. [Google Scholar] [CrossRef]
- Lee, M.H.; Jang, S.H.; Chung, C.W. On the multistep ionizations in an argon inductively coupled plasma. Phys. Plasmas 2006, 13, 053502. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.H.; Chung, C.W. Self-consistent global model with multi-step ionizations in inductively coupled plasmas. Phys. Plasmas 2005, 12, 073501. [Google Scholar] [CrossRef]
- Gudmundsson, J.T. On the effect of the electron energy distribution on the plasma parameters of an argon discharge: A global (volume-averaged) model study. Plasma Sources Sci. Technol. 2001, 10, 76. [Google Scholar] [CrossRef]
- Toneli, D.A. A volume averaged global model study of the influence of the electron energy distribution and the wall material on an oxygen discharge. J. Phys. D Appl. Phys. 2015, 48, 495203. [Google Scholar] [CrossRef]
- Magaldi, B.V.; Pessoa, R.S.; da Sobrinho, A.S. A global model study of argon plasma chemistry used as propellant of a gridded ion thruster. Rev. Bras. Apll. Vac. 2021, 40. [Google Scholar] [CrossRef]
- Kortshagen, U.; Heil, B.G. Kinetic Two-Dimensional Modeling of Inductively Coupled Plasmas Based on a Hybrid Kinetic Approach. IEEE Trans. Plasma Sci. 1999, 27, 5. [Google Scholar] [CrossRef]
- Loureiro, J.; Amorim, J. Kinetics and Spectroscopy of Low Temperature Plasmas; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Gyergyek, T.; Kovacic, J.; Gomez, I.; Gunn, J.P.; Costea, S.; Mozetic, M. Kinetic model of an inverted sheath in a bounded plasma system. Phys. Plasmas 2020, 27, 023520. [Google Scholar] [CrossRef]
- Wen, D.-Q.; Liu, W.; Gao, F.; Lieberman, M.A.; Wang, Y.-N. A hybrid model of radio frequency biased inductively coupled plasma discharges: Description of model and experimental validation in argon. Plasma Sources Sci. Technol. 2016, 25, 045009. [Google Scholar] [CrossRef]
- Lieberman, M.A.; Lichtenberg, A.J. Principle of Plasma Discharges and Materials Processing, 2nd ed.; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Pessoa, R.S.; Sismanoglu, B.N.; Gomes, M.P.; Medeiros, H.S.; Sagás, J.C.; Roberto, M.; Maciel, H.S.; Petraconi, G. Chemistry Studies of Low Pressure Argon Discharges: Experiments and Simulation. In Argon: Production, Characteristics and Applications; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2013. [Google Scholar]
- Roberto, M.; Smith, H.B.; Verboncoeur, J.P. Influence of Metastable Atoms in Radio-Frequency Argon Discharges. IEEE Trans. Plasma Sci. 2003, 31, 6. [Google Scholar] [CrossRef]
- Lymberopoulos, D.L.; Economou, D.J. Fluid simulations of glow discharges: Effect of metastable atoms in argon. J. Appl. Phys. 1993, 73, 8. [Google Scholar] [CrossRef] [Green Version]
- Toshikazu, S.; Toshiaki, M. Effect of metastables on a sustaining mechanism in inductively coupled plasma in Ar. J. Appl. Phys. 2005, 98, 113304. [Google Scholar] [CrossRef]
- Lee, Y.K.; Chung, C.W. Ionization in inductively coupled argon plasmas studied by optical emission spectroscopy. J. Appl. Phys. 2011, 109, 013306. [Google Scholar] [CrossRef]
- Hong, Y.H.H.; Kim, J.H.; Kim, T.W.; Lee, H.W.; Lee, M.Y.; Chung, C.H. Experimental investigation on optimal plasma generation in inductively coupled plasma. Phys. Plasmas 2021, 28, 053507. [Google Scholar] [CrossRef]
- Lee, C.; Lieberman, M.A. Global model of Ar, O2, Cl2, and Ar/O2 high-density plasma discharges. J. Vac. Sci. Technol. A 1995, 13, 368. [Google Scholar] [CrossRef]
- Freitas, F.M.; Pessoa, R.S.; Maciel, H.S.; Petraconi Filho, G. Comparisons between Langmuir probe measurements and global model of a capacitively coupled rf argon discharge. Rev. Bras. Apl. Vac. 2008, 27, 211. [Google Scholar]
- Hjartarson, A.T.; Thorsteinsson, E.G.; Gudmundsson, J.T. Low pressure hydrogen discharges diluted with argon explored using a global model. Plasma Sources Sci. Technol. 2010, 19, 065008. [Google Scholar] [CrossRef]
- Lee, Y.K.; Lee, M.H.; Chung, C.W. Experimental measurement of the total energy losses in a low pressure inductively coupled argon plasma. Appl. Phys. Lett. 2009, 95, 111501. [Google Scholar] [CrossRef]
- Lee, Y.K.; Ku, J.H.; Chung, C.H. Measurements of the total energy lost per electron–ion pair lost in low-pressure inductive argon, helium, oxygen and nitrogen discharge. Plasma Sources Sci. Technol. 2011, 20, 015005. [Google Scholar] [CrossRef]
- Ku, J.H.; Lee, Y.K.; Chung, C.W. Measurement of the total energy losses per electron-ion lost in various mixed gas inductively coupled plasmas. Phys. Plasmas 2010, 17, 043508. [Google Scholar] [CrossRef]
- Kim, J.Y.; Kim, Y.C.; Kim, Y.S.; Chung, C.W. Effect of the electron energy distribution on total energy loss with argon in inductively coupled plasmas. Phys. Plasmas 2015, 22, 013501. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® v. 5.4; COMSOL AB: Stockholm, Sweden. Available online: www.comsol.com (accessed on 15 August 2021).
- Straub, H.C.; Renault, P.; Lindsay, B.G.; Smith, K.A.; Stebbings, R.F. Absolute partial and total cross sections for electron-impact ionization of argon from threshold to 1000 eV. Phys. Rev. A 1995, 52, 1115. [Google Scholar] [CrossRef]
- Ali, M.A.; Stone, P. Electron impact ionization of metastable rare gases: He, Ne and Ar. Int. J. Mass Spectrom. 2008, 271, 51. [Google Scholar] [CrossRef]
- Deutsch, H.; Becker, K.; Grum-Grzhimailo, A.N.; Bartschat, K.; Summers, H.; Probst, M.; Matt-Leubner, S.; Märk, T.D. Calculated cross sections for the electron-impact ionization of excited argon atoms using the DM formalism. Int. J. Mass Spectrom. 2004, 233, 39. [Google Scholar] [CrossRef]
- Mityureva, A.A.; Smirnov, V.V. Integral Electronic Excitation Cross Sections of Hydrogen Atom Levels, A. Opt. Spectrosc. 2006, 101, 338–343. [Google Scholar] [CrossRef]
- Hayashi, M. A Set of Electron-Ar Cross Sections with 25 Excited States. 2003. Available online: https://iopscience.iop.org/0022-3727/38/10/014/media/argon-cs.pdf (accessed on 15 March 2021).
- Ferreira, C.M.; Loureiro, J.; Richard, A. Populations in the metastable and the resonance levels of argon and stepwise ionization effects in a lowpressure argon positive column. J. Appl. Phys. 1985, 57, 82. [Google Scholar] [CrossRef]
- Gudmundsson, J.T.; Thorsteinsson, E.G. Oxygen discharges diluted with argon: Dissociation processes. Plasma Sources Sci. Technol. 2007, 16, 399. [Google Scholar] [CrossRef]
- Bassett, N.L.; Economou, D.J. Effect of Cl2 additions to an argon glow discharge. J. Appl. Phys. 1994, 75, 1931. [Google Scholar] [CrossRef] [Green Version]
- Kannari, F.; Obara, M.; Fujioka, T. An advanced kinetic model of electron beam excited KrF lasers including the vibrational relaxation in KrF(B) and collisional mixing of KrF(B.C). J. Appl. Phys. 1985, 57, 4309. [Google Scholar] [CrossRef]
- Hurst, G.S.; Wagner, E.B.; Payne, M.G. Energy transfer from the resonance states Ar(1P1) and Ar(3P1) to ethylene. J. Chem. Phys. 1974, 61, 3680. [Google Scholar]
- Godyak, V.A.; Piejak, R.B.; Alexandrovich, B.M. Electron energy distribution function measurements and plasma parameters in inductively coupled argon plasma. Plasma Sources Sci. Technol. 2002, 11, 525. [Google Scholar] [CrossRef]
- Godyak, V.A. Electrical and plasma parameters of ICP with high coupling efficienc. Plasma Sources Sci. Technol. 2011, 20, 025004. [Google Scholar] [CrossRef] [Green Version]
- Jang, D.; Uhm, H.S.; Jang, D.; Hur, M.S.; Suk, H. Electron density characterization of inductively- coupled argon plasmas by the terahertz time- domain spectroscopy. Plasma Sources Sci. Technol. 2016, 25, 065008. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).