Thermal Analysis and Crystallization of Bioactive Glass “1d” in the SiO2-CaO-MgO-P2O5-CaF2-Na2O Compositional System
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of Glass and Glass–Ceramics
2.2. Thermal Analyses and Assessment of Crystallization Kinetics
2.3. Characterization of Samples
3. Results and Discussion
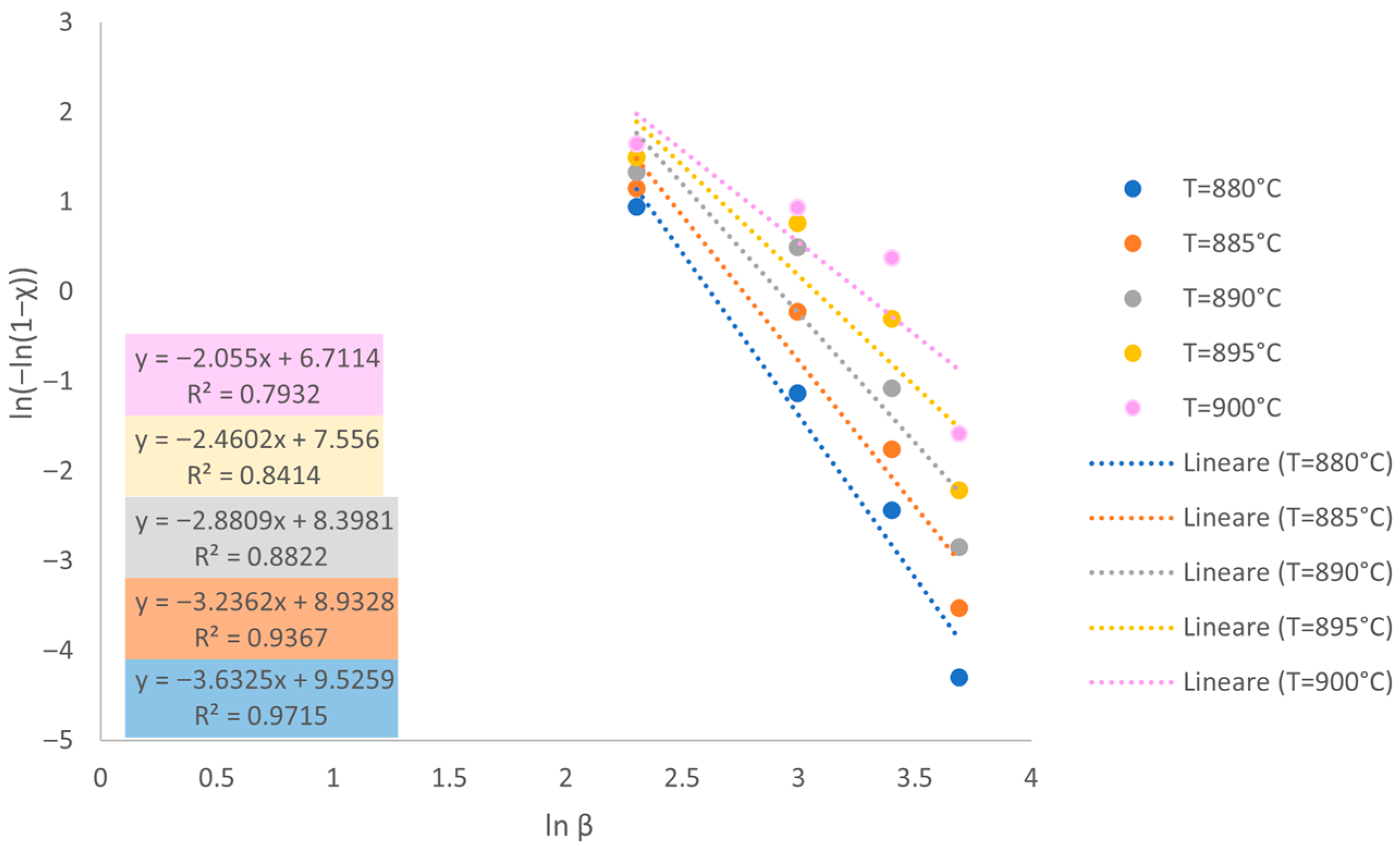
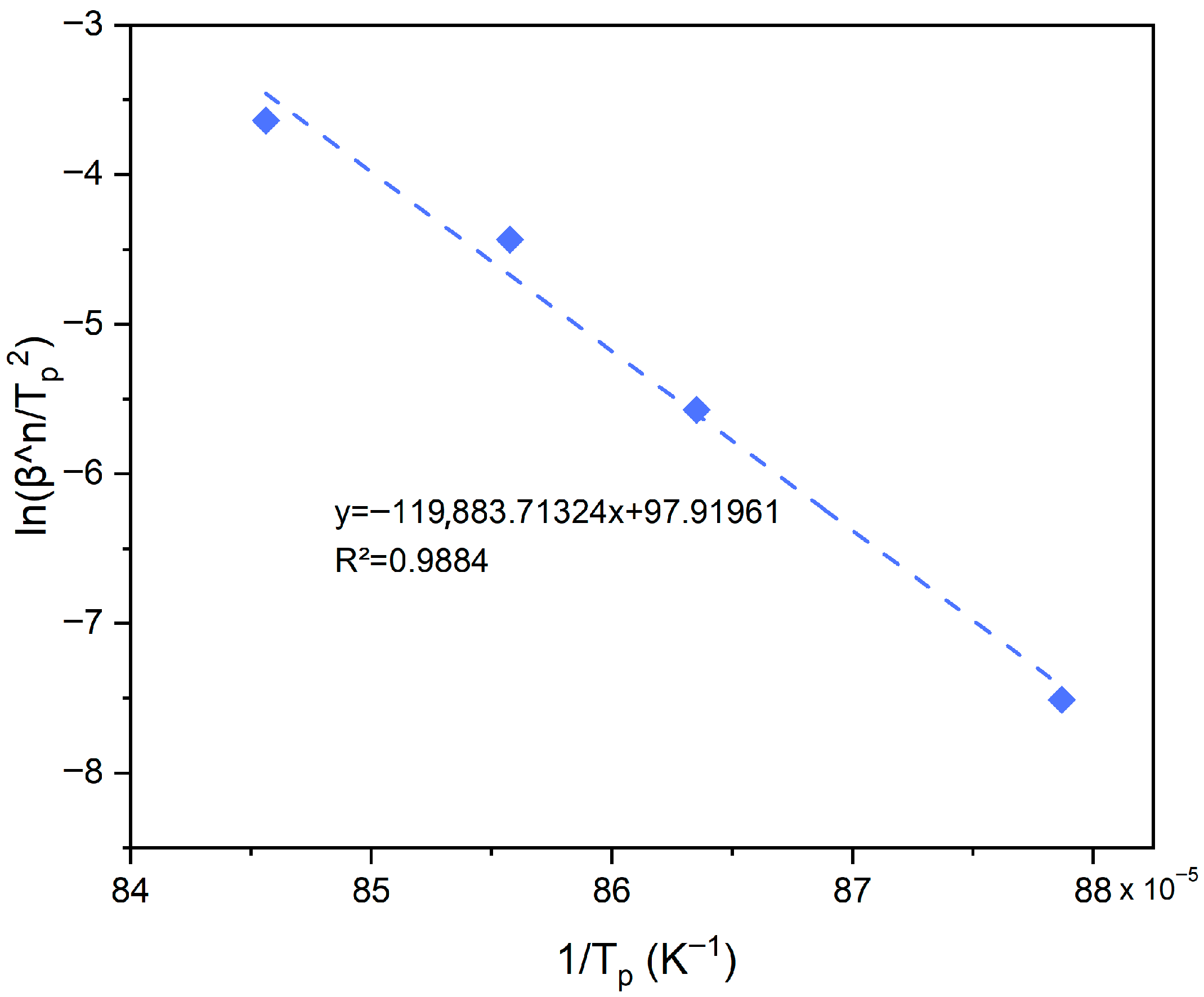
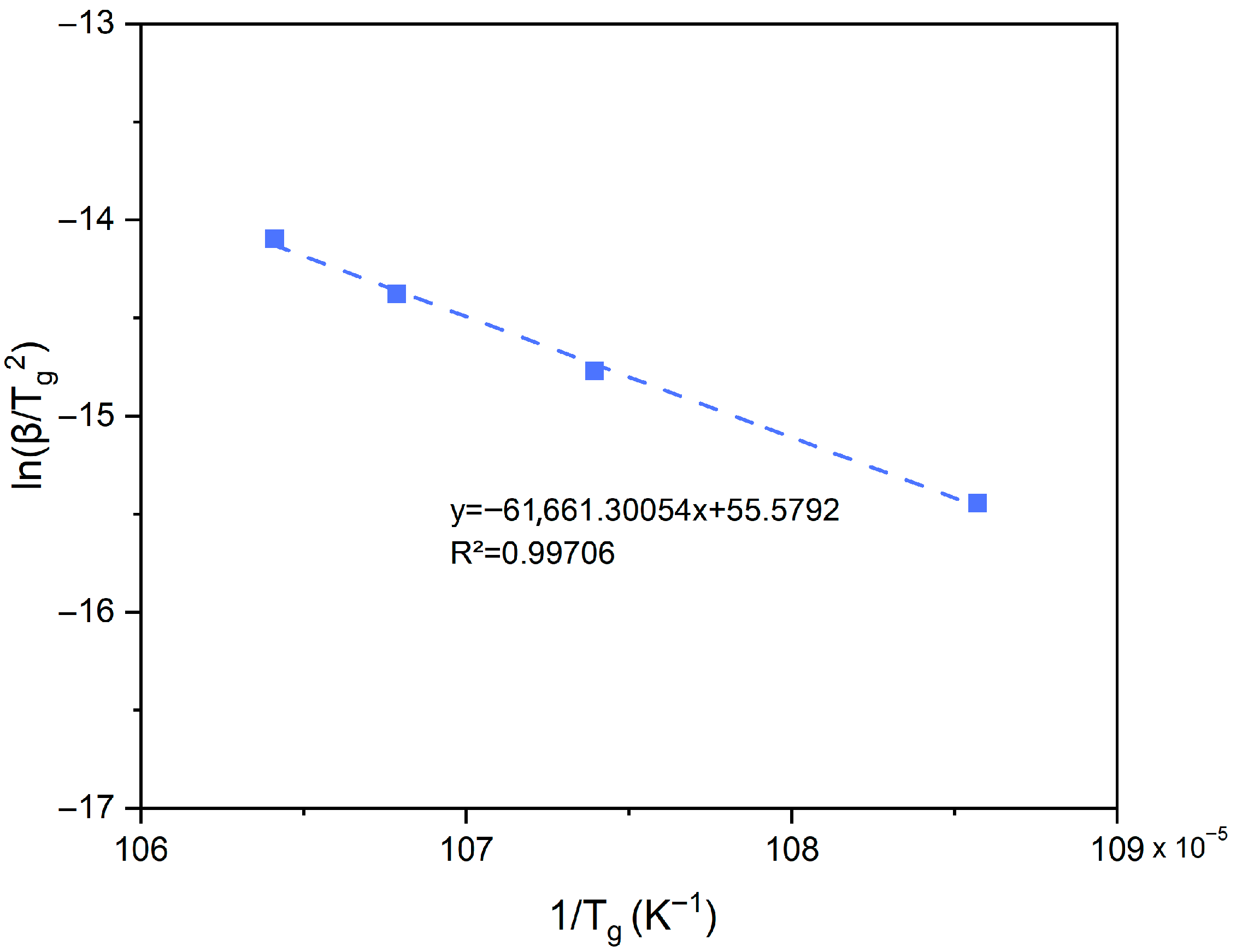
3.1. Thermal Properties and Assessment of Crystallization Energy
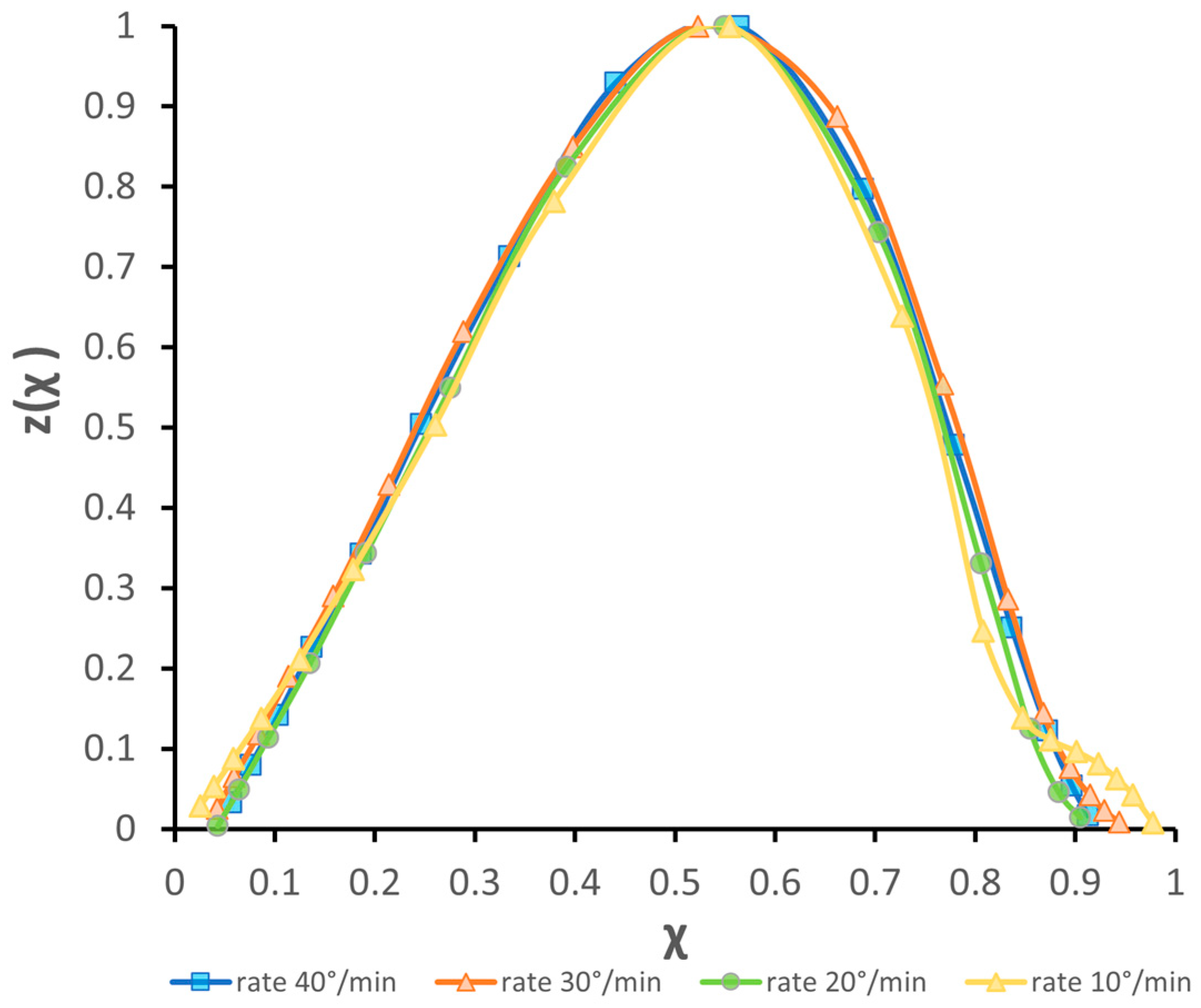
3.2. Sintering Ability Against Crystallization
3.3. Discussion of Model Applicability
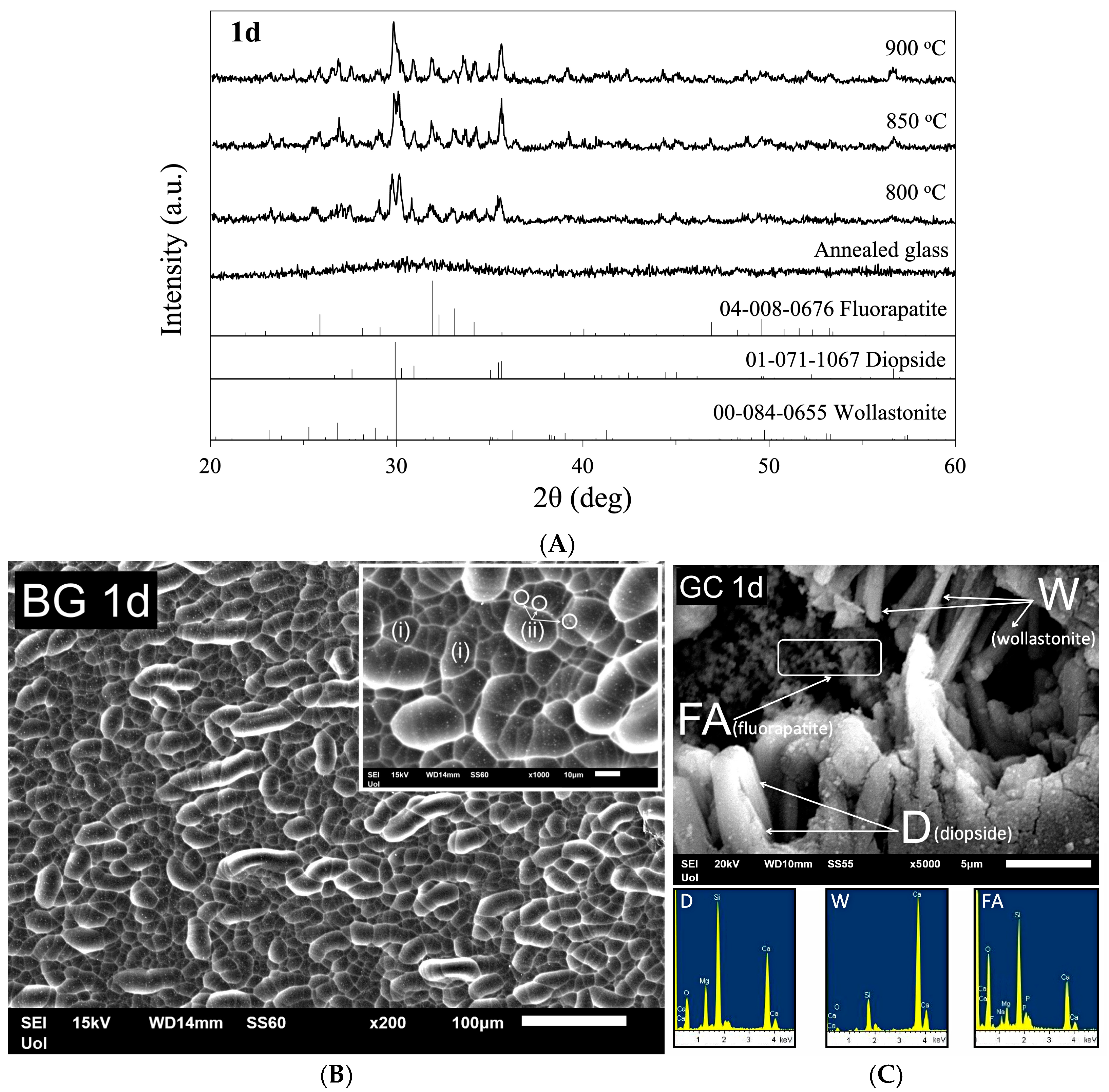
3.4. Glass–Ceramic 1d (GC1d) Through Devitrification of BG1d
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hench, L.L. The story of Bioglass®. J. Mater. Sci. Mater. Med. 2006, 17, 967–978. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.; Pigott, G.H.; Schoen, F.J.; Hench, L.L. Toxicology and biocompatibility of bioglasses. J. Biomed. Mater. Res. 1981, 15, 805–817. [Google Scholar] [CrossRef] [PubMed]
- Hench, L.L. Genetic design of bioactive glass. J. Eur. Ceram. Soc. 2009, 29, 1257–1265. [Google Scholar] [CrossRef]
- Miguez-Pacheco, V.; Hench, L.L.; Boccaccini, A.R. Bioactive glasses beyond bone and teeth: Emerging applications in contact with soft tissues. Acta Biomater. 2015, 13, 1–15. [Google Scholar] [CrossRef]
- Kargozar, S.; Hamzehlou, S.; Baino, F. Potential of Bioactive Glasses for Cardiac and Pulmonary Tissue Engineering. Materials 2017, 10, 1429. [Google Scholar] [CrossRef]
- Brink, M.; Turunen, T.; Happonen, R.P.; Yli-Urpo, A. Compositional dependence of bioactivity of glasses in the system Na2O- K2O-MgO-Cao-B2O3-P2O5-SiO2. J. Biomed. Mater. Res. 1997, 37, 114–121. [Google Scholar] [CrossRef]
- Abodunrin, O.D.; El Mabrouk, K.; Bricha, M. A review on borate bioactive glasses (BBG): Effect of doping elements, degradation, and applications. J. Mater. Chem. B. 2023, 11, 955. [Google Scholar] [CrossRef]
- Andersson, O.H.; Liu, G.; Karlsson, K.H.; Niemi, L.; Miettinen, J.; Juhanoja, J. In vivo behaviour of glasses in the SiO2-Na2O-CaO-P2O5-Al2O3-B2O3 system. J. Mater. Sci. Mater. Med. 1990, 1, 219–227. [Google Scholar] [CrossRef]
- Knowles, J.C. Phosphate based glasses for biomedical applications. J. Mater. Chem. 2003, 13, 2395–2401. [Google Scholar] [CrossRef]
- Montazerian, M.; Zanotto, E.D. History and trends of bioactive glass-ceramics. J. Biomed. Mater. Res. A 2016, 104, 1231–1249. [Google Scholar] [CrossRef]
- Montazerian, M.; Baino, F.; Fiume, E.; Migneco, C.; Alaghmandfard, A.; Sedighi, O.; DeCeanne, A.V.; Wilkinson, C.J.; Mauro, J.C. Glass-ceramics in dentistry: Fundamentals, technologies, experimental techniques, applications, and open issues. Prog. Mater. Sci. 2023, 132, 101023. [Google Scholar] [CrossRef]
- Lefebvre, L.; Gremillard, L.; Chevalier, J.; Zenati, R.; Bernache-Assolant, D. Sintering behaviour of 45S5 bioactive glass. Acta Biomater. 2008, 4, 1894–1903. [Google Scholar] [CrossRef] [PubMed]
- The Sintering Range of Porous Bioactive Glasses. Available online: https://www.researchgate.net/publication/233521778_The_Sintering_Range_of_Porous_Bioactive_Glasses (accessed on 25 August 2025).
- Tulyaganov, D.U.; Agathopoulos, S.; Ventura, J.M.; Karakassides, M.A.; Fabrichnaya, O.; Ferreira, J.M.F. Synthesis of glass–ceramics in the CaO-MgO-SiO2 system with B2O3, P2O5, Na2O and CaF2 additives. J. Eur. Ceram. Soc. 2006, 26, 1463–1471. [Google Scholar] [CrossRef]
- Tulyaganov, D.U.; Agathopoulos, S.; Dimitriadis, K.; Fernandes, H.R.; Gabrieli, R.; Baino, F. The Story, Properties and Applications of Bioactive Glass ‘1d’: From Concept to Early Clinical Trials. Inorganics 2024, 12, 224. [Google Scholar] [CrossRef]
- Tulyaganov, D.U.; Agathopoulos, S.; Valerio, P.; Balamurugan, A.; Saranti, A.; Karakassides, M.A.; Ferreira, J.M.F. Synthesis, bioactivity and preliminary biocompatibility studies of glasses in the system CaO-MgO-SiO2-Na2O-P2O5-CaF2. J. Mater. Sci. Mater. Med. 2011, 22, 217–227. [Google Scholar] [CrossRef]
- Tulyaganov, D.U.; Makhkamov, M.E.; Urazbaev, A.; Goel, A.; Ferreira, J.M.F. Synthesis, processing and characterization of a bioactive glass composition for bone regeneration. Ceram. Int. 2013, 39, 2519–2526. [Google Scholar] [CrossRef]
- Schmitz, S.I.; Widholz, B.; Essers, C.; Becker, M.; Tulyaganov, D.; Moghaddam, A.; de Juan, I.G.; Westhauser, F. Superior biocompatibility and comparable osteoinductive properties: Sodium-reduced fluoride-containing bioactive glass belonging to the CaO-MgO-SiO2 system as a promising alternative to 45S5 bioactive glass. Bioact. Mater. 2020, 5, 55–65. [Google Scholar] [CrossRef]
- Baino, F.; Tulyaganov, D.U.; Kahharov, Z.; Rahdar, A.; Verné, E. Foam-Replicated Diopside/Fluorapatite/Wollastonite-Based Glass–Ceramic Scaffolds. Ceramics 2022, 5, 120–130. [Google Scholar] [CrossRef]
- Baino, F.; Gaido, F.; Gabrieli, R.; Alidoost, D.; Schiavi, A.; Mohammadi, M.; Schwentenwein, M.; Tulyaganov, D.; Verné, E. Vat photopolymerization of ultra-porous bioactive glass foams. Open Ceram. 2024, 20, 100690. [Google Scholar] [CrossRef]
- Dimitriadis, K.; Vasilopoulos, K.C.; Vaimakis, T.C.; Karakassides, M.A.; Tulyaganov, D.U.; Agathopoulos, S. Synthesis of glass-ceramics in the Na2O/K2O-CaO-MgO-SiO2-P2O5-CaF2 system as candidate materials for dental applications. Int. J. Appl. Ceram. Technol. 2020, 17, 2025–2035. [Google Scholar] [CrossRef]
- Dimitriadis, K.; Moschovas, D.; Tulyaganov, D.U.; Agathopoulos, S. Development of novel bioactive glass-ceramics in the Na2O/K2O-CaO-MgO-SiO2-P2O5-CaF2 system. J. Non-Cryst. Solids 2020, 533, 119936. [Google Scholar] [CrossRef]
- Dimitriadis, K.; Tulyaganov, D.U.; Vasilopoulos, K.C.; Karakassides, M.A.; Agathopoulos, S. Influence of K and Mg substitutions on the synthesis and the properties of CaO-MgO-SiO2/Na2O, P2O5, CaF2 bioactive glasses. J. Non-Cryst. Solids 2021, 573, 121140. [Google Scholar] [CrossRef]
- Baino, F.; Fiume, E. Quantifying the effect of particle size on the crystallization of 45S5 bioactive glass. Mater. Lett. 2018, 224, 54–58. [Google Scholar] [CrossRef]
- Schiavi, A.; Gaido, F.; Gabrieli, R.; Alidoost, D.; Schwentenwein, M.; Mohammadi, M.; Tulyaganov, D.; Verné, E.; Baino, F. Permeability and tomography-based microstructural analysis of ultra-porous bioactive glass scaffolds. Mater. Lett. 2025, 384, 138064. [Google Scholar] [CrossRef]
- Kansal, I.; Tulyaganov, D.U.; Goel, A.; Pascual, M.J.; Ferreira, J.M.F. Structural analysis and thermal behavior of diopside-fluorapatite- wollastonite-based glasses and glass-ceramics. Acta Biomater. 2010, 6, 4380–4388. [Google Scholar] [CrossRef]
- Kissinger, H.E. Variation of Peak Temperature with Heating Rate in Differential Thermal Analysis. J. Res. Natl. Bur. Stand. 1956, 57, 217. [Google Scholar] [CrossRef]
- Matusita, K.; Sakka, S. Kinetic study of crystallization of glass by differential thermal analysis—Criterion on application of Kissinger plot. J. Non-Cryst. Solids 1980, 38–39, 741–746. [Google Scholar] [CrossRef]
- Matusita, K.; Komatsu, T.; Yokota, R. Kinetics of non-isothermal crystallization process and activation energy for crystal growth in amorphous materials. J. Mater. Sci. 1984, 19, 291–296. [Google Scholar] [CrossRef]
- Francis, A.A.; Rawlings, R.D.; Sweeney, R.; Boccaccini, A.R. Crystallization kinetic of glass particles prepared from a mixture of coal ash and soda-lime cullet glass. J. Non Cryst. Solids 2004, 333, 187–193. [Google Scholar] [CrossRef]
- Ozawa, T. Kinetics of non-isothermal crystallization. Polymer 1971, 12, 150–158. [Google Scholar] [CrossRef]
- Augis, J.A.; Bennett, J.E. Calculation of the Avrami parameters for heterogeneous solid state reactions using a modification of the Kissinger method. J. Therm. Anal. 1978, 13, 283–292. [Google Scholar] [CrossRef]
- Malek, J. Kinetic analysis of crystallization processes in amorphous materials. Thermochim. Acta 2000, 355, 239–253. [Google Scholar] [CrossRef]
- Málek, J.; Mitsuhashi, T. Testing method for the Johnson-Mehl-Avrami equation in kinetic analysis of crystallization processes. J. Am. Ceram. Society 2004, 83, 2103–2105. [Google Scholar] [CrossRef]
- Lara, C.; Pascual, M.J.; Durán, A. Glass-forming ability, sinterability and thermal properties in the systems RO-BaO-SiO2 (R = Mg, Zn). J. Non Cryst. Solids 2004, 348, 149–155. [Google Scholar] [CrossRef]
- Hrubý, A. Evaluation of glass-forming tendency by means of DTA. Czechoslov. J. Phys. 1972, 22, 1187–1193. [Google Scholar] [CrossRef]
- Baino, F.; Ferraris, M.; Bretcanu, O.; Verné, E.; Vitale-Brovarone, C. Optimization of composition, structure and mechanical strength of bioactive 3-D glass-ceramic scaffolds for bone substitution. J. Biomater. Appl. 2013, 27, 872–890. [Google Scholar] [CrossRef]
- Massera, J.; Mayran, M.; Rocherullé, J.; Hupa, L. Crystallization behavior of phosphate glasses and its impact on the glasses’ bioactivity. J. Mater. Sci. 2015, 50, 3091–3102. [Google Scholar] [CrossRef]
- Gotor, F.J.; Criado, J.M.; Málek, J. Limitations of the Augis and Bennett Method for Kinetic Analysis of the Crystallization of Glasses and Conditions for Correct Use. J. Am. Ceram. Soc. 2001, 84, 1797–1802. [Google Scholar] [CrossRef]
- Joraid, A.A. Limitation of the Johnson–Mehl–Avrami (JMA) formula for kinetic analysis of the crystallization of a chalcogenide glass. Thermochim. Acta 2005, 436, 78–82. [Google Scholar] [CrossRef]
- Moharramand, A.H.; Rasheddy, M.S. A Simple Method for Crystallization Kinetics Determination and Its Application to Ge10Te35As55 Glass. Phys. Status Solidi (A) 1998, 169, 33–41. [Google Scholar] [CrossRef]
- Pǎcurariu, C.; Lazǎu, R.I.; Lazǎu, I.; Tiţa, D. Kinetics of non-isothermal crystallization of some glass-ceramics based on basalt. J. Therm. Anal. Calorim. 2007, 88, 647–652. [Google Scholar] [CrossRef]
- Ray, C.S.; Day, D.E. Identifying internal and surface crystallization by differential thermal analysis for the glass-to-crystal transformations. Thermochim. Acta 1996, 280–281, 163–174. [Google Scholar] [CrossRef]
- Agathopoulos, S.; Tulyaganov, D.U. Bioglasses and Glass-Ceramics in the Na2O-CaO-MgO-SiO2-P2O5-CaF2 System. In Bioceramics and Biocomposites: From Research to Clinical Practice; Wiley Online Library: Hoboken, NJ, USA, 2019; pp. 123–148. [Google Scholar] [CrossRef]
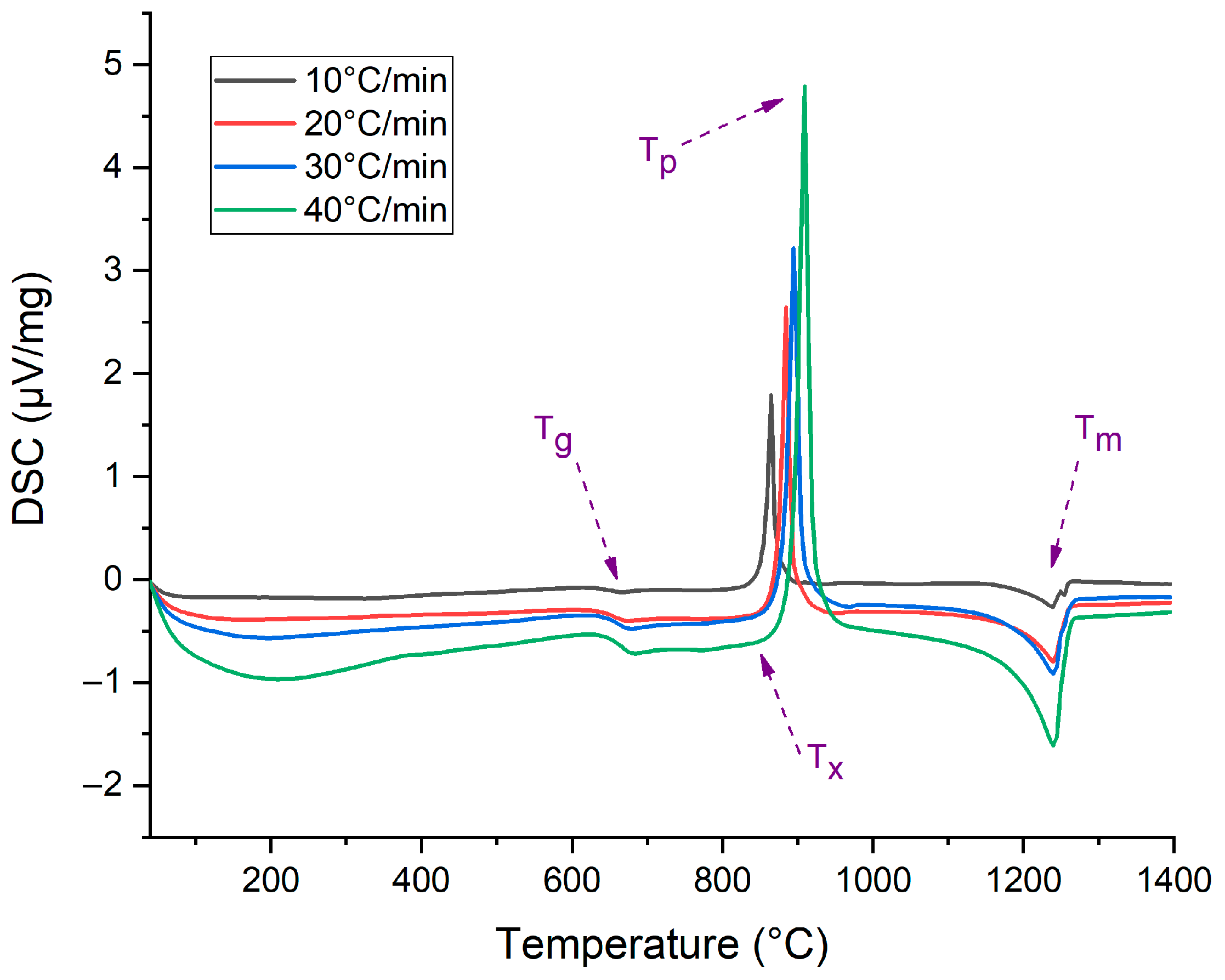

| β (°C/min) | Tg (°C) | Tx (°C) | Tp (°C) | Tm (°C) |
|---|---|---|---|---|
| 10 | 647.9 | 836.0 | 864.9 | 1238.8 |
| 20 | 658.0 | 853.0 | 884.9 | 1240.1 |
| 30 | 663.3 | 860.0 | 895.4 | 1240.1 |
| 40 | 666.6 | 865.0 | 909.4 | 1240.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigano, V.; Tulyaganov, D.U.; Dimitriadis, K.; Agathopoulos, S.; Baino, F. Thermal Analysis and Crystallization of Bioactive Glass “1d” in the SiO2-CaO-MgO-P2O5-CaF2-Na2O Compositional System. Ceramics 2025, 8, 145. https://doi.org/10.3390/ceramics8040145
Rigano V, Tulyaganov DU, Dimitriadis K, Agathopoulos S, Baino F. Thermal Analysis and Crystallization of Bioactive Glass “1d” in the SiO2-CaO-MgO-P2O5-CaF2-Na2O Compositional System. Ceramics. 2025; 8(4):145. https://doi.org/10.3390/ceramics8040145
Chicago/Turabian StyleRigano, Valentina, Dilshat U. Tulyaganov, Konstantinos Dimitriadis, Simeon Agathopoulos, and Francesco Baino. 2025. "Thermal Analysis and Crystallization of Bioactive Glass “1d” in the SiO2-CaO-MgO-P2O5-CaF2-Na2O Compositional System" Ceramics 8, no. 4: 145. https://doi.org/10.3390/ceramics8040145
APA StyleRigano, V., Tulyaganov, D. U., Dimitriadis, K., Agathopoulos, S., & Baino, F. (2025). Thermal Analysis and Crystallization of Bioactive Glass “1d” in the SiO2-CaO-MgO-P2O5-CaF2-Na2O Compositional System. Ceramics, 8(4), 145. https://doi.org/10.3390/ceramics8040145










