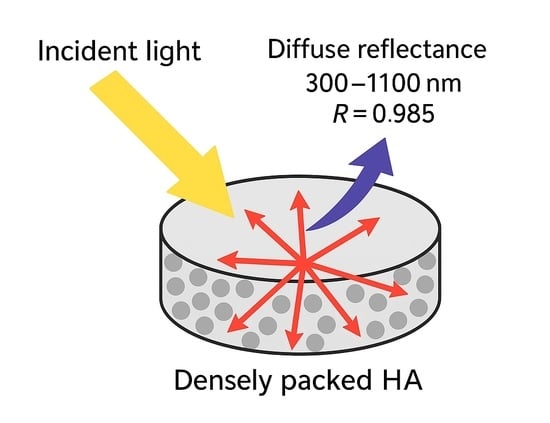
Light Transfer Properties of Densely Packed Hydroxyapatite Bioceramic Nanocrystallite Aggregates: Why Do These Substances Have an Extremely High Albedo?

Abstract

Radiation transfer in layers of densely packed aggregates of hydroxyapatite nanoparticles was studied for a spectral range from 300 to 1100 nm using diffuse reflectance measurements and the modeling of the light transfer properties of the layers. The studied samples of dispersed biogenic hydroxyapatite were obtained from animal bone material (bovine bones) using fast pyrolysis followed by grinding and pressing into tablets. A distinctive feature is the high reflectivity (high albedo) of the obtained samples, which is practically independent of the wavelength in the studied spectral range and comparable to the reflectivity of the diffuse reflectance standard based on Spectralon. The modeling of the light transfer properties of the studied samples within the framework of the effective medium theory (using coherent potential approximation) made it possible to establish the weak dependence of the mean scattering-free path and the mean transport-free path of light propagation in the medium on the wavelength, which is consistent with the features observed in the experiment. Possible prospects for the use of nanostructured hydroxyapatite as photonic material are discussed.

1. Introduction

Nowadays, the abundance of fundamental and applied works devoted to the study of various properties of hydroxyapatite (HA) and HA-based materials reflects the growing interest in various aspects of the application of these substances. HA is a natural mineral form of calcium apatite with the chemical composition of Ca₁₀(PO₄)₆(OH)₂. At present, the main HA applications are related to biomedicine due to its non-toxicity and biocompatibility; in addition, this material is hypoallergenic, insoluble in water, heat-resistant, and has the properties of isomorphic substitution and affinity adsorption. HA-based materials and products cover a wide range of practical applications in dentistry and implantology, traumatology and orthopedics, maxillofacial and ENT surgery, cosmetology, therapy, pharmacology, and hygiene [1,2]. Recent studies have shown possible prospects of applying HA nanoparticles as the material platform for drug and gene delivery, biovisualization, magnetic resonance applications, cell separation, and hyperthermia treatment [3,4,5].

The versatility of HA materials lies in the fact that, due to their modification, functionalization, and ion doping properties, they can be used not only in biomedicine but in other areas as well [6]. The structure of apatites allows for large variations in the composition specified by the general formula (M₁₀(XO₄)₆Z₂), including the partial or complete substitution of both cationic and anionic centers, the formation of non-stoichiometric forms, and solid solutions. The structure of apatite can include more than half of the elements existing in nature [7]. Studies of functionalized HA have shown the potential for its application as a promising heterogeneous catalyst [8,9,10,11] and photocatalyst [12] in the creation of energy storage/conversion elements, including supercapacitors, solar cells, fuel cells, etc. [13,14,15]. Nanocrystalline HA exhibits piezo-, pyro- and ferroelectric properties [16]. It has been shown that the isomorphic modification of calcium apatite by 3-d-metal atoms demonstrates a general tendency to decrease the bandgap with an increasing number of 3-d-metal atoms [17,18,19]. Recently, attention has been paid to HA of biogenic origin since the cost of its production is significantly lower than HA of synthetic origin, and the quality of the resulting material in a number of indicators, such as biocompatibility, is even higher [20].

Among the diverse physicochemical properties of bulk and nanostructured HA, optical properties may also be of particular interest for various applications. In particular, the use of Fe-doped HA as a promising material for sunscreen filters and screens was discussed in [21]. HA nanoparticles can be considered low-refractive-index additives for the formation of transparent polymer powder coatings [22]. The effects of nano-HA additives for the long-term UV protection of polyester composite materials under accelerated weathering conditions are demonstrated in this work. The electronic band structure and corresponding optoelectronic properties of HA were theoretically analyzed in [23] using the first-principles approach.

The use of dispersed multiple scattering systems based on nanostructured or microstructured HA is also of particular interest due to the relatively low refractive index of HA (around 1.64) compared to other widely used photonic materials based on wide-bandgap semiconductors and dielectrics. These materials are titanium dioxide with a refractive index varying between 2.87 and 2.47 in the spectral range from 400 nm to 1100 nm; zinc monoxide with $n=$ 2.105 at ${\lambda }_0=$ 450 nm and $n=$ 1.938 at ${\lambda }_0=$ 1125 nm; and sapphire with $n=$ 2.105 at ${\lambda }_0=$ 450 nm and $n=$ 1.938 at ${\lambda }_0=$ 1125 nm [24]. Low $n$ values of HA nano- and microparticles lead to the significantly higher sensitivity of the light transfer parameters of HA-based dispersed systems to changes in the refractive index of particle-containing matrix media compared to the above-mentioned materials. This opens the way, for example, to the synthesis of dispersed photonic systems with the possibility of external control of their scattering properties. The additional doping of particles to ensure selective absorption in certain spectral ranges may expand the functionality of such systems for optoelectronic and photonic applications.

The aim of this work was to conduct an experimental study and modeling of the features of radiation transfer in dispersed systems based on densely packed HA nanoparticles in the near UV, visible, and near IR ranges, leading, in particular, to their very high diffuse reflectivity in this spectral range.

2. Materials and Methods

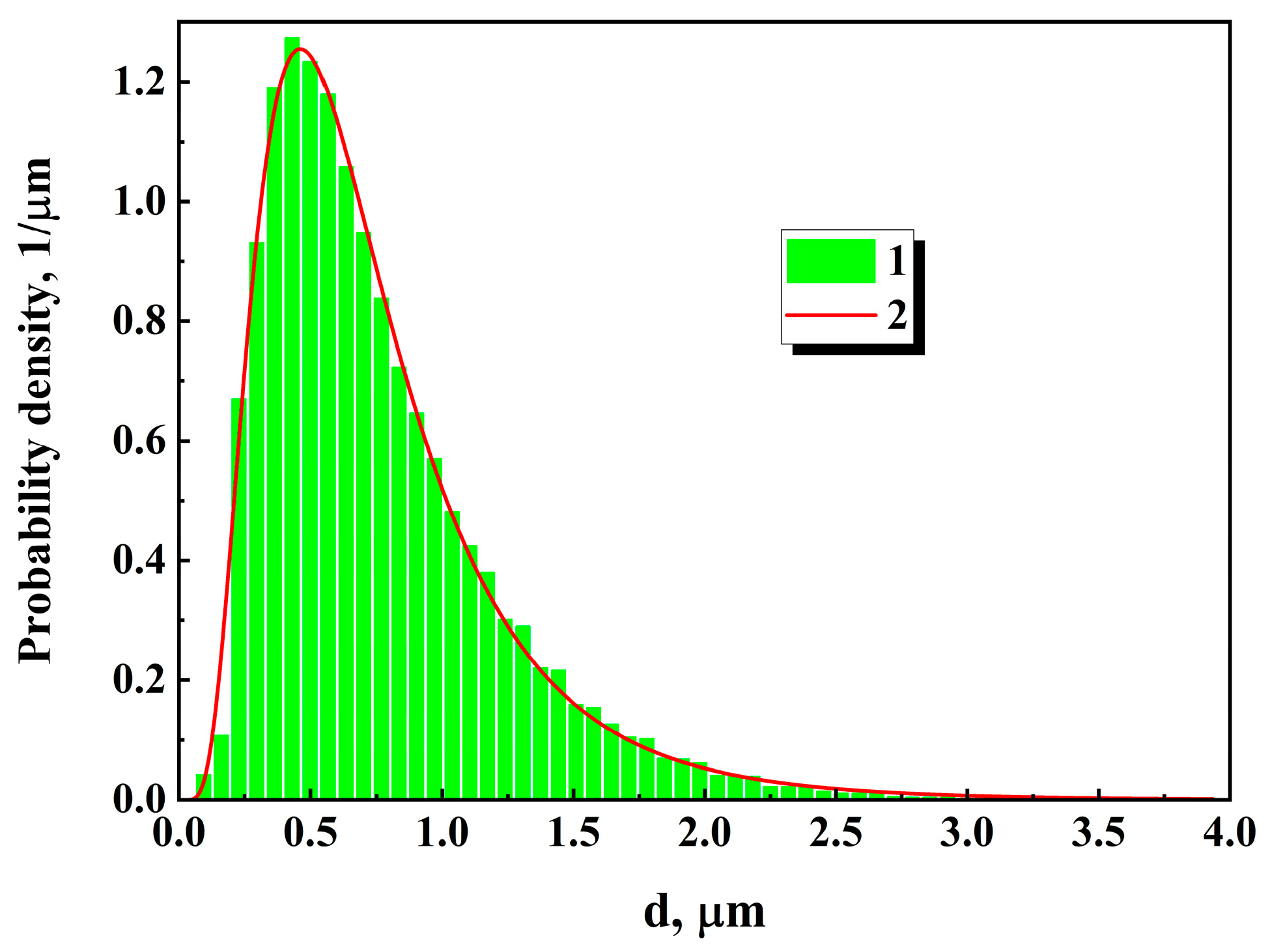
2.1. Synthesis and Characterization of HA Powders

Raw HA samples were obtained from bovine bones using a fast pyrolysis procedure. In this procedure, the bones were first defatted in boiling water and cleared of tendons and cartilage. At the next stage, the bones were crushed into 3–8 mm thick fragments and dried. The fast pyrolysis was carried out using a heat treatment of a certain amount (300 g) of the prepared bone fragments at the temperature of (850 ± 30) °C in a preheated muffle furnace. The treatment duration was equal to 30 min. This procedure ensured the thermal destruction of the organic components of the bone to a gaseous state and the removal of pyrolysis gas. In particular, preliminary experiments were carried out on pyrolysis in the temperature range from 600 °C to 1000 °C with a treatment time of 30 min, followed by an analysis of the chemical composition of the obtained samples (see below). It was established that only at the pyrolysis temperature of 600 °C was there a residual fraction of bioorganic components (approximately 4% by weight) in the obtained samples. At higher pyrolysis temperatures, starting from 700 °C, bioorganic residues were practically absent.

The released mineral part (HA) after the treatment did not change in shape and looked like a hard white substance without visually noticeable impurities. The provided X-ray phase analysis indicated correspondence between the X-ray data for the thermally treated bone fragments and well-established X-ray data for HA. In addition, the presence of spectral lines related to vibrations of phosphate, hydroxyl, and carbonate anion groups in the infrared spectra confirmed the chemical structure of HA for the obtained samples. The chemical composition of the obtained samples was analyzed using an Infralum FT-801 FTIR spectrometer (Lumex Instruments, St. Petersburg, Russia) and a Spectroscan Max-GV X-ray fluorescence spectrometer (Spectron LLC, St. Petersburg, Russia). It was found that the samples contained calcium in a mass fraction of about 37.9% (as Ca₁₀O₂H₂CO₃), phosphorus in a mass fraction of about 17.2% (as P₆O₂₄), silicon (about 0.1%, as SiO₂), and sulfur (about 0.1%, as SO₄). The mass fraction of other elements did not exceed 0.01%. Accordingly, it was concluded that the examined substance was hydroxyapatite Ca₁₀(PO₄)₆(CO₃OH)₂ containing a carbonate anionic group (approximately 2–4% by weight). Another conclusion formed was that the studied samples were completely inorganic without any residual bioorganic components or heavy metals.

For further study, the obtained samples of biogenic HA were ground to a powdered state using a specially designed laboratory prototype of a rotor-vortex disintegrator and separated using a sizing sieve with a minimum mesh of 40 µm. The particle size distribution in the obtained HA powder was analyzed using a laser diffractometer Analysette 22 (the product of FRITSCH GmbH—Milling and Sizing, (FRITSCH GmbH, Idar-Oberstein, Germany). After analyzing portions of the HA powders in accordance with procedures recommended by the producer of the Analysette 22 producer, the obtained raw data were further processed to quantify the particle size distribution and to compare it with probability distributions characteristic of various dispersive systems. Figure 1 shows the typical histogram of particle sizes for the examined system together with the approximating lognormal distribution.

$$\rho \left(d\right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma d}}\cdot \exp \left\{-{\displaystyle \frac{{\left\{\ln \left(d/\tilde{d}\right)\right\}}^2}{2{\sigma }^2}}\right\}$$

(1)

The following fitting parameters were used: $\sigma =$ 0.5812 ± 0.045 and $\tilde{d}=$ (0.6478 ± 0.0035) µm. The near-to-perfect agreement between the empirical particle size distribution and the model lognormal distribution is obvious; it can be mentioned that a variety of evolving dispersive systems consisting of small particles, which tend to aggregate, often exhibit close-to-lognormal distributions of particle sizes at the intermediate or final stage of their evolution (see, e.g., [25]). Using the fitting lognormal distribution, the modal ($d_{\mathrm{mod}}$) and average ($〈d〉$) particle sizes in the synthesized HA powders can be evaluated as $d_{\mathrm{mod}}=\tilde{d}/\exp \left({\sigma }^2\right)\approx$ 0.462 µm and $〈d〉=\tilde{d}\cdot \exp \left({\sigma }^2/2\right)\approx$ 0.668 µm.

The powder samples were also analyzed using scanning (SEM) and transmission (TEM) electron microscopy. In the case of TEM analysis, the samples were dispersed in alcohol using an ultrasonic bath; after this, the particle suspensions were applied to a porous carbon film, dried, and examined. The morphology of the particle aggregates was studied using a scanning electron microscope at an accelerating voltage of 20–30 kV. Figure 2 represents the typical TEM (Figure 2a) and SEM (Figure 2b) images obtained at various magnifications. Analysis of the obtained TEM and SEM images allowed us to conclude that the basic structural units of the obtained samples are flat, hexagonal HA nanocrystallites with characteristic dimensions of about 50–100 nm (Figure 2a). During powder processing, they combine into larger particles with submicron and micron sizes (Figure 2b) with the size distribution presented in Figure 1.

The prepared powder samples were pressed into round tablets with a diameter of 13 mm and a thickness $L$ of (3 ± 0.2) mm for further measurements of their reflectivity in the near IR, visible, and near UV ranges (from 300 nm to 1100 nm). Pressing was carried out using a specially designed laboratory press at a compacting pressure of 6.0 × 10⁵ Pa; the mechanical properties of the obtained tablets (no shedding, resistance to fracture, etc.) allowed for multiple spectral tests to be carried out while maintaining care in handling and storage. The reported density of monolithic HA samples was at around 3.14 g/cm³ (see, e.g., [26]), while the bulk density of the prepared powder samples was about (0.80 ± 0.04) g/cm³. After pressing, the bulk density of the obtained tablets was equal to (2.02 ± 0.09) g/cm³. Thus, the prepared tablets were characterized by high values of the volume fraction of the HA component (around 0.64); this value is close to the theoretical limit of the volume fraction in the case of the face-centered cubic (FCC) packing of equal-sized hard spheres (≈0.74). Accordingly, we can expect that pressing would cause remarkable changes in the size distribution of HA particles compared to that presented in Figure 3; in particular, a shift in $d_{\mathrm{mod}}$ and $〈d〉$ to lower values was expected.

One of the key factors when considering the scattering and absorption properties of various materials is their wavelength dependences of refractive ($n\left({\lambda }_0\right)$) and absorption ($k\left({\lambda }_0\right)$) indices (here, ${\lambda }_0$ denotes the wavelength value in free space). In the literature, the values of $n$ for HA are usually given at around 1.6 for the visible, near IR, and near UV regions (see, e.g., [22]). The absorption index for this spectral range was taken to be 0, except for wavelengths shorter than 300 nm. In this work, the model values of $n\left({\lambda }_0\right)$ and $k\left({\lambda }_0\right)$ were used in calculations of the light transport properties of the layered HA particles. These model values were recovered from the reported theoretical data on the behavior of the dielectric function $\epsilon \left(E_{ph}\right)={\epsilon }^{\prime }\left(E_{ph}\right)+{\epsilon }^{″}\left(E_{ph}\right)$ of bulk HA depending on the photon energy $E_{ph}$ [23]. In [23], the functions ${\epsilon }^{\prime }\left(E_{ph}\right)$ and ${\epsilon }^{″}\left(E_{ph}\right)$ were theoretically obtained on the basis of the density hybrid-functional theory and many-body perturbation theory. The indices $n\left({\lambda }_0\right)$ and $k\left({\lambda }_0\right)$ were recovered from the dataset (${\epsilon }^{\prime }\left(E_{ph}\right)$,${\epsilon }^{″}\left(E_{ph}\right)$) presented in [23] using the following formulae (see, e.g., [27]):

$$\begin{array}{l}n\left({\lambda }_0\right)=\sqrt{{\displaystyle \frac{\sqrt{{\left[{\epsilon }^{\prime }\left(E_{ph}\right)\right]}^2+{\left[{\epsilon }^{″}\left(E_{ph}\right)\right]}^2}+{\left[{\epsilon }^{″}\left(E_{ph}\right)\right]}^2}{2}}};\\ k\left({\lambda }_0\right)=\sqrt{{\displaystyle \frac{\sqrt{{\left[{\epsilon }^{\prime }\left(E_{ph}\right)\right]}^2+{\left[{\epsilon }^{″}\left(E_{ph}\right)\right]}^2}-{\left[{\epsilon }^{″}\left(E_{ph}\right)\right]}^2}{2}}},\\ {\lambda }_0\left[\mathrm{nm}\right]\approx 1239/E_{ph}\left[\mathrm{eV}\right].\end{array}$$

(2)

Figure 3 displays the recovered dependence $n\left({\lambda }_0\right)$ for the spectral region of interest; the recovered absorption index $k\left({\lambda }_0\right)$ is equal to zero up to the edge of the fundamental absorption band at $E_{ph}$ ≈ 5.2 eV (${\lambda }_0$ ≈ 238 nm). The expressed dispersion of $n\left({\lambda }_0\right)$ in the spectral range from 200 nm to 500 nm should be mentioned; this feature is typical for dielectrics and wide-bandgap semiconductors near the fundamental absorption band.

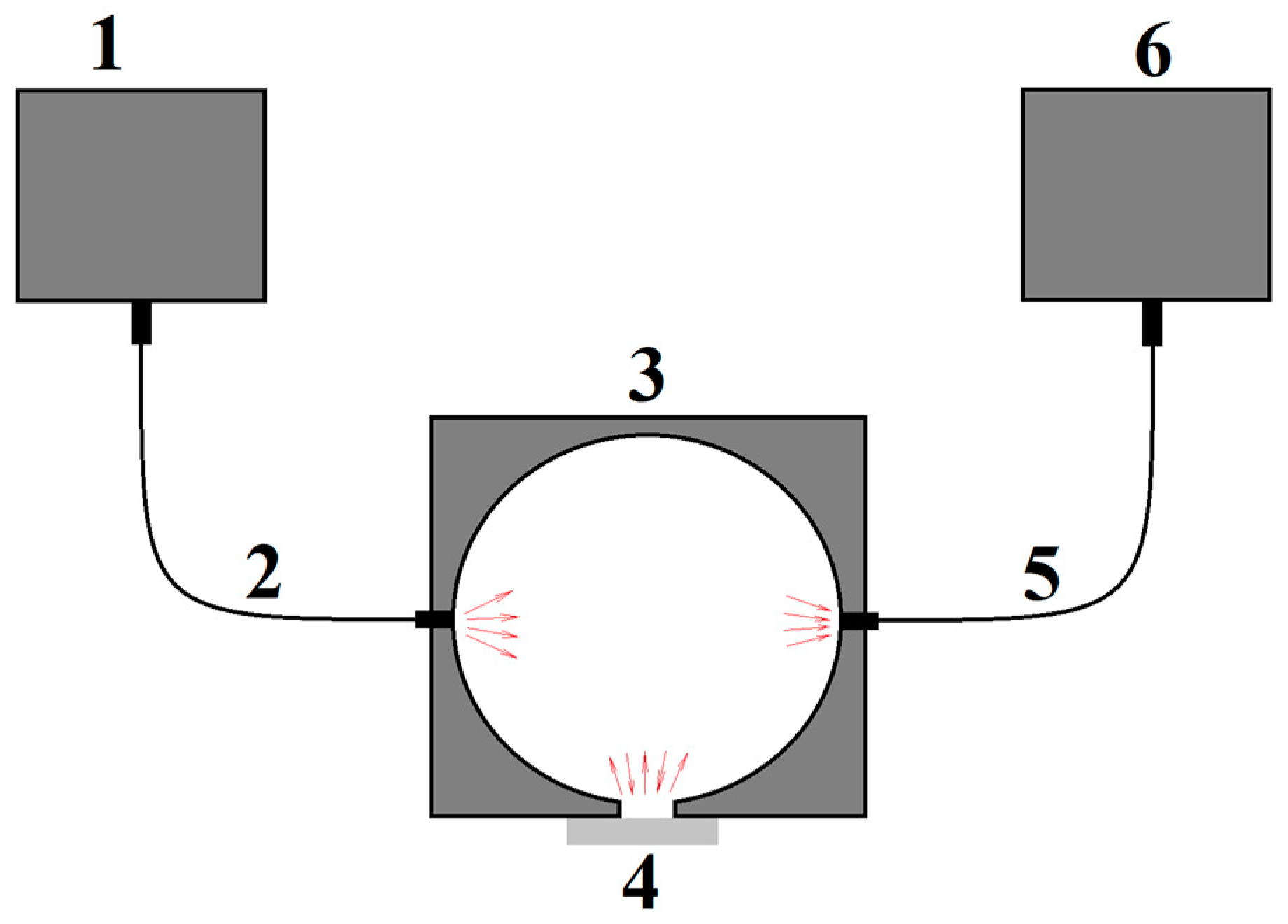
2.2. Diffuse Reflectance Spectroscopy of the Prepared Samples

Figure 4 displays the schematic of the experimental setup used to acquire the diffuse reflectance spectra $R_d\left({\lambda }_0\right)$ of the pressed samples of HA powders in the wavelength range from 300 nm to 1100 nm. Acquisition of the spectra was provided using wide-band illumination source 1, integrating sphere 3 for the diffuse illumination of the samples and collection of backscattered light, and spectrometer 6. All the units were connected with each other by fiber-optic patchcords 2 and 5 (the P200-2-UV-VIS type from the Ocean Optics Co., Orlando, FL, USA). The switchable halogen–deuterium light-emitting unit (type DH-2000-BAL, the product of the Ocean Optics Co.) was applied as unit 1; the diffuse transmittance spectra were recorded using the USB-spectrometer QE65000 (Ocean Optics, Orlando, FL, USA). The four-port integrating sphere (IS236A-4, the product of Thorlabs Co., NJ, USA) was used as unit 3.

During the experiment, multiple spectral runs (five times) were performed for each of the five samples obtained under the same conditions. Before the collection of the spectral data from the pressed HA samples, the spectra-acquiring system presented in Figure 4 was calibrated using the WS-1-SL white reflectance standard (Ocean Optics, Orlando, FL, USA). Diffuse reflectance spectra of the WS-1-SL standard were also acquired 5 times. The collected set of spectral data was preprocessed using smoothing in the spectral domain and averaging of the smoothed spectra (over 25 outputs were run for the HA samples, and 5 outputs were run for the standard). The smoothing in the spectral domain was carried out by applying an adjacent averaging procedure with a 21-point running window, which was provided using OriginPro 2021 software. This preprocessing procedure allowed us to decrease the level of spectral noise significantly. The preprocessed data were further used to recover the wavelength-dependent diffuse reflection coefficient $R_d\left({\lambda }_0\right)$ of the pressed HA samples in relation to the WS-1-SL standard (see Section 3.1).

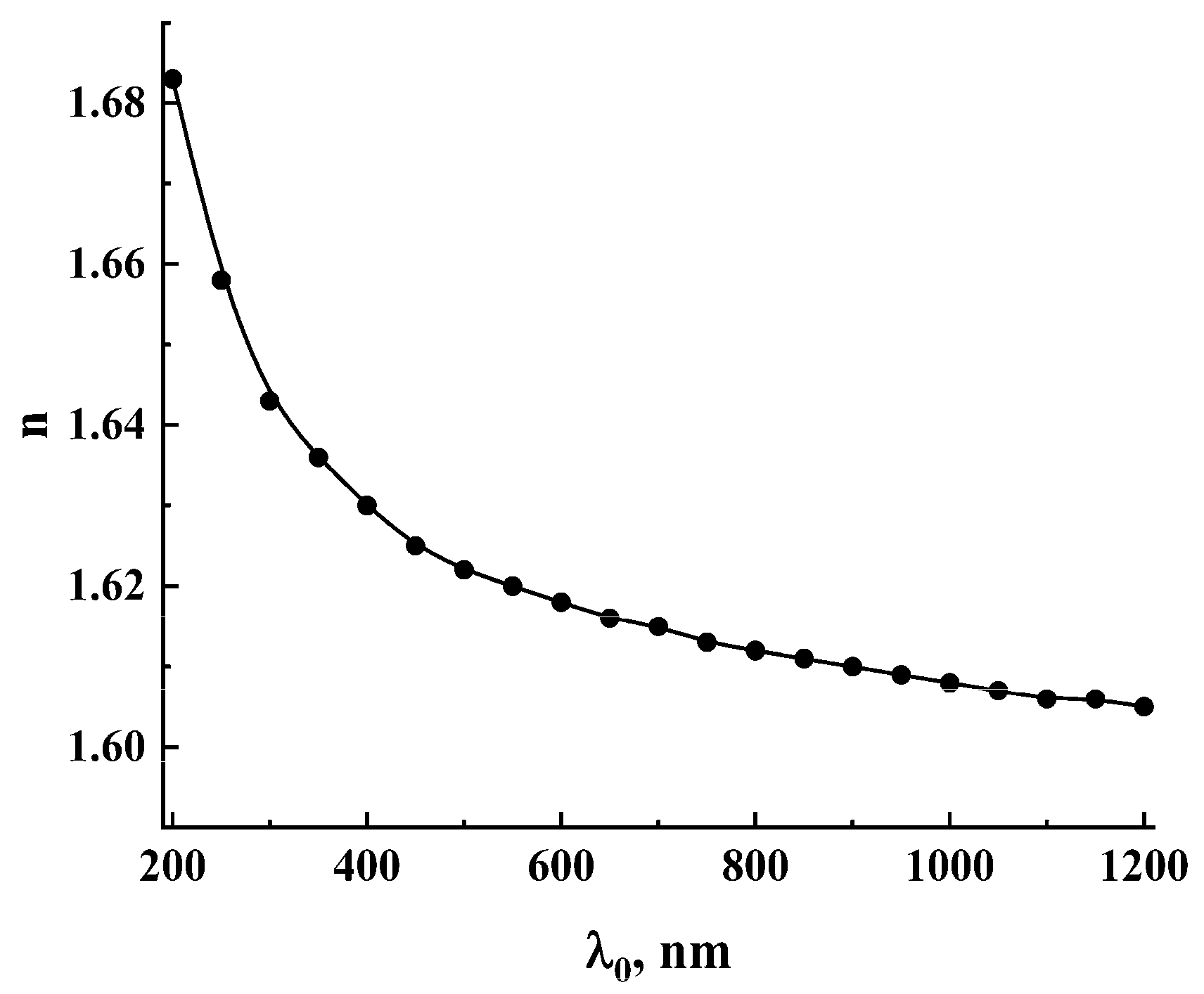
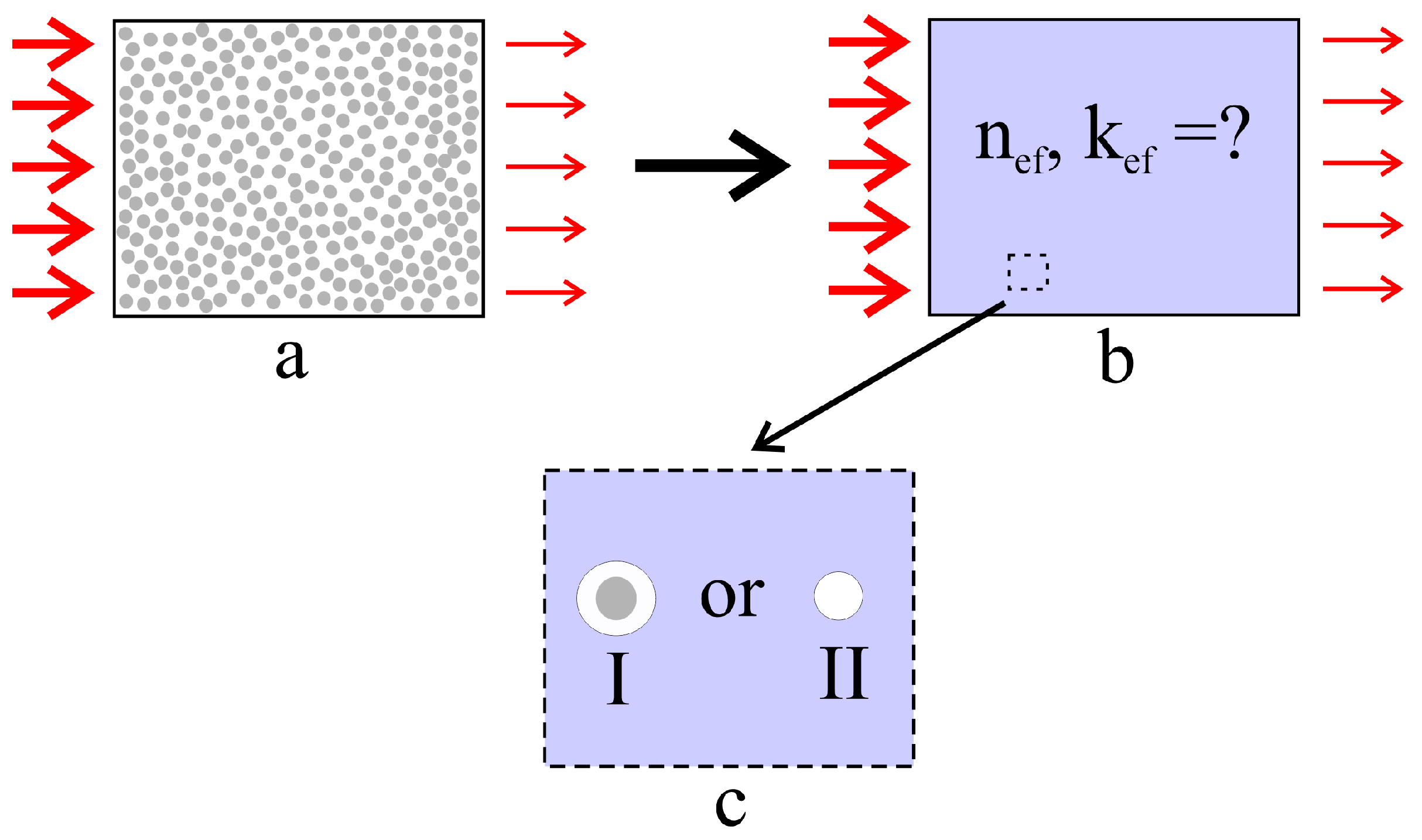
2.3. Modeling of the Light Transfer Properties of HA Layers Using an Effective Medium Approach

The observed high reflectivity of layers of close-packed HA particles can be considered in terms of the radiative transfer theory (RTT), taking into account the influence of the structural characteristics of the examined materials on their light transfer properties. In the RTT framework (see, e.g., [28]), the radiation transfer in random media is controlled by the following set of characteristic spatial scales, which are the reciprocals of the scattering (${\mu }_s$) and absorption (${\mu }_a$) coefficients: $l=1/{\mu }_s$ (the mean scattering-free path, SMFP) and $l_a=1/{\mu }_a$ (the absorption length). In the case of random media with pronounced anisotropic scattering at the microscopic level (i.e., consisting of large particles), an additional characteristic scale named the mean transport-free path (TMFP, $l^{*}$) was introduced. The physical meaning of $l$ and $l^{*}$ can be considered in terms of the discrete scattering model describing the formation of a multiple scattered light field in random media as a result of the superposition of partial light waves undergoing random sequences of scattering events due to interactions with scattering particles in the medium. In this case, the SMFP value is interpreted as the ensemble-averaged propagation path passed by a partial wave between two sequential scattering events. The propagation path, in which information about the initial direction of the light wave is completely lost, determines the mean transport-free path (in other words, the characteristic scale of transformation of a directed light beam into diffuse radiation). The $l^{*}$ value relates to $l$ as $l^{*}=l/\left(1-g\right)$, where $g=〈\cos \theta 〉$ is the scattering anisotropy factor or the average cosine of the scattering angle in a single scattering event [28]. In the so-called Mie scattering mode, $g$ approaches 1 and l* >> l; on the contrary, the Rayleigh scattering mode specific for random ensembles of small-sized particles is characterized by $g\approx$0 and $l^{*}\approx l$. Typically, the “conventional” randomly structured scattering systems are characterized by non-negative values of $g$: 0 $\le g\le$ 1. At the same time, some systems with a particular order of the scatter arrangement [29] or consisting of highly absorbing particles with $k>n$ exhibit negative values of the scattering anisotropy factor (i.e., dominating backscattering).

Figure 5 presents a qualitative interpretation of the diffuse reflection of radiation by a layer of a random non-absorbing medium illuminated by diffusely scattered light (these conditions correspond to those used in the experiment; see Figure 4). Diffusing waves propagate in the layer due to random sequences of scattering events, after which they leave the layer. In this geometry, the probe radiation penetrates into the layer to a certain depth $z_{pen}$, proportional to $l^{*}$. If $z_{pen}$ is less than the layer thickness $L$, then the diffuse reflection coefficient $R_d$ turns out to be significantly less than 1 due to the outflow of part of the diffusing waves through the lower boundary of the layer. In the case $z_{pen}\ll L$, $R_d$ approaches 1.

The relationship between $l,l^{*}$ and structural (the average size $〈d〉$ and shape of scattering sites and their volume fraction $f_p$ in the system) and optical properties (the refractive indices of scattering sites $n_p$ and matrix medium $n_m$) for a given wavelength ${\lambda }_0$ of propagating radiation is very ambiguous. Accordingly, it is strongly governed by a set of factors (primarily, the volume fraction $f_p$ of the scattering component and the ratio between $〈d〉$ and ${\lambda }_0$). In particular, this ambiguity manifests itself in the difficulty of classifying a scattering system for the $f_p$ values around 0.5: determining whether the scattering system is an ensemble of scattering particles of type 1 in a matrix medium of type 2 or a matrix medium of type 1 with inclusions of type 2. In the case of significantly different scattering efficiencies for type 1/type 2 and type 2/type 1 combinations, the scattering systems differ radically in their values of optical transport parameters and their behavior with changes in the structural characteristics and wavelength of the probing radiation. A gradual increase in the volume fraction of inclusions in the matrix medium will probably lead to a switch in the scattering mechanism at a certain value of $f_p$, which can be interpreted as an optical immersion effect. This behavior was observed, in particular, in layers of densely packed anatase nanoparticles with increasing packing density [30] and in foamed liquids during their transition to a dry foam state [31]. It should be noted that the examined layers of close-packed HA particles with a volume fraction of HA of about 0.6 can also cause ambiguity in interpretation: should they be considered as ensembles of HA particles in an air matrix or as ensembles of air inclusions in an HA matrix.

The key principle (Figure 6) of effective medium models applied for calculations of optical transport parameters $l$ and $l^{*}$ of spatially heterogeneous random media (Figure 6a) consists of considering a spatially homogeneous effective medium with a complex refractive index (Figure 6b) instead of a modeled spatially inhomogeneous non-absorbing medium. Accordingly, the refractive index $n_{ef}$ and absorption index $k_{ef}$ of the model’s effective medium are tuned in the modeling process in such a way as to minimize the effect of replacing the local volume of the effective medium with a probe local volume simulating a fragment of the real medium. Various criteria for minimizing the influence of such a replacement can be considered, which can be reduced, for example, to find $n_{ef,\min }$ and $k_{ef,\min }$ values corresponding to the minimum (ideally zero) value of the extinction of the cross-section of the probe volume in the effective medium. In addition, another criterion can be based on the minimal value of the forward scattering amplitude or the minimal difference between the average electromagnetic energy density inside and outside the probe volume, etc. After finishing the minimization procedure, the effective refractive index of the modeled spatially heterogeneous medium is established equal to $n_{ef,\min }$, and the SMFP value is calculated as $l=\lambda /2\pi k_{ef,\min }$ (this relation directly follows on from the similarity of the effects of absorption and extinction during electromagnetic wave propagation postulated in the effective medium models).

The scattering properties of layers of close-packed HA particles were modeled using a version of the effective medium model known as the coated coherent potential approximation (CCPA) and implemented by C. Soukoulis et al. [32,33,34]. In the framework of the CCPA approach, two types of model probe objects embedded in a spatially homogeneous effective medium with attenuation were considered (Figure 6c). The first of them was a dielectric sphere with a refractive index of $n_p$, which is surrounded by a coating with a refractive index of $n_m$. The second type is a homogeneous sphere with the refractive index of $n_m$. Here, $n_p$ and $n_m$ are the refractive indices of scattering sites and a matrix medium in a real scattering system. The geometric parameters of the probe units (the radius $R_c$ of the core and the thickness $h_c$ of the coating in the first type object and the radius $R_{II}$ of the second type object) are evaluated from the structural properties (the average volume $V$ of scattering sites and their volume fraction $f_p$) of the real scattering system. In particular, the radii of the coated sphere $R_I=R_c+h_c$ and the second-type sphere are evaluated as follows:

$$\begin{array}{l}{R}_I=z\cdot \sqrt[3]{{\displaystyle \frac{3V}{4\pi \left[f\left(z^3-1\right)-1\right]}}};\\ R_{II}=z\cdot \sqrt[3]{{\displaystyle \frac{3V\left[1-f\left(V_I/V\right)\right]}{4\pi }}},\end{array}$$

(3)

where $V_I$ is the volume of the first-type probe unit and $z$ is the specially introduced correction parameter approximately equal to 1.65. In accordance with [32], this value ensures the physical validity of the CCPA model in a wide interval of ${\lambda }_0$ and in a wide range of $f_p$ values, beginning from the weak scattering limit $\left(f_p\to 0\right)$ and ending in the case of the dense face-centered cubic (FCC) packing of equal-sized hard spheres ($f_p\approx$ 0.74).

In terms of this approach, the following functional is set to zero by finding the values of the refraction ($n_{ef}$) and absorption ($k_{ef}$) indices of the model effective medium:

$$f\left(\mathrm{0,0}\right)=p_I{f}_I\left(\mathrm{0,0}\right)+p_{II}{f}_{II}\left(\mathrm{0,0}\right)=0$$

(4)

where $f_I(0,0)$ and $f_{II}(0,0)$ are the forward scattering amplitudes for the first- and second-type probe scatters embedded in the effective medium and illuminated by a plane electromagnetic wave with a wavelength of ${\lambda }_0$. Accordingly, $p_I$ and $p_{II}$ define the probabilities of finding the first- and second-type probe scatterers under the condition of a random choice. These probabilities are related to the volumes of the real scattering site $V$, the first-type probe scatter $V_I$, and second-type probe scatter $V_{II}$ as follows:

$${\displaystyle \frac{p_{II}}{p_I}}={\displaystyle \frac{V-f{V}_{II}}{f{V}_I}}$$

(5)

using the obvious normalization condition: $p_I+p_{II}=1$. The forward scattering amplitudes $f_I(0,0)$ and $f_{II}(0,0)$ for the coated and homogeneous probe scatters are calculated in the framework of the Mie scattering theory as the sums of the scattering series coefficients $a_l,b_l$:

$$f_{I,II}\left(0,0\right)={\displaystyle \frac{i}{2q}}{\displaystyle \sum _{l=1}^{l_{\max }}\left(2l+1\right)\left(a_l^{I,II}+b_l^{I,II}\right)}$$

(6)

Here $q$ is the complex propagation constant in the effective medium defined as follows:

$$q={\displaystyle \frac{2\pi }{{\lambda }_0}}{\left({\epsilon }_{ef}\right)}^{0.5}={\displaystyle \frac{2\pi n_{ef}}{{\lambda }_0}}+{\displaystyle \frac{i}{2l}}$$

(7)

and the upper limit $l_{\max }$ of summation is determined by the rate of convergence of the $a_l,b_l$ coefficients to 0. The procedure of calculating $a_l^{I,II}$ and $b_l^{I,II}$ for the coated and homogeneous spherical scatters in the framework of Mie theory is described in detail in [27].

The CCPA technique has been repeatedly verified numerically and experimentally for multiple scattering media with various structural and dielectric properties (see, e.g., [30,32,33,34]). In this study, the coated CPA approach was applied to analyze the effect of the high reflectivity of densely packed HA particles in terms of the weak dependence of their scattering coefficient, which reflects the reciprocal of the scattering coefficient on the wavelength under the condition of weak absorbance of probe radiation in the examined systems. In contrast to the computational approach previously used by C. Soukoulis and co-workers [32], which was based on the numerical solution of Equation (1) for the complex function $f(0,0)$, we applied the procedure of minimizing the goal function equal to the absolute value $\left|f(0,0)\right|$.

As an example, Figure 7 displays the typical model distributions of the goal function $\left|f(0,0)\right|$ on the ($n_{ef},k_{ef}$) coordinate plane for the scattering systems imitating various HA-based dispersive systems ($n_p$ is around 1.6; see Figure 3; $n_m=$ 1.0) with various values of $R_c$ at various wavelengths ${\lambda }_0$. The $n_{ef\min },k_{ef\min }$ values corresponding to the $\left|f(0,0)\right|$ minima are marked with white dotted lines. The expected tendency for $n_{ef\min }$ and $k_{ef\min }$ to increase (that is, for the phase velocity of light $c/n_{ef,\min }$ in the system and the SMFP value to decrease) with the increasing ratio $R_c/{\lambda }_0$ is obvious.

In the course of modeling, the positions of $\left|f(0,0)\right|$ minima on the $n_{ef},k_{ef}$ coordinate plane for the HA-associated scattering systems were found using Broyden’s method [35] with an accuracy of ±0.0005 for $n_{ef,\min }$ and $k_{ef,\min }$. After this, the SMFP value $l$ for a given scattering system at a given wavelength ${\lambda }_0$ was evaluated as $l\approx {\lambda }_0/2\pi k_{ef,\min }$; the found value of $n_{ef,\min }$ determined the phase velocity of light in the medium at ${\lambda }_0$. Note that the distribution of $\left|f(0,0)\right|$ for large scatter particles (Figure 7b), in addition to the minimum at $n_{ef,\min }$ ≈ 1.491, $k_{ef,\min }$ ≈ 0.0594 marked by dotted lines, is characterized by the occurrence of two more local minima of $\left|f(0,0)\right|$ at the points with coordinates $n_{ef}$ ≈ 1.072, $k_{ef}$ ≈ 0.0566, and $n_{ef}$ ≈ 1.92, $k_{ef}$ ≈ 0.0889. However, these additional local minima are significantly less deep than the marked minimum. Moreover, the values of the effective refractive index of the model medium corresponding to these side minima are completely and physically unrealistic for the analyzed multiple scattering systems.

The CCPA approach can also be applied to estimate the mean transport-free path $l^{*}$ of radiation propagation in random media with a high-volume fraction $f_p$ of scattering particles [33]. The procedure is generally similar to the above-described procedure for determining $n_{ef}$ and $k_{ef}$; however, the minimized goal function is the difference between the extinction cross-section ${\sigma }_{ext}$ and the asymmetry cross-section ${\sigma }_{as}$ [27] of the probe scatters in the simulated effective medium:

$$f_{tr}\left(k^{\prime }\right)=p_I\left[{\sigma }_{ext,I}\left(k^{\prime }\right)-{\sigma }_{ass,I}\left(k^{\prime }\right)\right]+p_{II}\left[{\sigma }_{ext,II}\left(k^{\prime }\right)-{\sigma }_{ass,II}\left(k^{\prime }\right)\right]$$

(8)

The parameters introduced in this case are the real part $n_{ef}$ of the effective refractive index found at the first stage of modeling, the refractive indices of the scatterers and the matrix medium, the average radius and volume fraction of the scatterers in the real system, and the radiation wavelength. The variable parameter when minimizing the absolute value of $f_{tr}\left(k^{\prime }\right)$ is the new value of the absorption index $k^{\prime }$ of the effective medium. The TMFP value is determined as $l^{*}={\lambda }_0/2\pi {k^{\prime }}_{\min }$, where ${k^{\prime }}_{\min }$ corresponds to the minimum of $\left|f_{tr}\left(k^{\prime }\right)\right|$.

3. Results

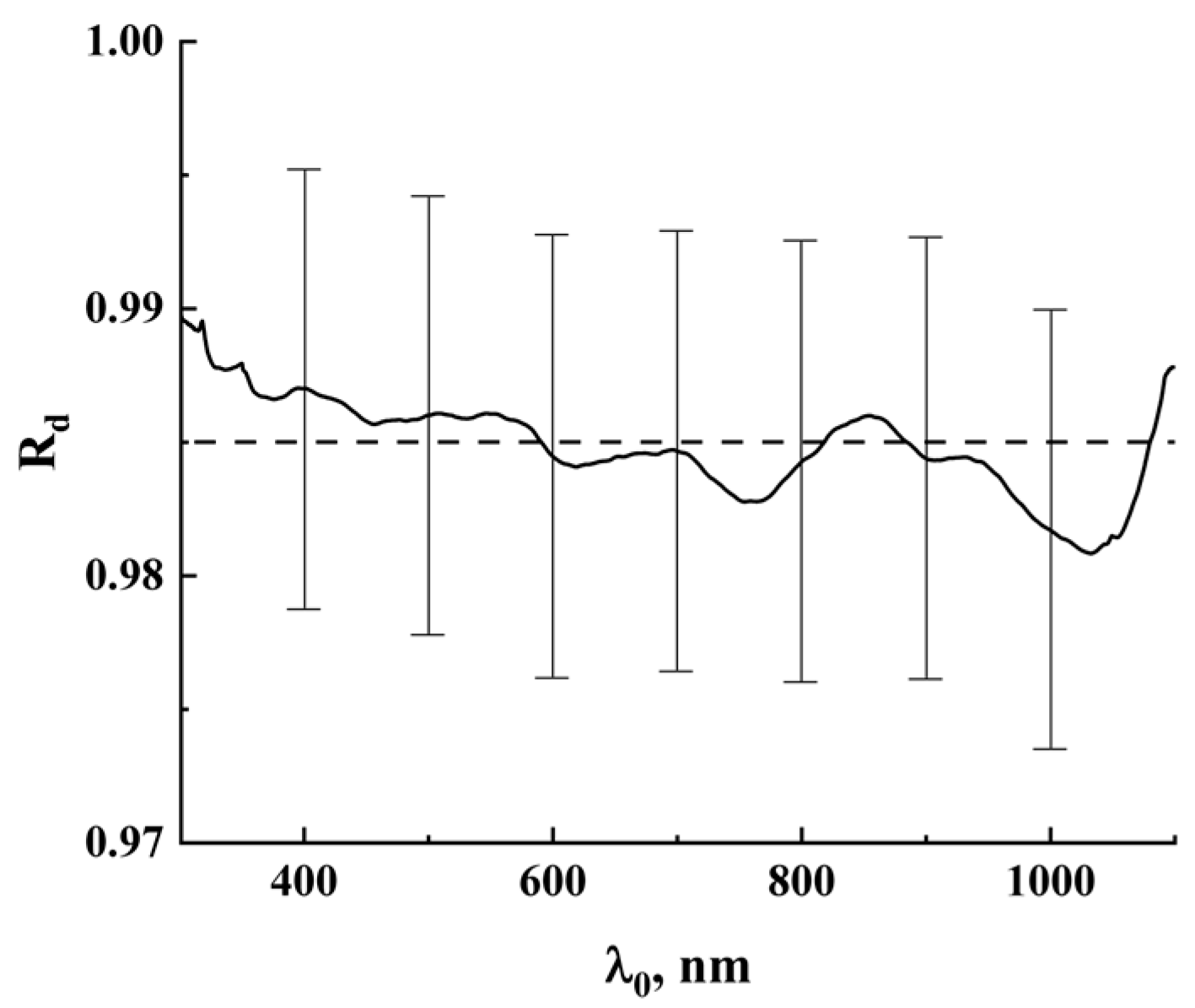
3.1. Diffuse Reflectivity of HA Layers in near UV, Visible, and near IR Ranges

Figure 8 displays the obtained diffuse reflectance spectrum $R_d\left({\lambda }_0\right)$ for the examined layers of densely packed HA particles in the spectrum range from 300 nm to 1100 nm. It was obtained in relation to the reflectivity of the diffuse reflectance standard WS-1-SL after the above-described preprocessing procedure (see Section 2.2). The error bars displayed correspond to the significance level of 0.95 and rather indicate the influence of random instrumental and preprocessing errors. It should be noted that the distribution of $R_d$ values was highly homogeneous over the spectral range examined. In particular, there was a slight trend towards an increase in $R_d$ in the short-wave region; however, the order of difference between the $R_d$ values at 1100 nm and 300 nm was small (≈0.005) and significantly less than the $R_d$ value averaged over the examined spectral range ($\overline{R_d}\approx$ 0.985, marked by a dashed line in Figure 8). This spectral homogeneity, in combination with large values of reflectivity, allows for the interpretation of the examined HA layers as a substance with very high albedo. Below 300 nm, a decrease in $R_d$ for the systems examined was expected due to the inter-band transition in HA [23].

Considering the so-called Kubelka–Munk function $F\left({\lambda }_0\right)={\left[1-R_d\left({\lambda }_0\right)\right]}^2/2R_d\left({\lambda }_0\right)$ (see, e.g., [36]), we can postulate its weak dependence on ${\lambda }_0$ and the small value of the order of 1 × 10⁻⁴ in the examined spectral range. Taking into account the fact that $F\left(\lambda \right)\propto K\left(\lambda \right)/S\left(\lambda \right)$, where $K\left(\lambda \right)$ and $S\left(\lambda \right)$ are the phenomenological dimensionless coefficients characterizing absorption and scattering losses in the two-flux consideration of the radiation transfer in multiple scattering systems, it can be concluded that a strong dominance of $S\left(\lambda \right)$ was found compared to $K\left(\lambda \right)$ in the range from 300 nm to 1100 nm. The coefficients $K\left(\lambda \right)$ and $S\left(\lambda \right)$ can be considered in terms of the characteristic scales of scattering and absorption of the diffusing light in the random media (i.e., the values of $l$ and $l_a$); in particular, the similar approach taken in the analysis of the Kubelka–Munk two-flux model was discussed in [37]. Taking into account the fact that the $l$ value must be replaced by $l^{*}$ in consideration of diffusing light transfer in random media with anisotropic scattering $\left(l^{*}>l\right)$, we arrived at the following relationship: l << l*.

The relationship between the characteristic value of $l^{*}$ and the geometric thickness $L$ of the examined samples, which leads to their high reflectivity, can also be considered in terms of the diffusion approximation. For layers of non-absorbing random media, the diffuse transfer of radiation is characterized by the following obvious relationship between the coefficients of diffuse reflection $R_d$ and the transmission $T_d$ of the layer: $R_d+T_d=1$. Thus, the following relationship holds: $T_d\le$ 0.015. On the other hand, the value of $T_d$ in the diffusion mode can be expressed as follows (see, e.g., [38]):

$$T_d\approx {\displaystyle \frac{\left(1+Z_1\right)l^{*}}{L+\left(Z_1+Z_2\right)l^{*}}}$$

(9)

where $Z_1$, $Z_2$ are the normalized values of the extrapolation length for the top and bottom boundaries of the layer depending on the reflectivity of the boundaries. In the case of air–layer interfaces $Z_1=Z_2=Z\approx 2\left(1+R_b\right)/3\left(1-R_b\right)$, where $R_b$ is the interface reflectivity. Assuming that the effective refractive index of the examined layers is close to 1.5 in the visible region and using the dependence of $R_b$ on the ratio of the reflective indices of a scattering medium and the surrounding space presented in [39], we can roughly estimate $R_b$ as ≈0.6. Accordingly, the value of $Z$ can be estimated as ≈2.67. With this value and $T_d\le$ 0.015, the ratio of the TMFP value to the geometric thickness of the sample can be presented as $l^{*}/L\le$ 5.6 × 10⁻³. With $L\approx$ 3.0 mm, the upper estimate of the TMFP value for the examined samples study is about 13 µm; this estimate is compared to the results of the CCPA modeling of light transfer parameters for the HA-based dense systems presented in the following Section 3.2.

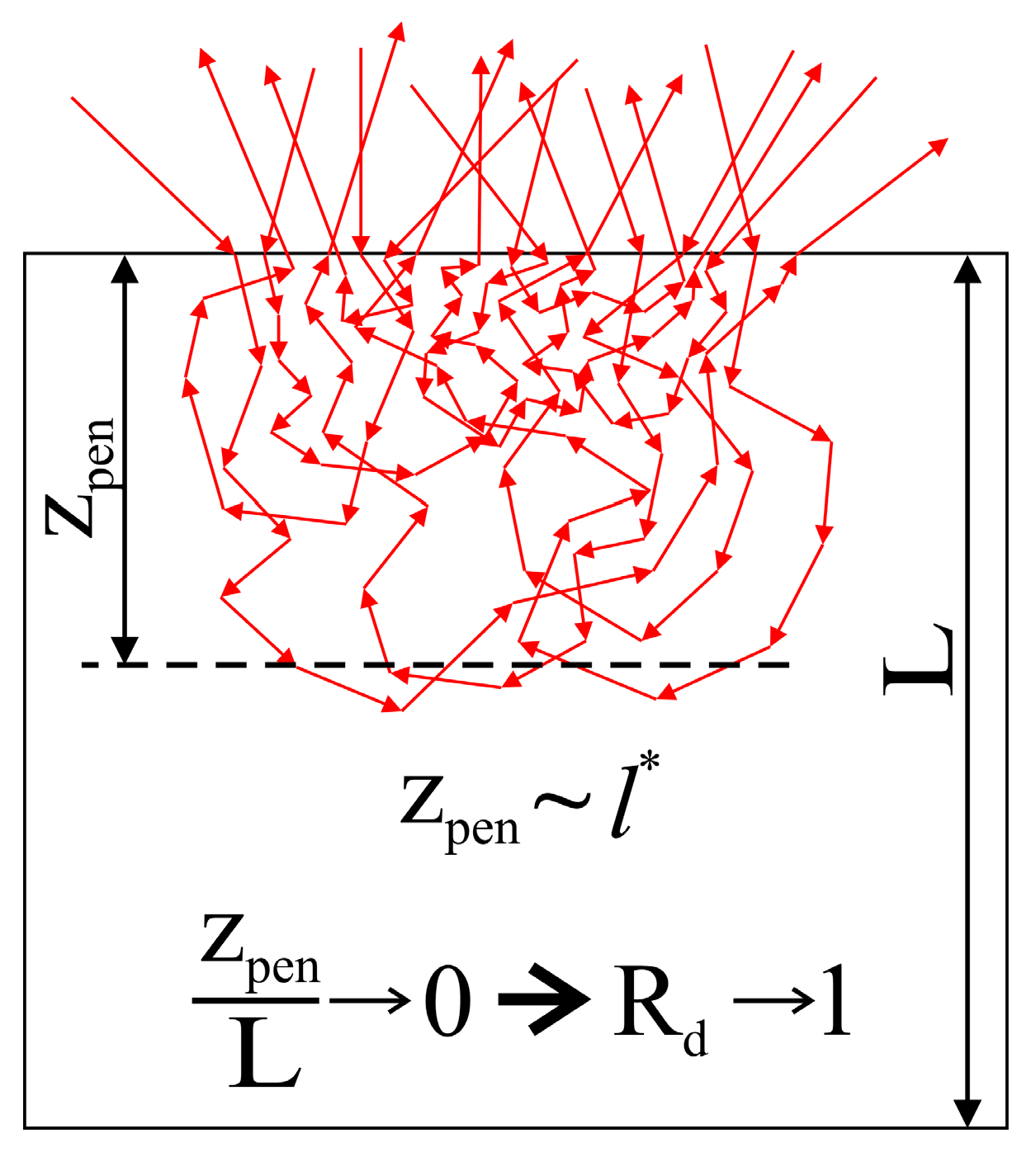
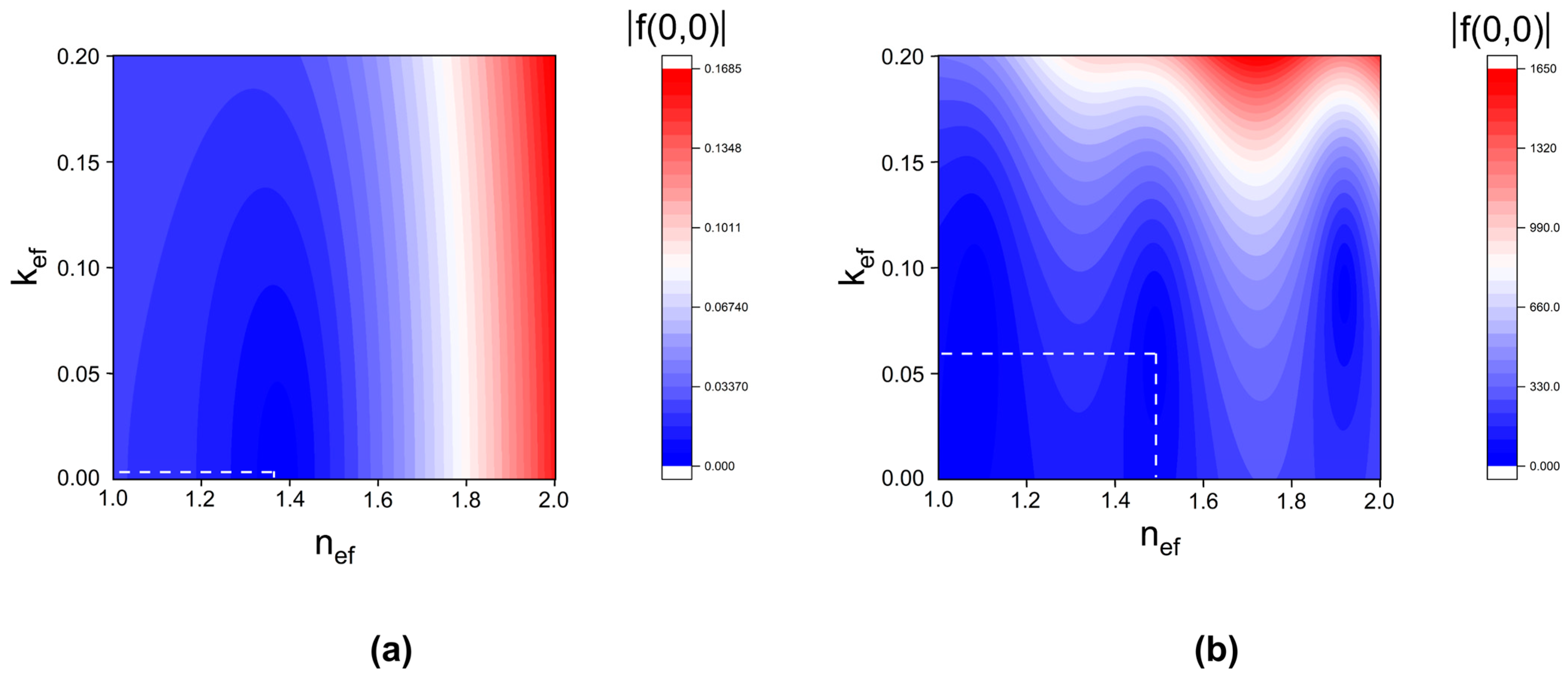
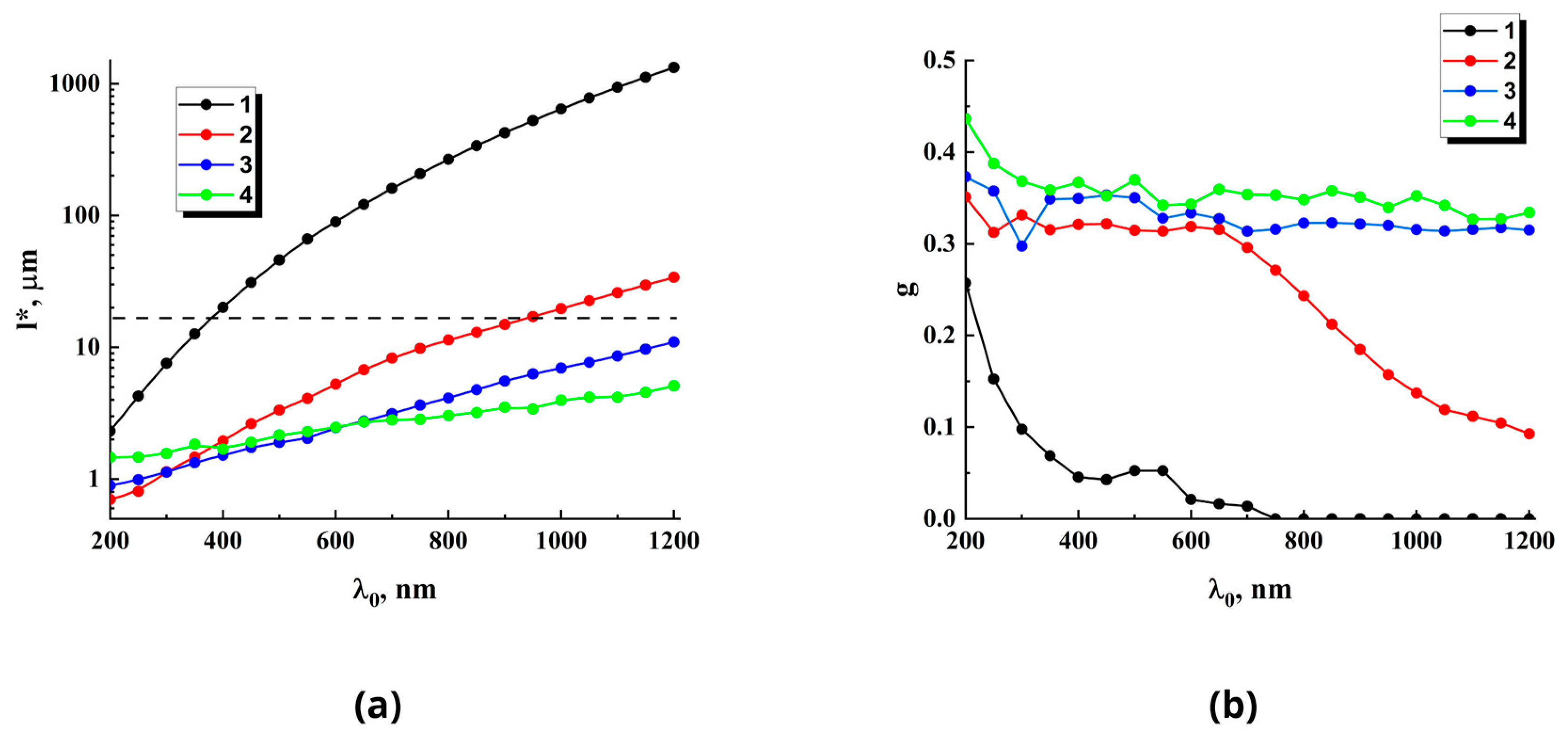
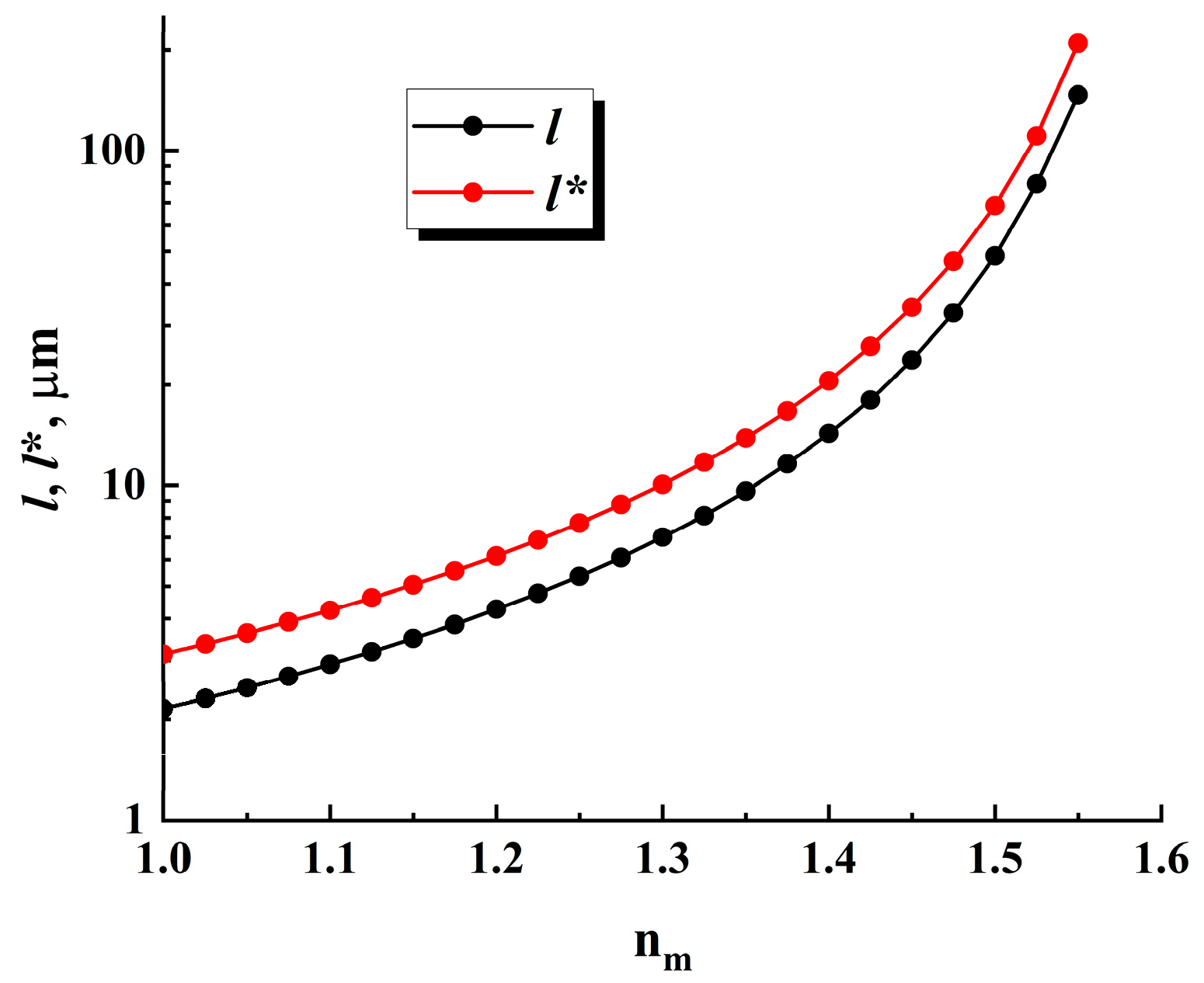
3.2. Model Data on the Light Transfer Properties of HA-Imitating Multiple Scattering Systems

Figure 9 displays the model dependencies $l^{*}\left({\lambda }_0\right)$ for the HA-imitating effective media with various scatter sizes $R_c$, which were obtained for the scatter volume fraction of $f_p=$ 0.65 using the above-described CCPA modeling. Modeling was carried out for the wavelengths ${\lambda }_0$ in the range from 200 nm to 1200 nm; values of the HA refractive index were taken from the recovered data presented in Figure 3. The $l^{*}$ values were estimated as $l\approx {\lambda }_0/2\pi k_{ef,\min }$ and further transformed to $l^{*}$ as $l^{*}=l\cdot \left(k_{ef,\min }/{k^{\prime }}_{\min }\right)$; the corresponding model values of the scattering anisotropy factor $g=1-{k^{\prime }}_{\min }/k_{ef,\min }$ are displayed in Figure 9b. The dashed line in Figure 9 marks the threshold value of $l^{*}$ corresponding to $R_d$ values of at least 0.98 over the entire spectral range from 200 nm to 1200 nm. Note that we consider the model system to be non-absorbing at ${\lambda }_0=$ 200 nm, while for real HA-based systems, this wavelength is slightly below the edge of the fundamental absorption band, and some absorption certainly occurs. However, this assumption does not have a significant impact on the main results of this work.

4. Discussion

It should be noted that the presented results of CCPA modeling for the light transfer parameters of HA-imitating scattering systems are approximate and rather semi-qualitative in nature due to certain limitations of the model. One of these limitations relates to the lack of consideration of the polydispersity and morphology of the modeled systems. The only input parameters considered were the radius $R_c$ of the scattering sphere, equal in volume to the average volume of particles in the simulated medium, and the volume fraction $f_p$ of particles in the medium. The shape of the particles and the properties of their size distribution remain outside our attention. In addition, it was noted in [32] that for $f_p$ values approaching the extreme value of ≈0.74 corresponding to FCC packing for hard spheres, the model gave significant errors in estimating $l$ and $l^{*}$. In our case, the volume fraction of particles in pressed samples was not far from this extreme value.

Nevertheless, the obtained model results are in reasonable agreement with the experimentally observed close-to-uniform behavior of the spectral distribution of reflectivity and the high values of this quantity for the examined samples in the spectral range from 300 nm to 1100 nm (Figure 8). This indicates that the thickness $L$ of the samples studied is many times greater than the values of $l^{*}$ in the entire analyzed spectral range. In addition, the observed trend towards a slight increase in the diffuse reflectivity of the samples in the short-wavelength region can be interpreted as the effect of a decrease in $l^{*}$. The decrease in the TMFP value is due to the combined effect of both an increase in the scatter refractive index $n_p$ (see Figure 3) and an increase in the ratio $〈d〉/{\lambda }_0$ of the scatter average size to the wavelength. This combined effect can be considered within the framework of the CCPA approach.

The question arises about the characteristic size of scattering centers in close-packed layers of HA particles. As noted above, the basic structural element is HA nanocrystallites with a size between 50 nm and 100 nm that aggregate into larger particles during the production of samples. Thus, the examined samples can be considered in the framework of the effective medium model as an ensemble of nanocrystallites uniformly (in the macroscopic sense) distributed in the air matrix (a fine-grained system) or an ensemble of nanocrystallite aggregates of a much larger characteristic size (a coarse-grained system). From the point of view of radiation transfer theory, two multiple scattering systems with the same values of $f_p$, but with significantly different sizes of scattering centers will, under certain conditions, differ radically in their values of light transfer parameters $l$ and $l^{*}$. This issue is explicitly reflected by the model data presented in Figure 9a. It is obvious that finer-grained scattering structures did not provide the high albedo values observed in the experiment in the spectral range from 300 nm to 1100 nm. In particular, the model system with $R_c=$ 50 nm is characterized by a certain dip in reflectivity in the near-IR region and the long-wavelength interval of the visible range. This should result in the bluish coloration of the fine-grained samples in diffuse-reflected light.

Based on the obtained model data, it can be concluded that the alignment of the dependence $R_d\left({\lambda }_0\right)$ over the entire spectral range from 200 nm to 1200 nm to the level observed in the experiment occurred at $R_c\ge$ 300 nm. It should be noted that, in accordance with the modeling results (Figure 9a), the average particle size in the raw hydroxyapatite powders $〈d〉\approx$ 0.67 µm, determined using laser diffractometry (see Section 2.1), corresponded fairly to the experimentally observed behavior of $R_d\left({\lambda }_0\right)$.

Following the principles of the theory of light scattering by particles, one can consider the ratio of the characteristic particle size (i.e., $2R_c$) to the wavelength of light in the particle material ${\lambda }_0/n_p$ as an important parameter characterizing the scattering efficiency of particles. In particular, the parameter $2R_c{n}_p/{\lambda }_0$ for model medium 1 (Figure 9) varies from ≈0.27 to ≈1.68 when ${\lambda }_0$ changes from 1200 nm to 200 nm. For other model media, these changes are, respectively, from ≈1.07 to ≈6.73 (medium 2), ≈2.14 to ≈13.46 (medium 3), and from ≈4.28 to ≈26.92 (medium 4). It should be noted that the CCPA modeling of the light transfer properties of densely packed TiO₂ particles ($R_c=$ 110 nm, $f_p=$ 0.36, $n_p\approx$ 2.73) showed the weak dependence of the ratio $l/R_c$ on the wavelength for $2R_c{n}_p/{\lambda }_0$ > 2; under this condition, this ratio approached a value of about 0.6 [32]. In our case, the consideration of the behavior of the model values of $l$ in relation to $R_c$ at the short-wavelength edge of the examined spectral interval gave the following values for model systems 2–4: ≈2.27 (2), ≈1.4 (3), ≈1.03 (4). It is necessary to take into account significant differences in the structural and optical characteristics of the scattering medium modeled in [32] and the HA-imitating model systems considered in this work. In addition, the trends in the behavior of the $l^{*}\left({\lambda }_0\right)$ dependencies (2–4) in Figure 9, at short wavelengths, allow us to assume that they are gradually saturated to the state $l^{*}\propto R_c$ with the proportionality constant of the order of one.

Another important question from the point of view of light transfer in dense multiple scattering media is the proximity of the parameters of the examined systems (primarily $l^{*}$ and $n_{ef}$) to the so-called light localization threshold (see, e.g., [40]) determined by the following condition: $\tilde{k}{l}^{*}=1$, where $\tilde{k}$ is the wavenumber of propagating light in the medium. Below the localization threshold, the nature of radiation transfer is radically different from conventional diffusion transfer, but we will not dwell on this popular topic in detail (for reference, see the numerous works on this topic). We will only note that obtaining random multiple scattering media with $\tilde{k}{l}^{*}\le 1$ (i.e., small values of $\tilde{k}$ and $l^{*}$) using traditional methods (the selection of particles with high refractive indices and the use of high particle packing densities) is practically impossible due to the abundance of fundamental limitations. In our case, the estimates of $\tilde{k}{l}^{*}$ for the examined model systems can be considered an indirect confirmation of the physical consistency of the modeling procedure since the parameters $n_{ef\min },k_{ef\min }$ leading to $\tilde{k}{l}^{*}\le 1$ are physically unreasonable. In the framework of our consideration, the localization parameter can be presented as follows:

$$\tilde{k}{l}^{*}={\displaystyle \frac{2\pi n_{ef\min }}{{\lambda }_0}}\cdot {\displaystyle \frac{{\lambda }_0}{2\pi {k^{\prime }}_{\min }}}={\displaystyle \frac{n_{ef\min }}{{k^{\prime }}_{\min }}}$$

(10)

Figure 10 displays the dependencies $\tilde{k}{l}^{*}\left({\lambda }_0\right)$ for the modeled systems (1–4); it can be seen that for all model systems, the parameter $\tilde{k}{l}^{*}$ is greater than one by many times, which indicates the conventional diffusion mode of radiation transfer in the entire analyzed range of wavelengths.

In addition, an important issue concerns the expected sensitivity of the light transfer parameters $l$ and $l^{*}$ of HA-based dispersed systems to changes in the refractive index of the matrix medium $n_m$. This issue arises, for example, in the case of the synthesis of various types of UV-protective coatings, which are transparent in the visible range. It may also be of interest from the point of view of biomedical technologies based on the effect of the optical clearing of biological tissues and various tissue-engineered structures when exposed to liquid immersion agents [41]. Moreover, the use of liquids or polymers as matrix media that are transparent in the optical range and characterized by the sensitivity of the refractive index to external influences (temperature, field, etc.) makes it possible to create new types of controlled photonic materials with a dispersed structure (for example, tunable diffusers). An example of the model dependences of $l$ and $l^{*}$ on $n_m$ for a system of closely packed aggregates of HA nanocrystallites with $R_c=$ 200 nm and $f=$ 0.65 at the wavelength ${\lambda }_0=$ 700 nm (which corresponds to the long-wavelength edge of the visible region and is characterized by larger values of $l$ and $l^{*}$ compared to the short-wavelength edge of the visible region) is shown in Figure 11. These dependencies allow for the rough estimation of the matrix replacement effect; in particular, replacing air as a matrix medium in the model structure with water with a refractive index of $n_m\approx$ a leads to an approximately four-fold increase in $l^{*}$ a (and, accordingly, the depth of penetration of the probing radiation into the system). This can be useful, for instance, in the light diffusion characterization of HA-based functional materials for tissue engineering and regenerative medicine applying optical coherence tomography (OCT).

The consideration of dependencies similar to that presented in Figure 11 for different average particle sizes and their volume fraction in a matrix medium with a known refractive index allows one to select the range of characteristics of HA-based dispersive photonic materials (in particular, the thickness $L$) in a way that satisfies the required criteria. For example, in the case of the synthesis of UV-protective layers in a polymer matrix based on HA particles that are partially transparent in the visible range, it is necessary to select $〈d〉$ and $f_p$ in such a way that in the range from 400 nm to 700 nm, the following condition is satisfied: $l\left(\lambda =400 \mathrm{nm}\right)>L$. On the contrary, when synthesizing highly reflective coatings for the visible range, it is necessary to meet the condition $l^{*}\left(\lambda =400 \mathrm{nm}\right)\le L/20$. In addition, one of the possible interesting applications of HA-based dispersive systems is their use as random matrix media with enhanced induced fluorescence emission under the influence of external laser pumping (the so-called random lasing systems; see, e.g., [42]). In particular, variations in $l^{*}$ due to changes in $〈d〉,f_p,n_m$ allows one to tune the ratio $L/l^{*}$ to produce the best condition to amplify the component of the fluorescent output induced [43].

5. Conclusions

Thus, the high reflectivity of ensembles of closely packed HA nanoparticle aggregates in the near IR, visible, and near UV regions (up to the edge of the fundamental absorption band at ≈238 nm) is due to the effective multiple scattering of light on nanoparticle aggregates with characteristic sizes exceeding 300 nm. The estimated values of the light penetration depth in the above-mentioned spectral range into air-filled HA-based dispersive media are of the order of several micrometers (in any case, for the samples under study, they do not exceed 15 µm). One of the possible applications of dispersive materials based on hydroxyapatite is the synthesis of coatings with a high degree of whiteness, which, due to the relatively low cost of the raw materials and good optical parameters, can create competition with other popular coatings with a high albedo (for example, PTFE).

HA-based dispersive materials are also of particular interest as matrix media in studies of fundamental features of energy transfer at the microscopic level in fluorescing liquids under external laser excitation of the fluorescence output. In particular, the appropriately high sensitivity of the light transfer parameters of these materials to their structural characteristics allows for the selection of these matrices on the basis of a criterion of high efficiency regarding the interaction between propagating fluorescent radiation and the ensembles of excited fluorophore molecules.

Further studies will be aimed at refining model concepts for the features of radiation transfer in HA-based dispersive media with various structures, as well as further developing methods for optical diagnostics of such systems (in particular, based on the coherent backscattering effect).