Heat Treatment-Driven Structural and Morphological Transformation Under Non-Parametric Tests on Metal–Ceramic-Sputtered Coatings
Abstract
1. Introduction
1.1. TiWN and TiWC Transition Metal–Ceramic Coatings
1.2. Relevance of Statistical Treatment on Materials Science
1.3. Statistical Techniques
- a.
- The data are ordinal and do not meet the precision of interval data;
- b.
- There are serious concerns about extreme deviation from normal distribution;
- c.
- There is a considerable difference in the number of subjects for each comparative group.
- 1.
- Determine the ranks (use average rank in the case of ties).
- 2.
- Determine the overall average rank.
- 3.
- Determine the number of cases in each category, determine the average rank per category, and square the difference with the overall average rank, then multiply by the number of cases in the category.
- 4.
- Sum up the last column.
- 5.
- For each rank, subtract the overall rank average and square the result.
- 6.
- Sum up the results of step 5.
- 7.
- Determine the H-value statistics. The exact distribution of H is complicated. It depends on the sample size, n1, n2, …, nk, and so it is not practical to tabulate its values beyond a small number of samples. When k or n is large, the exact distribution of H under H0 can be approximated by the distribution with (k − 1) degrees of freedom. For this purpose, we state the K-W theorem without proof.
- 8.
- Determine the degrees of freedom.
- 9.
- Use a bilateral distribution to determine the critical value.
2. Materials and Methods
2.1. Coating Growth
2.2. Preparation of Sample and Thermal Treatment
2.3. Characterization
2.4. Statistical Analysis
3. Results and Discussion
3.1. Data Experimental Analyses
3.1.1. XRD Patterns
3.1.2. Determination of Crystallite Size by Scherrer Formula
Crystalline Size Forescated Data by SMA
3.1.3. Top View by Optical Microscopy
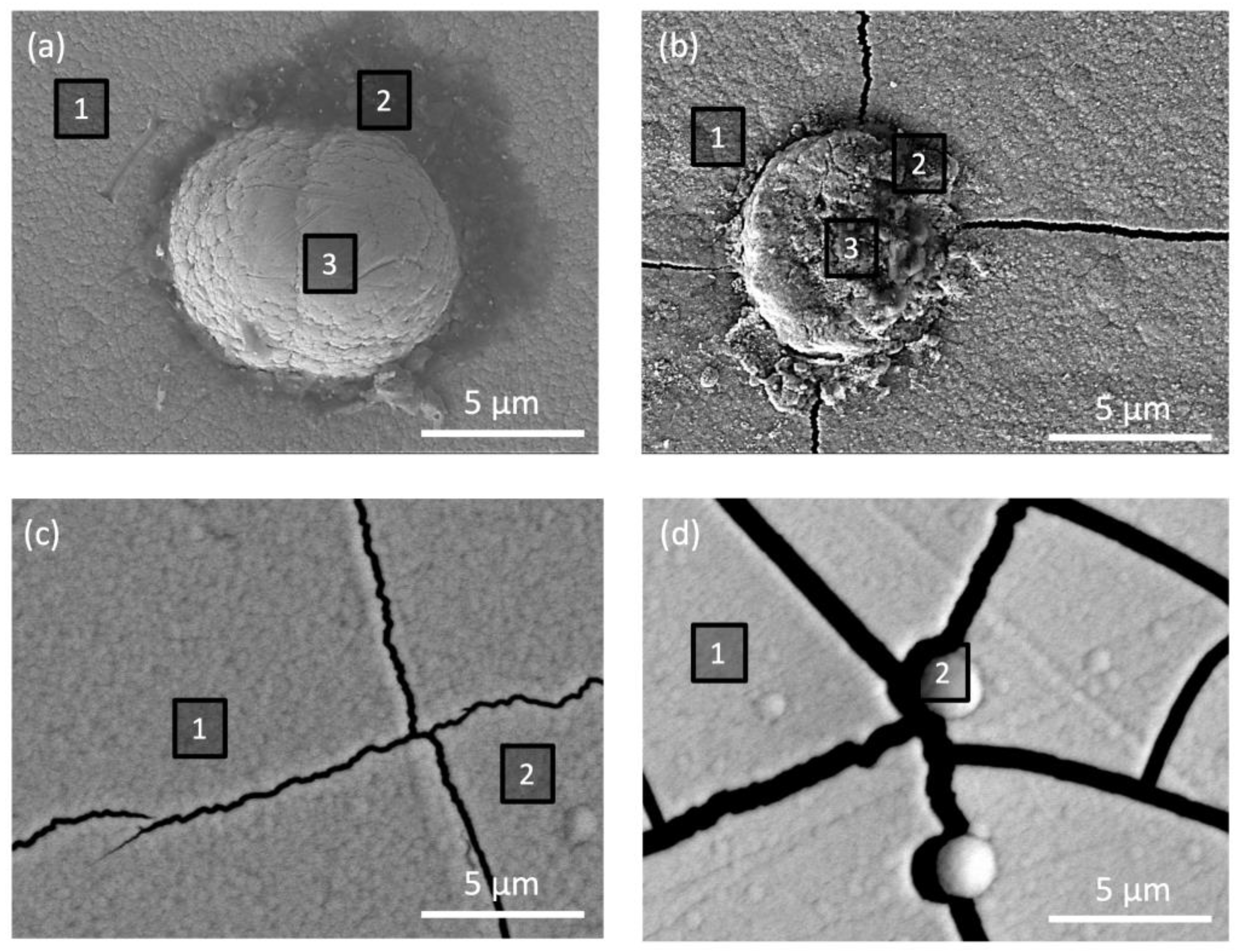
3.1.4. Scanning Electron Microscopy
3.1.5. Chemical Composition by EDS
3.2. Statistical Results
3.2.1. Normality Test
3.2.2. Dependent Relationship Paired Sample Test
3.2.3. K-W Hypothesis
3.2.4. K-W Procedure Step-by-Step
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Habashi, F. Titanium, physical and chemical properties. In Encyclopedia of metalloproteins; Kretsinger, R.H., Uversky, V.N., Permyakov, E.A., Eds.; Springer: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Barzan, M. Chapter 3: Titanium. In Smart Materials for Biomedical Applications; Springer Nature: New York, NY, USA, 2022; Available online: https://www.researchgate.net/publication/359355707_chapter_3_Titanium (accessed on 1 January 2024).
- Raj, P.P.; Sridhar, R.; Pugazhenthi, R.; Anbuchezhiyan, G.; Ganesh, M. Investigating the mechanical properties of tungsten carbide metal matrix composites with Al 6061. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Greger, M.; Čížek, L.; Widomska, M. Structure and mechanical properties of formed tungsten-based materials. J. Mater. Process. Technol. 2004, 157–158, 683–687. [Google Scholar] [CrossRef]
- Gren, M.; Fransson, E.; Ångqvist, M.; Erhart, P.; Wahnström, G. Modeling of vibrational and configurational degrees of freedom in hexagonal and cubic tungsten carbide at high temperatures. Phys. Rev. Mater. 2021, 5, 033804. [Google Scholar] [CrossRef]
- Ndumia, J.N.; Kang, M.; Lin, J.; Liu, J.; Li, H. Influence of Heat Treatment on the Microstructure and Wear Properties of Arc-Sprayed FeCrAl/Al Coating. Coatings 2022, 12, 374. [Google Scholar] [CrossRef]
- Hu, R.; Zhang, J.; Wang, R.; Zhang, C.; Xie, Z.; Zhang, Y.; Li, G.; Lu, X. Effect of heat treatment on microstructure and properties of WC reinforced co-based composite coating on copper. Mater. Lett. 2022, 319, 132262. [Google Scholar] [CrossRef]
- Reddy GV, A.; Naveen Kumar, K.; Sattar, S.A.; Shetty, H.D.; Guru Prakash, N.; Imran Jafri, R.; Devaraja, C.; BC, M.; CS, K.; Premkumar, R.; et al. Effect of post annealing on DC magnetron sputtered tungsten oxide (WO3) thin films for smart window applications. Phys. B Condens. Matter 2023, 664, 414996. [Google Scholar] [CrossRef]
- Zaid, M.H.M.; Matori, K.A.; Aziz, S.H.A.; Kamari, H.M.; Fen, Y.W.; Yaakob, Y.; Sa’at, N.K.; Gürol, A.; Şakar, E. Effect of heat treatment temperature to the crystal growth and optical performance of Mn3O4 doped α-Zn2SiO4 based glass-ceramics. Results Phys. 2019, 15, 102569. [Google Scholar] [CrossRef]
- Dong, W.; Yang, X.; Zhang, Z.; Wang, K.; Liu, B. Microstructural evolution and performance analysis of WC-11Co reinforced iron matrix composites. Mater. Des. 2024, 239, 112753. [Google Scholar] [CrossRef]
- Sinojiya, R.J.; Paulachan, P.; Chamasemani, F.F.; Bodlos, R.; Hammer, R.; Zálešák, J.; Reisinger, M.; Scheiber, D.; Keckes, J.; Romaner, L.; et al. Probing the composition dependence of residual stress distribution in tungsten-titanium nanocrystalline thin films. Commun. Mater. 2023, 4, 11. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, Y.; Cheng, W.; Chen, Y.; Gu, J. High temperature oxidation behavior of CoCrFeNiMo0.2 high-entropy alloy coatings produced by laser cladding. Mater. Today Commun. 2024, 39, 108639. [Google Scholar] [CrossRef]
- Uchiyama, H.; Okada, M.; Ogawa, D.; Kozuka, H. Crystallization and densification of alkoxide-derived titania films: Effect of the amount of H2O in the precursor solutions. J. Asian Ceram. Soc. 2013, 1, 248–256. [Google Scholar] [CrossRef]
- He, K.; Chen, N.; Wang, C.; Wei, L.; Chen, J. Method for determining crystal grain size by X-Ray Diffraction. Cryst. Res. Technol. 2018, 53, 1700157. [Google Scholar] [CrossRef]
- Taghipour, M.; Eslami, A.; Salehi, M.; Bahrami, A. An investigation on anti-coking behavior of gas phase aluminide coatings applied on a high performance micro alloyed (HP-MA) steel. Surf. Coat. Technol. 2020, 388, 125607. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, S.Y.; Park, J.S. Influence of Heat Treatment on the Microstructure and Properties of Copper Coatings Deposited by D.C. Sputtering. J. Alloys Compd. 2021, 867, 158778. [Google Scholar] [CrossRef]
- Martínez, R.A.; García, L.F. Comparative Analysis of Experimental and Statistical Methods in Evaluating Niobium Coatings Applied by D.C. Sputtering. Thin Solid Film. 2018, 654, 85–92. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Wang, H. Impact of Heat Treatment on the Adhesion of Ceramic Coatings Deposited by D.C. Sputtering. Ceram. Int. 2022, 48, 3521–3530. [Google Scholar] [CrossRef]
- Field, A. Discovering Statistics Using IBM SPSS Statistics, 5th ed.; Sage Publications: Washington, DC, USA, 2018. [Google Scholar]
- Bickman, L.; Rog, D.J. The SAGE Handbook of Applied Social Research Methods, 2nd ed.; Sage Publications: Washington, DC, USA, 2008; ISBN 9781412950312. [Google Scholar] [CrossRef]
- Rosenthal, R.; Rosnow, R.L. Essentials of Behavioral Research: Methods and Data Analysis, 3rd ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Hedges, L.V.; Olkin, I. Statistical Methods for Meta-Analysis; Academic Press: Cambridge, MA, USA, 1985; ISBN 978-0-08-057065-5. [Google Scholar] [CrossRef]
- Lai, K.; Kelley, K. Accuracy in parameter estimation for ANCOVA and ANOVA contrasts: Sample size planning via narrow confidence intervals. Br. J. Math. Stat. Psychol. 2011, 65, 350–370. [Google Scholar] [CrossRef]
- Grigoriev, S.N.; Nikitin, N.; Yanushevich, O.; Kriheli, N.; Kramar, O.; Khmyrov, R.; Idarmachev, I.; Peretyagin, P. Experimental and Statistical Analysis of the Effect of Heat Treatment on Surface Roughness and Mechanical Properties of Thin-Walled Samples Obtained by Selective Laser Melting from the Material AlSi10Mg. Materials 2023, 16, 7326. [Google Scholar] [CrossRef]
- Forthofer, R.N.; Lee, E.S.; Hernández, M. 9-Nonparametric Tests. In Biostatistics, 2nd ed.; Forthofer, R.N., Lee, E.S., Hernández, M., Eds.; Academic Press: Cambridge, MA, USA, 2007; pp. 249–268. ISBN 9780123694928. [Google Scholar] [CrossRef]
- Sharma, S.K.; Sharma, V. Comparative Analysis of Machine Learning Techniques in Sale Forecasting. Int. J. Comput. Appl. 2012, 53, 51–54. [Google Scholar] [CrossRef]
- Ahad, N.A.; Yin, T.S.; Abdul, R.O.; Che, R.Y. Sensitivity of normality tests to non-normal data. Sain Malays. 2011, 40, 637–641. [Google Scholar]
- Kolmogorov, A. Foundations of the Theory of Probability, 2nd ed.; Chelsea: New York, NY, USA, 1956. [Google Scholar]
- Smirnov, S. Beschreibung einer neuen Acartia-Art aus dem Japanischen Meer nebst einiger Bemerkungen uber die Untergattung Euacartia Steuer. Zool. Anz. 1936, 114, 87–92. [Google Scholar]
- Anderson, T.W.; Darling, D.A. Asymptotic theory of certain “goodness-of-fit” criteria based on stochastic processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Anderson, T.W. On the distribution of the two-sample Cramer-von Mises criterion. Ann. Math. Stat. 1962, 33, 1148–1169. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality. Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Razali, N.M.; Yap, B. Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Walpole, E.R.; Raymond, H.M.; Sharon, L.M.; Kevin, Y. Probability and statistics for engineers and scientists. In Nonparametric Statistics; Prentice Hall: Hoboken, NJ, USA, 2007; Chapter 16; p. 684. [Google Scholar]
- Nwobi, F.; Akanno, F.C. Power comparison of ANOVA and Kruskal–Wallis tests when error assumptions are violated. Adv. Methodol. Stat. Metod. Zv. 2021, 18, 53–71. [Google Scholar] [CrossRef]
- Lachenbruch, P.A.; Clements, P.J. ANOVA, Kruskal-Wallis normal scores and unequal variance. Commun. Stat.-Theory Methods 1991, 20, 107–126. [Google Scholar] [CrossRef]
- Fan, C.; Zhang, D.; Cun-Hui, Z. On sample size of the Kruskal-Wallis test with application to a Mouse Peritoneal Cavity Study. Biometrics 2011, 67, 213–224. [Google Scholar] [CrossRef]
- MacFarland, T.W.; Yates, J.M. Kruskal-Wallis H test of One-way analysis of Variance (ANOVA) by Ranks. In Introduction to Nonparametric Statistics for Biological Sciences Using R; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Ostertagová, E.; Ostertag, O.; Kováč, J. 2014 Methodology and application of the Kruskal-Wallis test. Appl. Mech. Mater. 2014, 611, 115–120. [Google Scholar] [CrossRef]
- Ramachandran, K.M.; Tsolcos, C.P. Chapter 12—Nonparametric test. In Mathematical Statistics with Applications in R, 2nd ed.; Academic Press: Cambridge, MA, USA, 2015; pp. 589–637. ISBN 9780124171138. [Google Scholar] [CrossRef]
- Puth, M.T.; Neuhäuser, M.; Ruxton, G.D. Effective use of Spearman’s and Kendall’s correlation coefficients for association between two measured traits. Anim. Behav. 2015, 102, 77–84. [Google Scholar] [CrossRef]
- Kumar, A.J.; Abirami, S. Aspect-based opinion ranking framework for product reviews using a Spearman’s rank correlation coefficient method. Inf. Sci. 2018, 460–461, 23–41. [Google Scholar] [CrossRef]
- Al-Hameed, A.A.K. Spearman’s correlation coefficient in statistical analysis. Int. J. Nonlinear Anal. Appl. 2022, 13, 3249–3255. [Google Scholar] [CrossRef]
- Motulsky, H.J. Nonparametric Tests with Small and Large Samples. GraphPad Statistics Guide. 2016. Available online: https://www.graphpad.com/guides/prism/latest/statistics/choosing_parametric_vs__nonpar.htm (accessed on 24 April 2024).
- Hansun, S.A. New approach of moving average method in time series analysis. In Proceedings of the Conference on New Media Studies (CoNMedia), Tangerang, Indonesia, 27–28 November 2013; pp. 1–4. [Google Scholar] [CrossRef]
- González-Hernández, A.; Morales-Cepeda, A.B.; Flores, M.M.; Caicedo, J.C.; Aperador, W.; César, A. Electrochemical Properties of TiWN/TiWC Multilayer Coatings Deposited by RF-Magnetron Sputtering on AISI 1060. Coatings 2021, 11, 797. [Google Scholar] [CrossRef]
- Tong, H.; Kou, Z.; Zhao, M.; Zhuang, D.; Wang, C.; Li, Y.; Wang, H.; Jia, M. Optimization of the photoelectric performances of Mg and Al co-doped ZnO films. Appl. Surf. Sci. 2023, 638, 158007. [Google Scholar] [CrossRef]
- Aryanto, D.; Sudiro, T.; Wismogroho, A.S. Correlations between Structural and Hardness of Fe-50%Al Coating Prepared by Mechanical Alloying. Piston J. Tech. Eng. 2018, 1, 289674. [Google Scholar] [CrossRef]
- Erdoğan, N.N.; Başyiğit, A.B. An approach on determining micro-strain and crystallite size values of thermal spray barrier coated Inconel 601 super alloy. Int. J. Mater. Eng. Technol. 2023, 6, 21–25. [Google Scholar]
- Kung-Hsu, H.; Yun-Feng, C.; Sha-Ming, C.; Chia-Hua, C. The heat treatment effect on the structure and mechanical properties of electrodeposited nano grain size Ni–W alloy coatings. Thin Solid Film. 2010, 518, 7535–7540. [Google Scholar] [CrossRef]
- Acosta-Humánez, F.; Almanza, O.; Vargas-Hernández, C. Effect of sintering temperature on the structure and mean crystallite size of Zn1−xCoxO (x = 0.01–0.05) samples. Superf. Y Vacío 2014, 27, 43–48. [Google Scholar]
- Guo, D.W.Y.; Fernandez, R.; Zhao, L.; Jodoin, B. Cold spray for production of in-situ nanocrystallite MCrAlY coatings—Part I: Process analysis and microstructure characterization. Surf. Coat. Technol. 2021, 409, 126854. [Google Scholar] [CrossRef]
- Alaneme, K.; Okotete, E.A. Recrystallization mechanisms and microstructure development in emerging metallic materials: A review. J. Sci. Adv. Mater. Devices 2019, 4, 19–33. [Google Scholar] [CrossRef]
- Dhanasekaran, V.; Mahalingan, T.; Chamdramoha, R. Post heat treatment effect on electrochemically synthesized CuO thin films. ECS Trans. 2013, 45, 73–78. [Google Scholar] [CrossRef]
- Piao, Y.; Le, K.C. Thermodynamic theory of dislocation/grain boundary interaction. Contin. Mech. Thermodyn. 2022, 34, 763–780. [Google Scholar] [CrossRef]
- Lakhotkin, Y.; Kukushkin, R. Growth mechanism and structure peculiarities of tungsten-rhenium coatings. J. De Phys. IV Proc. 1991, 2, C2-729–C2-733. [Google Scholar] [CrossRef]
- VanVoorhis, C.R.W.; Morgan, B.L. Understanding Power and Rules of Thumb for Determining Sample Sizes. Tutor. Quant. Methods Psychol. 2007, 3, 43–50. [Google Scholar] [CrossRef]
- Pitthan, E.; Tran, T.T.; Moldarev, D.; Rubel, M.; Rimetzhofer, D.P. Influence of thermal annealing and of the substrate on sputter-deposited thin films from EUROFER97 on tungsten. Nucl. Mater. Energy 2023, 35, 101449. [Google Scholar] [CrossRef]
- Zong, N.; Jing, T.; Liu, Y. Influence of internal cracking on carbide precipitation in continuous casting bloom induced by soft reduction technology and the resulting segregated band in hot-rolled wire rods. Arch. Metall. Mater. 2022, 67, 73–82. [Google Scholar] [CrossRef]
- Kusmono, B.C.; Salim, U.A. Effects of cold rolling and annealing time of fatigue Resistencia of AA5052 Aluminum alloy. IJE Trans. C Asp. 2021, 34, 2189–2197. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Barman, T.K.; Prasanta, S. Co-deposition of W and Mo in electroless Ni–B coating and its effect on the surface morphology, structure, and tribological behavior. J. Mater. Des. Appl. 2021, 235, 149–161. [Google Scholar] [CrossRef]
- Qian, D.; Xue, J.; Zhang, A.; Li, Y.; Tamura, N.; Song, Z.; Chen, K. Statistical study of ductility-dip cracking induced plastic deformation in polycrystalline laser 3D printed Ni-based superalloy. Sci. Rep. 2017, 7, 2859. [Google Scholar] [CrossRef]
- Hubicki, R.; Richert, M.; Wiewióra, M. An Experimental Study of Temperature Effect on Properties of Nitride Layers on X37CrMoV51 Tool Steel Used in Extrusion Aluminum Industry. Materials 2020, 13, 2311. [Google Scholar] [CrossRef]
- Kim, T.K.; Park, J.H. More about the basic assumptions of t-test: Normality and sample size. Statistical Round. Korean J. Anesthesiol. 2019, 72, 331–335. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.J.; Liu, Q.; Lee, L.; Wei, D. Relationship between the structure, physicochemical properties and in vitro digestibility of rice starches with different amylose contents. Food Hydrocoll. 2011, 25, 968–975. [Google Scholar] [CrossRef]
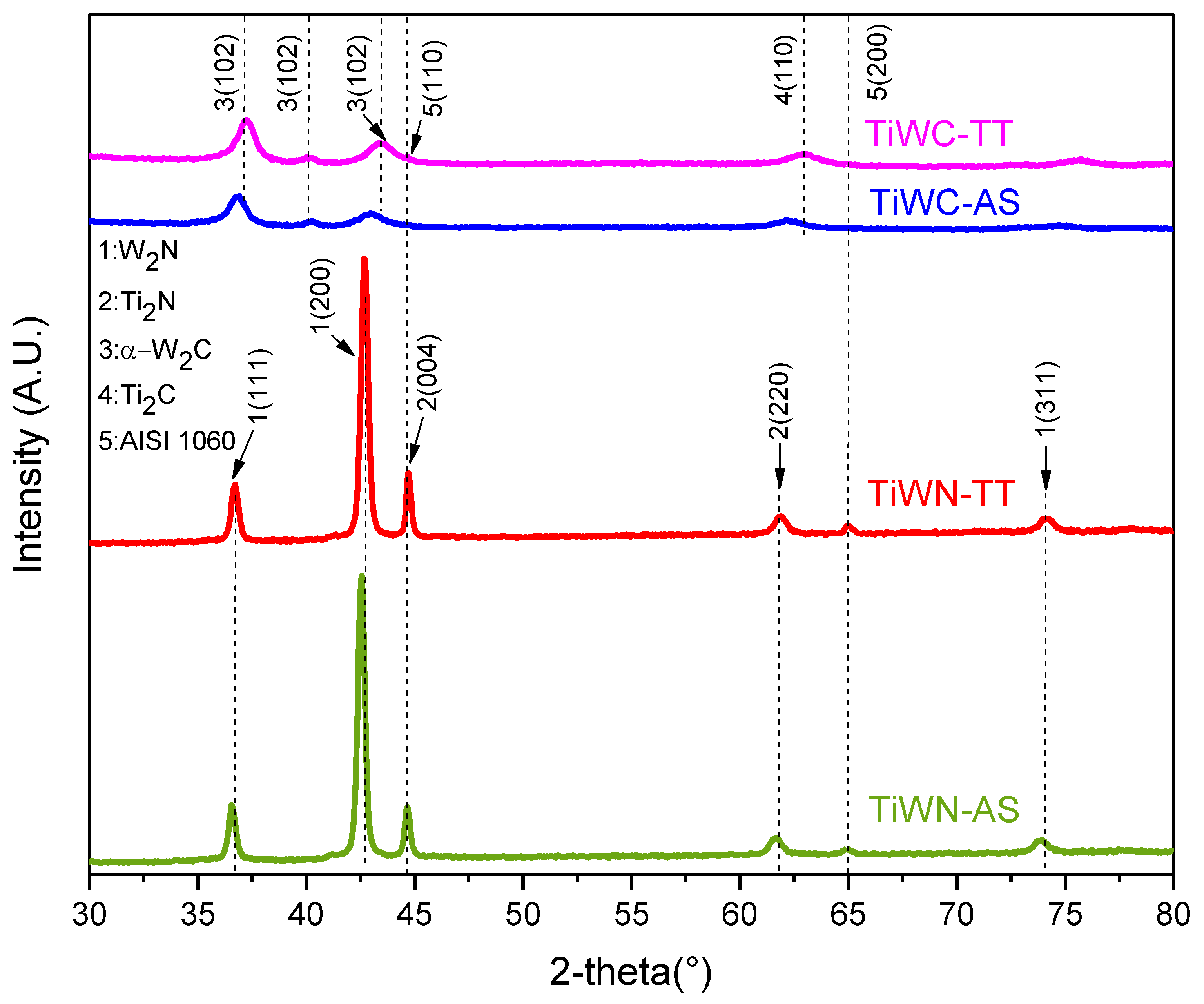
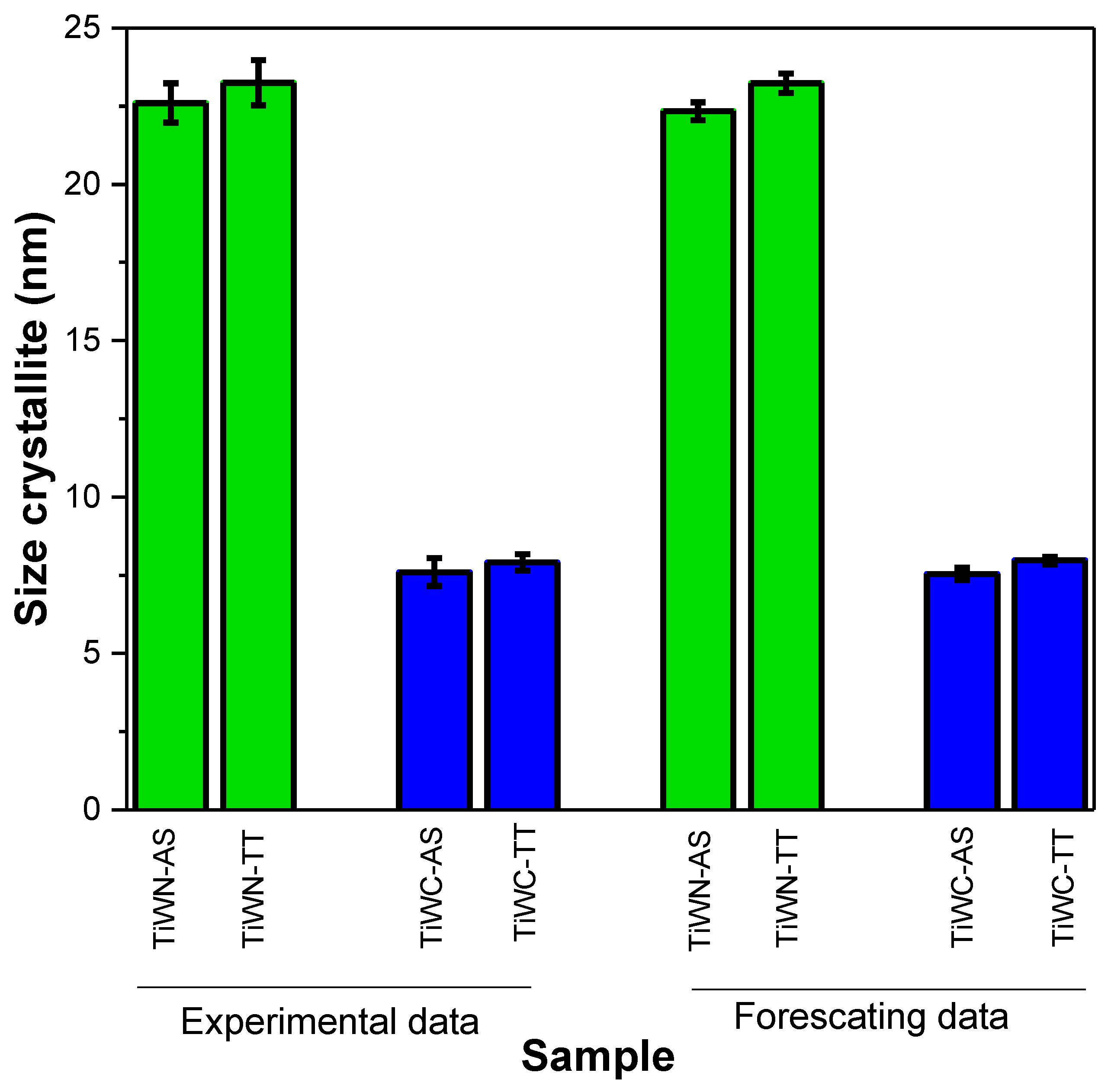

| Material | Peak Intensity 2θ (°) | FMHW β (°) | Crystallite Size (nm) | Microstrain (ε) | Dislocation Density (δ) |
|---|---|---|---|---|---|
| TiWN-AS | 42.56 | 0.40092 | 22.20 ± 0.63 | 4.49 × 10−3 | 2.03 × 10−3 |
| TiWN-TT | 42.54 | 0.38287 | 23.25 ± 0.72 | 4.29 × 10−3 | 1.85 × 10−3 |
| TiWC-AS | 36.88 | 1.15049 | 7.60 ± 0.45 | 1.51 × 10−2 | 1.73 × 10−3 |
| TiWC-TT | 37.22 | 1.10597 | 7.91 ± 0.26 | 1.43 × 10−2 | 1.60 × 10−3 |
| Sample/Data | Experimental Data | Forecasting Data | Statistic Parameter | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Av. | S.D. | S.E. | |
| TiWN-AS | 21.69 | 22 | 22.91 | 22.2 | 22.37 | 22.49 | 22.36 | 22.41 | 22.42 | 22.39 | 22.41 | 22.41 | 22.34 | 0.29 | 0.08 |
| TiWN-TT | 23.72 | 22.41 | 23.61 | 23.25 | 23.09 | 23.32 | 23.22 | 23.21 | 23.25 | 23.23 | 23.23 | 23.24 | 23.23 | 0.31 | 0.09 |
| TiWC-AS | 7.63 | 8.02 | 7.13 | 7.59 | 7.59 | 7.44 | 7.54 | 7.52 | 7.5 | 7.52 | 7.52 | 7.51 | 7.54 | 0.20 | 0.06 |
| TiWC-TT | 7.62 | 8.03 | 8.1 | 7.91 | 8.01 | 8.01 | 7.98 | 8 | 8 | 7.99 | 8 | 7.99 | 7.97 | 0.12 | 0.03 |
| Figure/ Sample | Point Selected | C | N | O | W | Ti |
|---|---|---|---|---|---|---|
| (a) TiWN-AS | 1 | 3.75 | 10.82 | 9.20 | 75.54 | 0.69 |
| 2 | 3.54 | 11.95 | 11.09 | 70.01 | 3.41 | |
| 3 | - | - | 18.35 | 67.75 | 13.9 | |
| (b) TiWN-TT | 1 | 33.0 | - | 29.35 | 31.39 | 6.26 |
| 2 | - | - | 54.91 | 29.15 | 15.94 | |
| 3 | - | - | 9.35 | 74.41 | 16.24 | |
| (c) TiWC-AS | 1 | - | 15.3 | 12.74 | 63.53 | 8.43 |
| 2 | 19.06 | - | 20.15 | 58.72 | 2.07 | |
| (d) TiWC-TT | 1 | 4.07 | - | 12.45 | 72.6 | 10.88 |
| 2 | - | 6.15 | 12.40 | 78.46 | 2.99 |
| Sample | Normality Test | Dependent (rs) | K-W | |||
|---|---|---|---|---|---|---|
| Shapiro–Wilk (p-Value) | Spearman Rank (p-Value) | H-Value (Bilateral) | C-Value | |||
| N = 48 | N = 12 | N = 48 | N = 12 | |||
| TiWN-AS | 0.034 | 0.252 | 42.30 | 15.19 | 7.81 | 3.84 |
| TiWN-TT | 0.010 | |||||
| TiWC-AS | 0.010 | −0.343 | 12.40 | |||
| TiWC-TT | 0.010 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamboa-Soto, F.; Bautista-García, R.; Llanes-Gil López, D.I.; Bermea, J.E.; Tinoco Mendiola, R.; Olive-Méndez, S.F.; González-Hernández, A. Heat Treatment-Driven Structural and Morphological Transformation Under Non-Parametric Tests on Metal–Ceramic-Sputtered Coatings. Ceramics 2025, 8, 25. https://doi.org/10.3390/ceramics8010025
Gamboa-Soto F, Bautista-García R, Llanes-Gil López DI, Bermea JE, Tinoco Mendiola R, Olive-Méndez SF, González-Hernández A. Heat Treatment-Driven Structural and Morphological Transformation Under Non-Parametric Tests on Metal–Ceramic-Sputtered Coatings. Ceramics. 2025; 8(1):25. https://doi.org/10.3390/ceramics8010025
Chicago/Turabian StyleGamboa-Soto, Federico, Roberto Bautista-García, Diana I. Llanes-Gil López, Juan E. Bermea, René Tinoco Mendiola, Sion F. Olive-Méndez, and Andrés González-Hernández. 2025. "Heat Treatment-Driven Structural and Morphological Transformation Under Non-Parametric Tests on Metal–Ceramic-Sputtered Coatings" Ceramics 8, no. 1: 25. https://doi.org/10.3390/ceramics8010025
APA StyleGamboa-Soto, F., Bautista-García, R., Llanes-Gil López, D. I., Bermea, J. E., Tinoco Mendiola, R., Olive-Méndez, S. F., & González-Hernández, A. (2025). Heat Treatment-Driven Structural and Morphological Transformation Under Non-Parametric Tests on Metal–Ceramic-Sputtered Coatings. Ceramics, 8(1), 25. https://doi.org/10.3390/ceramics8010025






