Study on Microwave Dielectric Materials an Adjustable Temperature Drift Coefficient and a High Dielectric Constant

Abstract

This paper reports the dielectric characterizations of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramics prepared using a solid-state reaction method with various x values. X-ray diffraction spectroscopy analyses showed that the crystal structure of these pure samples was orthorhombic perovskite. With increasing Sn⁴⁺ content, the lattice constant and unit cell volume increased, while the dielectric constant decreased because of the ionic polarizability decreasing. Moreover, a maximum Q × f value of 5242 (GHz), a dielectric constant (ε_r) of 91.23, and a temperature coefficient (τ_f) of +810 ppm/°C were achieved for samples sintered at 1350 °C for 4 h. The microwave dielectric characterization was found to be strongly correlated with the sintering temperature, and the best performance was achieved for the sample sintered at 1350 °C. (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ possesses a promising potential to be a τ_f compensator for a near-zero τ_f dielectric ceramic applied in wireless communication systems.

1. Introduction

With the rapid increase in requirements for 6G communication and broadcasting via satellite, the evolution of dielectric resonator materials for microwave frequency applications is urgently needed. The dielectric ceramics used in microwave applications should have outstanding dielectric performances such as a high permittivity ε_r, a low dielectric loss (i.e., high Q × f value), and a near-zero temperature coefficient τ_f at a resonant frequency [1,2,3]. Several kinds of dielectric materials have been investigated to satisfy these requirements for applying in microwave bands [4,5,6]. Perovskites that possess the general ABO₃ Bravais lattice have been widely studied for dielectric ceramics and play an important role in the manufacture of electronic components, resulting from their high permittivity and high reliability for practical applications [7,8]. Around the 1990s, numerous microwave dielectric ceramics with a high permittivity were proposed and realized, such as (A¹⁺_0.5A³⁺_0.5)TiO₃, BaO-Ln₂O₃–TiO₂, CaO–Li₂O-Ln₂O₃–TiO₂, and Pb-based ceramics [9,10,11]. Among these materials, CaTiO₃ sintered at 1400 °C for 4 h was proposed as a τ_f compensator because of its high positive τ_f of about 800 ppm/°C and demonstrated a ε_r value of 170 and a Q × f value of 3600 GHz [12,13]. Afterwards, related CaTiO₃-based materials and their microwave characteristics were also documented by many researchers due to the high permittivity and large τ_f of the dielectric materials [14,15,16]. Furthermore, Ca_1−xLa_2x/3TiO₃ ceramics, which are solid solution materials with La³⁺ substitution for Ca²⁺ ions in CaTiO₃, are upgraded materials for τ_f compensators. Hung et al. fabricated Ca_1−xLa_2x/3TiO₃ ceramics by sintering at 1450 °C for 4 hrs and using a conventional solid-state reaction method and demonstrated their optimum microwave dielectric performances of ε_r = 117.4, Q × f = 13,375 GHz, and τ_f = 217.2 at x = 0.4 (i.e., Ca_0.6La_0.2667TiO₃) [17,18]. Compared to CaTiO₃, Ca_0.6La_0.2667TiO₃ exhibited a higher Q×f value, but the Ca_0.6La_0.2667TiO₃ ceramics require a much higher sintering temperature (ST) of approximately 1450 °C, meaning a high energy consumption for industrial applications. Therefore, it is necessary to improve the microwave dielectric performance and reduce the thermal budget of ABO₃ ceramics. In this work, the partial substitution of Sn⁴⁺ for Ti⁴⁺ in (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramics was fabricated because the ionic radius 60.5 pm of Ti⁴⁺ is near 69 pm of Sn⁴⁺. Solid solution systems of dielectric ceramic (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ were synthesized using the solid-state reaction method with various x values. It was found that (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ sintered at 1350 °C for 4 h possessed the highest Q × f value, a moderate permittivity, and a temperature coefficient through adjusting the x value. Hence, this kind of ceramic material not only has excellent dielectric performance but also can save a lot of energy consumption and reduce production costs during the production process. On the other hand, microstructure observations of the sintered sample surfaces were examined by scanning electron microscopy (SEM, Philips XL-40FEG, FEI Company, Hillsboro, OR, USA). The crystalline phases of the calcined powder were identified by X-ray powder diffraction (XRD) analysis using Cu-Kα radiation with a 2θ range from 20° to 80°. As a result of systematic discussion of the results, the correlations between morphologies, the amount of Sn⁴⁺ cations, and the microwave dielectric properties of the samples were determined.

2. Experimental Procedure

The (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramic samples were prepared by a solid-state reaction method. The samples were calcined at 1100 °C (4 h) and sintered at temperatures from 1250 to 1425 °C (4 h). The starting materials were oxide powders CaCO₃, TiO₂, SrCO₃, and SnO₂, with a high purity of 99.9%. The starting materials were mixed according to the stoichiometry of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃, and ground in distilled water for 10 h in a baling mill with agate balls. In order to form the desired composition (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃, the calcined powder was mixed with PVA solution as a binder and milled for 5hrs again. Subsequently, the pellets of 11 mm diameter and 5 mm thickness were pressed by uniaxial pressing. After debinding, these pellets were sintered at various temperatures for 4 h, whereas the heating and cooling rates of a heater were both set at 10 °C/min. Characterization of phase structure, microstructure, and electrical properties of the samples was performed using the X-ray diffraction (XRD) method with Cu-Ka radiation, and the microstructures of the sintered sample surfaces were examined by scanning electron microscopy (SEM, Philips XL-40FEG), and the bulk densities of the samples were measured by the Archimedes method. Furthermore, the microwave dielectric properties were evaluated using the Hakki and Colman’s dielectric resonant TE₀₁₁ and TE_01δ methods [19,20], the HP8757D network analyzer, and a HP8350 sweep oscillator. The temperature coefficients were evaluated at a resonant frequency in the temperature range of 20–80 °C. A general technique was used to estimate the temperature coefficient τ_f through measuring a resonant frequency at a certain temperature, namely, a sample was placed on a test set with a thermostat in the temperature range from 20 °C to 80 °C. The temperature coefficient of a resonant frequency was evaluated by Equation (1):

$${\mathsf{\tau }}_{\mathrm{f}}={\displaystyle \frac{f_{80}-f_{20}}{60f_{20}}}\times {10}^6(\mathrm{ppm}/°\mathrm{C})$$

(1)

where f_T is the resonant frequency of the dielectric resonator at a temperature of T (°C).

3. Results and Discussion

A tolerance factor t is helpful in predicting the stability of the perovskite structure, and the t value is typically in the range from 0.748 to 1.333 [21].

Table 1. Lattice parameters, cell volumes, ionic polarizabilities, and ε_r data for sintered (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ sintered at 1350 °C.

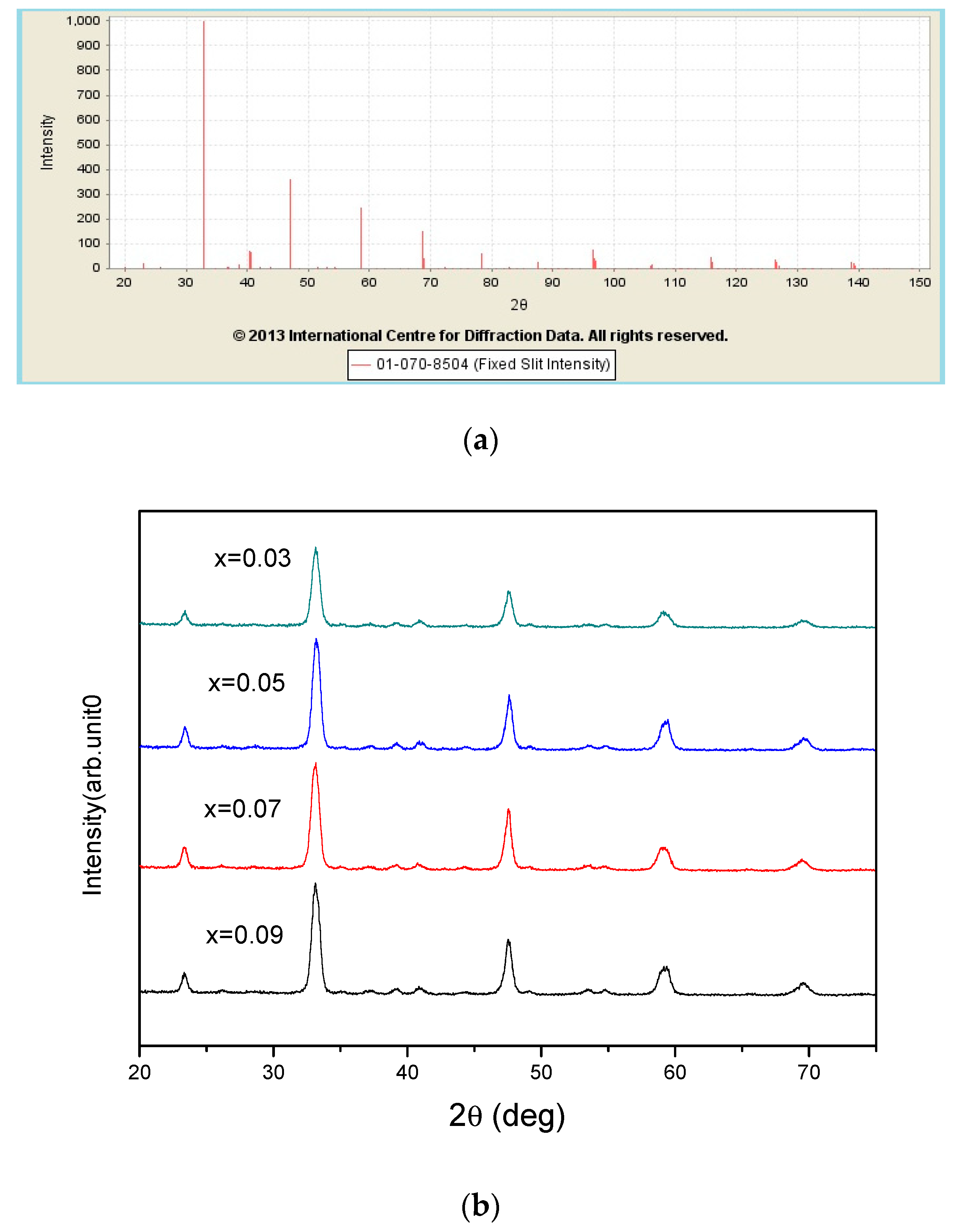
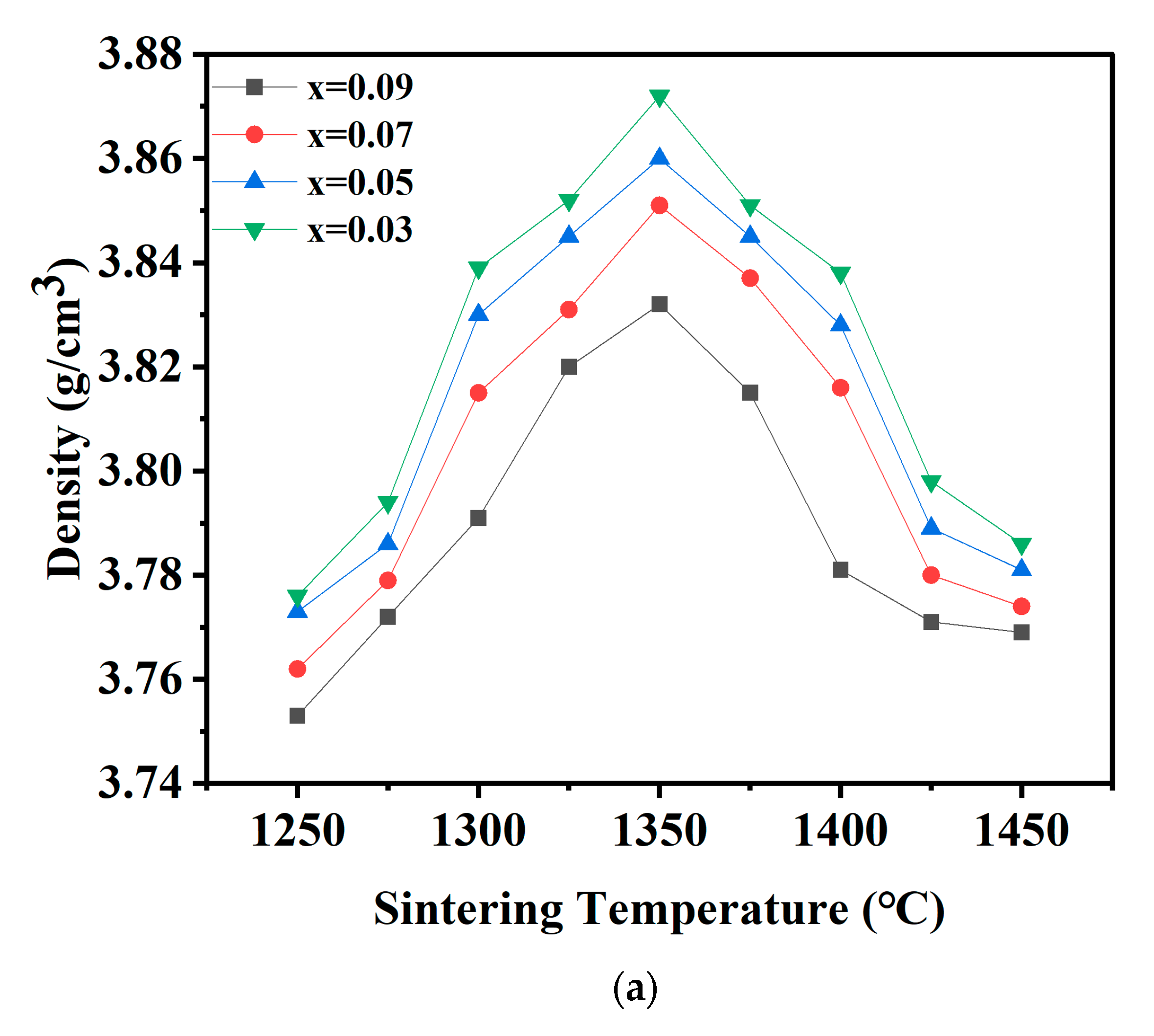
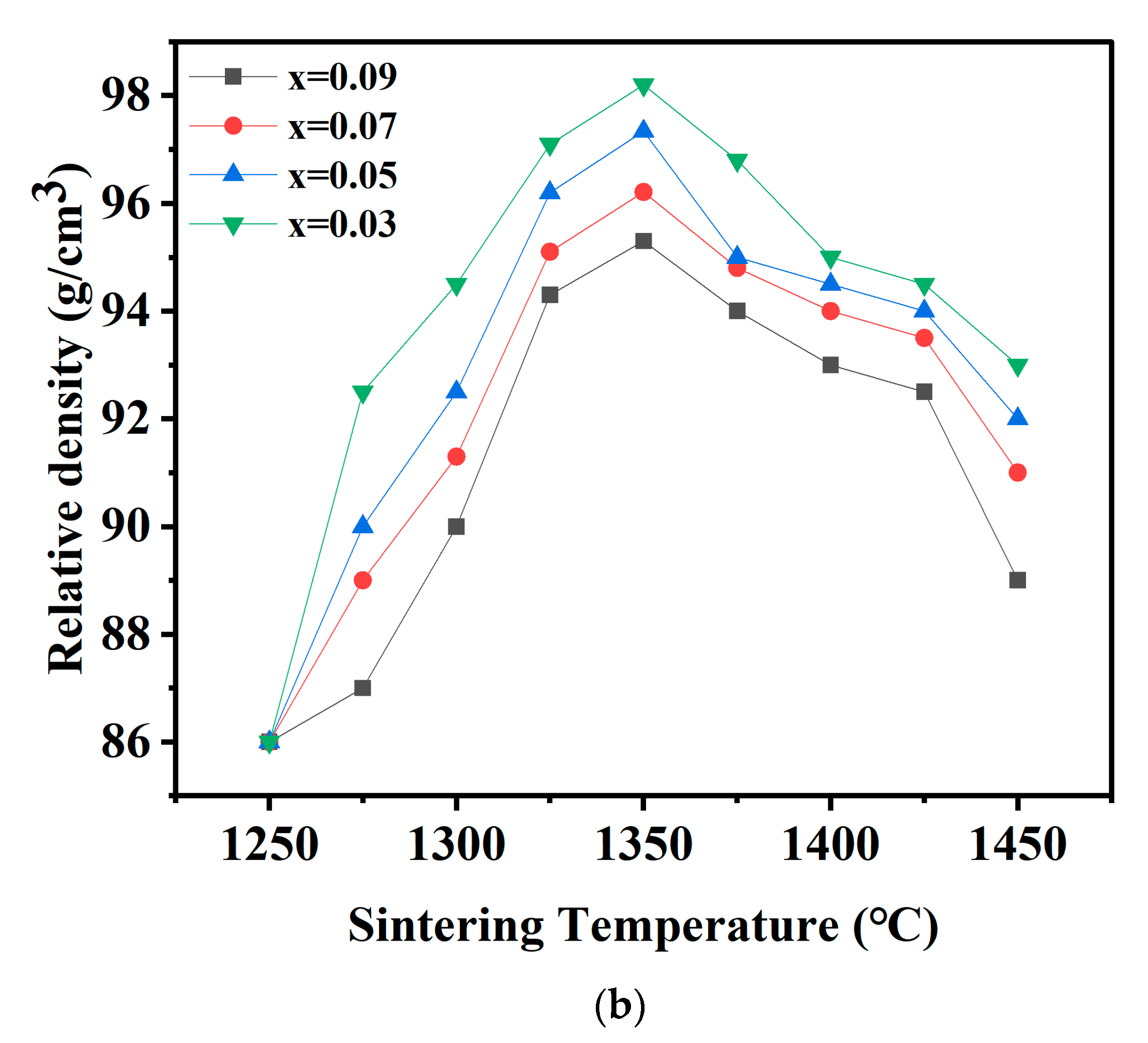
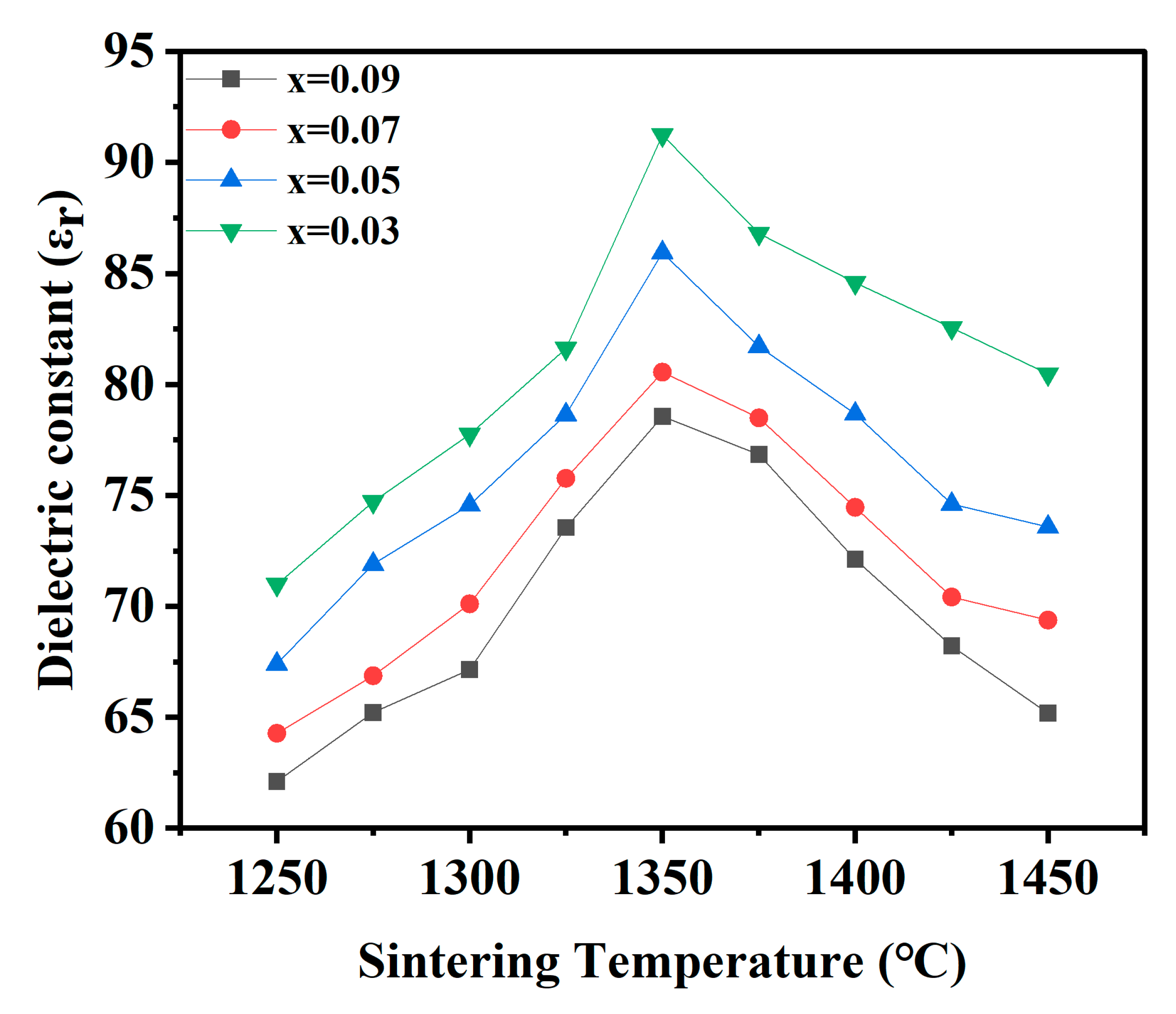
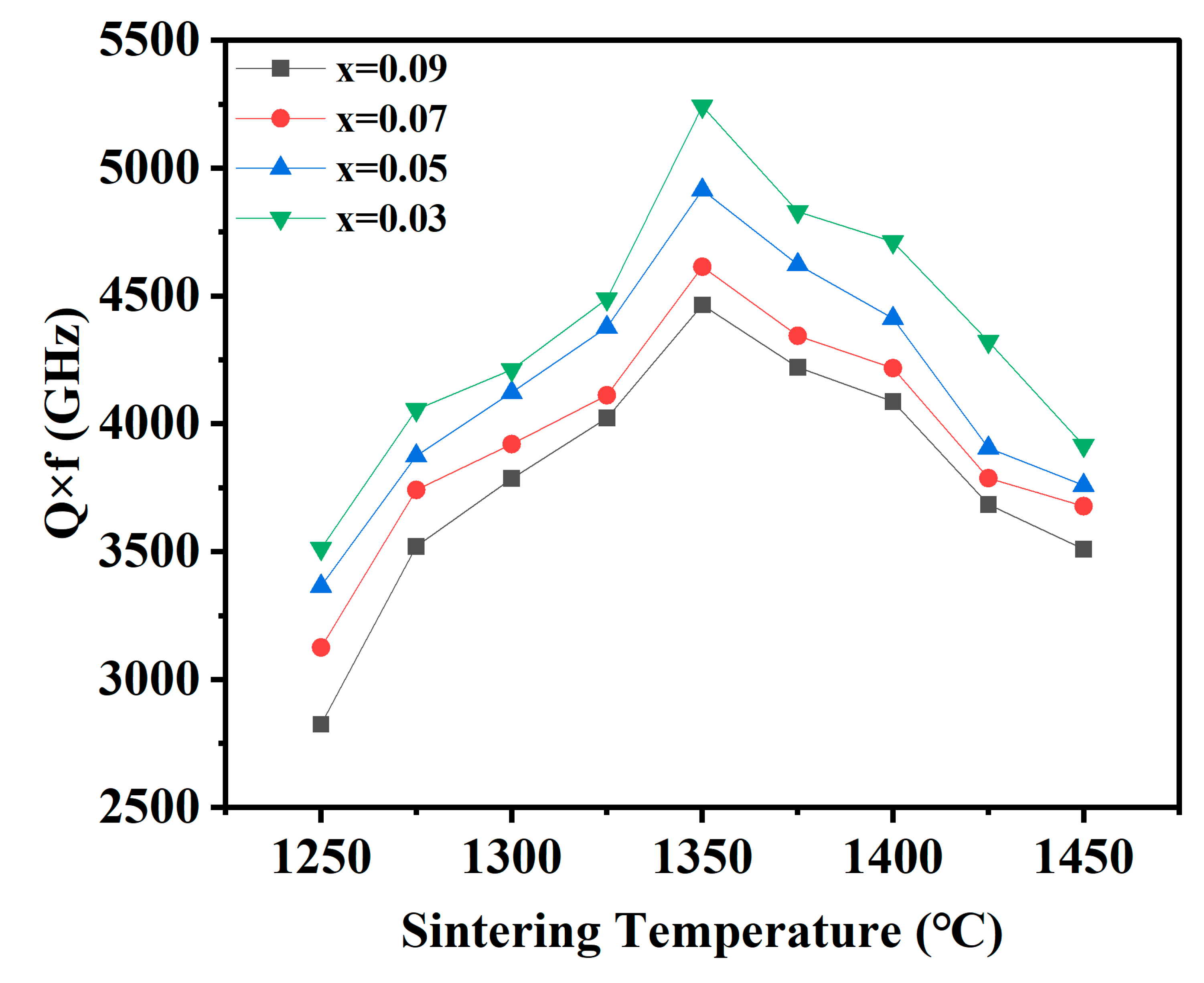
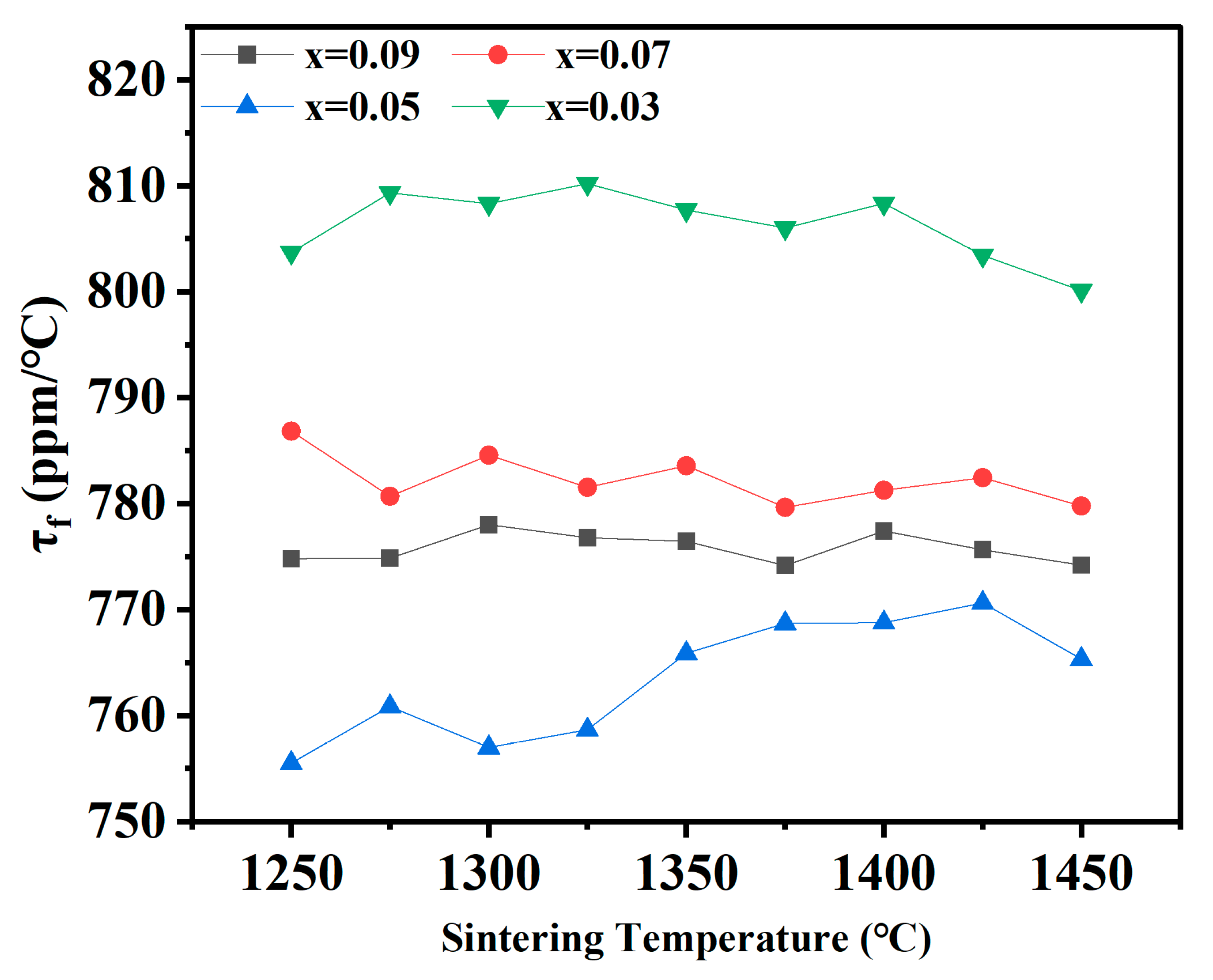
x =	0.03	0.05	0.07	0.09
a = b = c (Å)	6.2046	6.2055	6.2066	6.2081
	$\pm$2.6224	$\pm$2.6238	$\pm$2.6248	$\pm$2.6265
Vm (Å3)	238.8589	238.9628	239.09	239.263
αm(theory)	12.171	12.169	12.165	12.167
αm(exp)	11.98	11.961	11.952	11.934
Dielectric (cal.)	92.35	86.43	92.12	79.89
Dielectric (measured)	91.24	85.94	80.55	78.56
Tolerance factor	0.94731	0.94621	0.94538	0.94501

shows the tolerance factors and other parameters of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramics with various compositions x. The tolerance factor t, which is defined by $t=(R_A+R_O)/\sqrt{2}(R_B+R_O)$ in the ABO₃ perovskite, was calculated after taking the average ionic radius of a corresponding ionic for (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ [22]. In this equation, R_A and R_B are the average ionic radii of A and B cations, and R_O is the radius of O²⁻ at an appropriate coordination site, respectively. The near 0.95 value of a tolerance factor demonstrates that a (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramic has good stability in this study.

Table 2 reveals the lattice parameter, cell volume, ionic polarizabilities, and ε_r data measured at a frequency of 10 GHz for selected ceramics of the perovskite (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃. With the increased replacement of Sn⁴⁺ for Ti⁴⁺, both the lattice constant and unit cell volume increase. The dielectric constant decreased with increasing Sn⁴⁺ content because ionic polarizabilities decreased.

Figure 1a depicts the XRD patterns of (Ca_0.75Sr_0.25)TiO₃ ceramics sintered at 1350 °C. The obvious diffraction peaks are located at 32.8°, 40.44°, 47.11°, 58.54°, and 68.77°. All diffraction peaks can be indexed from a standard PDF card (ICDD-PDF #01-070-8504), and no second phase was observed, which confirms that a continuous solid solution has been formed. By reason of slight Sn⁴⁺ substitution in composition, Figure 1b reveals the X-ray diffraction patterns of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ (x = 0.03~0.09) ceramics sintered at 1350 °C for 4 hrs. Likewise, all the peaks indicate that the structure of a (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramic is the same as a cubic perovskite, and the detection of a minor phase by X-ray is not found, i.e., the second phase is not observed. The clear diffraction peaks of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ are located at 33.9°, 47.6°, 59.8°, and 69.17°, and those of (Ca_0.75Sr_0.25)TiO₃ are located at 32.80°, 40.44°, 47.11°, 58.54°, and 68.77°. There is no obvious deviation, but the peak intensity of the (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ phase increases slightly with the x value. Since the radii of Sn⁴⁺ and Ti⁴⁺ ions are similar, the measured XRD diffraction pattern of a sample does not produce significant deviation. In all XRD patterns shown in Figure 1 and Figure 2, the perovskite structure (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ is the main phase without any second phase. In addition, the SEM images of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ (x = 0.03) ceramics sintered at different temperatures for 4hrs are revealed in Figure 2. As seen in Figure 2e, the sample with x = 0.03 sintered at 1350 °C has the most regular and microstructure compared with other compounds sintered at different temperatures. The size of the grains grew with increasing the sintering temperature until 1350 °C. By the Archimedes method, the apparent densities of the (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramics with x = 0.03–0.09 sintered at different temperatures (1125–1450 °C) for 4hrs are measured and shown in Figure 3. The density of a sample increased with the sintering temperature from 1250 to 1350 °C, while it decreased at the higher temperatures. This phenomenon indicates that the best sintering temperature of a (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramic is 1350 °C, as observed in Figure 2e. Moreover, a relatively low density of 3.752–3.776 g/cm³ is observed for every sample sintered at 1250 °C, which is mainly attributed to a porous morphology as shown in Figure 2a. By contrast, specimens sintered at 1350 °C revealed high apparent densities, in particular, the highest value of 3.875 g/cm³ appeared when x = 0.03, referring to a dense and uniform microstructure of a (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramic. Figure 3b shows the variations in relative densities of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramics with respect to sintering temperature. At a sintering temperature of 1350 °C, the relative density exceeds 97.8%. There is a strong correlation between relative density, sintering temperatures, and relative permittivities. The relative permittivities exhibit a similar trend to that of relative density as a function of sintering temperature due to the inverse relationship between density and porosity.

A dielectric constant ${\mathsf{\epsilon }}_{\mathrm{r}}$ of a (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ (x = 0.03~0.09) ceramic is dependent on the sintering temperature and Sn⁴⁺ substitution, as demonstrated in Figure 4. It is well known that many factors, including porosity, density, secondary phases, polarizability, and structure characteristics, are able to change the dielectric constant values of the microwave dielectric ceramics.

As shown in Figure 4, the ${\mathsf{\epsilon }}_{\mathrm{r}}$ curves showed a similar trend to those of the apparent density, so that the density was assumed to play an important role in determining the dielectric constant of a sample. Both a maximum ${\mathsf{\epsilon }}_{\mathrm{r}}$ of 91.23 and the highest density of 3.875 g/cm³ were achieved for a specimen with x = 0.03 sintered at 1350 °C. Additionally, the dielectric constant of a microwave dielectric ceramic is known to be affected by ionic polarizability [23]; the ε_r values of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ increased with Sn⁴⁺ substitution for Ti⁴⁺, as mentioned above. The ionic polarizabilities (α_obs) of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ were estimated in order to clarify the effects of Zn substitution for Mg on the dielectric constant by using the Clausius–Mosotti equation:

$${\epsilon }_r={\displaystyle \frac{3{\mathit{V}}_m+8\mathit{\pi }{\mathit{\alpha }}_m}{3{\mathit{V}}_m-4\mathit{\pi }{\alpha }_{\mathit{m}}}}$$

(2)

Here, ε_r, V_m, and α_m are the relative permittivity, molar volume, and macroscopic polarizability, respectively. Using the experimental relative permittivity data and unit cell volume data, the macroscopic polarizability, α_m, was calculated. The theoretical polarizability data in Table 1 show an almost sigmoidal increase with increasing Zn²⁺ content, while the unit cell volume increased with x. The relative permittivity increased with α_m; when the value of α_m approached 3V_m/4π, the relative permittivity increased very rapidly. It has also been reported that the macroscopic polarizability of complex systems with an ideal symmetry can be determined from the summation of the polarizability of the constituent cations such that,

α_m = Σα(ions)

(3)

The theoretical polarizability (denoted as α_m(theory)) values calculated according to Equation (2) are compared with the “experimental” polarizability denoted as α_m(exp) determined using the Claussius–Mossotti relation, Equation (2) in Table 1. It is noted that α_m(exp) for the (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ end member is larger than the α_m(theory) value; the α_m(exp) values are larger than α_m(theory). Shannon [24] suggested that deviations from additivity of ionic polarizability arise when the compression or rattling of cations occur in the structural sites as the cation sizes are varied. The lower α_m(exp) value for (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ may thus be due to compression effects caused by the large difference between the ionic polarizabilities of Sn⁴⁺ and Ti⁴⁺. This agrees with the harmonic-oscillator model [25]. Internal factors, such as lattice vibration mode, impact the Q × f value of microwave loss. The presence of cation ordering can often result in an increase in Q × f; thus, its absence may frequently lead to a decrease in Q × f [26]. The decrease in Q × f in mixed systems has been associated by some with the loss of cation ordering in ordered cation compounds [27].

However, it should be noted that the reduction of the Q × f value can be due to either intrinsic (i.e., lattice-related) or extrinsic mechanisms. At microwave frequencies, the unloaded quality factor is said to be dependent on extrinsic factors like secondary phases, density, and oxygen vacancies. The Q × f value increases to its maximum value and subsequently decreases as the sintering temperature rises. Figure 5 demonstrates the quality factor values of samples sintered at various temperatures from 1250 °C to 1450 °C for 4 h. Generally speaking, the Q × f values can be affected by both the intrinsic and extrinsic losses. The former is caused by lattice vibration modes, while the latter may be caused by some factors such as secondary phases, grain boundaries, oxygen vacancies, densification, and porosity.

Figure 5 reveals that the variation of a Q × f curve for every compound has a trend similar to that of a density curve, meaning that the microwave property can be influenced by the densification and sintering temperature. All the Q × f curves climb upwards with the increase in sintering temperature up to 1350 °C and then bend downwards. The Q × f value of a (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramic sintered at 1350 °C reached a maximum of 5242 GHz, which could be ascribed to the enhancement of densification and elimination of pores by raising the temperature. The main factor leading to a low Q × f value of a sample is crystal defects caused by pores, just like the pores found in low-density samples. Another possible reason should be the dampening of the optical branch in lattice vibration due to the larger Sn⁴⁺ ions substitution for Ti⁴⁺ ions. Thus, both the ordering and disordering structural features can effectively influence the intrinsic losses of a dielectric.

The ${\mathsf{\tau }}_{\mathrm{f}}$ values of (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ (x = 0.03~0.09) samples at different sintering temperatures are demonstrated in Figure 6.

The relationship between the temperature coefficient of resonant frequency (TCF) and the temperature coefficient of dielectric constant (TCK), as well as the thermal expansion coefficient (α), is stated in Equation (4) [28]:

$$\mathrm{TCF}=({\displaystyle \frac{\mathrm{TCK}}{2}}+{\alpha }_L)$$

(4)

The linear thermal expansion coefficient, denoted as L, is a constant in ceramics and directly affects the temperature coefficient of capacitance (TCF) through its relationship with TCK. The temperature dependence of the dielectric constant (TCK) can be expressed as three terms (A, B, and C) in Equation (5) [29]:

$$\begin{array}{l}\mathit{T}\mathit{C}\mathit{K}={\displaystyle \frac{(\mathsf{\epsilon }-1)(\mathsf{\epsilon }+2)}{\epsilon }}\times ({\displaystyle \frac{1}{{\alpha }_m}}({\displaystyle \frac{\mathsf{\partial }{\alpha }_m}{\mathsf{\partial }T}})+{\displaystyle \frac{1}{{\alpha }_m}}({\displaystyle \frac{\mathsf{\partial }{\alpha }_m}{\mathsf{\partial }V}}){({\displaystyle \frac{\mathsf{\partial }V}{\mathsf{\partial }T}})}_P-{\displaystyle \frac{1}{V}}{({\displaystyle \frac{\mathsf{\partial }V}{\mathsf{\partial }T}})}_p)\\ ={\displaystyle \frac{(\epsilon -1)(\epsilon -2)}{\epsilon }}(A+B+C)\end{array}$$

(5)

where and V denote the polarizability and volume, respectively. The term A (commonly negative) represents the direct dependence of the polarizability on temperature. B and C represent the increase in the polarizability and the decrease in the number of polarizable ions in the unit cell, respectively; the unit cell volume increased with an increase in temperature. The B and C terms typically exhibit the highest magnitudes but possess opposite signs, rendering them of comparable value. Hence, (B + C) has a small positive value. TCK is increased by an increase in the tilting of oxygen octahedra in the perovskite structure, which corresponds to a decrease in TCF by Equation (4).

Table 2. Microwave dielectric parameters measured at a frequency of 10 GHz for selected ceramics based on the perovskite structure.

Samples	εr	Q × f (GHz)	τf (°C)	Sintering Temperature (°C)	Reference
Ca0.8Sr0.2TiO3	181	1000	+991	1350	[1]
Ca0.6La0.2667TiO3	117.4	13000	+217	1450	[30]
SrTiO3	290	4200	+1700	1400	[31]
(Ca0.95Sr0.05)(Ti1−xSnx)O3	92	10,000	+810	1350	This work

Table 2. Microwave dielectric parameters measured at a frequency of 10 GHz for selected ceramics based on the perovskite structure.

Samples	εr	Q × f (GHz)	τf (°C)	Sintering Temperature (°C)	Reference
Ca0.8Sr0.2TiO3	181	1000	+991	1350	[1]
Ca0.6La0.2667TiO3	117.4	13000	+217	1450	[30]
SrTiO3	290	4200	+1700	1400	[31]
(Ca0.95Sr0.05)(Ti1−xSnx)O3	92	10,000	+810	1350	This work

A ${\mathsf{\tau }}_{\mathrm{f}}$ is well known to be related to the composition, additives, and secondary phases of a material. When the x value increases from 0.03 to 0.09, the ${\mathsf{\tau }}_{\mathrm{f}}$ value changes from 750 ppm/°C to 810 ppm/°C. It can be observed from Figure 6 that ${\mathsf{\tau }}_{\mathrm{f}}$ does not change dramatically when the sintering temperature or x value increases. When x = 0.03 and the sintered temperature is 1350 ℃, ${\mathsf{\tau }}_{\mathrm{f}}$ = +810 ppm/°C. It is speculated that the change in sintering temperature and the amount of Sn⁴⁺ substitution have no effect on a ${\mathsf{\tau }}_{\mathrm{f}}$, and there is no relationship between ${\mathsf{\tau }}_{\mathrm{f}}$ with an apparent density, ${\mathsf{\epsilon }}_{\mathrm{r}}$, or the Q × f value.

4. Conclusions

A (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramic with high performance was successfully achieved. It was concluded that the best dielectric properties were observed for samples with x = 0.03 prepared at sintering temperature of 1350 °C: a maximum Q−f value = 5242 (GHz), a dielectric constant ε_r = 91.23, the highest density of 3.875 g/cm³ due to a dense and uniform microstructure of the samples, and a temperature coefficient of +810 ppm/°C. The microwave dielectric characterization is found to be strongly correlated with the sintering temperature and the amount of Sn⁴⁺ substitution in a (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ ceramic. Finally, it was concluded that (Ca_0.95Sr_0.05)(Ti_1−xSn_x)O₃ possessed a promising potential to be a compensator for a near-zero dielectric ceramic used in wireless communication systems.