A Multi-Teacher Knowledge Distillation Framework with Aggregation Techniques for Lightweight Deep Models
Abstract
1. Introduction
1.1. Motivation
1.2. Contributions
- A novel iterative Multi-Round Parallel Multi-Teacher KD (MPMTD) framework is proposed to enable adaptive and strategic teacher aggregation, enhancing scalability, robustness, and efficiency.
- Robust aggregation techniques from Federated Learning are introduced into the multi-teacher distillation context to address issues such as noise, conflicting predictions, and adversarial teacher behavior.
- A comprehensive evaluation of individual and combined aggregation methods is conducted, providing insights into their respective strengths and limitations.
- Aggregation is investigated at multiple levels, including both output-level and loss-level fusion, to assess their impact on student model performance.
- The optimal number of distillation rounds is identified, showing that most performance gains plateau after 2–5 rounds, thereby informing trade-offs between convergence and computational cost for edge deployment.
- The framework is validated under a cross-modal distillation setting (RGB teachers to grayscale student) on a real-world agricultural dataset with fixed splits, demonstrating its practical relevance for low-resource scenarios and real-time applications.
1.3. Organization
2. Background and Preliminaries
2.1. Edge Devices
2.2. Computational Resource Constraints and Deployment Challenges
2.2.1. Computational Resource Constraints
2.2.2. Deployment Challenges
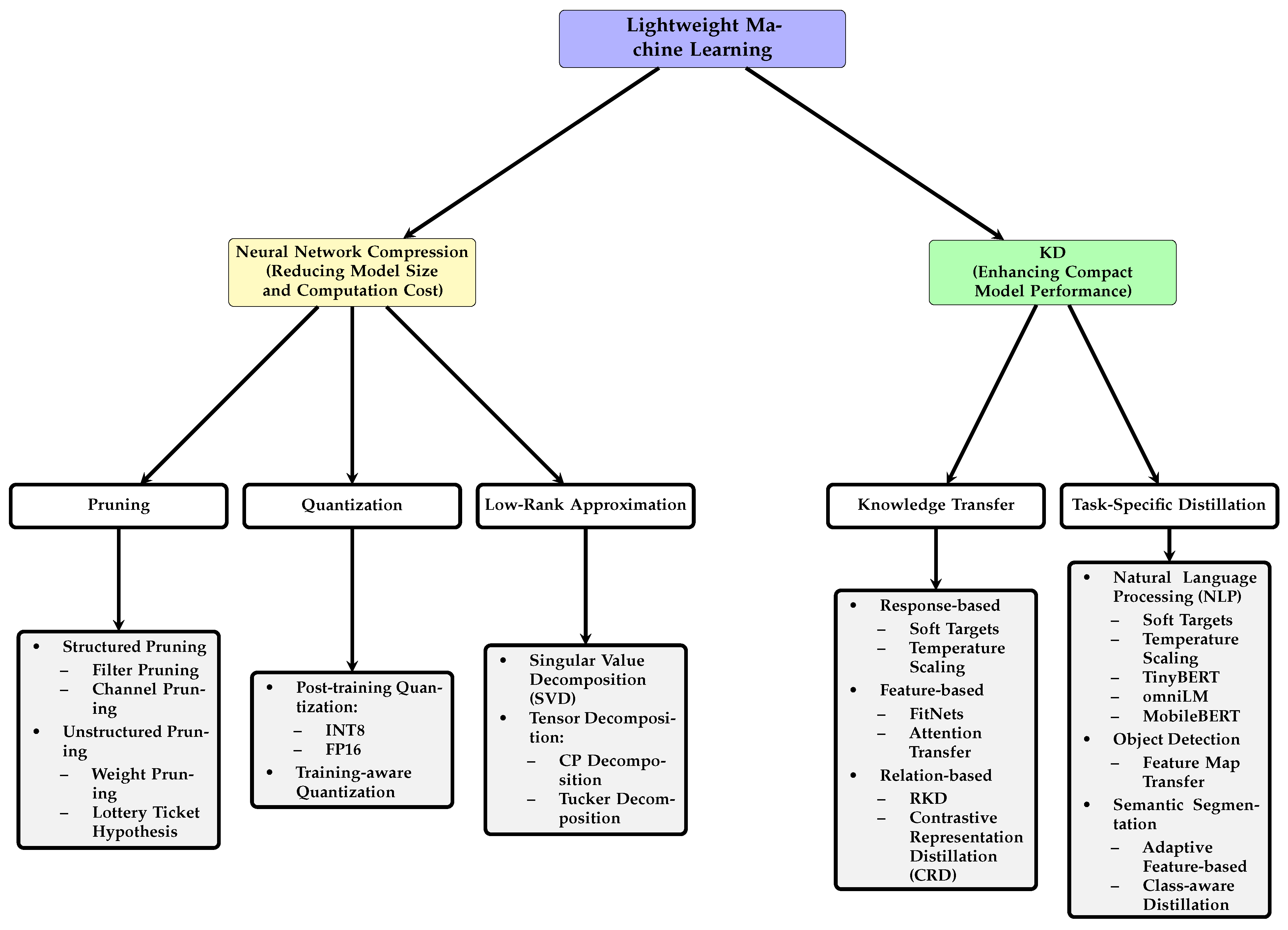
2.3. Neural Network Compression
2.4. KD
- is a weighting factor that balances the two loss terms;
- denotes the true labels;
- represents the student’s predictions with ;
- and are the softened output probabilities of the teacher and student models, respectively;
- is included to account for the gradients’ scaling effect due to the temperature T.
2.5. MT-KD Approaches
2.6. Aggregation Techniques in MT-KD
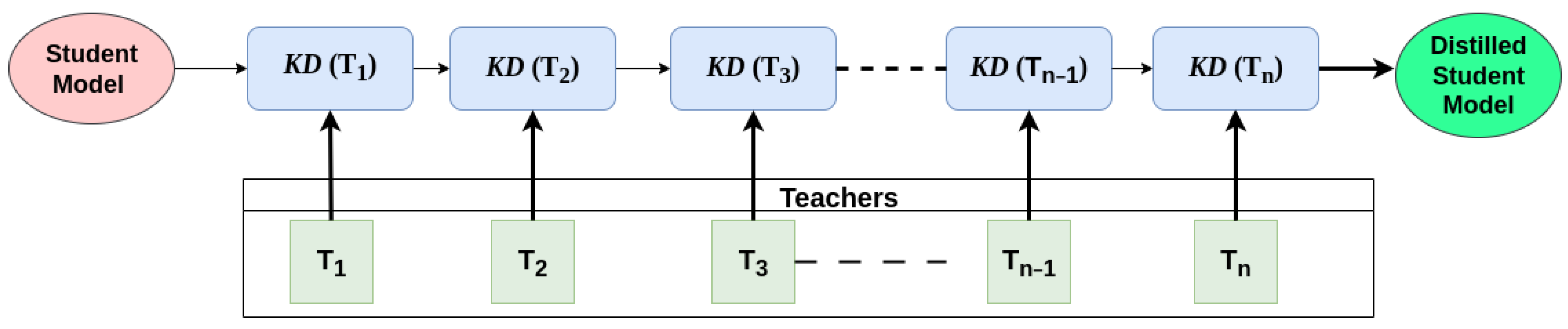
2.6.1. Parallel Aggregation
2.6.2. Successive Aggregation
2.7. Aggregation Techniques in FL
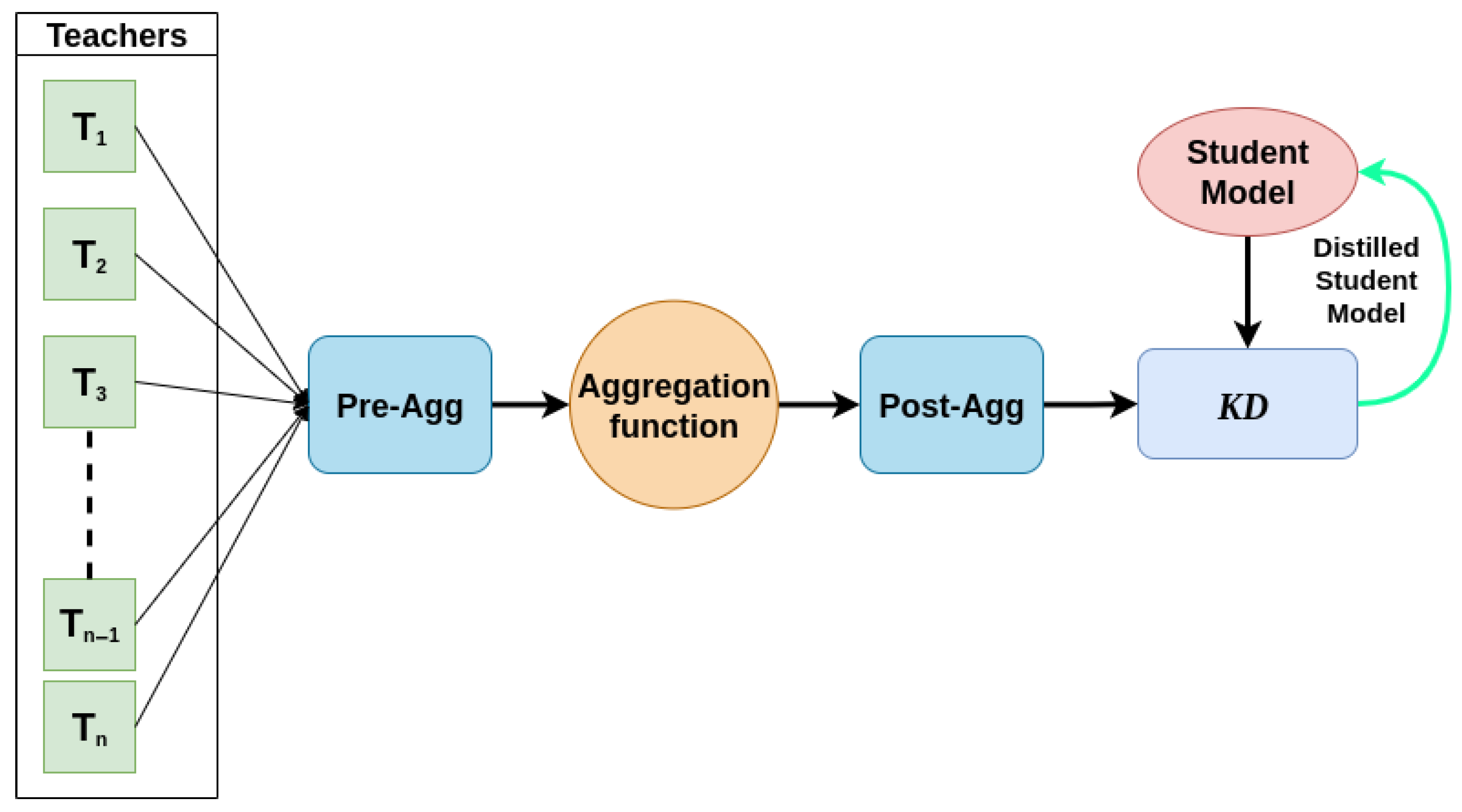
2.8. Overview of Aggregation Strategies
2.9. Aggregation Function
| Algorithm 1: Krum Aggregation for Multi-Teacher KD. |
 |
| Algorithm 2: Byzantine-Resilient Aggregation (Trimmed Mean). |
Input: Set of teacher models , input x, trim fraction c Output: Aggregated prediction
|
3. Prposed Method
3.1. Aggregation Levels in MT-KD
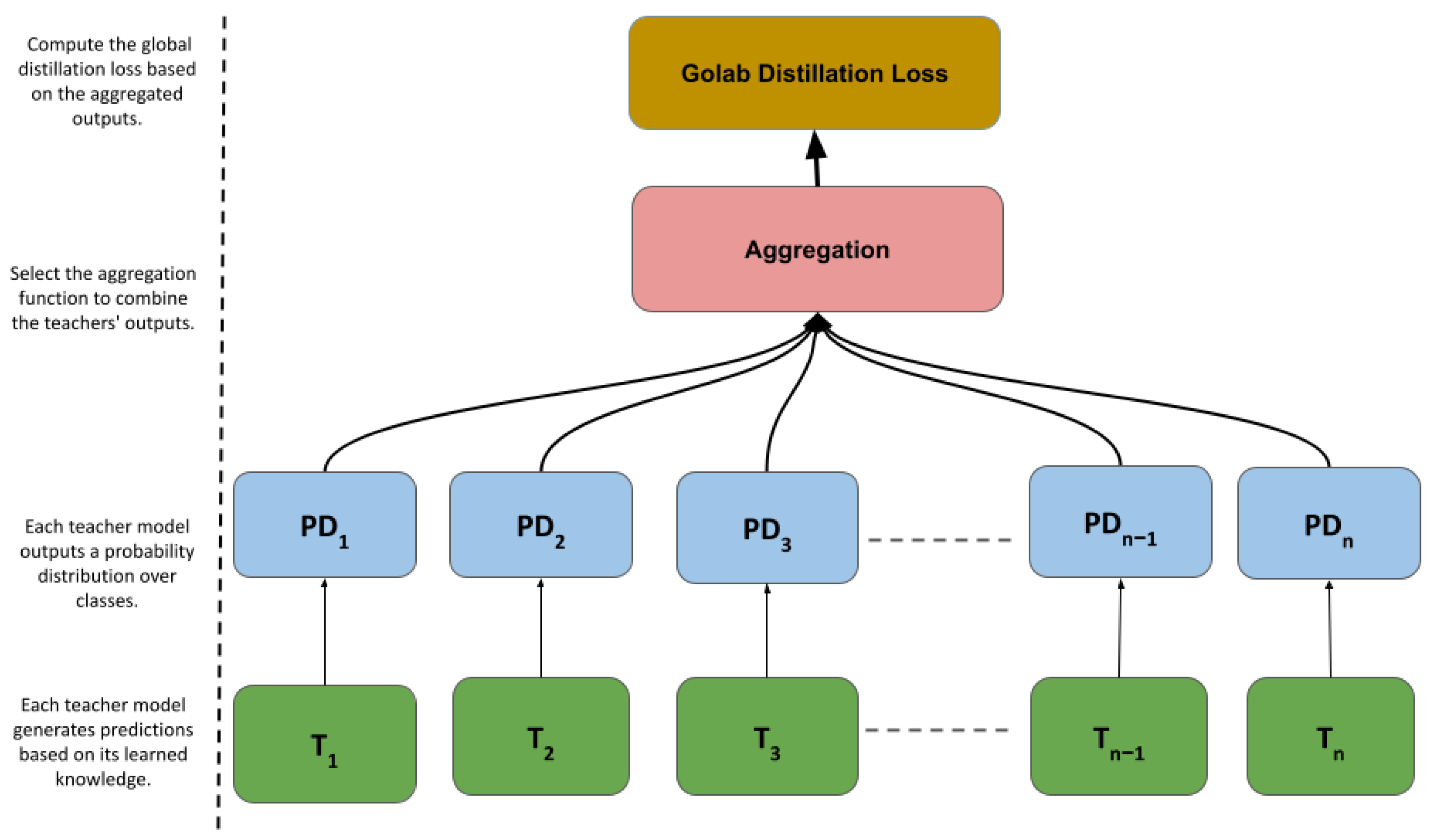
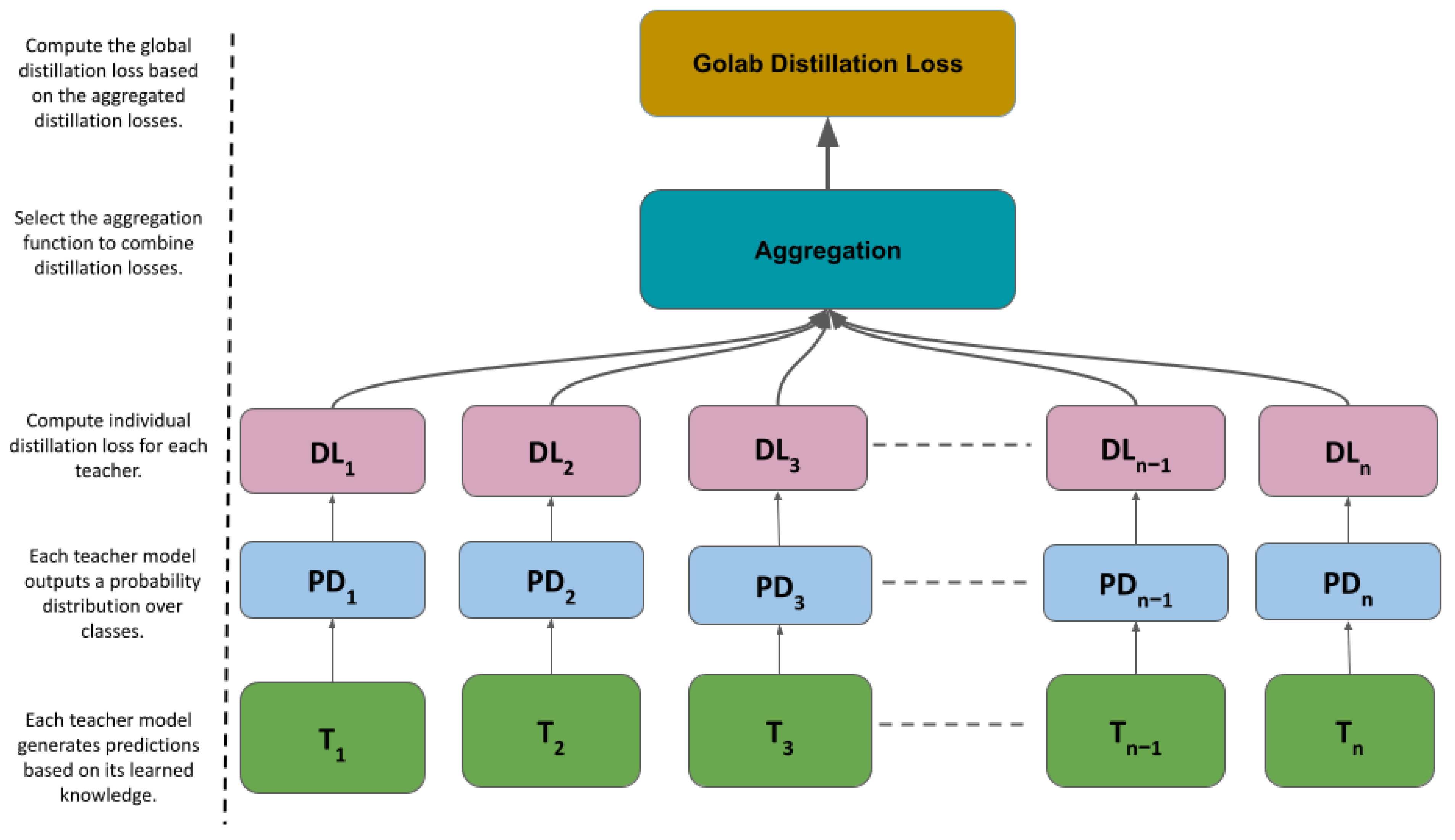
3.1.1. PD
3.1.2. DL
3.1.3. Comparison of Aggregation Levels
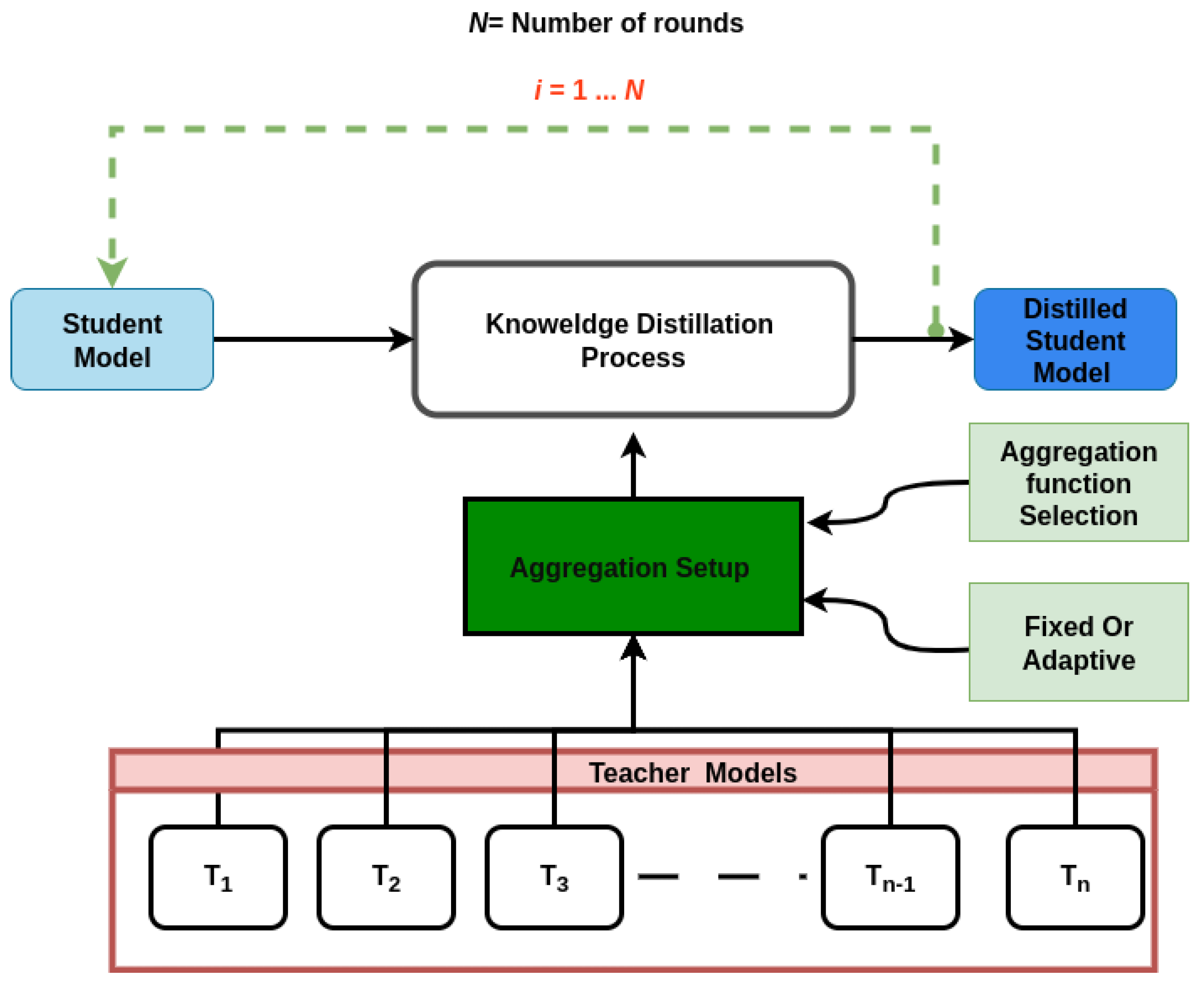
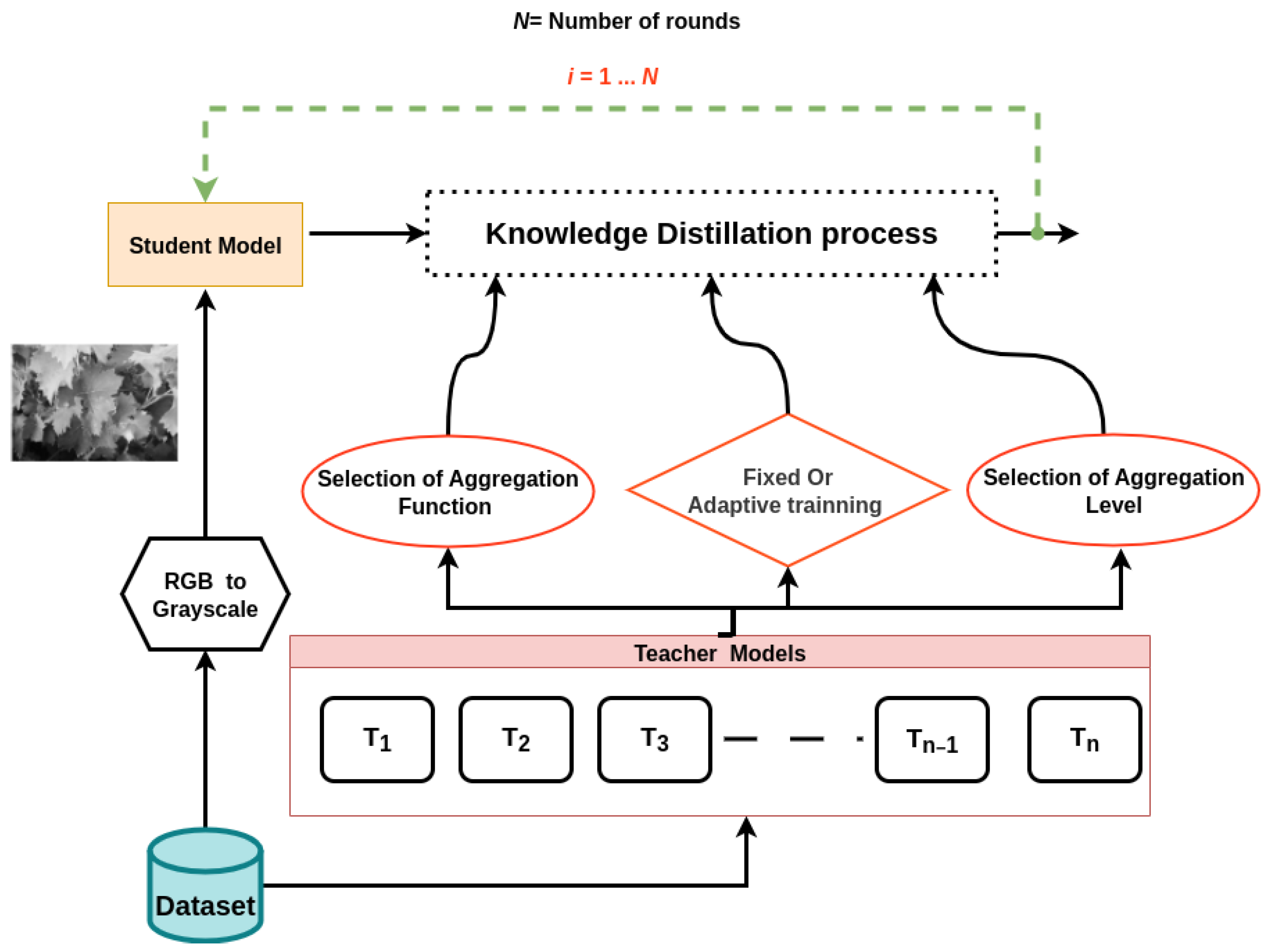
3.2. Proposed Method: MPMTD Framework
3.3. Fixed Aggregation Strategy
- represents a fixed mathematical aggregation method used for all rounds.
- is the input at the selected aggregation level, meaning the following:
- −
- If the aggregation level is DL, then (distillation loss from teacher i).
- −
- If the aggregation level is Proba, then (probability distribution from teacher i).
3.4. Adaptive Multi-Round Aggregation Strategy
- Alternating DL and PD aggregation: switching between DL-level aggregation and PD-level aggregation across rounds. For example, DL-based aggregation may be used in round t, followed by PD-based aggregation in round , and then back to DL.
- Iterative aggregation with DL Level: using different aggregation methods (e.g., mean, median, Byzantine, Krum, weighted) in each round while maintaining a consistent aggregation level at DL.
- Iterative aggregation with PD Level: similar to the previous approach but consistently using probability distribution–level aggregation (PD) instead of DL.
4. Experimental Results
4.1. Methodology Overview
4.1.1. Dataset Description
4.1.2. Data Preprocessing
- Rescaling: Images were resized to align with the model input dimensions.
- Normalization: Pixel values were scaled to the [0, 1] range to accelerate convergence and enhance training stability.
- Data augmentation: Techniques such as rotation, flipping, and random cropping were applied to enhance generalization.
- Grayscale conversion: Images processed for the student model were converted from RGB (224 × 224 × 3) to grayscale (224 × 224 × 1). This step significantly reduces computational complexity while preserving key visual information for classification.
4.1.3. Data Splitting
- Training set: 70% of the dataset (randomly sampled in each run).
- Validation set: 15% of the dataset (randomly sampled in each run).
- Test set: 15% of the dataset (remains unchanged across experiments).
4.1.4. Student Model Training
4.1.5. Teacher Model Training
4.1.6. Evaluation Metrics
- Accuracy: The proportion of correctly classified samples, computed as follows:
- F1-score: The harmonic mean of precision and recall, particularly useful for handling imbalanced datasets, is calculated as follows:
- Confusion matrix: This provides a granular breakdown of classification performance, capturing True Positives (TP), False Positives (FP), True Negatives (TN), and False Negatives (FN).
- Computational efficiency: Computational efficiency is measured by the following:
- −
- Parameter count: The total number of trainable parameters.
- −
- Inference time: The average time required for the model to classify a single image.
4.1.7. Experimental Setup
4.2. KD Process
4.3. Baseline Performance
4.4. Individual Aggregation Analysis
Performance Metrics Overview
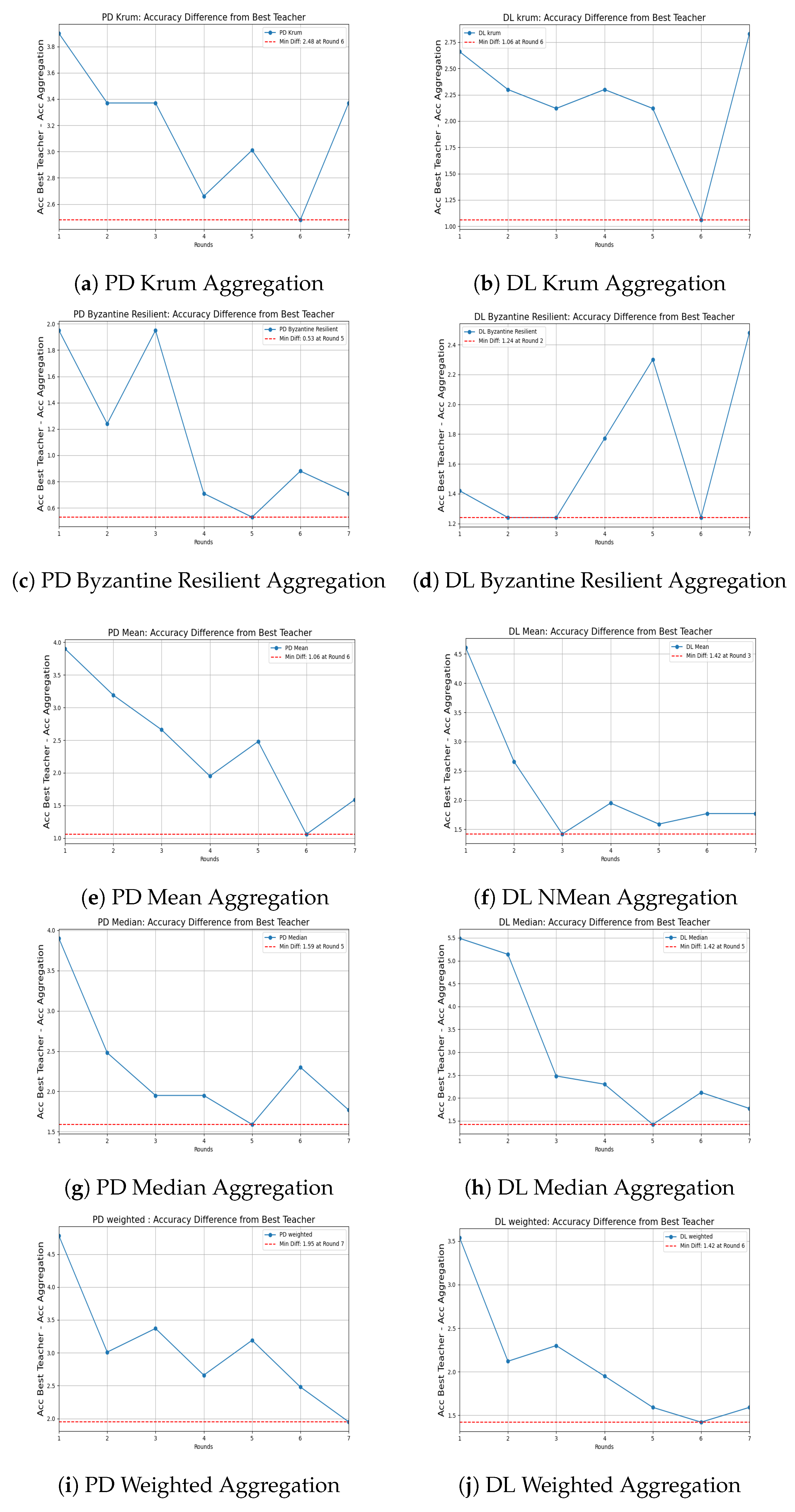
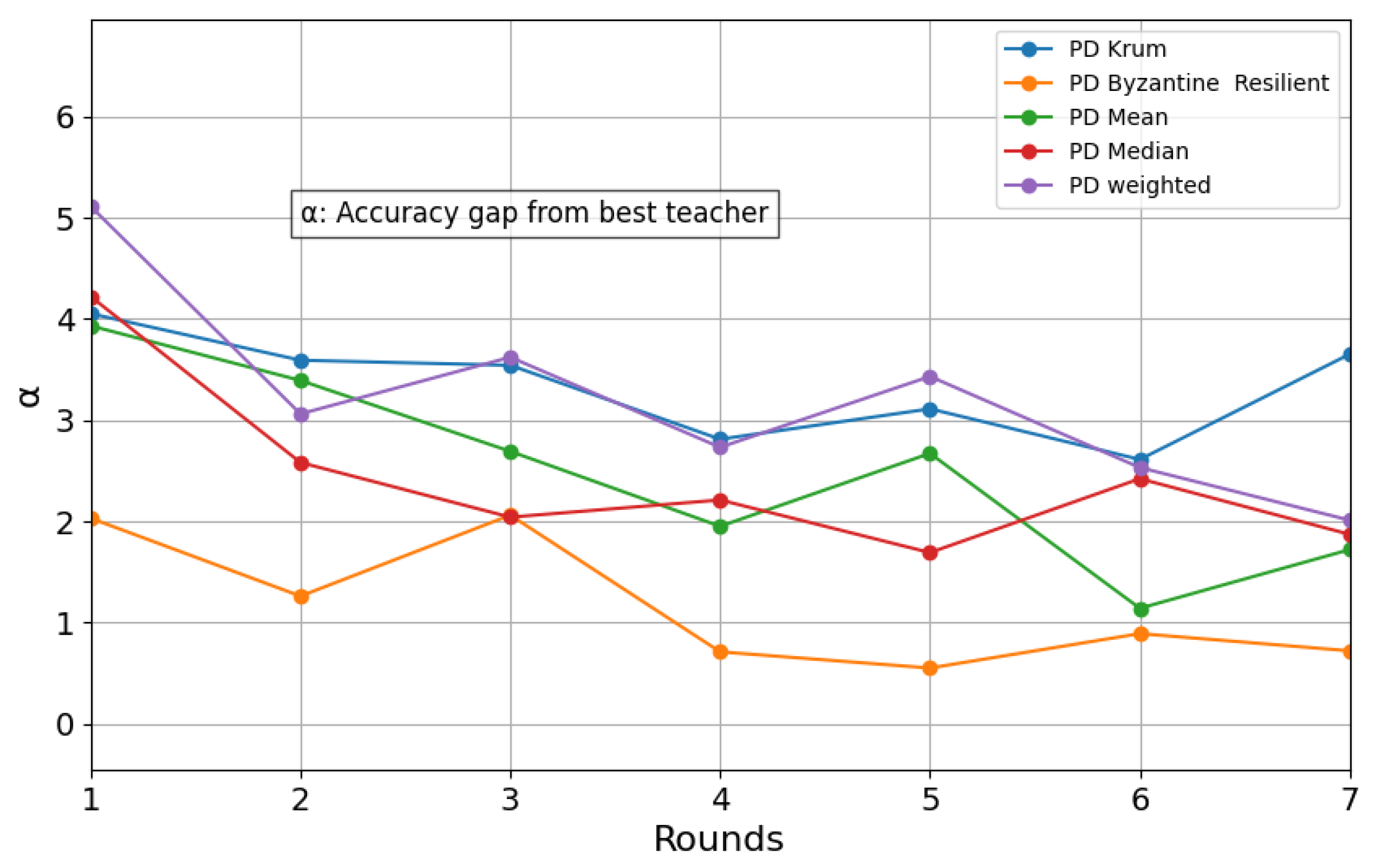
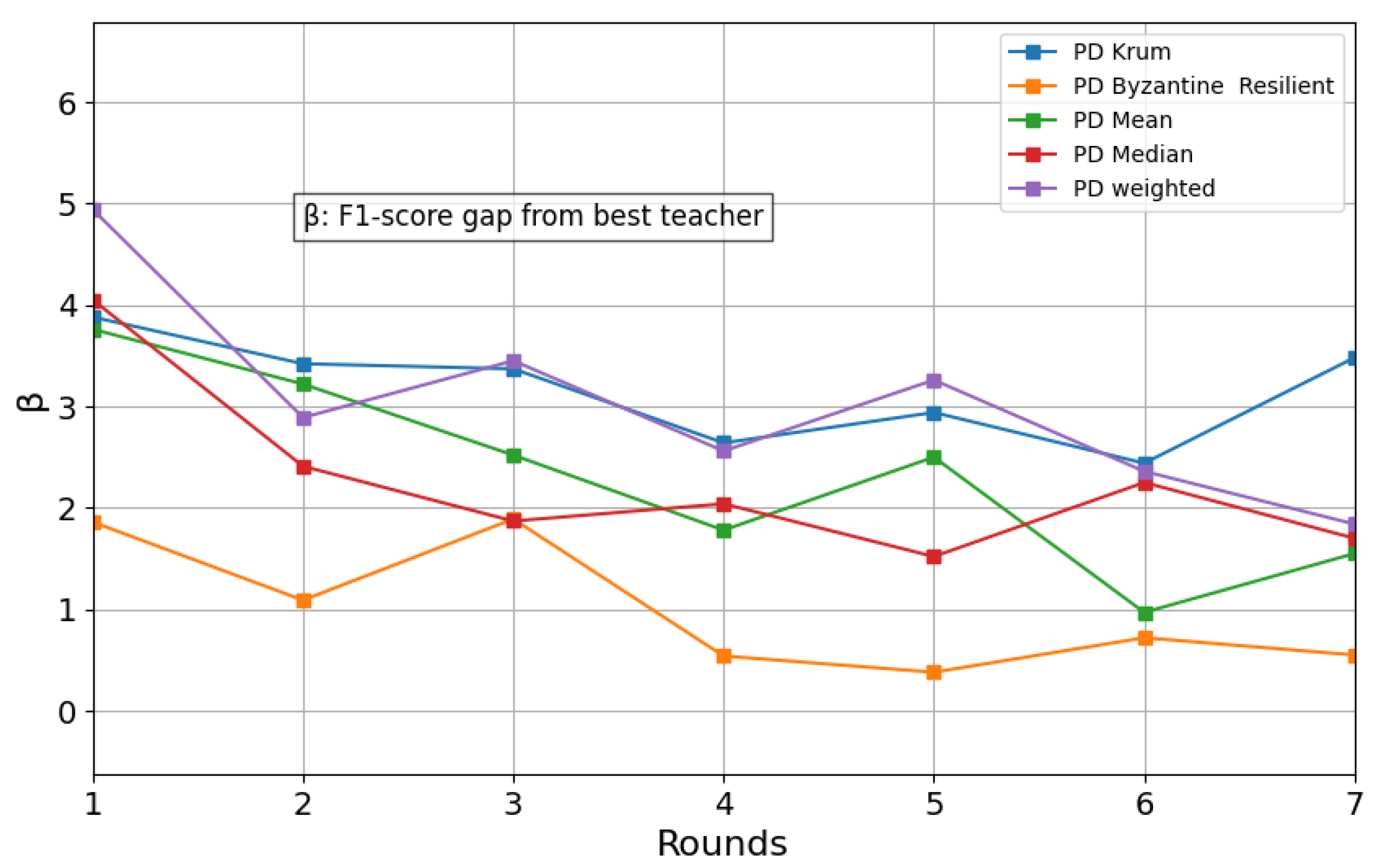
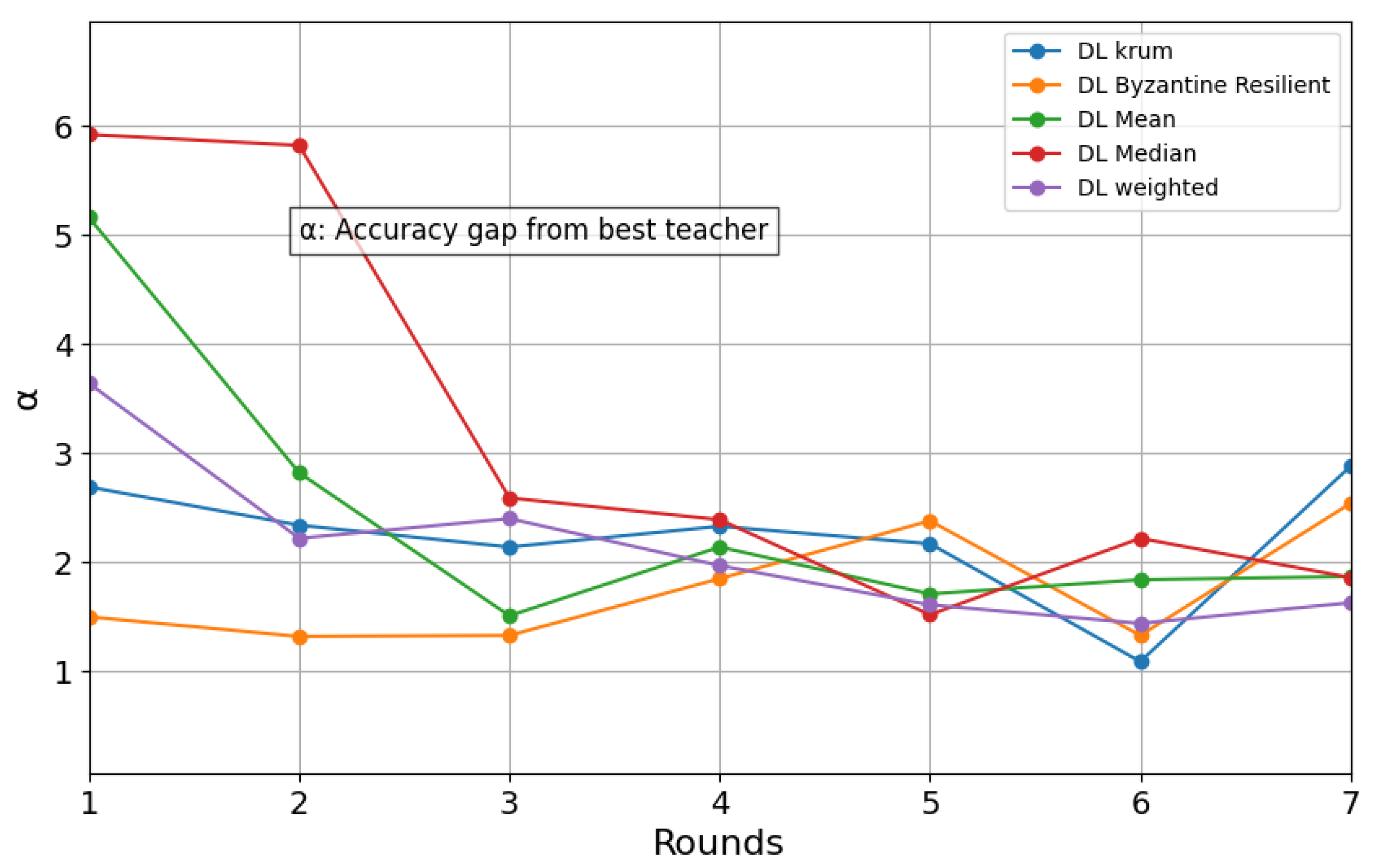
4.5. Accuracy Difference Between Best Teacher and Student over Training Rounds
4.5.1. Performance Analysis
- Byzantine-Resilient aggregation achieves the fastest convergence, reducing the accuracy difference to 0.53 at Round 5, indicating strong robustness and efficient knowledge transfer.
- Mean aggregation steadily reduces the gap, reaching its minimum difference of 1.06 at Round 6, showing a balanced learning curve.
- Weighted aggregation also shows improvement, but it takes longer, with the smallest accuracy difference being 1.95 at Round 7.
- Krum aggregation demonstrates slower convergence, with more fluctuations, and a final minimum difference of 2.48 at Round 6.
4.5.2. Visualization of Accuracy Difference Trends
4.5.3. Optimal Number of Rounds
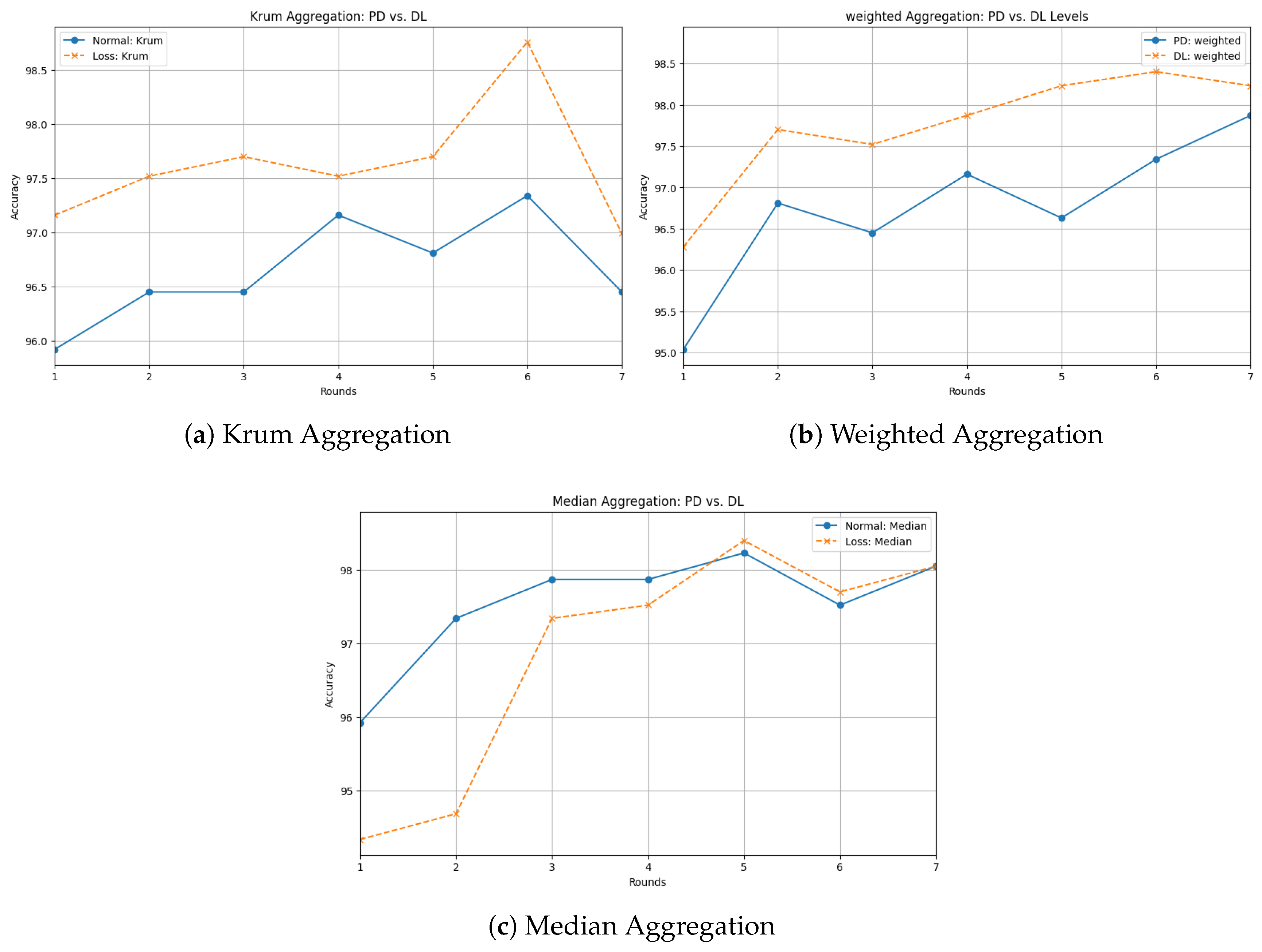
4.6. Evaluation of PD vs. DL Aggregation
4.6.1. Aggregation Methods Where Loss-Based Aggregation Outperforms Probability-Based Aggregation
4.6.2. Aggregation Methods Where Probability-Based Aggregation Outperforms Loss-Based Aggregation
4.6.3. Interpretation of Results
- Loss-based aggregation leads to more stable learning in methods like Krum, Weighted, and Median aggregation. These approaches seem to benefit from refining student training signals at the loss level, allowing the model to learn in a smoother, more structured way.
- Probability-based aggregation tends to generalize better for methods like Byzantine Resilient and Mean aggregation. In these cases, relying on the direct probability outputs of multiple teachers provides a more effective guiding signal for the student model, reducing the need for complex loss-based adjustments.
- No single strategy is universally best as the effectiveness of an aggregation technique depends on the context. This suggests that a hybrid approach that dynamically switches between probability and loss-based aggregation could be an even better strategy, depending on the training conditions and the presence of adversarial influences.
4.7. Evaluation of PL-Level and DL-Level Aggregation Strategies
4.7.1. Performance of PL-Level Aggregation
4.7.2. Performance of DL-Level Aggregation
4.8. Multi-Round Aggregation with Varying Techniques per Round
4.8.1. Mixed-Level Aggregation Across Rounds
4.8.2. Same-Level Aggregation Across Rounds
- DL Aggregation: Aggregation is consistently applied at the distillation loss-level across all rounds. This experiment examines whether DL-based aggregation leads to smoother convergence and better generalization.
- Probability Distribution Aggregation: Aggregation is performed at the probability distribution level in every round. This experiment assesses whether directly averaging teacher probability outputs results in superior model performance.
5. Discussion
5.1. Advantages and Contributions
5.2. Limitations and Challenges
5.3. Real-World Applications
5.4. Future Research Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ML | Machine Learning |
| KD | Knowledge Distillation |
| CNN | Convolutional Neural Network |
| IoT | Internet of Things |
| MT-KD | Multi-Teacher Knowledge Distillation |
| MPMTD | Multi-Round Parallel Multi-Teacher Distillation |
| CA-MKD | Confidence-Aware Multi-Teacher KD |
| DL | Distillation Loss |
| PD | Probability Distribution |
| PL | Probability Level |
| KL | Kullback–Leibler |
| RGB | Red, Green, Blue (Color Channels) |
| DDKD | Direct Data Knowledge Distillation |
| SKD | Self-Knowledge Distillation |
| TS | Teacher–Student |
| ViTs | Vision Transformers |
References
- Sharifani, K.; Amini, M. Machine learning and deep learning: A review of methods and applications. World Inf. Technol. Eng. J. 2023, 10, 3897–3904. [Google Scholar]
- Menghani, G. Efficient deep learning: A survey on making deep learning models smaller, faster, and better. ACM Comput. Surv. 2023, 55, 1–37. [Google Scholar] [CrossRef]
- Capra, M.; Peloso, R.; Masera, G.; Ruo Roch, M.; Martina, M. Edge computing: A survey on the hardware requirements in the internet of things world. Future Internet 2019, 11, 100. [Google Scholar] [CrossRef]
- Kim, H.; Khan, M.U.K.; Kyung, C.M. Efficient neural network compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12569–12577. [Google Scholar]
- Phuong, M.; Lampert, C. Towards understanding knowledge distillation. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 5142–5151. [Google Scholar]
- Chen, C.; Zhang, P.; Zhang, H.; Dai, J.; Yi, Y.; Zhang, H.; Zhang, Y. Deep learning on computational-resource-limited platforms: A survey. Mob. Inf. Syst. 2020, 2020, 8454327. [Google Scholar] [CrossRef]
- Liang, X.; Wu, L.; Li, J.; Qin, T.; Zhang, M.; Liu, T.Y. Multi-teacher distillation with single model for neural machine translation. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 992–1002. [Google Scholar] [CrossRef]
- Ye, X.; Jiang, R.; Tian, X.; Zhang, R.; Chen, Y. Knowledge Distillation via Multi-Teacher Feature Ensemble. IEEE Signal Process. Lett. 2024, 31, 566–570. [Google Scholar] [CrossRef]
- Zhu, E.Y.; Zhao, C.; Yang, H.; Li, J.; Wu, Y.; Ding, R. A Comprehensive Review of Knowledge Distillation-Methods, Applications, and Future Directions. Int. J. Innov. Res. Comput. Sci. Technol. 2024, 12, 106–112. [Google Scholar] [CrossRef]
- Long, J.; Yin, Z.; Han, Y.; Huang, W. MKDAT: Multi-Level Knowledge Distillation with Adaptive Temperature for Distantly Supervised Relation Extraction. Information 2024, 15, 382. [Google Scholar] [CrossRef]
- Jiang, Y.; Feng, C.; Zhang, F.; Bull, D. MTKD: Multi-teacher knowledge distillation for image super-resolution. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 364–382. [Google Scholar]
- Zhang, T.; Liu, Y. MTUW-GAN: A Multi-Teacher Knowledge Distillation Generative Adversarial Network for Underwater Image Enhancement. Appl. Sci. 2024, 14, 529. [Google Scholar] [CrossRef]
- Krichen, M.; Abdalzaher, M.S.; Shaaban, M.; Aburukba, R. Lightweight AI for Drones: A Survey. In Proceedings of the 2025 7th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 8–10 April 2025; pp. 1–6. [Google Scholar]
- Li, W.; Hu, D.; Wang, D. The Design of a Lightweight AI Robot for Logistics Handling. In Proceedings of the 2024 10th International Conference on Mechanical and Electronics Engineering (ICMEE), Xi’an, China, 27–29 December 2024; pp. 195–200. [Google Scholar]
- Chen, L.; Ding, Q.; Zou, Q.; Chen, Z.; Li, L. DenseLightNet: A light-weight vehicle detection network for autonomous driving. IEEE Trans. Ind. Electron. 2020, 67, 10600–10609. [Google Scholar] [CrossRef]
- Sipola, T.; Alatalo, J.; Kokkonen, T.; Rantonen, M. Artificial intelligence in the IoT era: A review of edge AI hardware and software. In Proceedings of the 2022 31st Conference of Open Innovations Association (FRUCT), Helsinki, Finland, 27–29 April 2022; pp. 320–331. [Google Scholar]
- Asal, B.; Can, A.B. Ensemble-Based Knowledge Distillation for Video Anomaly Detection. Appl. Sci. 2024, 14, 1032. [Google Scholar] [CrossRef]
- Nanayakkara, S.I.; Pokhrel, S.R.; Li, G. Understanding global aggregation and optimization of federated learning. Future Gener. Comput. Syst. 2024, 159, 114–133. [Google Scholar] [CrossRef]
- Khraisat, A.; Alazab, A.; Singh, S.; Jan, T.; Gomez, A., Jr. Survey on federated learning for intrusion detection system: Concept, architectures, aggregation strategies, challenges, and future directions. ACM Comput. Surv. 2024, 57, 1–38. [Google Scholar] [CrossRef]
- Ni, L.; Gong, X.; Li, J.; Tang, Y.; Luan, Z.; Zhang, J. rfedfw: Secure and trustable aggregation scheme for byzantine-robust federated learning in internet of things. Inf. Sci. 2024, 653, 119784. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, Z.; Weng, W.; Yu, W.; Zhou, J. DE-MKD: Decoupled Multi-Teacher Knowledge Distillation Based on Entropy. Mathematics 2024, 12, 1672. [Google Scholar] [CrossRef]
- Mu, X.; Antwi-Afari, M.F. The applications of Internet of Things (IoT) in industrial management: A science mapping review. Int. J. Prod. Res. 2024, 62, 1928–1952. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Reddy, N.V.; Reddy, A.; Pranavadithya, S.; Kumar, J.J. A critical review on agricultural robots. Int. J. Mech. Eng. Technol. 2016, 7, 183–188. [Google Scholar]
- Hoffpauir, K.; Simmons, J.; Schmidt, N.; Pittala, R.; Briggs, I.; Makani, S.; Jararweh, Y. A survey on edge intelligence and lightweight machine learning support for future applications and services. Acm J. Data Inf. Qual. 2023, 15, 1–30. [Google Scholar] [CrossRef]
- Hu, X.; Chu, L.; Pei, J.; Liu, W.; Bian, J. Model complexity of deep learning: A survey. Knowl. Inf. Syst. 2021, 63, 2585–2619. [Google Scholar] [CrossRef]
- Waisberg, E.; Ong, J.; Masalkhi, M.; Kamran, S.A.; Zaman, N.; Sarker, P.; Lee, A.G.; Tavakkoli, A. GPT-4: A new era of artificial intelligence in medicine. Ir. J. Med. Sci. (1971-) 2023, 192, 3197–3200. [Google Scholar] [CrossRef]
- Raghu, M.; Unterthiner, T.; Kornblith, S.; Zhang, C.; Dosovitskiy, A. Do vision transformers see like convolutional neural networks? Adv. Neural Inf. Process. Syst. 2021, 34, 12116–12128. [Google Scholar]
- Gao, Y.; Liu, Y.; Zhang, H.; Li, Z.; Zhu, Y.; Lin, H.; Yang, M. Estimating GPU memory consumption of deep learning models. In Proceedings of the 28th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Virtual Event, 8–13 November 2020; pp. 1342–1352. [Google Scholar]
- Sree, S.R.; Vyshnavi, S.; Jayapandian, N. Real-world application of machine learning and deep learning. In Proceedings of the 2019 International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 27–29 November 2019; pp. 1069–1073. [Google Scholar]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A survey of autonomous driving: Common practices and emerging technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Liu, Z. Fermatean fuzzy similarity measures based on Tanimoto and Sørensen coefficients with applications to pattern classification, medical diagnosis and clustering analysis. Eng. Appl. Artif. Intell. 2024, 132, 107878. [Google Scholar] [CrossRef]
- Kaleem, S.; Sohail, A.; Babar, M.; Ahmad, A.; Tariq, M.U. A hybrid model for energy-efficient Green Internet of Things enabled intelligent transportation systems using federated learning. Internet Things 2024, 25, 101038. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, M.; Shi, J.Q. A survey on deep neural network pruning: Taxonomy, comparison, analysis, and recommendations. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 10558–10578. [Google Scholar] [CrossRef]
- Lang, J.; Guo, Z.; Huang, S. A comprehensive study on quantization techniques for large language models. In Proceedings of the 2024 4th International Conference on Artificial Intelligence, Robotics, and Communication (ICAIRC), Xiamen, China, 27–29 December 2024; pp. 224–231. [Google Scholar]
- Cai, G.; Li, J.; Liu, X.; Chen, Z.; Zhang, H. Learning and compressing: Low-rank matrix factorization for deep neural network compression. Appl. Sci. 2023, 13, 2704. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, S.; Wang, Y.; Huan, W. Review of research on lightweight convolutional neural networks. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 1713–1720. [Google Scholar]
- Gou, J.; Yu, B.; Maybank, S.; Tao, D. Knowledge Distillation: A Survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, G.; Xie, Z.; Ma, J.; Huang, J.X. A diversity-enhanced knowledge distillation model for practical math word problem solving. Inf. Process. Manag. 2025, 62, 104059. [Google Scholar] [CrossRef]
- Zhao, B.; Cui, Q.; Song, R.; Qiu, Y.; Liang, J. Decoupled knowledge distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11953–11962. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Wang, C. Adaptive Multi-Teacher Knowledge Distillation with Meta-Learning. arXiv 2023, arXiv:2306.06634. [Google Scholar] [CrossRef]
- Loussaief, E.B.; Rashwan, H.A.; Ayad, M.; Khalid, A.; Puig, D. Adaptive weighted multi-teacher distillation for efficient medical imaging segmentation with limited data. Knowl.-Based Syst. 2025, 315, 113196. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Z.; Bai, L.; Ji, S.; Ai, B.; Wang, X.; Philip, S.Y. Multi-Level Knowledge Distillation with Positional Encoding Enhancement. Pattern Recognit. 2025, 163, 111458. [Google Scholar] [CrossRef]
- Yang, C.; An, Z.; Cai, L.; Xu, Y. Hierarchical self-supervised augmented knowledge distillation. arXiv 2021, arXiv:2107.13715. [Google Scholar]
- Li, W.; Wang, J.; Ren, T.; Li, F.; Zhang, J.; Wu, Z. Learning accurate, speedy, lightweight CNNs via instance-specific multi-teacher knowledge distillation for distracted driver posture identification. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17922–17935. [Google Scholar] [CrossRef]
- Ma, Y.; Jiang, X.; Guan, N.; Yi, W. Anomaly detection based on multi-teacher knowledge distillation. J. Syst. Archit. 2023, 138, 102861. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, Z.; Xiao, J.; Wei, C.; Wang, H.; Yuille, A.L.; Zhou, Y.; Xie, C. Masked autoencoders enable efficient knowledge distillers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 24256–24265. [Google Scholar]
- Zhang, Y.; Xiang, T.; Hospedales, T.M.; Lu, H. Deep Mutual Learning. In Proceedings of the CVPR, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Liu, Y.; Cao, J.; Li, B.; Yuan, C.; Hu, W.; Li, Y.; Duan, Y. Knowledge distillation via instance relationship graph. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7096–7104. [Google Scholar]
- Liu, Y.; Zhang, K.; Hou, C.; Wang, J.; Ji, R. Adaptive multi-teacher multi-level knowledge distillation. Neurocomputing 2020, 415, 106–113. [Google Scholar] [CrossRef]
- Zhang, L.; Bao, C.; Ma, K. Self-distillation: Towards efficient and compact neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4388–4403. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Wang, C. Confidence-aware multi-teacher knowledge distillation. In Proceedings of the ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 4498–4502. [Google Scholar]
- Cao, S.; Li, M.; Hays, J.; Ramanan, D.; Wang, Y.X.; Gui, L. Learning lightweight object detectors via multi-teacher progressive distillation. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 3577–3598. [Google Scholar]
- Mukherjee, S.; Awadallah, A. XtremeDistil: Multi-stage distillation for massive multilingual models. arXiv 2020, arXiv:2004.05686. [Google Scholar]
- Lee, Y.; Wu, W. QMKD: A Two-Stage Approach to Enhance Multi-Teacher Knowledge Distillation. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; pp. 1–7. [Google Scholar]
- Sun, T.; Li, D.; Wang, B. Decentralized federated averaging. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4289–4301. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Wang, J.; Liu, Q.; Liang, H.; Joshi, G.; Poor, H.V. A novel framework for the analysis and design of heterogeneous federated learning. IEEE Trans. Signal Process. 2021, 69, 5234–5249. [Google Scholar] [CrossRef]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach. Adv. Neural Inf. Process. Syst. 2020, 33, 3557–3568. [Google Scholar]
- Arivazhagan, M.G.; Aggarwal, V.; Singh, A.K.; Choudhary, S. Federated learning with personalization layers. arXiv 2019, arXiv:1912.00818. [Google Scholar] [CrossRef]
- Wei, W.; Liu, L.; Wu, Y.; Su, G.; Iyengar, A. Gradient-leakage resilient federated learning. In Proceedings of the 2021 IEEE 41st International Conference on Distributed Computing Systems (ICDCS), Washington, DC, USA, 7–10 July 2021; pp. 797–807. [Google Scholar]
- De Carvalho, M. Mean, what do you Mean? Am. Stat. 2016, 70, 270–274. [Google Scholar] [CrossRef]
- Dor, D.; Zwick, U. Selecting the median. Siam J. Comput. 1999, 28, 1722–1758. [Google Scholar] [CrossRef]
- Taheri, R.; Arabikhan, F.; Gegov, A.; Akbari, N. Robust aggregation function in federated learning. In Proceedings of the International Conference on Information and Knowledge Systems, Portsmouth, UK, 22–23 June 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 168–175. [Google Scholar]
- So, J.; Güler, B.; Avestimehr, A.S. Byzantine-resilient secure federated learning. IEEE J. Sel. Areas Commun. 2020, 39, 2168–2181. [Google Scholar] [CrossRef]
- Mylonas, N.; Malounas, I.; Mouseti, S.; Vali, E.; Espejo-Garcia, B.; Fountas, S. Eden library: A long-term database for storing agricultural multi-sensor datasets from uav and proximal platforms. Smart Agric. Technol. 2022, 2, 100028. [Google Scholar] [CrossRef]




| Variable | Description |
|---|---|
| Set of N teacher models. | |
| The i-th teacher model. | |
| Probability distribution produced by teacher for input x. | |
| Aggregated probability distribution from all teachers for input x. | |
| N | Number of teacher models. |
| Weight assigned to teacher in Weighted Mean Aggregation. | |
| Pairwise Euclidean distance between predictions of teachers and . | |
| Sum of distances from teacher to its nearest teachers. | |
| f | Number of faulty or adversarial teachers. |
| Selected teacher with the smallest sum of distances in Krum Aggregation. | |
| c | Number of extreme teacher predictions to trim in Byzantine-Resilient aggregation. |
| Set of the highest and lowest c teacher predictions in Byzantine-Resilient Aggregation. | |
| Weighting factor balancing cross-entropy loss and KL divergence loss in KD. | |
| True labels for the input data. | |
| Predictions of the student model with temperature . | |
| Softened output probabilities of the teacher model with temperature T. | |
| Softened output probabilities of the student model with temperature T. | |
| CE | Cross-entropy loss function. |
| KL | Kullback–Leibler divergence loss function. |
| Adaptive coefficient balancing aggregation methods at distillation loss (DL) and probability distribution (Proba) levels in adaptive aggregation. | |
| Fixed mathematical aggregation method used in fixed aggregation strategy. | |
| Input at the selected aggregation level (either distillation loss or probability distribution ). | |
| Student model parameters at round t. | |
| Aggregation method applied at round t in adaptive aggregation. |
| Issue | Description |
|---|---|
| Scalability | The difficulty of deploying models across distributed or federated systems, where bandwidth and computational resources are unevenly distributed. |
| Hardware Constraints | The limited computational capabilities of edge devices and embedded systems. |
| Cost-Efficiency | The financial and environmental cost of running large-scale models in production. |
| Technique | Description | Advantages | Disadvantages |
|---|---|---|---|
| Pruning | Removing less important connections/neurons | Reduces model size and computational cost | Can require retraining; unstructured pruning can be difficult to accelerate on hardware |
| Quantization | Reducing precision of weights/activations | Reduces memory footprint and can improve inference speed | Can lead to accuracy loss if not performed carefully |
| Low-Rank Factorization | Decomposing weight matrices | Reduces the number of parameters | Can be computationally expensive; may not be suitable for all architectures |
| Compact Architectures | Designing efficient architectures | Reduces model size and computational cost from the outset | Requires careful architectural design; may not achieve the same accuracy as larger models |
| KD | Transferring knowledge from a large teacher to a smaller student | Can improve student performance beyond training from scratch | Requires training a large teacher model |
| Aggregation Technique | Pre-Aggregation | Aggregation | Post-Aggregation |
|---|---|---|---|
| Mean | Collect all teacher outputs | Compute average of values | Store and analyze trends |
| Median | Sort data | Select middle value | Reduce impact of outliers |
| Weighted Mean | Assign weights based on importance | Compute weighted sum | Adjust based on reliability scores |
| Krum | Compute pairwise distances between predictions | Select prediction closest to majority | Improve robustness against adversarial inputs |
| Byzantine-Resilient | Sort and identify extreme values | Remove top and bottom outliers, then compute mean | Ensure robustness against corrupted teachers |
| Aggregation Technique | Description | Steps | Mathematical Formulation |
|---|---|---|---|
| Mean [63] | Computes the average of teacher predictions. This method is computationally efficient but sensitive to outliers. |
| |
| Median [64] | Uses the median of teacher predictions to reduce sensitivity to outliers. This method is robust to extreme values. |
| |
| Weighted Mean [51] | Assigns weights to teachers based on their reliability or accuracy. This method prioritizes more reliable teachers. |
| |
| Krum [65] | Selects the teacher whose prediction is closest to the majority. This method is robust to adversarial or unreliable teachers. |
| |
| Byzantine-Resilient [66] | Removes a fraction of extreme teacher predictions before computing the mean. This method is robust to adversarial or unreliable teachers. |
|
| Aggregation Level | Description | Characteristics |
|---|---|---|
| PD | Combines soft predictions from teachers into a single target distribution for the student | Simplifies the learning process but may dilute teacher-specific insights. Suitable for consistent teacher outputs. |
| DL | Computes and combines the distillation loss for each teacher independently | Preserves teacher diversity and allows flexibility but can be computationally intensive. Effective for heterogeneous teacher outputs. |
| Aggregation Level | Advantages | Limitations |
|---|---|---|
| PD |
|
|
| DL |
|
|
| Teacher Model | Accuracy (%) | F1-Score (%) | Recall (%) | Precision (%) | Parameter Count | Parameter Ratio (to Student) |
|---|---|---|---|---|---|---|
| MobileNet V1 | 99.82 | 98.2 | 98.5 | 98.4 | 3,220,000 | 9.99 |
| ResNet50 | 99.64 | 99.65 | 99.7 | 99.6 | 23,590,000 | 73.2 |
| Xception | 99.46 | 99.36 | 99.4 | 99.3 | 22,910,480 | 71.1 |
| EfficientNetB0 | 99.61 | 98.6 | 98.9 | 98.7 | 5,300,000 | 16.45 |
| Setting | Accuracy (%) | F1-Score (%) | Recall (%) | Precision (%) |
|---|---|---|---|---|
| Without KD | 94.31 | 94.06 | 94.10 | 94.00 |
| With KD (one Teacher) | 96.85 | 96.66 | 96.70 | 96.62 |
| Aggregation/Teacher | Round Number | Metrics (%) | |||
|---|---|---|---|---|---|
| Accuracy | Recall | Precision | F1-Score | ||
| Best Teacher | - | 99.82 | 98.5 | 98.4 | 98.2 |
| Krum-Based PD | 1 | 95.92 | 95.32 | 95.18 | 95.77 |
| 13 * | 97.52 | 97.12 | 97.24 | 97.38 | |
| Krum-Based DL | 1 | 97.16 | 96.78 | 96.85 | 97.13 |
| 6 * | 98.76 | 98.45 | 98.62 | 98.73 | |
| Byzantine-Resilient DL | 1 | 98.40 | 98.11 | 98.22 | 98.32 |
| 2 * | 98.58 | 98.47 | 98.51 | 98.50 | |
| Byzantine-Resilient PD | 1 | 97.87 | 97.64 | 97.72 | 97.79 |
| 5 * | 99.29 | 99.18 | 99.21 | 99.27 | |
| Mean-Based PD | 1 | 95.92 | 95.56 | 95.71 | 95.89 |
| 6 * | 98.76 | 98.63 | 98.67 | 98.68 | |
| Mean-Based DL | 1 | 95.21 | 94.85 | 94.81 | 94.66 |
| 10 * | 98.40 | 98.31 | 98.33 | 98.29 | |
| Median-Based PD | 1 | 95.92 | 95.50 | 95.63 | 95.60 |
| 10 * | 98.40 | 98.28 | 98.32 | 98.31 | |
| Median-Based DL | 1 | 94.33 | 94.07 | 94.12 | 93.90 |
| 11 * | 98.58 | 98.44 | 98.48 | 98.34 | |
| M-Weighted PD | 1 | 95.04 | 94.82 | 94.91 | 94.71 |
| 9 * | 98.05 | 97.86 | 97.92 | 97.99 | |
| M-Weighted DL | 1 | 97.87 | 97.69 | 97.76 | 97.79 |
| 15 * | 98.76 | 98.71 | 98.74 | 98.75 | |
| Aggregation Method | Best Round |
|---|---|
| Krum Aggregation (PD) | 6 |
| Krum Aggregation (DL) | 6 |
| Byzantine Resilient Aggregation (PD) | 5 |
| Byzantine Resilient Aggregation (DL) | 2 |
| Mean Aggregation (PD) | 6 |
| Mean Aggregation (DL) | 3 |
| Median Aggregation (PD) | 5 |
| Median Aggregation (DL) | 5 |
| Weighted Aggregation (PD) | 7 |
| Weighted Aggregation (DL) | 6 |
| Aggregation Method | Best Aggregation Level (PD or DL) |
|---|---|
| Krum Aggregation | DL Aggregation |
| Byzantine-Resilient Aggregation | PD Aggregation |
| Mean Aggregation | PD Aggregation |
| Median Aggregation | DL Aggregation |
| Weighted Aggregation | DL Aggregation |
| Round | Aggregation Method | Accuracy (%) | Weighted Precision (%) | Weighted Recall (%) | Weighted F1-Score (%) |
|---|---|---|---|---|---|
| 1 | Byzantine-Resilient DL Aggregation | 95.57 | 95.24 | 95.57 | 95.20 |
| 2 | Byzantine-Resilient DL Aggregation | 96.63 | 97.26 | 96.63 | 96.53 |
| 3 | Byzantine-Resilient Probability Aggregation | 96.99 | 97.46 | 96.99 | 96.96 |
| 4 | Byzantine-Resilient Probability Aggregation | 98.23 | 98.32 | 98.23 | 98.22 |
| 5 | Krum-Based DL Aggregation | 98.58 | 98.62 | 98.58 | 98.56 |
| 6 | Krum-Based DL Aggregation | 98.76 | 98.85 | 98.76 | 98.74 |
| 7 | Mean-Based DL Aggregation | 98.90 | 98.92 | 98.90 | 98.89 |
| Round | Aggregation | Accuracy | Recall | Precision | F1-Score |
|---|---|---|---|---|---|
| 1 | Krum DL | 95.70 | 95.55 | 95.65 | 95.60 |
| 2 | Byzantine-Resilient DL | 97.00 | 96.85 | 96.90 | 96.87 |
| 3 | Mean DL | 97.40 | 97.20 | 97.30 | 97.25 |
| 4 | Weighted DL | 97.80 | 97.65 | 97.70 | 97.68 |
| 5 | Byzantine-Resilient DL | 98.00 | 97.85 | 97.90 | 97.87 |
| 6 | Median DL | 98.20 | 98.05 | 98.10 | 98.07 |
| 7 | Weighted DL | 98.35 | 98.20 | 98.25 | 98.23 |
| Round | Aggregation | Accuracy | Recall | Precision | F1-Score |
|---|---|---|---|---|---|
| 1 | Krum Probability | 95.56 | 95.40 | 95.50 | 95.45 |
| 2 | Byzantine-Resilient Probability | 96.89 | 96.70 | 96.80 | 96.75 |
| 3 | Mean Probability | 97.23 | 97.00 | 97.10 | 97.05 |
| 4 | Weighted Probability | 97.64 | 97.50 | 97.55 | 97.52 |
| 5 | Byzantine-Resilient Probability | 97.85 | 97.70 | 97.75 | 97.72 |
| 6 | Median Probability | 98.10 | 98.00 | 98.05 | 98.02 |
| 7 | Weighted Probability | 98.25 | 98.15 | 98.20 | 98.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamdi, A.; Noura, H.N.; Azar, J. A Multi-Teacher Knowledge Distillation Framework with Aggregation Techniques for Lightweight Deep Models. Appl. Syst. Innov. 2025, 8, 146. https://doi.org/10.3390/asi8050146
Hamdi A, Noura HN, Azar J. A Multi-Teacher Knowledge Distillation Framework with Aggregation Techniques for Lightweight Deep Models. Applied System Innovation. 2025; 8(5):146. https://doi.org/10.3390/asi8050146
Chicago/Turabian StyleHamdi, Ahmed, Hassan N. Noura, and Joseph Azar. 2025. "A Multi-Teacher Knowledge Distillation Framework with Aggregation Techniques for Lightweight Deep Models" Applied System Innovation 8, no. 5: 146. https://doi.org/10.3390/asi8050146
APA StyleHamdi, A., Noura, H. N., & Azar, J. (2025). A Multi-Teacher Knowledge Distillation Framework with Aggregation Techniques for Lightweight Deep Models. Applied System Innovation, 8(5), 146. https://doi.org/10.3390/asi8050146






