Optimizing Bus Driver Scheduling: A Set Covering Approach for Reducing Transportation Costs

Abstract

Cutting operational costs is a critical component for transportation agencies. To reduce these costs, agencies must optimize their scheduling. Typically, the total operating costs of transport include vehicle expenses and driver wages. Solving such tasks is complex, and optimal planning is usually broken down into multiple stages. These stages can include vehicle scheduling, driver shift planning, and driver assignment. This paper focuses specifically on developing a near-optimal driver schedule for a specified set of vehicle schedules. It shows how to efficiently assign drivers to predetermined optimal vehicle routes while ensuring compliance with regulatory constraints on driving hours. We address this challenge using a mathematical model based on the set covering problem, building on a framework established perviously. The set covering problem is typically formulated as an integer programming problem, solvable through column generation techniques. Our algorithm combines this method with heuristics, taking into account the practical aspects of the problem. The article also presents a computational analysis of the method using benchmark and real data.

1. Introduction

This paper addresses an important part of the operational planning of public transport services: the planning of driver schedules. The solution methods presented apply to public bus transportation.

Driver scheduling is a crucial component of operational planning for public transportation systems. Public transportation service planning can be divided into several phases. Strategic planning, which usually includes the design of bus routes, is the initial step. Tactical planning encompasses the second and third phases, which focus on establishing service frequencies and schedules, typically determined by the local council. Operational planning includes the final phases, such as arranging drivers, vehicles, and rostering. For example, you can find a detailed description of these phases, models, etc. in [1]. Excellent reviews covering strategic and tactical phases are provided in [2], and many books and studies also address electric vehicles [3,4,5,6,7].

Reducing operating costs is a major goal for transportation firms, as these costs are mostly driven by the cost of vehicles (for example, fuel costs) and their drivers (for example, fuel costs and driver wages). Vehicle scheduling, vehicle assignment, driver scheduling, and driver rostering are the four stages of operations planning [8].

Vehicle scheduling creates daily vehicle shifts based on the available fleet, ensuring that all scheduled trips are covered (see [9]). Movements of vehicles without passengers, or deadhead trips, are allowed between two planned trips t₁ and t₂ as long as the travel time for the deadhead trip does not exceed the interval between t₁’s arrival and t₂’s departure. Between the arrival station of t₁ and the departure station of t₂, these deadhead trips take place. We also consider a pull-out at the beginning of the day and a pull-in at the end of the day to be a deadhead trip, if the corresponding stations are different from the depot. Typically, vehicle schedules produce appropriate schedules that meet the requirements of the timetable, such as departure times and locations of the trips. Several mathematical models for solving vehicle scheduling problems have been developed over recent decades. Today, the most widely used models formulate the problem as an integer multi-commodity network flow problem (see [10,11,12,13]). In this model, optimal scheduling can be computed as a solution to a linear integer programming problem. The problem can also be formulated as a set covering or set partitioning problem (see, for example, [14,15]). All models, including single- and multi-depot ones, are reviewed in detail in [16].

The vehicle assignment step assigns specific buses to the schedule to meet specific requirements (for example, the maximum distance without refueling for natural gas buses is specified [17]). After this stage, every vehicle shift is assigned to its own bus.

The driver scheduling phase [18] entails assigning drivers to work shifts that meet daily requirements. These limitations include laws that control driving hours, rest intervals, overall work hours, and required breaks between work phases. For example, the maximum time to drive without breaks and the maximum working time per day are prescribed. The most popular approach to solve this problem is to study set partitioning (see [19]) and its relaxation, the set covering model (see [20]). Typically, the solution can be generated in two ways: either by generating a feasible solution satisfying the constraints [21] and iteratively improving it, or by selecting the best among the large number of feasible solutions generated [22]. Numerous types of algorithms have been employed to tackle the problem. Among these, it is worth mentioning the integer programming models (see [23]), the metaheuristic method based on evolutionary principles [22], or algorithms based on the fuzzy method [24].

Driver rostering assigns drivers to shifts over a set period (e.g., weeks or months), while ensuring compliance with scheduling requirements. This includes managing vacation days and meeting minimum rest requirements, such as Sundays off. In transport, split shifts are common, especially on weekdays, to match peak periods (e.g., morning and afternoon commute peaks) with a “two-hump camel back” demand profile. Methods and applications of staff scheduling and rostering are summarized in [25].

Various software modules exist to support operational planning, either manually or interactively, typically as part of a decision support system.

Several integrated models for public transportation incorporate some of the processes mentioned above (see [1,26,27,28,29,30]). However, these models are typically only relevant to medium-sized problems because of their problem size restrictions, which force them to simplify driving regulations or reduce the overall number of rules. Finding a driving schedule that works well is essential to cut operating expenses. Bodin et al. [10] emphasized the importance of this issue as early as the 1980s. They showed that most operational costs are attributable to driver costs, which are typically higher than the average costs associated with cars, using the example of public transportation in North America. Recently, integrated methods have been used in several forms in various related fields, for example, in the optimization of electric buses and rail transport. In [31], Wang et al. integrated timetabling with vehicle scheduling for urban rail transit, while in [32], Teng et al. used a similar integration for electric buses. In [33], Mo et al. investigated integrated models for paratransit services.

Our Contribution

In the field of vehicle scheduling, the idea of Kliewer et al. [11], the so-called time–space network (TSN) model was a significant advance in the literature in reducing the computational complexity of the model. Its basic idea is presented in Section 2. The model has shown favorable properties, and it has been incorporated into driver scheduling models [26,28,34]. The model continues to play an important role in the mathematical modeling of transportation problems today [35,36,37,38]. We use these ideas in our work.

Similarly to the method presented in [26], we construct a driver schedule for an existing optimal vehicle schedule. This is computed by solving a set partitioning problem using column generation. We need column generation because it is not possible to generate all possible shifts since the number of shifts can be very large. In contrast to [26], we generate the driver shifts for the initial column set using a heuristic that is fully adapted to the existing vehicle scheduling and generates shifts that satisfy all rules. Empirical observations show that heuristics are faster than solving a driver scheduling problem. We generate new shifts using a TSN-based shift generation network, similar to the method presented in [28] for another type of integrated problem. This allows us to generate shifts consisting of an arbitrary number of workpieces, which is consistent with the rules we use. Due to the complexity of the rules, it is necessary to incorporate a special checker in the generation network, enabling the handling of more complex rules in addition to the usual resource-based method. This is also an important difference compared to the methods mentioned above. These rules are also described in Section 3.

In Section 2 we describe the technique for calculating vehicle schedules, required by the driver scheduling module. Section 3 contains the driver scheduling method. Finally, Section 4 contains conclusions. The preliminary results of this article are published in the extended abstract [39].

2. Constructing Vehicle Schedules

We outline the process for constructing vehicle schedules. The first step is to create a hypothetical vehicle schedule, and the second is vehicle assignment, the act of allocating certain vehicles to these schedules. The vehicle assignment module and the vehicle scheduling module, respectively, are responsible for these two stages in our system.

The vehicle scheduling module receives the following inputs:

• Information about the trips, including the departure and arrival times, the geographical locations of the departure and arrival stations, the type of vehicle needed, running distance, and category (local or regional).
• Vehicle types and related data, such as fuel type and range, running costs for normal and deadhead trips per km.
• Extra geographic information, including depot-specific characteristics, such as GPS coordinates, number of parking places, suitability for short- or long-term parking, and eligibility for breaks (the required distances and times between the geographic locations can be given or can be calculated from the GPS coordinates).

Various events, including passenger and deadhead trips, are included in vehicle schedules. The multi-depot vehicle scheduling model uses vehicles from particular depots to produce a daily schedule for the fleet. One predefined limitation is the composition of the fleet, which is the total number of vehicles of each category, such as normal, low-floor, and long vehicles.

The following specifications must be met by the vehicle schedule:

• Each trip must be assigned to a single vehicle.
• For vehicle shifts to be practical, they must adhere to the following:

  (a)

  Begin and conclude at the same depot.

  (b)

  Assignments must be completed without scheduling conflicts.

• Every depot’s capacity restrictions must be adhered to.
• Requirements for compatibility between depots and journeys must be met.

The following are the general goals of the vehicle scheduling problem:

• Minimize the number of vehicles required.
• Minimize the total distance or duration of deadhead trips.
• Find an optimal (minimum) weighted sum of these costs.

The total cost of a vehicle’s daily operation, which varies based on the type of vehicle, is represented by the cost of each vehicle leaving a depot in our cost model. Every vehicle trip also has a variable cost, which is determined by multiplying the cost per kilometer by the distance traveled. These expenses serve as the basis for the objective function that aims to minimize them.

The vehicle scheduling problem has been the subject of several studies published over the last few decades, using a variety of models (see [1] for a summary and comparison of these models and methodologies). Two typical models are used to describe the multi-depot vehicle scheduling problem (MDVSP): the time–space network model (created by Natalie Kliewer et al. in 2006 [11]) and the connection-based network model (as proposed by Andreas Löbel in 1997 [12]). An integer programming (IP) model is solved by both formulations; however, as shown in [11], the time–space network model has fewer arcs. In this study, we use the latter approach for the daily vehicle scheduling software.

Figure 1 shows an example time–space network. There are five geographic locations; two are depots. These locations are represented by horizontal lines that contain the nodes of the network. The nodes represent the departure and arrival times of the trips from or to that station. Various types of edges appear in the network, representing trips, deadheads, and waiting events. Figure 1 uses different colors to distinguish the types of edges:

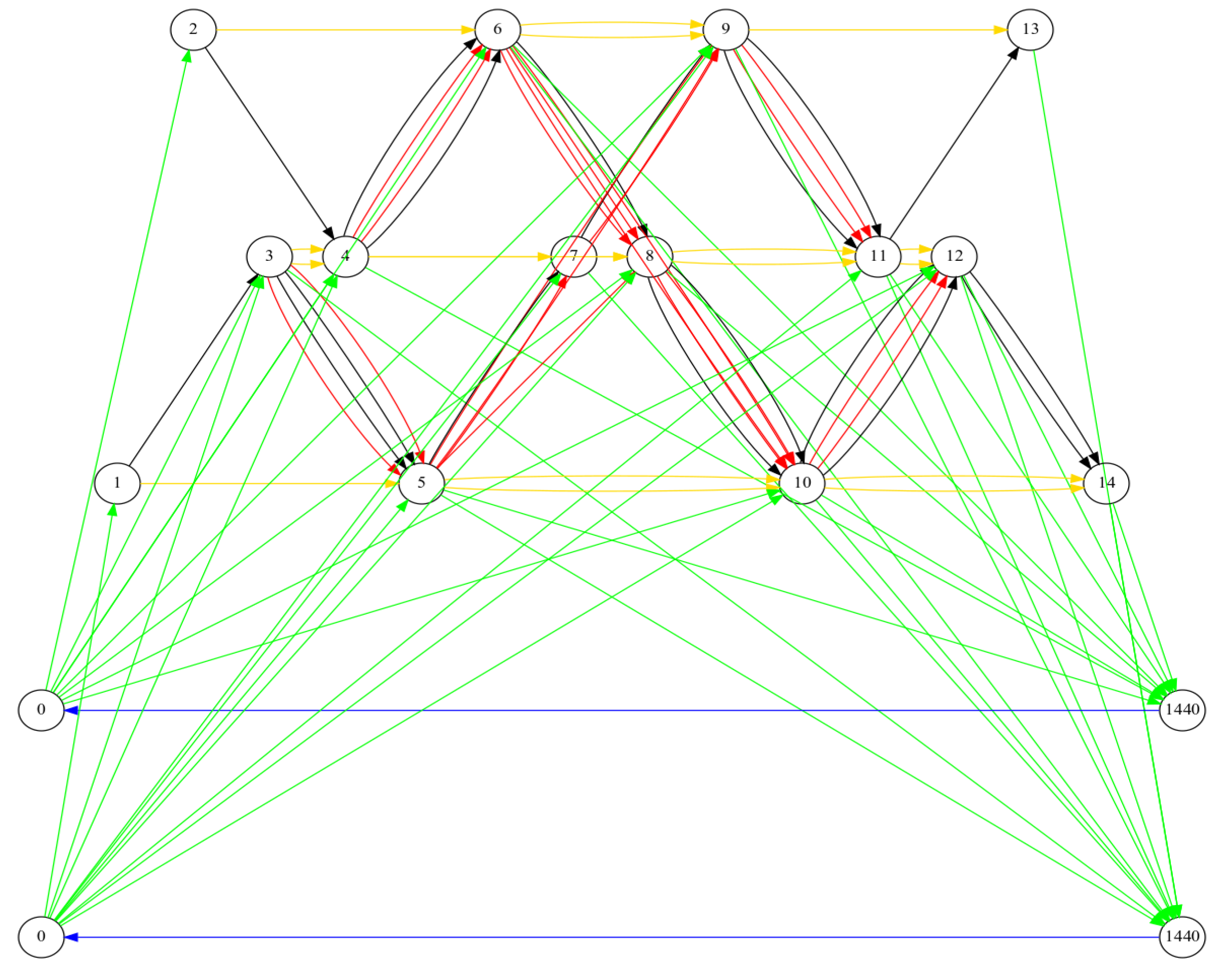
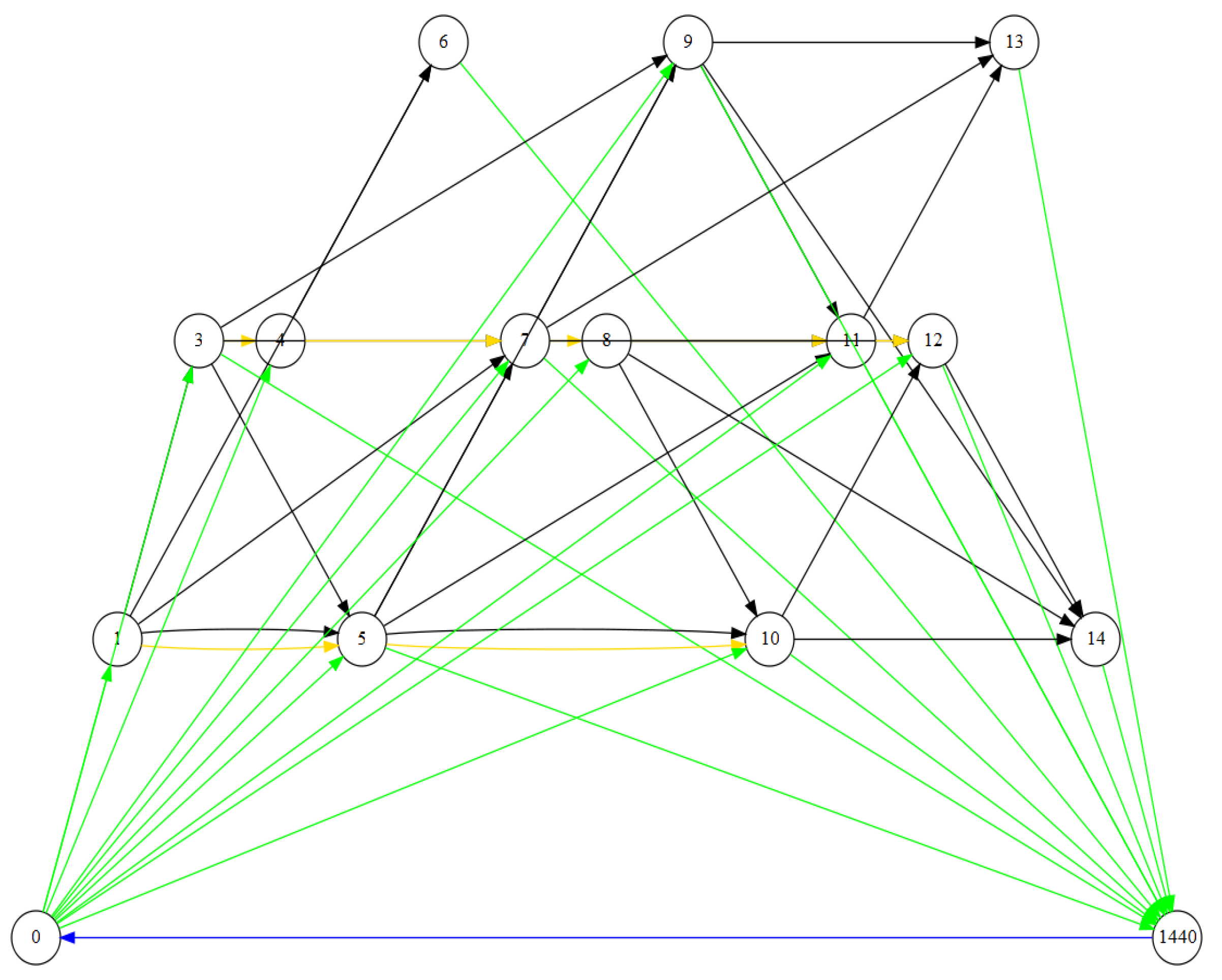
• The green edges represent deadhead trips to and from the depots.
• The red edges represent deadhead trips between the two stations.
• The yellow edges represent waiting.
• The black edges represent trips.

Multiple edges may occur between some nodes since there are two depots.

We use a specialized assignment model in our system’s vehicle assignment module and formulate the problem using linear programming (LP) [17]. This section also addresses vehicle refueling criteria. The input data for the assignment module consist of geographical location data, particular vehicle attributes, and hypothetical vehicle timetables. (We talk about theoretical vehicle scheduling because there is no specific vehicle, e.g., identified by registration number allocated to a shift.) Vehicle fuel types are also included.

Vehicle schedules with precise vehicle identification are included in the output of the vehicle assignment module. In addition, vehicle shifts include specific vehicle events, such as parking and maintenance. The current state of the vehicle (such as the distance driven without refueling and the time elapsed since the last maintenance) and its specifications (such as its maximum range) are among the limitations of the problem. The vehicle assignment module is described in our previous paper [17].

The input of driver planning comes from the phases of vehicle scheduling and assignment; therefore, vehicle schedules and assignments must be given in advance.

Figure 1. An example time–space network of 12 trips.

Figure 1. An example time–space network of 12 trips.

3. Constructing Driver Schedules

Now, we will discuss some concepts regarding mandatory driving legislation and driver schedules. We will then discuss a method for scheduling drivers.

• Operating guidelines as limitations on driver scheduling

To start with, we define a few keywords and concepts associated with driver employment rules. A valid sequence of trips and deadhead trips is called a “workpiece”. “Valid” in this context refers to the possibility of a single driver completing the sequence without interruption. There are some events in driver shifts. For example, events can be special activities that take place at the beginning and end of the shift, which require driving and other events such as shift breaks, vehicle maintenance time intervals, etc. In general, additional rules and regulatory requirements apply to drivers’ daily, weekly, and monthly work schedules. However, these parameters are normally covered in the rostering step. Moreover, specific needs must also be considered, such as the type of driver’s license required for a certain shift.

Some regulations established by the EU must be considered with regard to the driver schedule, including

• The maximum number of hours that one can drive in a day;
• The laws governing the longest period that a driver may spend behind the wheel;
• The minimum amounts of time needed for rests, breaks, etc.

and local regulations, like the following:

• Types of the events and shifts;
• Extra local regulations concerning breaks and the maximum number of working hours (per day).

We will briefly review the set of work guidelines we take into account. First, we present the general rules, established by the EU.

• A driver cannot exceed 9 h of driving per day, with a maximum of two exceptions per week where it can be extended to 10 h.
• Breaks of at least 45 min must be taken after every 4.5 h of driving.
• A break can be divided into two periods, where the first is at least 15 min and the second is at least 30 min (which must be completed after 4.5 h of driving)

The specific local rules for breaks that we must take into account are as follows. These rules mainly apply to working and duty time and not to driving time. Working time may also include other special paid activities such as required waiting, administrative, and maintenance activities.

• Only specified areas (stations) are allowed for the minimum and maximum duration of breaks, which are 15 and 30 min long, respectively.
• The driver must take the first work break no later than five hours and fifty-nine minutes into the shift.
• If the driver works a shift for more than eight hours, a second break must start after working for 8 h and 59 min.
• If the shift exceeds nine hours, the driver must start a third break before nine hours and 59 min.
• A shift consists of three periods: the first six hours, the second two hours, and the third one hour. A break may only occur once during a period.
• The driver is exempt from taking a break if the rest period starts earlier and the shift is finished before the end of the period.

Extra guidelines for operation:

• If there is no two-hour or longer rest interval during the shift, there must be a minimum 12 h rest period after the shift. The rest period following the shift must be at least 9 h if there is at least a 2 h break during the shift. If this is not the case, the total length of the longest break during the shift plus the rest period following the shift must be at least 12 h.
• The driver must take a minimum of an 80 min break if their shift is broken into two parts. Short breaks are not allowed during a split shift. A shift must be classified as split if it has a minimum 80 min break. A split shift can have two or more components. In the latter scenario, there must be a minimum of 80 min of rest time between each of the next two shift halves; however, the total of these rest periods cannot exceed five hours.
• The driver has administrative time at the start and end of a shift. When a shift is split, there is an administrative period at the beginning and end of each part of the shift. They last about five minutes each. A driver change also has an administration period that lasts five minutes.
• There are certain paid events throughout a driver shift:
  • A half-hour maintenance window for vehicles;
  • A 10 min special administrative period.
  These activities must be offered in blocks of at least five minutes (or in multiples of five).

There are two 2 min breaks for passengers to board and disembark from buses before and after each trip.

In addition, if a shift is shorter than four hours, the full four hours of work must be compensated.

We also implement our approach in regional public transport. The following are the driver regulations for regional public transport:

• The shifts of the drivers are classified based on the duration of the trips. We refer to a shift as a long shift if it includes a trip of more than 50 km; otherwise, it is referred to as a short shift.
• After 4.5 h of nonstop driving during long shifts, drivers must take a work break of at least 45 min. There are two possible lengths for this break: the first should be at least 15 min, and the second should be at least 30 min. Each period may be extended, but the order cannot be altered.
• A maximum of nine hours may be spent driving on up to three days per week. There is a maximum driving limit of 56 h per week, which doubles to 90 h in two weeks.
• There is a minimum of 11 h of rest per 24 h. It can be split into two minimal periods: three hours and nine hours.
• The minimum weekly rest period is 45 h; this can be lowered to 36 h, but the three weeks that follow must make up for the lost time.

• Our method to solve the driver scheduling problem

We then present our driver scheduling module’s specification and optimization criteria.

The input of this module consists of

• Vehicle schedules;
• Vehicle data;
• Driver data (driving license types, contract types);
• Geographical locations.

The driver schedules that are generated must adhere to the established guidelines. It follows that our job is to plan the workpieces and other daily events while adhering to the limitations (daily rules).

In driver scheduling, the cost model is often the total weighted sum of the drivers’ fees and the number of shifts. Our objective function aims to minimize the overall cost, which is the sum of the expenses associated with each driver and the number of schedules.

3.1. The Set Covering Formulation Used as the Mathematical Basis for Driver Scheduling

The set cover, or a remarkably similar set partitioning strategy, is the most frequently used mathematical model for driver scheduling in the literature. Numerous articles (e.g., [20,26,28,34]) apply this approach to solve the driver scheduling problem.

We can formulate the driver scheduling problem as a 0–1 programming problem by using the set covering model, specifically,

$$\sum _{d\in D}\sum _{k\in K^d}{c}_k^d{x}_k^d\to \min ,$$

$$\sum _{d\in D}\sum _{k\in K^d\left(t\right)}{x}_k^d\ge 1\mathrm{for}\forall t\in T,$$

$$x_k^d\in \left\{0, 1\right\},d\in D,k\in K^d,$$

where:

• T is the set of timetabled trips to be covered;
• D is the set of depots;
• K^d is the set of possible driver shifts from depot d;
• K^d(t) is the set of driver shifts covering trip t from depot d;
• $c_k^d$ is the cost of shift k from depot d;
• $x_k^d$ is the variable indicating if shift k from depot d is included in the solution or not.

The main difficulty when solving the problem with the abovementioned set covering model is that the number of possible combinations of driver shifts is very large. Therefore, they cannot be generated directly. Every driver’s shift must adhere to all guidelines and specifications. As a result, we fix the issue using a column generation technique. This approach is widely used in the literature and has numerous uses [40].

The following is a heuristic algorithm that we use to address this issue:

• The algorithm of the solution

• Step 1 Generate all feasible workpieces from vehicle schedules to form an initial set of columns.
• Step 2 Using the current column set K, solve the relaxed master problem. Save the dual program’s information as well as the current lower bound.
• Step 3 Determine new columns with a negative reduced cost by solving the pricing problem for each depot. Add these new columns to the existing set.
• Step 4 Proceed to Step 2 if Step 3 contains new columns with negative reduced costs and the number of steps is less than a specified parameter.
• Step 5 Solve the IP problem and build an integer solution with the current column set.

In Step 1 we create the initial driver shifts for column generation using a heuristic that generates all the valid workpieces depending on four parameters from the events of the existing vehicle shifts. These parameters are the minimum and maximum working times and the minimum and maximum number of trips. For each vehicle shift, the method iterates through all the events of the shift and, starting from that event, systematically generates all the valid workpieces beginning with that event. Then with these, we cover each vehicle shift, using the adapted version of the greedy set partition algorithm defined by Chvatal in [41].

The initial driver shifts are made up of all valid workpieces used for this partition. The pseudocode of the algorithms used in Steps 1 is given in Algorithms 1 and 2

Algorithm 1 Generate workpieces from a vehicle schedule.

1: function GenWP (A, i, $MINWT,MAXWT,MINNT,MAXNT$) 2:     ▹ $\begin{array}{l}A: \mathrm{Array} \mathrm{of} \mathrm{vehicle} \mathrm{schedules}, MINWT,MAXWT: \mathrm{Working} \mathrm{time} \mathrm{parameters}, MINWT,MAXWT:\\ \mathrm{Parameters} \mathrm{for} \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{trips}\end{array}$ 3:     ▹ i: Index of the actual vehicle schedule 4:     $output\leftarrow \varnothing$ 5:     ▹ $output$: Set of the generated workpieces 6:     $E\leftarrow A\left[i\right]$ 7:     ▹E: Array of events of the ith vehicle schedule 8:     $m\leftarrow Length\left(E\right)$ 9:     for $j=1$ to m do 10:         $wT\leftarrow 0$ 11:         ▹$wT$: The accumulated working time in schedule E, starting from the jth event 12:         $nT\leftarrow 0$ 13:         ▹$nT$: The number of trips in schedule E, starting from the jth event 14:         $k\leftarrow j$ 15:         while $wT\le MAXWT$ and $nT\le MAXNT$ and $k\le m$ do 16:            $wT\leftarrow wT+E\left[k\right].workTime$ 17:            if $E\left[k\right].type$ = TRIP then 18:                $nT\leftarrow nT+1$ 19:            end if 20:            if $wT\ge MINWT$ and $nT\ge MINNT$ then 21:                $wP\leftarrow \varnothing$ 22:                ▹$wP$: The array containing the events of the actual workpiece 23:                for $l=j$ to k do 24:                    $wP$.add($E\left[l\right]$) 25:                end for 26:                Add $wP$ to the $output$ 27:            end if 28:            $k\leftarrow k+1$ 29:         end while 30:     end for 31:     return $output$ 32: end function

Algorithm 2 Solve a set partition problem for each vehicle schedule by a greedy heuristic to obtain the initial driver shifts

1: function InitialDriverShifts(A, $MINWT,MAXWT,MINNT,MAXNT$) 2:     ▹ $\begin{array}{l}A: \mathrm{Array} \mathrm{of} \mathrm{vehicle} \mathrm{schedules}, MINWT,MAXWT: \mathrm{Working} \mathrm{time} \mathrm{parameters}, MINWT,MAXWT:\\ \mathrm{Parameters} \mathrm{for} \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{trips}\end{array}$ 3:     $n\leftarrow Length\left(A\right)$ 4:     $output\leftarrow \varnothing$ 5:     for $i=1$ to n do 6:         S $\leftarrow GenWP(A,i,MINWT,MAXWT,MINNT,MAXNT)$ 7:         ▹S: Set of the workpieces generated from the ith vehicle schedule 8:         while $S\ne \varnothing$ do 9:            Find $s\in S$ containing the most events 10:            Add s to $output$ 11:            for all $q\in S$ do 12:                if $s\cap q\ne \varnothing$ then 13:                    $S\leftarrow S-q$ 14:                end if 15:            end for 16:         end while 17:     end for 18:     return $output$ 19: end function

In Step 2 we use LP-relaxation, i.e., we solve the model without the integrality constraints.

In order to select the new columns for each depot, we solve the so-called pricing problem described in Step 3. To do this, we apply the concept of [28] to solve a resource-constrained shortest path problem on a given time–space network (N,E) with a given resource set R. We use the basic label setting algorithm described in [28].

We considered the additional regulations as well, but resources cannot verify all of the rules. In the pricing problem, additional steps are taken to verify the accuracy of the shifts that are generated using the more intricate drivers’ rules. Invalid shifts are excluded and do not appear in the generator. The generator stores several negative reduced cost driver shifts, which will be candidates as the new columns. A parameter determines the maximum number of new columns that can be included in the model.

The structure of the time–space network is similar to that for trips. However, this time the edges of the network are not the trips, but the workpieces. This time, the nodes of the network will be the start and end points of the workpieces on each time line, which are assigned to the end stations. Each generation network also has a depot timeline that represents the current depot. There are four types of edges in the network; these are the pull-in, pull-out, workpiece, and waiting. The pull-in and pull-out edges always start from the depot and lead to the initial node of each workpiece. The workpiece edges are defined by the departure and arrival time and location of the respective workpiece. In the time lines, the workpieces are connected by waiting edges. Theoretically, it is also possible for the waiting to be done by travel, but in our model this type of waiting is not allowed.

In the generator network, certain conditions can be controlled by using resources. Different resources can be assigned to each shift, usually more than one at a time. These express different constraints on the shifts, such as maximum working time, number of work segments included, etc. The resource values for each shift can be calculated using a function. These functions are called resource functions. The driver shifts are described by means of paths; the functions are constructed in such a way that the function value is obtained by summing the values taken at the edges of the path. For more information on resource functions, see, for example, [28,42]. The values of the resource functions for the edges of our time–space network model are given in

Table 1. Cost and resource consumption of the different types of edge of the time space network used by the pricing problem. Here, the * symbol means multiplication.

Edge Type	Cost	Resources (Length is Measured in Time)
		Working time	Shift Duration	Driving Time	Number of Workpieces
Pull-in	Fixed value	Length	Length	Length	0
Pull-out	0	Length	Length	Length	0
Workpiece	Length * Unit cost	Length	Length	Length	1
Waiting	0	0	Length	0	0

.

In our model, the following four resources are used:

• The maximum working time;
• The maximum shift duration;
• The maximum number of workpieces;
• The maximum driving time.

Figure 2 shows an example TSN generator corresponding to our model. The notation is the same as in Figure 1, except that here the black edges represent valid workpieces and not trips, and the red edges are missing.

Formally, the pricing problem on a given TSN $(N,E)$ can be stated as

$$\begin{array}{c}\hfill \sum _{e\in E}{\tilde{c}}_e{x}_e\to \min ,\end{array}$$

supposing that

$$\begin{array}{c}\hfill \sum _{e\in n^{+}}{x}_e-\sum _{e\in n^{-}}{x}_e=\left\{\begin{array}{c}1,\mathrm{if}n\mathrm{is}\mathrm{a}\mathrm{source}\mathrm{node},\hfill \\ 0,\mathrm{if}n\in N\mathrm{and}n\mathrm{is}\mathrm{not}\mathrm{source}\mathrm{and}\mathrm{not}\mathrm{destination}\mathrm{node}\hfill \\ -1,\mathrm{if}n\mathrm{is}\mathrm{a}\mathrm{destination}\mathrm{node},\hfill \end{array}\right.,\end{array}$$

(1)

$$\begin{array}{cc}\hfill & a^r\le \sum _{e\in E}{d}_e^r{x}_e\le f^r,\mathrm{for}\mathrm{each}r\in R,\hfill \end{array}$$

(2)

$$\begin{array}{c}\hfill x_e\in \left\{0,1\right\},\mathrm{for}\mathrm{each}e\in E.\end{array}$$

In the objective function, ${\tilde{c}}_e$ is the reduced cost of edge e, obtained by subtracting the dual value from the original cost value. The binary variable $x_e$ indicates whether the edge e is included in the optimal driver shift. The equations described by Formula (1) express that the driver shift must move continuously from the source to the destination. $n^{+}$ is the set of edges that leave node n, while $n^{-}$ is the set of edges that enter node n. Inequalities (2) imply that regular shifts must satisfy all the criteria defined in the model, e.g., they must not be shorter or longer than a given duration, they must not contain only limited driving time, etc. For each edge, in addition to cost, there are also resource values for each element of the resource set R. These can be, for example, the values defined in Table 1. Here, $a^r$ is the lower bound and $f^r$ is the upper bound for the resource $r\in R$. $d_e^r$ is the corresponding resource consumption for edge e and resource r. The solution of the model gives the regular shift with the lowest reduced cost, which is what we are looking for.

The mentioned resource functions can only be used if the value of the function is obtained as the sum of the values of the events included in the shift. We can compare the values obtained in this way to the appropriate limits. However, as we saw in the introductory part of this chapter, local rules can be special, requiring more complicated conditions to be checked. These include, for example, the different break rules for long and short shifts, or the maintenance and administration periods required for shifts. Such rules can only be checked using a special method. We implement a procedure as part of the shift generator, which checks each incomplete shift to see if it is suitable for placing break events and places the necessary events in the case of already completed shift candidates, thus checking feasibility. Inappropriate shifts are removed from the generator.

3.2. Computational Results

The algorithm was first tested on publicly available benchmark data. For this purpose, we selected 20 inputs from the randomly generated data sets discussed in [43,44]. One type of data set, called $A200$, contains 200 trips and 2 depots. The other type, which is called $A400$, has 400 trips in each data series, also served by 2 depots. Huisman et al. in [44] discuss in detail the behavior of their combined vehicle and driver scheduling algorithms developed for these data sets.

Table 2. Computational results of the algorithm on random benchmark A200.

Problem	Number of Vehicles	Number of Driver Shifts	Total
#1	19	37	56
#2	21	38	59
#3	18	33	51
#4	17	32	49
#5	20	37	57
#6	16	32	48
#7	18	33	51
#8	20	38	58
#9	23	42	65
#10	12	24	36
Averages	18.4	34.6	53

and

Table 3. Computational results of the algorithm on random benchmark A400.

Problem	Number of Vehicles	Number of Driver Shifts	Total
#1	34	68	102
#2	35	66	101
#3	34	62	96
#4	29	55	84
#5	35	66	101
#6	29	57	86
#7	32	60	92
#8	36	69	105
#9	43	77	120
#10	22	45	67
Averages	32.9	62.5	95.4

show the results of the algorithm described in this paper for these data sets. Although an exact comparison with the results in that paper is not possible, it can be seen that the average number of vehicle schedules is exactly the same, while the number of driver shifts is similar for both input categories. In [44], the average number of driver shifts for the data set $A200$ varies between $40.7$ and $44.5$, while in our case it is $34.6$, and for the data set $A400$ in [44], it varies between $73.2$ and $74.9$, while in our case it is $62.5$. Since the cost function used and the criteria for the driver shifts may differ, the comparison cannot be considered exact, but the results show that for the same data series our algorithm gives similar results to the previous combined methods. As can be seen in the model description, our objective function minimizes the total cost of the driver schedules using optimal vehicle schedules. The objective function used in [44] minimizes the sum of the cost of the vehicle and the driver schedules. Although the exact values of the objective function are not given in [44], this can cause the average number of drivers to be slightly lower when using our model. The number of drivers can also be influenced by the rules, which in our case may also differ from those used in the referenced publication.

The main parameters used in our tests, which correspond to the criteria of the transport company involved in our development, are as follows.

• Minimum length of the workpieces: 30 min;
• Maximum length of the workpieces: 300 min;
• Minimum number of trips per workpiece: 1;
• Maximum number of trips per workpiece: not limited;
• Maximum number of workpieces per shift: 3;
• Maximum working time and shift duration: 720 min;
• Maximum driving time: 540 min.

Break rules are checked according to the rules described above.

We also use our approach in local and regional public transportation scenarios. The results appear to be encouraging, and the estimated half-hour run times for medium-sized problems are reasonable.

The calculations performed for the Szeged Regional Bus Transport Company are shown in Table 4.

The table shows the number of trips, the number of iterations made by the column generation solver, and the running times. The PC used is configured with an Intel i7-10700 2.90GHz CPU, and 16GB RAM.

In each of the above real-world examples, trips are serviced from three depots, including one larger one (Depot 2) and two smaller ones (Depot 1 and Depot 3). In Table 5, Table 6 and Table 7, we analyze the behavior of the column generation for these depots. The tables contain the following data:

• INS: Initial number of driver shifts, i.e., columns;
• FNS: The final number of driver shifts after solving the integer model;
• IOV: Initial value of the objective function;
• FROV: Final value of the objective function for the relaxed problem;
• FIOV: Final value of the objective function for the integer problem;
• RG%: Relative gap.

Table 4. Computational results for some real-world problems.

Problem	Number of Trips	Number of Vehicles	Number of Drivers	Number of CG Iterations	Time (minutes)
#1	830	99	225	104	2
#2	902	107	229	143	3
#3	900	105	229	155	3
#4	951	104	201	188	6
#5	1465	175	292	286	30
#6	1467	175	297	272	29
#7	1483	174	298	223	21

Table 4. Computational results for some real-world problems.

Problem	Number of Trips	Number of Vehicles	Number of Drivers	Number of CG Iterations	Time (minutes)
#1	830	99	225	104	2
#2	902	107	229	143	3
#3	900	105	229	155	3
#4	951	104	201	188	6
#5	1465	175	292	286	30
#6	1467	175	297	272	29
#7	1483	174	298	223	21

Table 5. Number of schedules and values of the objective function for depot 1.

Problem	Depot 1
	INS	FNS	IOV	FROV	FIOV	RG%
#1	76	58	781,674	603,116	603,116	0
#2	60	36	632,574	360,320.601	377,021	4.42
#3	60	36	632,574	360,320.601	377,021	4.42
#4	69	43	727,607	419,176.834	445,501	5.91
#5	93	49	951,707	496,062.845	507,398	2.23
#6	93	57	973,703	574,549.559	590,071	2.63
#7	90	52	943,671	531,940.470	538,806	1.27

Table 5. Number of schedules and values of the objective function for depot 1.

Problem	Depot 1
	INS	FNS	IOV	FROV	FIOV	RG%
#1	76	58	781,674	603,116	603,116	0
#2	60	36	632,574	360,320.601	377,021	4.42
#3	60	36	632,574	360,320.601	377,021	4.42
#4	69	43	727,607	419,176.834	445,501	5.91
#5	93	49	951,707	496,062.845	507,398	2.23
#6	93	57	973,703	574,549.559	590,071	2.63
#7	90	52	943,671	531,940.470	538,806	1.27

Table 6. Number of schedules and values of the objective function for depot 2.

Problem	Depot 2
	INS	FNS	IOV	FROV	FIOV	RG%
#1	227	158	2,405,062	1,658,725.778	1,676,210	1.04
#2	190	119	2,032,993	1,228,429.196	1,254,494	2.07
#3	190	122	2,043,245	1,267,100.875	1,285,449	1.42
#4	209	119	2,258,083	1,245,889.563	1,271,081	1.98
#5	322	194	3,450,365	2,014,750.609	2,050,696	1.75
#6	321	192	3,434,485	2,003,882.411	2,038,130	1.68
#7	326	195	3,485,790	2,035,322.634	2,060,903	1.24

Table 6. Number of schedules and values of the objective function for depot 2.

Problem	Depot 2
	INS	FNS	IOV	FROV	FIOV	RG%
#1	227	158	2,405,062	1,658,725.778	1,676,210	1.04
#2	190	119	2,032,993	1,228,429.196	1,254,494	2.07
#3	190	122	2,043,245	1,267,100.875	1,285,449	1.42
#4	209	119	2,258,083	1,245,889.563	1,271,081	1.98
#5	322	194	3,450,365	2,014,750.609	2,050,696	1.75
#6	321	192	3,434,485	2,003,882.411	2,038,130	1.68
#7	326	195	3,485,790	2,035,322.634	2,060,903	1.24

Table 7. Number of schedules and values of the objective function for depot 3.

Problem	Depot 3
	INS	FNS	IOV	FROV	FIOV	RG%
#1	11	9	105,632	95,177	95,177	0
#2	75	74	910,375	895,845	895,845	0
#3	72	71	910,375	851,249	851,249	0
#4	39	39	474,073	474,073	474,073	0
#5	49	49	613,759	613,441	613,441	0
#6	48	48	603,821	603,503	603,503	0
#7	55	51	671,171	627,329	627,329	0

Table 7. Number of schedules and values of the objective function for depot 3.

Problem	Depot 3
	INS	FNS	IOV	FROV	FIOV	RG%
#1	11	9	105,632	95,177	95,177	0
#2	75	74	910,375	895,845	895,845	0
#3	72	71	910,375	851,249	851,249	0
#4	39	39	474,073	474,073	474,073	0
#5	49	49	613,759	613,441	613,441	0
#6	48	48	603,821	603,503	603,503	0
#7	55	51	671,171	627,329	627,329	0

4. Conclusions

In this study, we introduced a novel and application-oriented approach to integrated vehicle and bus driver scheduling using a set covering formulation for the driver scheduling part with an efficient column generation framework and a heuristic for initial shift generation. Unlike previous methods, our approach constructs the initial column set using a heuristic fully adapted to the given vehicle schedules, ensuring compliance with all operational and regulatory rules. This eliminates the need to generate infeasible shifts and reduces the computational overhead. Furthermore, the method uses a time–space network-based shift generator enhanced with a special feasibility checker, enabling the incorporation of complex, locally specific break and rest regulations that are often oversimplified or ignored in existing models. The originality of this work lies in its combination of three elements: (1) a problem-specific heuristic for initial solution construction, (2) integration of sophisticated regulatory constraints into the column generation process through a dedicated rule checking mechanism, and (3) demonstrated applicability to large-scale, real-world public transportation scenarios with competitive performance against benchmark results. The adaptability and practicality of the method are further validated through the successful deployment in the Szeged public bus transport system, showing that it can bridge the gap between theoretical optimization models and operational decision making.