1. Introduction
A number of low-probability, high-impact events, such as extreme disasters, episodic failures, and deliberate attacks, are threatening the stable operation of power systems. In 2012, Hurricane Sandy damaged the distribution system in New York State, USA, and more than eight million customers suffered power outages [
1]. The Ukrainian power grid was deliberately attacked in 2015, leaving a large number of residents without power for several hours [
2]. Heavy rains in Zhengzhou, China, in 2021 disrupted more than 500 power lines and knocked out power to more than 400 neighborhoods [
3]. Enhancing the resilience of distribution systems to extreme events has received widespread attention.
The ability of the power system to withstand extreme events and quickly restore power is referred to as resilience [
4]. Resilience is defined primarily through vulnerability and recoverability. Vulnerability refers to the loss of power system load shedding suffering disruptive events, while recoverability refers to the repair speed at which the power system returns to normal operation after disruption [
5]. These involve two periods: pre-disaster protection and post-disaster restoration. In general, measures for pre-disaster protection include reinforcing transmission lines [
6], reinforcing nodes [
7], deploying distributed generators [
8], etc. Post-disaster restoration measures include repairing lines and nodes [
9], reconfiguring topology [
10], dispatching mobile emergency generators (MEG) [
11], and more.
For confined power networks like ships, a centralized emergency control strategy is proposed to manage disturbances in multi-terminal Voltage–Source–Converter (VSC)-based power systems [
12]. In [
13], strategies to enhance power system resilience against high-impact low-probability (HILP) events are reviewed, focusing on safeguarding systems with high renewable penetration.
Existing models set the impact of extreme disasters on system components only in terms of whether or not the system components are damaged. Previous studies have only classified components into two states: normal operation and damaged. However, in practice, different disaster intensities can cause different levels of damage to components, and the repair time required for damaged components to return to normal operation varies. Ref. [
14] discusses the problem of defense resource allocation regarding the uncertainty in the number of failed components, but less consideration is given to uncertainty in the repair phase. Ref. [
15] considers the uncertainty in the number of failed components and the uncertainty in the damage intensity, but only optimizes the deployment of mobile emergency power without considering other defense measures. This suggests that there is a research gap regarding the enhancement of power system resilience in terms of considering the uncertainty in the repair time.
Stochastic programming (SP) [
16] and robust optimization (RO) [
17] are the two main approaches used to address the uncertainty. The SP assumes that the uncertain variables follow a specific probability distribution and are solved based on the expected value of all possible scenarios. In contrast, the RO constructs box or polyhedral ambiguity sets to limit the range of variation of the parameters and seeks the best solution in the worst-case scenario. However, both SP and RO have limitations [
18]. SP requires precise probability distributions for uncertain parameters, which often rely on a large amount of valid historical data [
19]. RO aims to cope with solutions in low-probability, high-impact scenarios, but the solutions obtained by considering only extreme scenarios are too conservative [
20]. In contrast, distributed robust optimization (DRO) avoids being overly conservative while ensuring the robustness of the solution. It requires only partial probabilistic information about uncertain parameters to construct moment-based or distance-based ambiguity sets and generates decisions based on the worst probability distributions in these ambiguity sets, thus reducing the potential risks associated with uncertainty and providing better solutions. Recent advances in deep learning also offer alternative resilience solutions. Ref. [
21] pioneered a decentralized Deep Q-Network for attack-response coordination, while [
22] embedded physical constraints in PPO algorithms for partial observability scenarios. However, these methods require large historical samples for reliable policy convergence, whereas Wasserstein-based DRO operates with partial distribution information.
The defender–attacker–defender (DAD) model simulates the interaction between the defending and attacking sides and ultimately obtains better defense resource deployment strategies [
23]. It takes into account (i) defense decisions: the development of optimal resource allocation strategies to minimize load-shedding losses and defense costs; (ii) attack behavior: the identification of the combination of critical components that can cause the greatest load-shedding losses to the system; and (iii) recovery behavior: the rapid restoration of the system after components have been taken out of service through the scheduling of maintenance team (MT) and emergency power supply. The model essentially contains only the game decisions of two intelligences, the defender and the attacker, so the tri-level model is mainly transformed into a two-stage model structure for the solution process, which contains a master problem and a sub-problem. Ref. [
24] solves the inner max–min model using an implicit enumeration algorithm after transforming it into max–max using strong duality theory. This reduces the size of the traversal solution method by exploiting the properties of 0–1 variables. In [
25], the two-stage model is solved by the Benders decomposition method, which approximates the optimal solution step by step through the cutting plane. Ref. [
23] proposes a column and constraint generation (C&CG) method to solve the DAD model, which effectively reduces the number of solution iterations by continuously generating new variables and constraints for the master problem.
However, with the continuous enrichment of disaster resilience enhancement methods and the increasing complexity of the scale of the resource dispatch problem, there are some non-convex cases in the DAD model that are unable to satisfy the KKT condition and cannot be solved by using the dual solution for the inner max–min model. The tri-level structure induces triple-exponential complexity in the worst case, aligning with interdiction problems which exhibit structural similarities to several NP-hard combinatorial optimization problems. In [
26], with the help of the special characteristics of the DAD model, the objective functions of the main problem and the subproblem are relaxed and shifted to the maximization of the number of defense components and the number of damaged components, respectively. Then, the super valid inequalities (SVIs) are incorporated into the subproblem, which forces the attacker to find at least one unbroken component to destroy within the available budget. Each iteration produces a different inequality than the previous one while constantly updating the best solutions. As a result, due to the limitations of the attack budget and the number of candidate component sets, the subproblem eventually becomes infeasible because it cannot satisfy all the inequalities added to the model. The ensemble coverage algorithm then ends with the optimal attack solution and feeds it back to the main problem [
27]. Ref. [
5] follows the subproblem-solving method of [
26] and improves the main problem-solving efficiency by using the Benders decomposition method. However, Ref. [
28] proved that the solution efficiency of C&CG is better than that of the Bender decomposition method, which implies that there still exists a faster method for solving mixed-integer models that do not satisfy the KKT condition.
Table 1 compares the key features of resilience enhancement models in different literature.
To improve the resilience of the system to withstand extreme damage, this paper proposes a defense resource allocation method based on a tri-level defender–attacker–defender model. This method can deploy defense resources to protect critical components before the grid suffers damage, to mitigate grid losses, and enhance resilience. Meanwhile, a distributionally robust optimization model is proposed to mitigate the uncertainty of repair time due to different damage intensities. The main contributions of this paper are summarized as follows:
A tri-level DAD optimization model is developed to consider the restoration process of the grid, so as to obtain the optimal deployment strategy of defense resources and enhance the system resilience.
A distributionally robust optimization (DRO) model is proposed to provide a robust solution to the resource allocation problem by considering the impact of repair time uncertainty on the return of the system to normal operation.
An algorithm combining the set covering method and column and constraint generation is developed to quickly solve the mixed integer model, and the optimal resource allocation plan is obtained by using the iterative relationship between the master problem and the subproblems.
The rest of this paper is organized as follows.
Section 2 describes the proposed TDR-DAD model in detail.
Section 3 presents the SC-C&CG solution method. In order to verify the validity of the proposed model and solution method,
Section 4 shows the case study and the corresponding results. Finally,
Section 5 summarizes the work of this paper and future perspectives.
2. Problem Formulation
2.1. Overall System Framework
Uncertainty in the damage intensity is modelled using a Wasserstein distance-based DRO to strike a balance between robustness and conservativeness. The proposed resilience enhancement model adopts a tri-level DAD framework to address coordinated decision-making under extreme contingencies. This Stackelberg game-theoretic structure comprises three interdependent decision layers: (1) pre-event defense resource allocation, (2) worst-case attack identification, and (3) post-attack emergency recovery. The distinctive strength of the DAD framework lies in its ability to simultaneously optimize proactive hardening measures and reactive recovery strategies against extreme events.
In the first stage, defensive resources are pre-allocated to reinforce critical transmission lines and nodes, while MEGs and MTs are strategically positioned to ensure redundancy. The subsequent attacker layer solves the bilevel optimization problem to identify the most disruptive attack strategy that maximizes grid damage, considering both line outages and generator incapacitation. The final defender stage implements emergency response actions, where available MEGs and MTs are dispatched for rapid power supply restoration and repair crews are optimally routed to mitigate cascading failures and restore normal operations.
Notably, the recovery phase is specifically designed for contingency scenarios derived from the identified worst-case attack strategies. This formulation generates two critical outputs: (1) a robust allocation plan for reinforcing the deployment of resources, MEGs, and MTs and (2) a methodological framework guiding emergency repair operations. While the model prioritizes preventive defense strategies through min–max optimization, it intentionally excludes real-time repair scheduling from the decision variables to maintain computational tractability.
2.2. Uncertainty Modelling
Repair time is used to model the uncertainty in representing damage intensity. The greater the damage intensity, the longer the repair time. An ambiguity set is constructed to address the inherent uncertainty by using the Wasserstein distance metric. This approach enables the incorporation of all possible probability distributions while requiring only partial information about the underlying distribution. The proposed methodology determines the optimal reinforcement strategy by considering the worst-case probability distribution within the constructed ambiguity set, rather than relying on a predetermined distribution. This novel approach yields a more robust and realistic reinforcement strategy that is particularly suitable for power system applications.
Given two probability distributions
and
, the Wasserstein distance is defined as the minimum transport cost to move
to
with minimum transport cost, with a general norm
. The formulation of the ambiguity set model is briefly described as follows.
S is the maximum Wasserstein distance between any pair of distributions in
.
N is the number of historical data.
is the confidence level for the distribution information. For any
,
, there is the cost of moving a Dirac point mass from
to
, equal to
.
represents the set which contains all candidate joint contingency distributions. The distributionally robust ambiguity set
, constructed to hedge against the uncertainty of disaster intensity, is defined as a Wasserstein ball encapsulating all probability distributions
within a prescribed radius
from an empirical reference distribution
(e.g., the empirical distribution derived from historical data). Mathematically,
The first term represents obeying a distribution, the second term represents the true distribution being restricted to the Wasserstein radius of the empirical distribution, and the third and fourth terms represent being a positive distribution with a total probability of 1. controls the conservativeness of the model by regulating the deviation from the empirical distribution. The construction of ambiguity sets plays a key role in the development of system resilience enhancement scenarios. It covers all possible distributions of the repair time and finds the worst-case distribution from them to ensure that the defense scheme is effective in safeguarding the power supply when the system is damaged. This setup not only enhances the robustness of the system in the face of extreme disasters and deliberate attacks but also avoids the conservativeness of the scenarios developed by considering only the worst-case scenarios. Therefore, constructing an appropriate ambiguity set is crucial to resolving the uncertainty of the model parameters.
2.3. Objective Function
The proposed tri-level optimization framework aims to address the strategic inner dependencies between proactive grid hardening, adversarial attack selection, and adaptive recovery operations. Central to this formulation is a nested objective function that rigorously encodes the sequential decision-making logic of the DAD paradigm: defensive investments precede attack realization, which in turn governs post-event recovery efficacy. This structure ensures resilience planning which simultaneously optimizes preventive measures against worst-case disruptions while maintaining cost-effectiveness.
The objective function is structured hierarchically to reflect three critical operational dimensions: (1) Preventive Cost Minimization: Front-loaded investments in infrastructure hardening and mobile resource deployment; (2) Adversarial Risk Maximization: Explicitly quantifying the benefits of the attacker compromising critical components; and (3) Operational Resilience Maximization: Adaptive load shedding minimization under compromised grid conditions.
where
,
, and
are the decision variables for the three levels of optimization, respectively.
and
represent the distribution ambiguity sets for the number of attack resources and repair time, respectively, and
and
are the corresponding probability distributions.
is the defense resource cost.
is the benefit to the attacker from damaging the grid.
and
are the load-shedding loss and operation cost of the damaged grid.
2.3.1. First Layer Optimization
The objective function of the first level is to minimize the cost of defense, and the pertinent objective function and decision variables are as in Equations (5) and (6).
where
and
are the set of lines and buses.
and
represent the cost required to defend the line
l and node
n, respectively.
and
are binary variables, equal to 1 for protecting the line
l or the node
n and 0 otherwise.
represents the initial deployment location of the MEG
k, and
denotes the location of the MT
r. It is worth noting that this will create discrete feasible regions, leading to non-convexity in the strategy space.
2.3.2. Second Layer Optimization
The objective of the second layer of the optimization model is to find the most destructive attack scenario in the constructed set of distributional ambiguities. The specific objective function and decision variables are elaborated in Equations (7) and (8).
where
and
represent the destruction priority, the value of which is determined by the actual importance of each node or line.
and
are binary variables, equal to 1 for attacking the line
l or the node
n and 0 otherwise.
2.3.3. Third Layer Optimization
The purpose of the third layer is to minimize the total load-shedding loss caused by the damage before the grid returns to normal operation, following the determination of the defense scheme and damage strategy in the first two layers, respectively. Equations (
9)–(
11) show the details of the objective function and decision variables.
where
is the time set.
represents the coefficient of the load-shedding loss.
and
are the operation costs of the MT and MEG.
is the load shedding after the restoration phase.
,
,
,
,
,
, and
are binary variables.
and
are equal to 0, indicating that the line
l or node
n is disconnected during the sabotage operation, and 1 otherwise.
and
are equal to 1, meaning that the line
l or node
n is reactivated at time
t.
and
are the trajectories of the repair team recorded with the matrix. When it stops at the damaged components (equal to 1), it can be considered to repair the component.
equals 1 denotes that MEG is powering node
n at time
t.
and
are the generated power of MEG and generator at node
n at time
t.
is the power flow on line
l at time
t.
represents the load shedding at node
n at time
t.
denotes the phase angle at node
n at time
t.
By integrating these components through a min–max–min operator sequence, the model captures the inherent asymmetry among defensive preparedness, attack, and restoration actions. The mathematical nesting ensures defensive strategies are evaluated against their effectiveness in limiting both direct attack impacts and subsequent restoration challenges, thereby aligning theoretical robustness with practical grid operational requirements.
2.4. Constraints
The constraint structure must systematically bridge expected hardening measures, disruption scenarios, and recovery countermeasures while explicitly addressing the inherent uncertainty: attack intensity constraints (as reflected in the time to repair components). The uncertainties propagate in both directions in the decision hierarchy—pre-event defenses change the attacker’s decision space, while post-event maintenance scheduling influences the formulation of defenses. To realize this interdependence, we construct constraints through three mutually recursive levels: (1) pre-disaster defense resource allocation under budget constraints, (2) adversarial attack selection considering limited attack resources and attack benefits, and (3) post-disaster restoration coordination integrating grid current balancing, MEG scheduling, and MT scheduling. It is worth noting that in constructing the constraints of the model, the big-M method is used to linearize the possible nonlinear terms, where M denotes a large constant.
2.4.1. First-Layer Constraints
The deployment of protection resources is an important part of system resilience enhancement, and by hardening some of the lines and nodes, the impact of extreme disasters and deliberate attacks can be effectively resisted. Specific constraints on the deployment of the defense resources are detailed below:
is the defense resource budget.
R and
K are the number of MTs and MEGs. Constraint (
12) represents the budgetary constraints on the investment of total defense resources. Constraints (13) and (14) limit the initial number of MT and MEG deployments.
2.4.2. Section-Layer Constraints
The second layer involves identifying the optimal disruption strategies under different attack resource scenarios for the attacker. Disrupting some of the lines and nodes in the grid can cause maximum load shedding during grid operation. The specific constraints are as follows:
is the attack resource budget. Constraint (
17) means that the maximum number of destroyed components cannot exceed the attack budget.
2.4.3. Third-Layer Constraints
The third layer focuses on constraints on the dispatch of restorative resources and the generation power regulation. Constraints (20)–(55) provide a full breakdown of the model construction.
Component state constraints:
Constraints (20) and (21) represent the state of the line or node. Constraints (22) and (23) indicate whether the damaged components are repaired at time t. Constraints (24) and (25) emphasize that the disconnected nodes and lines will not be repaired until the next time.
MT dispatching constraints:
Since the matrix facilitates the recording of trajectories, is used instead of the line l with start point n and end point m. R is the MT set. and represent the set of routes for each MT and MEG, which are derived from the Dijkstra algorithm. is the travel time on line l for MT r. M in constraints (29)–(55) denotes a good constant. Constraints (26)–(28) indicate trip coherence, i.e., the MTs can only drive into the adjacent roadway at the next moment. Constraints (29) and (30) show that maintenance tasks cannot be interrupted. Constraints (31) and (32) show that once an MT starts work, it must be completed before the next component is repaired. Constraints (33)–(35) limits repairs to one team per destroyed component and one component per team per repair. Constraints (36)–(38) represent the amount of time the MT has to work to ensure that the component is returned to normal, while and represent the amount of time required to repair the damaged component. Constraints (39) and (40) denote the time required to bring the component back to normal. The product of binary variables , , and introduce nonlinear, non-convex terms.
MEG operating constraints:
K is the set of MEGs. Constraints (41)–(43) indicate trip coherence, i.e., the MEG can only drive into the adjacent roadway at the next moment. Constraints (44)–(46) specify a maximum of one MEG per bus. Constraint (47) emphasizes the journey dispatch time of the MEGs. is the travel time on line l for MEG k. Constraint (48) shows that the power supply to the MEG cannot be interrupted unless component maintenance is completed. Constraint (49) limits the power generated by the MEG at node n.
Power balance constraints:
Constraint (
50) ensures the power inflow and outflow balance at each bus
n.
denotes the load demand at bus
n. Constraints (51)–(53) show the upper and lower limits associated with line and node states. Constraint (54) limits the power generation at bus
n. Constraint (55) calculates the power flow on the transmission lines. The multiplicative term
is bilinear, creating non-convexity.
4. Case Study
To evaluate the effectiveness of the proposed tri-level distribution robust optimization model and the SC-C&CG algorithm, a case study is conducted on the modified IEEE 24-bus [
30] test systems, which are mainly based on the topology of the distributed distribution network of these two systems operating as a mesh. Due to the broad range of the transmission network, the total simulation time is set to 14 days, with a unit time of 1 day. The maintenance time scenarios are set to [1, 2, 3, 4] days with the corresponding probability distributions of [0.40, 0.30, 0.20, 0.10] depending on the damage intensity. Experience distribution is obtained from historical data and can be adjusted according to different regional conditions. The power network structure used in this study is rigorously tested based on the Matpower software to ensure the authenticity of the results. The model is developed in MATLAB R2021b using the YALMIP toolbox and solved using the commercial solver GUROBI. Computational simulations are performed on a laptop equipped with an Intel Core i7-9750H CPU and 16 GB of RAM.
4.1. Experimental Setting
The power is uniformly set at kW. For the defender, the unit cost of protection of a line is USD 900/km, and the cost of protection of each line is obtained by multiplying its length by the unit cost. The cost of defending the bus is USD 100,000. For the attacker, the destruction priority of the line and bus is set to 1 and 2, respectively. The cost of breaking the line and the bus is USD 10,000 and USD 20,000, respectively. The cost of defending the line and bus is USD 15,000. The cost per unit of time for the load-shedding loss is USD 100/kW. The fuel cost of the MEG is USD 200/day. The defense budget is set to USD 30,000. The attack budget is set to USD 50,000. The destruction priority of the bus and the line is set to 2 and 1, respectively. The system is equipped with two 100 kW MEGs and two MTs. The MEG can only supply power to the buses in which they are located and cannot support the demands of the entire system through grid integration. Each bus has enough fuel to keep the MEG running until the system is repaired.
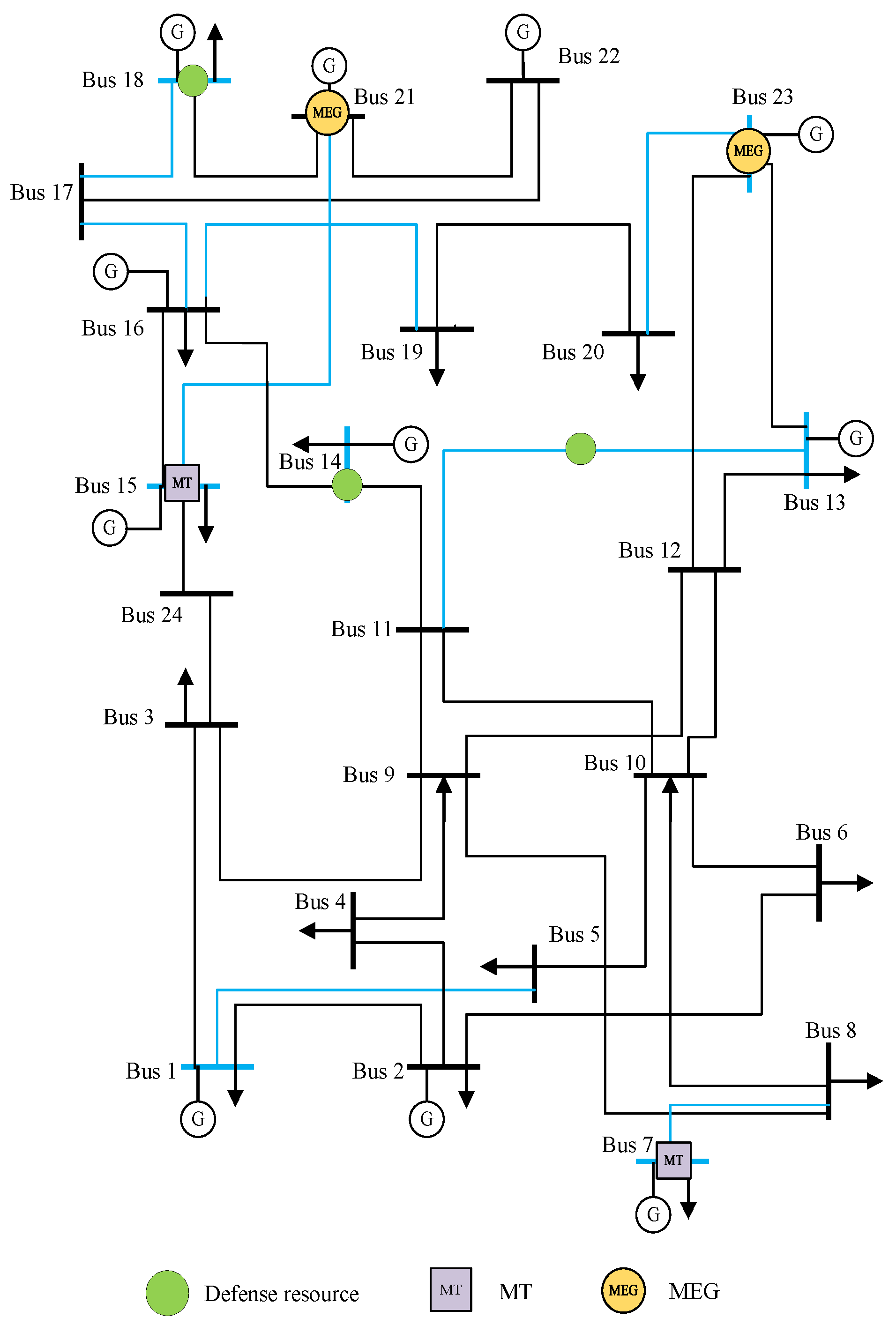
The modified 24-bus system consists of 11 generation buses, 17 load buses, and 34 lines. The system voltage is set to 10 kV to match the MEG dispatch, and the topology is shown in
Figure 1. The top 25% of candidate nodes and line sets after screening by load centrality are marked in red.
4.2. Computational Results
The results calculated in the IEEE 24-bus system are shown in
Figure 1, where the protection scheme includes line 11–13 and buses 14 and 18. The MEG is pre-deployed at buses 21 and 23, and the MT is pre-deployed at buses 7 and 15.
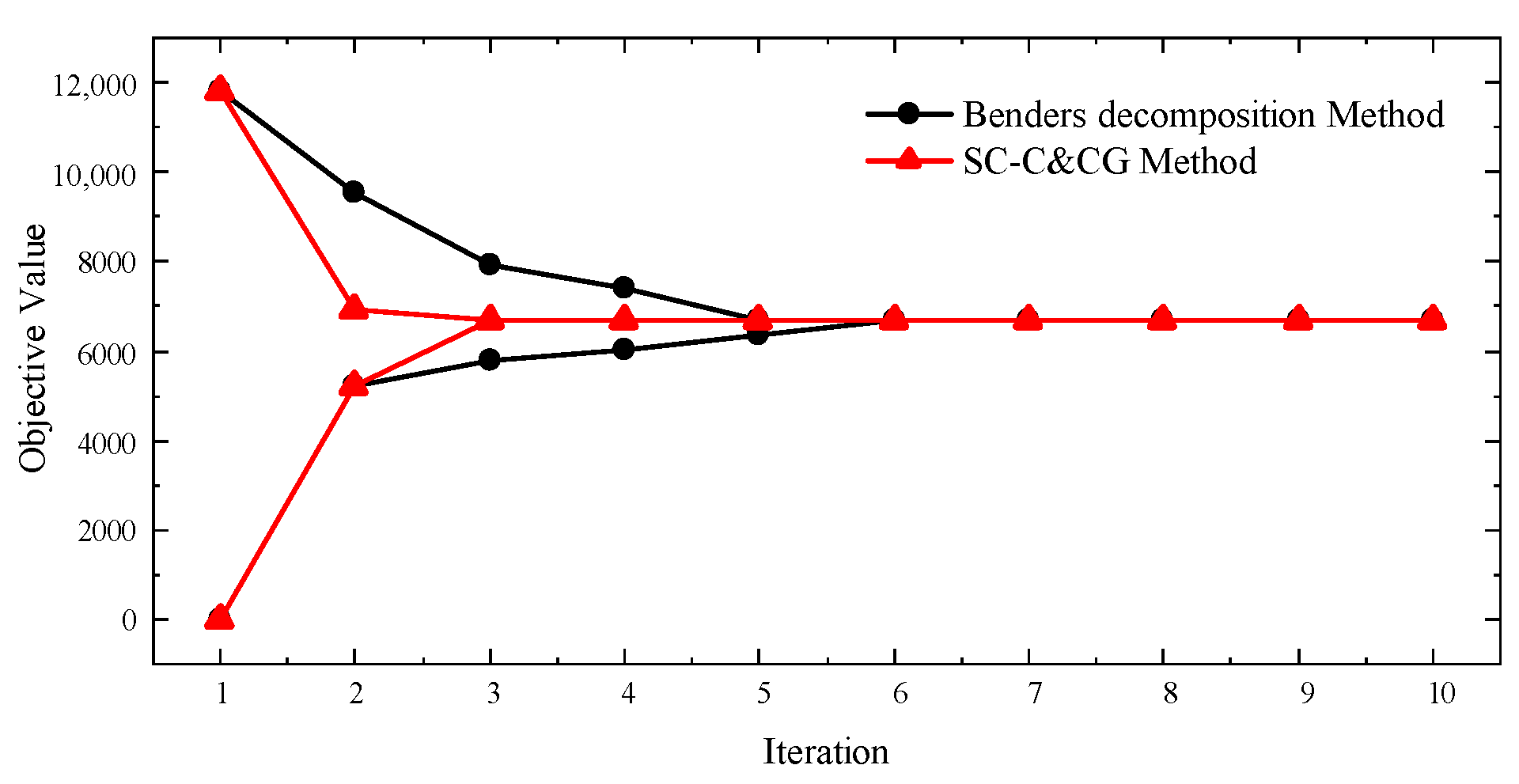
The model yielded results after only three iterations within 1462 s, and the convergence of the upper and lower bounds of the model is shown in
Figure 2. The number of iterations using the Benders decomposition method is much greater than that of the proposed method, and the time required is 3274 s. The worst probability distribution in the constructed distribution ambiguity set is obtained as [0.4067, 0.3022, 0.1978, 0.0933].
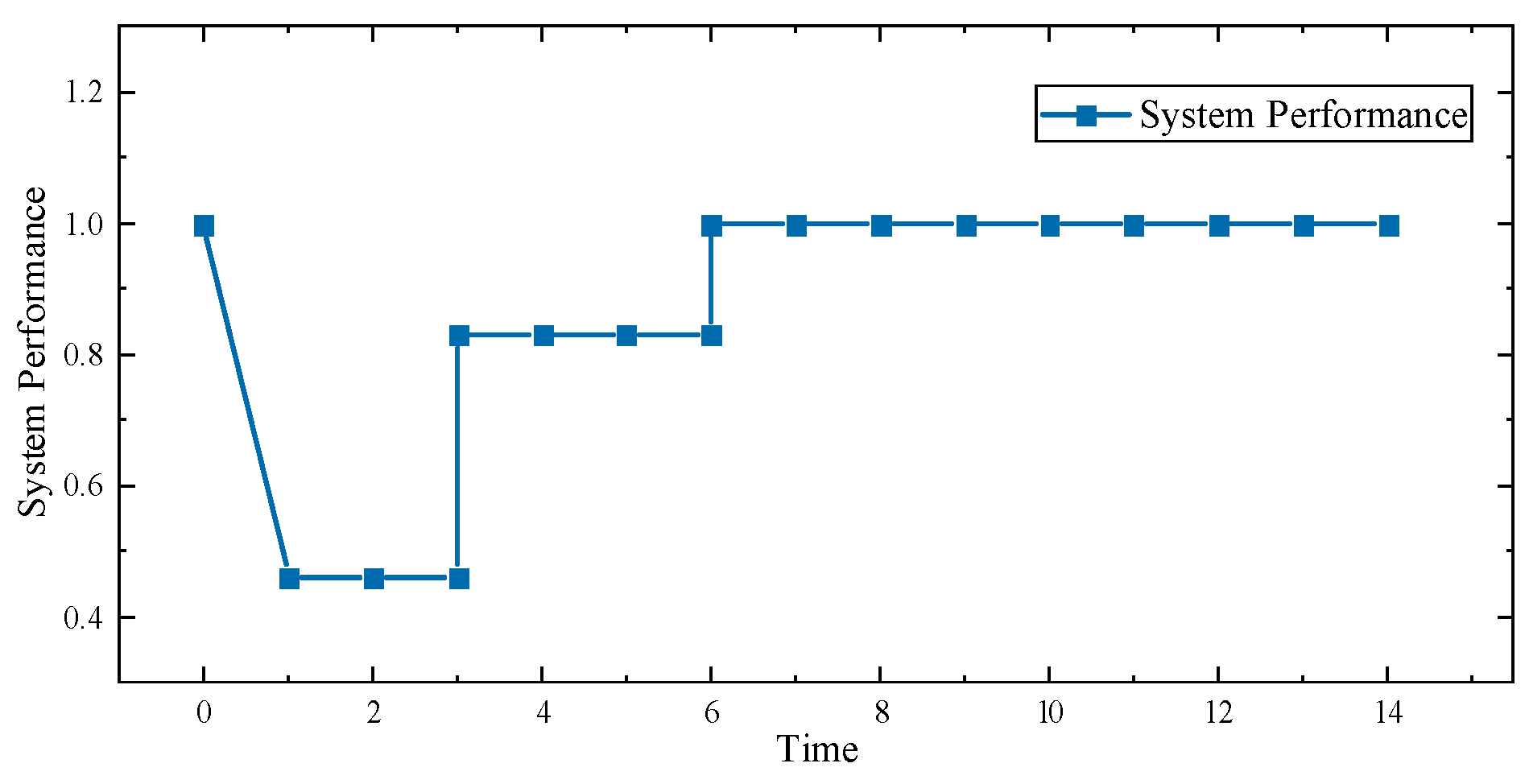
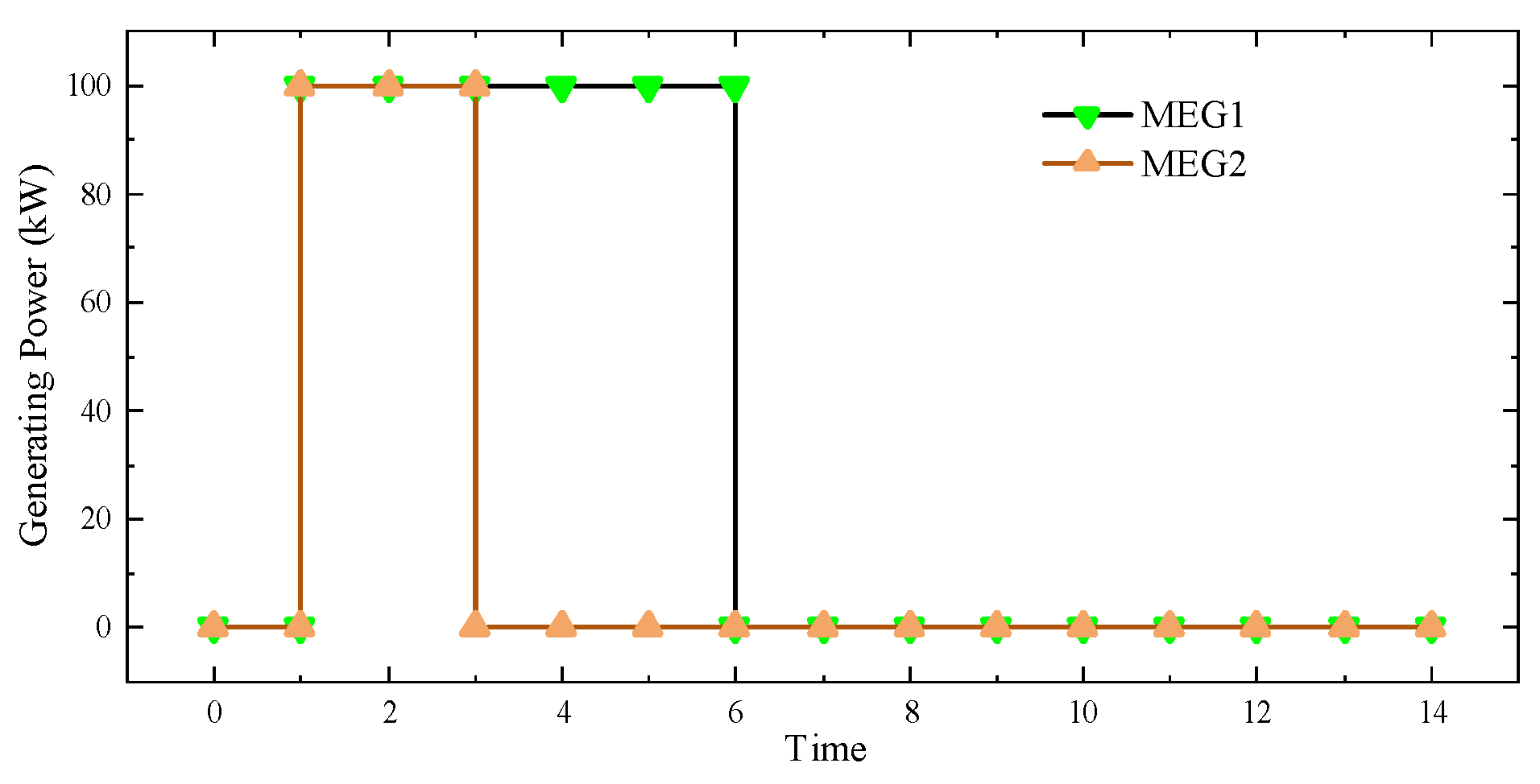
Figure 3 and
Figure 4 show the status of the system during the two-day repair period. As shown in the figures, the system immediately began power adjustments and dispatched repair teams after the damage occurred. At time point 1, both MEGs began generating power, and MEG 2 stopped its emergency power supply on the third day, while MEG 1 continued to operate until the sixth day, at which point the entire system returned to normal. This is because MT takes one day to schedule damaged nodes and two days to repair them.
4.3. Comparison of Uncertainty Modeling Methods
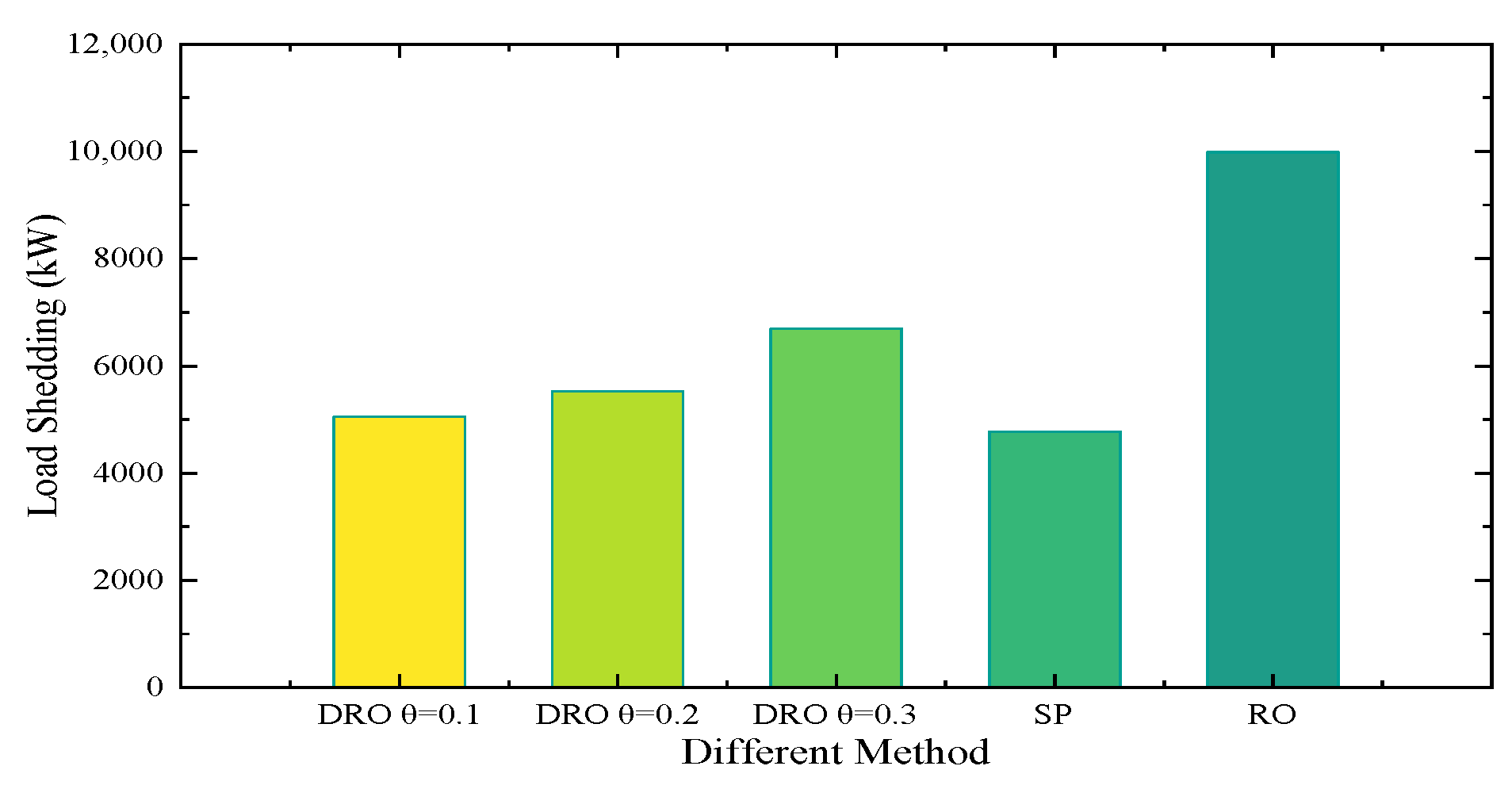
This section evaluates the utility of various methods for addressing repair time uncertainty. The main uncertainty modeling methods are SP, RO, and DRO. Given the repair time scenarios [1, 2, 3, 4] and the empirical distributions [0.4, 0.3, 0.2, 0.1], experimental comparisons are made in the case of the same defense and attack budget, and the results under the different methods are shown in
Figure 5.
This figure clearly shows that RO yields the largest load-shedding loss because it considers all possible scenarios, resulting in an overly conservative solution. SP has the smallest load-shedding loss because the method solves only for a specific distribution. The value of DRO then shows a balanced solution that avoids being overly conservative and also avoids being overly dependent on the exact distribution of the information. This is because the DRO method makes full use of historical data to build the ambiguity set of distributions based on the empirical distribution, thus covering a wider range of distributions. This extension enhances the robustness of the solution. The robustness can also change as the radius of the Wasserstein sphere changes, which demonstrates the flexibility of the DRO method.
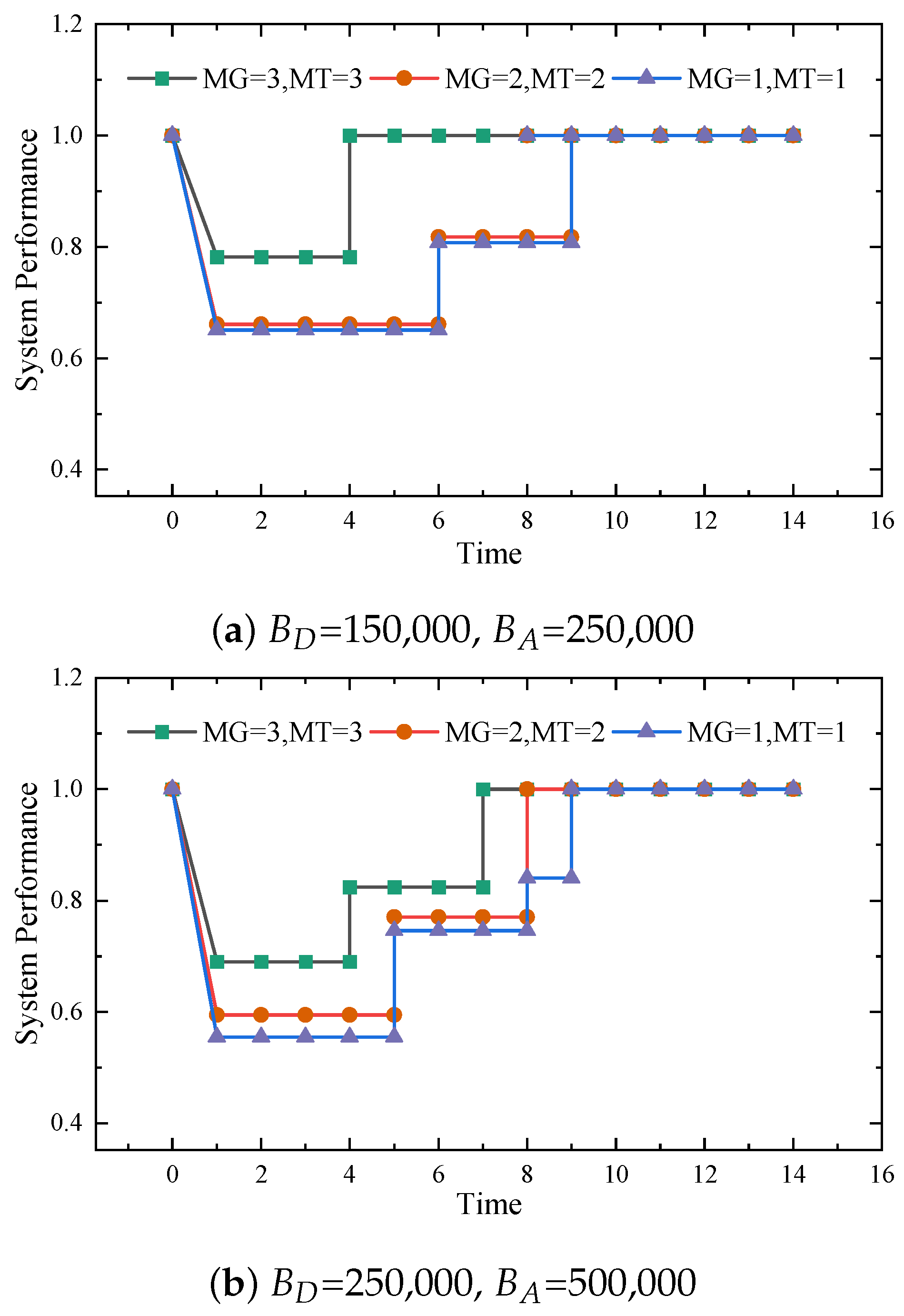
4.4. Comparison of the Number of Different Scheduling Resources
This section explores the impact of changes in the number of recovery resources on the system recovery process under different attack and defense budgets. Recovery resources are mainly the MEGs and MTs working in the recovery process. The purpose of this analysis is to investigate the effect of different numbers of recovery resources on the system recovery speed to ensure the consistency of the results. The budgets of defense and attack are set as [(150,000, 250,000), (250,000, 500,000)], and the combinations of MEGs and MTs are set as [(1,1), (2,2), (3,3)]. Multiple experiments are conducted based on the setup scenario, as shown in
Figure 6.
This figure shows the recovery speed of the system for different scenarios. In the initial phase, the system suffers damage, and the load satisfaction rate decreases. Then, the defender starts dispatching MEGs and MTs until the whole system fully recovers. Obviously, using multiple MEGs and MTs can speed up the recovery process because multiple MTs can run in parallel, thus allowing the system to return to normal operation faster. From this figure, it can be seen that the greater the number of MEGs, the less the system performance degrades after damage. The higher the number of recovery resources, the faster the system returns to normal operation.
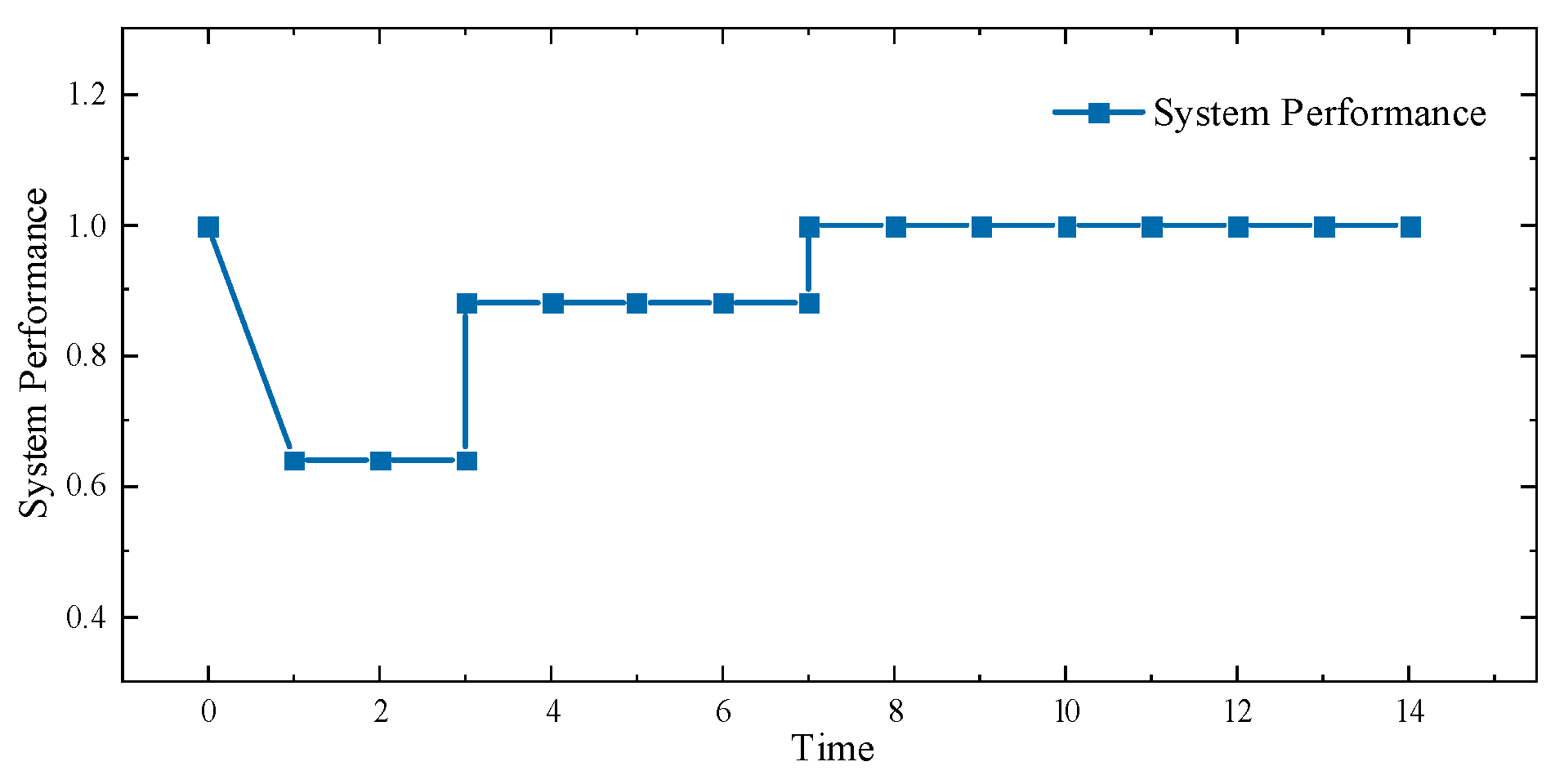
4.5. Effect Verification of the 118-Bus System
To assess the scalability of large-scale systems, the IEEE 118-bus system is used for validation. This larger system includes 118 buses, 186 transmission lines, 54 generation buses, and 99 load buses, providing a realistic scale for resilience studies. We set the same attack budget and defense budget, and conducted the test with a repair time of two days.
The changes in the load satisfaction rate of the power grid are shown in
Figure 7. It can be seen that under the same budget, as the scale of the power grid increases, the impact of damage to the power grid decreases, but the larger mobility space also leads to longer recovery times.