Abstract
Designing propulsion systems for agricultural drones involves a repetitive process that is both expensive and time-intensive. At the same time, conducting comprehensive experimental tests demands specialized equipment and strict safety protocols. In this work, the design and assessment of the propulsion system (propeller, motor, and battery) for large-sized drones in agricultural applications are conducted using numerical methods. To properly predict and validate the performance of a brushless direct current motor, a three half-bridge inverter circuit, featuring a trapezoidal commutation, is implemented and constructed. First, the propeller is studied using the finite volume method, obtaining a maximum variation of 6.32% for thrust and 10.1% for torque. Additionally, an electromagnetic analysis on a commercial brushless direct current motor (BLDC) using JMAG software from JSOL corporation (JMAG designer 23.2, Cd.Obregón, México) resulted in 4.43% deviation from experimental electrical measurements. The selected propulsion system is implemented in a 30 kg drone, where motor performance is evaluated for two instants of time in a typical agriculture trajectory. The findings demonstrate that numerical methods provide valuable insights in large-sized unmanned aerial vehicle (UAV) design, decreasing the experimental tests conducted and accelerating implementation time.
1. Introduction
High-efficiency electric machines have gained significant interest in modern technological industries, such as automation and robotics, home appliances, and electromobility, where electric motors represent over half of the electricity expenses and about two-thirds of the total power consumption. Out of the vast catalog of electric machines, the brushless permanent magnet motor (PM motor), characterized by an electronically controlled commutation stands out by its high torque density, good efficiency, and versatility. The use of PM motors in appliances is supposed to provide up to a 42% energy reduction, compared to conventional alternating current motor appliances, and its implementation in ground and aerial vehicles allows for high power efficiency at low speeds. Multi-copter Unmanned aerial vehicles (MUAV) are used in various fields for their hovering capabilities and maneuverability [1]. However, these precise characteristics make them the least efficient aerial robot by depending entirely on actuators to generate lift. On the other hand, modern battery technology imposes limitations on flight time, negatively impacting all drone applications. The propulsion system, directly relates to the efficiency and performance of the vehicle. A lot of effort in early drone design is consequently directed towards designing and selecting the ideal elements for the desired operating range, commonly executed empirically by testing multiple element combinations [2].
In large-sized MUAVs, a high torque-to-weight ratio and efficiency make the brushless DC motor (BLDC) the preferred PM motor. Its typical rectangular wave-formed current reproduces electronically the physical brushes characteristic of the direct current (DC) motor, thus producing an alternating current (AC) signal to operate, making it fundamentally an AC machine. This driving technique allows for considerable energy loss reduction and broader commutation options for specific applications. This flexibility comes at the expense of driving complexity, requiring an electronic speed controller (ESC) to operate [3]. The ESC includes the power electronics, rotor position detection methods, and controllers needed to generate the trapezoidal commutation commonly used in low- and medium-end agriculture unmanned aerial vehicles.
Several works address the design and analysis of BLDC motors. In [4], electromagnetic analysis in a switched reluctance, induction, and BLDC motor using ANSYS Maxwell software was conducted. The BLDC motor proved to be the most efficient and offered the highest torque density in the desired operating range. The differences in inner and outer brushless motors were discussed in [5], highlighting the superior power-to-weight ratio and torque density of outrunners, making them ideal for agriculture UAV applications where high inertia and low to medium speeds are desired. The electromagnetic radial flux property of BLDC motors allows for a good field distribution and reduced dimensions, while their surface magnet rotor structure, typically found in drones, offers mechanical simplicity and improved controllability. Recent works focus on the multi-step analysis and optimization of electric machines using important geometric characteristics as input parameters. The finite element method is used for pre-manufacture output evaluation, with particular interest in efficiency, torque, and output power. In [6], the influence of magnet geometry on cogging torque is investigated. Through the use of both analytical and numerical methods, the most influential motor harmonics are weakened through eccentric magnet shapes, effectively reducing torque ripple up to 90 percent, resulting in quieter and less fault-prone motors, while in [7], a novel back-electromotive-force detection method is presented. The improved technique allows for a full motor operating range and smooth start, by combining two different sensorless detection methods. Few works address the analysis of BLDC motors for drone design purposes.
In [8], the electronic speed controller, motor and propeller are modeled analytically to evaluate the Field-Oriented Control (FOC) and trapezoidal performance in real drone scenarios. The nested PI controllers of the FOC commutations translate into higher computational requirements and electronic complexity in the ESC; while the out-performance of the FOC architecture is evident, the 1% efficiency improvement does not vindicate the superior costs and weight compared to the trapezoidal commutation in agriculture UAV. On the other hand, in [9], the design and electromagnetic analysis of a BLDC motor for a large-sized multi-rotor were conducted using ANSYS Maxwell software. The design requirements are defined by a systematic propulsion system assessment using analytical equations.
Despite the progress made in BLDC motor analysis regarding drone applications, some challenges and limitations have been identified. These include a lack of BLDC motor analysis methodology in electric machine-dedicated simulation tools such as JMAG software, the use of numerical methods to select the optimal motor–propeller combination, and numerical efficiency assessment of propulsion system elements focused on UAV autonomy to ensure longer flying times in drone agriculture applications.
The contributions of this work are as follows:
- Electromagnetic performance assessment of a BLDC motor in agricultural drone applications using JMAG software.
- Validation of the electronic speed controller circuit with trapezoidal commutation in JMAG. The reliability of the circuit is demonstrated by comparing the generated driving signals against commercial and in-house-built electronic speed controllers.
- The use of Computational Fluid Dynamics and the finite element method (through JMAG), to assess the optimal motor–propeller combination.
- Propulsion system design focused on multi-rotor autonomy. The propulsion system was implemented and tested in a large-sized UAV for agriculture.
These contributions address the challenges of traditional propulsion system design and assessment, such as depending on large application-based drone databases and extensive experimental testing. The rest of this paper is organized as follows: Section 2 presents the design requirements and initial sizing of the agriculture UAV. Additionally, the performance of a commercial drone propeller is evaluated using Computational Fluid Dynamics (CFD). The methodology of electromagnetic analysis using JMAG, the analysis of a commercial BLDC motor, and the trapezoidal commutation technique are introduced in Section 3. In Section 4, the lithium-ion polymer (LiPo) battery characteristics for the application are defined, and through the computation of the efficiency of the BLDC motor, the drone autonomy in hover conditions is predicted. Finally, in Section 5, some conclusions and final comments are provided.
2. Propulsion System Design in Agriculture Multi-Rotor UAVs
This section provides the specific characteristics of agricultural applications in UAVs. The iterative nature of agricultural drone propulsion system design makes it costly and time-consuming. The extensive experimental tests require specialized equipment and rigorous safety measures. Numerical methods can be included in the design process to reduce the number of experimental tests conducted. The propulsion system consists of the battery technology, the electronic speed controller, the BLDC motor, and the propeller. The mass distribution in commercial agriculture drones is shown in Figure 1; the propulsion system takes up to 24% of the nominal take-off weight. Compared to other large-sized drone applications, agriculture UAVs focus on structure integrity and payload, sacrificing autonomy. The most important design requirements are divided into four categories and introduced in Table 1.
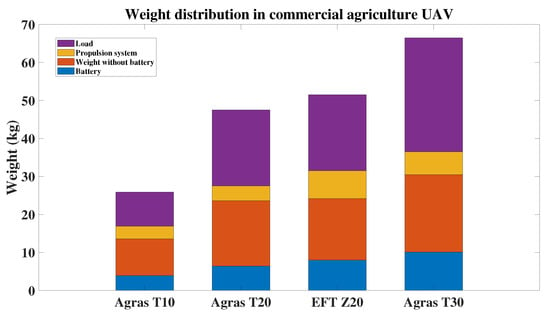
Figure 1.
Mass distribution in commercial agriculture UAVs.

Table 1.
Basic UAV design requirements for agriculture applications.
In order to find an efficient propeller–motor combination with an appropriate specific energy source while fitting into the desired wheelbase of the vehicle, the maximum propeller diameter is calculated.
A maximum D1 distance of 265 cm for transportability and a minimum D3 distance of 5 cm were set for a hexarotor with the configuration shown in Figure 2. Equation (1) expresses the maximum allowable propeller diameter in terms of D3 and D1, resulting in a 33.4 inch maximum diameter.
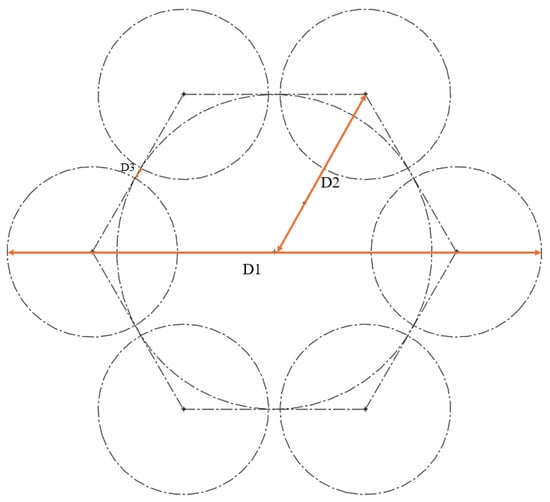
Figure 2.
Propeller and overall skeleton size characterization.
2.1. Propeller
In this section, the sizing and aerodynamic analysis of a commercial propeller using CFD, is presented. The numerical computation of propeller torque, thrust, and efficiency marks the beginning of the propulsion system design methodology. The typical thrust-to-weight ratio in commercial agriculture drones goes from 1.6 to 2.0 [10]. This relation provides good drone maneuverability to external disturbances by reaching a hover state close to the half-throttle capacity. The multi-rotor studied in this paper had a nominal take-off weight of 30 kg and a maximum desired thrust of 470.88 N, aiming for a 1.6 ratio. According to [2], the optimal propeller diameter can be sized with Equation (2). The air density is dependent on flight altitude and ambient temperature, while the optimum angular velocity is obtained from the propeller manufacturer and reported in Table 2. The propeller chosen was the T-Motor carbon fiber, 31.2 × 10.2, which also fits with the maximum allowable propeller diameter for the UAV.
where is the air density, N is the maximum optimum angular velocity, is the propeller thrust coefficient, and is the theoretical maximum thrust.

Table 2.
Propeller sizing variables [2].
Selecting the right propeller for the imposed design requirements and agriculture application characteristics implies finding a propeller capable of efficiently providing the maximum desired thrust of 470.88 N, so that the flight-time objectives are accomplished. For a hexarotor configuration, each propeller must deliver at least 78.48 N. Computational Fluid Dynamics can be used to evaluate the fit of the propeller chosen.
2.1.1. CFD
The essence of Computational Fluid Dynamics (CFD) in multi-rotors revolves around numerically resolving the Navier–Stokes equations for viscous and incompressible fluids in a three-dimensional space:
where is the fluid viscosity, p is the pressure, U is the velocity field, and F denotes the source terms encompassing the mass forces acting on the body.
Propeller performance can be assessed through spatially averaged solutions using Moving Reference Frames (MRFs) and Reynolds-Averaged Navier–Stokes (RANS) equations [11]:
where denotes the Reynolds stresses, accounting for turbulent effects.
MRFs allow for flow modeling around moving parts in steady-state conditions by including acceleration terms in the RANS momentum equations [12]. For an absolute velocity formulation, the additional term takes the following form:
where and are the angular and absolute velocity, respectively.
The low-to-medium Reynolds numbers characteristic of agriculture multi-rotors require turbulence models capable of appropriately solving viscous effects (adverse pressure gradient flows) near the propeller and free shear flows away from it [13,14]. For this, the shear-stress transport (SST) turbulence model is employed in addition to the RANS equations. This hybrid model utilizes the empirical formulation near the boundary layer for its numerical stability while switching to the robust model in the free-stream region. The superior accuracy and good convergence of this model in multi-rotor applications had made it widely used in the literature [15].
2.1.2. Boundary Conditions
The computational domain consists of two cell zones: a static region and moving region (Figure 3). It is in the inner, moving domain that the propeller is located and the rotational speed assigned. As for the outer region, the inlet, outlet, and wall enclose a stationary cylinder. The general characteristics and dimensions are defined as follows:
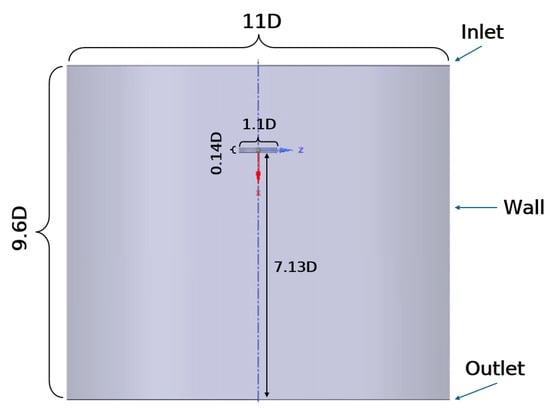
Figure 3.
Geometric characteristics of CFD domain.
- Static domain: A cylinder of 11D (11 times the propeller’s diameter) in diameter and 9.6D in height.
- Moving domain: A cylinder of 1.1D in diameter and witth a height of 0.14D.
- Boundary conditions: The inlet and outlet correspond to the atmospheric pressure (1 atm) in an absolute frame, reproducing hover conditions. Similarly, the no-slip condition was set to the outer wall and propeller (Table 3).
 Table 3. Boundary conditions for propeller analysis using CFD.
Table 3. Boundary conditions for propeller analysis using CFD. - Interface treatment: Absolute formulation.
A CFD analysis of the propeller (Figure 4) defines the optimum velocity and torque in a range of 2400–3000 RPM and torque of 1.75–2.88 Nm with an efficiency of 9.66–7.56 g/W. These values were compared and confirmed with T-motor online data.

Figure 4.
Three-dimensional CAD design of 31.2 × 10.2 carbon fiber propeller.
The thrust–speed and torque–speed curves for the propeller from the CFD analysis show their characteristic quadratic dependence on speed (Figure 5 and Figure 6). The propeller is expected to reach about 3000 rpm to comply with the maximum thrust and thrust-to-weight ratio previously defined. However, nominal operation is enclosed in a 2200 to 2600 rpm range. The propeller efficiency is commonly delivered in grams per watt to denote the propeller’s capacity of generating lift per watt consumed (Figure 7). Table 4 presents the thrust and torque CFD result validation against reported data from the manufacturer.
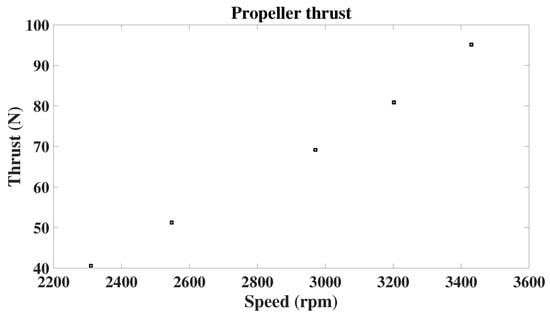
Figure 5.
Thrust–speed curve for the range of interest from CFD analysis.
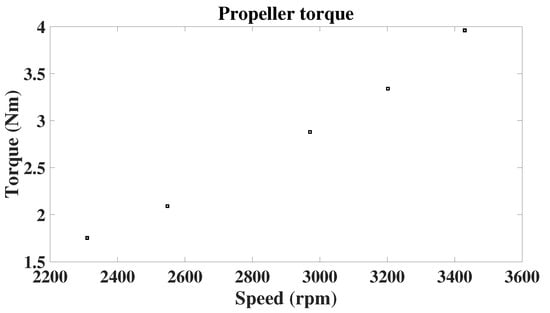
Figure 6.
Torque–speed curve for the range of interest from CFD analysis.
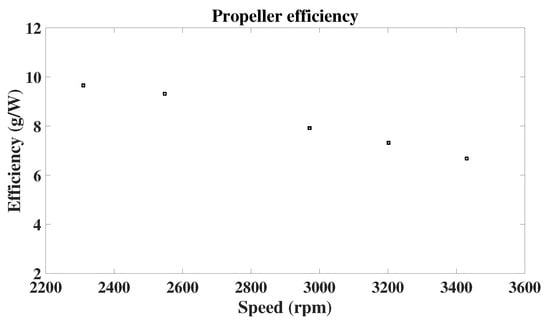
Figure 7.
Efficiency–speed curve for the range of interest from CFD analysis.

Table 4.
Thrust and torque validation: numerical and manufacturer data.
With the optimal torque and velocity range with this propeller for this application, the task now is to select the BLDC motor capable of efficiently providing that mechanical power.
3. Bldc Motor Analysis
In this section, a commercial outrunner BLDC motor for large-sized drones is analyzed and assessed for the desired operating range. Numerical methods provide valuable operational insights in electric machine analysis. They are widely used for output evaluation after exhaustive analytical design work, making them ideal tools for this work.
3.1. Electromagnetic Analysis in Time Domain for Electric Machines
JMAG is a software package for electric machine analysis using the finite element method to solve the governing equations of electromagnetic, thermal, and structural phenomena. Regarding motor operation, Maxwell’s equations are used to relate electric and magnetic fields to electric charges within the machine. The electromagnetic field in transient state is expressed as
where A is the magnetic vector potential, is the electric conductivity, and is the magnetic reluctivity.
Additionally, the external circuit equation introduces the effects of the electric supply and control:
where V is the stator phase voltage, R is the total stator phase resistance, i is the stator phase current, is the total cross-section area of stator windings, L is the ending winding inductance, and s is the total cross-sectional area of the stator winding, one turn per coil side.
The following motion equation describes the rotation of the rotor:
where is the total moment of inertia, is the rotor speed, is the electromagnetic torque, D is the damping coefficient, and is the shaft torque. These equations are coupled together and matched in the air gap region of the motor.
3.2. Boundary Conditions
The computational domain comprises three zones: a stator, rotor, and air region (Figure 8). The rotational motion and nodal force calculation are set to the rotor region. Similarly, to properly capture the flux leakage outside the motor material, the surrounding air region is defined as five times the rotor diameter. The rest of the domain characteristics are as follows:
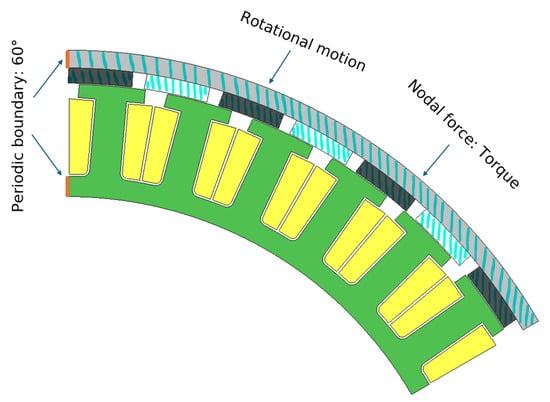
Figure 8.
Boundary conditions: electric motor simulation.
- Static domain: iron core and winding.
- Moving domain: rotor and outside air region (diameter of 543 mm).
- Boundary conditions: rotation periodic boundary with 60 degree periodicity and a slide condition in the air gap.
3.3. U12 KV 120 Motor Description
The selected test motor was the outrunner U12 II KV 120 from T-Motor. It is a medium-end BLDC motor for heavy-lift aerial vehicles, with its basic parameters shown in Table 5. Its high power factor allows for future upgrades and improvements.

Table 5.
Motor parameters.
Outrunner BLDC motors in agriculture drone applications typically have a long pole number and short length–diameter ratio to account for torque-demanding load requirements and relatively low speeds [16]. The 36-slot–42-magnet configuration of the test motor results in a small pole pitch, which reduces the electrical loss characteristic of larger diameters, while the superior split ratio ensures a high overall volume. The CAD design shows the rotor’s greater axial length compared to the magnets (Figure 9). A yoke flux spreads to the cup material, thus increasing the effective magnetic area, allowing for thinner cup dimensions even when paramagnetic materials such as aluminum are used. The cross-sectional view of the motor reveals the rotational symmetry characteristic of salient pole designs; thus, a low winding inductance and reluctance torque is expected. The surface magnet configuration allows for an air gap tolerance of 0.2 mm without compromising significant flux density.

Figure 9.
Three-dimensional CAD U12II motor design.
Motor manufacturers do not provide detailed material characteristics; some assumptions were needed for the simulation (see Table 6).

Table 6.
Motor materials.
The permanent magnet in the U12 II is the arc magnet N42UH, with a radial magnetic pattern and a 1.5 mm width or 7.5 times the air gap length, as suggested by the literature. With a maximum working temperature of 180 °C and a remanence of 1.3 T. However, the working temperature should be kept below 120 °C to avoid significant demagnetization, as the magnetic hysteresis curve collapses over 80% on higher temperatures [17].
Figure 10 shows the winding configuration of the U12 motor. Concentrated winding reduces copper losses and allows for fault tolerance between coils, while its high cogging torque frequency translates into low cogging torque (Figure 11). Compared to a single winding layer, the double-layer winding reduces the increase in the conductor AC resistance as the frequency increases (Figure 12), by having 0.85 slots per magnet pole, and thus a coil span of 1 (Table 7). Shorter end-turn lengths can be used, reducing winding resistance and the overall motor volume. The definition of the coil placement in the slot region of the stator sets the back electromotive force (BEMF) ideally as a trapezoidal-shaped form. This BEMF is then softened by the conductor inductance and pole-to-pole leakage [18], resulting in a rounded, sinusoidal waveform (Figure 13).
Figure 10.
U12II winding configuration.
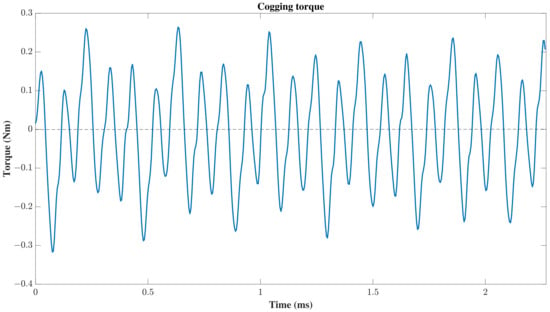
Figure 11.
Cogging torque in the U12II motor with 2548 rpm.
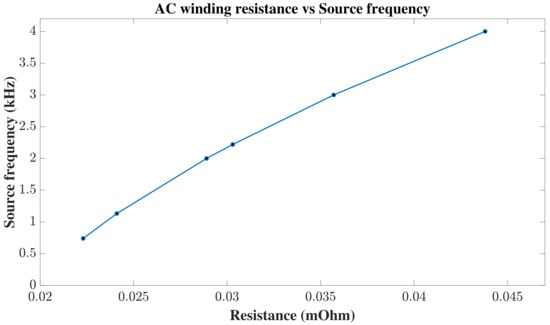
Figure 12.
Copper resistance evolution regarding source frequency.

Table 7.
Winding characteristics.
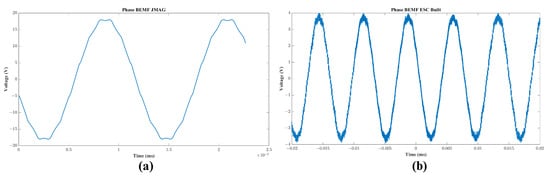
Figure 13.
BEMF: (a) JMAG simulation, (b) measured using a designed ESC with trapezoidal commutation.
The low slot fill factor relates to the low KV (motor velocity constant) rating. While the use of higher conductor gauges increases the copper losses, the stranded parallel wiring reduces this effect and facilitates the winding process. Table 8 shows the typical KV range for large-sized UAVs in agriculture applications. Low KV is desired for vertical take-off configurations to achieve high efficiency at low speeds [19].

Table 8.
Typical KV for two different drone applications.
Based on the analysis of the motor characteristics and application fit, the following section introduces the driving technique that correctly reproduces the experimental behavior of the commercial ESC.
3.4. Six-Step Commutation
Trapezoidal commutation is a low-cost technique often used in agricultural UAV applications. Its electronic simplicity lies in the six-step nature of the driving signal, disregarding the use of dead-time circuits, complex filters, and rotor position detection methods. During a complete electrical cycle, the current and voltage waveforms undergo six transitions, that is, a different current mode every 60 degrees (Figure 14). In any instant of time, current flows through two of three lines in a controlled fashion [20]. The floating line can then be used to lead the timing of the transitions required to produce a maximum torque output by detecting the zero-crossing of the BEMF [21]. Pulse width modulation (PWM) is used to control the voltage input to the motors and thus regulate the motor speed. The most popular PWM drive signal scheme in BLDC motors is that in which only high-side MOSFETs are controlled using the PWM signal (Figure 15), while the rest only receive ON-OFF states [7].
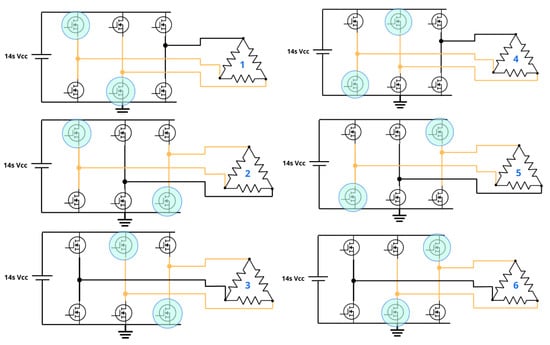
Figure 14.
Six-step trapezoidal commutation for a three-phase motor with delta termination.
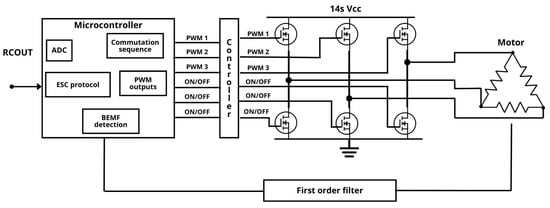
Figure 15.
Electronic speed controller for a three-phase electric motor with delta connection using trapezoidal commutation.
In practice, the three-half-bridge topology is used to create six-step power signal commutation and zero-crossing via resistors, filters, and comparators.
Figure 16 shows the ESC implemented in JMAG. The circuit scheme includes a rotor position detection algorithm that commands the six-step commutation to the three-half-bridge circuit model switches. The PWM’s duty cycle is regulated through a modulation ratio, emulating a radio control signal or throttle percentage from a flight controller. Additionally, the inverter is energized with a current source corresponding to experimental measurements. The circuit inputs for a 60% throttle capacity are shown in Table 9, and the corresponding electromagnetic flux density and flux lines appear in Figure 17.
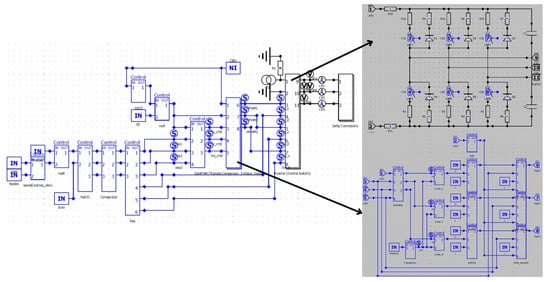
Figure 16.
JMAG circuit for trapezoidal commutation and motor delta connection.

Table 9.
Circuit parameters for a 60% throttle capacity.
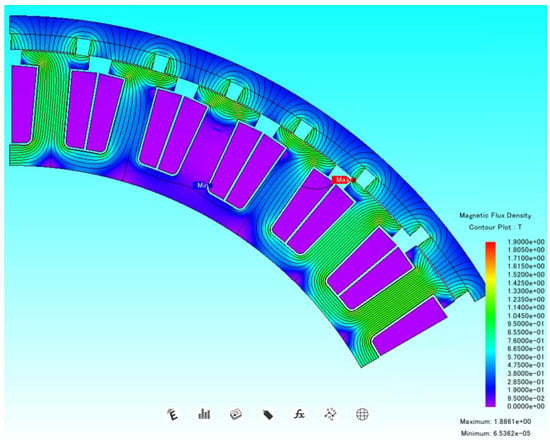
Figure 17.
Magnetic flux density and flux lines for 60% throttle.
The overall good outer-to-inner diameter ratio of the stator can be observed in the nominal magnetic flux density. The relatively thin stator yoke accounts for the larger slot depth. In keeping the magnetic flux density below 1.7 T and maintaining a good operating temperature, fewer iron losses are expected.
3.5. Jmag Trapezoidal Commutation Validation
In order to validate the current and voltage waveforms of the commutation circuit in JMAG, an ESC featuring trapezoidal commutation was constructed. The square-wave current form of the JMAG simulation, the ESC constructed, and the Flame 100A 14s from T-Motor are shown in Figure 18, with good agreement. The experimental setup consists of the U12KV120 BLDC motor, the 31.2 × 10.2 inch carbon fiber propeller from the T-motor, and a 14s LiPo battery. Initial static thrust tests were performed with the A622 AC/DC current probe and the Herelink V1.1 remote controller to supply precise throttle values. The experimental setup can be observed at the following link: https://youtu.be/QTqWmrk4BxM (accessed on 1 June 2025). The driving signal is supplied instantaneously in the static thrust test. Contrasted with the gradual speed increment in nominal flight operation, increased heat production and higher initial peak current demand are expected.
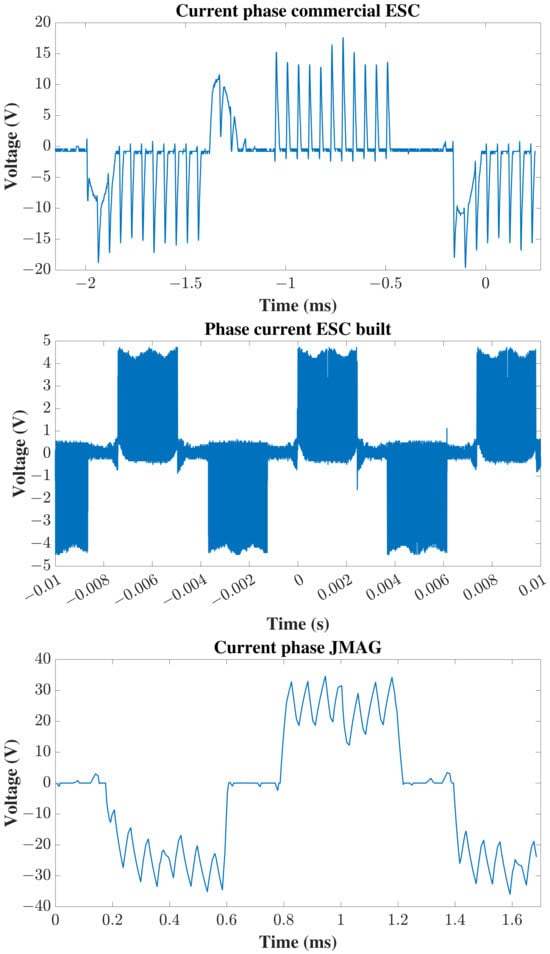
Figure 18.
Phase current qualitative comparison: (top) commercial ESC, (middle) designed ESC, (bottom) JMAG.
Motor inductance and chopping frequency effects are present in the experimentally measured current, causing current ripples in polarity reversals. These effects are considerably weakened in the phase current from JMAG.
Similarly, the trapezoidal-wave voltage form of the JMAG simulation, the constructed ESC, and the Flame 100A 14s from the T-Motor are shown in Figure 19. The superimposed BEMF can be observed in the measured experimental line voltage.
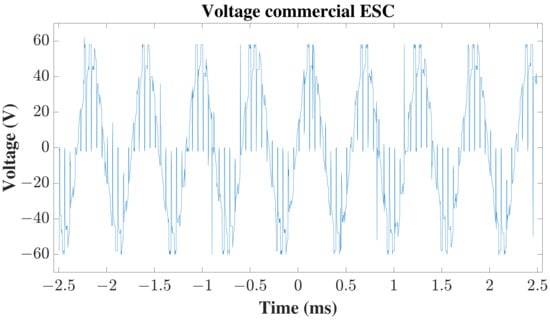
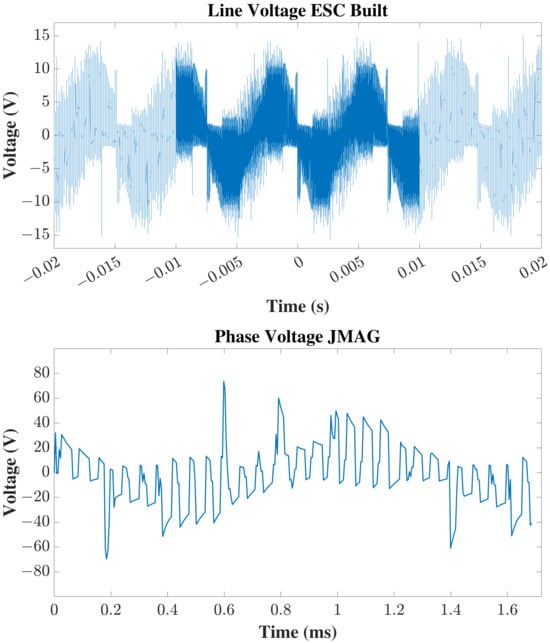
Figure 19.
Line voltages qualitative comparison: (top) commercial ESC, (middle) designed ESC, (bottom) JMAG.
The driving signals corresponding to 70% throttle are presented in Figure 20 with the phase and line root mean square value (RMS). The quantitative comparison shows a maximum variation of 3.5% from experimental measurements (Table 10).
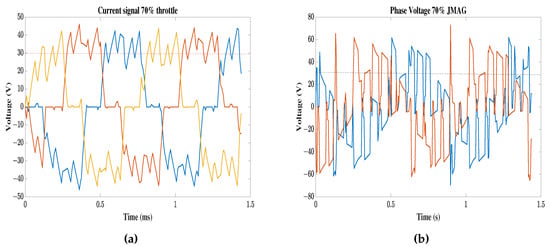
Figure 20.
Driving signals for 70% throttle from JMAG. (a) Phase currents from JMAG. (b) Line voltages from JMAG.

Table 10.
Quantitative comparison: JMAG and experimental driving signals for a 70% trottle.
Similarly, the phase current and line voltages for 40% throttle are presented in Figure 21. Table 11 shows a 4.43% error compared to experimental measurements.
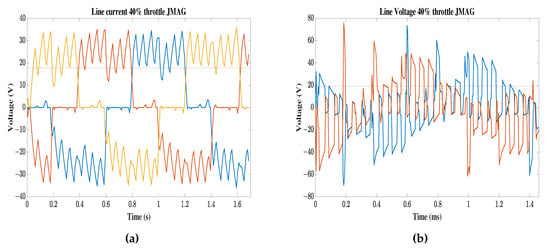
Figure 21.
Driving signals for 40% throttle from JMAG. (a) Phase currents from JMAG. (b) Line voltages from JMAG.

Table 11.
Quantitative comparison: JMAG and experimental driving signals for 40% throttle.
After validating the driving signal waveforms and root mean square values, the efficiency and performance of the motor in specific operating ranges are presented.
4. Results and Discussion
4.1. Efficiency and Autonomy
Efficiency maps (EMs) are contour plots used to relate torque, speed, and efficiency in electric machine applications. EMs allow for the evaluation of design choices taken throughout motor development and represent a powerful tool with which to assess electric machines’ performance in specific load cases. However, in order to obtain accurate EM results, motor loss components should be considered [22]. Out of the various components, the joule and core losses represent the highest power dissipation in electric machines on electrical vehicle applications. The core loss frequency-based approach in JMAG allows for accurate results [22], while the Finite Element Analysis (FEA) technique permits individual part loss analysis. Additionally, windage and friction losses (mechanical loss) can be considered in the efficiency map computation.
A reduced efficiency map for the U12II motor is shown in Figure 22, where the maximum efficiency reaches 79.3% for the specified operating range. The total losses, excluding converter contributions, are reported in Figure 23.
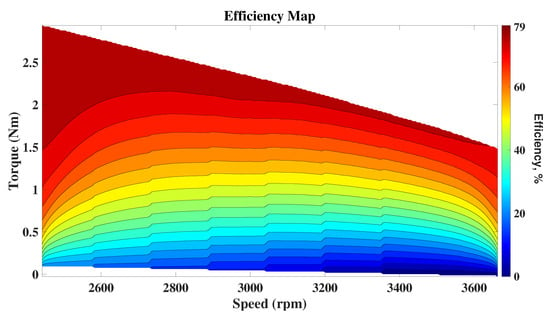
Figure 22.
Reduced motor efficiency map obtained for the expected velocity range.
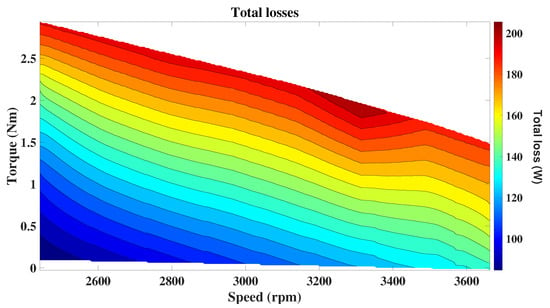
Figure 23.
Total losses for the expected velocity range.
Iron losses are highly dependent on source frequency, flux density, and core characteristics [22]. And they represent the highest loss contribution (Figure 24). On the other hand, copper losses directly relate to winding current, motor torque, and speed, becoming significant in high-torque low-speed applications (Figure 25). Velocity effects dominate in mechanical loss contributions; in assuming a 6 W/k rpm mechanical loss [23], the low-speed characteristics of UAV agriculture applications account for up to 10.69% of the total losses (Figure 26).
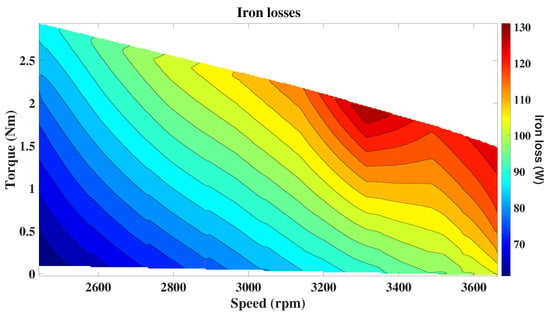
Figure 24.
Iron losses for the expected velocity range.
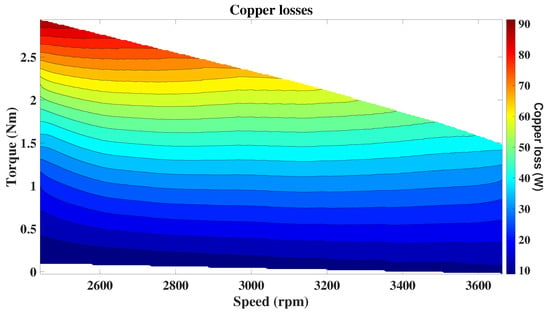
Figure 25.
Copper losses for the expected velocity range.
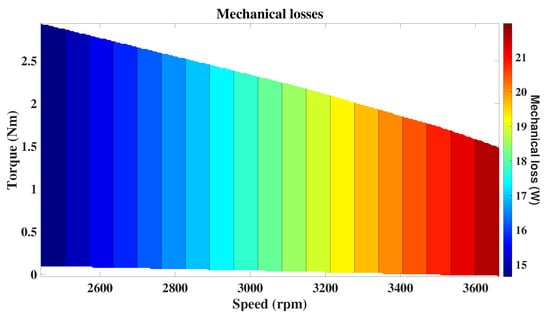
Figure 26.
Mechanical losses for the expected velocity range.
For a battery with a 40 percent minimum reserve capacity, assuming a linear consumption behavior and hover conditions, Equation (10) from [24] can be used to obtain the battery capacity and minimum C-rate.
and
where is the battery capacity in Ah; , the flight time in minutes; , the hover current; and , the minimum C-rate. Through the use of the design requirements and values obtained in the electromagnetic analysis, the battery chosen was the Tattu 28 Ah 14SP1, with a continuous C-rate of 6.07 and burst C-rate of 7.85.
For the chosen battery, the overall propeller–motor efficiency can be related with autonomy as
where , , and are the power of the battery, the total mass of the UAV in grams, and the motor efficiency, respectively.
With the data obtained from Figure 7, to have a 12-min flight time, the motor efficiency should be above 75%. From Figure 22, it is clear that for a vehicle mostly in hover mode, the U12II KV120 motor will suffice. Agriculture UAV applications set the starting torque in a medium-duty range category using large inertia loads [25]. At the same time, the load characteristics of the propeller set a linear relationship between thrust and torque, evolving with the square of the speed, while the power of the motor increases to the third power of the angular velocity. The starting torque can be used to evaluate the capacity of the motor to deliver torque in the required time. The torque needed to drive the load with a specific acceleration is given by the acceleration torque:
where is the acceleration of the load, is the rotor moment of inertia, and is the load moment of inertia. The power ratio related to the motor is given by
The maximum acceleration of the motor is then expressed as
With [kgm2], [kgm2], and Nm,
The motor can be accelerated from 0 to 1002 rpm in a second.
4.2. Implementation
The implementation of the selected propulsion system is shown in Figure 27 with the conditions imposed in Table 12. The vehicle was flown in autonomous mode after defining a trajectory characteristic of agriculture applications (Figure 28). The peak power consumed corresponds to take-off (Figure 29): demanding up to 22% more power than the rest of the trajectory. From Figure 30, it is in the turning points that the rest of the local maximum power demands occur.

Figure 27.
Propulsion system implementation in a 30 kg large-sized hexarotor.

Table 12.
Flight conditions.
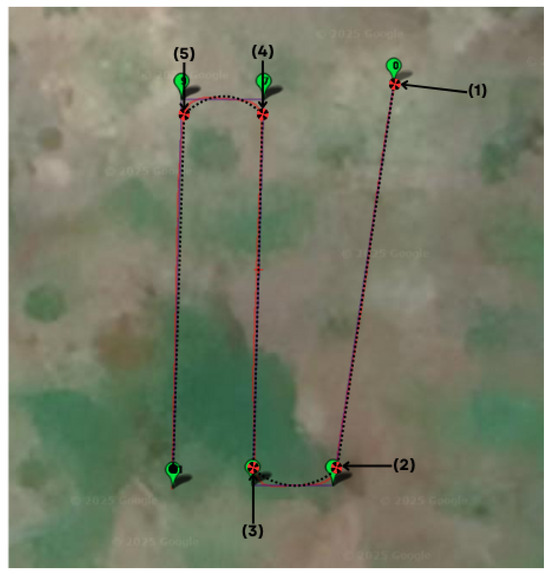
Figure 28.
Trajectory for autonomous flight mode emulating an agriculture application.
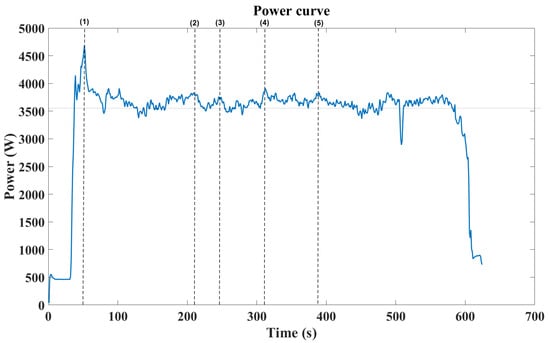
Figure 29.
Power consumption evolution throughout the imposed trajectory.
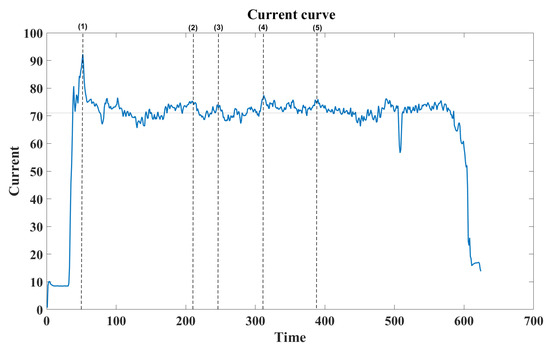
Figure 30.
Evolution of the battery current in the defined trajectory.
In order to examine the agricultural UAV trajectory, points one and four were subjected to analysis, representing take-off and the maximum power consumption state immediately after. Assuming equal conditions for all six motors, Table 13 presents the results and simulation inputs for take-off. A DT6236B digital tachometer was used in the static thrust tests to obtain the required simulation speed for the angular velocity definition on the rotor in JMAG. Additionally, the coupled motor–propeller system via the motor shaft transfers the mechanical power from the motor to the propeller; thus, the torque and mechanical power from the CFD analysis and electromagnetic analysis are compared in Table 13, showing a maximum variation of 3.5% from the manufacturer’s data. The motor torque and phase currents from JMAG are shown in Figure 31 and Figure 32, respectively.

Table 13.
Motor–propeller conditions and results for take-off in the specified trajectory.
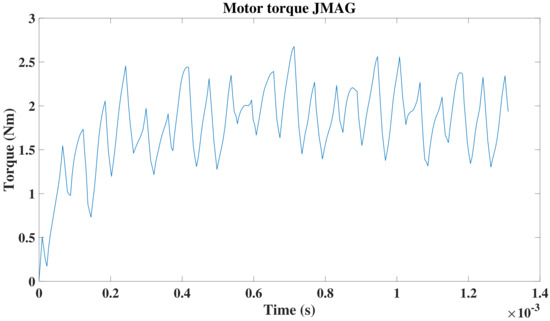
Figure 31.
Motor torque from JMAG corresponding to take-off.

Figure 32.
Three-phase currents from JMAG corresponding to take-off state.
The simulation inputs, experimental electrical measurements, and numerical results corresponding to point four are presented in Table 14. The overall efficiency of the motor–propeller combination goes down to 7.075 g/W, while the mechanical power between the manufacturer’s data, the propeller simulation, and electromagnetic analysis of the BLDC motor results in a maximum variation of 5.4%. In the context of multi-rotor UAVs for agriculture applications, these deviations represent a subtle contribution to the overall performance of the vehicle. From Figure 29 and Figure 30, it is clear that the larger effective propeller area and high inertia of the drone reduce the need for high dynamics and pronounced accelerations even in complex scenarios such as agriculture application trajectories, whereas in small multi-rotors, the reduced propeller area and high thrust-to-weight ratios entail a higher dependency on motor and propeller dynamics.

Table 14.
Motor–propeller conditions and results for point four in the specified trajectory.
The torque ripple amplitude result of the magnetic configuration is observed in Figure 33.
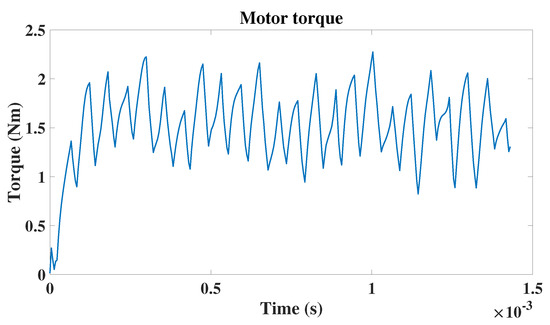
Figure 33.
Motor torque from JMAG corresponding to point four conditions.
The qualitative comparison between numerical and experimental currents and voltages is introduced in Figure 34 and Figure 35. The amplitude of the square waveform shows good agreement.
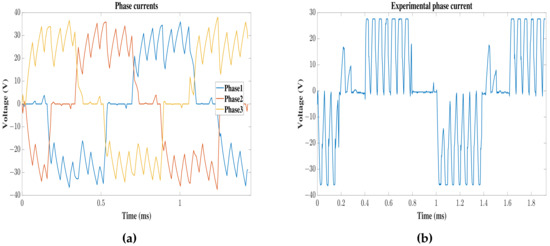
Figure 34.
Motor phase currents for point four in the defined trajectory. (a) Three-phase currents obtained from JMAG. (b) Phase current measured in the static thrust test.
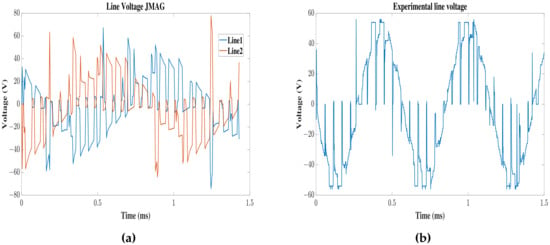
Figure 35.
Motor line voltages for point four in the defined trajectory. (a) Two voltage lines from JMAG. (b) Experimental line voltage measured.
Figure 36 shows the current evolution for a hover autonomy test with the parameters defined in Table 15. The current draw between translational flight and hover presents a maximum variation of 5.2 A at any time instant after take-off, reaching 11.6 min of flight time.
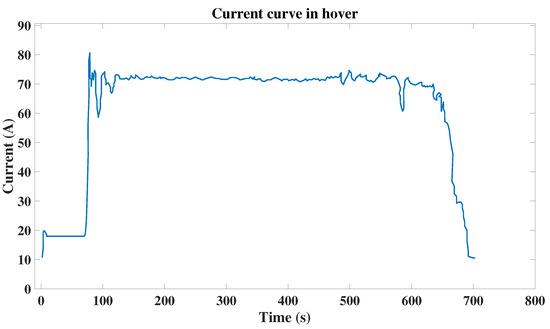
Figure 36.
Current curve for hover test.

Table 15.
Comparative analysis of large-sized multi-rotors.
A comparative analysis between the proposed drone, commercial drones, and a coaxial multi-rotor designed from a market trend evaluation [26] is presented in Table 15. The proposed drone outperforms the Agras T10 and the coaxial drone in flight time; however, the Agras T20 presents the highest autonomy in the list by maintaining a low motor KV and an optimized structure. For the proposed drone to be more competitive, structural analysis can be implemented to optimize mass and increase flight time.
5. Conclusions
This paper proposed a propulsion system design methodology for UAV agriculture applications focused on BLCD motor analysis. A numerical approach was used to evaluate a commercial propeller and motor under the specified range. Once the design requirements of this application were explored, the assessment strategy began with the propeller sizing and aerodynamic analysis using the finite volume method, where thrust–speed, torque–speed, and efficiency–speed curves were obtained with 6.32% thrust and 10.1% torque maximum deviation from experimental results. Additionally, an electromagnetic study using JMAG was used to evaluate the fit of a BLDC motor with the design requirements. Appropriate driving signal generation permits accurate motor performance evaluation; for this, a trapezoidal commutation circuit was implemented. Together with the right energy source, the selection of an efficient motor–propeller combination that complies with the desired flying time was obtained. The findings demonstrate that numerical methods provide valuable insights in large-sized UAV design, decreasing the experimental tests conducted and accelerating implementation time. Further research should focus on the thermal effects of the power electronics and electric motors in drone performance, allowing for more accurate electric machine evaluation. Similarly, turbulence models with a higher number of transport equations can be implemented with transient simulations to improve numerical results in the aerodynamic analysis of drone propellers. Regarding the drone structure, structural analysis will provide valuable insights in material assessment and optimization.
Author Contributions
Conceptualization, J.d.l.C.S., J.J.G.-A. and J.Y.R.-M.; data curation, G.O.-T., S.E.G.-C., H.M.B.-A., M.R.-M. and M.A.L.-O.; formal analysis, J.J.G.-A., J.Y.R.-M., J.P.-R. and O.A.V.-L.; investigation, M.A.Z.-G., F.D.J.S.-V., H.M.B.-A. and M.A.L.-O.; methodology, J.d.l.C.S., J.J.G.-A., M.A.Z.-G., J.P.-R. and O.A.V.-L.; software, S.E.G.-C. and M.R.-M.; validation, G.O.-T.; writing—original draft, J.J.G.-A.; writing—review and editing, J.Y.R.-M., G.O.-T., F.D.J.S.-V., S.E.G.-C., H.M.B.-A. and M.A.L.-O. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would also like to express their gratitude to the Jalisco State Council of Science and Technology (COECyTJAL) for the Call for Proposals of the Jalisco Scientific Development Fund to Address Social Challenges 2022 (FODECIJAL 2022), with grant number 10105-2022, for their financial support, which made this work possible.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the Motion Capture Laboratory at the University of Guadalajara, Los Valles University Center, for granting access to their equipment and facilities. Additionally, the authors would also like to thank the Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCYT) for the scholarship awarded to carry out my master studies in physics, mathematics, and sciences with mathematics orientation.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Ortiz-Torres, G.; Zurita-Gil, M.A.; Rumbo-Morales, J.Y.; Sorcia-Vázquez, F.D.J.; Avalos, J.J.G.; Pérez-Vidal, A.F.; Ramos-Martinez, M.B.; Pascual, E.M.; Juárez, M.A. Integrating Actuator Fault-Tolerant Control and Deep-Learning-Based NDVI Estimation for Precision Agriculture with a Hexacopter UAV. AgriEngineering 2024, 6, 2768–2794. [Google Scholar] [CrossRef]
- Dai, X.; Quan, Q.; Ren, J.; Cai, K.Y. An analytical design-optimization method for electric propulsion systems of multicopter UAVs with desired hovering endurance. IEEE/ASME Trans. Mechatron. 2019, 24, 228–239. [Google Scholar] [CrossRef]
- Mohanraj, D.; Aruldavid, R.; Verma, R.; Sathiyasekar, K.; Barnawi, A.B.; Chokkalingam, B.; Mihet-Popa, L. A Review of BLDC Motor: State of Art, Advanced Control Techniques, and Applications. IEEE Access 2022, 10, 54833–54869. [Google Scholar] [CrossRef]
- Gecer, B.; Tosun, O.; Apaydin, H.; Serteller, N.F.O. Comparative analysis of SRM, BLDC and induction motor using ANSYS/Maxwell. In Proceedings of the International Conference on Electrical, Computer, Communications and Mechatronics Engineering, ICECCME 2021, Mauritius, 7–8 October 2021. [Google Scholar] [CrossRef]
- BBVL, D.; Singh, D.P.; Kuppa, S.K.; Rao, M.J. Design optimization of drone BLDC motor for delivery service applications. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, X.; Zhao, W.; Ji, J.; Hu, J. Influence of magnet shape on the cogging torque of a surface-mounted permanent magnet motor. Chin. J. Electr. Eng. 2019, 5, 40–50. [Google Scholar] [CrossRef]
- Shao, J.; Nolan, D.; Hopkins, T. A novel direct back EMF detection for sensorless brushless DC (BLDC) motor drives. In Proceedings of the Applied Power Electronics Conference and Exposition (APEC 2002), Dallas, TX, USA, 10–14 March 2002; Volume 1, pp. 33–37. [Google Scholar] [CrossRef]
- Bosso, A.; Conficoni, C.; Raggini, D.; Tilli, A. A Computational-Effective Field-Oriented Control Strategy for Accurate and Efficient Electric Propulsion of Unmanned Aerial Vehicles. IEEE/ASME Trans. Mechatron. 2021, 26, 1501–1511. [Google Scholar] [CrossRef]
- Ozer, K.; Yilmaz, M. Design and Analysis of a High Power Density Brushless DC Motor for a Multi-Rotor Unmanned Aircraft. In Proceedings of the 2021 13th International Conference on Electrical and Electronics Engineering, ELECO 2021, Bursa, Turkey, 25–27 November 2021; pp. 378–382. [Google Scholar] [CrossRef]
- Gutierrez-Rivera, M.E.; Rumbo-Morales, J.Y.; Ortiz-Torres, G.; Gascon-Avalos, J.J.; Sorcia-Vázquez, F.D.; Torres-Cantero, C.A.; Buenabad-Arias, H.M.; Guillen-Escamilla, I.; López-Osorio, M.A.; Zurita-Gil, M.A.; et al. Design, Construction and Finite Element Analysis of a Hexacopter for Precision Agriculture Applications. Modelling 2024, 5, 1239–1267. [Google Scholar] [CrossRef]
- Zhu, H.; Nie, H.; Zhang, L.; Wei, X.; Zhang, M. Design and assessment of octocopter drones with improved aerodynamic efficiency and performance. Aerosp. Sci. Technol. 2020, 106, 106206. [Google Scholar] [CrossRef]
- Christodoulou, K.; Vozinidis, M.; Karanatsios, A.; Karipidis, E.; Katsanevakis, F.; Vlahostergios, Z. Aerodynamic analysis of a quadcopter drone propeller with the use of computational fluid dynamics. Chem. Eng. Trans. 2019, 76, 181–186. [Google Scholar] [CrossRef]
- Winslow, J.; Otsuka, H.; Govindarajan, B.; Chopra, I. Basic understanding of airfoil characteristics at low Reynolds numbers (104–105). Aerosp. Res. Cent. 2017, 55, 1050–1061. [Google Scholar] [CrossRef]
- Yousefi, K.; Razeghi, A. Determination of the critical reynolds number for flow over symmetric NACA airfoils. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Loureiro, E.V.; Oliveira, N.L.; Hallak, P.H.; de Souza Bastos, F.; Rocha, L.M.; Delmonte, R.G.P.; de Castro Lemonge, A.C. Evaluation of low fidelity and CFD methods for the aerodynamic performance of a small propeller. Aerosp. Sci. Technol. 2021, 108, 106402. [Google Scholar] [CrossRef]
- Hendershot, J.; Miller, T. Design of Brushless Permanent-Magnet Machines, 2nd ed.; Motor Design Books: Venice, FL, USA, 2022. [Google Scholar]
- Arnold Magnetic Technologies. N42UH: Sintered Neodymium Iron Boron Magnets; Technical Report; Arnold Magnetic Technologies: Rochester, NY, USA, 2017. [Google Scholar]
- Duane, H. Brushless Permanent Magnet Motor Design, 2nd ed.; Magna Physics Publishing: Madison, WI, USA, 2006. [Google Scholar]
- Carev, V.; Roháč, J.; Šipoš, M.; Schmirler, M. A Multilayer Brushless DC Motor for Heavy Lift Drones. Energies 2021, 14, 2504. [Google Scholar] [CrossRef]
- Lee, T.Y.; Seo, M.K.; Kim, Y.J.; Jung, S.Y. Design and Torque Ripple Analysis of Brush-less DC Motor According to Delta Winding Connection. J. Magn. 2015, 20, 166–175. [Google Scholar] [CrossRef]
- Shao, J. An improved microcontroller-based sensorless brushless DC (BLDC) motor drive for automotive applications. IEEE Trans. Ind. Appl. 2006, 42, 1216–1221. [Google Scholar] [CrossRef]
- Roshandel, E.; Mahmoudi, A.; Kahourzade, S.; Yazdani, A.; Shafiullah, G.M. Losses in Efficiency Maps of Electric Vehicles: An Overview. Energies 2021, 14, 7805. [Google Scholar] [CrossRef]
- Nayak, D.S.; Shivarudraswamy, R. Loss and Efficiency Analysis of BLDC Motor and Universal Motor by Mathematical Modelling in the Mixer Grinder. J. Inst. Eng. (India) Ser. B 2022, 103, 517–523. [Google Scholar] [CrossRef]
- Shi, D.; Dai, X.; Zhang, X.; Quan, Q. A practical performance evaluation method for electric multicopters. IEEE/ASME Trans. Mechatron. 2017, 22, 1337–1348. [Google Scholar] [CrossRef]
- Agrawal, K.C. Electrical Power Engineering: Reference & Applications Handbook, 1st ed.; Suryodaya Books: New Delhi, India, 2017; p. 1129. [Google Scholar]
- Ong, W.; Srigrarom, S.; Hesse, H. Design methodology for heavy-lift unmanned aerial vehicles with coaxial rotors. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).