A Markov Chain-Based Stochastic Queuing Model for Evaluating the Impact of Shared Bus Lane on Intersection

Abstract

The introduction of Bus Rapid Transit (BRT) systems has the potential to alleviate urban traffic congestion. However, in certain cities in China, the increasing prevalence of privately owned vehicles, combined with the underutilization of bus lanes due to infrequent bus departures, has contributed to heightened congestion in general lanes. The advent of Internet of Things (IoT) technology offers a promising opportunity to develop intelligent public transportation systems, facilitating efficient management through seamless information transmission to end devices. This paper presents an IoT-based shared bus lane (IoT-SBL) that integrates intersection information, real-time traffic queuing conditions, and bus location data to encourage passenger vehicles to utilize the bus lane. This encouragement can be communicated through traditional signaling methods or future Infrastructure-to-Vehicle (I2V) and Vehicle-to-Vehicle (V2V) communication technologies. To evaluate the effectiveness of the IoT-SBL strategy, we proposed a stochastic model that incorporates queuing effects and derived a series of performance metrics through model analysis. The experimental findings indicated that the IoT-SBL strategy significantly reduces vehicle queuing, decreases vehicle delays, enhances intersection throughput efficiency, and lowers fuel consumption compared to the traditional bus lane strategy.

1. Introduction

Bus Rapid Transit (BRT) systems have emerged as an effective solution for urban transportation challenges, especially in cities facing traffic congestion, pollution, and inefficiencies in traditional public transit [1]. BRT is widely recognized for offering high-quality, cost-effective services with modern, high-capacity vehicles and dedicated bus lanes. These lanes are designed to prioritize buses over general traffic, ensuring faster and more reliable service by avoiding delays caused by congestion. In densely populated urban environments with limited road space, the implementation of BRT systems can substantially alleviate transit challenges and contribute to more sustainable urban mobility [2]. However, BRT implementation is not without its complexities, especially regarding its impact on the overall road network and the potential exacerbation of congestion for private vehicles [3,4].

A key challenge with dedicated bus lanes is their potential to reduce road capacity for general traffic [5]. While bus lanes increase the efficiency and speed of bus services, they may also limit the capacity for private vehicles, which can contribute to higher congestion elsewhere in the urban road network [6]. This situation is particularly problematic in cities with already constrained infrastructure. Balancing the priority given to buses with the flow of general traffic is a persistent challenge that requires innovative solutions to ensure BRT systems effectively serve all road users [7,8].

One promising approach to mitigate the negative effects of dedicated bus lanes on general traffic is the concept of the Intermittent Bus Lane (IBL). The foundational principles of IBL systems were first introduced by Viegas and Lu, who analyzed the viability of such systems [9,10,11]. Unlike traditional bus lanes, IBLs are designed to allow general traffic to use the bus lane when no buses are present, thus optimizing road use and reducing congestion. Initially proposed to enhance flexibility, IBL systems allow private vehicles to utilize the bus lane during off-peak periods, which helps reduce congestion without compromising bus service efficiency [12]. This concept has gained traction as a potential solution to balance bus priority and general traffic flow when the bus lane is underutilized [13].

In practice, the operation of an IBL involves dynamic control systems, such as Variable Message Signs (VMS) and embedded longitudinal “spiral” lights, which inform drivers of approaching buses and indicate when it is prohibited to enter the bus lane. These systems aim to minimize disruptions to bus operations while allowing general vehicles to use the lane when no buses are present. Thus, the lane functions as a bus-only lane when buses are approaching but is open to general traffic at other times. The intermittent bus lane concept provides a potential means to reduce congestion while preserving the efficiency benefits of BRT systems [14].

Despite the initial promise of IBLs, a significant design flaw was revealed in earlier studies [14,15]. Specifically, the framework allowed general vehicles to enter the bus lane ahead of an approaching bus, without requiring those already in the lane to exit. This led to the formation of queues, causing delays for buses and reducing the overall efficiency of the system. This raised concerns about the effectiveness of IBL systems in maintaining bus priority [16,17].

To address this issue, several studies proposed modifications to the IBL system to ensure buses retain priority [12,18,19]. These modifications focused on requiring vehicles in the bus lane to exit when a bus is approaching, thus preventing the formation of queues and maintaining bus operations. This led to the development of the Bus Lane with Intermittent Priority (BLIP) concept, a refined version of the IBL system. The BLIP concept integrates strategies to clear the lane of general vehicles ahead of an approaching bus, minimizing delays and preserving bus priority.

Ongoing research into BLIP systems has emphasized their importance in urban transport and traffic management. Advanced simulation models and empirical data have been used to explore optimal designs and implementations for these systems [20]. The success of BLIP systems depends not only on the technical design of the lane but also on the broader traffic management strategies employed in conjunction, including real-time traffic monitoring, dynamic control systems, and coordinated traffic signal management to prioritize buses effectively without disrupting general traffic flow [21].

In recent years, a growing body of literature has explored the application of intermittent bus lane systems in cities worldwide [22,23]. Research has focused on the potential for these systems to enhance both public transportation efficiency and overall traffic flow. The design and operation of IBL and BLIP systems vary significantly based on local factors, including traffic patterns, road infrastructure, and public transport ridership. As such, the successful implementation of these systems requires a careful consideration of contextual factors and the use of advanced modeling techniques to optimize system performance.

The evolution of BRT and intermittent priority bus lane systems underscores the need for continued innovation in urban transport. As cities grow and face increasing congestion, the development of systems like IBL and BLIP will play a crucial role in creating more sustainable and efficient transportation networks. Through thoughtful design, effective management, and the integration of advanced technologies, cities can enhance the performance of their public transportation systems while simultaneously addressing the challenges of urban congestion.

This paper addressed these challenges by proposing an IoT-SBL strategy, which integrates real-time traffic data, intersection conditions, and bus location information to optimize bus lane usage. Through the analysis of this approach, we aimed to evaluate the potential for IoT-SBL to reduce congestion, enhance bus priority, and improve the overall efficiency of urban transportation systems.

2. IoT-Based Shared Bus Lane System (IoT-SBL)

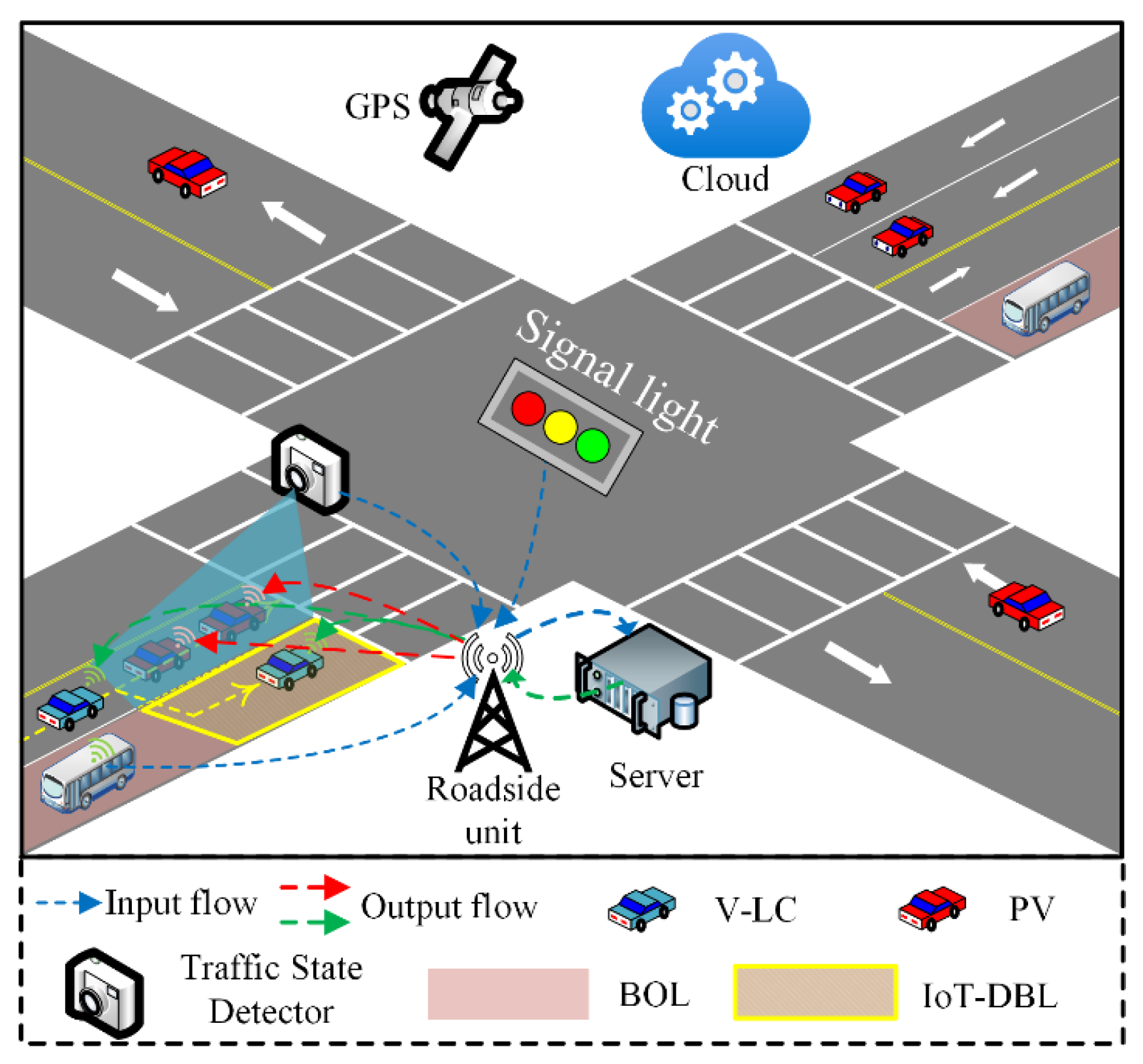
The IoT-SBL system proposed in this paper, as illustrated in Figure 1, aims to enhance the throughput efficiency of signal intersections, reduce vehicle queues and delays, and minimize fuel consumption. This system is designed to operate on both bus lanes and general-purpose lanes, utilizing loop detectors or cameras positioned near or above the lanes to monitor real-time traffic conditions.

Buses are equipped with GPS and wireless communication technologies to obtain real-time spatial-temporal data. This information is collected by roadside units and transmitted to a central server for analysis and processing, enabling informed planning and decision-making. The decision-making process is activated under two specific conditions: (1) when the queue length of private vehicles exceeds a predetermined threshold, indicating congestion; and (2) when all private vehicles within the IoT-SBL area must be cleared prior to the arrival of a bus.

Once these conditions are met, a command is issued to private vehicles, instructing them to yield access to the bus lane. The expectation is that drivers may utilize the bus lane when no bus is present; however, as a bus approaches, private vehicles will be cleared from the lane and prohibited from entering to ensure smooth transit for public transport.

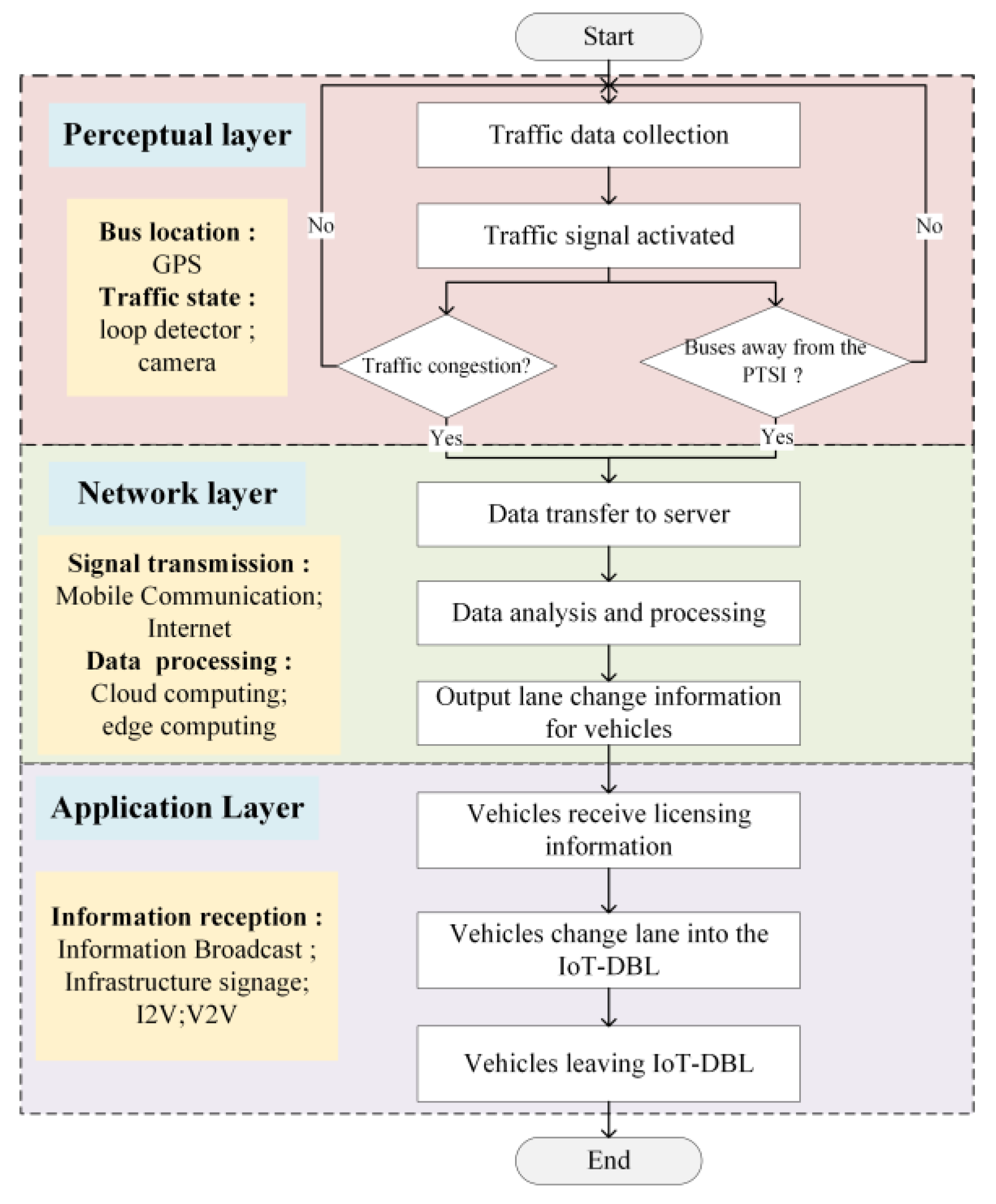
The comprehensive architecture of the IoT-based intelligent bus lane, illustrated in Figure 2, consists of three distinct layers: the perception layer, the network transmission layer, and the application layer.

In the perception layer, real-time traffic conditions are monitored through intersection cameras or pre-installed loop detectors. The current position of buses is transmitted in real time via GPS or the bus’s integrated Wi-Fi module, while the intersection’s signal status is communicated to the edge processing unit through IoT protocols. The network transmission layer serves as a conduit for relaying the collected traffic signal statuses, bus position data, and intersection signal light statuses to the roadside unit for processing. At the application layer, the roadside unit makes decisions based on the processed information, allocating signals to vehicles equipped with Vehicle-to-Everything (V2X) capabilities. This effectively guides connected vehicles into the bus lane. For the specific case of isolated intersections considered in this study, it is advisable to avoid uploading data to a centralized server for processing. Instead, edge processing significantly reduces the volume of data that requires analysis and facilitates rapid real-time decision-making.

The core of the entire system architecture consists of three modules:

(1)

Traffic Data Collection Module: Responsible for receiving real-time traffic queuing information detected by loop detectors or cameras, as well as spatial and temporal information of buses, and transmitting it to the server via roadside units.

(2)

Lane Change Information Decision-Making Strategy: By integrating the collected traffic information, the server makes lane change decisions for private vehicles, ensuring compliance with traffic rules and constraints.

(3)

Private Vehicles Driver Lane Change Information Acceptance Module: Processed information from the server can be transmitted through the roadside unit to relevant signs, including vertical signal indicators, or displayed in real time on the onboard monitor using more intelligent I2V and V2V communication.

3. Methods

The proposed IoT-SBL strategy may result in significant variations in vehicle queuing at signalized intersections, contingent upon the type of traffic present (e.g., buses versus private vehicles). Given the unpredictable nature of traffic demand, it is essential to conduct a thorough evaluation of how the implementation of the IoT-SBL strategy impacts the queuing behavior of vehicles at these intersections. To this end, this section introduces a stochastic queuing model designed to analyze and assess the performance of the IoT-SBL strategy. By integrating stochastic elements, this model aims to provide a comprehensive examination of the dynamic and probabilistic characteristics of queuing at traffic signals influenced by the proposed IoT-SBL strategy.

3.1. Model Description

To develop an accurate probabilistic model of the queuing process at a prioritized signal intersection utilizing the IoT-SBL strategy, this study is based on two key assumptions: (1) The time axis is divided into equal intervals, with $T$ representing the average minimum time between two consecutive vehicles entering the intersection during the green phase. Each vehicle’s service begins or ends strictly at the boundary of these time intervals; (2) Vehicle arrivals at the intersection occur randomly and independently across different intervals. By adopting a discrete-time approach and assuming independent and identically distributed arrivals, we can characterize the queue lengths at intersection boundaries as discrete-time Markov chains.

The signal intersection functions as a queuing system with fixed cycles of green and red lights, where vehicles face delays if another vehicle is present during the green phase or if they arrive during the red phase. We denote the duration of red and green lights as $M$ and $N,$ respectively, with the interval between successive vehicles passing the stop line represented as $T$. This interval can be subdivided into shorter segments, $M=mT$ and $N=nT$. The model makes two primary assumptions: (1) Arrivals of private cars at the intersection follow a Poisson process, and (2) A maximum of two private vehicles may pass through the intersection in each time interval.

3.2. Stochastic Queuing Model Based on Markov Chain

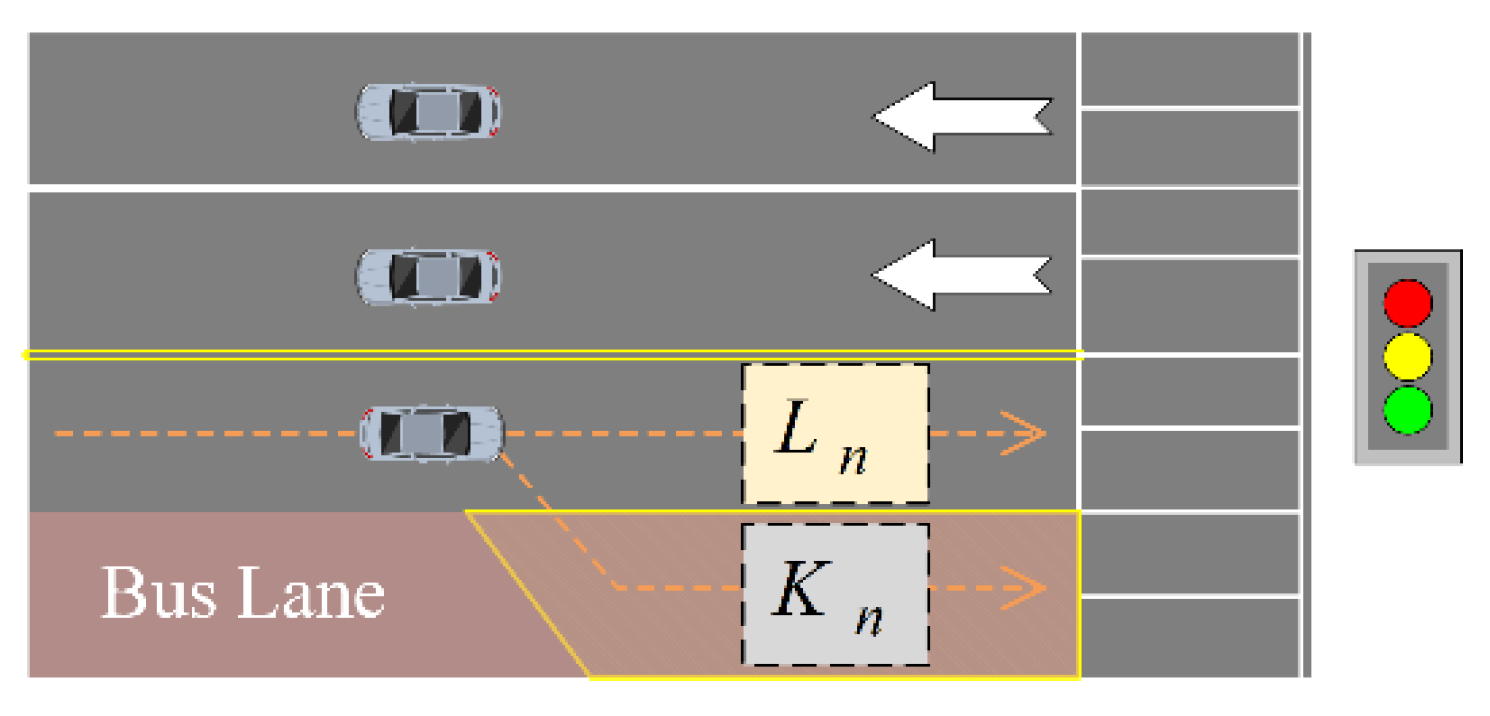
In Figure 3, within the context of the IoT-SBL strategy, the vehicle queue in front of the signalized intersection stop line is segmented into two categories: private vehicles in the regular lane and private vehicles in the dynamic bus lane. We denote $L_t$ and $K_t$ as the numbers of queued private vehicles in the regular lane and the dynamic bus lane at time $t$, respectively. Additionally, $S_t$ represents the number of time intervals that have elapsed since the last green light phase at the intersection. This framework characterizes the traffic queuing system at that moment under the IoT-SBL strategy as $\{L_t,K_t,S_t,t>0\}$, where $L_t\ge 0,0\le K_t\le V,{1\le S}_t\le G+R$. In the proposed model, $\mathrm{V}$ denotes the maximum capacity of the dynamic bus lane (i.e., the maximum number of private vehicles permitted in the IoT-SBL). For numerical experiments, $V$ is set to 15 vehicles, based on typical urban road configurations (e.g., a 200 m lane length with an average vehicle spacing of 13 m). Consequently, $K_t$ operates within $0\le K_t\le 15$. While ${ L}_t$ (regular lane queue) has no theoretical upper limit, its practical range is constrained by traffic demand, signal cycle duration, and intersection discharge capacity.

The signaling system, denoted as ${\{S}_t,t>0\}$, is governed by the signal intersection and is characterized as a deterministic process within a state space defined by $\{\mathrm{1,2}\dots m,m+1\dots m+n\}$. In this state space, each signal state corresponds to consecutive time intervals $T$ during the signaling cycle of the intersection. Private vehicles arrive randomly and independently, with access to the IoT-SBL or the ability to depart from the PTSI stop line only at the boundaries of these time intervals. Consequently, the established traffic queuing mechanism can be effectively represented as a semi-regenerative process $\{L_t,K_t,S_t,t>0\}$, which can be analyzed through traditional methods of traffic queuing dynamics.

We define $(t_n=nT,n\ge 0)$ as the termination time of the nth time slot. Here, $L_n=L\left(t_n\right)$ denotes the number of private vehicles in the regular lane, while $K_n=K\left(t_n\right)$ represents the count of private vehicles in the IoT-SBL. Additionally, $S_n=S\left(t_n\right)$ indicates the number of time intervals that have elapsed since the start of the most recent green light phase at the signal intersection, beginning from time n. The overall signaling state throughout the complete cycle can be represented as $S_n$. Given that private vehicles can only enter the IoT-SBL or exit the signal intersection stop line at the boundaries of the time intervals, the system state can be characterized by $\{L_n,K_n,S_n,n>0\}$.

In the semi-regenerative process $\{L_{t_n},K_{t_n},S_{t_n},t_n>0\}$, the associated Markovian update process can be illustrated by $\{L_t,K_t,S_t,t>0\}$ Consequently, the embedded Markov chain is further defined as $\{L_n,K_n,S_n,n>0\}$.

Let l and k represent the counts of private vehicles in the social lane and the IoT-SBL, respectively, while s indicates the signal state at time t. The state space $\varnothing$ of the process $\{L_n,K_n,S_n,n>0\}$ is defined as follows:

$$\begin{gathered} \varnothing =\left\{\left(l,0,s\right),l\ge \mathrm{0,1}\le s\le g+r\right\} \\ \cup \left\{\left(l,k,s\right),0\le l\le V,1\le k\le \min \left(k,V\right),V-l\le s\le V-k\right\} \\ \cup \left\{\left(l,k,s\right),l\ge V,1\le k\le \min \left(k,V\right),1\le s\le V-k\right\} \\ \cup \left\{\left(l,k,s\right),l\ge V,1\le k\le \min \left(k,V\right),g+l\le s\le c\right\} \end{gathered}$$

(1)

Queuing the state space in lexicographic order, the one-step probability transition matrix of an embedded Markov chain $\{L_n,K_n,S_n,n>0\}$ can be derived as follows:

$$\mathbb{Q}=\left[\begin{array}{ccccccc}{\mathcal{F}}_{\mathrm{0,0}}& {\mathcal{F}}_{\mathrm{0,1}}& \dots & {\mathcal{F}}_{0,V}& {\mathcal{F}}_{0,V+1}& {\mathcal{F}}_{0,V+2}& \dots \\ {\mathcal{F}}_{\mathrm{1,0}}& {\mathcal{F}}_{\mathrm{1,1}}& \dots & {\mathcal{F}}_{1,V}& {\mathcal{F}}_{1,V+1}& {\mathcal{F}}_{1,V+2}& \dots \\ & \ddots & ⋮& ⋮& ⋮& ⋮& ⋮\\ & & \ddots & {\mathcal{F}}_{V,V}& {\mathcal{F}}_{V,V+1}& {\mathcal{F}}_{V,V+2}& \dots \\ & & & {\mathcal{F}}_{V+1,V}& {\mathcal{F}}_{V+1,V+1}& {\mathcal{F}}_{V+1,V+2}& \dots \\ & & & & {\mathcal{F}}_{V+2,V+1}& {\mathcal{F}}_{V+2,V+2}& \dots \\ & & & & ⋮& \ddots & \ddots \end{array}\right]$$

(2)

By using the above repartitioning, the transfer matrix $\mathbb{Q}$ can be expressed as:

$$\mathbb{Q}=\left[\begin{array}{ccccc}{\mathcal{B}}_0& {\mathcal{B}}_1& {\mathcal{B}}_2& {\mathcal{B}}_3& \dots \\ C& A_1& A_2& A_3& \dots \\ & A_0& A_1& A_2& ⋮\\ & & \ddots & \ddots & \dots \end{array}\right]$$

(3)

where

$${\mathcal{B}}_0=\left[\begin{array}{cccc}{\mathcal{F}}_{\mathrm{0,0}}& {\mathcal{F}}_{\mathrm{0,1}}& \dots & {\mathcal{F}}_{0,V}\\ {\mathcal{F}}_{\mathrm{1,0}}& {\mathcal{F}}_{\mathrm{1,1}}& \dots & {\mathcal{F}}_{1,V}\\ & \ddots & ⋮& ⋮\\ & & \ddots & {\mathcal{F}}_{V,V}\end{array}\right] {\mathcal{B}}_1=\left[\begin{array}{c}{\mathcal{F}}_{0,V+1}\\ {\mathcal{F}}_{1,V+1}\\ ⋮\\ {\mathcal{F}}_{V,V+1}\end{array}\right]$$

$${\mathcal{B}}_2=\left[\begin{array}{c}{\mathcal{F}}_{0,V+2}\\ {\mathcal{F}}_{1,V+2}\\ ⋮\\ {\mathcal{F}}_{V,V+2}\end{array}\right] {\mathcal{B}}_3=\left[\begin{array}{c}{\mathcal{F}}_{0,V+3}\\ {\mathcal{F}}_{1,V+3}\\ ⋮\\ {\mathcal{F}}_{V,V+3}\end{array}\right]$$

3.3. Model Solving Algorithm

The structure of the transfer matrix $\mathbb{Q}$ indicates that it is of type M/G/1. According to Neuts [24] and matrix analysis methods, the matrix $A={\sum }_{i=0}^{\infty }{A}_i$ has a unique probability vector $\pi$ only when it is ergodic, which gives the matrix $\mathbb{Q}$ a unique probability distribution $x$. The equation for solving $\pi$ is as follows:

$$\pi A=\pi ;\pi e=1$$

(4)

Define $\beta ={\sum }_{i=0}^{\infty }{i\mathcal{B}}_i$. The matrix a is ergodic if and only if

$$\rho =\pi \beta \le 1$$

(5)

Therefore, if condition (3) holds, a steady-state probability vector x exists for matrix $\mathbb{Q}$. To achieve this, as recommended in Ramaswami [25], it is first necessary to compute matrix $G$, which is the smallest nonnegative solution of $G={\sum }_{i=0}^{\infty }{A}_i{G}^i$. The computation of matrix $G$ involves a recursive procedure, which presents an advancement compared to the methods described in Neuts [24] and Hu et al. [26]. A concise overview of this procedure is provided here, with further details available in Latouche [27] regarding the numerical method.

$$\begin{gathered} G=\underset{n\to \infty }{\mathit{lim}}{G}_n \\ {G}_1={(I-A_1)}^{-1}{A}_0 \\ {G}_{n+1}={(I-{\sum }_{i=1}^{\infty }{A}_1{G}_n^{i-1})}^{-1}{A}_0, n>1 \end{gathered}$$

(6)

where $I$ is a unit matrix of the same dimension as matrix $A$, and it is necessary to terminate the calculation at an optimal n to attain the desired numerical precision.

Let ${\hslash }_{l,k,s}, i\ge \mathrm{0,0}\le k\le \mathit{min}\left(i,V\right),1\le s\le g+r$ represent the steady-state probability vector of the queuing system $\mathbb{Q}$. This vector reflects the probability of having $l$ private vehicles in the regular lane and $k$ private vehicles in the IoT-SBL at time $s$ when the signal from the signal intersection is active. We can denote the overall steady-state probability vector as $\hslash ={{[\hslash }_{l,k,s}]}_l$, where $l\ge 0$.

$$\mathrm{\hslash }=({\mathrm{\hslash }}_0,{\mathrm{\hslash }}_1,\dots {,\mathrm{\hslash }}_{\mathrm{V}},{\mathrm{\hslash }}_{\mathrm{V}+1}\dots )$$

(7)

where

$$\begin{gathered} {\hslash }_{i,j}=\left[{(\hslash }_{00}\right),{{(\hslash }_{10},\hslash }_{11}),\dots {,(\hslash }_{V,0},{\hslash }_{V,1},\dots {,\hslash }_{V,V})], 0\le j\le i\le V \\ {\hslash }_i=[{(\hslash }_{V,0}\dots {(\hslash }_{V,V}),{(\hslash }_{V+\mathrm{1,0}}\dots {(\hslash }_{V+1,V}),\dots ], i>V \end{gathered}$$

For the solution of ${\hslash }_{l,k,s}$, a recursive formula that can be computed quickly and efficiently as follows:

$${\hslash }^l=\left[{\hslash }^0{\overline{\mathcal{B}}}_l+{\sum }_{k=1}^{l-1}{\hslash }^k{\overline{A}}_{l-k+1}\right]{\left(I-{\overline{A}}_1\right)}^{-1}, l\ge 1$$

(8)

where

$${\overline{\mathcal{B}}}_n={\mathcal{B}}_n+{\overline{\mathcal{B}}}_{n+1}G, {\overline{ A}}_n=A_n+{\overline{A}}_{n+1}G, n\ge 1$$

In order to compute ${\hslash }^l$ in (8) above, the solution ${\hslash }^0$. Therefore, we introduce the matrix $K$.

$$\mathrm{K}={\mathcal{B}}_0+{\overline{\mathcal{B}}}_1{\left(\mathrm{I}-{\overline{\mathrm{A}}}_1\right)}^{-1}\mathrm{C}$$

(9)

and

$$\mathcal{H}={\overline{\mathcal{B}}}_1\mathrm{G}={\sum }_{\mathrm{n}=1}^{\mathrm{\infty }}{\mathcal{B}}_{\mathrm{n}}{\mathrm{G}}^{\mathrm{n}}$$

(10)

Thus, we can get ${\mathrm{\hslash }}^0$

$${\mathrm{\hslash }}^0=\mathsf{\kappa }/\mathcal{g}$$

(11)

where $\kappa$ is the steady-state distribution vector of $K$, which is obtained by the following equation:

$$\kappa K=\kappa ;\kappa e=1$$

(12)

and

$$\mathcal{g}=1+{\displaystyle \frac{\kappa }{1-\rho }}[\beta +(\mathcal{B}-\mathcal{H}){(I-A+e\pi )}^{-1}\alpha ]$$

(13)

where $\mathcal{B}={\sum }_{n=1}^{\mathrm{\infty }}{\mathcal{B}}_n,\alpha ={\sum }_{n=1}^{\mathrm{\infty }}{nA}_{n}e,$ and $e$ is the same unit column vector.

4. Performance Evaluation Indicators

The implementation of the IoT-SBL strategy introduces variability in traffic demand, making it difficult to evaluate its performance using a single metric. Traditional metrics like average queue length and delay provide static, aggregated insights but fail to capture the transient queuing dynamics inherent to the IoT-SBL strategy. For instance, average delay does not reflect temporal variations in queue formation during signal cycles, such as spikes during red phases or rapid dissipation during green phases. Similarly, average queue length masks critical patterns like maximum queue lengths at cycle endpoints, which are vital for assessing intersection congestion. To address this, our model introduces dynamic metrics (e.g., maximum queue length, intersection efficiency) that account for time-dependent fluctuations and lane-specific queuing behavior.

4.1. Average Queue Length and Delay

Assessing the average queue length and delay is essential for evaluating the effectiveness of IoT-SBL strategies. In this study, we define $E\left(L\right)$ as the average total number of private vehicles positioned in front of the signal intersection stop line, encompassing those in both the social lane and the IoT-SBL. This metric serves as a key indicator of traffic congestion levels.

$$E\left(L\right)={\displaystyle \frac{\lambda T}{2}}+{\sum }_{l+k=0}^{\infty }{\sum }_{s=1}^{g+r}\left(l+k\right){\hslash }_{l,k,s}$$

(14)

By the Little Law, we can obtain the mean delay as follows:

$$E\left(W\right)={\displaystyle \frac{E\left(L\right)}{\lambda }}={\displaystyle \frac{T}{2}}+{\displaystyle \frac{{\sum }_{l+k=0}^{\infty }{\sum }_{s=1}^{g+r}\left(l+k\right){\hslash }_{l,k,s}}{\lambda }}$$

(15)

4.2. Average Queue Length on the Social Lane

The number of vehicles waiting in the social lane serves as a visual representation of the IoT-SBL strategy’s effectiveness when compared to the average total queue size. We denote this count as $E\left(L_{GL}\right)$. This metric offers valuable insights into the operational efficiency of the IoT-SBL strategy and its impact on overall traffic flow and queuing behavior.

$$E\left(L_{GL}\right)={\displaystyle \frac{\lambda T}{2}}+{\sum }_{l=0}^{\infty }{\sum }_{k=0}^V{\sum }_{s=1}^{g+r}k{\hslash }_{l,k,s}$$

(16)

4.3. Average Maximum Queue Length

In practical scenarios, as the signal intersection signaling cycle progresses, vehicles begin to queue during the red phase, lining up behind the stop line, and subsequently moving during the green phase. Consequently, the longest queue length under the IoT-SBL strategy is observed at the end of the red phase. We denote $E\left(L_{max}\right)$ as the maximum total number of private vehicles at the signal intersection and $E\left(L_{GL-max}\right)$ as the maximum number of vehicles in the social lane. This observation enables us to establish the following expressions:

$$E\left(L_{max}\right)={\displaystyle \frac{\lambda T}{2}}+{\sum }_{l=0}^{\infty }{\sum }_{k=0}^V(l+k){\hslash }_{l,k,c}$$

(17)

$$E\left(L_{GL-max}\right)={\displaystyle \frac{\lambda T}{2}}+{\sum }_{l=0}^{\infty }{\sum }_{k=0}^{V}k{\hslash }_{l,k,c}$$

(18)

4.4. Intersection Traffic Efficiency

Traffic efficiency is a critical indicator of the overall performance of signalized intersections. It is defined as the number of vehicles that traverse the intersection during the green phase of the signal cycle. Additionally, we denote the total number of vehicles arriving throughout the entire duration of the green light, which can be quantified accordingly.

$$Te=E\left(L_{max}\right)-E\left(L_{GL-max}\right)+\lambda gT$$

(19)

Beginning with the red-light phase, we define the total number of vehicles in the system as $S$. This total encompasses vehicles that arrive during the current signal cycle and those arriving at the conclusion of the green light phase, expressed as $S=\lambda gT+E\left(L_{max}\right)$. Additionally, $\chi$ denotes the traffic efficiency at the intersection as follows:

$$\chi ={\displaystyle \frac{Te}{S}}\times 100\%=(1-{\displaystyle \frac{E\left(L_{max}\right)}{E\left(L_{GL-max}\right)+\lambda gT}})\times 100\%$$

(20)

5. Numerical Experiments

This section examines the operational performance metrics of the Priority Traffic Signal Intersection under two distinct strategies: the bus-only lane and the IoT-SBL approach. Key metrics analyzed include vehicle queue lengths, delays, and intersection efficiency. The findings underscore the potential of the IoT-SBL strategy to improve traffic performance at the intersection. All queue lengths are measured in passenger car unit (pcus), assuming homogeneous traffic flow. While motorcycles, trucks, and buses may exhibit different occupancy and acceleration behaviors, this study focuses on passenger vehicles to isolate the effects of the IoT-SBL strategy. Future work will incorporate heterogeneous traffic using equivalence coefficients (e.g., 1 pcu for a car, 0.5 pcu for a motorcycle, 2 pcus for a truck or bus) to better reflect real-world conditions.

The numerical experiments evaluated the IoT-SBL strategy across four saturation levels ($V/C=0.1, 0.5, 0.9, 0.97$) to represent low-to-extreme traffic conditions. Key variables include bus departure frequency and IoT-SBL capacity, reflecting typical urban traffic configurations.

The experiments presented in this section are based on simulated traffic scenarios generated using the proposed queuing model. Parameters such as signal cycle duration and saturation levels were selected to represent typical urban intersection conditions.

5.1. Impact of IoT-SBL Strategy on Queue Length

This article investigated the application of IoT-SBL technology, which allows passenger vehicles to access the bus-only lane, thereby increasing traffic capacity for these vehicles and alleviating congestion in general traffic lanes. This section analyzes fluctuations in vehicle queue lengths during a single signal cycle at the Priority Traffic Signal Intersection, offering insights into the effectiveness of the proposed strategy.

The signal cycle comprises a 60 s red phase and a 40 s green phase. Lost time (e.g., startup delays during phase transitions) is accounted for by assuming that vehicles begin moving at the start of the green phase after a brief transition interval, which is embedded within the fixed cycle duration. The all-red phase, typically used for intersection clearance, is not explicitly modeled here, as the analysis focuses on queuing dynamics during the active red and green phases. Figure 4 illustrates the variation in the number of vehicles in regular lanes throughout the entire signal cycle under different traffic control strategies, particularly at various saturation levels. The outer circle represents the signal cycle in seconds, while the inner circle denotes the average queue length in passenger car units (pcus).

In Figure 4a, at a saturation level of 0.1, the queue length observed with the IoT-SBL strategy closely mirrors that of the bus-only lane strategy, showing only minor improvements. However, as the saturation level increases, the differences in vehicle queue lengths between the two strategies become more pronounced. Figure 4b depicts a saturation level of 0.5, while Figure 4c,d illustrate saturation levels of 0.9 and 0.97, respectively.

The outer circles denote the signal cycle duration (seconds) while the inner circles show average queue lengths (pcus). At $V/C=0.97$, ${ L}_t$ peaks at 28 vehicles (traditional lane) vs. 15 vehicles (IoT-SBL), while ${ K}_t$ reaches 12 vehicles. With each increase in saturation, it is evident that the IoT-SBL strategy significantly reduces queue lengths compared to the bus lane strategy. This analysis highlights the potential of IoT-SBL in optimizing traffic flow and enhancing overall intersection performance, particularly in high-saturation scenarios, ultimately contributing to a more efficient transportation system.

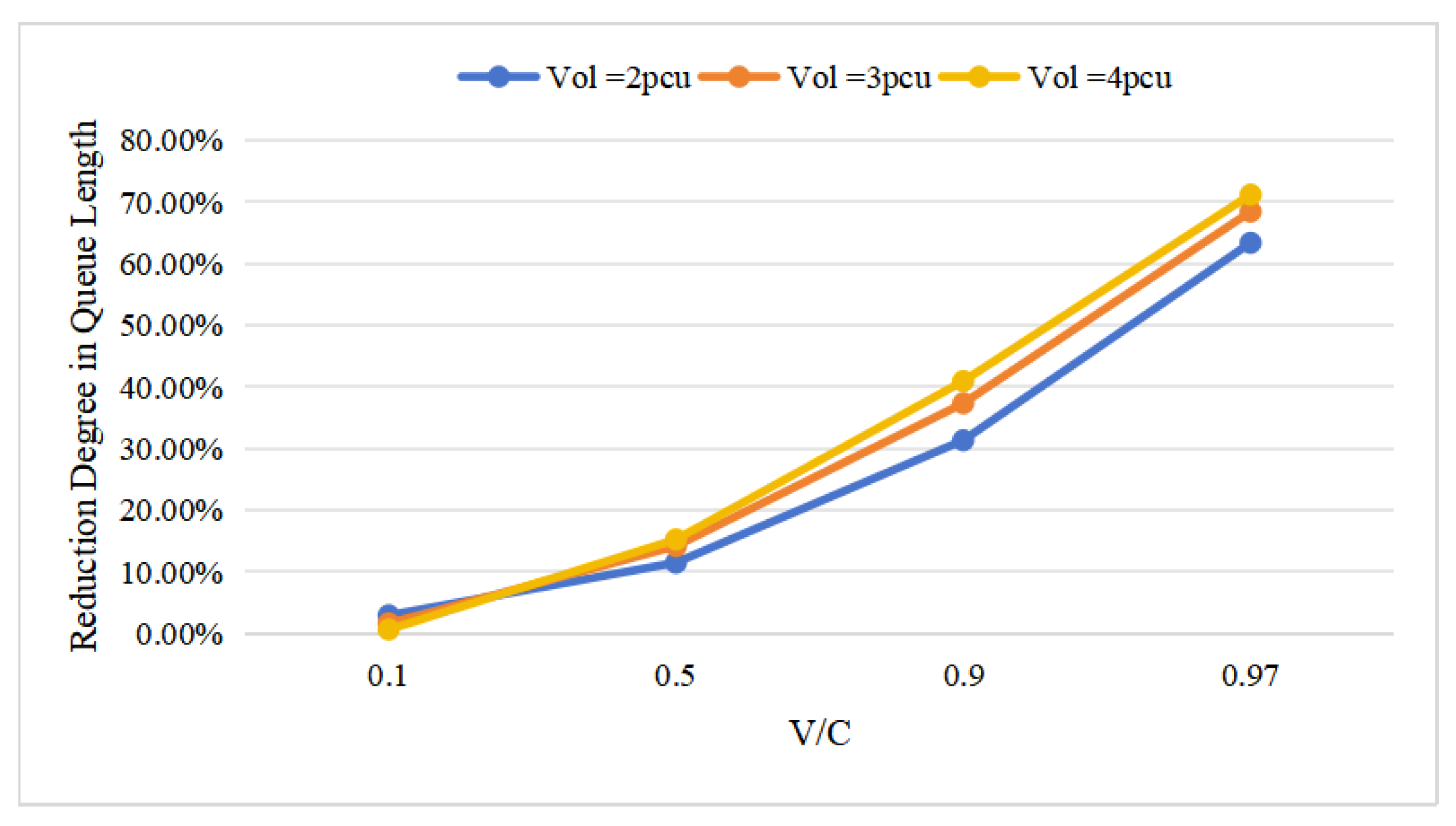
The impact of the IoT-SBL strategy on reducing vehicle queue lengths across various saturation levels is depicted in Figure 5. At a saturation level of 0.1, the IoT-SBL strategy achieves a queue length reduction of up to 2.91%. Conversely, at a saturation level of 0.97, this reduction can reach an impressive 71.15%. The findings presented in Figure 4 and Figure 5 align with expectations, as the traditional bus lane strategy effectively manages traffic under low saturation conditions, rendering the IoT-SBL strategy less critical. However, as saturation levels increase, the traditional bus lane strategy becomes progressively less effective in handling high traffic volumes, underscoring the advantages of the IoT-SBL strategy in these scenarios. Additionally, it is important to note that the performance of the IoT-SBL strategy is contingent upon its capacity, which is primarily influenced by the prevailing traffic volume.

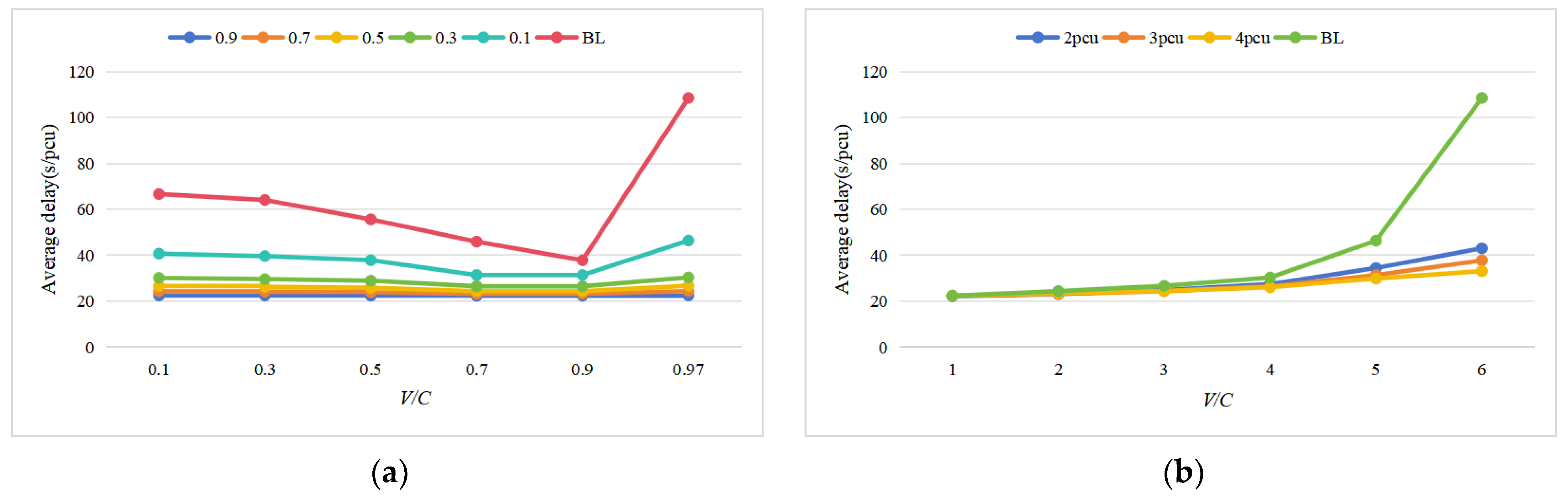
5.2. Impact of IoT-SBL Strategy on Delay

Delay is a critical metric that significantly impacts the overall assessment of the performance of the signal intersection. It provides essential insights into the efficiency and effectiveness of the transportation system, serving as a key indicator of its functionality and operational success. This subsection focuses on a comprehensive analysis of how the IoT-SBL strategy affects vehicle delays. By comparing the performance of two different strategies across various saturation levels, this analysis aims to highlight the effectiveness of the IoT-SBL strategy in mitigating vehicle delays, ultimately contributing to a better understanding of its potential benefits for real-world transportation systems.

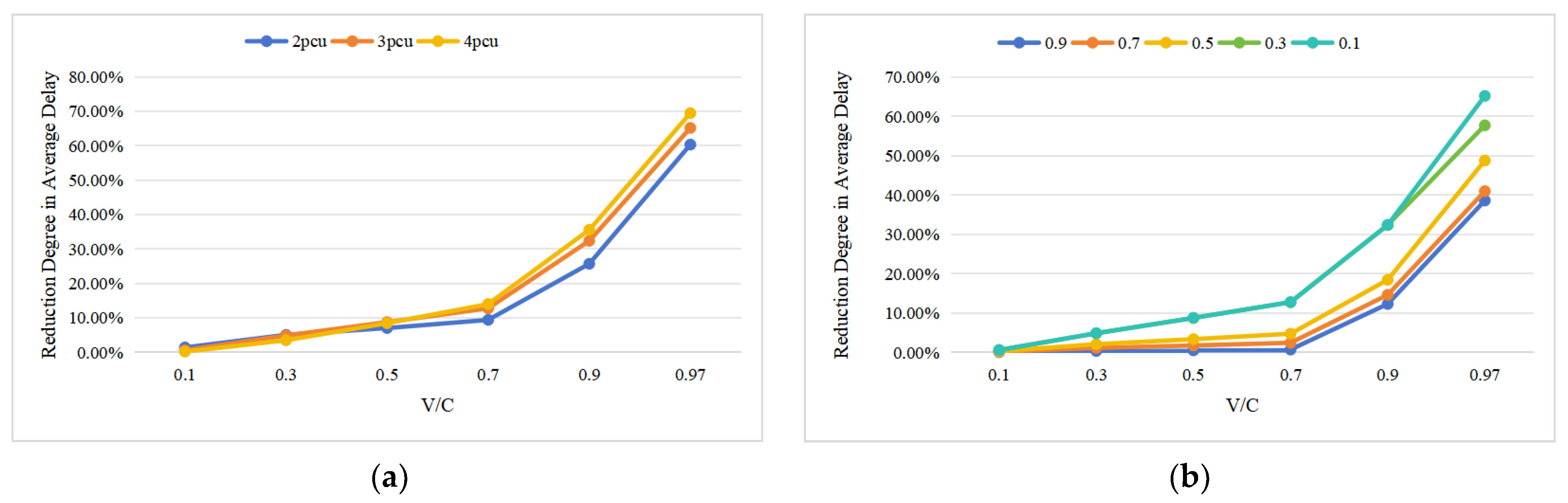
Figure 6a presents a comparison of different IoT-SBL strategies against the bus lane strategy at varying saturation levels and capacities. At saturation levels below 0.5, both strategies demonstrate similar vehicle delays, as the signal intersection operates without congestion due to low saturation. However, as saturation levels exceed 0.5, particularly reaching 0.97, the advantages of the IoT-SBL strategy become increasingly evident. During this higher saturation, the traditional bus lane strategy experiences a significant rise in vehicle delays, while the IoT-SBL strategy manages to maintain delays within an acceptable range.

Furthermore, the IoT-SBL strategy’s capacity to reduce vehicle delays is less than 10% at lower saturation levels but escalates to an impressive 69.48% when saturation reaches 0.97. This underscores that the effectiveness of the IoT-SBL strategy is closely tied to its capacity, emphasizing the importance of establishing optimal capacity to maximize its performance across varying saturation conditions.

Figure 6b examines how varying bus departure frequencies affect the IoT-SBL strategy. Interestingly, the trends in vehicle delays across different saturation levels reflect those observed in Figure 7. It is important to note that bus departure frequency plays a crucial role in influencing vehicle delays, particularly at elevated saturation levels. When departure frequencies are excessively high, they can diminish the effectiveness of the IoT-SBL strategy by interfering with the prioritization of public transportation. As shown in Figure 7, there is a significant variation of 26.59% in vehicle delays caused by different bus departure frequencies at the same saturation level. Despite these fluctuations, the IoT-SBL strategy maintains a consistent level of performance across all scenarios, regardless of the departure frequency employed.

5.3. Impact of IoT-SBL Intersection Efficiency

Intersection efficiency is another key indicator for evaluating the performance of the signal intersection, primarily reflecting the capacity for emitting vehicles during the green light cycle. Like the analysis of delays, it assesses throughput efficiency at various saturation levels under two different strategies

Figure 8a compares the throughput efficiency of various IoT-SBL strategies with different capacities against the bus lane strategy. The blue line indicates the performance of the bus lane strategy, while the other colored lines represent the IoT-SBL strategies with varying capacities. It is clear that when the saturation level of the intersection is below 0.7, both strategies achieve a throughput efficiency of approximately 95%, indicating that the current signal intersection can effectively accommodate the vehicle flow. However, as saturation levels rise, the throughput efficiency of the signal intersection under the bus lane strategy declines linearly. By the time saturation reaches 0.97, the efficiency plummets to below 50%. In contrast, the IoT-SBL strategy manages to sustain the signal intersection’s throughput efficiency at around 90%, even under these high saturation conditions.

Figure 8b further underscores the effectiveness of the IoT-SBL strategy in enhancing the throughput efficiency of the signal intersection. It also reveals that bus departure frequency has a significant impact on the performance of the IoT-SBL strategy. Notably, the effectiveness of the IoT-SBL strategy increases as the frequency of bus departures decreases. First, this emphasizes the importance of IoT-SBL capacity for optimizing signal intersection throughput efficiency. At lower saturation levels, the IoT-SBL strategy is less engaged, so the capacity does not significantly affect throughput efficiency. For instance, at a saturation of 0.1, the improvement in signal intersection throughput efficiency is merely 2.02% across all scenarios. In contrast, at a saturation level of 0.97, the enhancement in throughput efficiency ranges from 86.22% to 100.11%, demonstrating that proper IoT-SBL capacity is crucial for maximizing the improvement in signal intersection throughput efficiency.

Additionally, bus departure frequency also impacts the throughput efficiency of the signal intersection. Like the previous observation, the effect on throughput efficiency enhancement is minimal at low saturation levels. However, at a saturation of 0.97, the degree of enhancement in signal intersection throughput efficiency varies from 41.22% to 93.62%, representing a substantial range of 52.4%. This indicates that bus departure frequency plays a significant role in influencing the improvement of signal intersection throughput efficiency.

6. Conclusions

This study developed a stochastic queuing framework to evaluate the IoT-SBL coordination strategy under time-varying traffic demand. By modeling vehicle arrivals via a Markov Arrival Process and incorporating real-time bus priority and lane-switching logic, the proposed method demonstrated significant advantages in managing intersection queues and improving overall efficiency.

Our findings align with those of Eichler and Daganzo [19], who reported that intermittent bus lanes reduced average delays by 15–30% under moderate saturation. However, the proposed IoT-SBL strategy achieved up to 71% queue length reduction at V/C = 0.97 due to its real-time responsiveness and integrated coordination via IoT. At low saturation levels (V/C < 0.5), our results show that the advantage of IoT-SBL diminishes, in agreement with observations by Zhu [13], where traditional bus lane strategies perform comparably.

Practically, IoT-SBL is most beneficial in corridors where saturation exceeds 0.5, especially under peak-hour congestion. For intersections with V/C ratios above 0.7, the strategy can reduce average delays by 40–70% and maintain intersection throughput above 90%. These benefits are particularly evident in urban settings with frequent bus operations (e.g., departure intervals less than 10 min) and high private vehicle demand.

The IoT-SBL strategy is inherently adaptable to diverse urban environments. Key parameters (e.g., lane capacity, signal phases) can be calibrated to local traffic patterns, infrastructure capabilities, and policy frameworks. Future work will explore case studies in cities with varying congestion profiles and IoT readiness to validate universal applicability. While the IoT-SBL strategy demonstrates efficacy under fixed saturation levels, real-world implementation requires adaptation to dynamic traffic fluctuations. Future work will incorporate time-varying parameters to address this gap.