An Agent-Based Simulation and Optimization Approach for Sustainable Urban Logistics: A Case Study in Lisbon
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
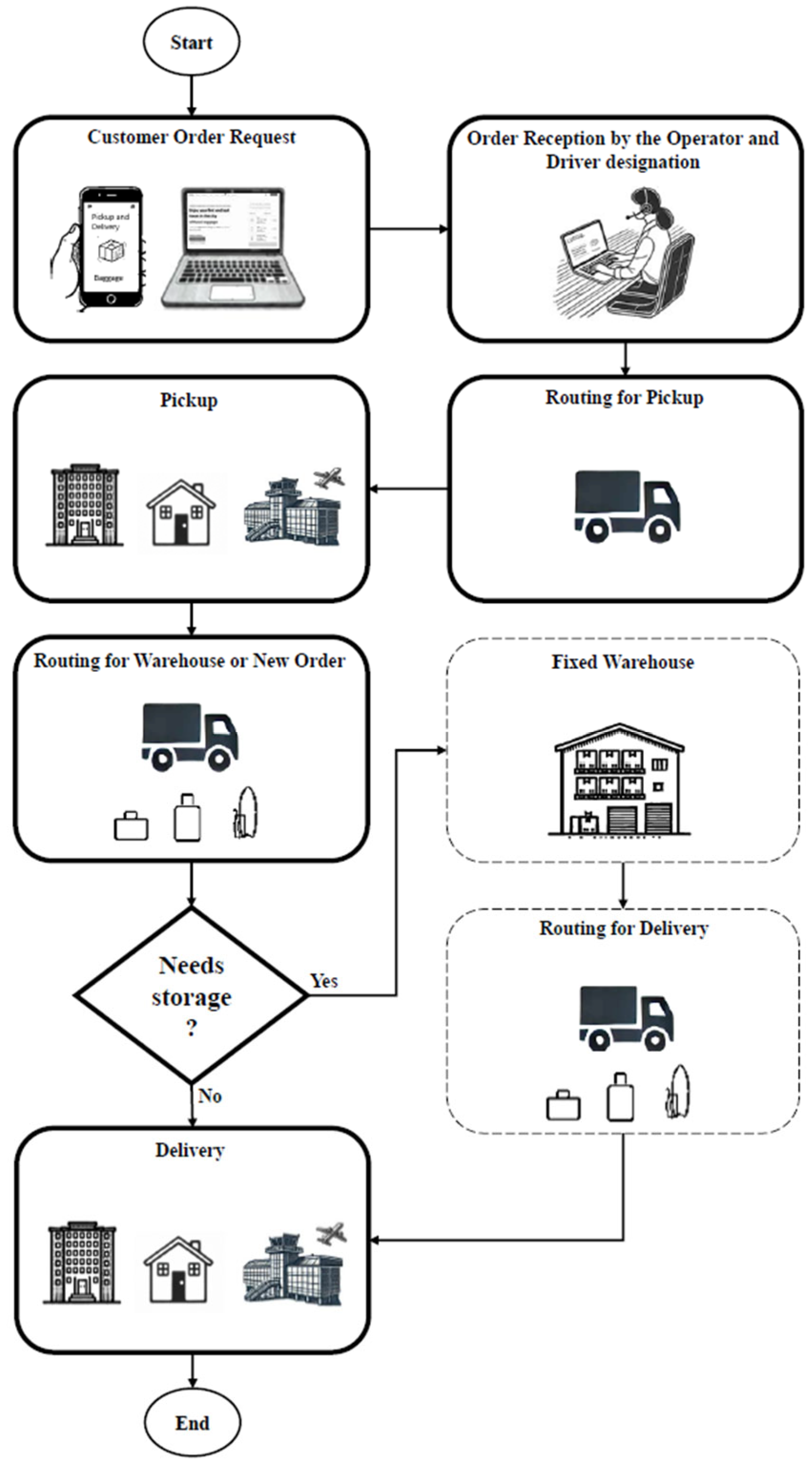
3.1. Conceptual Model
- Order: Represents customer requests for pickup and delivery|Attributes include size (small: 1 unit, medium: 2 units, large: 4 units), geographic coordinates for pickup and delivery, and specific time windows.
- Vehicles/Drivers: Responsible for transporting luggage between locations|Attributes include maximum capacity (24 units), dynamic positioning during operations, and estimated travel time based on geographic distances.
- Warehouses: Fixed locations for temporary storage of luggage, used when operational constraints prevent direct delivery|Attributes include storage capacity and associated operational costs.
- Order Classification and Allocation: Orders are assigned to vehicles based on their size and the vehicle’s available capacity, ensuring the total does not exceed 24 units.
- Storage Decisions:
- ○
- If the pickup date and the delivery date do not match, the goods are sent to a warehouse.
- ○
- Condition 2: If the vehicle has sufficient capacity, it acts as a mobile warehouse.
- ○
- Condition 3: If the vehicle does not have sufficient capacity, the goods are sent to a warehouse with the help of a vehicle designated for this situation.
- Time Window Compliance: Pickup and delivery times are subject to a 10 min tolerance to account for operational delays.
- Safety Assurance: Once the baggage is collected, the company under study assumes full responsibility for its safe transportation and storage.
- The simulation captures interactions between agents, such as:
- Vehicles consolidating or exchanging cargo at meeting points to optimize routes and capacity usage.
- Dynamic reassignment of orders based on real-time changes in vehicle availability and capacity.
- Capacity utilization: percentage of vehicle capacity utilized.
- Time: task time and length of time luggage remains in storage facilities.
- Distance travel: the distance per task and total for all vehicles.
- Number of Vehicles Used: Total vehicles required to fulfill all orders.
- Time Window Adherence: Percentage of pickups and deliveries completed within the allowed time tolerance.
- CO2 Emissions: Estimated carbon dioxide emissions based on the distance traveled and fuel consumption of diesel vehicles, used to assess the environmental impact of each scenario.
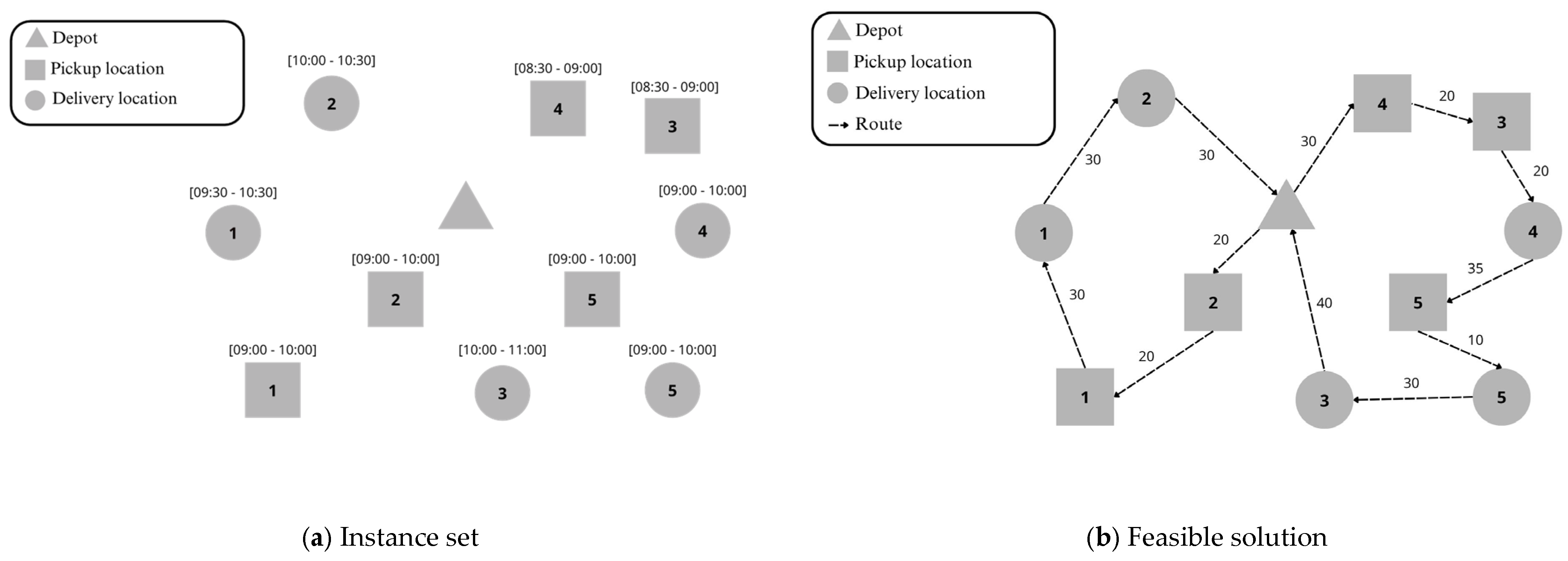
3.2. Mathematical Model Formulation
3.3. Agent-Based Simulation Using Anylogic
Implementation of ABS Model
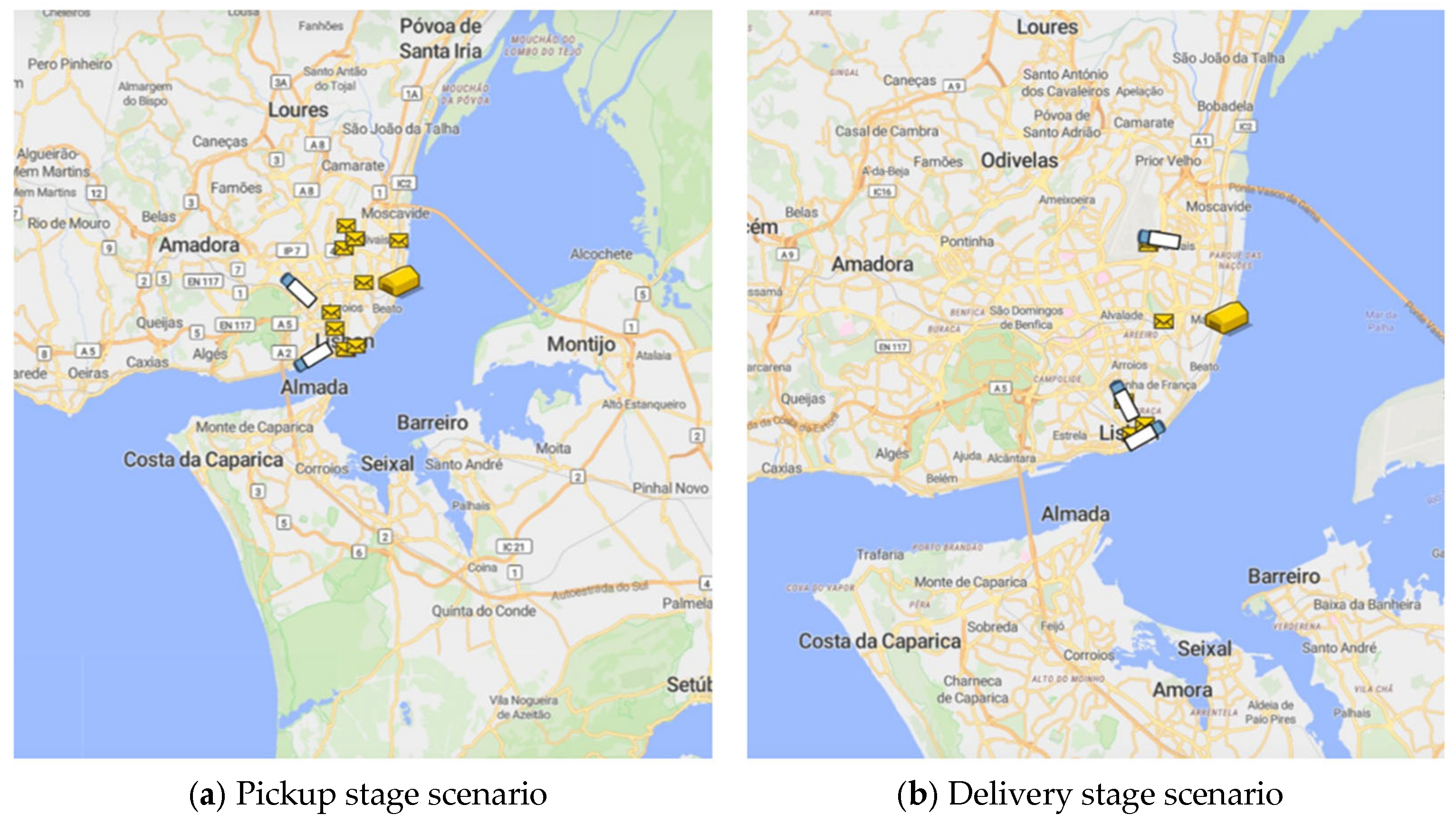
4. Case Study of Lisbon
5. Results and Discussion
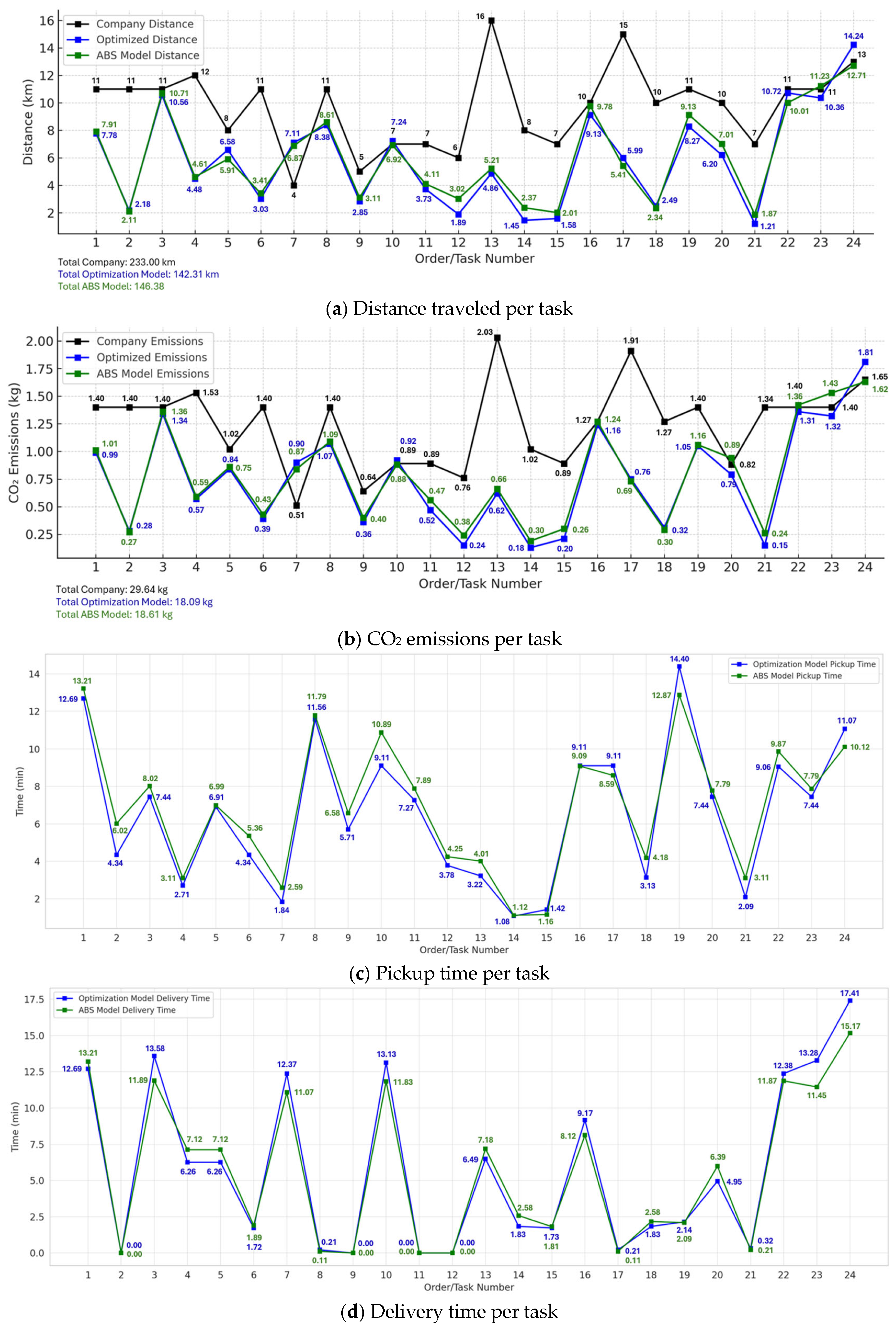
5.1. Scenario 1: Current Scenario
5.2. Scenario 2: Optimal Scenario
5.3. Limitations
6. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goetz, A.R. Transport Challenges in Rapidly Growing Cities: Is There a Magic Bullet? Transp. Rev. 2019, 39, 701–705. [Google Scholar] [CrossRef]
- Moreno, R.P.; Lopes, R.B.; Ferreira, J.V.; Ramos, A.L.; Correia, D. A Study of the Main Mathematical Models Used in Mobility, Storage, Pickup and Delivery in Urban Logistics: A Systematic Review. Systems 2024, 12, 374. [Google Scholar] [CrossRef]
- Lagorio, A.; Pinto, R.; Golini, R. Research in Urban Logistics: A Systematic Literature Review. Int. J. Phys. Distrib. Logist. Manag. 2016, 46, 908–931. [Google Scholar] [CrossRef]
- Frederhausen, S.; Klumpp, M. Commercial Electric Vehicle Routing in Urban Logistics: A Systematic Literature Review. In Data Science in Maritime and City Logistics: Data-driven Solutions for Logistics and Sustainability. Proceedings of the Hamburg International Conference of Logistics (HICL); Jahn, C., Kersten, W., Ringle, C.M., Eds.; epubli GmbH: Berlin, Germany, 2020; Volume 30, pp. 33–69. [Google Scholar]
- Mitrović-Minić, S.; Laporte, G. The Pickup and Delivery Problem with Time Windows and Transshipment. INFOR 2006, 44, 217–227. [Google Scholar] [CrossRef]
- Lyu, Z.; Yu, A.J. The Pickup and Delivery Problem with Transshipments: Critical Review of Two Existing Models and a New Formulation. Eur. J. Oper. Res. 2023, 305, 260–270. [Google Scholar] [CrossRef]
- Wolfinger, D. A Large Neighborhood Search for the Pickup and Delivery Problem with Time Windows, Split Loads and Transshipments. Comput. Oper. Res. 2021, 126, 105110. [Google Scholar] [CrossRef]
- Min, H. The Multiple Vehicle Routing Problem with Simultaneous Delivery and Pick-up Points. Transp. Res. Part Gen. 1989, 23, 377–386. [Google Scholar] [CrossRef]
- Martinez, L.M.; Correia, G.H.A.; Viegas, J.M. An Agent-Based Simulation Model to Assess the Impacts of Introducing a Shared-Taxi System: An Application to Lisbon (Portugal). J. Adv. Transp. 2015, 49, 475–495. [Google Scholar] [CrossRef]
- Murarețu, I.; Bădică, C. Optimal Agent-Based Pickup and Delivery with Time Windows and Electric Vehicles. Appl. Sci. 2024, 14, 7528. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; Nordfjaern, T.; Klöckner, C.A. A Systematic Review of the Agent-Based Modelling/Simulation Paradigm in Mobility Transition. Technol. Forecast. Soc. Chang. 2022, 184, 122011. [Google Scholar] [CrossRef]
- Rao, C.; Goh, M.; Zhao, Y.; Zheng, J. Location Selection of City Logistics Centers under Sustainability. Transp. Res. Part Transp. Environ. 2015, 36, 29–44. [Google Scholar] [CrossRef]
- Anily, S.; Hassin, R. The Swapping Problem. Networks 1992, 22, 419–433. [Google Scholar] [CrossRef]
- Santos, D.O.; Xavier, E.C. Taxi and Ride Sharing: A Dynamic Dial-a-Ride Problem with Money as an Incentive. Expert Syst. Appl. 2015, 42, 6728–6737. [Google Scholar] [CrossRef]
- Tadei, R.; Perboli, G.; Ricciardi, N.; Baldi, M.M. The Capacitated Transshipment Location Problem with Stochastic Handling Utilities at the Facilities. Int. Trans. Oper. Res. 2012, 19, 789–807. [Google Scholar] [CrossRef]
- Abreu, A.P. The Robust Pickup and Delivery Problem with Time Windows. Master’s Thesis, Federal University of São Carlos, São Carlos, Brazil, 2025. [Google Scholar]
- Khanna, A.; Liu, F.; Gupta, S.; Pavia, S.; Mukhopadhyay, A.; Dubey, A. PDPTW-DB: MILP-Based Offline Route Planning for PDPTW with Driver Breaks. In Proceedings of the 26th International Conference on Distributed Computing and Networking, Hyderabad, India, 4–7 January 2025; pp. 73–83. [Google Scholar]
- Dridi, I.H.; Kammarti, R.; Ksouri, M.; Borne, P. Genetic Algorithm for Mulicriteria Optimization of a Multi-Pickup and Delivery Problem with Time Windows. In Proceedings of the 13th IFAC Symposium on Information Control Problems in Manufacturing: Moscow, Russia, 3–5 June 2009; Volume 42, pp. 1538–1543. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, L.; Li, Z.; Lev, B. An Adaptive Genetic Algorithm with Neighborhood Search for Integrated O2O Takeaway Order Assignment and Delivery Optimization by E-Bikes with Varied Compartments. Appl. Soft Comput. 2024, 167, 112277. [Google Scholar] [CrossRef]
- Helo, P.; Rouzafzoon, J. An Agent-Based Simulation and Logistics Optimization Model for Managing Uncertain Demand in Forest Supply Chains. Supply Chain Anal. 2023, 4, 100042. [Google Scholar] [CrossRef]
- Karney, C.F.F. Algorithms for Geodesics. J. Geod. 2013, 87, 43–55. [Google Scholar] [CrossRef]
- AnyLogic: Simulation Modeling Software Tools & Solutions for Business. Available online: https://www.anylogic.com/ (accessed on 5 April 2025).
- Miller, C.E.; Tucker, A.W.; Zemlin, R.A. Integer Programming Formulation of Traveling Salesman Problems. J. ACM 1960, 7, 326–329. [Google Scholar] [CrossRef]
- Attajer, A.; Darmoul, S.; Chaabane, S.; Riane, F.; Sallez, Y. Benchmarking Simulation Software Capabilities Against Distributed Control Requirements: FlexSim vs. AnyLogic. In Service Oriented, Holonic and Multi-Agent Manufacturing Systems for Industry of the Future; Borangiu, T., Trentesaux, D., Leitão, P., Cardin, O., Lamouri, S., Eds.; Springer International Publishing: Cham, Germany, 2021; pp. 520–531. [Google Scholar]
- Hussein, M.; Karam, A.; Eltoukhy, A.E.E.; Darko, A.; Zayed, T. Optimized Multimodal Logistics Planning of Modular Integrated Construction Using Hybrid Multi-Agent and Metamodeling. Autom. Constr. 2023, 145, 104637. [Google Scholar] [CrossRef]
- Abdelmageed, S.; Abdelkhalek, S.; Hussien, M.; Zayed, T. A Hybrid Simulation Model for Modules Installation in Modular Integrated Construction Projects. Int. J. Constr. Manag. 2024, 24, 1407–1418. [Google Scholar] [CrossRef]
- Santiyuda, G.; Wardoyo, R.; Pulungan, R.; Yu, V.F. Multi-Objective Reinforcement Learning for Bi-Objective Time-Dependent Pickup and Delivery Problem with Late Penalties. Eng. Appl. Artif. Intell. 2024, 128, 107381. [Google Scholar] [CrossRef]
- Armenta-Déu, C. Environmental Impact of Urban Surface Transportation: Influence of Driving Mode and Drivers’ Attitudes. Pollutants 2025, 5, 5. [Google Scholar] [CrossRef]

| Notation | Description |
|---|---|
| Parameters | |
| quantity of baggage associated to request | |
| traveling distance between the arc using the vehicle | |
| traveling time between the arc | |
| earliest time that the request can be picked up at the location | |
| latest time that the request can be delivered at the location | |
| Variables | |
| 1 if vehicle travels through the arc , 0 otherwise. | |
| 1 if request is transported by vehicle through the arc , 0 otherwise. | |
| auxiliary variable used for sub-tour elimination, indicating the rank order in which node is visited (see Miller et al. [23]) | |
| arrival time for vehicle at location | |
| departure time for vehicle at location |
| Agent | Attribute | Description |
|---|---|---|
| Order/Task | Date | Date for Pickup and delivery |
| Time | Time for collection and delivery | |
| Address | Location of collection and delivery (latitude and longitude) | |
| Dimension | Dimensions of the merchandise | |
| Vehicles/Driver | Capacity | Volume/weight of the merchandise |
| Load Capacity | Vehicle carrying capacity | |
| Address Time | Time to reach the location | |
| Warehouse | Storage Cost | Cost associated with storage |
| Storage Capacity | Maximum supported volume |
| Driver Pickup–Delivery | Pickup Date | Pickup Time | Delivery Date | Delivery Time | Baggage Volume | Pickup (Latitude, Longitude) | Delivery (Latitude, Longitude) |
|---|---|---|---|---|---|---|---|
| B–A | 31 December 2022 | 12:00 | 6 January 2023 | 18:30 | 8 | (38.708603, 9.152313) | (38.729587, 9.145609) |
| B–B | 5 January 2023 | 10:00 | 5 January 2023 | 18:00 | 3 | (38.708603, 9.152313) | (38.768882, −9.129371) |
| A–A | 5 January 2023 | 08:00 | 5 January 2023 | 15:00 | 3 | (38.770698, −9.128416) | (38.709128, 9.131975) |
| B–B | 5 January 2023 | 11:00 | 5 January 2023 | 17:00 | 13 | (38.709886, −9.136901) | (38.768888, −9.129258) |
| A–A | 5 January 2023 | 11:00 | 5 January 2023 | 17:00 | 5 | (38.740775, −9.132096) | (38.768888, −9.129258) |
| A–A | 5 January 2023 | 10:00 | 5 January 2023 | 19:00 | 1 | (38.713089, 9.128038) | (38.763894, −9.136909) |
| B–B | 6 January 2023 | 09:00 | 6 January 2023 | 15:30 | 3 | (38.713419, −9.136630) | (38.768888, −9.129258) |
| B–B | 6 January 2023 | 08:45 | 6 January 2023 | 17:30 | 6 | (38.711479, −9.146890) | (38.768888, −9.129258) |
| B–B | 6 January 2023 | 11:00 | 6 January 2023 | 18:30 | 2 | (38.732004, −9.130959) | (38.763894, −9.136909) |
| A–A | 6 January 2023 | 15:00 | 7 January 2023 | 11:00 | 4 | (38.710027, −9.136163) | (38.768888, −9.129258) |
| A–A | 6 January 2023 | 08:00 | 6 January 2023 | 16:30 | 2 | (38.768888, −9.129258) | (38.709628, 9.135127) |
| A–B | 6 January 2023 | 11:00 | 6 January 2023 | 16:30 | 3 | (38.714964, −9.131438) | (38.768888, −9.129258) |
| A–A | 6 January 2023 | 10:30 | 6 January 2023 | 17:00 | 3 | (38.709268, 9.146129) | (38.767842, 9.099344) |
| B–B | 6 January 2023 | 11:30 | 6 January 2023 | 17:00 | 2 | (38.713236, 9.125640) | (38.775593, 9.135366) |
| B–B | 6 January 2023 | 09:30 | 6 January 2023 | 18:00 | 2 | (38.718769, −9.132179) | (38.763894, −9.136909) |
| A–A | 6 January 2023 | 09:00 | 6 January 2023 | 14:00 | 4 | (38.768990, −9.129261) | (38.711616, 9.128668) |
| A–A | 6 January 2023 | 13:30 | 6 January 2023 | 17:30 | 4 | (38.740243, −9.166652) | (38.720934, 9.143161) |
| C–C | 7 January 2023 | 10:30 | 7 January 2023 | 16:00 | 2 | (38.709903, −9.134395) | (38.763554, 9.137307) |
| C–C | 7 January 2023 | 10:00 | 7 January 2023 | 18:00 | 3 | (38.708603, 9.152313) | (38.770012, −9.128149) |
| A–A | 7 January 2023 | 08:30 | 9 January 2023 | 14:30 | 8 | (38.770698, −9.128416) | (38.768882, −9.129371) |
| C–B | 8 January 2023 | 10:30 | 8 January 2023 | 18:00 | 9 | (38.714284, −9.130639) | (38.768888, −9.129258) |
| C–B | 8 January 2023 | 10:00 | 8 January 2023 | 15:30 | 5 | (38.721265, −9.138722) | (38.770012, −9.128149) |
| B–B | 8 January 2023 | 10:00 | 8 January 2023 | 16:00 | 3 | (38.770698, −9.128416) | (38.711139, 9.135703) |
| B–B | 9 January 2023 | 09:38 | 9 January 2023 | 11:45 | 2 | (38.711377, −9.142813) | (38.785560, 9.110437) |
| Driver Pickup–Delivery | Pickup Date/Time | Delivery Date/Time | Real Distance Traveled (KM) | ABS Model (KM) | Real Cost (EUR per KM) | ABS Model Cost (EUR per KM) | Warehouse Cost (EUR) |
|---|---|---|---|---|---|---|---|
| B–A | 31 December 2022 12:00 | 6 January 2023 18:30 | 11 | 9.3 | 5.50 | 4.65 | 30.00 |
| B–B | 5 January 2023 10:00 | 5 January 2023 18:00 | 11 | 7.5 | 5.50 | 3.75 | - |
| A–A | 5 January 2023 8:00 | 5 January 2023 15:00 | 11 | 11.7 | 5.50 | 5.85 | - |
| B–B | 5 January 2023 11:00 | 5 January 2023 17:00 | 12 | 11.6 | 6.00 | 5.80 | - |
| A–A | 5 January 2023 11:00 | 5 January 2023 17:00 | 8 | 7.3 | 4.00 | 3.65 | - |
| A–A | 5 January 2023 10:00 | 5 January 2023 19:00 | 11 | 11.4 | 5.50 | 5.70 | - |
| B–B | 6 January 2023 9:00 | 6 January 2023 15:30 | 4 | 3.7 | 2.00 | 1.85 | - |
| B–B | 6 January 2023 8:45 | 6 January 2023 17:30 | 11 | 11.2 | 5.50 | 5.60 | - |
| B–B | 6 January 2023 11:00 | 6 January 2023 18:30 | 5 | 3.8 | 2.50 | 1.90 | - |
| A–A | 6 January 2023 15:00 | 7 January 2023 11:00 | 7 | 6.3 | 3.50 | 3.15 | 5.0 |
| A–A | 6 January 2023 8:00 | 6 January 2023 16:30 | 7 | 5.7 | 3.50 | 2.85 | - |
| A–B | 6 January 2023 11:00 | 6 January 2023 16:30 | 6 | 4.8 | 3.00 | 2.40 | - |
| A–A | 6 January 2023 10:30 | 6 January 2023 17:00 | 16 | 19.8 | 8.00 | 9.90 | - |
| B–B | 6 January 2023 11:30 | 6 January 2023 17:00 | 8 | 6.7 | 4.00 | 3.35 | - |
| B–B | 6 January 2023 9:30 | 6 January 2023 18:00 | 7 | 3.3 | 3.50 | 1.65 | - |
| A–A | 6 January 2023 9:00 | 6 January 2023 14:00 | 10 | 8.8 | 5.00 | 4.40 | - |
| A–A | 6 January 2023 13:30 | 6 January 2023 17:30 | 15 | 18.4 | 7.50 | 9.20 | - |
| C–C | 7 January 2023 10:30 | 7 January 2023 16:00 | 10 | 7.7 | 5.00 | 3.85 | - |
| C–C | 7 January 2023 10:00 | 7 January 2023 18:00 | 11 | 9.8 | 5.50 | 4.90 | - |
| A–A | 7 January 2023 8:30 | 9 January 2023 14:30 | 10 | 9.6 | 5.00 | 4.80 | 10.00 |
| C–B | 8 January 2023 10:30 | 8 January 2023 18:00 | 7 | 8.5 | 3.50 | 4.25 | - |
| C–B | 8 January 2023 10:00 | 8 January 2023 15:30 | 11 | 11.9 | 3.50 | 5.95 | - |
| B–B | 8 January 2023 10:00 | 8 January 2023 16:00 | 11 | 12.3 | 5.50 | 6.15 | - |
| B–B | 9 January 2023 9:38 | 9 January 2023 11:45 | 13 | 12.7 | 6.50 | 6.35 | - |
| Real Order Pickup Date/Time | Real Order Delivery Date/Time | Company Distance (KM) | Optimization Optimal Distance (KM) | ABS Model Optimal Distance (KM) | Real Cost (EUR per KM) | Optimized Cost (EUR per KM) | ABS Model Optimal Cost (EUR per KM) | Optimized Time (Pickup—Delivery) | ABS Time (Pickup—Delivery) | Time Window Adherence (Optimization/Simulation) | Warehouse Usage (Yes/No) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 31 December 2022 12:00 | 6 January 2023 18:30 | 11 | 7.78 | 7.91 | 5.50 | 3.89 | 3.96 | 10:50–18:20 | 10:48–18:26 | Yes—Yes | Yes |
| 5 January 2023 10:00 | 5 January 2023 18:00 | 11 | 2.18 | 2.11 | 5.50 | 1.09 | 1.06 | 10:00–17:50 | 09:57–17:59 | Yes—Yes | No |
| 5 January 2023 08:00 | 5 January 2023 15:00 | 11 | 10.56 | 10.71 | 5.50 | 5.28 | 5.36 | 08:10–14:50 | 08:12–14:57 | Yes *—Yes * | No |
| 5 January 2023 11:00 | 5 January 2023 17:00 | 12 | 4.48 | 4.61 | 6.00 | 2.24 | 2.31 | 10:57–16:50 | 11:02–17:01 | Yes—Yes * | No |
| 0 January 2023 11:00 | 5 January 2023 17:00 | 8 | 6.58 | 5.91 | 4.00 | 3.29 | 2.96 | 11:00–16:50 | 11:17–16:55 | Yes—Yes | No |
| 5 January 2023 10:00 | 5 January 2023 19:00 | 11 | 3.03 | 3.41 | 5.50 | 1.52 | 1.71 | 09:55–18:50 | 09:59–18:58 | Yes—Yes | No |
| 6 January 2023 09:00 | 6 January 2023 15:30 | 4 | 7.11 | 6.87 | 2.00 | 3.56 | 3.44 | 08:50–15:20 | 09:04–15:28 | Yes—Yes | No |
| 6 January 2023 08:45 | 6 January 2023 17:30 | 11 | 8.38 | 8.61 | 5.50 | 4.19 | 4.31 | 08:45–17:20 | 08:45–17:26 | Yes—Yes | No |
| 6 January 2023 11:00 | 6 January 2023 18:30 | 5 | 2.85 | 3.11 | 2.50 | 1.43 | 1.56 | 10:50–18:30 | 11:00–18:36 | Yes—Yes * | No |
| 6 January 2023 15:00 | 7 January 2023 11:00 | 7 | 7.24 | 6.92 | 3.50 | 3.62 | 3.46 | 14:50–10:50 | 14:54–11:00 | Yes—Yes | Yes |
| 6 January 2023 08:00 | 6 January 2023 16:30 | 7 | 3.73 | 4.11 | 3.50 | 1.87 | 2.06 | 08:10–16:20 | 08:17–16:27 | Yes—Yes | No |
| 6 January 2023 11:00 | 6 January 2023 16:30 | 6 | 1.89 | 3.02 | 3.00 | 0.95 | 1.51 | 10:53–16:20 | 10:59–16:30 | Yes—Yes | No |
| 6 January 2023 10:30 | 6 January 2023 17:00 | 16 | 4.86 | 5.21 | 8.00 | 2.43 | 2.61 | 10:20–17:00 | 10:28–17:03 | Yes—Yes * | No |
| 6 January 2023 11:30 | 6 January 2023 17:00 | 8 | 1.45 | 2.37 | 4.00 | 0.73 | 1.19 | 11:20–16:50 | 11:24–16:59 | Yes—Yes | No |
| 6 January 2023 09:30 | 6 January 2023 18:00 | 7 | 1.58 | 2.01 | 3.50 | 0.79 | 1.01 | 09:20–17:50 | 09:27–18:03 | Yes—Yes * | No |
| 6 January 2023 09:00 | 6 January 2023 14:00 | 10 | 9.13 | 9.78 | 5.00 | 4.57 | 4.89 | 08:50–13:50 | 08:58–13:59 | Yesc– Yes | No |
| 6 January 2023 13:30 | 6 January 2023 17:30 | 15 | 5.99 | 5.41 | 7.50 | 3.00 | 2.71 | 13:20–17:20 | 13:30–17:29 | Yes—Yes | No |
| 7 January 2023 10:30 | 7 January 2023 16:00 | 10 | 2.49 | 2.34 | 5.00 | 1.25 | 1.17 | 10:20–15:50 | 10:27–15:59 | Yes—Yes | No |
| 7 January 2023 10:00 | 7 January 2023 18:00 | 11 | 8.27 | 9.13 | 5.50 | 4.14 | 4.57 | 09:50–17:50 | 09:57–18:00 | Yes—Yes | No |
| 7 January 2023 08:30 | 9 January 2023 14:30 | 10 | 6.20 | 7.01 | 5.00 | 3.10 | 3.51 | 08:20–14:30 | 08:30–14:29 | Yes—Yes | Yes |
| 8 January 2023 10:30 | 8 January 2023 18:00 | 7 | 1.21 | 1.87 | 3.50 | 0.61 | 0.94 | 10:20–17:50 | 10:29–18:00 | Yes—Yes | No |
| 8 January 2023 10:00 | 8 January 2023 15:30 | 11 | 10.72 | 10.01 | 3.50 | 5.36 | 5.01 | 09:50–15:20 | 09:52–15:29 | Yes—Yes | No |
| 8 January 2023 10:00 | 8 January 2023 16:00 | 11 | 10.36 | 11.23 | 5.50 | 5.18 | 5.62 | 09:50–15:50 | 09:50–15:59 | Yes—Yes | No |
| 9 January 2023 09:38 | 9 January 2023 11:45 | 13 | 14.24 | 12.71 | 6.50 | 7.12 | 6.36 | 09:28–11:35 | 09:30–11:41 | Yes—Yes | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, R.P.R.; Lopes, R.B.; Ramos, A.L.; Ferreira, J.V.; Correia, D.; Melo, I.E.S.d. An Agent-Based Simulation and Optimization Approach for Sustainable Urban Logistics: A Case Study in Lisbon. Appl. Syst. Innov. 2025, 8, 66. https://doi.org/10.3390/asi8030066
Moreno RPR, Lopes RB, Ramos AL, Ferreira JV, Correia D, Melo IESd. An Agent-Based Simulation and Optimization Approach for Sustainable Urban Logistics: A Case Study in Lisbon. Applied System Innovation. 2025; 8(3):66. https://doi.org/10.3390/asi8030066
Chicago/Turabian StyleMoreno, Renan Paula Ramos, Rui Borges Lopes, Ana Luísa Ramos, José Vasconcelos Ferreira, Diogo Correia, and Igor Eduardo Santos de Melo. 2025. "An Agent-Based Simulation and Optimization Approach for Sustainable Urban Logistics: A Case Study in Lisbon" Applied System Innovation 8, no. 3: 66. https://doi.org/10.3390/asi8030066
APA StyleMoreno, R. P. R., Lopes, R. B., Ramos, A. L., Ferreira, J. V., Correia, D., & Melo, I. E. S. d. (2025). An Agent-Based Simulation and Optimization Approach for Sustainable Urban Logistics: A Case Study in Lisbon. Applied System Innovation, 8(3), 66. https://doi.org/10.3390/asi8030066









