Development of a Control System for Pressure Distribution During Gas Production in a Structurally Complex Field
Abstract
1. Introduction
2. Materials
3. Methods
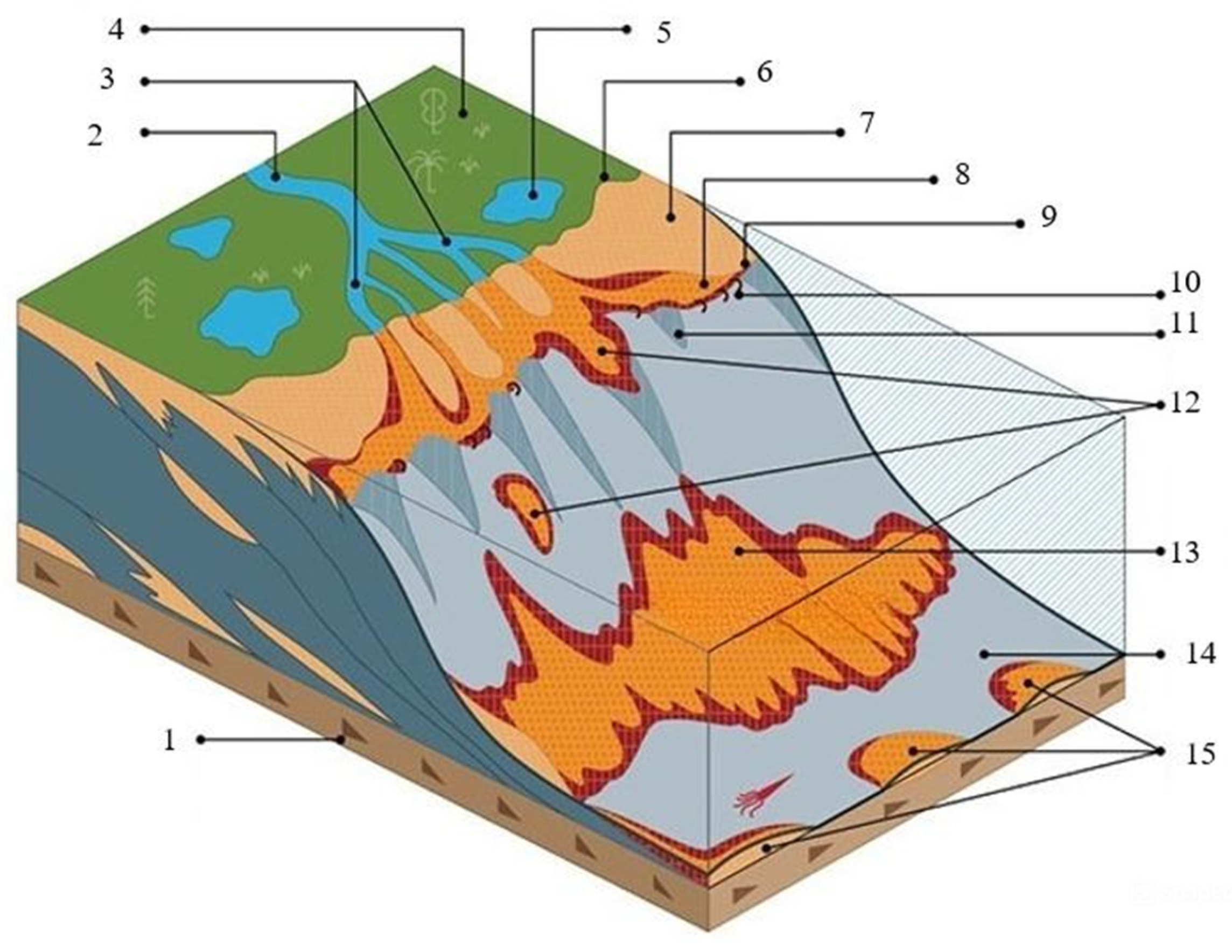
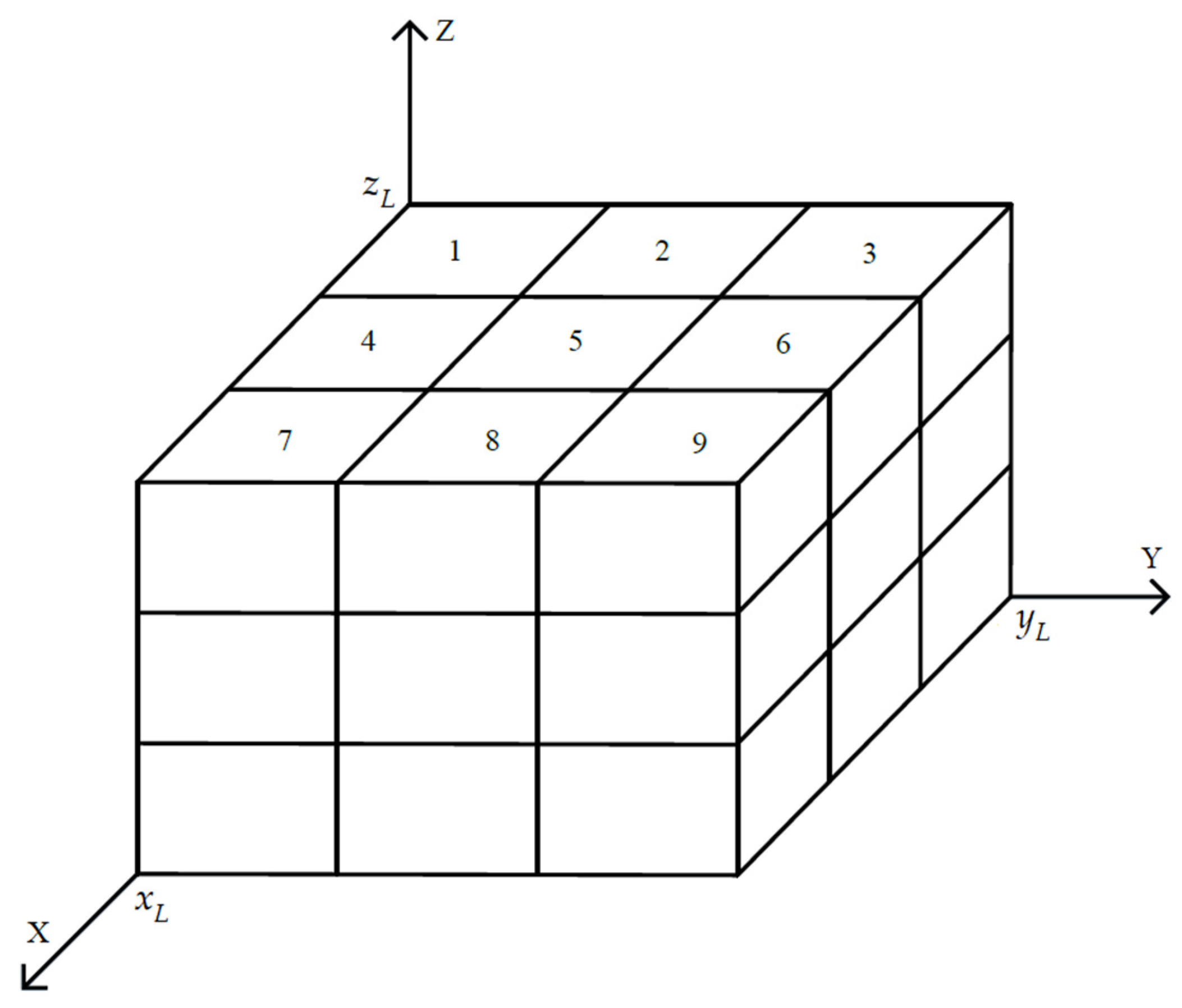
4. Development of a Mathematical Model of Pressure Distribution in a Structurally Complex Reservoir
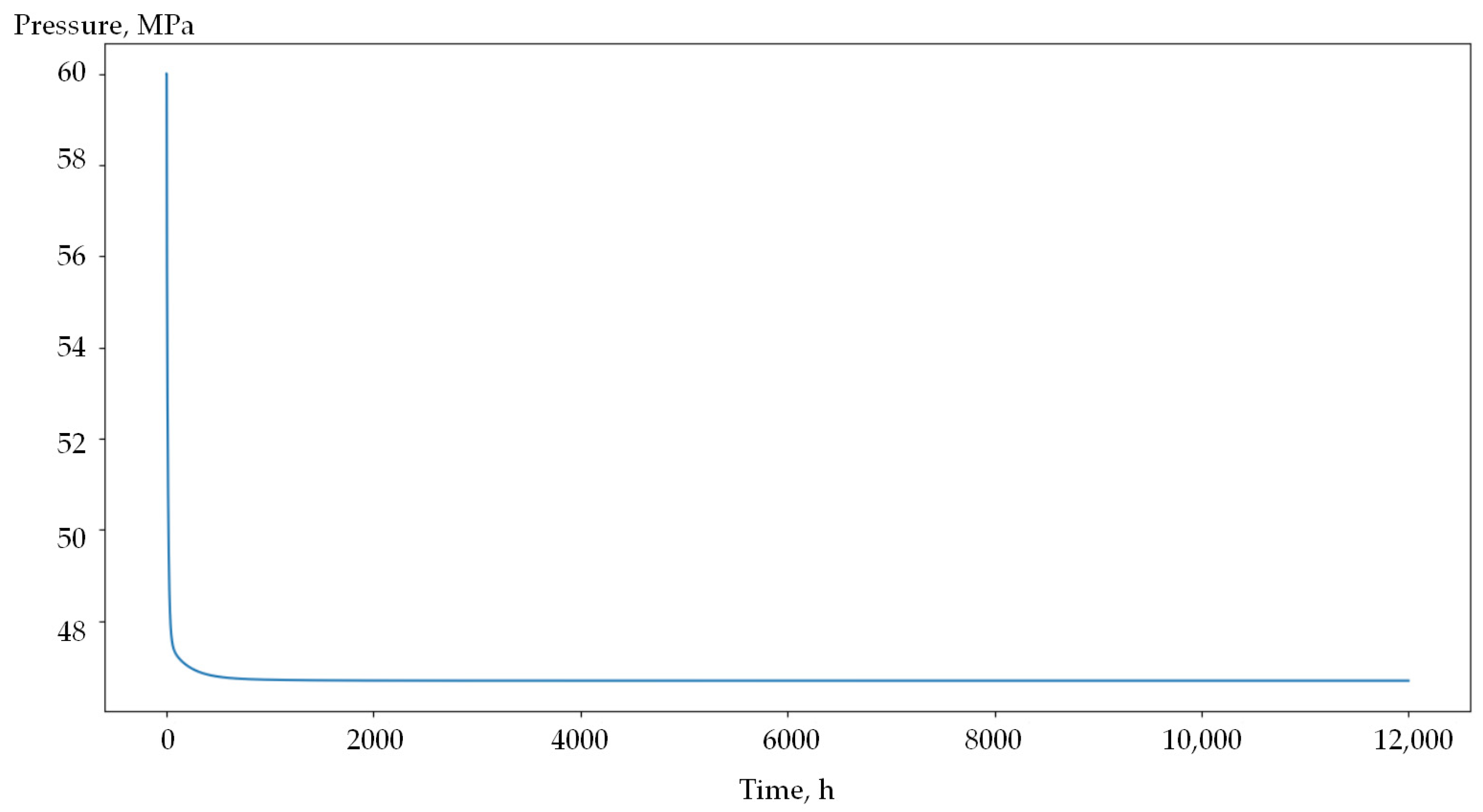
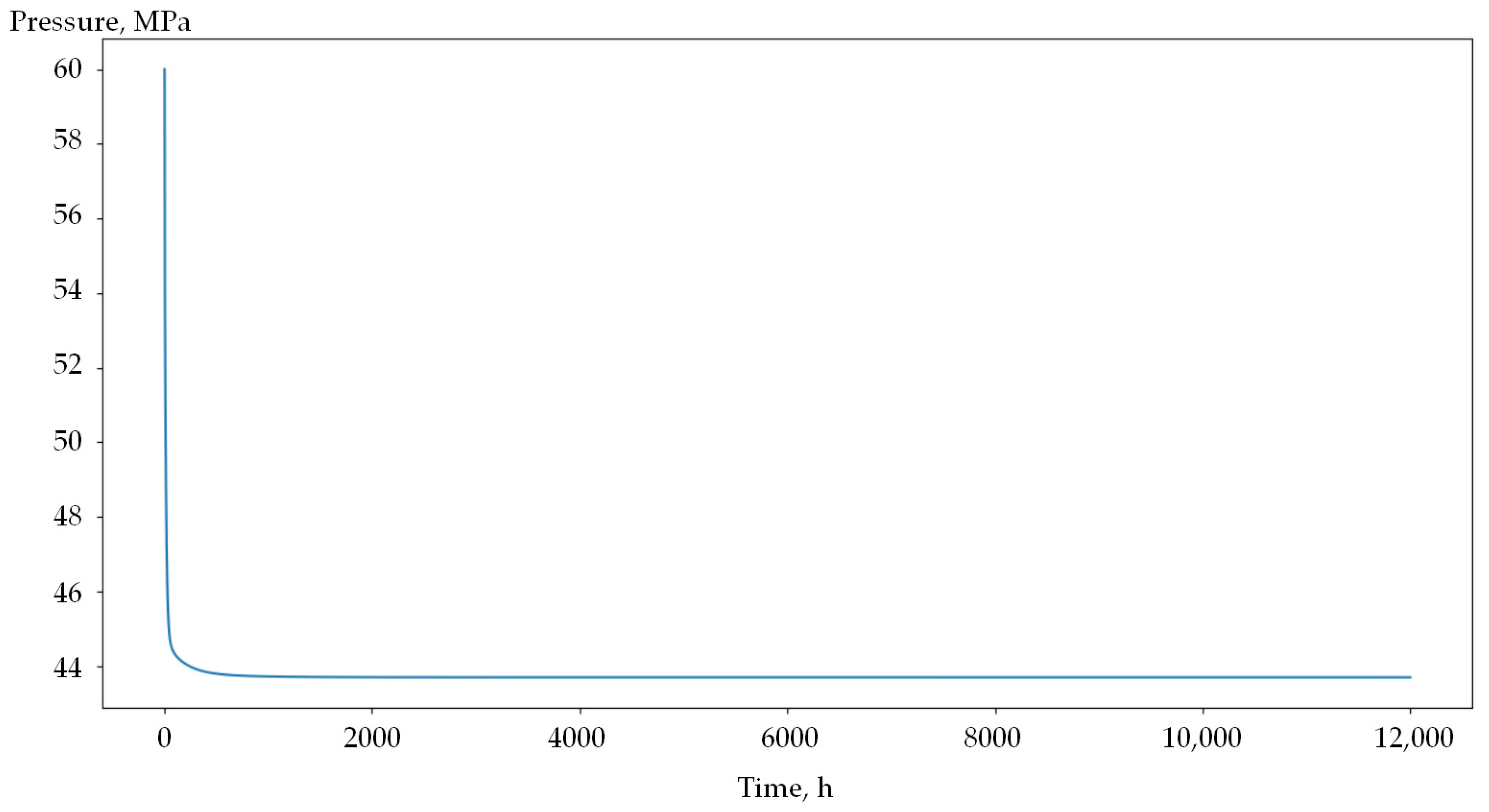
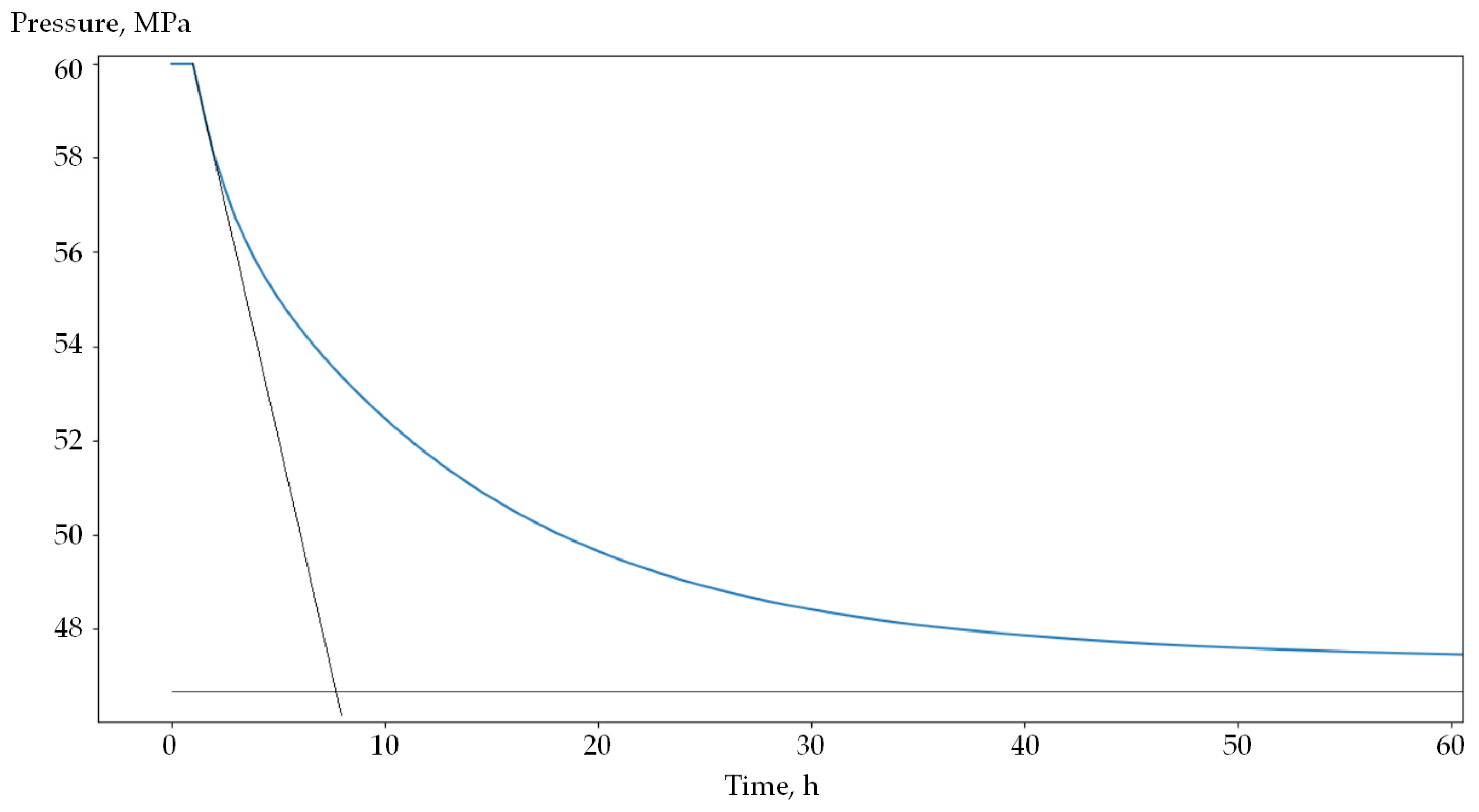
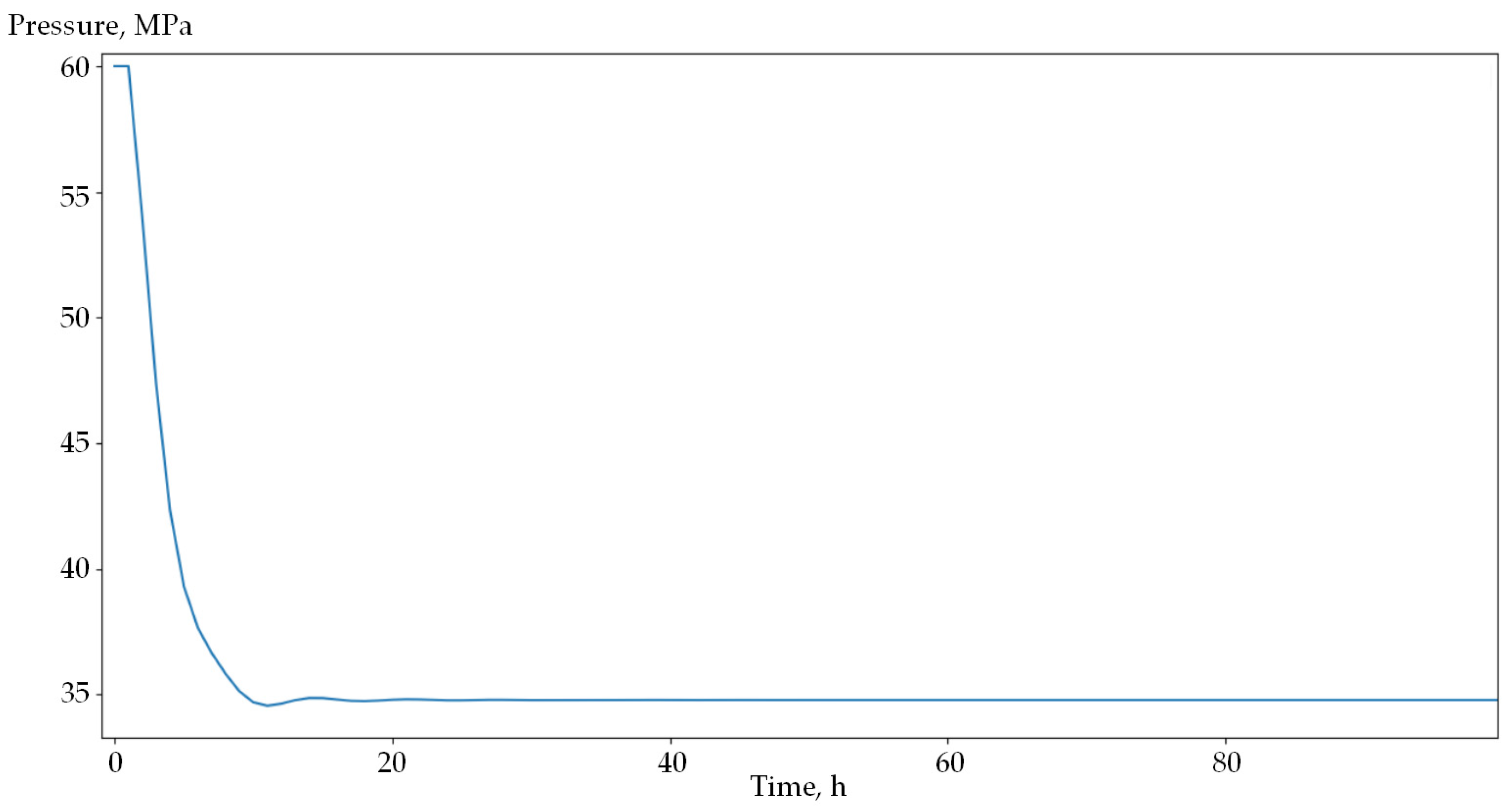
5. Results
- Gas-bearing reservoir with a complex geological structure is an object with distributed parameters since the pressure in the reservoir is distributed over the deposit (spatial coordinates), and the task of pressure field control is set;
- The synthesised pressure field control system has good quality indicators.
6. Discussion
- Allows to regulate the geometric values of depression funnels and increases the gas and condensate recovery factor;
- The possibility of realising control actions not on a specific point but on the required area as a whole will reduce the process of fluid backflow;
- Allows to prevent premature watering and related financial costs.
7. Conclusions
- Mathematical model of a gas-bearing reservoir as an object with distributed parameters, with given initial and boundary conditions, has been obtained;
- A distributed system of pressure field control in a structurally complex gas field was developed;
- It is revealed that the proposed approach will allow controlling the geometric dimensions of depression funnels;
- The quality and performance of the synthesised system were analyzed;
- Recommendations on the application of the proposed system in practice were formed.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bratskikh, D.S.; Romasheva, N.V.; Konopelko, A.Y.; Nikolaychuk, L.A. Model of Supply Chain Management in the Oil and Gas Industry Using Digital Technologies. OIJ 2024, 2024, 120–125. [Google Scholar] [CrossRef]
- Safiullin, R.N.; Safiullin, R.R.; Sorokin, K.V.; Kuzmin, K.A.; Rudko, V.A. Integral Assessment of Influence Mechanism of Heavy Particle Generator on Hydrocarbon Composition of Vehicles Motor Fuel. Int. J. Eng. 2024, 37, 1700–1706. [Google Scholar] [CrossRef]
- Litvinenko, V. The Role of Hydrocarbons in the Global Energy Agenda: The Focus on Liquefied Natural Gas. Resources 2020, 9, 59. [Google Scholar] [CrossRef]
- Jia, C.; Pang, X.; Song, Y. The Mechanism of Unconventional Hydrocarbon Formation: Hydrocarbon Self-Sealing and Intermolecular Forces. Pet. Explor. Dev. 2021, 48, 507–526. [Google Scholar] [CrossRef]
- Zhu, W.-Y.; Chen, Z.; Shang, X.-C. Multiphysical field coupling in unconventional oil and gas reservoirs. Chin. J. Eng. 2023, 45, 1045–1056. [Google Scholar] [CrossRef]
- Hong, L.; Jin, P.; Xiaolu, W.; Xinan, Y.; Qing, L. Analysis of Interlayer Interference and Research of Development Strategy of Multilayer Commingled Production Gas Reservoir. Energy Procedia 2012, 16, 1341–1347. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, J.; Tang, X. Unconventional Natural Gas Accumulation System. Nat. Gas Ind. B 2022, 9, 9–19. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, D.-H.; Wang, W.-H.; Jiang, T.-X.; Xue, Z.-J. Development of Unconventional Gas and Technologies Adopted in China. Energy Geosci. 2020, 1, 55–68. [Google Scholar] [CrossRef]
- Shklyarskiy, Y.; Andreeva, I.; Sutikno, T.; Jopri, M.H. Energy Management in Hybrid Complexes Based on Wind Generation and Hydrogen Storage. Bull. Electr. Eng. Inform. 2024, 13, 1483–1494. [Google Scholar] [CrossRef]
- Yao, J.; Ding, Y.; Sun, H.; Fan, D.; Wang, M.; Jia, C. Productivity Analysis of Fractured Horizontal Wells in Tight Gas Reservoirs Using a Gas–Water Two-Phase Flow Model with Consideration of a Threshold Pressure Gradient. Energy Fuels 2023, 37, 8190–8198. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.; Tsvetkov, P.; Koshenkova, A.; Skvortsov, I.; Andreeva, I.; Vorobeva, V. A Methodology for Forecasting the KPIs of a Region’s Development: Case of the Russian Arctic. Sustainability 2024, 16, 6597. [Google Scholar] [CrossRef]
- Prishchepa, O.; Aleksandrova, T. Study of thermodynamic processes of the Earth from the position of the genesis of hydrocarbons at great depths. J. Min. Inst. 2024, 269, 685–686. [Google Scholar]
- Prischepa, O.M.; Lutsky, D.S.; Kireev, S.B.; Sinitsa, N.V. Thermodynamic modelling as a basis for predicting phase states of hydrocarbon fluids at large and ultra-large depths. J. Min. Inst. 2024, 269, 815–832. [Google Scholar]
- Wei, M.; Zhou, J.; Duan, Y.; Long, T.; Duan, X.; Zhao, L.; Du, Y.; Hou, P. Prediction of Pressure and Temperature Profiles for Two-Phase Flow in Multilayered Gas Wells by DTS Data. Geoenergy Sci. Eng. 2024, 234, 212615. [Google Scholar] [CrossRef]
- Tao, X.; Okere, C.J.; Su, G.; Zheng, L. Experimental and Theoretical Evaluation of Interlayer Interference in Multi-Layer Commingled Gas Production of Tight Gas Reservoirs. J. Pet. Sci. Eng. 2022, 208, 109731. [Google Scholar] [CrossRef]
- Wang, C.-W.; Jia, C.-S.; Peng, X.-L.; Chen, Z.; Zhu, S.-Y.; Sun, H.-S.; Zhang, J. Effects of Wellbore Interference on Concurrent Gas Production from Multi-Layered Tight Sands: A Case Study in Eastern Ordos Basin, China. J. Pet. Sci. Eng. 2019, 179, 707–715. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, B.-R.; Zhao, Y.-L.; Zhang, L.-H.; Qiao, X.-Y.; Zhang, L.; Guo, J.-J.; Thanh, H.V. Inter-Layer Interference for Multi-Layered Tight Gas Reservoir in the Absence and Presence of Movable Water. Pet. Sci. 2024, 21, 1751–1764. [Google Scholar] [CrossRef]
- Yu, Y.; Lin, L.; Zhai, C.; Chen, H.; Wang, Y.; Li, Y.; Deng, X. Impacts of Lithologic Characteristics and Diagenesis on Reservoir Quality of the 4th Member of the Upper Triassic Xujiahe Formation Tight Gas Sandstones in the Western Sichuan Basin, Southwest China. Mar. Pet. Geol. 2019, 107, 1–19. [Google Scholar] [CrossRef]
- Zeng, F.; Liu, B.; Zhang, C.; Zhang, G.; Gao, J.; Liu, J.; Ostadhassan, M. Accumulation and Distribution of Natural Gas Reservoir in Volcanic Active Area: A Case Study of the Cretaceous Yingcheng Formation in the Dehui Fault Depression, Songliao Basin, NE China. Geofluids 2021, 2021, e2900224. [Google Scholar] [CrossRef]
- Zhong, X.; Zhu, Y.; Liu, L.; Yang, H.; Li, Y.; Xie, Y.; Liu, L. The Characteristics and Influencing Factors of Permeability Stress Sensitivity of Tight Sandstone Reservoirs. J. Pet. Sci. Eng. 2020, 191, 107221. [Google Scholar] [CrossRef]
- Olhin, A.; Vishnyakov, A. Pore Structure and Permeability of Tight-Pore Sandstones: Quantitative Test of the Lattice–Boltzmann Method. Appl. Sci. 2023, 13, 9112. [Google Scholar] [CrossRef]
- Orlov, D.; Ebadi, M.; Muravleva, E.; Volkhonskiy, D.; Erofeev, A.; Savenkov, E.; Balashov, V.; Belozerov, B.; Krutko, V.; Yakimchuk, I.; et al. Different Methods of Permeability Calculation in Digital Twins of Tight Sandstones. J. Nat. Gas Sci. Eng. 2021, 87, 103750. [Google Scholar] [CrossRef]
- Zhao, D.; Hou, J.; Sarma, H.; Guo, W.; Liu, Y.; Xie, P.; Dou, L.; Chen, R.; Zhang, Z. Pore Throat Heterogeneity of Different Lithofacies and Diagenetic Effects in Gravelly Braided River Deposits: Implications for Understanding the Formation Process of High-Quality Reservoirs. Geoenergy Sci. Eng. 2023, 221, 111309. [Google Scholar] [CrossRef]
- Afagwu, C.; Alafnan, S.; Mahmoud, M.A.; Patil, S. Permeability Model for Shale and Ultra-Tight Gas Formations: Critical Insights into the Impact of Dynamic Adsorption. Energy Rep. 2021, 7, 3302–3316. [Google Scholar] [CrossRef]
- Ding, J.; Yan, C.; He, Y.; Wang, C. Secondary Formation Damage of Low-Pressure Layer during Commingled Production in Multilayered Tight Gas Reservoirs. Sci Rep 2019, 9, 17542. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Mei, S.; Tao, Z.; Hou, S. An Experimental Investigation of Gas Permeability of a Low Permeability Sandstone under Deviatoric Loading with Loading/Unloading Cycles. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 173. [Google Scholar] [CrossRef]
- Pszonka, J.; Godlewski, P.; Fheed, A.; Dwornik, M.; Schulz, B.; Wendorff, M. Identifica-tion and quantification of intergranular volume using SEM automated mineralogy. Mar. Pet. Geol. 2024, 162, 106708. [Google Scholar] [CrossRef]
- Pszonka, J.; Götze, J. Quantitative estimate of interstitial clays in sandstones using Nomarski differential interference contrast (DIC) microscopy and image analysis. J. Pet. Sci. Eng. 2018, 161, 582–589. [Google Scholar] [CrossRef]
- Chai, X.; Tian, L.; Dong, P.; Wang, C.; Peng, L.; Wang, H. Study on Recovery Factor and Interlayer Interference Mechanism of Multilayer Co-Production in Tight Gas Reservoir with High Heterogeneity and Multi-Pressure Systems. J. Pet. Sci. Eng. 2022, 210, 109699. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, R.; Xu, X.; Sun, Z.; Yuan, Z.; Ma, K.; Jiang, B.; Kang, B.; Chen, G.; Li, C. The Pressure Buildup Well Test Analysis Considering Stress Sensitivity Effect for Deepwater Composite Gas Reservoir with High Temperature and Pressure. Geofluids 2021, 2021, e5054246. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Zhang, L.; Tang, H.; Xiong, Y.; Guo, J.; Shan, B. Laws of Gas and Water Flow and Mechanism of Reservoir Drying in Tight Sandstone Gas Reservoirs. Nat. Gas Ind. B 2021, 8, 195–204. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, T.; Jia, C.; Li, X.; Wu, K.; He, M. Numerical Simulation on Natural Gas Migration and Accumulation in Sweet Spots of Tight Reservoir. J. Nat. Gas Sci. Eng. 2020, 81, 103454. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Z.; Fu, S.; Li, A.; Zhong, J. Research on Transformation of Connate Water to Movable Water in Water-Bearing Tight Gas Reservoirs. Energies 2023, 16, 6961. [Google Scholar] [CrossRef]
- Bera, A.; Kumar, S.; Foroozesh, J.; Gharavi, A. Multiphysics Gas Transport in Nanoporous Unconventional Reservoirs: Challenges of Mathematical Modelling. J. Nat. Gas Sci. Eng. 2022, 103, 104649. [Google Scholar] [CrossRef]
- Asadulagi, M.-A.M.; Pershin, I.M.; Tsapleva, V.V. Research on Hydrolithospheric Processes Using the Results of Groundwater Inflow Testing. Water 2024, 16, 487. [Google Scholar] [CrossRef]
- Ilyushin, Y.; Talanov, N. Development of Methods and Models for Assessing Technical Condition of Mines and Underground Structures. Int. J. Eng. 2025, 38, 1659–1666. [Google Scholar] [CrossRef]
- Pervukhin, D.; Kotov, D.; Trushnikov, V. Development of a Conceptual Model for the Information and Control System of an Autonomous Underwater Vehicle for Solving Problems in the Mineral and Raw Materials Complex. Energies 2024, 17, 5916. [Google Scholar] [CrossRef]
- Tulyakov, T.; Afanaseva, O. Development of a Methodology for Introducing Robotic Devices for Technical Inspection of Power Lines Based on Data Mining. In Proceedings of the II International Scientific Forum on Sustainable Development and Innovation (WFSDI 2023): Conference Proceedings, Porto, Portugal, 27–28 April 2023; Institute of Digital Economics and Law LLC: Ekaterinburg, Russia, 2024; pp. 2018–2026. [Google Scholar]
- Boronko, E.A.; Novozhilov, I.M. Designing an Information System for Monitoring the Electromagnetic Field of a Power Plant. In Proceedings of the 2024 Conference of Young Researchers in Electrical and Electronic Engineering (ElCon), Saint Petersburg, Russia, 29–31 January 2024; pp. 331–334. [Google Scholar] [CrossRef]
- Romashin, D.V. Application of Artificial Intelligence to Improve the Efficiency of Monitoring and Diagnosing the Condition of Complex Technical Objects. In Proceedings of the 2024 Conference of Young Researchers in Electrical and Electronic Engineering (ElCon), Saint Petersburg, Russia, 29–31 January 2024; pp. 485–488. [Google Scholar] [CrossRef]
- Borodkin, V.N.; Kurchikov, A.R.; Melnikov, A.V.; Khramtsova, A.V. Formation Model and Textural Features of Rocks of the Achimov Complex in the North of Western Siberia; TyumGNGU: Tyumen, Russia, 2011; 84p. [Google Scholar]
- Arkhipov, V.N.; Zakharenko, V.A.; Dubrovin, A.A.V.; Starikov, M.A. Assessment of applicability of gas enhanced oil recovery methods for development of hard-to-recover reserves of objects-analogues of Achimov deposits. Expo. Oil Gas 2023, 1, 46–53. [Google Scholar] [CrossRef]
- Punanova, S.A. Hydrocarbon accumulations of Achimov deposits of the northern regions of Western Siberia. Expo. Oil Gas 2020, 3, 10–13. [Google Scholar] [CrossRef]
- Zakharov, L.A.; Martyushev, D.A.; Ponomareva, I.N. Predicting dynamic formation pressure using artificial intelligence methods. J. Min. Inst. 2022, 253, 23–32. [Google Scholar] [CrossRef]
- Martyushev, D.A.; Ponomareva, I.N.; Shen, W. Adaptation of transient well test results. J. Min. Inst. 2023, 264, 919–925. [Google Scholar]
- Abramkin, S.E.; Dushun, S.E. Implementation of Complex Control Algorithms at a Gas Production Enterprise. In Proceedings of the 2022 XXV International Conference on Soft Computing and Measurements (SCM), Saint Petersburg, Russia, 25–27 May 2022; pp. 56–59. [Google Scholar] [CrossRef]
- Gharavi, A.; Abbas, K.A.; Hassan, M.G.; Haddad, M.; Ghoochaninejad, H.; Alasmar, R.; Al-Saegh, S.; Yousefi, P.; Shigidi, I. Unconventional Reservoir Characterization and Formation Evaluation: A Case Study of a Tight Sandstone Reservoir in West Africa. Energies 2023, 16, 7572. [Google Scholar] [CrossRef]
- Lv, M.; Xue, B.; Guo, W.; Li, J.; Guan, B. Novel Calculation Method to Predict Gas–Water Two-Phase Production for the Fractured Tight-Gas Horizontal Well. J. Pet. Explor. Prod. Technol. 2024, 14, 255–269. [Google Scholar] [CrossRef]
- Tao, H.; Yan, L.I.U.; Jianhua, H.E.; Tairan, Y.E.; Hucheng, D.; Ruixue, L.I.; Kesai, L.I.; Jiawei, Z. Evaluation method and engineering application of in−situ stress of deep tight sandstone reservoir in the second member of Xujiahe Formation in Xiaoquan−Fenggu area, western Sichuan. Geol. China 2024, 51, 89–104. [Google Scholar] [CrossRef]
- Mal’Tsev, P.A.; Abramkin, S.E.; Plotnikov, A.V.; Martirosyan, K.V. A Conceptual Model of Controlled Gas Production Processes in Fields with a Complex Geological Structure. In Proceedings of the 2024 XXVII International Conference on Soft Computing and Measurements (SCM), Saint Petersburg, Russia, 22–24 May 2024; pp. 107–110. [Google Scholar] [CrossRef]
- Pervukhin, D.A.; Davardoost, H.; Gasimov, E.; Hawezy, A.L.J. Optimizing Multimodal Logistics in Petroleum Supply Chains Using Linear Goal Programming: A Case Study on South Pars Gas Field Development. Int. J. Eng. 2025, 38, 1909–1921. [Google Scholar] [CrossRef]
- Eremeeva, A.M.; Ilyushin, Y.V. Temperature Control During Storage of Raw Materials in the Process of Biodiesel Fuel Production. Inventions 2025, 10, 7. [Google Scholar] [CrossRef]
- Martirosyan, A.V.; Martirosyan, K.V.; Grudyaeva, E.K.; Chernyshev, A.B. Calculation of the Temperature Maximum Value Access Time at the Observation Point. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), St. Petersburg, Russia, 26–29 January 2021; pp. 1014–1018. [Google Scholar] [CrossRef]
- Pershin, I.M. Frequency Concept of Analysis and Synthesis of Systems with Distributed Parameters: Monograph; Ministry of Science and Higher Education of the Russian Federation, North Caucasus Federal University: Pyatigorsk, Russia, 2021; p. 171. [Google Scholar]
- Leibenzon, L.S. Collected Works. Volume 2. Underground Hydrogasdynamics; USSR Academy of Sciences: Moscow, Russia, 1953; 544p. [Google Scholar]
- Basiev, K.S.; Kochina, I.N.; Maksimov, V.M. Underground Hydromechanics: Textbook for Universities; Nedra: Moscow, Russia, 1993; p. 416. [Google Scholar]
- Pershin, I.M.; Tsapleva, V.V.; Malkov, A.V.; Pomelyayko, I.S. Designing a distributed well pad control system. In Proceedings of the System Synthesis and Applied Synergetics: Collection of Scientific Papers of the X All-Russian Scientific Conference, Nizhny Arkhyz Settlement, Russia, 28 September 2021; pp. 330–336. [Google Scholar] [CrossRef]
- Alotaibi, M.; Alotaibi, S.; Weijermars, R. Stream and Potential Functions for Transient Flow Simulations in Porous Media with Pressure-Controlled Well Systems. Fluids 2023, 8, 160. [Google Scholar] [CrossRef]
- Cheng, M.; Xue, W.; Guo, Z.; Hou, M.; Wang, C. Development of Large-Scale Tight Gas Sandstone Reservoirs and Recommendations for Stable Production—The Example of the Sulige Gas Field in the Ordos Basin. Sustainability 2023, 15, 9933. [Google Scholar] [CrossRef]
- Pan, H.; Jiang, Y.; Guo, G.; Yang, C.; Deng, H.; Zhu, X.; Zeng, Q.; Song, L.; Cao, J.; Wang, Z.; et al. Pore-Throat Structure Characteristics and Fluid Mobility Analysis of Tight Sandstone Reservoirs in Shaximiao Formation, Central Sichuan. Geol. J. 2023, 58, 4243–4256. [Google Scholar] [CrossRef]
- Sirota, D.D. Development of a computer model of unsteady gas filtration taking into account the inhomogeneity of the formation filtration properties. In Proceedings of the 2020 XXIII International Conference on Soft Computing and Measurements (SCM), Saint Petersburg, Russia, 27–29 May 2020; pp. 193–197. [Google Scholar]
- Hu, C.; Wang, F.; Liu, Y.; Zhi, J. Three-Dimensional Lattice Boltzmann Simulation of Gas-Water Transport in Tight Sandstone Porous Media: Influence of Microscopic Surface Forces. Energy Sci. Eng. 2020, 8, 1924–1940. [Google Scholar] [CrossRef]
- Ilyushin, Y.V.; Asadulagi, M.-A.M. Development of a Distributed Control System for the Hydrodynamic Processes of Aquifers, Taking into Account Stochastic Disturbing Factors. Water 2023, 15, 770. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kukharova, T.; Maltsev, P.; Novozhilov, I. Development of a Control System for Pressure Distribution During Gas Production in a Structurally Complex Field. Appl. Syst. Innov. 2025, 8, 51. https://doi.org/10.3390/asi8020051
Kukharova T, Maltsev P, Novozhilov I. Development of a Control System for Pressure Distribution During Gas Production in a Structurally Complex Field. Applied System Innovation. 2025; 8(2):51. https://doi.org/10.3390/asi8020051
Chicago/Turabian StyleKukharova, Tatyana, Pavel Maltsev, and Igor Novozhilov. 2025. "Development of a Control System for Pressure Distribution During Gas Production in a Structurally Complex Field" Applied System Innovation 8, no. 2: 51. https://doi.org/10.3390/asi8020051
APA StyleKukharova, T., Maltsev, P., & Novozhilov, I. (2025). Development of a Control System for Pressure Distribution During Gas Production in a Structurally Complex Field. Applied System Innovation, 8(2), 51. https://doi.org/10.3390/asi8020051






