Application of Artificial Neural Networks for Power Load Prediction in Critical Infrastructure: A Comparative Case Study

Abstract

This article aims to assess the effectiveness of state-of-the-art artificial neural network (ANN) models in time series analysis, specifically focusing on their application in prediction tasks of critical infrastructures (CIs). To accomplish this, shallow models with nearly identical numbers of trainable parameters are constructed and examined. The dataset, which includes 120,884 hourly electricity consumption records, is divided into three subsets (25%, 50%, and the entire dataset) to examine the effect of increasing training data. Additionally, the same models are trained and evaluated for univariable and multivariable data to evaluate the impact of including more features. The case study specifically focuses on predicting electricity consumption using load information from Norway. The results of this study confirm that LSTM models emerge as the best-performed model, surpassing other models as data volume and feature increase. Notably, for training datasets ranging from 2000 to 22,000 instances, GRU exhibits superior accuracy, while in the 22,000 to 42,000 range, LSTM and BiLSTM are the best. When the training dataset is within 42,000 to 360,000, LSTM and ConvLSTM prove to be good choices in terms of accuracy. Convolutional-based models exhibit superior performance in terms of computational efficiency. The convolutional 1D univariable model emerges as a standout choice for scenarios where training time is critical, sacrificing only 0.000105 in accuracy while a threefold improvement in training time is gained. For training datasets lower than 22,000, feature inclusion does not enhance any of the ANN model’s performance. In datasets exceeding 22,000 instances, ANN models display no consistent pattern regarding feature inclusion, though LSTM, Conv1D, Conv2D, ConvLSTM, and FCN tend to benefit. BiLSTM, GRU, and Transformer do not benefit from feature inclusion, regardless of the training dataset size. Moreover, Transformers exhibit inefficiency in time series forecasting due to their permutation-invariant self-attention mechanism, neglecting the crucial role of sequence order, as evidenced by their poor performance across all three datasets in this study. These results provide valuable insights into the capabilities of ANN models and their effective usage in the context of CI prediction tasks.

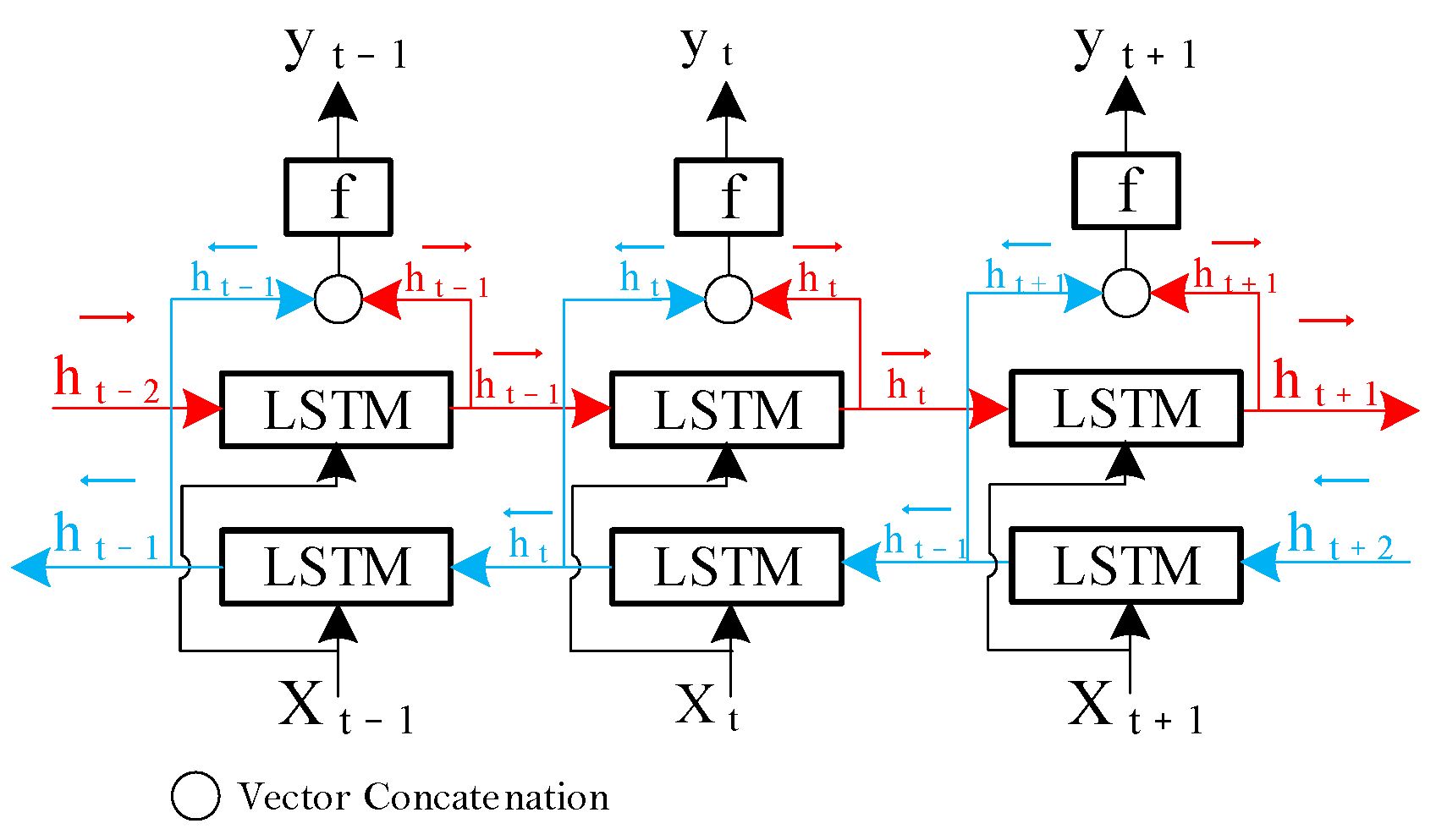
1. Introduction

The emergence of new technologies, such as automated transport, digitalization, e-maintenance, IoT, cloud computing, big data analytics, virtual reality (VR), and Industry 4.0 concepts, has opened avenues for more the efficient and sustainable management of Critical Infrastructures (CIs) [1,2,3]. In particular, recent advancements in machine learning, particularly in the field of artificial neural networks (ANNs), have shown great promise in overcoming the limitations of traditional approaches and improving their performance [4,5,6]. For instance, Bucher and Most [7] have used ANNs to estimate limit state functions in nonlinear structural analysis using the response surface method. Shuliang Wang et al. [8] employed deep learning techniques for vulnerability analysis of CIs. Guzman et al. [9] demonstrated the power of ANNs in improving accuracy in risk assessment of critical infrastructure. One of the primary objectives of this study is to demonstrate the efficacy of ANNs in the electric power load forecasting of CIs. Notably, research reports [10,11] indicate that a reduction of 1% in power load prediction error can result in savings of up to GBP 10 million in electricity power operational costs. Thus, selecting the most suitable ANN model in power load forecasting can lead to substantial cost savings and contribute to a more sustainable power system. Moreover, with a better understanding of ANN’s architects and performances, researchers and practitioners can find suitable applications for challenges inherent to the complex nature of CIs more efficiently and effectively. Ongoing research and development in ANN models continue to enhance their capabilities, providing opportunities for further improvements in the performance, reliability, and resilience of CIs.

Load forecasting is typically categorized into three subcategories: short-term (hourly to a few weeks ahead), medium-term (beyond a week to a few months ahead), and long-term (forecasting consumption for the next year to a few years ahead) [12]. Short-term load forecasting (STLF) primarily deals with power distribution aspects such as unit commitment, load switching, load balancing, and dispatching. Medium-term load forecasting (MTLF) aids in the efficient scheduling of fuel supplies and proper operation and maintenance activities. Long-term load forecasting (LTLF) supports infrastructure development, including planning new power plants and distribution networks. Developing accurate forecasting models facilitates efficient and economical supply and demand management for both customers and suppliers, leading to a more sustainable power system. Numerous models, methods, and techniques have been developed in academia and industry for power load forecasting, broadly categorized as multi-factor forecasting methods and time series methods [13]. Time series methods further consist of statistical models, machine learning models, and hybrid models [13]. Conventionally, statistical models such as multiple linear regression [14,15,16], general exponential smoothing [17,18,19], and autoregressive integrated moving averages (ARIMA) have been widely used for power load forecasting [20,21,22]. These methods often require the time series data to be stationary (i.e., constant mean, variance, and serial correlation). While these approaches can handle univariate data, they are single-step forecast models that necessitate extensive preprocessing and explicit definitions of input characteristics [23]. Machine learning models such as Support Vector Machines (SVM) [24,25,26], Bayesian Belief Networks [20,27], and Principal Component Analysis (PCA) [15,28] have also been employed in power load forecasting. For instance, Jain and Satish [26] utilized SVM for short-term load forecasting and demonstrated that applying a threshold between the daily average load of training input patterns enhances the accuracy of SVM predictions. There are plenty of studies that have shown the ANN models outperform machine learning and statistical models such as ARIMA [29,30,31,32,33]; therefore, the focus of this study is on deep learning models.

ANNs, a central component of machine learning methods known as deep learning, have expanded the capabilities of machine learning models by enabling complex pattern recognition in multivariable input data. ANNs learn functional relationships and patterns between inputs and outputs without requiring the explicit extraction of these relationships. Moreover, they can handle intrinsic challenges associated with electric power loads, such as periodicity, seasonality, and sequential dependence among electricity consumption data sequences. Long Short-Term Memory (LSTM), introduced by Hochreiter and Schmidhuber [34], emerged as a solution to address the backpropagation and long-term dependency issues in Recurrent Neural Networks (RNNs). LSTM has since become one of the most widely used RNNs in time series analysis, including load forecasting [32,35,36]. Over time, a diverse range of ANN architectures have been developed to tackle various forecasting problems. These architectures that are commonly used in load forecasting include Fully Connected Networks (FCNs) [37,38,39], RNNs [29,30,40,41], Gated Recurrent Units (GRU) [42,43], Convolutional Neural Networks (CNNs) [44,45,46], Bidirectional LSTM networks (BiLSTMs) and Transformers, which have been highly successful in Natural Language Processing (NLP). For instance, Zhao, et al. [47] proposed a transformer-based model for day-ahead electricity load forecasting. Additionally, hybrid approaches combining different ANN architectures, each with its unique characteristics, have also been used in electricity power load forecasting. A hybrid CNN-LSTM-BiLSTM with attention mechanism [31], a combination of CNN and LSTM [48], and a hybrid BiLSTM-Auto Encoder [49], are a combination of evaluated models in the present study. As an example, Rafi, et al. [50] have developed a hybrid CNN-LSTM model, where CNN layers are commonly used for feature extraction, while LSTM layers are responsible for sequence learning.

Despite the wide range of ANN models mentioned here for electric load forecasting, a comprehensive comparison of their performance is lacking. For example, reference [51] is a comparative study of RNN, GRU, BiLSTM, and LSTM models for the short-term charging load forecasting of electric vehicles. The hybrid CNN-LSTM, Convolutional 1D and 2D, FCNs, and Transformer models are also included in the present study to include most of the state-of-the-art ANN models. Moreover, the effect of available data, features, and the training time for each model is also evaluated, which gives a better understanding of the ANN model’s performance. Therefore, this research tries to bridge a critical gap in the literature where a comprehensive comparative analysis of cutting-edge ANNs in prediction tasks has not been thoroughly evaluated or explored considering available data, features, and training time.

The rest of this paper is structured as follows: Section 2 provides a concise overview of the ANN models used in this study. In Section 3, the comprehensive case study is presented detailing data collection, data preprocessing, building the ANN models, defining the evaluation metrics, training and testing the models, and finally, the result of experiments. Section 4 provides a discussion of the results in the light of similar research. Ultimately, Section 5 offers the conclusion.

2. The ANN Models—A Brief Review

In this study, the focus is on the application of ANNs in time series forecasting, and the following section provides a brief introduction to the architectures used in this study. For simplicity, only the equations for the forward propagation of inputs are presented. The backward propagation is performed by calculating the derivatives of the loss function concerning the weights and biases, enabling the assessment of their impact on the error and subsequent updates.

2.1. Densely or Fully Connected Networks (FCNs)

The fully connected neural network (FCN) employs a linear transformation on its inputs [52,53]. This connectivity allows for a comprehensive exploration of the relationships between the inputs and outputs. The output of a fully connected unit can be obtained by taking the dot product of the inputs and weights, adding the bias term, and passing the result through an activation function ($f$), as shown in Equation (1).

$$y_{jk}\left(x\right)=f\left({\displaystyle \sum }_{i=1}^n(w_{jk} . x_i)+b_{jk}\right)$$

(1)

where each input ($x_i$) is connected to every output ($y_{jk}\left(x\right)$) through a set of weights ($w_{jk}$) and biases ($b_{jk}$).

2.2. Long Short-Term Memory Networks (LSTMs)

Long short-term memory (LSTM) was introduced by Hochreiter and Schmidhuber [34] to tackle the long-term dependencies problem in recurrent neural networks (RNNs). An LSTM consists of input, forget, and output gates, enabling them to retain the important information from the past and discard the irrelevant. As shown in Figure 1, the forget gate ($f_t)$ plays a crucial role in determining which information to discard from the cell state $\left(C_{t-1}\right)$ which is commonly written as:

$$f_t=\sigma \left(W_f .\left[h_{t-1},x_t\right]+b_f\right)$$

(2)

The input gate selectively determines what new information (from the input and previous hidden state ($\left[h_{t-1},x_t\right]$) should be passed into the cell state, as shown in Equation (3).

$$i_t=\sigma \left(W_i .\left[h_{t-1},x_t\right]+b_i\right)$$

(3)

Once the forget and update values have been determined, the previous cell state $\left(C_{t-1}\right)$ can be updated accordingly; thus, the new candidate’s equation is written as:

$${\tilde{C}}_t=\tan \mathrm{h}\left(W_c .\left[h_{t-1},x_t\right]+b_c\right)$$

(4)

By performing these operations, the LSTM effectively combines the relevant information from the previous state with the newly computed candidate values, resulting in an updated cell state ($C_t$) that reflects the desired modifications. The updated cell state is calculated as follows:

$$C_t=f_t\times C_{t-1}+i_t\times {\tilde{C}}_t$$

(5)

The output gate ($o_t$) uses a sigmoid function and determines which portion of the cell state should be transmitted as the output.

$$o_t=\sigma \left(W_0 .\left[h_{t-1},x_t\right]+b_o\right)$$

(6)

Finally, the current hidden state ($h_t$) is updated as follows:

$$h_t=o_t\times \tan \mathrm{h}(C_t)$$

(7)

where $f_t$, $i_t$, ${\tilde{C}}_t$ are forget, input gates, outputs, and the candidate values for the current time step t; $\sigma$ and $\tan \mathrm{h}$ are the sigmoid and hyperbolic tangent activation functions; $W_f$, $W_i$, $W_c$ are forget, input gates and candidate value weight matrices; $\left[h_{t-1},x_t\right]$ is a concatenation of the previous hidden state ($h_{t-1}$) and curet input values ($x_t$); and $b_f,b_i,b_c$ are forget, input gates and candidate values biases.

2.3. Gated Recurrent Units Networks (GRUs)

The Gated recurrent networks (GRU) are similar to LSTMs, but without the need for a separate memory cell, introduced by Cho, et al. [54]. They consist of two gates instead of three: the update gate and the reset gate, illustrated in Figure 2. The reset gate decides which information from the previous hidden state ($h_{t-1}$) should be used to compute the candidate hidden state (${\tilde{h}}_t$). The update gate decides which information from the previous hidden state ($h_{t-1}$) should be combined with the candidate hidden state to produce the updated hidden state ($h_t$).

The reset gate ($r_t)$:

$$r_t=\sigma \left(W_r .\left[h_{t-1},x_t\right]+b_r\right)$$

(8)

The update gate ($z_t$):

$$z_t=\sigma \left(W_z .\left[h_{t-1},x_t\right]+b_z\right)$$

(9)

The hidden state candidate (${\tilde{h}}_t$):

$${\tilde{h}}_t=\tanh \left(W_h .\left[(r_t\times h_{t-1}),x_t\right]+b_c\right)$$

(10)

Finally, the output of the GRU is determined by combining updated values of the previous hidden state $\left(1-z_t\right)\times h_{t-1}$ with the updated current memory content of the cell ($z_t\times {\tilde{h}}_t$).

$$h_t=\left(1-z_t\right)\times h_{t-1}+z_t\times {\tilde{h}}_t$$

(11)

where $\sigma$ and $\tan \mathrm{h}$ are the sigmoid and hyperbolic tangent activation functions; $W_r$, $W_z$, $W_h$ are reset, update gates and hidden state candidate weight matrices; $\left[h_{t-1},x_t\right]$ is a concatenation of previous hidden state ($h_{t-1}$) and curet input values ($x_t$); and $b_r,b_z,b_c$ are reset, update gates and hidden state candidate biases.

2.4. Bidirectional LSTM Networks (BiLSTMs)

Schuster and Paliwal [55] introduced Bidirectional LSTM to overcome the limitation of accessing only past information by enabling the network to simultaneously consider present and future information through positive and negative time directions. This architecture consists of two LSTMs: one processing the input in the forward direction and the other in the backward direction, allowing the network to incorporate both forward and backward information at each step, as shown in Figure 3.

The outputs of both the forward $\overrightarrow{h}$ (from $t-n$ to $t+n$) and backward $\overleftarrow{h}\left(\mathrm{from}t+n\mathrm{to}t-n\right)$ directions are computed using Equation (12).

$$y_t=f\left(\left[\overrightarrow{ h}, \overleftarrow{ h} \right]\right)$$

(12)

where the final output ($y_t$) of the BiLSTM at any given time obtained from concatenating, summing, averaging, or multiplying the forward ($\overrightarrow{h}$) and backward ($\overleftarrow{h}$) outputs. This combined output typically undergoes a sigmoid activation function.

2.5. Convolutional Neural Networks (CNNs)

Unlike LSTMs, which were initially developed for sequential data such as time series analysis, CNNs were originally designed to leverage spatial correlations in data [56,57,58]. They excel at processing grid-like data structures, such as images and speech data. The core operation in CNNs is convolution Equation (13), which involves sliding one function over another and summing the overlapping areas within a sliding window.

$$x\ast k={{\displaystyle \int }}_{-\infty }^{\infty }{x}_{\tau }k\left(t-\tau \right)d\tau$$

(13)

In practice, a kernel or filter is applied to the receptive field, and the convolution operation calculates the dot product of the kernel and receptive field as the kernel shifts across the input and generates feature map ($x\ast k$). Different layers in a CNN use varying numbers and sizes of kernels to extract features, starting with simpler ones like colors and edges and progressing to more abstract patterns, textures, and shapes. This process is illustrated in Figure 4 and Equations (14) and (15), where a 2D kernel slides through the input, producing a feature map by summing the cross-products of kernel values and receptive field values.

$$\alpha =\left(ae+bf+cg+dh\right)$$

(14)

$$\beta =\left(af+bi+ch+dj\right)$$

(15)

The final part of the network, known as the classification section, utilizes the extracted information for specific tasks like classification and prediction. The network can be designed without a flattened layer, which transforms the output of the convolutional layer into probabilities, by using only a dense layer with similar functionality. The number of dense units in this layer depends on the number of classes or features to be predicted. The output of each convolutional layer is computed by convolving the kernel with the receptive field, adding a bias term, and passing the result through an activation function, commonly the rectified linear unit (ReLU). The ReLU activation function returns the input value if it is greater than zero, and zero otherwise, as shown in Equation (16).

$$y_j\left(x\right)=f\left({\displaystyle \sum }_{i=1}^n(K_{ij}\ast x_i)+b_j\right)$$

(16)

where $y_j\left(x\right)$ is the output of the convolution operation at index j for the input i ($x_i$), $K_{ij}$ is the kernel (weight) connecting input i to output j, and $b_j$ is the bias for output j, and $f$ is the activation function.

2.6. Convolutional LSTM (ConvLSTM)

The convolutional LSTM (ConvLSTM), shares similarities with the LSTM and the CNN, which is a hybrid of them. However, instead of input matrix multiplications, it employs convolutional operations, as demonstrated in Figure 5.

2.7. Transformer Networks

The transformer, introduced by Vaswani, et al. [59] in their paper called “Attention is All You Need”, revolutionized sequence modeling using an attention mechanism instead of the bidirectional LSTM enabling parallel processing of inputs, and handling longer dependencies in sequences. Unlike RNNs, which naturally encode the position of inputs in the sequence, transformers require positional encoding to identify the positions of the inputs in the sequence. The transformer model, initially designed for Natural Language Processing (NLP) tasks (see Figure 6), has been further developed for various applications, including image [60], and video [61] classifications.

The attention mechanism was introduced by [62] and initially utilized bidirectional LSTM to establish similar weights. Eventually, various methods were developed to compute dynamic similarity weights between input elements (keys) with respect to specific outputs (queries). These methods include additive, multiplicative (dot product), scaled multiplicative, general, biased general, activated general, and similarity [63]. The scaled dot product approach scales the dot product of the query and the transposed key values ($Q_i{K}^T{}_i)$ based on the input dimensions ($d_k{}_i$ in Equation (17)). These similarity weights are then multiplied by the input sequence (values) to emphasize specific elements within the sequence. To introduce nonlinearity, fully connected units (FC) are used in the first and last linear layers, as depicted in Figure 7. A multi-head scaled dot product attention mechanism with a mask layer for selectively masking (filter future values commonly) certain parts of the input is shown in Figure 7.

Given a set of queries (Q), keys (K), and values (V), and the number of attention heads (h), the scaled dot product attention scores (Attention (Q, K, V)) for each head (i) are calculated as:

$$Attention\left(Q, K, V\right)=SoftMax\left(\frac{Q_i{K}^T{}_i}{\sqrt{d_k{}_i}}\right)V_i$$

(17)

The output for each head:

$$hea{d}_i=Attention\left(Q W_i^Q, K W_i^K, V W_i^V\right)$$

(18)

Concatenate the outputs of all heads:

$$MultiHead\left(Q, K, V\right)=Concat \left(hea{d}_1,\dots ,hea{d}_i\right)W^O$$

(19)

where $SoftMax$ is the SoftMax function, which normalizes the attention scores, $\sqrt{d_k{}_i}$ is the square root of the dimension of the key vectors, used for scaling to prevent gradients from becoming too small, and $W_i^Q,W_i^K,W_i^V,and{W}^O$ are the learnable weight matrix for queries (Q), keys (K), and values (V), and the output projection.

The collection of attention units (represented by red blocks in Figure 7) integrates information from different perspectives of queries, keys, and values, like the use of multiple kernels in CNNs. This mechanism allows the model to focus on different parts of the input for different tasks or aspects, making it more flexible and capable of capturing various patterns in the data.

2.8. The ANN Models Used in this Study

In this study, the following models are used to see their performances in the prediction task in CIs as a case study in electric power utilities, see

Table 1. The ANNs models used in this study.

Model	#Parameters
FCN Univariable and Multivariable	407,001 and 411,001
Convolutional 1D Univariable and Multivariable	420,519 and 422,565
Convolutional 2D Univariable and Multivariable	424,009 and 444,818
ConvLSTM 2D Univariable and Multivariable	417,117 and 443,037
LSTM Univariable and Multivariable	424,029 and 429,169
GRU Univariable and Multivariable	416,237 and 420,077
BiLSTM Univariable and Multivariable	414,385 and 419,505
Transformer Univariable and Multivariable	423,873 and 432,265

.

The models are structured into two parts: the features extraction, which consists of three layers, and the prediction part, which is similar for all models and consists of a flattened layer and then a dense layer, followed by dropout and finally another dense layer. As an example, the architects of the one-dimensional convolutional model (Conv1D) are shown in

Table 2. The architects of convolutional 1D.

Layer	Output Shape	#Parameters	Part
Conv1D	(None, 24, 256)	12,542	Features extraction
Conv1D	(None, 24, 128)	262,272
Conv1D	(None, 24, 24)	24,600
Flatten	(None, 576)	0	Prediction
Dense	(None, 128)	73,856
Dropout	(None, 128)	0
Dense	(None, 1)	129
Total Trainable Parameters: 363,161

(the architects of other models can be seen in Appendix A).

Moreover, to see the effects of including other features such as temperature in power consumption, the same models are trained to evaluate the performance of multivariable models as well.

3. Case Study—The ANN Models for Load Forecasting

Electricity infrastructure is a crucial component of modern society and ranks among the most vital of the Critical Infrastructures (CIs). In Norway, electric grids play a significant role in supplying electricity to millions of households and businesses through an intricate and susceptible network comprising power plants, transmission lines, and distribution networks. Electricity is the primary energy source in Norway, with a consumption of 104,438 Terawatt-hours (TWh) in 2021, heavily influenced by prevailing weather conditions. In this study, the electricity consumption in Norway serves as input data for predicting Artificial Neural Network (ANN) models. Using ANN models requires some specific procedures, regardless of the problem and the task involved, and can be divided into six steps, as shown in Figure 8. It starts by collecting the data around the problem at state in the required format to build, train, and use the ANN models for any given task.

Shallow ANN models explained in Section 2 with almost the same number of layers and the same number of trainable parameters are constructed, trained, and tested following the steps in Figure 8 and will be discussed in detail in the following sections.

3.1. Data Collection

The data includes Norway’s hourly electricity consumption in megawatts (MW) and average air temperatures in Celsius (°C) from Alna and Bygdøy weather stations in Oslo as a proxy of Norway’s average air temperature from 1 January 2009 to 21 October 2022, as shown in Figure 9. These data are collected from the central collection and publication of electricity generation and the Norwegian meteorological institute [64,65]. Moreover, as the hourly eclectic power consumptions and the temperatures do not change dramatically from previous hours, the Nan values and empty records are filled with previous values.

3.2. Data Preprocessing

It is very important to clean, preprocess, and prepare appropriately for the required formatted data for ANNs models. First, the data can consist of outliers, noises, and Nan values that have undesirable effects on the study. Outliers can be due to the variability in the data, data extraction, data exchange errors, recording, and human errors among many other reasons. Therefore, the recordings that do not fall within three standard divisions (SD) are considered outliers in this study based on the method suggested in reference [66]. Boxplot of monthly power load before the removal of outliers (a) and after the removal of outliers (b) can be seen from the boxplot in Figure 10. In total, there are only 122 records removed from 121,004; hourly electric power consumption records are removed as outliers from the dataset.

Electric power load data has daily, seasonality, and yearly periodicities. To capture these periodicities, the sine and cosine of the days and years are used to capture periodicity in the days and seasonality in the years. These features with the temperatures are used for multivariable ANN modeling in prediction tasks. There is a correlation between these features; for example, electric consumption is affected by temperatures. As can be seen from Figure 11, there is a strong negative correlation between electric consumption, −0.789, and as the temperature goes up, the energy consumption decreases.

Normalization of data has many benefits, such as reducing prediction errors, reducing computational costs, and reducing the risk of overfitting the neural networks during the training [67,68]. In this study, Z-score normalization is used (Equation (20)) to normalize the data, as can be seen in Figure 12.

$$\mathsf{{\rm Z}}={\displaystyle \sum }_{i=1}^n\frac{x_i-\mu }{\delta }$$

(20)

where Z is the standardized value (Z-score) of the ith data point $x_i$, and $\mu$ and $\delta$ are the mean and the standard deviation of the dataset, respectively.

Finally, the dataset is split into training validation and test, 70%, 15%, and 15% respectively. The training data set is used for training the ANN models to learn hidden relationships, features, and patterns in the dataset. The validation set is used for validating the ANNs models’ performance during the training, and the test set is an unseen data set that provides an unbiased metric to evaluate the performance of the models after the training.

The previous 24 h are used as the sequences for training the ANN models. In the multivariable models, all the features are fed into the model, while in the univariable model, the variable of interest, which here is electric consumption, is fed into the model. Figure 13 and Figure 14 show some examples of the univariable and multivariable input sequences for training ANN models.

Moreover, to evaluate the effect of the number of input data on the performance of different ANN models, the data are divided into three parts (100%, 50% and 25% of the dataset,

Table 3. The data in three datasets.

Date and Time	Hourly Records before Removing Outliers	Hourly Records after Removing Outliers
1 January 2009 00:00 to 21 October 2022 22:00	121,004	120,882
11 June 2015 07:00 to 21 October 2022 22:00	61,000	61,000
26 February 2019 15:00 to 21 October 2022 22:00	32,000	31,898

).

3.3. Evaluation Metrics

To evaluate the performance of ANN models the mean absolute error (MAE), mean square error (MSE), and root mean square error (RMSE) are used (Equations (21)–(23)) in this study.

$$MSE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(\left|x_i-{\widehat{x}}_i\right|\right)}^2$$

(21)

$$MAE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left(\left|x_i-{\widehat{x}}_i\right|\right)$$

(22)

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(\left|x_i-{\widehat{x}}_i\right|\right)}^2}$$

(23)

where $x_i$ is the ith value, ${\widehat{x}}_i$ is the corresponding predicted value, and n is the number of data points.

As ANN models become more complex, the explanation of how the models make such predictions or decision become more ambitious. Explainable artificial intelligence has gained a lot of attention recently for explaining how ANN models perform in any given task. The Shapley value is one of the common metrics to evaluate the average marginal contribution of any feature of output value produced by the ANN model.

$${ø}_i\left(f,x\right)={\displaystyle \sum }_{z^{\prime }\subseteq x^{\prime }}\frac{\left|z^{\prime }\right|!\left(M-\left|z^{\prime }\right|-1\right)!}{M!}[f_x\left(z^{\prime }\right)-f_x\left(z^{\prime }\right)\backslash i]$$

(24)

where ${ø}_i$ is the Shapley value for feature $i$, $f$ is the model, $x$ is the input data point, $z^{\prime }$ is the subset of data, $M$ is the number of features, and $f_x\left(z^{\prime }\right)$ and $f_x\left(z^{\prime }\right)\backslash i$ are the model output without and with feature $i$. In a nutshell, the Shapley value is calculated by computing a weighted average payoff gain that feature $i$ provides, included in all coalitions that exclude $i$.

3.4. Training ANN Models

The selected ANN models are trained for both using univariable and multivariable inputs. The previous 24 h are used as the input sequences for training, and the Adam optimizer with learning rate 0.001 is used for all the ANN models. All the models have trained on a workstation with CPU: dual intel Xeon gold 6248R (35.75 MB cache, 24 cores, 48 threads, 3.00 GHz to 4.00 GHz Turbo, 205 W) and GPU: NVIDIA RTX™ A5000, 24 GB GDDR6, 4 DP. Figure 15 shows the accuracy of the ANN models in training and validation datasets for 100 training epochs in 25% of the dataset. The accuracy of the ANN models in 100% and 50% of the datasets can be seen in Appendix B.

As can be seen, the LSTM, BiLSTM, ConvLSTM, and GRU models, which were originally developed for time series analysis, are more stable during the training as the error does not change dramatically from the previous step compared to the other models developed for including the time series analyses as well. In most of the models, the error decreases in 100 epochs of training in both validation and training datasets, except for the bidirectional LSTM (BIiLTM) multivariable model. In other words, this might be a sign of overfitting in the BiLTM multivariable model. Thus, the performance of this model is expected to be worse than the other models. Otherwise, this might be relevant to the probabilistic nature of ANN models, complexity and many other hyperparameters to be considered. This argument is true for the ConvLSTM2D univariable model in which the error does not show a decreasing pattern.

3.5. Experiments and Results

The ANN model’s performances based on the number of data they have trained on and the inclusion of features, Univariable and Multivariable, are shown in

Table 4. MAE of ANN models in validation and test dataset of three databases.

	25% of the Dataset		50% of the Dataset		The Whole Dataset
	Test	Validation	Test	Validation	Test	Validation
	MAE	MAE	MAE	MAE	MAE	MAE
LSTM Multivariable	0.00515	0.00490	0.01120	0.00400	0.004521	0.002426
ConvLSTM2D Univariable	0.00541	0.00467	0.01252	0.00317	0.00455	0.002653
Conv1D Univariable	0.00514	0.00470	0.01142	0.00462	0.004626	0.002984
ConvLSTM2D multivariable	0.00617	0.00568	0.00847	0.00413	0.004764	0.002551
LSTM Univariable	0.00482	0.00466	0.00750	0.00335	0.004886	0.003089
Conv2D multivariable	0.00639	0.00621	0.00876	0.00459	0.005036	0.003018
BiLSTM Univariable	0.00549	0.00483	0.00788	0.00329	0.005101	0.002754
Conv2D Univariable	0.00528	0.00450	0.00861	0.00330	0.005212	0.002713
BiLSTM Multivariable	0.00738	0.00735	0.01032	0.00392	0.005625	0.002694
Conv1D Multivariable	0.00614	0.00545	0.00916	0.00381	0.005758	0.002507
Transformer Univariable	0.00702	0.00631	0.00875	0.00355	0.006086	0.003589
FCN Multivariable	0.00722	0.00714	0.01222	0.00498	0.007994	0.004703
GRU Univariable	0.00471	0.00634	0.00912	0.00380	0.008551	0.005877
FCN Univariable	0.00713	0.00790	0.01098	0.00790	0.013184	0.011243
Transformer Multivariable	0.01814	0.01223	0.02112	0.01599	0.015608	0.010485
GRU Multivariable	0.00685	0.00663	0.01032	0.00280	0.033668	0.029053

.

For example, when the models are trained on 30,000 data, the GRU univariable model has the Mean Absolute Error (MAE) of 0.00471, but as the training data increases to 120,000, the GRU model performance decreases significantly (with MAE 0.008551). Another interesting result is that when using 50% of the data (60,000), models with the same structures have the worst performance, as opposed to the assumption that as the number of training data increases, the performance of the ANN model increases as well. But overall, using the whole data set has the lowest error, and it confirms this assumption. AS, the LSTM model that has trained on the whole dataset with all features, multivariable, has the best performance. This confirms the fact that including more data and features increases the performance of LSTM models for the power prediction task. Also, it might be true for some models such as convolutional 2D and FCNmodels. But, this is not true for all models, as in some cases like that of BiLSTM, GRU, and Transformer, the univariable model performs better regardless of the number of data that the model is trained on. In some cases, convolutional 1D and ConvLSTM2D univariable models have a lower error in the smallest and biggest dataset, but in the middle, with 50% of the data, the multivariable model performs better. As can be seen from the behavior of the ANN models, there is no evidence that including more features such as temperature and so on will reduce the error in the prediction, as in many cases this is not true. As can be seen from Figure 16, there is not a significant change in the range of errors when models are trained on the smallest dataset. But, the range of errors increases as the amount of data increases, with the most in 50% of the dataset.

The multivariable Transformer model is the only model that has an error of 0.01814, which is significantly more than the previous highest error, the BiLSTM multivariable model with an MAE of 0.00738, in 25% of the test data. By doubling the training data, the overall performance of models decreases, and there is more fluctuation in the range of error. Moreover, there are more models with higher errors (BiLSTM Multivariable, GRU Multivariable, FCN Univariable, LSTM Multivariable, Conv1D Univariable, FCN Multivariable, ConvLSTM2D Univariable, Transformer Multivariable), which have significantly more errors than that with the previous highest error, which is the Conv1D Multivariable model with an MAE of 0.00916. The models trained on the whole dataset have similar performance to when they are trained on 25% of the whole dataset with regard to the magnitude of errors with slightly lower values. For example, the MAE of the best model trained on the whole dataset, the LSTM multivariable, is 0.00019 less than the best model trained on 25% of the whole dataset, which is the GRU univariable. Moreover, to visualize the contribution of features in the prediction of Shapely values for the LSTM multivariable, the best-performing model, is shown in Figure 17. Interestingly, the periodicity in the day (cosine of the day) is more important than the temperature in the LSTM multivariable model’s performance.

On the other hand, there is always a tradeoff between the computational costs and the level of accuracy in choosing the best model for a specific task. Thus, considering the training time as an indicator of computational costs is useful in such scenarios. As shown in

Table 5. Training time of ANN models for three databases.

Training Time [Seconds]
	25% of the Dataset	50% of the Dataset	The Whole Dataset
Conv2D Multivariable	543.383	1176.480	1988.9845
Conv2D Univariable	549.978	1190.235	2020.693
Conv1D Univariable	576.131	1220.502	2120.209
Conv1D Multivariable	583.428	1269.449	2182.462
FCN Univariable	663.283	1389.063	2356.592
FCN Multivariable	662.267	1378.942	2371.775
GRU Univariable	1570.411	3361.053	5839.046
GRU Multivariable	1595.815	3390.978	5885.515
LSTM Univariable	1641.205	3524.260	5985.779
LSTM Multivariable	1650.034	3552.155	5989.320
BiLSTM Univariable	2916.908	6158.082	10,529.661
BiLSTM Multivariable	2968.764	6262.675	10,577.390
ConvLSTM2D Multivariable	3254.541	6852.926	12,261.736
ConvLSTM2D Univariable	3284.826	6824.547	12,286.509
Transformer Multivariable	4417.155	8887.481	15,052.959
Transformer Univariable	4962.736	10,004.780	17,675.277

, the convolutional models are the fastest models, and Transformer is the slowest model. For example, convolutional 2D multivariable is almost 8, 9 times faster than Transformer univariable. Considering the best-performing model, the LSTM multivariable (5989 s and MAE 0.004521), in the whole dataset with convolutional 2D multivariable (1989 s and MAE 0.005036) when sacrificing 0.000515 of accuracy, a 3-fold gain in training time will be achieved. Moreover, it is obvious that as the number of training data increases, the training time rises as well. When the number of training data doubled from 30,000 to 60,000, the training time almost doubled as well. By doubling the number of training data from 60,000 to 120,000, in this case, as the number of available data doubled, the training time will be 1.69 times higher (from 1176.48 to 1988.98 s).

Once the ANN models are trained, they can be used for the prediction of any given time in the future. Figure 18 and Figure 19 show the prediction of ANN models for the next 24 days of power consumption and the ANN model prediction with actual data in three different datasets.

4. Discussion

In this study, eight of the state-of-the-art ANN models for power load prediction are evaluated based on available dataset size (entire dataset, 50% and 25% of dataset) and the inclusion of features (univariable vs. multivariable). Due to the scarcity of comparable studies, the result of the present study is compared with aggregated comparable studies. The results of some of these studies where scales of data are the same were normalized for load prediction with relevant sequence time windows [48,49]. In addition, the number of hidden layers and other hyperparameters such as Adam optimizations are similar; thus, the results can be somehow compared, as shown in

Table 6. Comparison of the present study with some similar studies based on MAE.

	Reference [31]		Reference [48]		Reference [49]		Reference [51]		This Study
Features	4		1		32		6			1	6	1	6	1	6
Sequence window	120 [h]		20 [h]		1 [h]		15 [min]		24 [h]
Training data	2208		59,829		77,831		367,920			22,328	22,328	42,700	42,700	84,617	84,617
	Layers	MAE	Layers	MAE	Layers	MAE	Layers	MAE	Layers	MAE
Conv1D			5	0.008269					6	0.00514	0.00614	0.01142	0.00916	0.004626	0.005758
Conv2D			4	0.0088					6	0.00528	0.00639	0.00861	0.00876	0.005212	0.005036
ConvLSTM	*	5.061	6	0.006624	11	0.0057			6	0.00541	0.00617	0.01252	0.00847	0.00455	0.004764
LSTM	*	6.009	4	0.007345			4	0.55	4	0.00482	0.00515	0.0075	0.0112	0.004886	0.004521
BiLSTM					5	0.0066	4	0.8296	4	0.00549	0.00738	0.00788	0.01032	0.005101	0.005625
GRU							4	1.3269	5	0.00471	0.00685	0.00912	0.01032	0.008551	0.033668
* Is not given in the reference

and

Table 7. Comparison of the present study with similar study based on RSME.

Reference [33]				This Study
Features		4	10		6
Sequence window		168 [h]	24 [h]
Data size		1456	8723		22,328	42,700	84,617
	layers	RSME		layers	RSME
LSTM	2	0.197	0.097	5	0.04939	0.056421	0.044879
ConvLSTM	7	0.207	0.053	7	0.055561	0.057934	0.046501

. As can be seen from the result of reference [51] where the models are trained on 367,920 datapoints (biggest data size), GRU performs worse, which explains the increase in their error in the current study, with an MAE of 0.008551 for univariable and 0.033668 for multivariable in the entire dataset compared to 0.00471 and 0.00685 in 25% of the dataset. Thus, it can be concluded that for the time series, the training data are approximately in the range of 2000 and 22,000, The GRU is the best choice in shallow networks (4–11 layers) in terms of accuracy. When the raining data are below a threshold, 2208 and 1456, the performance of these shallow ANN models decreases drastically as the result of this study, and references [31,33] confirm this. It cannot be said exactly where this threshold for each model stands, and more investigation is needed to find such exact points for each model. Where the training data are in the range of approximately 22,000 and 42,000, the LSTM and BiLSTM are good choices in terms of accuracy as they have the best performances in this range (50% of the dataset and 42,700 training data).

Including more training data the performance of LSTM, Conv1D, and Conv2D improved significantly as they have a lower error with training on 84,617 data than the same models in reference [48], which are trained on 59,829 data. Therefore, it can be concluded that when the training data are between 840,00 and 367,920, LSTM, ConvLSTM, Conv1D, and Conv2D are good choices in terms of accuracy, as confirmed by the results of reference [51].

Surprisingly, when increasing the data from 25% to 50% of the data (42,700), the ANN models perform worse, contrary to the assumption that more training data leads to better performance (see Figure 20). The GRU is excluded from Figure 20 due to its high error in the entire dataset, moving the average error with more than 25% of the dataset.

By repeating the experiment, 50% of the dataset always shows the highest errors. This suggests that there is an optimal dataset size for each model regarding their depth (layers), and increasing or decreasing the data beyond that point might lead to overfitting. This finding emphasizes the need for careful data curation and model selection based on the ANN model, depth, dataset size, and features. These findings are aligned with [69], which emphasizes the threshold in which CNN models perform the best regarding training data size.

With the lowest dataset, all the univariable models perform better than the multivariable. This implies that when the range of data training is lower than 22,328, the feature inclusion does not improve the performance of ANN models. Moreover, including additional features is beneficial for Conv2D and FCN models when increasing the dataset from 42,700 to 84,617. However, this improvement is not observed when increasing the dataset from 22,000 to 42,700. When increasing the dataset from 22,328 to 42,700 only ConvLSTM and Conv1D performed better when including features, but this advantage diminishes when further increasing the dataset to 84,617. Considering these findings, it can be concluded that there is no consistent pattern or relationship observed among the ANN models when it comes to the inclusion of features. These findings are aligned with the results of reference [33,49], as they used 32 and 10 features in their study. Apart from the training data size, the number of layers contribute to the performance of ANN models. For example, in reference [33], just one LTSM layer with one dense layer is used, and they get a root mean square error (RMSE) of 0.097, which can be improved significantly by adding more layers. In addition, they achieved an RSME of 0.053 for ConvLSTM, which is more than the result of this study (0.046501). Apart from the data training size, the present study confirms that ConvLSTM performs better without including the features; thus, another reason might be the lower number of features in the present study—six compared to ten features in [33]. Including more features does not improve the performance of all other models, except LSTM, Conv2D, and FCN, which is confirmed by reference [70] where they concluded that adding more features does not always lead to better performance.

Ailing Zeng et al. [71] in a paper called “Are Transformers Effective for Time Series Forecasting?” have discussed the inefficiency of Transformers in time series forecasting. This inefficiency is due to temporal information loss, which is the result of the permutation invariant self-attention mechanism. In other words, in time series forecasting, the sequence order often plays an important role in which attention mechanism of Transformers is not considered. The results of this study confirm this argument, as the Transformer has the worst performance in all datasets.

The present study takes the training time into account as an important factor in selecting an ANN model in time series prediction tasks such as power load forecasting. The CNN models are among the fastest models, where Conv2D multivariable is the fastest model, followed by Conv2D univariable, Conv1D univariable, and Conv1D multivariable. The choice of the best model for any given task involves a tradeoff between computational costs and accuracy, making the Conv1D univariable a preferred option in applications where computational expenses are significant and small errors can be disregarded.

5. Conclusions

In this study, the effectiveness of state-of-the-art Artificial Neural Networks (ANNs) in time series analysis, particularly focusing on electricity consumption prediction—a critical task in power distribution utilities—is explored. Moreover, to better understand the performance of the ANN models regarding the available training data and the effect of features, the dataset is split into three parts. The models are trained with only electricity consumption one feature, called univariable, and multivariable models include six features, including temperature, sine and cosine of days and years to reflect periodicity in days and years. In comparing our research with prior studies, this study contributes insights into a better understanding of the state-of-the-art ANN model’s performance in time series analysis, specifically in electricity consumption prediction—a vital task for power distribution utilities. The present study has practical implications for practitioners and researchers in the efficient operation, management, and maintenance of Critical Infrastructures (CIs) through informed decision-making and strategy development, leveraging state-of-the-art ANN models. For example, in a scenario where available data fall between 2000 and 22,000 and there are not enough features available, a GRU model can be selected with high confidence with good accuracy. When the available data fall between 22,000 and 42,000 LSTM, BiLSTM can be selected with a high confidence of acceptable accuracy. Moreover, a CCN-based model such as Conv1D can be selected, where the computational expenses are significant.

The key findings of this study are as follows:

• The LSTM model, increasing data and features, outperforms other models, highlighting that when more data are available, feature inclusion enhances LSTM performance in power prediction.
• There is an optimal training dataset size for each model regarding their depth (layers), and increasing or decreasing the data beyond that point leads to overfitting.
• For the time series prediction task, when the training data are below 2000 in time series prediction, the performance of ANN models decreases dramatically.
• When the training data are in the range of 2000–22,000, the GRU is the best choice regarding accuracy.
• Where the training data fall in the range of 22,000–42,000, the LSTM and BiLSTM are good choices in terms of accuracy.
• Where the training data are between 42,000 and 360,000, LSTM, and ConvLSTM are good choices in terms of accuracy.
• Even though Conv1D and Conv2D did not appear in the top two best-performing models (Conv1D univariable third in 25% and entire data), they are good choices in terms of computational efficiency.
• When the range of data training is lower than 22,000, the feature inclusion does not improve the performance of any ANN model.
• When the number of training data are more than 22,000, the ANN models do not show any consistent pattern or relationship regarding the inclusion of features. But somehow, LSTM, Conv1D, Conv 2D, ConvLSTM, and FCN benefit from including features. Univariable models like BiLSTM, GRU, and Transformer consistently outperform multivariable models, irrespective of training data size.
• This study highlights the computational efficiency of convolutional neural networks in processing one-dimensional inputs like time series sequences. The convolutional 1D univariable model emerges as a standout choice for scenarios where training time is critical, sacrificing only 0.000105 in accuracy, and a threefold improvement in training time is gained.
• The shallow ANN models in this study exhibit poor performance with 50% of the data but excel with the smallest and largest datasets. This implies that each ANN model may have an ideal training dataset size concerning their layers and depths, and going beyond or below this point could result in overfitting. This underlines the importance of meticulous model selection, considering factors like available data, type of ANN model, depth, and available features.
• In line with Ailing Zeng et al.’s findings, Transformers exhibit inefficiency in time series forecasting due to their permutation-invariant self-attention mechanism, neglecting the crucial role of sequence order, as evidenced by their poor performance across all three datasets in this study.

Limitations and further works

• The ANN models used in this study are shallow networks within 5–6 layers of depth. Similar ANN models with deeper networks can be constructed to evaluate their performance regarding the training data size and feature inclusion.
• The range of data training size is roughly limited to 21,000 to 82,000. Moreover, the available dataset is divided into three parts only. It can be split more, and the ANN models can be trained on a wider training data range to find the exact range in which each model performs the best.
• The future inclusion for multivariable models is limited to temperature and periodicity in days a year (sine and cosine of days and years) with a total of six features. Datasets with more features can contribute to better the evaluation of univariable and multivariable models.
• More hybrid ANN models can be included to find the best models in the range of available data for each specific model.
• Further studies are required regarding hyperparameter tuning like neural architecture search methods, which are vital for fine-tuning hyperparameters and finding the best model in each range of available data.
• As a future direction for studying prediction tasks and incorporating the geographical coordinates of failures with historical failure data in CIs, ANN models can predict the potential future failure locations, contributing to proactive maintenance and the improved reliability of CIs.