Personalized E-Learning Recommender System Based on Autoencoders
Abstract
:1. Introduction
2. Motivation and Contributions
- A recommendation system based on collaborative filtering was developed to suggest various e-learning courses to learners.
- The system uses a dataset constructed by Kulkarni et al. [23] to analyze the performance of a recommendation model based on an autoencoder to recommend appropriate courses to learners.
- The proposed model was compared to four models: KNN, SVD, SVD++ and NMF.
- MAE and RMSE are the two metrics used to evaluate the performance of these models.
3. Related Work
4. Methodology and Preliminaries
- Learning each student’s behavior;
- Predicting the probability of consuming the courses provided. Learning is built based on learner–course interactions, which determine how each learner interacts with the courses presented.
4.1. Problem Definition
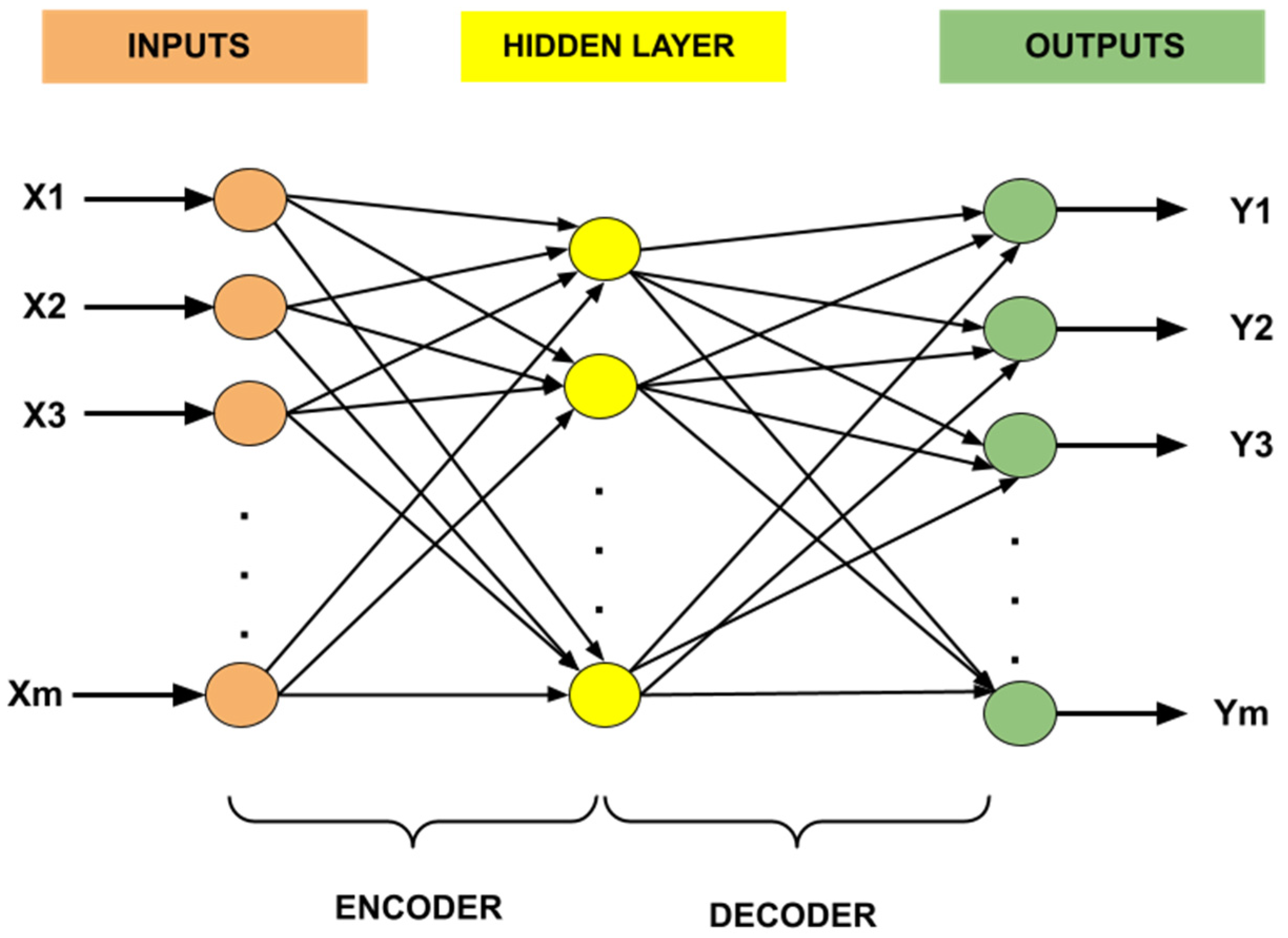
4.2. Autoencoder
- Configurable Parameters
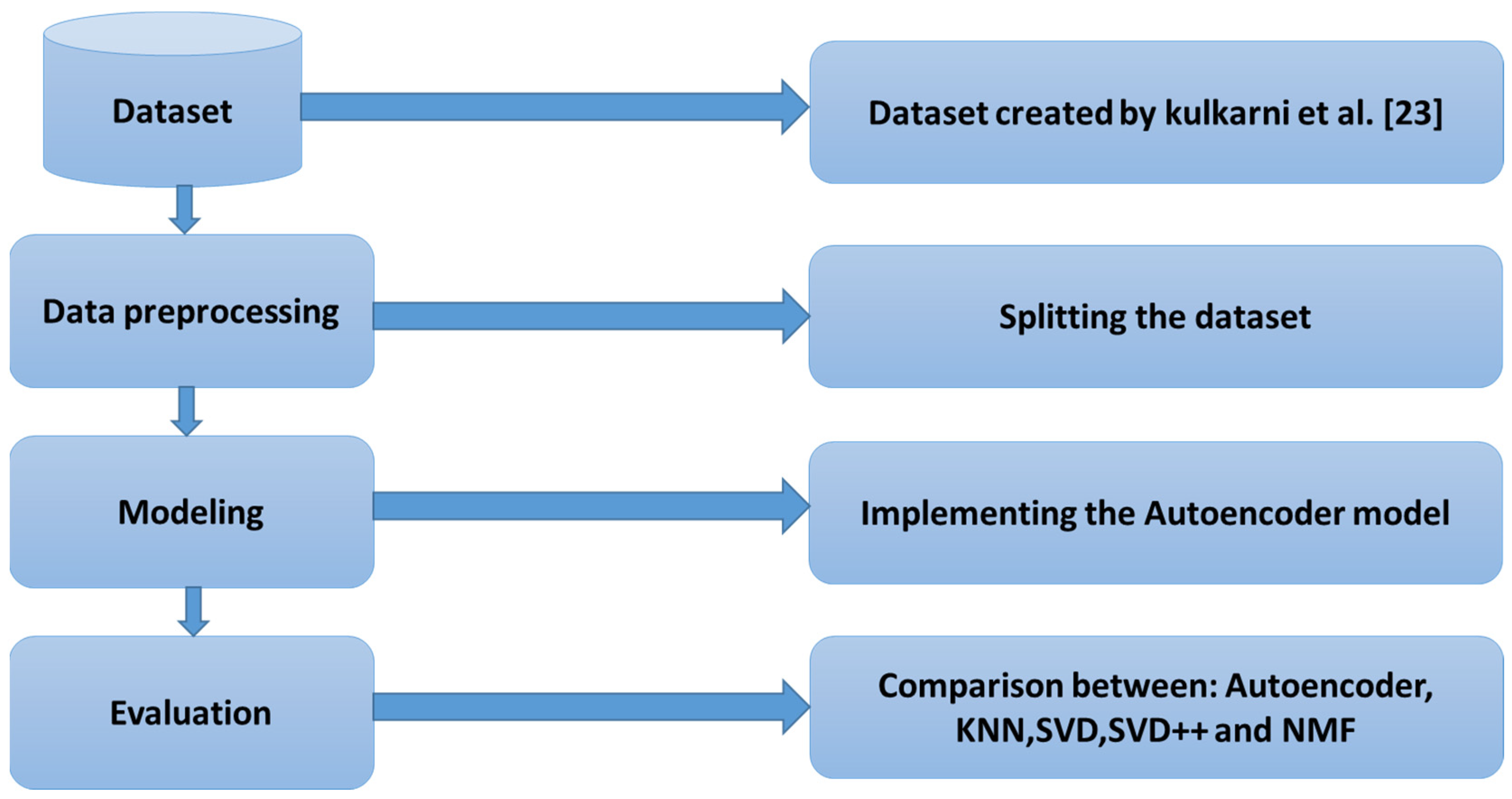
4.3. Procedure for Study
5. Experiments
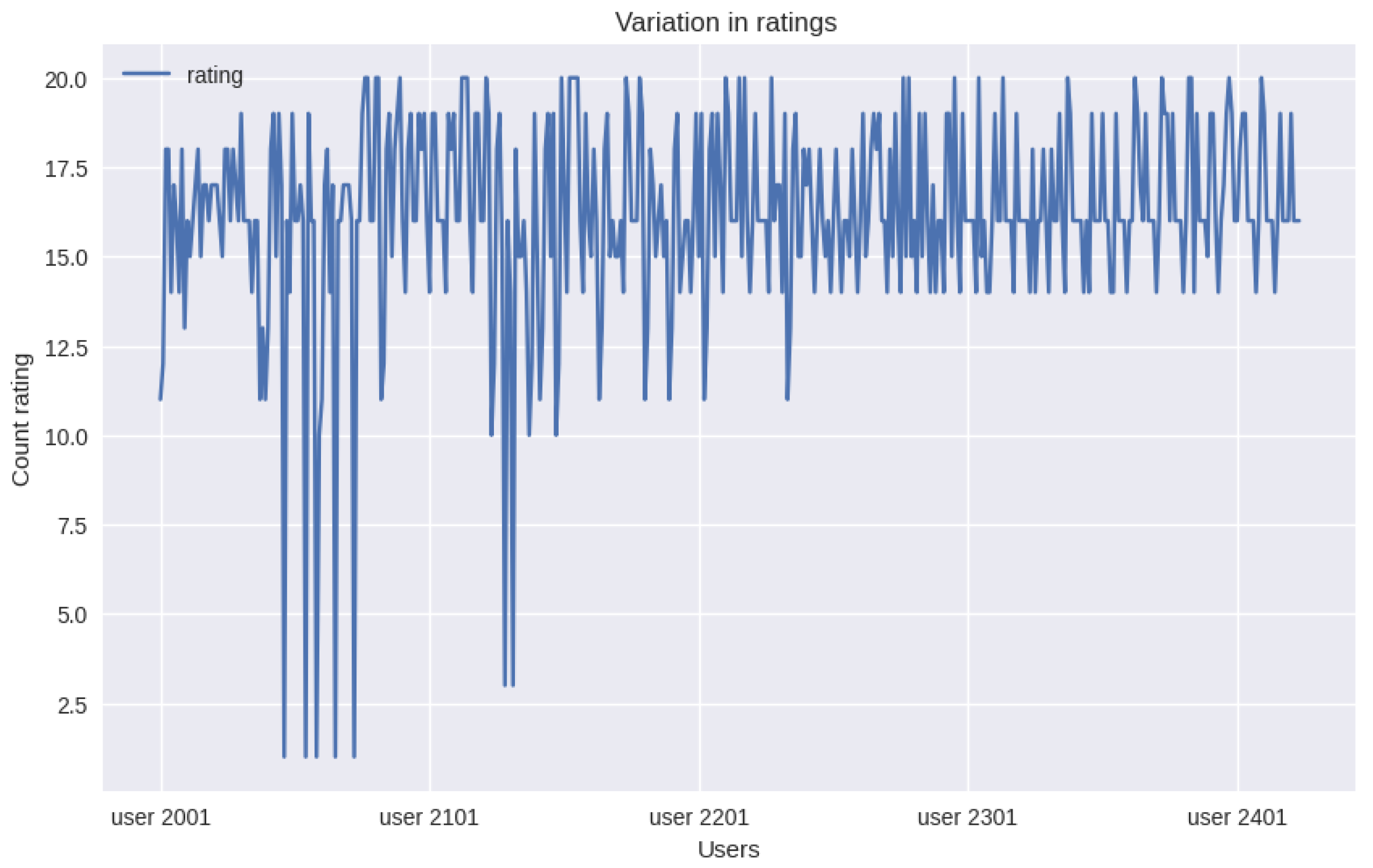
5.1. The Dataset
- User rating.csv contains user ratings and includes user ID, course ID and rating, as shown in Table 8.
- UserId identifies the user. Each user rated courses.
- CourseId identifies the course.
- Rating is the rating ranging from 1 to 5 on a scale of 5 stars.
- UserId identifies the user.
- Degree 1 is the user’s diploma.
- Degree 1 Specializations is the specialty of the user’s degree.
- Known languages are languages mastered by the user.
- Key Skills are the skills of the user.
- Career Objective is the career objective of the user.
- UserId, which identifies the user.
- Degree 1, which is the user’s diploma.
- Degree 1 Specializations, which is the specialty of the user’s degree.
- Campus, which is the name of the campus where the user is registered.
- Key Skills, which are the skills of the user.
5.2. Compared Methods
- KNN
- is the list of items that can be recommended.
- refers to the number of items to recommend.
- represents the “prediction of the rating that the recommender system provides to user for item ”.
- represents the “K-nearest neighbors” of the user named u who evaluated the item named .
- denotes the “actual rating given by the neighbor” user , which concerns item .
- is the average rating relative to user , which is calculated according to the rating history.
- represents the average rating relative to user , which is calculated according to the rating history.
- is the calculation of the similarity between users and based on distance metrics, such as cosine and Pearson’s correlation coefficient.
- SVD
- SVD++
- is the number of items.
- is the number of users.
- denotes the dimension obtained after the reduction in the matrix dimension.
- and are the deviations from the average values for user and item , respectively.
- represents the average value of all data.
- denotes the “number of items” that are assessed by user .
- denotes the “number of users” who have rated a specific item.
- represents the “number of items” that have been evaluated by multiple users;
- designates the left orthogonal of implicit matrix.
- are additional parameters added to values and for regularization [48].
- NMF
5.3. Evaluation Metrics
- represents the rating predicted for the user, and denotes the original rating of the user;
- indicates the total number of predicted ratings. Lower values of RMSE and MAE show better prediction accuracy.
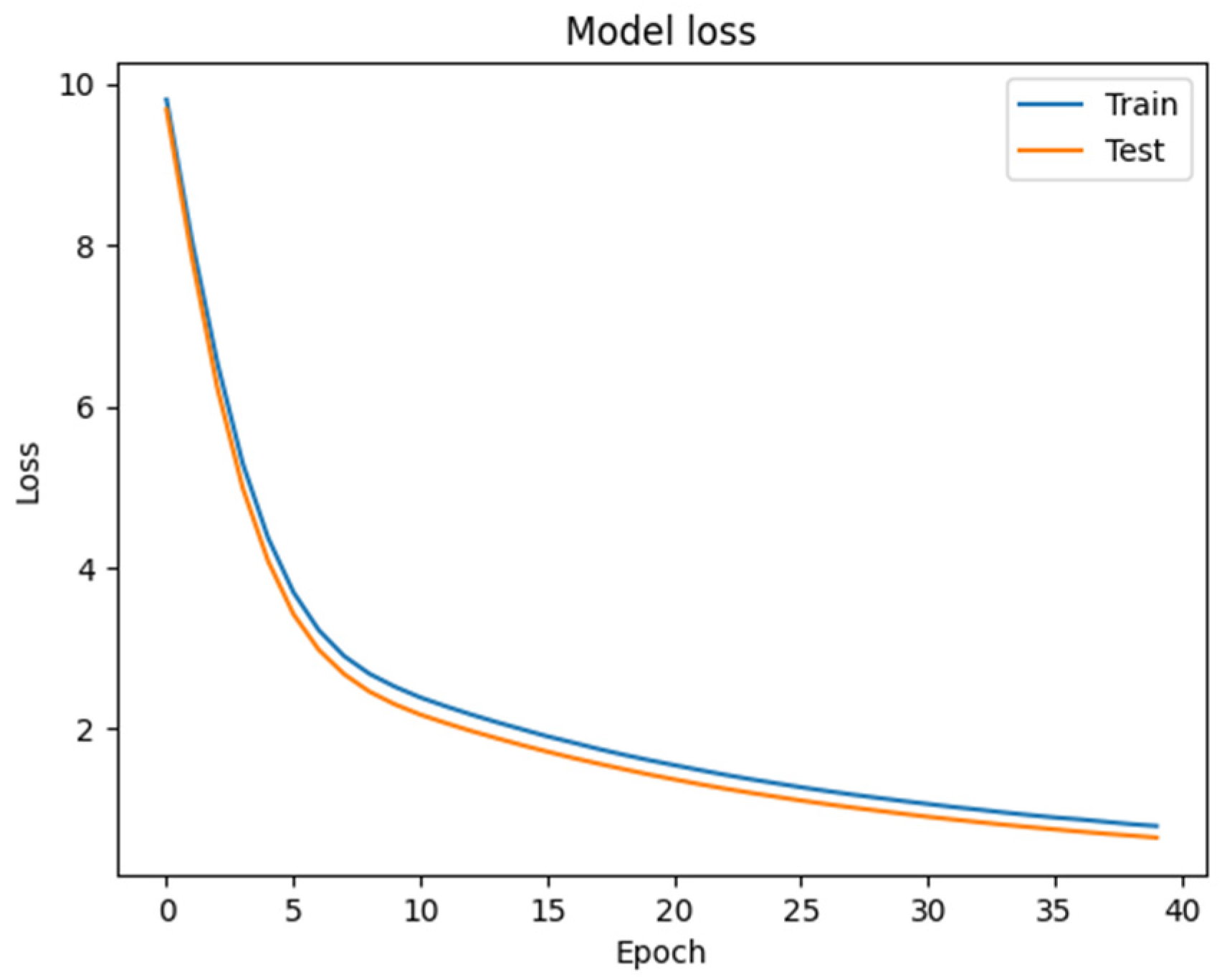
5.4. Implementation Details
6. Results
7. Discussion
- The autoencoder learns latent representations of user–element interactions, enabling them to capture more complex patterns.
- The autoencoder can handle both dense and sparse data.
- The autoencoder can be more scalable.
- The autoencoder can handle different types of data.
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, X.; Li, X.; Lu, M. A MultiView courses recommendation system based on deep learning. In Proceedings of the 2020 International Conference on Big Data and Informatization Education (ICBDIE), Zhangjiajie, China, 23–25 April 2020; pp. 502–506. [Google Scholar]
- Vesin, B.; Mangaroska, K.; Giannakos, M. Learning in smart environments: User-centered design and analytics of an adaptive learning system. Smart Learn. Environ. 2018, 5, 24. [Google Scholar] [CrossRef]
- Normadhi, N.B.A.; Shuib, L.; Nasir, H.N.M.; Bimba, A.; Idris, N.; Balakrishnan, V. Identification of personal traits in adaptive learning environment: Systematic literature review. Comput. Educ. 2019, 130, 168–190. [Google Scholar] [CrossRef]
- Troussas, C.; Sgouropoulou, C. Innovative Trends in Personalized Software Engineering and Information Systems: The Case of Intelligent and Adaptive e-Learning Systems; IOS Press: Amsterdam, The Netherland, 2020; Volume 324. [Google Scholar]
- Sridevi, M.; Rao, R.R.; Rao, M.V. A survey on recommender system. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 265. [Google Scholar]
- Kulkarni, P.V.; Rai, S.; Kale, R. Recommender System in eLearning: A Survey. In Proceeding of the International Conference on Computational Science and Applications, Online, 1–4 July 2020; Springer: Singapore, 2020; pp. 119–126. [Google Scholar]
- Lu, J.; Wu, D.; Mao, M.; Wang, W.; Zhang, G. Recommender system application developments: A survey. Decis. Support Syst. 2015, 74, 12–32. [Google Scholar] [CrossRef]
- Guo, Q.; Zhuang, F.; Qin, C.; Zhu, H.; Xie, X.; Xiong, H.; He, Q. A Survey on Knowledge Graph-Based Recommender Systems. IEEE Trans. Knowl. Data Eng. 2020, 34, 3549–3568. [Google Scholar] [CrossRef]
- Afsar, M.M.; Crump, T.; Far, B. Reinforcement Learning based Recommender Systems: A Survey. ACM Comput. Surv. 2022, 55, 1–38. [Google Scholar] [CrossRef]
- Alamdari, P.M.; Navimipour, N.J.; Hosseinzadeh, M.; Safaei, A.A.; Darwesh, A. A Systematic Study on the Recommender Systems in the E-Commerce. IEEE Access 2020, 8, 115694–115716. [Google Scholar] [CrossRef]
- Singhal, A.; Sinha, P.; Pant, R. Use of Deep Learning in Modern Recommendation System: A Summary of Recent Works. Int. J. Comput. Appl. 2017, 180, 17–22. [Google Scholar] [CrossRef]
- Kumar, P.; Thakur, R.S. Recommendation system techniques and related issues: A survey. Int. J. Inf. Technol. 2018, 10, 495–501. [Google Scholar] [CrossRef]
- Pazzani, M.J.; Billsus, D. Content-Based Recommendation Systems. In The Adaptive Web: Methods and Strategies of Web Personalization; Springer: Berlin/Heidelberg, Germany, 2007; pp. 325–341. [Google Scholar] [CrossRef]
- Mu, R.; Zeng, X.; Han, L. A Survey of Recommender Systems Based on Deep Learning. IEEE Access 2018, 6, 69009–69022. [Google Scholar] [CrossRef]
- Burke, R. Hybrid Web Recommender Systems. In The Adaptive Web; Brusilovsky, P., Kobsa, A., Nejdl, W., Eds.; LNCS 4321; Springer: Berlin/Heidelberg, Germany, 2007; pp. 377–408. [Google Scholar] [CrossRef]
- Chen, R.; Hua, Q.; Chang, Y.-S.; Wang, B.; Zhang, L.; Kong, X. A Survey of Collaborative Filtering-Based Recommender Systems: From Traditional Methods to Hybrid Methods Based on Social Networks. IEEE Access 2018, 6, 64301–64320. [Google Scholar] [CrossRef]
- Cui, Z.; Xu, X.; Xue, F.; Cai, X.; Cao, Y.; Zhang, W.; Chen, J. Personalized Recommendation System Based on Collaborative Filtering for IoT Scenarios. IEEE Trans. Serv. Comput. 2020, 13, 685–695. [Google Scholar] [CrossRef]
- Duan, R.; Jiang, C.; Jain, H.K. Combining review-based collaborative filtering and matrix factorization: A solution to rating’s sparsity problem. Decis. Support Syst. 2022, 156, 113748. [Google Scholar] [CrossRef]
- Verma, C.; Illés, Z.; Kumar, D. (SDGFI) Student’s Demographic and Geographic Feature Identification Using Machine Learning Techniques for Real-Time Automated Web Applications. Mathematics 2022, 10, 3093. [Google Scholar] [CrossRef]
- Alhijawi, B.; Kilani, Y. A collaborative filtering recommender system using genetic algorithm. Inf. Process. Manag. 2020, 57, 102310. [Google Scholar] [CrossRef]
- Wu, L.; He, X.; Wang, X.; Zhang, K.; Wang, M. A Survey on Accuracy-oriented Neural Recommendation: From Collaborative Filtering to Information-rich Recommendation. IEEE Trans. Knowl. Data Eng. 2022, 35, 4425–4445. [Google Scholar] [CrossRef]
- Da’u, A.; Salim, N. Recommendation system based on deep learning methods: A systematic review and new directions. Artif. Intell. Rev. 2020, 53, 2709–2748. [Google Scholar] [CrossRef]
- Kulkarni, P.V.; Rai, S.; Sachdeo, R.; Kale, R. Personalised eLearning Recommendation system. IEEE DataPort 2022. [Google Scholar] [CrossRef]
- Madani, Y.; Erritali, M.; Bengourram, J.; Sailhan, F. Social Collaborative Filtering Approach for Recommending Courses in an E-learning Platform. Procedia Comput. Sci. 2019, 151, 1164–1169. [Google Scholar] [CrossRef]
- Teodorescu, O.M.; Popescu, P.S.; Mihaescu, M.C. Taking e-Assessment Quizzes—A Case Study with an SVD Based Recommender System. In Intelligent Data Engineering and Automated Learning—IDEAL 2018; Lecture Notes in Computer Science; Yin, H., Camacho, D., Novais, P., Tallón-Ballesteros, A.J., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11314, pp. 829–837. [Google Scholar] [CrossRef]
- Li, T.; Ren, Y.; Ren, Y.; Wang, L.; Wang, L.; Wang, L. NMF-Based Privacy-Preserving Collaborative Filtering on Cloud Computing. In Proceedings of the 2019 International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Atlanta, GA, USA, 14–17 July 2019; pp. 476–481. [Google Scholar] [CrossRef]
- Anwar, T.; Uma, V. Comparative study of recommender system approaches and movie recommendation using collaborative filtering. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 426–436. [Google Scholar] [CrossRef]
- Zriaa, R.; Amali, S. A Comparative Study between K-Nearest Neighbors and K-Means Clustering Techniques of Collaborative Filtering in e-Learning Environment. In Innovations in Smart Cities Applications Volume 4. SCA 2020; Lecture Notes in Networks and Systems; Ahmed, M.B., Kara, İ.R., Santos, D., Sergeyeva, O., Boudhir, A.A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 183, pp. 268–282. [Google Scholar] [CrossRef]
- Al-Nafjan, A.; Alrashoudi, N.; Alrasheed, H. Recommendation System Algorithms on Location-Based Social Networks: Comparative Study. Information 2022, 13, 188. [Google Scholar] [CrossRef]
- Gomede, E.; de Barros, R.M.; de Souza Mendes, L. Deep auto encoders to adaptive E-learning recommender system. Comput. Educ. Artif. Intell. 2021, 2, 100009. [Google Scholar] [CrossRef]
- Sidi, L.; Klein, H. Neural Network-Based Collaborative Filtering for Question Sequencing. arXiv 2020, arXiv:2004.12212. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Zhang, G.; Lu, J. A recurrent neural network-based recommender system framework and prototype for sequential E-learning. In Developments of Artificial Intelligence Technologies in Computation and Robotics, Proceedings of the 14th International FLINS Conference (FLINS 2020), Cologne, Germany, 18–21 August 2020; World Scientific: Singapore, 2020; pp. 488–495. [Google Scholar]
- Tan, J.; Chang, L.; Liu, T.; Zhao, X. Attentional Autoencoder for Course Recommendation in MOOC with Course Relevance. In Proceedings of the 2020 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC), Chongqing, China, 29–30 October 2020; pp. 190–196. [Google Scholar]
- Zhang, H.; Huang, T.; Lv, Z.; Liu, S.; Yang, H. MOOCRC: A Highly Accurate Resource Recommendation Model for Use in MOOC Environments. Mob. Netw. Appl. 2019, 24, 34–46. [Google Scholar] [CrossRef]
- Gong, T.; Yao, X. Deep exercise recommendation model. Int. J. Model. Optim. 2019, 9, 18–23. [Google Scholar] [CrossRef]
- Ren, Z.; Ning, X.; Lan, A.S.; Rangwala, H. Grade Prediction with Neural Collaborative Filtering. In Proceedings of the 2019 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Washington, DC, USA, 5–8 October 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Pan, Y.; He, F.; Yu, H. Learning social representations with deep autoencoder for recommender system. World Wide Web 2020, 23, 2259–2279. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, Y.; Jin, X. A survey of autoencoder-based recommender systems. Front. Comput. Sci. 2020, 14, 430–450. [Google Scholar] [CrossRef]
- Ferreira, D.; Silva, S.; Abelha, A.; Machado, J. Recommendation System Using Autoencoders. Appl. Sci. 2020, 10, 5510. [Google Scholar] [CrossRef]
- Kuchaiev, O.; Ginsburg, B. Training Deep AutoEncoders for Collaborative Filtering. arXiv 2017, arXiv:1708.01715. [Google Scholar]
- Chen, S.; Guo, W. Auto-Encoders in Deep Learning—A Review with New Perspectives. Mathematics 2023, 11, 1777. [Google Scholar] [CrossRef]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation Functions: Comparison of trends in Practice and Research for Deep Learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Rasamoelina, A.D.; Adjailia, F.; Sinčák, P. A review of activation function for artificial neural network. In Proceedings of the 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 23–25 January 2020; pp. 281–286. [Google Scholar]
- Nguyen, L.V.; Vo, Q.-T.; Nguyen, T.-H. Adaptive KNN-Based Extended Collaborative Filtering Recommendation Services. Big Data Cogn. Comput. 2023, 7, 106. [Google Scholar] [CrossRef]
- Chen, V.X.; Tang, T.Y. Incorporating Singular Value Decomposition in User-based Collaborative Filtering Technique for a Movie Recommendation System: A Comparative Study in Proceeding of the 2019 the International Conference on Pattern Recognition and Artificial Intelligence—PRAI’19, Wenzhou, China, 26–28 August 2019; ACM Press: New York, NY, USA, 2019; pp. 12–15.
- Jiao, J.; Zhang, X.; Li, F.; Wang, Y. A Novel Learning Rate Function and Its Application on the SVD++ Recommendation Algorithm. IEEE Access 2019, 8, 14112–14122. [Google Scholar] [CrossRef]
- Yehuda, K. Factorization Meets the Neighborhood: A Multifaceted Collaborative Filtering Model. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 426–434. [Google Scholar]
- Al Sabaawi, A.; Karacan, H.; Yenice, Y. Two Models Based on Social Relations and SVD++ Method for Recommendation System. Int. J. Interact. Mob. Technol. (IJIM) 2021, 15, 70. [Google Scholar] [CrossRef]
- Eren, M.E.; Richards, L.E.; Bhattarai, M.; Yus, R.; Nicholas, C.; Alexandrov, B.S. FedSPLIT: One-Shot Federated Recommendation System Based on Non-negative Joint Matrix Factorization and Knowledge Distillation. arXiv 2022, arXiv:2205.02359. [Google Scholar]
- Zhang, F.; Gong, T.; Lee, V.E.; Zhao, G.; Rong, C.; Qu, G. Fast algorithms to evaluate collaborative filtering recommender systems. Knowl.-Based Syst. 2016, 96, 96–103. [Google Scholar] [CrossRef]

| Item 1 | Item 2 | Item 3 | Item 4 | Item 5 | |
|---|---|---|---|---|---|
| User1 | 3 | 2 | 3 | ||
| User2 | 4 | 3 | 4 | 3 | 5 |
| User3 | 3 | 3 | 5 | 4 | |
| User4 | 1 | 5 | 5 | 1 |
| Article | Machine Learning Method | Approach | Metric | Dataset | Item Types Recommended |
|---|---|---|---|---|---|
| [27] | SVD, SVD++, Co-clustering and K-NN | CF | -MAE -RMSE | MovieLens-100 K | Movie |
| [29] | SVD, SVD++, NMF | CF | -MAE -RMSE | Yelp dataset | Restaurant |
| [30] | Denoising autoencoders, deep autoencoders for collaborative filtering, deep autoencoders for collaborative filtering using content information | CF | -“Mean Average Precision” (MAP) -“Normalized Discounted Cumulative Gain” (NDCG) -“Personalization” (P) -“Coverage” -“Serendipity” (SAUC) | Interactions between students and learning objects from a “Massive Open Online Course” (MOOC) | Learning objects |
| [31] | Neural Collaborative Filtering (NCF) | -Average precision correlation (AP) | Algebra1 dataset | Question sequencing | |
| [34] | Deep belief networks (DBNs) | CF | RMSE | StarC MOOC platform of Central China Normal University | Course |
| [35] | Stacked denoising autoencoder (SDAE) with wide linear component | hybrid | Receiver operating characteristic (ROC) curve the area under ROC (AUC-ROC) | Dataset from an online education company | Exercises |
| Present Approach | Autoencoder | CF | MAERMSE | Dataset created by Kulkarni et al. [23] | Course |
| Hyperparameter | Meaning | Autoencoder |
|---|---|---|
| Activation | Function utilized by the neuron’s activation | SELU |
| Batch Size | The size of the sampler that the network is using | 64 |
| Epoch | The total number of iterations required for training the network | 40 |
| Loss Function | Compares the distance between the prediction output and the target values to determine the model’s performance | Mean square error (MSE) |
| Learning Rate | The rate at which synapse weights are updated | 0.0001 |
| Optimizer | “adaptive moment estimation” is an optimization algorithm | Adam |
| Activation Function | Advantages | Drawbacks |
|---|---|---|
| Sigmoid | -Simple to understand -Commonly utilized in shallow networks [42] | -Gradient saturation [42] -Slow convergence-Output is nonzero-centered |
| Tanh | -Output is zero-centered | -Vanishing gradient problem could not be solved using this function [42] |
| ReLU | -Faster learning | -Fragile during training, resulting in the death of some gradients [42] |
| SELU | -Not affected by vanishing gradient problems-Works well in standard feed-forward neural networks (FNNs) [43] | -“Internal covariate shift” problem |
| Activation Function | MAE | RMSE |
|---|---|---|
| SELU | 0.6042 | 0.8756 |
| Sigmoid | 1.9906 | 2.4077 |
| Relu | 0.7281 | 0.9987 |
| Tanh | 1.9624 | 2.3953 |
| Optimizer Algorithm | MAE | RMSE |
|---|---|---|
| Adam | 0.6042 | 0.8756 |
| SGD | 1.3769 | 1.7637 |
| Dataset | Users | Items | Ratings |
| 424 | 20 | 8480 |
| UserId | CourseId | |||||
| 1001 | 1002 | … | 1019 | 1020 | ||
| 2001 | 5 | 3 | … | 1 | 3 | |
| 2002 | 3 | 5 | … | 0 | 0 | |
| … | … | … | … | … | … | |
| 2423 | 2 | 5 | … | 5 | 5 | |
| 2424 | 0 | 0 | … | 2 | 3 | |
| UserId | Degree 1 | Degree 1 Specializations | Known Languages | Key Skills | Career Objective |
|---|---|---|---|---|---|
| 1001 | B.E. | Computer Science & Engineering | “English, Marathi, Hindi” | C, Java, Keras, Flask, DeepLearning, Selenium, cpp, TensorFlow, Machine Learning, Web Development Areas of interest Django, Python, Computer Vision, HTML, MySQL | “Computer Engineering student with good technical skills and problem solving abilities. include Computer Vision, Deep Learning, Machine Learning, and Research.” |
| 1002 | B.E. | Computer Science & Engineering | Hindi English | Java, Neural Networks, AI, Python, Html5, CPP | Interested in working under company offering AI/Neural Networking outlooks |
| … | … | … | … | … | … |
| 2045 | B.E. | Computer Science & Engineering | Html, Wordpress, Css, C, Drupal-(CMS) Adobe-Illustrator, HTML, Adobe-Photoshop, MYSQL, Bootstrap, Wordpress-(CMS), JavaScript-(Beginner) Python-(Beginner), CSS | To prove myself dedicated worthful and energetic support in an organization that gives me a scope to apply my knowledge and seeking a challenging position and providing benefits to the company with my performance | |
| 2046 | B.E. | Computer Science & Engineering | “Python, Robotics”, Win32-Sdk, JAVA, Operating-System | “To secure a challenging position where I can effectively contribute my skills as Software Professional, possessing competent Technical Skills.” |
| Sr | Degree 1 | Degree 1 Specializations | Campus | Key Skills |
|---|---|---|---|---|
| 1001 | B E | Mechanical, | MITCOE | CATIA |
| 1002 | B E | Mechanical, | MITCOE | CATIA |
| … | … | … | … | … |
| 10,999 | B E | Electronics Telecommunication Engineering | MITAOE | “AmazonWebServiCes, C CPP, Arduino, MongoDB, Linux, Golang, Microcontrollers, Gobot, InternetofThings, MATLAB, SQL, PHP” |
| 11,000 | B E | Electronics Telecommunication Engineering | MITAOE | “AmazonWebServiCes, C CPP, Arduino, MongoDB, Linux, Golang, Microcontrollers, Gobot, InternetofThings, MATLAB, SQL, PHP” |
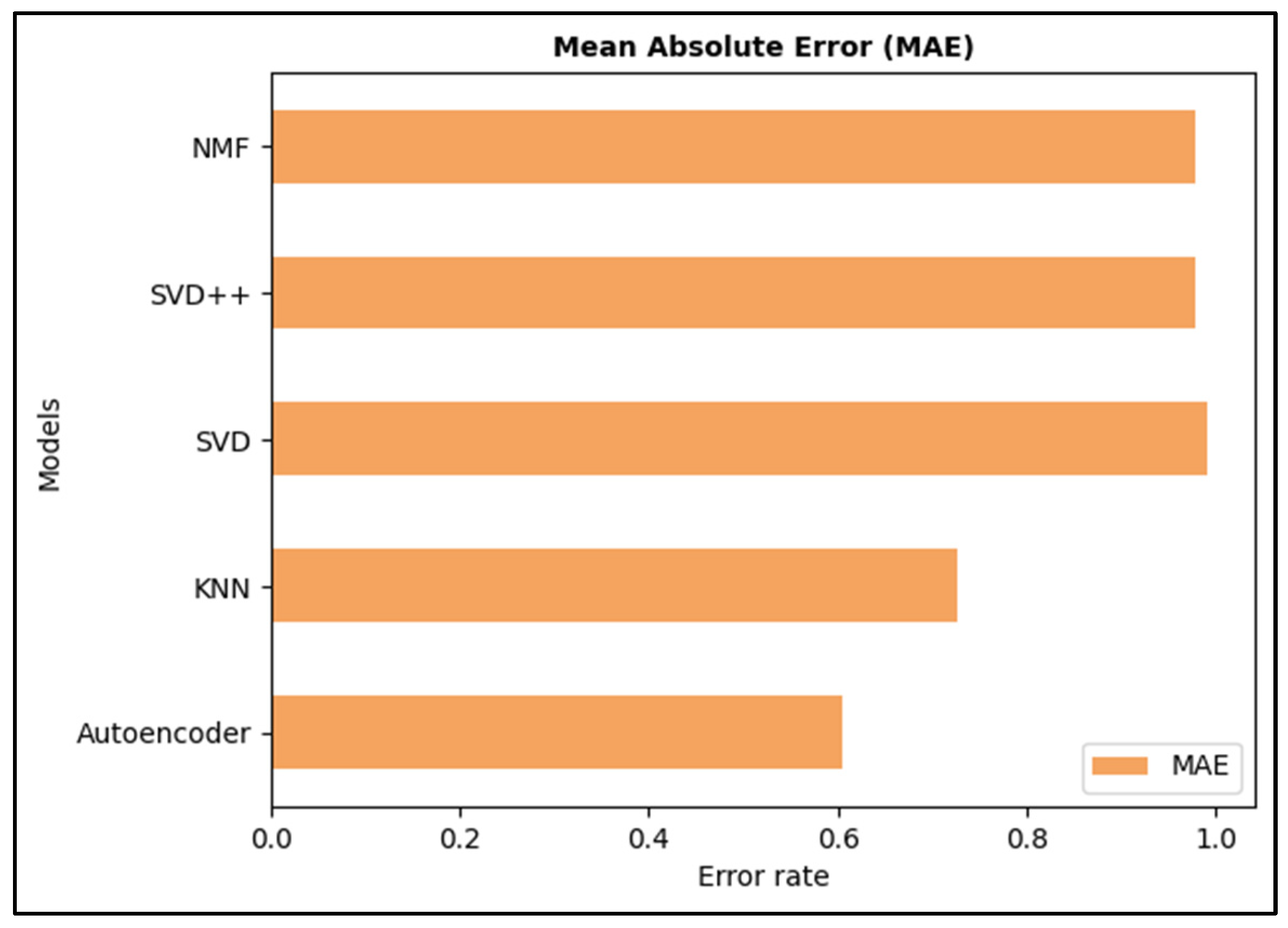
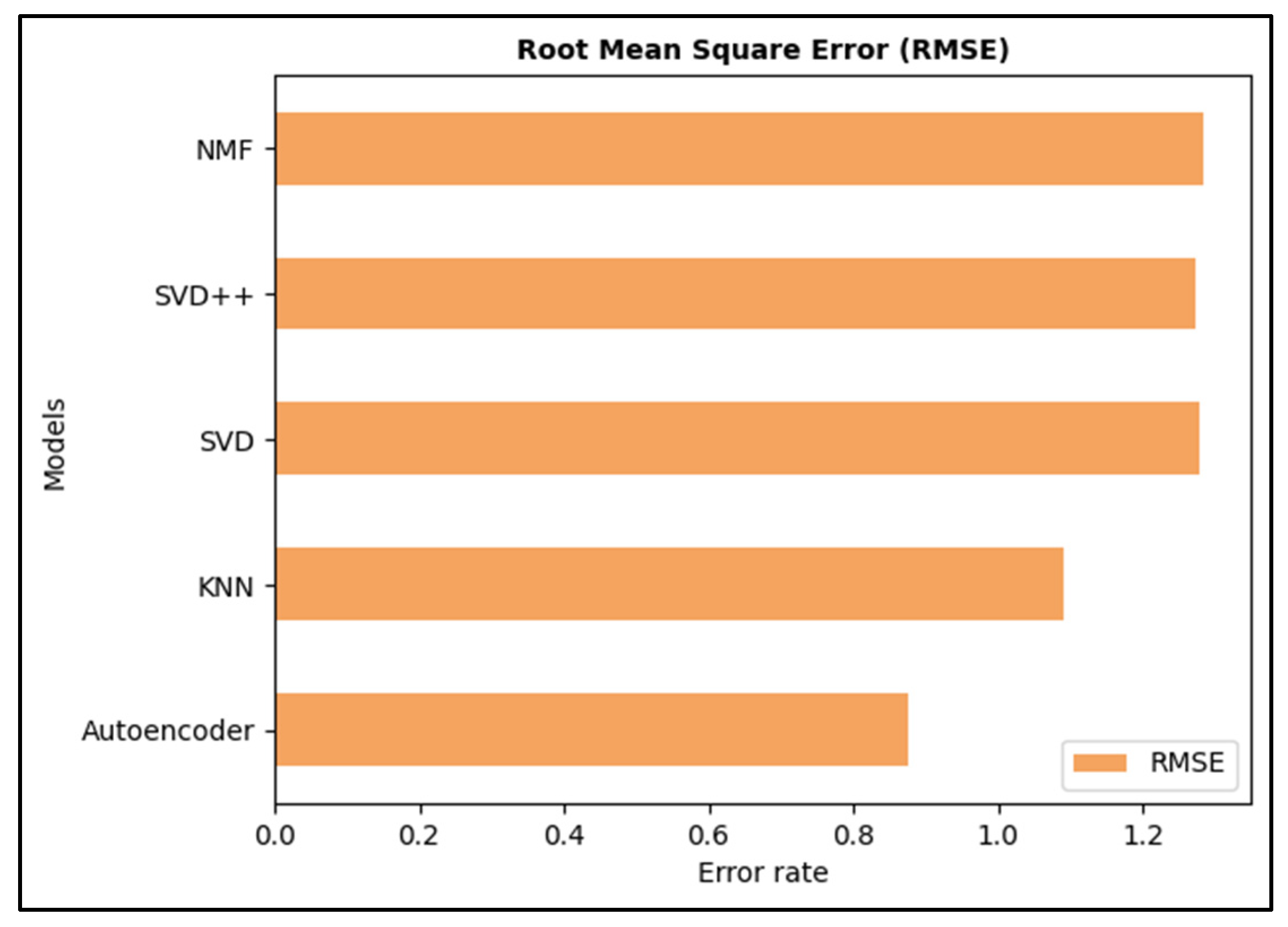
| Model | MAE | RMSE |
|---|---|---|
| KNN | 0.7259 | 1.0895 |
| SVD | 0.9922 | 1.2772 |
| SVD++ | 0.9796 | 1.2742 |
| NMF | 0.9781 | 1.2851 |
| Proposed model (autoencoder) | 0.6042 | 0.8756 |
| UserId | CourseId |
|---|---|
| 2012 | [1003, 1006, 1004] |
| 2027 | [1016, 1015, 1001] |
| 2141 | [1004, 1003, 1005] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Youbi El Idrissi, L.; Akharraz, I.; Ahaitouf, A. Personalized E-Learning Recommender System Based on Autoencoders. Appl. Syst. Innov. 2023, 6, 102. https://doi.org/10.3390/asi6060102
El Youbi El Idrissi L, Akharraz I, Ahaitouf A. Personalized E-Learning Recommender System Based on Autoencoders. Applied System Innovation. 2023; 6(6):102. https://doi.org/10.3390/asi6060102
Chicago/Turabian StyleEl Youbi El Idrissi, Lamyae, Ismail Akharraz, and Abdelaziz Ahaitouf. 2023. "Personalized E-Learning Recommender System Based on Autoencoders" Applied System Innovation 6, no. 6: 102. https://doi.org/10.3390/asi6060102
APA StyleEl Youbi El Idrissi, L., Akharraz, I., & Ahaitouf, A. (2023). Personalized E-Learning Recommender System Based on Autoencoders. Applied System Innovation, 6(6), 102. https://doi.org/10.3390/asi6060102






