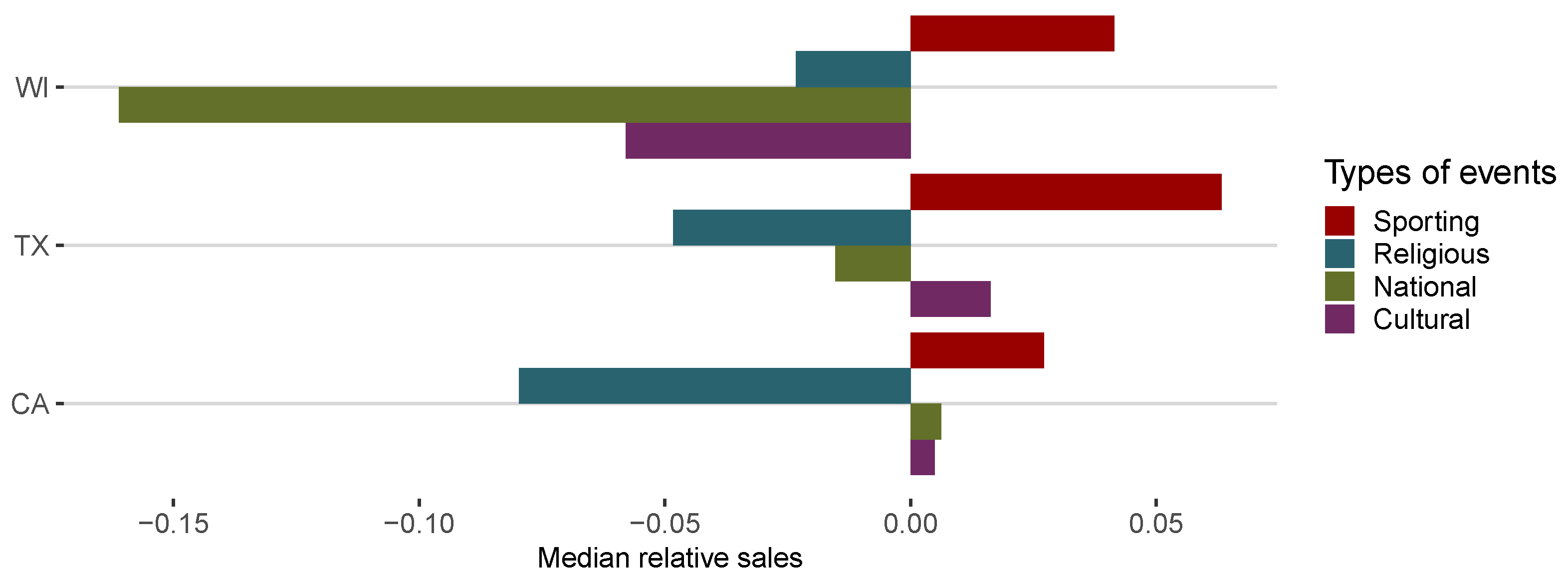1. Introduction
Accurate sales forecasts are of paramount importance to retailers as they heavily depend on them to effectively manage their supply chains and make crucial decisions related to marketing, logistics, finance, and human resources [
1]. Accurate sales forecasts help retailers determine how much inventory they need to purchase from their suppliers in order to meet customer demand. If the forecast is too low, they risk running out of stock and losing sales. If the forecast is too high, they risk overstocking and tying up cash in excess inventory. Sales forecasts also help retailers plan their logistics operations, such as determining how much warehouse space they need, how many trucks they need to transport goods, and how much labor is required to handle incoming and outgoing shipments. They also help retailers plan their marketing campaigns, such as determining which products to promote, which channels to use, and how much to spend on advertising. By having a clear understanding of expected sales volumes, retailers can more effectively allocate their marketing budgets. Accurate sales forecasts are also important for financial planning, such as budgeting and forecasting cash flow. Retailers need to know how much revenue they can expect in order to plan for expenses, investments, and debt repayment. Finally, sales forecasts are used by retailers to plan their staffing needs. They need to know how many employees they will need in their stores and warehouses in order to meet customer demand, and how much labor they will need to handle incoming and outgoing shipments [
2].
A global forecasting model, such as a recurrent neural network (RNN), is a model that uses information from multiple time series to make predictions [
3,
4]. This is in contrast to a univariate forecasting model like autoregressive integrated moving average (ARIMA) or exponential smoothing (ETS) [
5], which only use information from a single time series to make predictions. In a global forecasting model, the RNN is trained on multiple time series at once. Each time series is considered a separate input sequence, and the RNN is trained to capture the patterns and relationships between the different time series. This allows the model to make predictions for all of the time series simultaneously. One advantage of using a global forecasting model like an RNN is that it can capture complex dependencies between the different time series. For example, the sales of one product in a store may be influenced by the sales of a complementary product, or sales at one store may be influenced by sales at nearby stores. By using a global model that takes into account all of the relevant time series, we can better capture these relationships and make more accurate predictions [
6]. Another advantage of using a global model is that it can help reduce uncertainty in the individual time series. In some cases, individual time series may be noisy or exhibit erratic behavior. By using a global model that incorporates information from multiple time series, we can reduce the impact of these individual anomalies and improve the overall accuracy of the forecasts [
7].
In retail forecasting, covariates (also known as exogenous variables or features) can be used to help improve the accuracy of forecasts [
8]. Retail sales can be influenced by the time of year, as well as holidays, weekends, and other special events. Including calendar variables such as the day of week, month, and year can help capture these effects. Changes in price can also have a significant impact on sales. Including variables such as regular price, discount percentage, and promotional price can help capture these effects. Promotions, advertising, and other marketing activities can also influence sales. Including variables such as the type and frequency of marketing activities can help capture these effects. Weather conditions can affect the demand for certain products. Including variables such as temperature, precipitation, and wind speed can help capture these effects. The characteristics of a store’s local area can also influence sales. Including variables such as population density, median income, and age distribution can help capture these effects. Overall economic conditions can also influence sales. Including variables such as unemployment rate, GDP, and consumer confidence can help capture these effects.
The objective of this research was to explore how the accuracy of global forecasting models is influenced by incorporating various potential demand covariates, considering their potential effects on operational decisions. The subsequent structure of this paper is organized as follows: In
Section 2, we outline the developed forecasting framework designed for the evaluation study, while
Section 3 delves into its implementation details. Moving forward,
Section 4 unveils and discusses the obtained results, and finally, in
Section 5, we offer concluding remarks along with identifying potential areas for further research.
2. Autoregressive Neural Network Model
In this research, we employ a deep learning RNN sequence-to-sequence model known as DeepAR [
9], which represents a state-of-the-art algorithm specifically designed to tackle the intricate challenges inherent in time series forecasting. Developed by Amazon Web Services (AWS), DeepAR has demonstrated excellent performance across diverse domains such as finance, healthcare, and supply chain management. This success can be attributed to its inherent capability to capture complex temporal patterns and dependencies within data, which may remain obscured when using traditional forecasting methods [
10,
11]. A notable advantage of DeepAR lies in its built-in ability to model uncertainty, offering probabilistic forecasts [
12,
13]. This feature proves particularly crucial in decision-making processes that demand a nuanced assessment of both risks and opportunities. Furthermore, DeepAR’s flexibility in accommodating varying data characteristics and its adaptability to incorporate external covariates make it a versatile tool for enhancing the accuracy and reliability of predictions.
Let
denote the sales of product
i at time
t. The primary objective of DeepAR model is to forecast the conditional probability
P of future sales
using past sales
and additional information in the form of covariates
, where
represents the first time instant of the future and
T represents the last time instant of the future [
14]:
It is important to note that the time index t is relative, meaning that may not correspond to the initial time point of the time series. During training, we have access to in both the conditioning range and the prediction range . The former is used for encoding, while the latter is used for decoding in the sequence-to-sequence model. However, during inference (when we make predictions), is not available in the prediction range.
At each time step
t, the model produces an output represented by
:
This output is obtained by applying a multi-layer RNN with long short-term memory (LSTM) cells [
15] parameterized by
. The model is considered autoregressive because it takes the sales value from the previous time step
as input. Additionally, it is considered recurrent, as the output from the network at the previous time step
is given back as input at the next time step.
During training, we learn the model parameters by maximizing the log-likelihood of a chosen probability distribution using the equation:
Here, L denotes the likelihood of the distribution, N corresponds to the number of products, and represents a linear mapping from the function to the parameters of the distribution. DeepAR uses the entire time range to calculate the loss since the encoder model is identical to the decoder. DeepAR forecasts a single value at each step. However, during the inference phase, to predict several steps, the model repeatedly obtains forecasts for subsequent periods until the forecast horizon is reached. The model starts by generating samples from a probability distribution that has been trained on past sequences. The first prediction is made using these samples, and this prediction is then used as input to the model to make the next prediction. This process is repeated for each subsequent period. Because the predictions are derived from samples taken from the trained distribution, the model’s output is probabilistic. This means that the model does not produce a single deterministic value for each prediction, but rather a distribution of possible values. This distribution can be used to assess the forecasting accuracy of the model by providing a measure of the uncertainty associated with each prediction. The sampling mechanism also allows the model to be used to generate different forecasting scenarios. By sampling from the distribution of predictions, the model can be used to generate a range of possible outcomes, which can be used to inform decision making.
Sales data often exhibit a zero-inflated distribution, meaning that there are a significant number of observations that equal zero [
16]. This can pose a challenge for forecasting models, as they are typically not designed to handle zeros [
17,
18,
19,
20]. To address this challenge, we used the negative log-likelihood of the Tweedie distribution as our loss function [
21,
22]. The Tweedie distribution is a flexible distribution that can accommodate zero-inflated data, and the negative log-likelihood is a well-established loss function for Tweedie models. This approach allowed us to develop a forecasting model that was able to accurately predict both zero and non-zero sales.
Here, represents the gamma function, and and p denote the mean, dispersion, and power parameters, respectively. When p lies between 1 and 2, the distribution takes on the form of a compound Poisson-gamma distribution, which is frequently used for datasets displaying positive skewness and a significant number of zeros. The dispersion parameter regulates the level of diversity or heterogeneity in the data. A small value of suggests high dispersion in the data, whereas a large value indicates homogeneity.
3. Empirical Study
3.1. Dataset and Exploratory Analysis
In this study, we used the M5 competition dataset, which is a well-established and openly available dataset of hierarchical unit sales data from Walmart. The M5 dataset is widely used for forecasting research because it is credible and reproducible. The M5 dataset comprises 3049 items categorized under Hobbies, Foods, and Household. These categories are further divided into a total of seven departments. Specifically, the Foods category is subdivided into three distinct departments (Foods1, Foods2, and Foods3), while both the Hobbies and Household categories are each subdivided into two departments (Hobbies1, Hobbies2, Household1, and Household2) [
23]. These items are available for sale across 10 stores located in three states: California (CA), Texas (TX), and Wisconsin (WI). The state of California encompasses four stores (CA1, CA2, CA3, and CA4), whereas the states of Texas and Wisconsin each have three stores (TX1, TX2, and TX3; WI1, WI2, and WI3, respectively). The dataset covers a period of 5.4 years, from 29 January 2011 to 19 June 2016, on a daily basis, totaling 1969 days.
In addition to sales data, the M5 dataset also includes the regular price of each item, supplemental nutrition assistance program (SNAP) days, and special events that may impact sales. Approximately 8% of days in the dataset are marked by a special event, which is equivalent to around 160 events in the span of 1969 days. Of these events, around one-third are religious, such as Orthodox Christmas, while another one-third are national holidays, like Independence Day. The remaining third is divided into two-thirds encompassing cultural events, such as Valentine’s Day, and one-third sporting events, such as the Super Bowl (please see
Figure 1).
The SNAP is a federally funded initiative in the United States aiming to help individuals and families with low incomes to buy food. It was previously referred to as food stamps and is managed by the U.S. Department of Agriculture. As the largest nutrition assistance program in the nation, SNAP plays a crucial role in providing support for those in need of food assistance. The M5 dataset provides information on the SNAP in each state for each day. When we examine the proportion of days on which Walmart stores permit purchases with SNAP benefits, we observe that it is consistent across all three states: 650 days or 33%. SNAP benefits are available for exactly 10 days each month in all states, and these days occur on fixed dates that are the same for every month in every state. In California, SNAP benefits are available in the first 10 days of the month, while in Texas, benefits are available on the 1st, 3rd, 5th, 6th, 7th, 9th, 11th, 12th, 13th, and 15th days. In Wisconsin, SNAP benefits are available on the 2nd, 3rd, 5th, 6th, 8th, 9th, 11th, 12th, 14th, and 15th days. Notably, SNAP days occur in the first half of the month for all states.
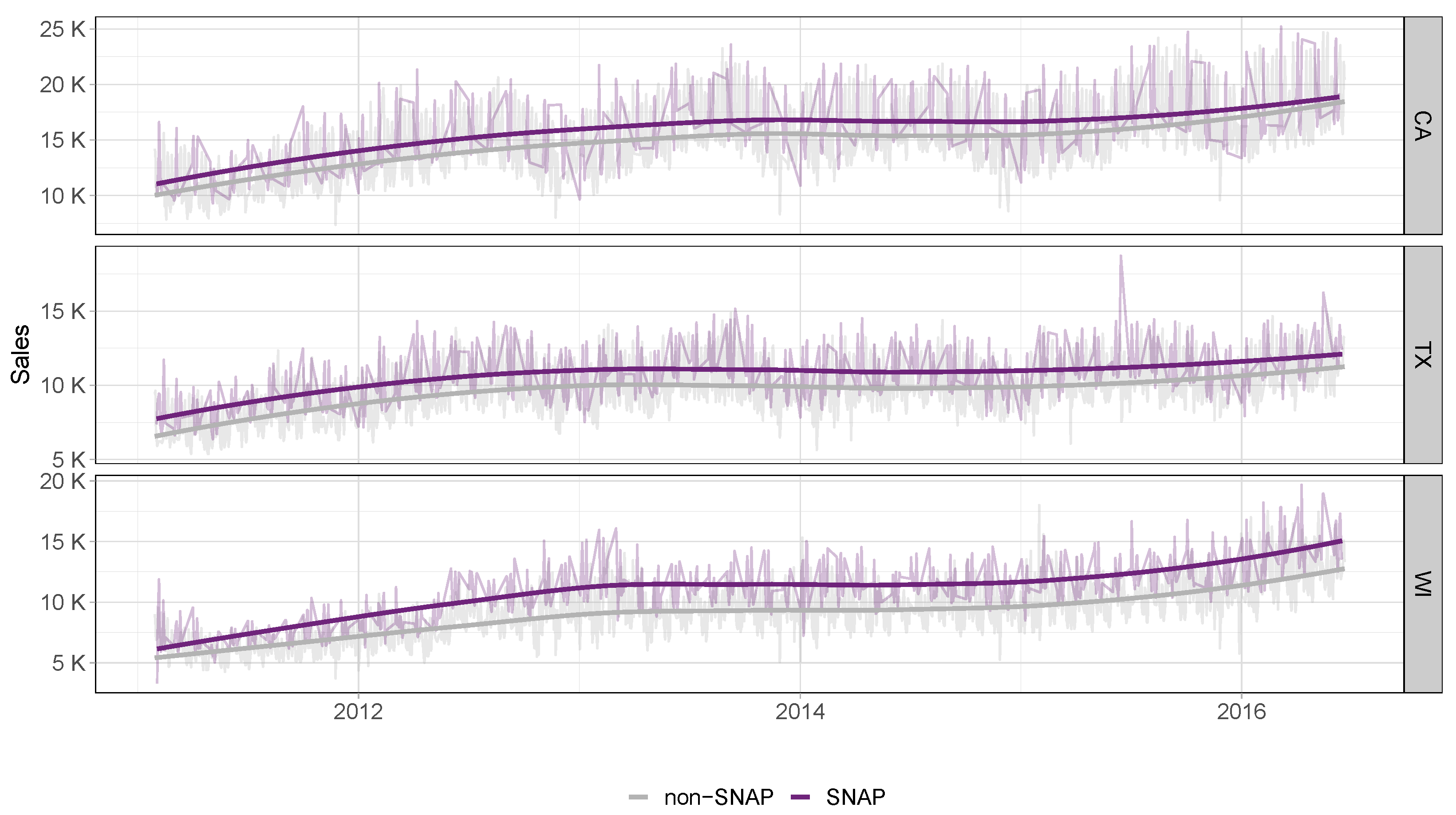
Figure 2 provides a comprehensive overview of the sales volume during SNAP and non-SNAP days in the three states: California, Texas, and Wisconsin. Although the daily time series are visible in the background, it is more informative to examine the smoothed representations. Our analysis shows that sales volumes are significantly higher on SNAP days compared to non-SNAP days in every state. The largest difference is observed in Wisconsin, while the variations over time are relatively minor. Specifically, the two curves in Wisconsin appear to reach their biggest difference at approximately 2013. However, as with all smoothing fits, it is important to exercise caution when examining data at the edges. In such cases, the results may be less reliable and should be interpreted with caution.
We also analyzed sales volumes during special event days versus non-event days in the three states (please see
Figure 3). Our findings suggest that special events slightly outsell non-event days in Texas before 2014, while afterward, their sales are similar. In California and Wisconsin, there is a drop in sales around the same time, but here it is from similar sales to lower sales. This pattern appears to be common, starting from 2013. Our analysis of event types is particularly interesting, especially for Wisconsin, where national events result in a considerable adverse effect on sales figures (
Figure 4). Additionally, Wisconsin stands alone as the sole state where cultural events experience lower sales figures, particularly when compared to Texas. On the other hand, religious events show a relatively minor but still unfavorable effect in Wisconsin, while sporting events have positive impacts in all three states.
The “Everyday Low Prices” policy has been a key driver of Walmart’s success, helping the company to establish a strong position in the highly competitive retail industry. The idea behind this policy is to provide customers with affordable pricing on a wide range of products throughout the year, rather than relying on the typical retail model of offering higher prices and occasional sales. By maintaining low prices every day, Walmart aims to attract and retain customers who value affordability and reliability in their shopping experience.
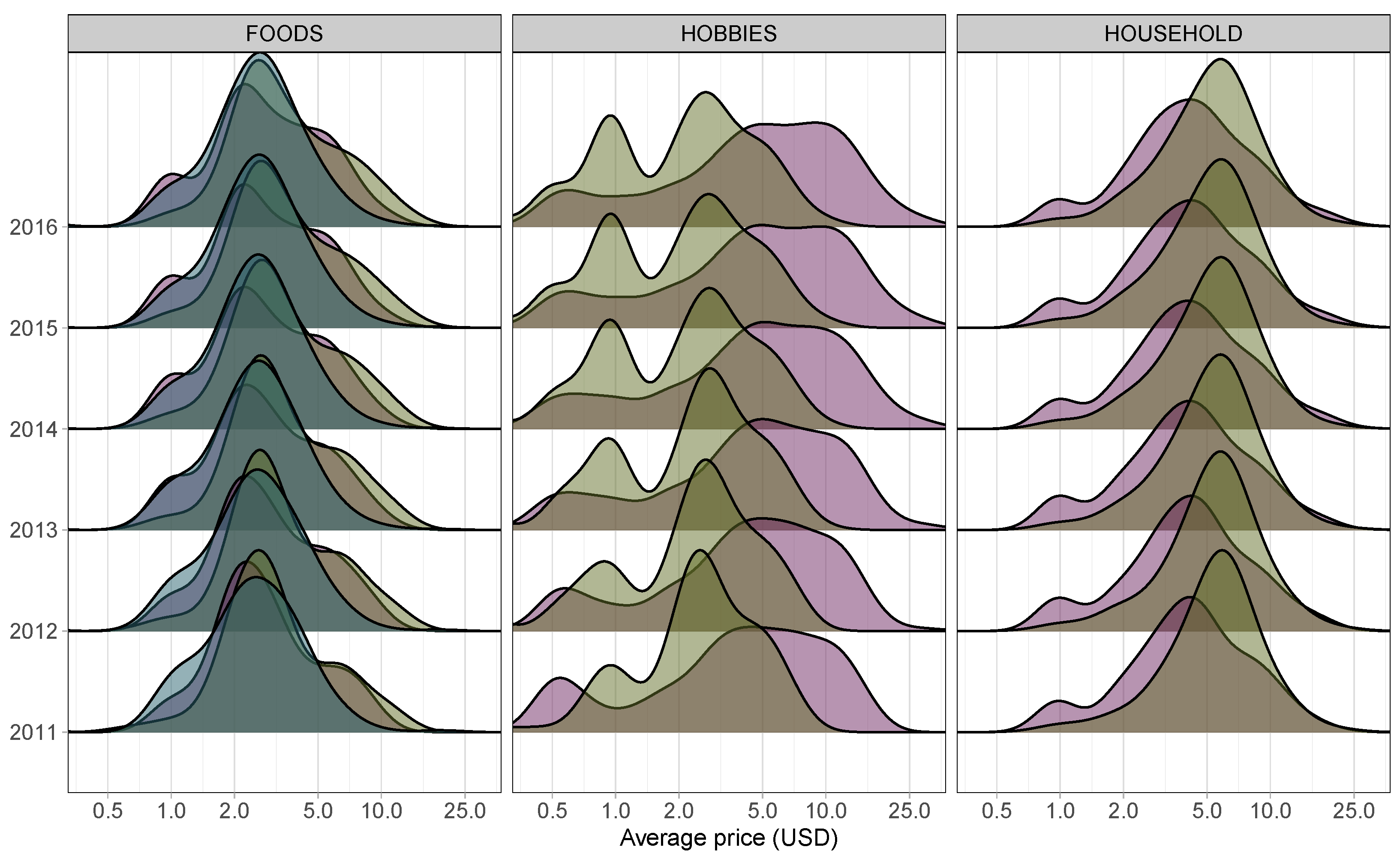
Figure 5 depicts overlapping density plots for weekly average price distributions within each category’s departments for each year from 2011 to 2016. As expected, the price distributions have remained relatively steady, experiencing only slight increases, likely attributed to inflation. However, distinct variations exist among the categories. On average, Foods items tend to be more affordable compared to Household items, whereas Hobbies items exhibit a broader range of prices, even displaying a secondary peak at lower price points. Within each category, there are also substantial differences. For instance, in the Foods category, department 3 (Foods3 in dark green) does not have a high-price tail. The Hobbies category exhibits the greatest diversity, with both departments displaying wide-ranging distributions. The Hobbies2 department (depicted in light green) showcases a bimodal structure, encompassing almost all items priced below USD 10, whereas the Hobbies1 department (in pink) exhibits notably higher prices. The price distributions in the Household category are quite similar, but the Household2 department (in light green) has a peak at clearly higher prices than the Household1 department (in pink). An interesting trend is visible in the Hobbies2 department, which becomes increasingly bimodal over time. The second peak at USD 1 is growing in importance, almost reaching the level of the main peak just above USD 2. Meanwhile, the small secondary peak at half a dollar in the Hobbies1 department (in pink) becomes flatter after 2012. Conversely, the Household departments remain very stable, while the Foods category shows small changes such as the relative growth of the USD 1 peak in the Foods1 department.
Furthermore, the M5 dataset encompasses details regarding the item ID (ranging from 1 to 3,049), the category ID (Foods, Hobbies, or Household), the department ID (Foods1, Foods2, Foods3, Hobbies1, Hobbies2, Household1, or Household2), the store ID (CA1, CA2, CA3, CA4, TX1, TX2, TX3, WI1, WI2, or WI3), as well as the state ID (CA, TX, or WI) for each individual item.
3.2. Features Engineering
There are two distinct types of features: sequential and categorical. Sequential features are represented as two-dimensional real-value data, encompassing both the time and channel dimensions. These sequential features are directly fed into the network without any additional manipulation.
On the other hand, categorical features undergo an embedding process before being fed into the network. During this process, the network learns embeddings through an embedding layer, which serves as a lookup table, mapping input values to trainable embeddings [
24].
Four distinct feature groups were taken into consideration: time-related features, price-related features, event-related features including SNAP days, and identification-related (ID) features. The first three groups of features are sequential, while the last group is categorical. Regarding time-related features, eight different value types were used: day, month, year, week of the month, week of the year, day of the year, weekday, and weekend indicator. Following the recommendation by [
9], all of these values, excluding the final one, were encoded to the range of
. The weekend indicator was encoded as a binary feature. For instance, in terms of the day values, day 1 is represented as the encoded value
, day 2 as
, day 29 as
, day 30 as
, and day 31 as
. Similarly, for the weekday, Monday is encoded as
, Tuesday as
, Wednesday as
, Thursday as 0, Friday as
, Saturday as
, and Sunday as
.
Three normalized price features were utilized, with normalization achieved through a standard score, i.e., price values were divided by the standard deviation after the mean value was subtracted. The first normalized price value was obtained for each item across all time, considering the disparities from the mean price. The second normalized price value was calculated within each item group that belonged to the same department, allowing for comparisons of the relative price of each item. In each item group associated with the same store, we computed the third normalized price value. This calculation allowed us to make relative price comparisons for each item.
We used three values representing the SNAP days from the M5 dataset, which is a binary feature indicating whether the three states permit SNAP purchases on specific dates, without making any changes to them. The calendar events, characterized by two-dimensional features with varying values based on time, underwent a similar encoding process, scaled to fit within the range of prior to being input into the network. Each event is defined by both its name and type. In total, thirty distinct events were considered, each with a corresponding encoded value: days without events were represented as , Chanukah End as , Christmas as , Cinco de Mayo as , Columbus Day as , Easter as , Eid al-Fitr as , Eid Al-Adha as , Father’s Day as , Halloween as , Independence Day as , Labor Day as , Lent Start as , Lent Week 2 as , Martin Luther King Day as , Memorial Day as 0, Mother’s Day as , NBA Finals End as , NBA Finals Start as , New Year as , Orthodox Christmas as , Orthodox Easter as , Pesach End as , Presidents’ Day as , Purim End as , Ramadan starts as , St. Patrick’s Day as , Super Bowl as , Thanksgiving as , Valentines Day as , and Veterans Day as . Each event falls within one of the following four types: days without events are encoded as , cultural events as , national events as 0, religious events as , and sporting events as . Given that some days have two calendar events, four event-related features were incorporated alongside the existing three SNAP features.
We considered five distinct identification-related features: the item ID, the category ID, the department ID, the store ID, and the state ID. Each of these features was encoded using integers ranging from 0 to one less than its cardinality. As these are one-dimensional features with constant values regardless of time, we replicated them within the time dimension after embedding, ensuring their dimensions matched with other features.
3.3. Evaluation Design
DeepAR global models were trained using the M5 dataset, consisting of 30,490 sales of products across the 10 stores.
The information about the short-term sales trend was derived using the sales data from the previous 28 days as inputs. We adopted the M5 competition’s framework, where the last 28 days of each time series (from 23 May 2016 to 19 June 2016) were reserved as a testing set for out-of-sample evaluation. The remaining data, spanning from 29 January 2011 to 22 May 2016 (a total of 1941 days), was used for training the models. In order to reach good accuracy results, it is essential to identify a high-performing model during the testing phase. Usually, a validation set is utilized to assess the most appropriate model. The success of a deep learning model is significantly impacted by various factors, including the values for hyperparameters and the values for the initial weights. In order to identify the best model, we used the final 28 days of in-sample training data, covering the period from 25 April 2016 to 22 May 2016, as the validation set. The hyperparameter optimization process was carried out using the Optuna optimization framework [
25], with the root mean squared error (RMSE) [
7] serving as the accuracy metric for model selection. To evaluate the significance of the different types of features, we included them individually and in various combinations, and compared their performance to the baseline case where no features were used.
We assessed the performance of the DeepAR models using two metrics commonly employed in the forecasting literature [
26]: the root mean squared scaled error (RMSSE) and the mean absolute scaled error (MASE):
where
is the sales of item
i at time
t and
is its forecast,
n is the length of the training set and
h is the forecast horizon. In this particular case study, the time frame considered for the forecast horizon is 28 days. Once calculated for each item, the RMSSE and the MASE were summarized across all items.
The RMSSE was the metric used to assess the accuracy of point forecasts in the M5 competition [
27]. RMSSE and MASE are two scale-independent measures that can be utilized to compare forecasts across different items with different scales and units. This is because they scale the forecast errors based on the MSE and MAE of the 1-step ahead in-sample naïve forecast errors, respectively. This ensures that the errors are measured in terms of their absolute or squared magnitude, which allows for fair comparisons across different products. Additionally, RMSSE and MASE differ in how they weight the errors. RMSSE uses squared errors, which emphasizes forecasts that closely adhere to the mean of the target series. MASE uses absolute errors, which emphasizes forecasts that closely adhere to the median of the target series. This difference in weighting allows for different perspectives on the underlying structure of the data.
4. Results and Discussion
Table 1 displays the results obtained from an empirical study employing the DeepAR model across various feature combinations, organized by the number of feature groups included. The seasonal naïve model is used as a benchmark. This simple time series forecasting model assumes that the future value of a series is equal to the most recent observed value from the same season. In this context, assuming a seasonal period of 7 days with daily data, as is the case here, the forecast for all future Monday values, for instance, mirrors the last observed Monday value, and so forth.
Table 1 highlights the most effective combination of features in boldface within the RMSSE and MASE columns.
Let us highlight the key observations in the results. Firstly, regardless of the error measure used, the DeepAR model with or without features consistently exhibits a significantly better performance compared to the univariate benchmark. The improvements in forecast accuracy are substantial, amounting to approximately 25.8% based on RMSSE. This underscores the advanced capabilities of the DeepAR model in time series forecasting.
Secondly, it is important to note that there are differences in the results between RMSSE and MASE. This difference is understandable since these error measures concentrate on distinct aspects of the distribution of the target variable.
Thirdly, the incorporation of time-, event-, and ID-related features consistently enhances the accuracy of the baseline DeepAR model, which lacks any covariates. This improvement aligns with expectations, given the significance of special events, sales dates, and item attributes in retail forecasting.
Fourthly, in general, the inclusion of price-related features does not lead to performance improvement in DeepAR models across various feature combinations. This result is unsurprising, especially in the context of a retailer like Walmart, where price distributions tend to remain relatively stable over the years.
Finally, the usefulness of ID-related features significantly surpasses those of time- and event-related features. However, the best performance is achieved when all three of these groups of features are used together, suggesting that the individual relevance of each type of feature is emphasized when the information is given jointly. This model’s performance (DeepAR + Events + Time + IDs) improved by 1.8% for RMSSE and 6.5% for MASE when compared to the baseline model without features.
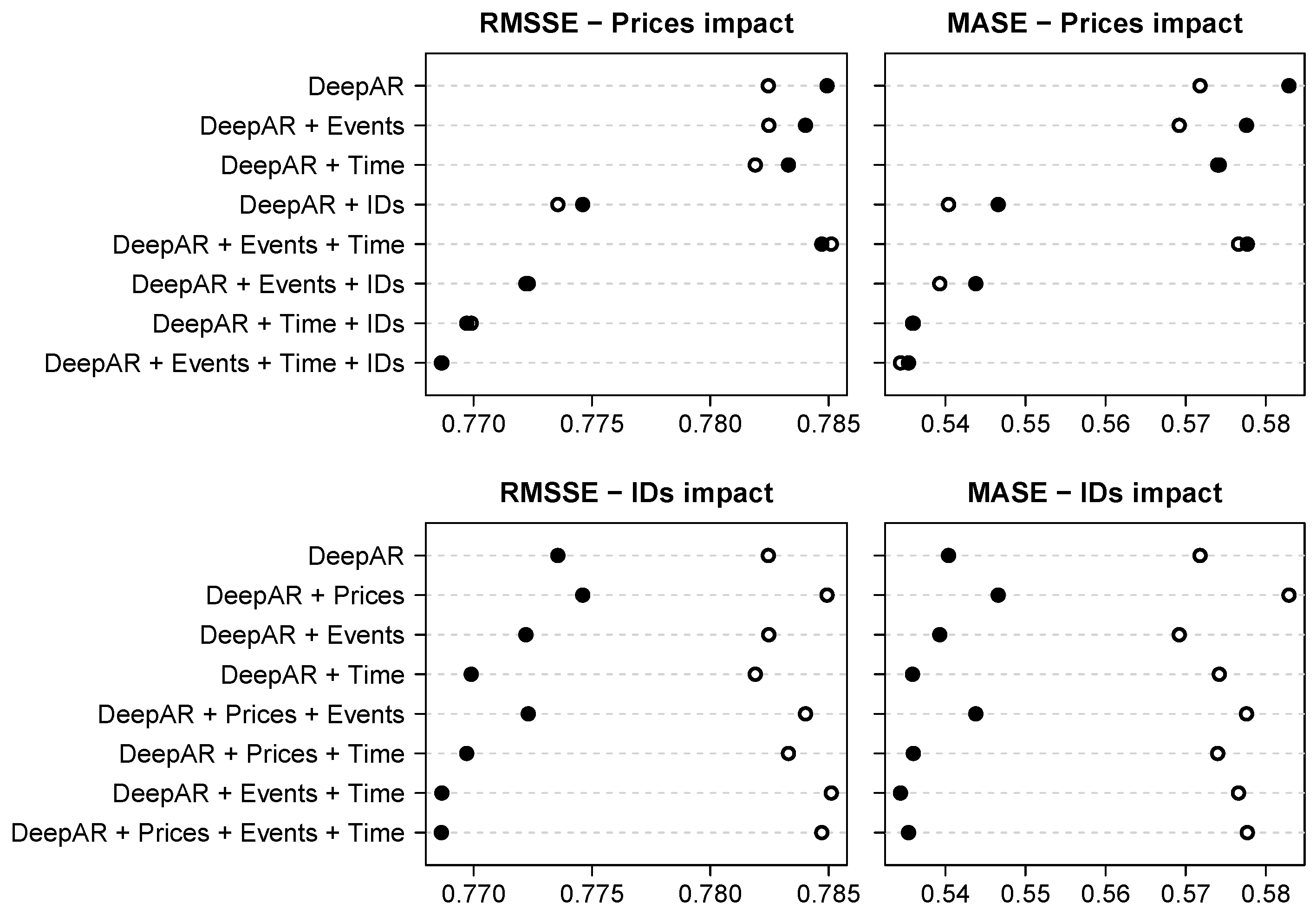
Additionally, in
Figure 6, we offer a comparison of how features related to prices and IDs affect the performance of DeepAR models across different feature combinations. Hollow dots represent errors from models without prices/IDs, while filled dots represent errors from models with prices/IDs. These figures unequivocally demonstrate that, regardless of the error measure used, the inclusion of price-related features never enhances the accuracy of any DeepAR model, regardless of the feature combination. Conversely, the addition of ID-related features consistently improves the forecasting performance of a DeepAR model, regardless of the feature combination used. The influence of time- and event-related features closely resembles that of the IDs, albeit with a less pronounced improvement (figures not displayed).
In the M5 dataset, we only had five distinct ID-related features: item ID, category ID, department ID, store ID, and state ID. However, in a real retail setting, there would be numerous additional attributes and features associated with each product. These may include details such as the product type, brand, size, and attributes that are relevant within specific subcategories (for example, “white vs. red” matters for wine but less so for beer, even though both fall under the category of “alcoholic beverages”). Leveraging these additional attributes is likely to result in even more significant improvements compared to solely relying on the five item IDs provided by the M5 dataset.
It is worth emphasizing that the importance of each feature type hinges on the specific application domain. It is expected that the significance of these specific features may vary in other application domains, and different features may assume a more prominent role.
5. Conclusions
Retailers heavily depend on accurate sales forecasts to effectively manage their supply chains and make informed decisions about purchasing, logistics, marketing, finance, and human resources. An advantage of using a global forecasting model, such as an RNN, is its ability to capture intricate dependencies and relationships between different time series. For instance, the sales of a complementary product can affect the sales of another product in a store, or the sales of a particular store can be influenced by the sales at nearby stores. By utilizing a comprehensive model that incorporates all relevant time series, we can more effectively capture these interrelationships and make more accurate predictions.
In retail forecasting, covariates such as calendar events, changes in pricing, and weather conditions can be employed to enhance the forecast accuracy. The objective of this study was to examine how the accuracy of global forecasting models is influenced by the inclusion of various possible demand covariates, considering their potential impact on operational decision making. To ensure the significance of our findings, we employed the widely recognized and openly accessible dataset from the M5 competition. We trained DeepAR global models using the complete M5 dataset, which comprises 30,490 product sales across ten stores.
To assess the significance of the different feature types, we included them both individually and in various combinations, comparing their performance against the baseline case where no features were used. The findings reveal that the DeepAR model, whether with or without additional features, consistently demonstrates a significantly superior performance compared to the univariate seasonal naïve benchmark. The inclusion of time, event, and ID-related features consistently enhances the accuracy of the baseline DeepAR model, which lacks any covariates. In general, the inclusion of price-related features does not lead to performance improvements in DeepAR models across various feature combinations. This observation is not surprising, especially in the context of a retailer like Walmart, which follows an “Everyday Low Prices” strategy, resulting in relatively stable price distributions. The utility of ID-related features greatly surpasses that of time and event-related features. However, the best performance is achieved when all three groups of features are used in combination, suggesting that the individual relevance of each feature type is accentuated when information from all sources is considered jointly. Overall, the best-performing model demonstrates a 1.8% improvement in RMSSE and a 6.5% improvement in MASE compared to the model without any additional features.