Unsupervised Classification of Human Activity with Hidden Semi-Markov Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Model Description
2.3. Model Validation
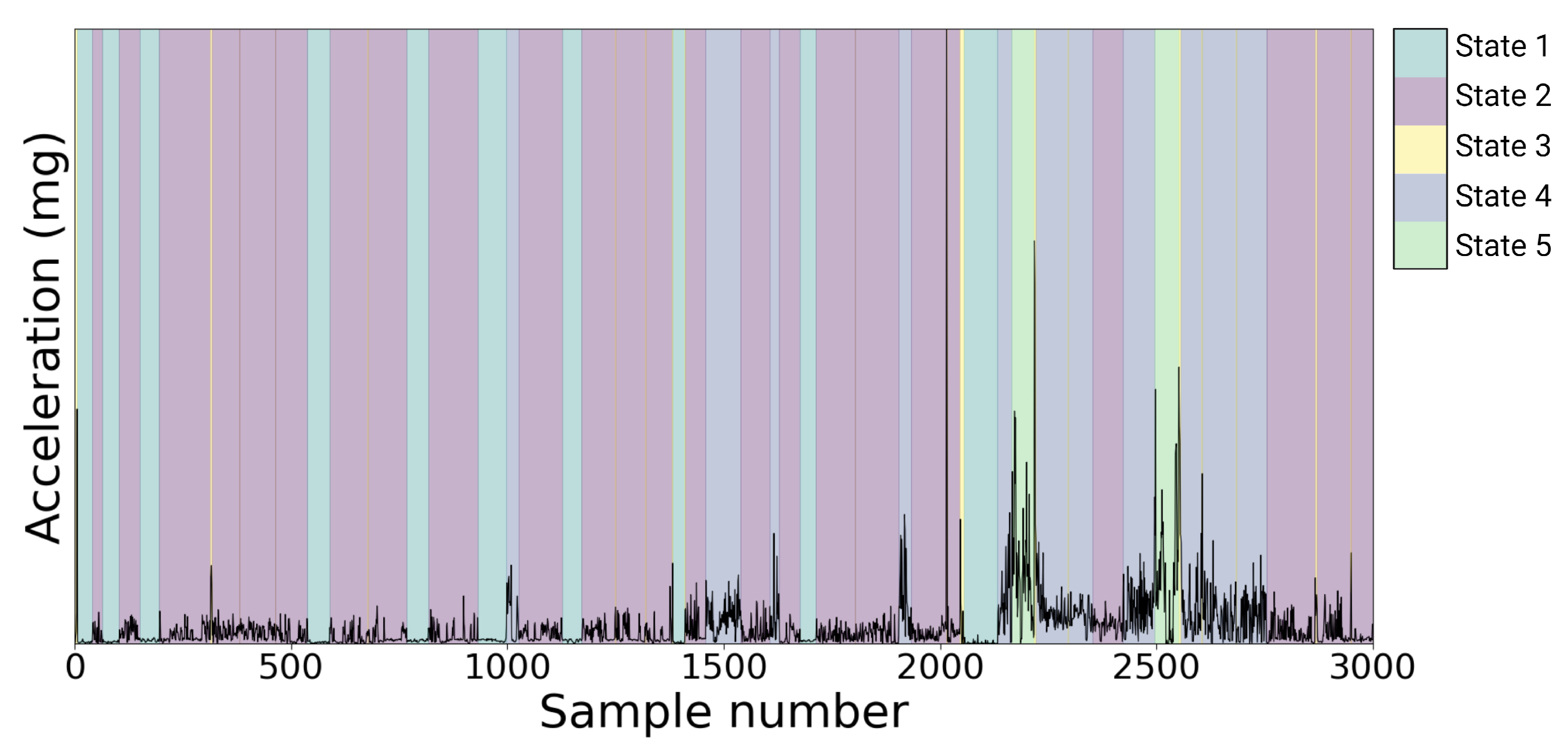
3. Results
3.1. Dataset Description
3.2. Model Selection
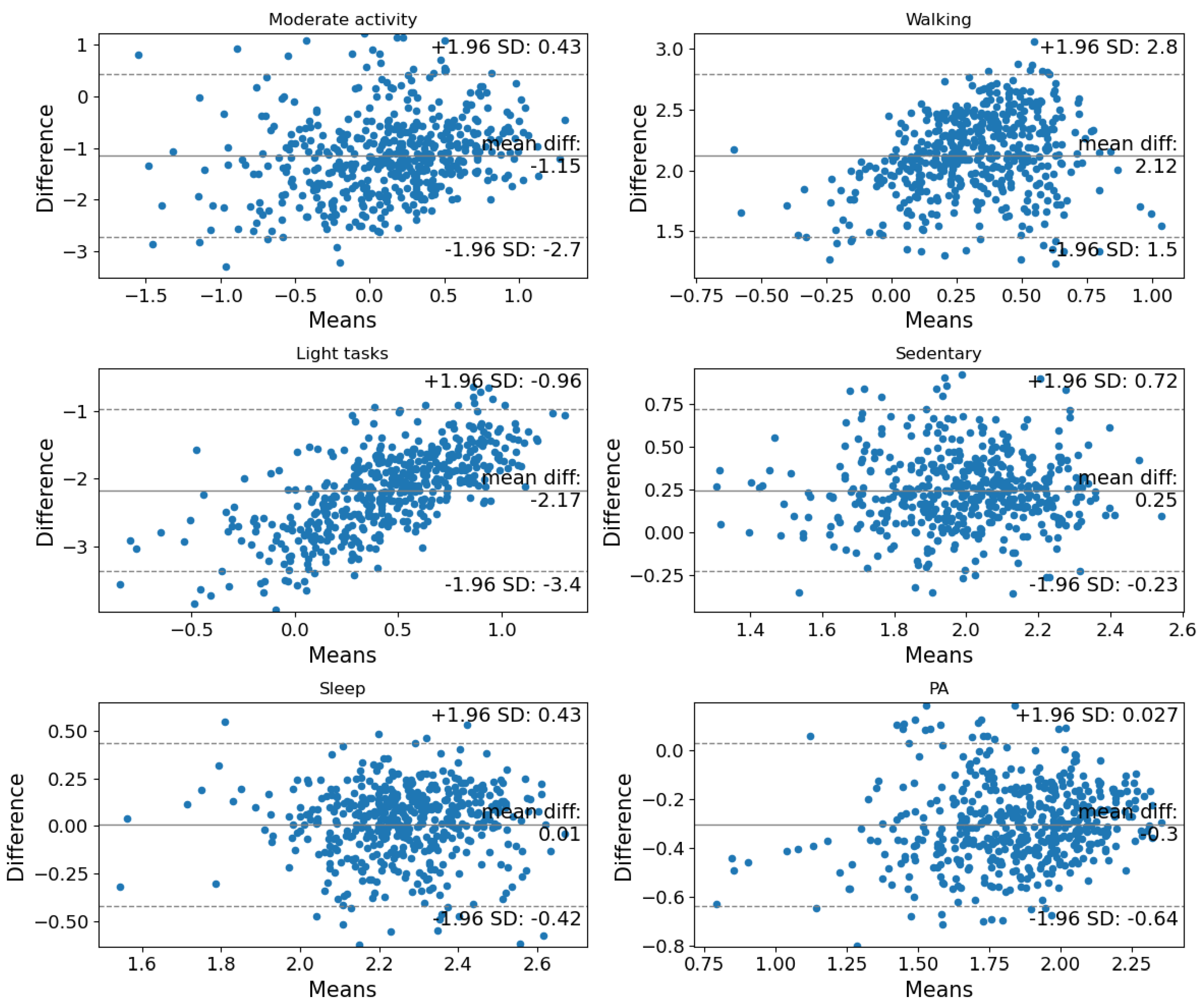
3.3. Model Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BMI | Body mass index |
| CPM | Counts-per-minute |
| HSMM | Hidden semi-Markov model |
| HSM | Hidden Markov model |
| MET | Metabolic equivalent |
| MPA | Moderate physical activity |
| PA | Physical activity |
| SB | Sedentary behaviour |
| WC | Waist circumference |
References
- Ekelund, U.; Steene-Johannessen, J.; Brown, W.J.; Fagerland, M.W.; Owen, N.; Powell, K.E.; Bauman, A.; Lee, I.M. Does physical activity attenuate, or even eliminate, the detrimental association of sitting time with mortality? A harmonised meta-analysis of data from more than 1 million men and women. Lancet 2016, 388, 1302–1310. [Google Scholar] [CrossRef]
- Ekelund, U.; Tarp, J.; Steene-Johannessen, J.; Hansen, B.H.; Jefferis, B.; Fagerland, M.W.; Whincup, P.; Diaz, K.M.; Hooker, S.P.; Chernofsky, A.; et al. Dose-response associations between accelerometry measured physical activity and sedentary time and all cause mortality: Systematic review and harmonised meta-analysis. BMJ 2019, 366, l4570. [Google Scholar] [CrossRef] [PubMed]
- Dempsey, P.C.; Biddle, S.J.; Buman, M.P.; Chastin, S.; Ekelund, U.; Friedenreich, C.M.; Katzmarzyk, P.T.; Leitzmann, M.F.; Stamatakis, E.; van der Ploeg, H.P.; et al. New global guidelines on sedentary behaviour and health for adults: Broadening the behavioural targets. Int. J. Behav. Nutr. Phys. Act. 2020, 17, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Tremblay, M.; Colley, R.; Saunders, T.; Healy, G.; Owen, N. Physiological and health implications of a sedentary lifestyle. Appl. Physiol. Nutr. Metab. 2010, 35, 725–740. [Google Scholar] [CrossRef]
- Haskell, W.L.; Lee, I.M.; Pate, R.R.; Powell, K.E.; Blair, S.N.; Franklin, B.A.; MacEra, C.A.; Heath, G.W.; Thompson, P.D.; Bauman, A. Physical activity and public health: Updated recommendation for adults from the American College of Sports Medicine and the American Heart Association. Med. Sci. Sport. Exerc. 2007, 39, 1423–1434. [Google Scholar] [CrossRef]
- Watson, K.B.; Carlson, S.A.; Carroll, D.D.; Fulton, J.E. Comparison of accelerometer cut points to estimate physical activity in US adults. J. Sport. Sci. 2014, 32, 660–669. [Google Scholar] [CrossRef]
- Willetts, M.; Hollowell, S.; Aslett, L.; Holmes, C.; Doherty, A. Statistical machine learning of sleep and physical activity phenotypes from sensor data in 96,220 UK Biobank participants. Sci. Rep. 2018, 8, 7961. [Google Scholar] [CrossRef]
- Farrahi, V.; Niemelä, M.; Kangas, M.; Korpelainen, R.; Jämsä, T. Calibration and validation of accelerometer-based activity monitors: A systematic review of machine-learning approaches. Gait Posture 2019, 68, 285–299. [Google Scholar] [CrossRef]
- Trabelsi, D.; Mohammed, S.; Chamroukhi, F.; Oukhellou, L.; Amirat, Y. An unsupervised approach for automatic activity recognition based on Hidden Markov Model regression. IEEE Trans. Autom. Sci. Eng. 2013, 10, 829–835. [Google Scholar] [CrossRef]
- Ong, W.H.; Koseki, T.; Palafox, L. An unsupervised approach for human activity detection and recognition. Int. J. Simul. Syst. Sci. Technol. 2013, 14, 42–49. [Google Scholar] [CrossRef]
- Weber, N. Unsupervised Learning in Human Activity Recognition: A First Foray Into Clustering Data Gathered from Wearable Sensors. Ph.D. Thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Duong, T.V.; Bui, H.H.; Phung, D.Q.; Venkatesh, S. Activity recognition and abnormality detection with the switching hidden semi-Markov model. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 838–845. [Google Scholar] [CrossRef]
- Van Kasteren, T.L.; Englebienne, G.; Kröse, B.J. Activity recognition using semi-Markov models on real world smart home datasets. J. Ambient Intell. Smart Environ. 2010, 2, 311–325. [Google Scholar] [CrossRef]
- Van Kuppevelt, D.; Heywood, J.; Hamer, M.; Sabia, S.; Fitzsimons, E.; Van Hees, V. Segmenting accelerometer data from daily life with unsupervised machine learning. PLoS ONE 2019, 14, e0208692. [Google Scholar] [CrossRef]
- Wirth, K.; Klenk, J.; Brefka, S.; Dallmeier, D.; Faehling, K.; Roqué i Figuls, M.; Tully, M.A.; Giné-Garriga, M.; Caserotti, P.; Salvà, A.; et al. Biomarkers associated with sedentary behaviour in older adults: A systematic review. Ageing Res. Rev. 2017, 35, 87–111. [Google Scholar] [CrossRef]
- Silva, B.G.C.; Silva, I.C.M.; Ekelund, U.; Brage, S.; Ong, K.K.; De Lucia Rolfe, E.; Lima, N.P.; da Silva, S.G.; de França, G.V.; Horta, B.L. Associations of physical activity and sedentary time with body composition in Brazilian young adults. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef]
- Sudlow, C.; Gallacher, J.; Allen, N.; Beral, V.; Burton, P.; Danesh, J.; Downey, P.; Elliott, P.; Green, J.; Landray, M.; et al. UK Biobank: An open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 2015, 12, 1–10. [Google Scholar] [CrossRef]
- Doherty, A.; Jackson, D.; Hammerla, N.; Plötz, T.; Olivier, P.; Granat, M.H.; White, T.; Van Hees, V.T.; Trenell, M.I.; Owen, C.G.; et al. Large scale population assessment of physical activity using wrist worn accelerometers: The UK Biobank study. PLoS ONE 2017, 12, e0169649. [Google Scholar] [CrossRef]
- Johnson, M.J.; Willsky, A.S. Bayesian nonparametric Hidden semi-Markov models. J. Mach. Learn. Res. 2013, 14, 673–701. [Google Scholar]
- Teh, Y.W. Dirichlet Process. Encycl. Mach. Learn. 2010, 1063, 280–287. [Google Scholar]
- Witowski, V.; Foraita, R.; Pitsiladis, Y.; Pigeot, I.; Wirsik, N. Using hidden Markov models to improve quantifying physical activity in accelerometer data—A simulation study. PLoS ONE 2014, 9, e114089. [Google Scholar] [CrossRef]
- Bland, M.J.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Chastin, S.F.M.; Palarea-Albaladejo, J.; Dontje, M.L.; Skelton, D.A. Combined effects of time spent in physical activity, sedentary behaviors and sleep on obesity and cardio-metabolic health markers: A novel compositional data analysis approach. PLoS ONE 2015, 10, e0139984. [Google Scholar] [CrossRef]
- Dumuid, D.; Pedišić, Ž.; Stanford, T.E.; Martín-Fernández, J.A.; Hron, K.; Maher, C.A.; Lewis, L.K.; Olds, T. The compositional isotemporal substitution model: A method for estimating changes in a health outcome for reallocation of time between sleep, physical activity and sedentary behaviour. Stat. Methods Med Res. 2019, 28, 846–857. [Google Scholar] [CrossRef]
- World Health Organization. Global Health Risks: Mortality and Burden of Disease Attributable to Selected Major Risks; WHO: Geneva, Switzerland, 2009. [Google Scholar]
- Slade, P.; Kochenderfer, M.; Delp, S.E.A. Sensing leg movement enhances wearable monitoring of energy expenditure. Nat. Commun. 2021, 12, 4312. [Google Scholar] [CrossRef]
- Slade, P.; Habib, A.; Hicks, J.L.; Delp, S.L. An Open-Source and Wearable System for Measuring 3D Human Motion in Real-Time. IEEE Trans. Biomed. Eng. 2022, 69, 678–688. [Google Scholar] [CrossRef]
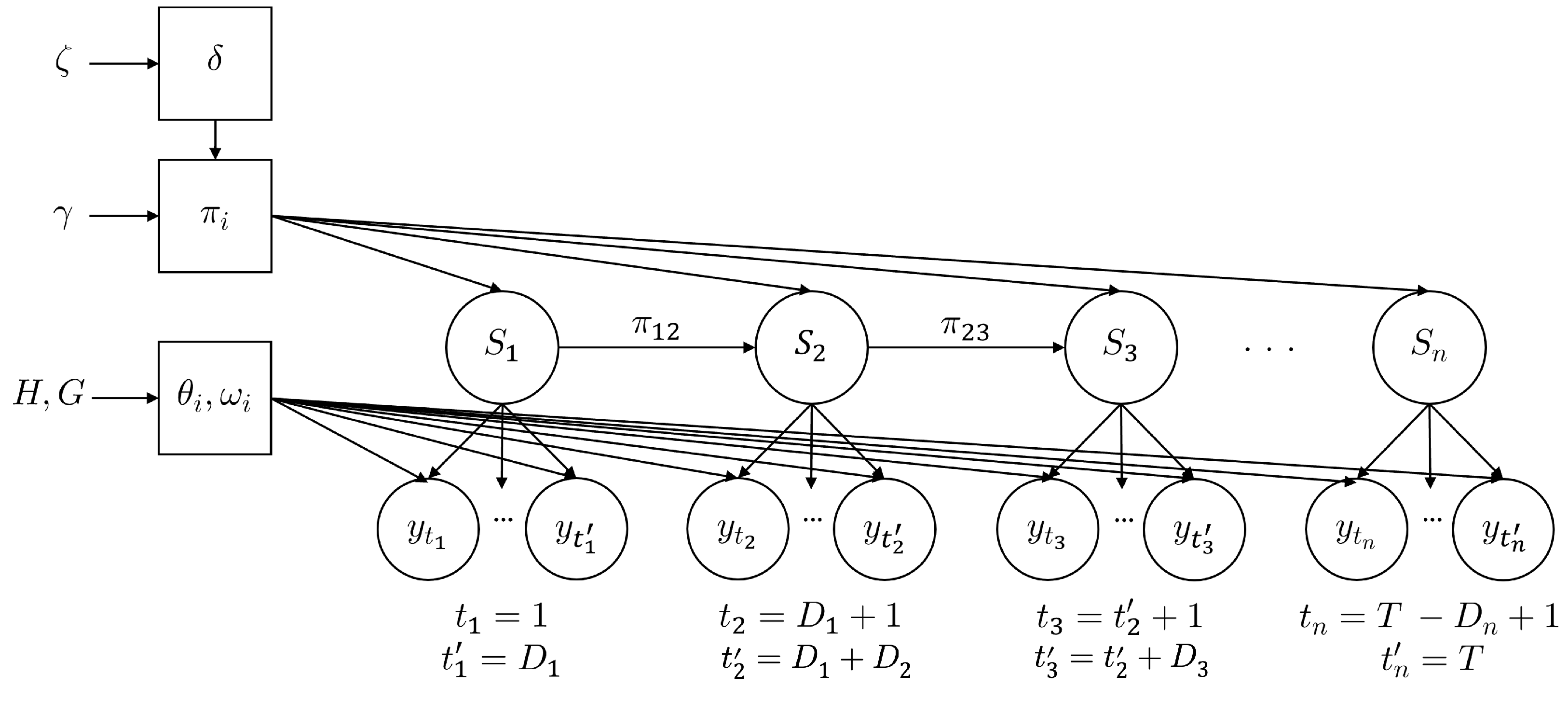
| Duration | Observations | |
|---|---|---|
| Distribution | Poisson | Gaussian |
| Parameters | , | |
| Conjugate prior | Gamma | Gaussian |
| Hyperparameter | , | , |
| Variable | n = 500 |
|---|---|
| Sex (% males) | 49 |
| Age (years) | 56.08 (7.89) |
| BMI (kg/m) | 29.57 (4.22) |
| Waist circumference (cm) | 95.46 (12.47) |
| MPA (hours/day) | 0.79 (0.54) |
| Walking (hours/day) | 4.16 (1.28) |
| Light tasks (hours/day) | 0.63 (0.37) |
| Sedentary time (hours/day) | 8.45 (1.94) |
| Sleep (hours/day) | 9.83 (1.91) |
| Overall activity (hours/day) | 5.58 (1.45) |
| Activity | Magnitude | X-Axis | Y-Axis | Z-Axis | Duration (s) |
|---|---|---|---|---|---|
| MPA | 0.084 (0.147) | −0.042 (0.536) | −0.078 (0.433) | 0.165 (0.634) | 44 |
| SB | 0.014 (0.022) | −0.077 (0.531) | −0.009 (0.527) | 0.14 (0.613) | 196 |
| Sleep | 0.003 (0.007) | −0.015 (0.495) | −0.006 (0.563) | 0.114 (0.649) | 471 |
| Light tasks | 0.049 (0.096) | −0.08 (0.446) | −0.065 (0.734) | 0.001 (0.411) | 53 |
| Walking | 0.088 (0.078) | −0.027 (0.563) | −0.091 (0.606) | −0.074 (0.401) | 125 |
| Average | 0.048 | −0.048 | −0.05 | 0.069 | 178 |
| Activity | Magnitude | Magnitude + Axes | Axes | Magnitude + Angles |
|---|---|---|---|---|
| MPA | 0.11 [0.02–0.19] | 0.12 [0.03–0.21] | 0.23 [0.15–0.31] | −0.02 [−0.11–0.07] |
| Walking | 0.5 [0.43–0.57] | 0.49 [0.42–0.56] | −0.06 [−0.15–0.03] | 0.45 [0.38–0.52] |
| Light tasks | 0.11 [0.03–0.2] | 0.1 [0.01–0.18] | 0.13 [0.04–0.21] | 0.04 [−0.05–0.12] |
| SB | 0.22 [0.13–0.3] | 0.26 [0.18–0.34] | −0.04 [−0.13–0.05] | 0.18 [−0.05–0.12] |
| Sleep | 0.35 [0.27–0.42] | 0.22 [0.14–0.30] | −0.12 [−0.21–−0.03] | 0.29 [0.21–0.37] |
| Overall PA | 0.59 [0.53–0.64] | 0.55 [0.48–0.61] | 0.03 [−0.06–0.12] | 0.48 [0.41–0.55] |
| Average (std) | 0.31 (0.2) | 0.29 (0.19) | 0.03 (0.13) | 0.09 (0.32) |
| Activity | Very Informative | Medium | Very Uninformative |
|---|---|---|---|
| MPA | 0.17 [0.08–0.25] | 0.11 [0.02–0.19] | 0.18 [0.1–0.2] |
| Walking | 0.35 [0.27–0.43] | 0.5 [0.43–0.57] | 0.28 [0.2–0.36] |
| Light tasks | 0.19 [0.10–0.27] | 0.11 [0.03–0.2] | 0.19 [0.1–0.27] |
| Sedentary | 0.37 [0.29–0.44] | 0.22 [0.13–0.3] | 0.48 [0.41–0.55] |
| Sleep | 0.34 [0.26–0.41] | 0.35 [0.27–0.42] | 0.39 [0.31–0.46] |
| Overall PA | 0.71 [0.67–0.75] | 0.59 [0.53–0.64] | 0.81 [0.31–0.84] |
| Average (std) | 0.36 (0.19) | 0.31 (0.2) | 0.39 (0.23) |
| Magnitude | Duration | ||
|---|---|---|---|
| Activity | (s) | ||
| Walking | 0.17 | 0.058 | 8 |
| Tasks | 0.04 | 0.001 | 308 |
| SB | 0.01 | 0.0001 | 366 |
| Sleeping | 0.002 | 3 | 452 |
| MPA | 0.11 | 0.005 | 254 |
| Outcome | Activity | Reference | Inferred |
|---|---|---|---|
| BMI (kg/m) | SB (h/day) | 3.27 *** | 4.51 *** |
| BMI (kg/m) | PA (h/day) | −3.43 *** | −2.74 ** |
| BMI (kg/m) | Sleep (h/day) | 0.16 | −1.77 * |
| WC (cm) | SB (h/day) | 9.96 *** | 12.54 *** |
| WC (cm) | PA (h/day) | −11.46 *** | −7.62 ** |
| WC (cm) | Sleep (h/day) | 1.51 | −4.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavallo, F.R.; Toumazou, C.; Nikolic, K. Unsupervised Classification of Human Activity with Hidden Semi-Markov Models. Appl. Syst. Innov. 2022, 5, 83. https://doi.org/10.3390/asi5040083
Cavallo FR, Toumazou C, Nikolic K. Unsupervised Classification of Human Activity with Hidden Semi-Markov Models. Applied System Innovation. 2022; 5(4):83. https://doi.org/10.3390/asi5040083
Chicago/Turabian StyleCavallo, Francesca Romana, Christofer Toumazou, and Konstantin Nikolic. 2022. "Unsupervised Classification of Human Activity with Hidden Semi-Markov Models" Applied System Innovation 5, no. 4: 83. https://doi.org/10.3390/asi5040083
APA StyleCavallo, F. R., Toumazou, C., & Nikolic, K. (2022). Unsupervised Classification of Human Activity with Hidden Semi-Markov Models. Applied System Innovation, 5(4), 83. https://doi.org/10.3390/asi5040083







