A Fuzzy Inference System for Unsupervised Deblurring of Motion Blur in Electron Beam Calibration

Abstract

This paper presents a novel method of restoring the electron beam (EB) measurements that are degraded by linear motion blur. This is based on a fuzzy inference system (FIS) and Wiener inverse filter, together providing autonomy, reliability, flexibility, and real-time execution. This system is capable of restoring highly degraded signals without requiring the exact knowledge of EB probe size. The FIS is formed of three inputs, eight fuzzy rules, and one output. The FIS is responsible for monitoring the restoration results, grading their validity, and choosing the one that yields to a better grade. These grades are produced autonomously by analyzing results of a Wiener inverse filter. To benchmark the performance of the system, ground truth signals obtained using an 18 μm wire probe were compared with the restorations. Main aims are therefore: (a) Provide unsupervised deblurring for device independent EB measurement; (b) improve the reliability of the process; and (c) apply deblurring without knowing the probe size. These further facilitate the deployment and manufacturing of EB probes as well as facilitate accurate and probe-independent EB characterization. This paper’s findings also makes restoration of previously collected EB measurements easier where the probe sizes are not known nor recorded.

1. Introduction

The main goal of fuzzy systems is to define and control sophisticated processes by incorporating and taking advantage of human knowledge and experience. Nowadays, fuzzy logics are widely used in industry for various applications ranging from cameras to cement kilns, trains, and vacuum cleaners [1]. Furthermore, deblurring techniques have versatile applications and they are either performed in spatial [2] or frequency domains [3,4,5]. Hosseinzadeh [6] modeled the electron beam (EB) measurement process with a linear motion blur and evaluated three of the well-established deblurring techniques for EB restoration. In this study [6], Hosseinzadeh used a Weiner inverse filter and blind Richardson-Lucy deconvolutions to restore the EB distribution and correct the measurements through deblurring. A simple motion blur is formulated in Equation (1).

$$g\left(x\right)=\int f\left(x\right)h\left(x\right)+n\left(x\right),$$

(1)

where in the spatial domain, $f$, $g$, $h$, and $n$ are the ground truth signal (EB distribution) of length $L_f$, degraded signal (measurement from probe), point spread function (PSF) of length $L_h$, and noise respectively. Their frequency domains are represented by uppercase letters $F,G$, and $H$. In the case of electron beam measurements, the ground truth signal is the distribution of EB and the degraded signal is the measurement acquired from the probe. The electron absorption of a slit or wire probe of size $L_h$ is modeled with a PSF kernel [6].

Linear motion blur point spread function has two distinct characteristics of motion direction and length ($L$) [7]. The PSF is known for having harmonically spaced vanishing magnitudes in the frequency domain due to its limited length in the spatial domain [8]. There are several approaches to estimate $L_h$ such as log power spectrum, cepstrum, bispectrum, and pitch detection algorithms. In image deblurring jargon, it is assumed that the frequency spectrum of $F$ is smooth and does not contain vanishing frequencies, hence any vanishing frequencies in $G$ are associated to $H$ [9,10]. However, this assumption usually does not hold for EB measurements, especially where the $L_f$ is in the same order of $L_h$. This similarity makes it complicated to distinguish between $L_f$ and $L_h$ and therefore compromises the deblurring process by an incorrect detection of null frequencies. Such an erroneous deblurring process is likely to produce an incorrect but convincing result, notably when $f$ and $h$ have remarkable cross-correlation. This ambiguity is likely to happen in EB measurements, because: (a) $f$ and $h$ are usually in the same order of magnitude and they have relatively high cross-correlation; and (b) the $L_f$ can be inconsistent. In Reference [6], a prior knowledge of $L_h$ is used to estimate the position of null frequency of $h$ from the spectrum analysis of $G$. Hosseinzadeh limited the spectrum of $G$ to ±15% of the nominal $L_h$ by applying a window to its log-power spectrum, thereby ignoring vanishing frequencies outside of this interval. This algorithm is available in Reference [11]. This strategy relies on knowing the $L_h$. Therefore, it is a good approach when it is known accurately. There are a few limitations with this method due to the varying nature of $L_f$ during the calibration and measurement process. As a result, the beam’s vanishing frequency (or its harmonics) can be located within the applied window and cause a false detection. Furthermore, if the inaccuracy of $L_h$ is more than 15%, the null frequency of $h$ is ignored by the window resulting in an erroneous restoration. In addition, any inaccuracy of more than ±15% cannot be compensated.

One solution to effectively address this uncertainty is to use fuzzy systems. Fuzzy inference systems are widely used to address instrumental uncertainties. A comprehensive review and explanation of fuzzy inference systems are provided in Reference [12].

It is known that a wrong estimation of $L_h$ can lead to drastic noise-like errors in the restorations [13]. Furthermore, utilizing deblurring techniques for industrial purposes requires real-time, reliable, and unsupervised methods. To satisfy these requirements, this article proposes a Wiener filter that is monitored by a fuzzy inference system. A Wiener filter is selected due to its simplicity, real-time execution, and superior performance in the restoration of linear motion blur [6]. The fuzzy inference system deals with the uncertainty of the deconvolution by monitoring the entire restoration process. This FIS is comprised of three crisp inputs that included the PSF length or probe size ($L_h$) deviation, attenuation of the vanishing frequencies, and deconvolution residue.

However, probe size deviation is an optional input, which is based on a previous rough knowledge of $L_h$. If $L_h$ is roughly known, it serves as a reference point from which the PSF length deviation is calculated. Therefore, unlike Reference [6], prior knowledge of $L_h$ does not limit the inaccuracy compensation to ±15%. It is demonstrated in Reference [6] that the spatial domain of $h$ has a sharper transition compared to the EB distribution ($f$). This is due to the semi-Gaussian distribution of $f$ compared to $h$. Therefore, vanishing frequencies of $h$ are expected to have higher attenuation or lower magnitude compared to $f$. Hence, the normalized magnitude of the detected null frequencies in $G$ are the second crisp input to the fuzzy inference systems. The last input of the system is the quantified deblurring artifacts that are introduced during the restoration of $f$ from $g$. The restored beam distributions are denoted as ($\widehat{f}$). These residual artifacts are inevitable and they increase as the $h$ deviates from its mathematical definition. Extraction of residues from $\widehat{f}$ is explained in section II. The output of the fuzzy system ($E_i$) is defuzzified to represent the quality of the restorations. This output is generated based on the definition of the fuzzy rules that are explained in the next section.

The rest of this paper is arranged as follows: Section 2 illustrates the details of FIS implementation. This includes specifying the crisp inputs and fuzzifying them, defining the membership functions, and formulating the fuzzy sets. The section continues by identifying the fuzzy rules and making an inference to generate the output. Section 3 presents the practical results of the proposed method and the ability of the system to distinguish the correct deblurring results. The values of membership functions parameters are provided and a comparison is made between implementing the fuzzy system with and without the knowledge of probe size ($L_h$).

2. Modeling and Implementation

As mentioned, when there is similarity between $L_f$ and $L_h$ it is difficult to discriminate between their null frequencies just by looking at $G$. This introduces an uncertainty and makes it hard to decide which null frequency belongs to the probe ($H$) because null frequencies can belong to either beam ($F$) or probe ($H$). To address the uncertainty of unsupervised $L_h$ detection, all the null frequencies in $G$ are identified and only the first two nulls with lowest frequencies are extracted while avoiding the harmonics. This implies that a maximum of two null frequencies (${\omega }_{i=1,2}$) are to be extracted from $G$. There are three possibilities based on the extracted number of null frequencies: (a) If no null frequency is detected due to $L_h\ll L_f$, then motion blur effect is negligible and deconvolution is not necessary; (b) if a single null frequency is detected as a result of $L_h\gg L_f$, then the deconvolution can progress without involving the fuzzy system as the null frequency belongs to $L_h$; (c) in case two null frequencies are extracted (${\omega }_1,{\omega }_2)$, two deconvolutions are performed where each of the deconvolutions are performed by adjusting their corresponding ${\widehat{L}}_{i=1,2}$ (${\widehat{L}}_{i=1,2}\propto 1/{\omega }_{i=1,2}$). This is done because both ${\omega }_1$ and ${\omega }_2$ could be belonging to $h$ of different sizes.

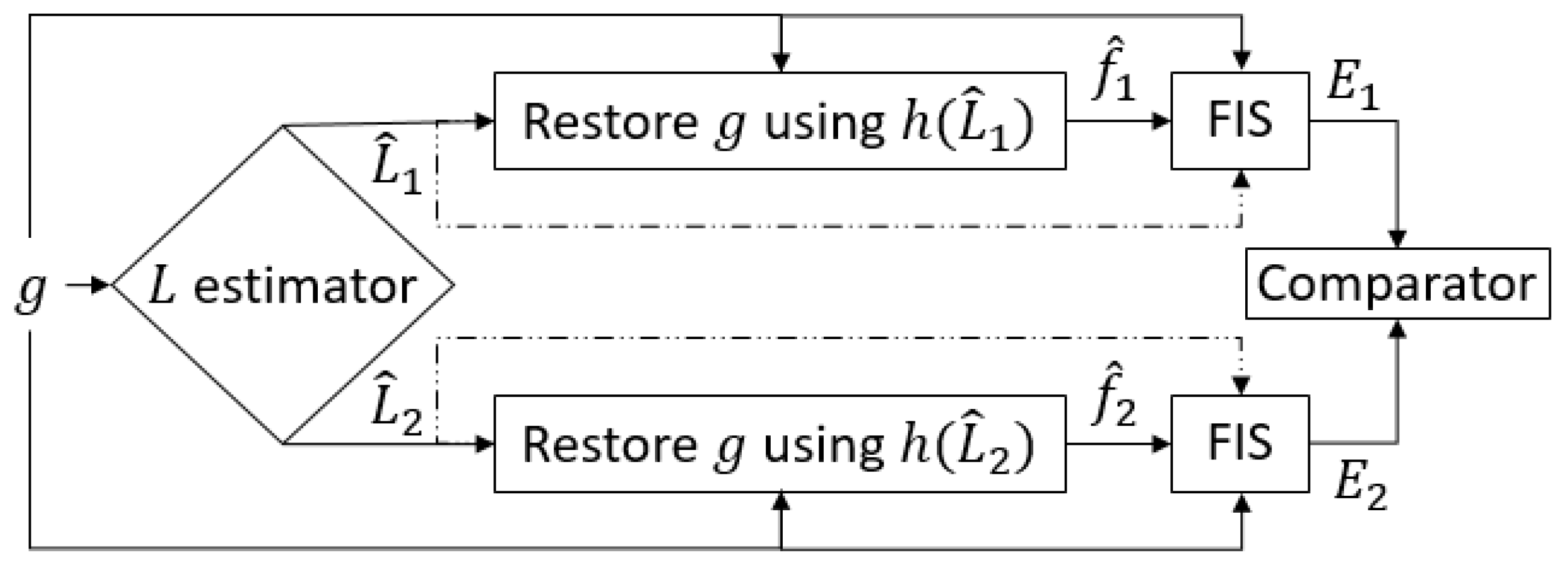
The FIS is defined with three merits to grade the deblurrings. Deblurrings are performed by two individual Weiner filters that use ${\widehat{L}}_1$ and ${\widehat{L}}_2$ resulting in ${\widehat{f}}_1$ and ${\widehat{f}}_2$ respectively. The fuzzy system produces a single crisp output deconvolution grade ($E_{i=1,2}$) for each restoration. The restoration process that produces a higher $E_i$ is then chosen as the correct process with its corresponding ${\widehat{L}}_i$ being the correct probe size ($L_h\leftarrow {\widehat{L}}_i$). A single layer (non-hierarchal) fuzzy inference system of three inputs and a single output is designed to evaluate the overall deblurring process. These inputs are: PSF length deviation, null frequency magnitude, and residue, and the deconvolution grade is the only output. These inputs and the output are explained in detail as follows.

2.1. PSF Length Deviation

As mentioned, ${\omega }_1$ and ${\omega }_2$ are extracted to accurately adjust the $L_h$ during the restoration process. By having rough prior knowledge of the probe size ($L_h$) and the estimated sizes (${\widehat{L}}_i$) from $G$, we can define PSF length deviation as the distance between the expected and the estimations ($|L_h-{\widehat{L}}_i|$). This definition converges to zero if the estimation is close to the prior knowledge, whereas it increases if ${\widehat{L}}_i$ is deviated from $L_h$. 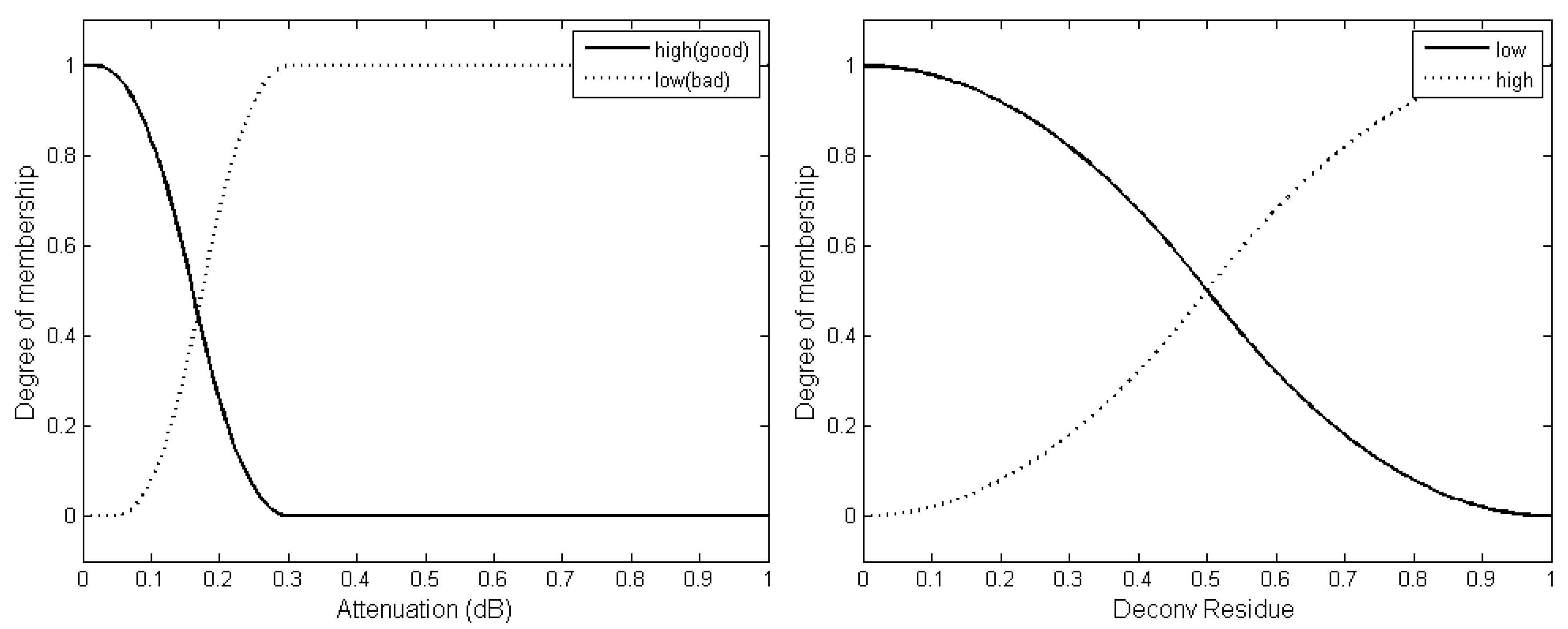Two fuzzy sets ($A_{far}$ & $A_{close}$) with membership functions of ${\mu }_m^{\prime }$ and ${\mu }_m$ are defined to account for the probe inaccuracy and assign a degree of membership to each ${\widehat{L}}_i$ based on its deviation from $L_h$. Membership functions are defined by polynomial-Z (zmf) and polynomial-S (smf). The $A_{close}$ fuzzy set definition and its membership function is formulated in Equation (2). A thorough evaluation of fuzzy membership functions are provided in Reference [14].

$$\begin{gathered} A_{close}=\{({\widehat{L}}_i,{\mu }_{m({\widehat{L}}_i)})|0<{\widehat{L}}_i<\infty ,m({\widehat{L}}_i)=\frac{2|L_h-{\widehat{L}}_i|}{L_h}\}, \\ {\mu }_m=\{\begin{array}{cc}1& m\le a_m\\ 1-2{\left(\frac{m-a_m}{c_m-a_m}\right)}^2& a_m<m\le \frac{a_m+c_m}{2}\\ 2{\left(\frac{m-c_m}{c_m-a_m}\right)}^2& \frac{a_m+c_m}{2}<m\le c_m\\ 0& m>c_m\end{array}, \end{gathered}$$

(2)

where $a_m$ and $c_m$ are the membership function parameters that are found heuristically through analysis of several measurements.

2.2. Null Frequency Magnitude

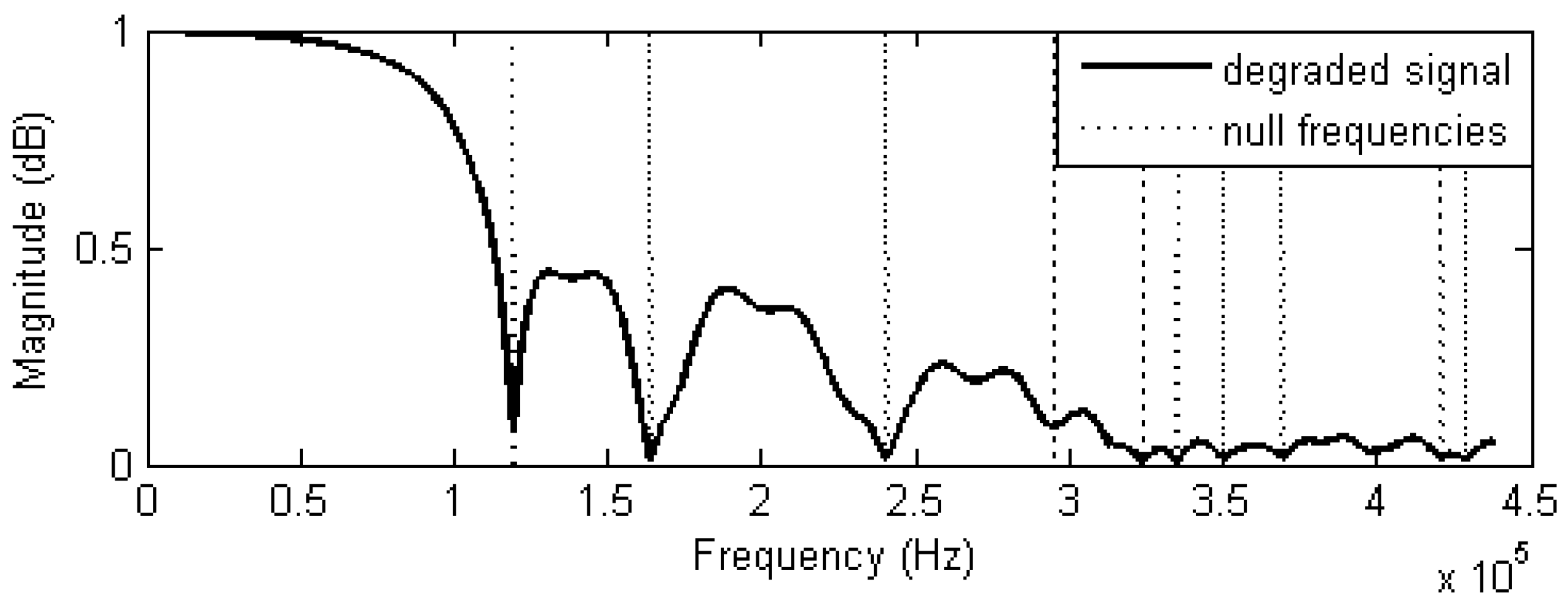
The second input of the fuzzy system is the magnitude of the extracted null frequencies. This is extracted from the normalized log-power spectrum of $g$ and has a dynamic range of 0 to 1 dB, demonstrated in Figure 1.

As explained, $h$ is most likely to have rapid spatial transitions compared to $f$. This implies that $H$ is likely to have the nulls with higher attenuation in $G$ (nulls with lower magnitude). As a result, two fuzzy sets ($B_{high}$ & $B_{Low}$) with membership functions of ${\mu }_o^{\prime }$ and ${\mu }_o$ are defined to assign a higher membership value to the nulls with more attenuation (or lower magnitude), whereas a lower degree of membership is assigned to less attenuated (higher magnitude) nulls. Membership functions are defined with zmf and sfm. $B_{Low}$ is formulated in Equation (3), where $G_N$ is the normalized frequency spectrum of the degraded signal $G$ and $a_o$ and $c_o$ are the membership function parameters. $A_{Far}$ membership function definition is similar to $B_{Low}$ as they are both defined by smf.

$$\begin{gathered} B_{Low}=\{({\widehat{L}}_i,{\mu }_{o({\widehat{L}}_i)}^{\prime })|0<{\widehat{L}}_i<\infty ,o({\widehat{L}}_i)=\log (|G_N({\widehat{L}}_i)+1|)\}, \\ {\mu }_o^{\prime }=\{\begin{array}{cc}0& o\le a_o\\ 2{\left(\frac{o-a_o}{c_o-a_o}\right)}^2& a_o<o\le \frac{a_o+c_o}{2}\\ 1-2{\left(\frac{o-c_o}{c_o-a_o}\right)}^2& \frac{a_o+c_o}{2}<o\le c_o\\ 1& o>c_o\end{array}, \end{gathered}$$

(3)

2.3. Deconvolution Artifact Residues

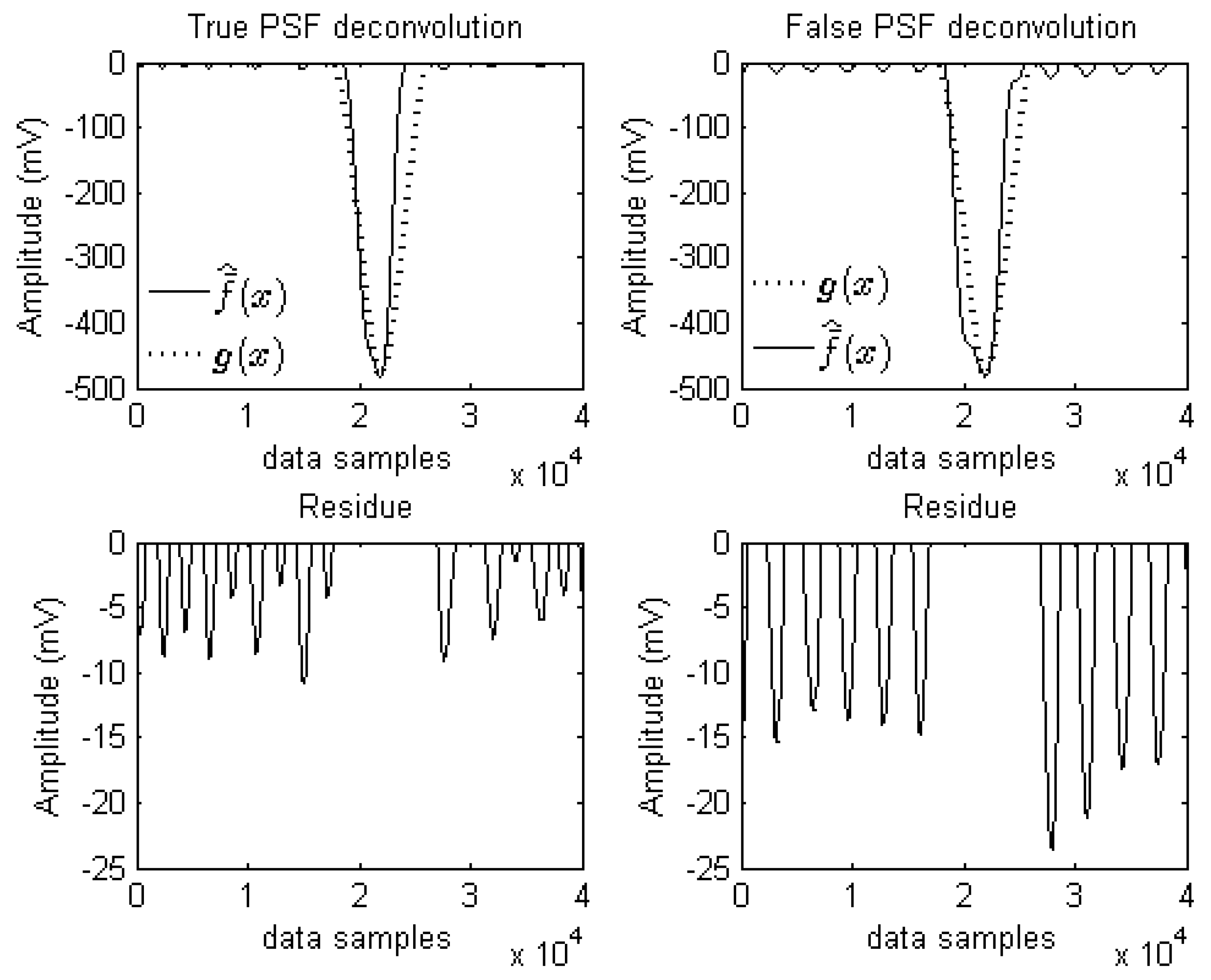
Deconvolutions are performed using the Wiener inverse filtering process in Equation (4).

$${\widehat{F}}_i=\frac{1}{H\left({\omega }_i\right)}\left[\frac{|H\left({\omega }_i\right){|}^2}{{\left|H\left({\omega }_i\right)\right|}^2+\frac{1}{SNR\left(\omega \right)}}\right]G\left(\omega \right),$$

(4)

where in the frequency domain, ${\widehat{F}}_i$ is the restored ground truth signal and $SNR$ is the signal-to-noise ratio. After the deconvolutions,${\widehat{f}}_{i=1,2}$ has shorter lengths in spatial domain compared to $g$. We first normalized $g$ and both of the restorations (${\widehat{f}}_{i=1,2}$) between $\left[0,-1\right]$, $g_N$ is then shifted so its minimum is matched with the minimums of each ${\widehat{f}}_i$ in the spatial domain to obtain ${\widehat{g}}_N$. Finally, every restoration residue ($r_i$) is quantified as in Equation (5).

$$r_i=\frac{4}{\int g\left(x\right)dx}·\int {\widehat{f}}_i\left(\tau \right)d\tau \hspace{1em}\hspace{1em}\{\tau \in x|{\widehat{g}}_N\left(\tau \right)>-0.05\},$$

(5)

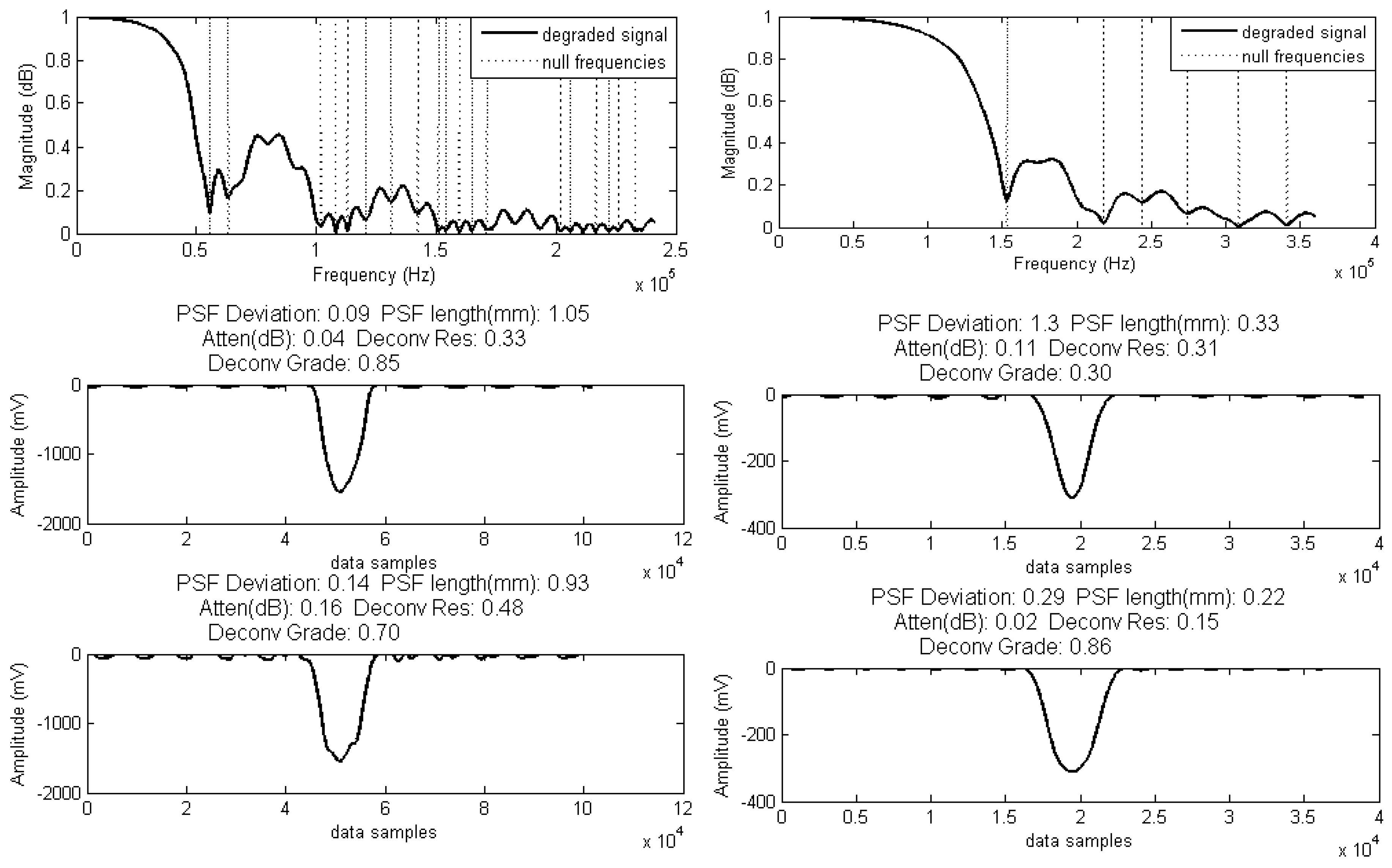
The deconvolution process using both of the extracted PSFs and their corresponding residues are showed in Figure 2. The deconvolution was performed with a Wiener inverse filter, where $h$ is formulated in Equation (6).

$$h_{{\widehat{L}}_i}\left(x\right)=\{\begin{array}{c}0\hspace{1em}\hspace{1em}o.w\\ 1\hspace{1em}\left|x\right|<\frac{{\widehat{L}}_i}{2}\end{array},$$

(6)

Two fuzzy sets ($C_{low}$ and $C_{high}$) are defined with membership functions of ${\mu }_r$ and ${\mu }_r^{\prime }$ using zmf and smf respectively, where the overall shape of the functions is determined by $a_r$ and $c_r$. These functions are designed to assign a higher degree of membership to the ${\widehat{L}}_i$ that produces a smaller number of residues after restoration.

2.4. Deconvolution Grade

All the combinations of the aforementioned inputs are used to form eight if–then rule statements with different weights. These statements, with their corresponding weights, are provided in

Table 1. Rule base formation criteria.

Antecedent			Consequence	Rule Weight
PSF Dev	Attenuation	Residue	Restoration Quality
${\mu }_m$	${\mu }_o$	${\mu }_r$	${\mu }_g$	1
${\mu }_m$	${\mu }_o$	${\mu }_r^{\prime }$	${\mu }_g$	0.66
${\mu }_m$	${\mu }_o^{\prime }$	${\mu }_r$	${\mu }_g$	0.66
${\mu }_m$	${\mu }_o^{\prime }$	${\mu }_r^{\prime }$	${\mu }_b$	0.66
${\mu }_m^{\prime }$	${\mu }_o$	${\mu }_r$	${\mu }_g$	0.66
${\mu }_m^{\prime }$	${\mu }_o$	${\mu }_r^{\prime }$	${\mu }_b$	0.66
${\mu }_m^{\prime }$	${\mu }_o^{\prime }$	${\mu }_r$	${\mu }_b$	0.66
${\mu }_m^{\prime }$	${\mu }_o^{\prime }$	${\mu }_r^{\prime }$	${\mu }_b$	1

. Fuzzy AND operator is then used for the implication of the fuzzy consequences.

Rule weight is added to scale the consequences and account for the certainty of the rules. The consequence is the restoration quality with two fuzzy sets $(D_{good}\&D_{bad})$ and membership functions of ${\mu }_q$ and ${\mu }_q^{\prime }$ respectively defined by smf and zmf. Aggregations of the rules are performed by using a Zadeh T-norm and defuzzifications are carried out by mean of maximum (MoM) method [15]. The resulting crisp values are the deconvolution grades $\left(E_{i=1,2}\right)$. Therefore, there is a grade $\left(E_{i=1,2}\right)$ for each deconvolution. In other words, for each ${\widehat{f}}_{i=1,2}$ that is deblurred by its corresponding $h_{{\widehat{L}}_{i=1,2}}$, there is an overall grade of restoration $\left(E_{i=1,2}\right)$. According to the definition of the consequence membership functions, a greater value of $E_i$ represents a better restoration and, on the contrary, a lower value of $E_i$ represents a possible erroneous process, ($E_i$ is ranging from 0 to 1). With this proposed system, if by mistake $L_f$ is used instead of $L_h$ in the formation of the $h$ (Equation (6)), then the resulting $E_i$ will be lower. Overall, $E_1$ and $E_2$ are used comparatively to determine and select the best restoration between ${\widehat{f}}_1$ and ${\widehat{f}}_2$ that are emerged from restoring a degraded sample ($g$). This proposed system and its overall restoration processes are demonstrated in Figure 3.

3. Practical Result

Membership Function Parameters

Membership function parameters were investigated pragmatically by testing the explained algorithm for various degraded EB measurement samples. In all degraded measurements, $h$ and $f$ had approximately similar sizes as a result of which ${\widehat{L}}_1\cong {\widehat{L}}_2$. The membership functions were designed with smooth transitions to provide a general solution and more flexibility, except for the attenuation. To further discriminate between $E_1$ and $E_2$, the attenuation membership function parameters were adjusted to have more emphasis between the interval of 0 to 0.3 dB. This intuitive definition was done by observing the magnitude of null frequencies in several degraded signals where the attenuation of the null frequencies was always under 0.3 dB. The membership function parameters are presented in

Table 2. Membership function definition details.

PSF Deviation				Attenuation				Residue				Restoration Quality
${\mu }_m$		${\mu }_m^{\prime }$		${\mu }_o$		${\mu }_o^{\prime }$		${\mu }_r$		${\mu }_r^{\prime }$		${\mu }_q$		${\mu }_q^{\prime }$
$a_m$	$c_m$	$a_m$	$c_m$	$a_o$	$c_o$	$a_o$	$c_o$	$a_r$	$c_r$	$a_r$	$c_r$	$a_q$	$c_q$	$a_q$	$c_q$
0.02	1	0.04	1	0.02	0.3	0.05	0.3	0	1	0	1	0	1	0	1

.

The membership functions of attenuation ($B_{high}$ & $B_{Low}$) and residue ($C_{low}\&C_{high}$) fuzzy sets are depicted in Figure 4, according to their values in Table 2. The fuzzy sets of PSF deviation and restoration quality were also defined with the similar membership functions to that of residues.

The analysis of a few of the samples are shown in Figure 5 and Figure 6. For a few of the EB measurements, the $L_h$ (probe sizes) were known to be 1.00, 0.20, and 0.40 mm respectively. The crisp fuzzy inputs and deconvolution grades $E_i$ were also provided for every sample. The restoration that resulted in the higher $E_i$ was selected by the system as the correct solution and its corresponding ${\widehat{L}}_i$ therefore represents the probe size (${\widehat{L}}_h\leftarrow {\widehat{L}}_i)$. To validate the proposed system with the ground truth signal ($f$) [6], both restorations (${\widehat{f}}_{1,2}$) were compared against their ground truth signal using cross-correlation. For the ${\widehat{f}}_i$ with the higher $E_i$, the cross-correlation of ${\widehat{f}}_i$ and $f$ also produced greater coefficients, supporting the accuracy and reliability of the system. As another benchmark, full width at half maximum (FWHM) analysis was used, as it is a popular measure in the EB calibration jargon. The FWHM of $f$ and the ${\widehat{f}}_i$ that had the higher $E_i$ produced a similar result, further confirming that the FIS had successfully identified the correct restoration process.

4. Conclusions and Discussion

The algorithm showed superior performance when a rough prior knowledge of $L_h$ was provided for the fuzzy inference system. The $\Delta E_i=\left(\left|E_1-E_2\right|\right)$ was greater than 0.5 thereby clearly identifying and segregating the correct deconvolution process. The algorithm was also tested without including the PSF knowledge, in which case $\Delta E_i$ was in the interval of 0.1 to 0.5, which was enough to confidently separate the correct deconvolution process.

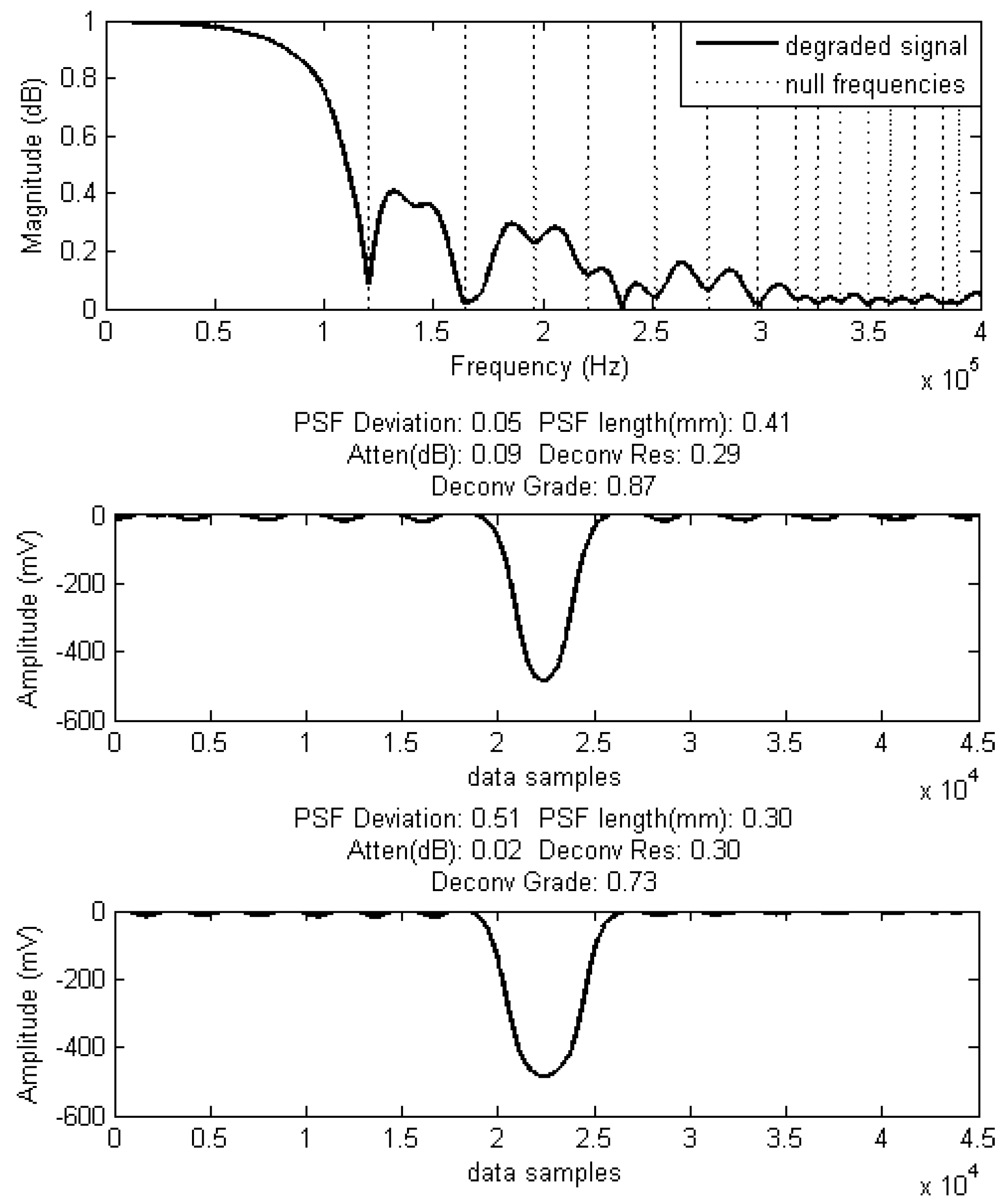
Figure 6 depicted a special case where $H$ had a null frequency at ${\omega }_h$ = 120 kHz with a normalized magnitude of 0.09 dB, whereas, $F$ null was at ${\omega }_f$ = 170 kHz with a magnitude of 0.02 dB and had four times higher attenuation. Although ${\omega }_f$ had a magnitude that was in its favor, the PSF deviation of 0.51 was not, yet the PSF deviation outweighed its low magnitude and the correct restoration was successfully distinguished with 14% separation in the deconvolution grades ($\left|E_1-E_2\right|$ = 0.14). This high attenuation of ${\omega }_f$ was most likely due to it being closer to the second harmonic of ${\omega }_h$ and, therefore, it experienced further attenuation. Nevertheless, owing to the FIS implementation, the correct restoration process was identified. All the possible rules were considered for the implementation of this FIS and its tuning was performed heuristically by an expert. However, clustering algorithms could be used for FIS with multiple inputs and membership functions to determine the optimum number of rules. Furthermore, adaptive FISs can be used to automate the tuning and learning process of the FIS in a more complicated and complex scenario.