Employing Robust Principal Component Analysis for Noise-Robust Speech Feature Extraction in Automatic Speech Recognition with the Structure of a Deep Neural Network
Abstract
:1. Introduction
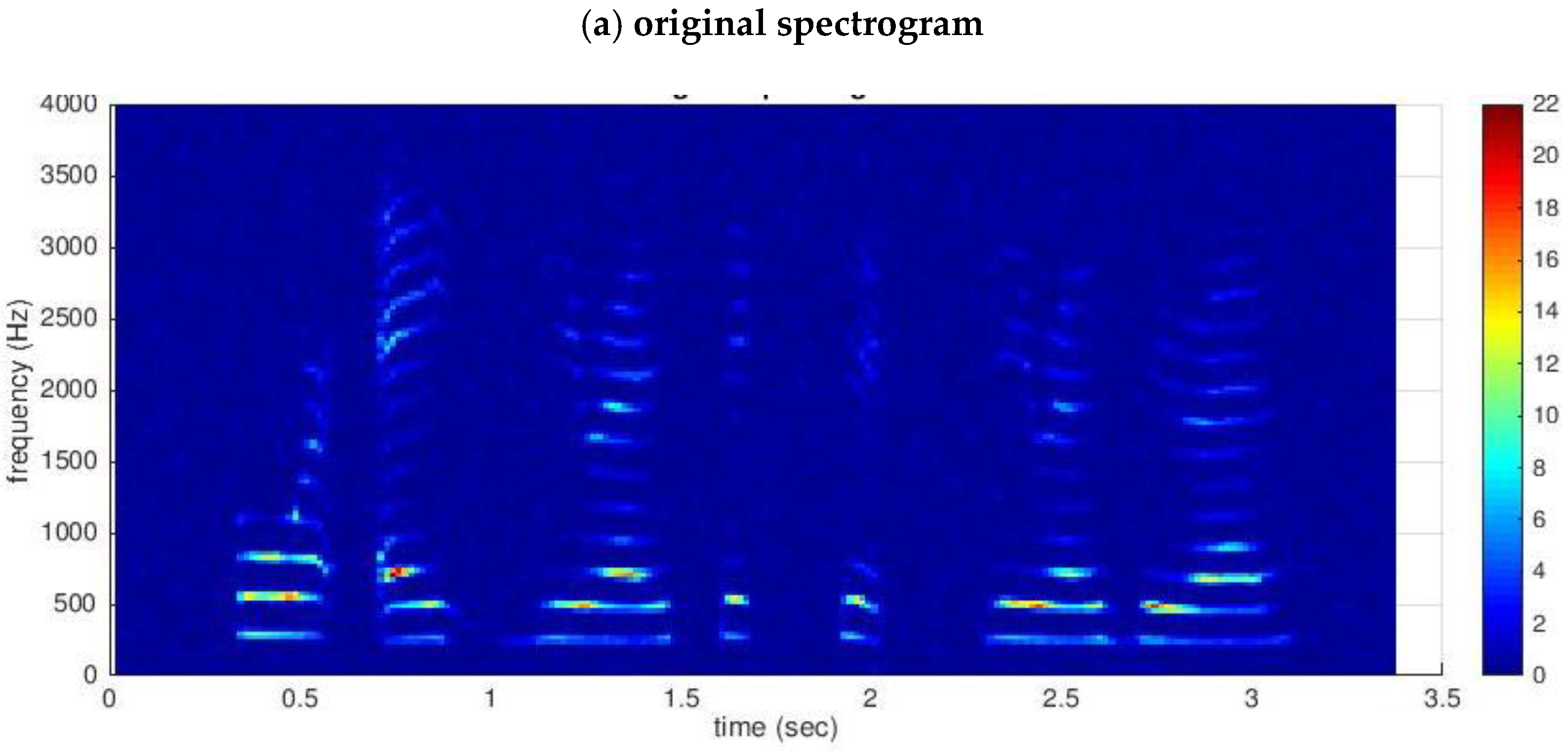
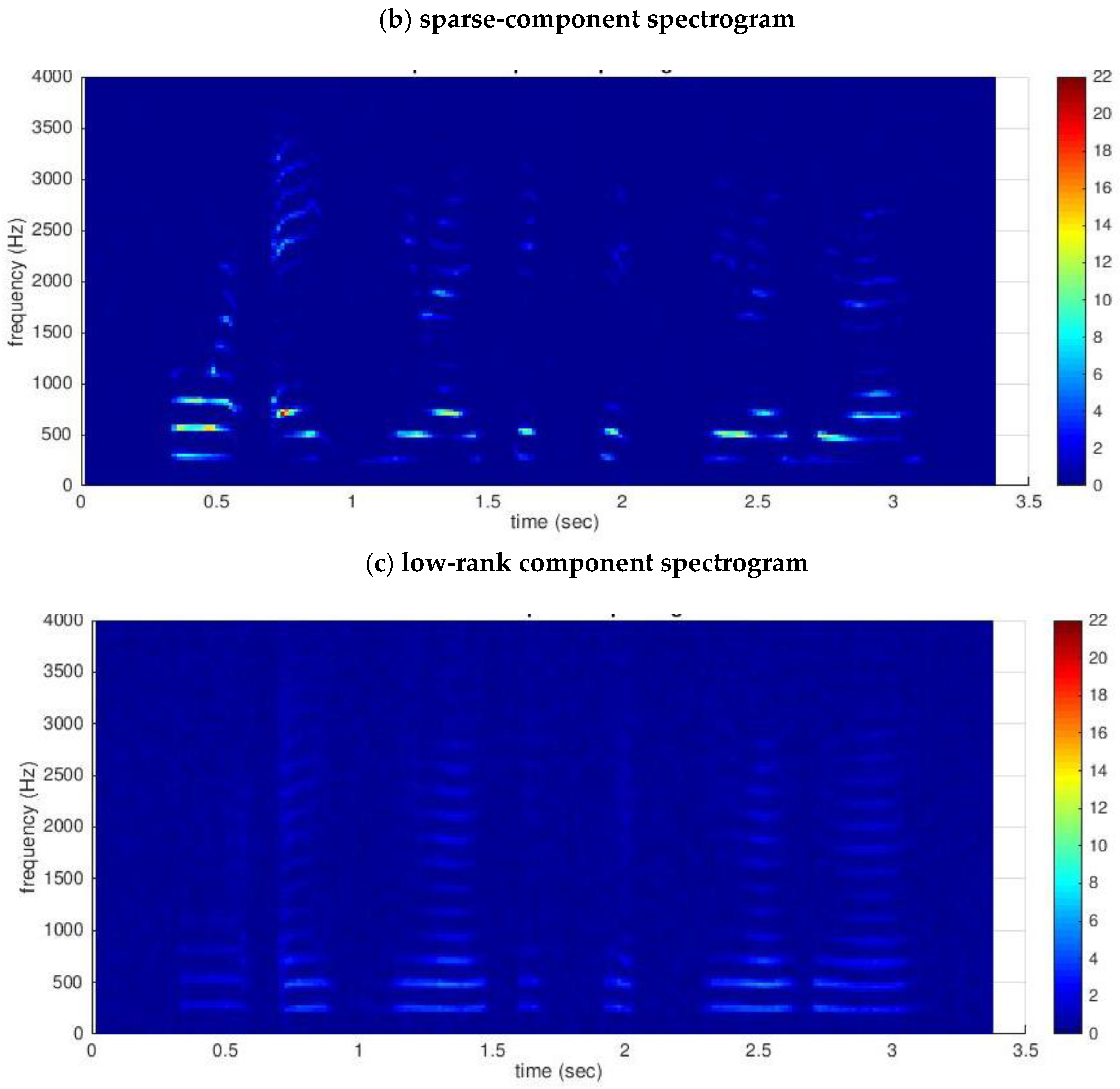
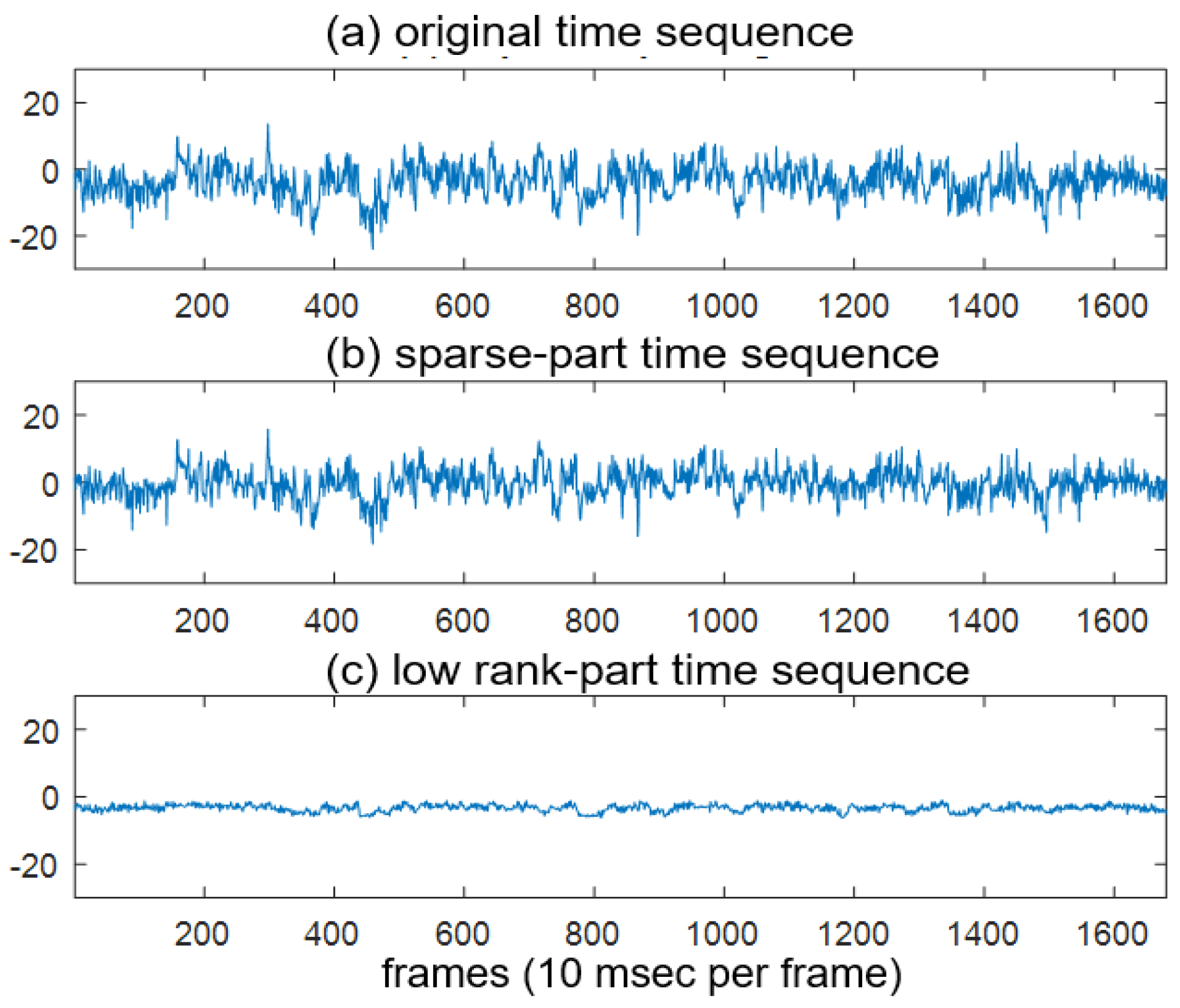
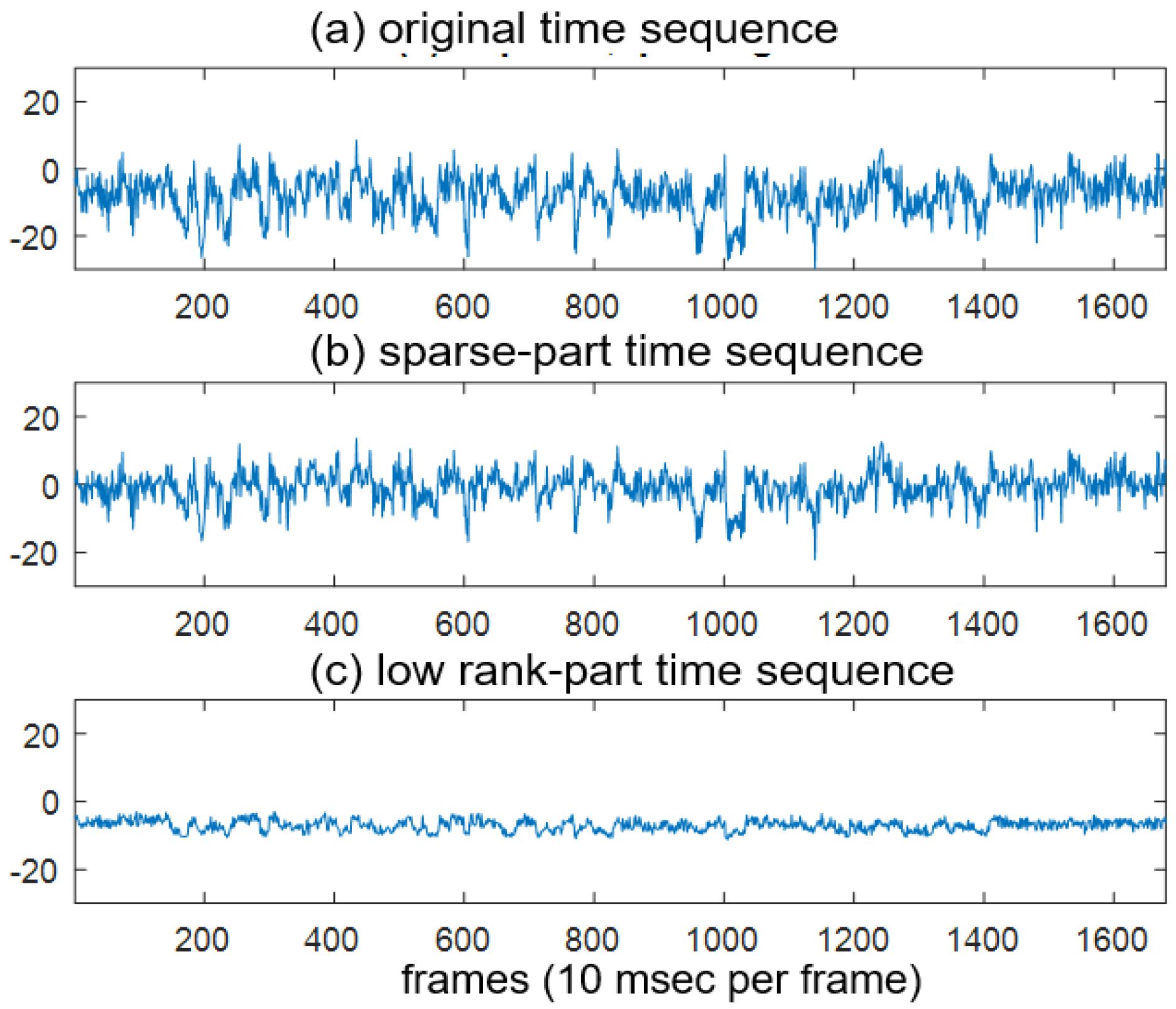
2. Robust Principal Component Analysis (RPCA)
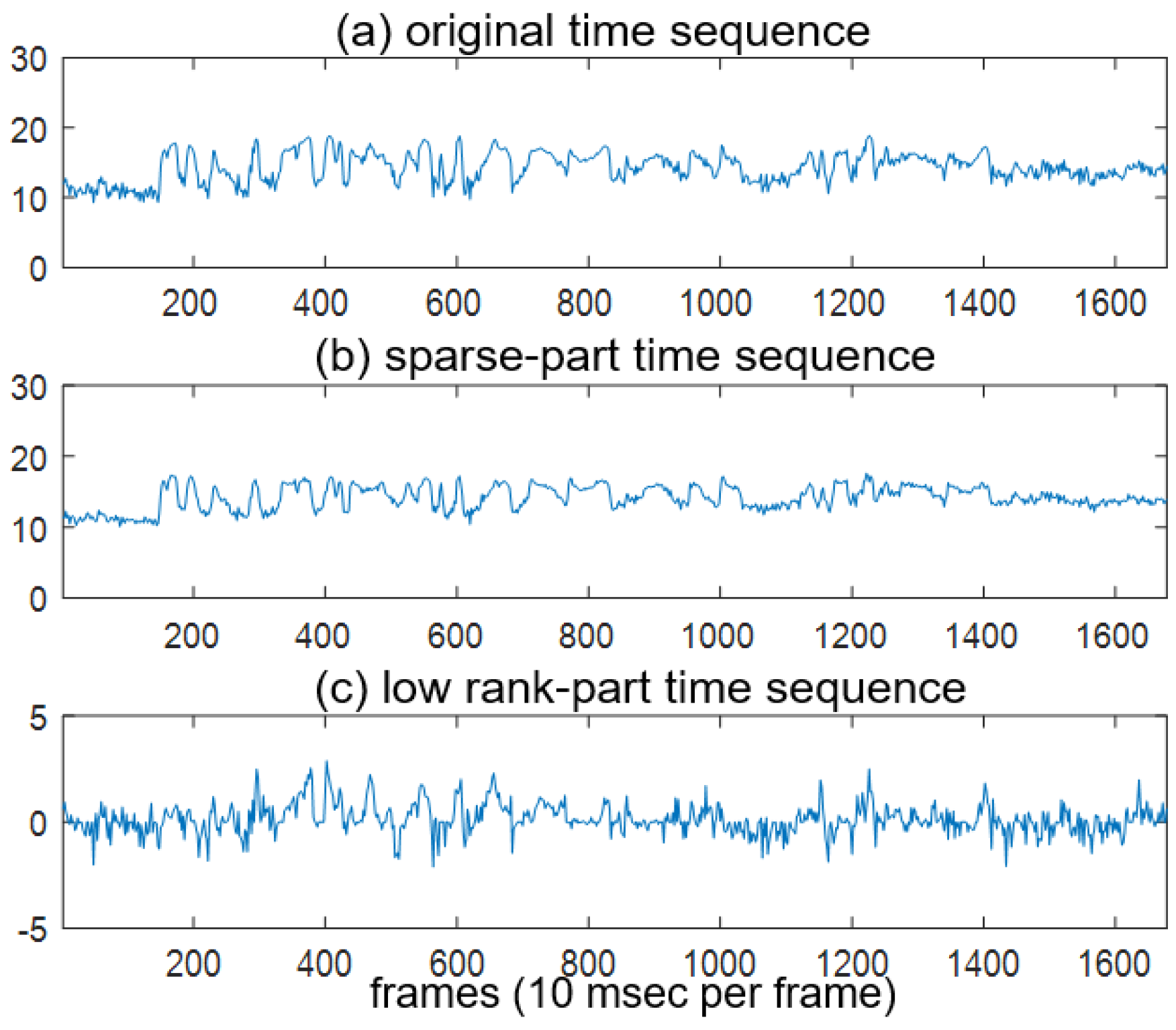
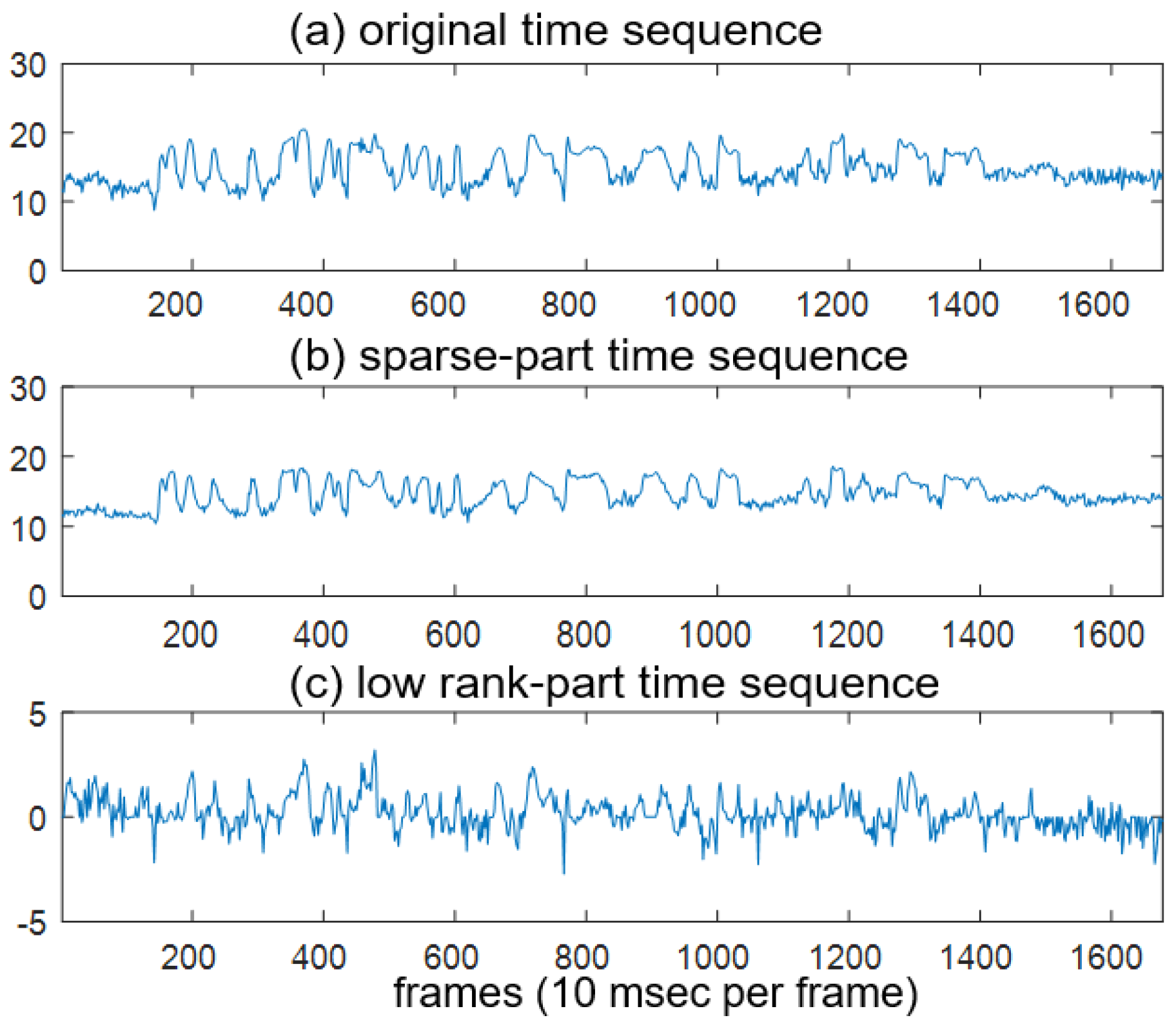
3. Proposed Method
4. Experimental Setup
5. Experimental Results and Discussions
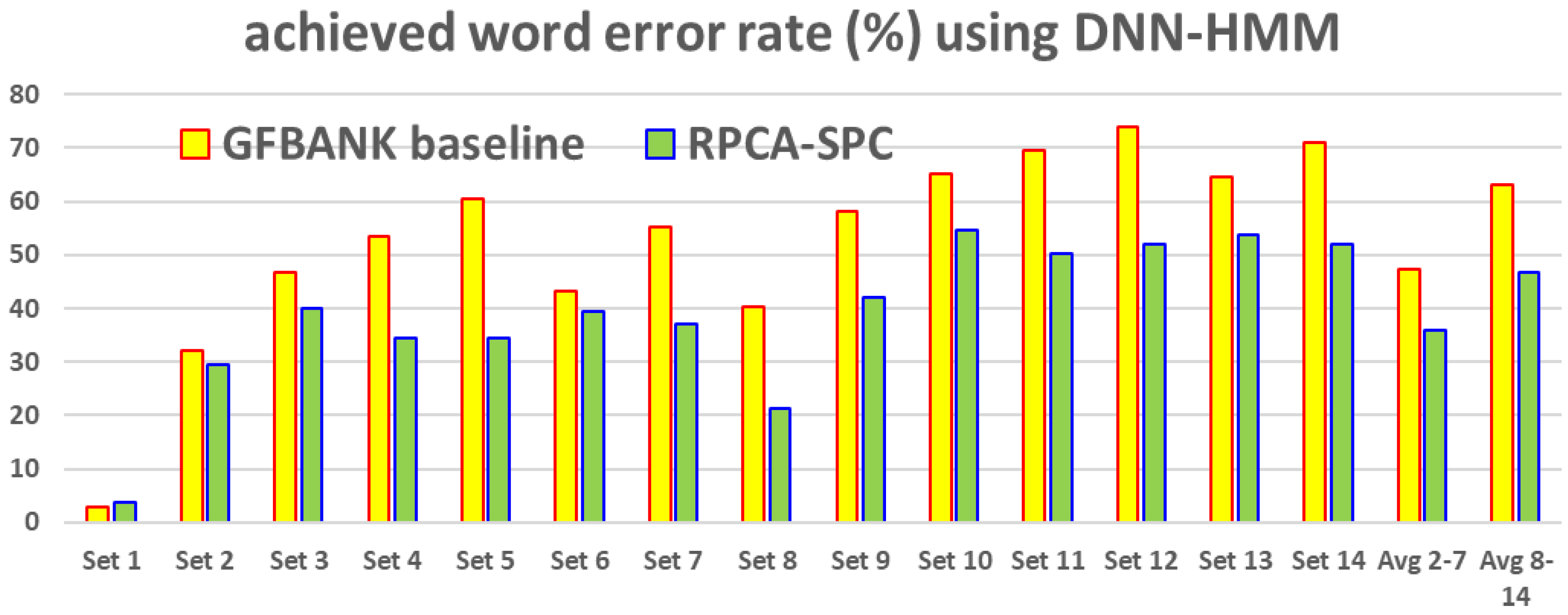
5.1. Individual Method
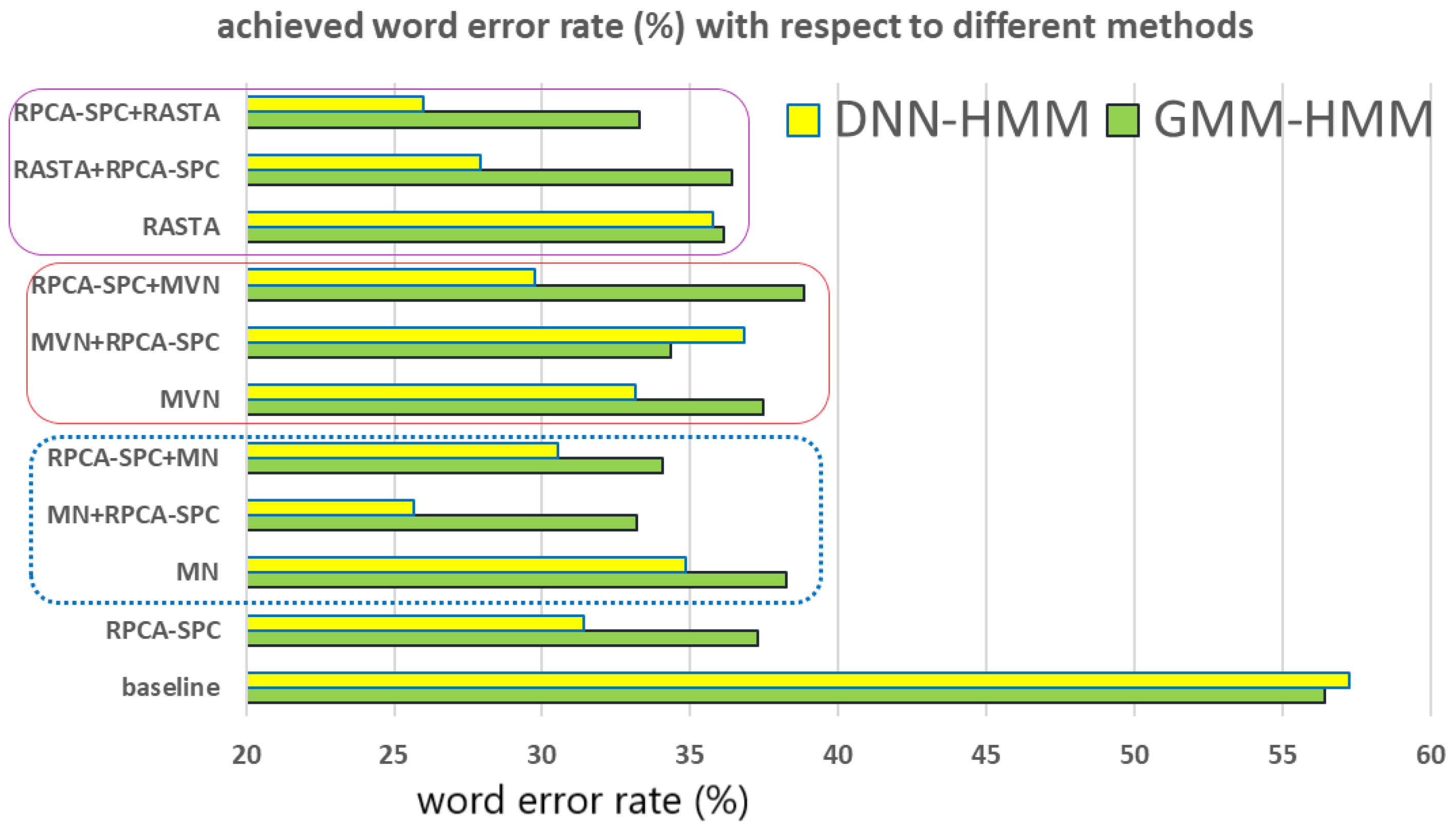
- Both MFCC and FBANK (with GMM-HMM and DNN-HMM as the acoustic models, respectively) give very low WERs for the clean noise-free set, i.e., Set 1. However, FBANK with DNN-HMM outperforms MFCC with GMM-HMM by giving even lower WERs, which is in general attributed to the deep learning scheme in DNN.
- As for the second sub-group, Sets 2–7, the WERs of both MFCC and FBANK are much higher in comparison with those obtained in Set 1. Thus, we observe that noise deteriorates the performance of speech recognition, and MFCC and FBANK are quite vulnerable to noise. In addition, comparing the WERs obtained from Sets 8–14 with those from Sets 1–7, we see that an extra channel distortion results in further degradation of recognition accuracy. Furthermore, unlike the clean noise-free case, FBANK with DNN-HMM behaves almost equally to MFCC with GMM-HMM, implying that the deep learning structure in acoustic modeling does not necessarily benefit the recognition accuracy under adverse environments.
- For the clean noise-free case, only MN behaves better than the baseline in promoting both MFCC (with GMM-HMM) and FBANK (with DNN-HMM), while the other methods including MVN, RASTA, and RPCA-SPC worsen the recognition accuracy of the baseline features in particular for the case of GMM-HMM. The probable explanation is as follows: Compared with the other methods, MN simply applies a subtraction operation and does the least change to the original features. By contrast, RASTA and RPCA-SPC always remove some components from speech features in Set 1, which does not have any noise distortion. Accordingly RASTA and PRCA-SPC corrupt clean noise-free speech features by diminishing speech-relevant information or introducing extra distortions.
- For the mismatched Test Sets (sets 2–7 and 8–14), RPCA-SPC is shown to substantially improve the recognition accuracy relative to the baseline, which undoubtedly shows the effectiveness of the newly proposed RPCA-SPC in enhancing noise robustness of speech features. These results also support our claim that extracting the sparse component in noisy speech features can highlight the clean-speech portion and/or reduce the pure noise portion.
- For the sets containing noise only (sets 2–7) and the sets containing both channel and noise interferences (sets 8–14), all the methods discussed here provide baseline features with significantly better recognition accuracy. For example, in Sets 2–7, RASTA shows around 23% and 21% in averaged accuracy improvement for the cases of DNN-HMM and GMM-HMM, respectively, and RPCA-SPC gives rise to an averaged accuracy improvement of around 25% and 20% for the cases of DNN-HMM and GMM-HMM, respectively. It is also shown that RPCA-SPC behaves better than MN, MVN, and RASTA in reducing the effect of noise and channel distortions on speech recognition for the case of DNN-HMM.
- For mismatched noise/channel cases, the recognition accuracy achieved by DNN-HMM is consistently superior to that by GMM-HMM, which coincides with the general idea that deep learning techniques benefit speech recognition. The proposed RPCA-SPC is shown to profit speech features under the DNN-HMM scenario in particular, giving lower word error rates than the other methods, and is thus revealed to further capture the speech-related information beyond what the DNN structure does.
5.2. The Cascade of RPCA with any of the Other Methods
- The series connection of RPCA-SPC with either of MN and RASTA behave better than each single component method for Sets 2–7 (containing noise) and Sets 8–14 (containing noise and channel interference). For example, in the case of DNN-HMM, MN + RPCA-SPC, and RPCA-SPC + MN give 25.67% and 30.53% in WER averaged over the 14 Sets, which are lower than those obtained by MN (34.83%) and RPCA-SPC (31.39%). Similarly, RASTA + RPCA-SPC and RPCA-SPC + RASTA give 27.92% and 25.97% in WER averaged over the 14 Sets, which are lower than those obtained by RASTA (35.75%) and RPCA-SPC (31.39%). These results again claim that the newly proposed RPCA-SPC serves as a promising technique that can extract noise-robust components in speech features either preprocessed/post-processed by MN, RASTA or not. In addition, MN + RPCA-SPC provides a relatively low WER value on average for the DNN-HMM scenario, indicating that it is quite suitable for use and development in the deep learning architecture of speech recognition;
- Unlike MN and RASTA, cascading MVN with RPCA-SPC does not necessarily gives better recognition results than MVN and RPCA-SPC alone. One possible reason is that MVN makes the features of all different channels behave like a common random variable with zero mean and unity variance, and thus the subsequent RPCA-SPC tends to view these features to be low-rank so as to discard a significant amount of them, which somewhat harms the recognition accuracy. In addition, For RPCA-SPC preprocessed features, MVN is likely to bring an over-normalization effect and diminishes the respective discriminating capability.
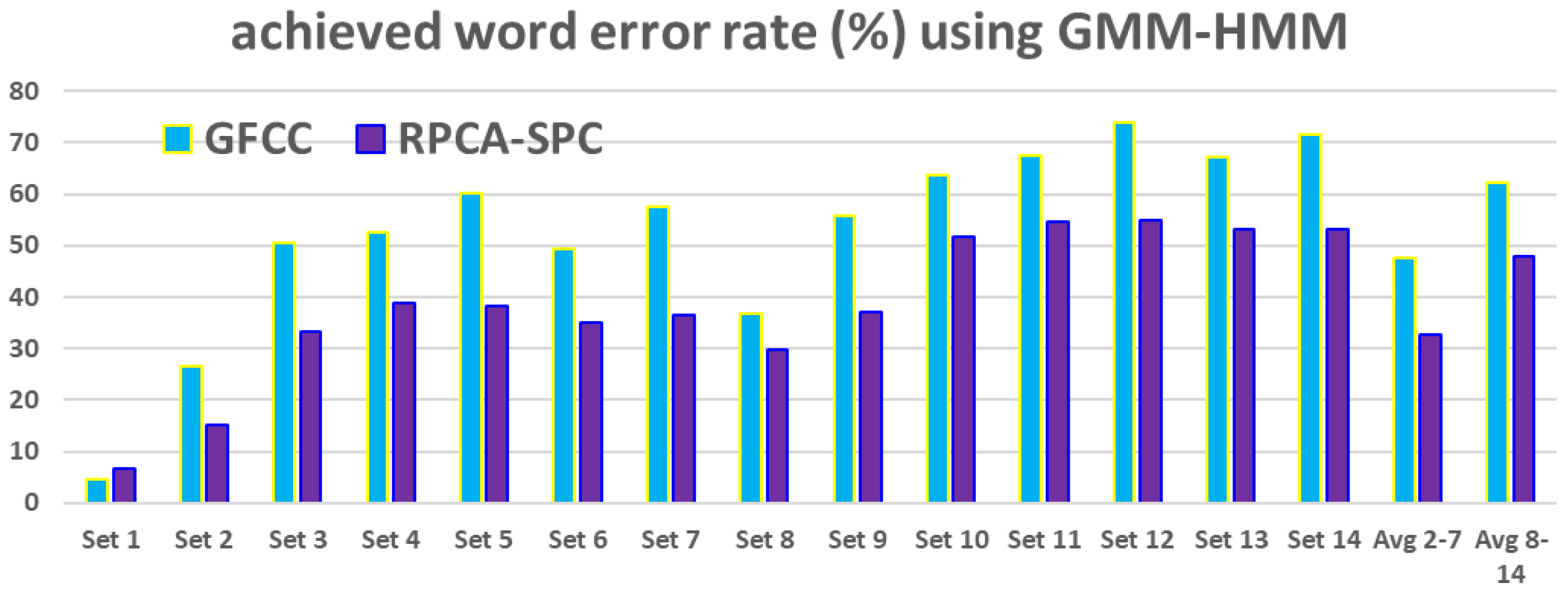
5.3. Performing RPCA-SPC on Gammatone-Filterbank Features
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hermansky, H. Perceptual linear predictive (PLP) analysis of speech. J. Acoust. Soc. Am. 1990, 87, 1738–1752. [Google Scholar] [CrossRef] [PubMed]
- Benesty, J.; Sondhi, M.M.; Huang, Y. Springer Handbook of Speech Processing; Springer: Berlin, Germany, 2008. [Google Scholar]
- Schlider, R.; Bezrukov, I.; Wagner, H.; Ney, H. Gammatone features and feature combination for large vocabulary Speech recognition. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Honolulu, HI, USA, 15–20 April 2007; Volume 4, pp. IV-649–IV-652. [Google Scholar]
- Berouti, M.; Schwartz, R.; Makhoul, J. Enhancement of speech corrupted by acoustic noise. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Washington, DC, USA, 2–4 April 1979; pp. 208–211. [Google Scholar]
- Boll, S. Suppression of acoustic noise in speech using spectral subtraction. IEEE Trans. Acoust. Speech Signal. Process. 1979, 27, 113–120. [Google Scholar] [CrossRef]
- Plapous, C.; Marro, C.; Scalart, P. Improved signal-to-noise ratio estimation for speech enhancement. IEEE Trans. Acoust. Speech Signal. Process. 2006, 14, 2098–2108. [Google Scholar] [CrossRef]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum mean-square error log-spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal. Process. 1985, 33, 443–445. [Google Scholar] [CrossRef]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal. Process. 1984, 32, 1109–1121. [Google Scholar] [CrossRef]
- Furui, S. Cepstral analysis technique for automatic speaker verification. IEEE Trans. Acoust. Speech Signal. Process. 1981, 29, 254–272. [Google Scholar] [CrossRef]
- Viikki, O.; Laurila, K. Cepstral domain segmental feature vector normalization for noise robust speech recognition. Speech Commun. 1998, 25, 133–147. [Google Scholar] [CrossRef]
- Hilger, F.; Ney, H. Quantile based histogram equalization for noise robust large vocabulary speech recognition. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 845–854. [Google Scholar] [CrossRef]
- Lin, S.H.; Chen, B.; Yeh, Y.M. Exploring the use of speech features and their corresponding distribution characteristics for robust speech recognition. IEEE Trans. Audio Speech Lang. Process. 2009, 17, 84–94. [Google Scholar] [CrossRef]
- Hermansky, H.; Morgan, N. RASTA processing of speech. IEEE Trans. Speech Audio Process. 1994, 2, 578–589. [Google Scholar] [CrossRef]
- Xiao, X.; Chng, E.S.; Li, H.Z. Normalization of the speech modulation spectra for robust speech recognition. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 1662–1674. [Google Scholar] [CrossRef]
- Chen, C.P.; Bilmes, J. MVA processing of speech features. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 257–270. [Google Scholar] [CrossRef]
- Sun, L.C.; Lee, L.S. Modulation spectrum equalization for improved robust speech recognition. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 828–843. [Google Scholar] [CrossRef]
- Hung, J.W.; Tu, W.H.; Lai, C.C. Improved modulation spectrum enhancement methods for robust speech recognition. Signal. Process. 2012, 92, 2791–2814. [Google Scholar] [CrossRef]
- Hung, J.W.; Hsieh, H.J.; Chen, B. Robust Speech Recognition via Enhancing the Complex-Valued Acoustic Spectrum in Modulation Domain. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 236–251. [Google Scholar] [CrossRef]
- Li, J.; Deng, L.; Gong, Y.; Haeb-Umbach, R. An overview of noise-robust automatic speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 745–777. [Google Scholar] [CrossRef]
- Leggetter, C.J.; Woodland, P.C. Maximum likelihood linear regression for speaker adaptation of continuous density hidden Markov models. Comput. Speech Lang. 1995, 9, 171–185. [Google Scholar] [CrossRef]
- Gales, M.J.F. Maximum likelihood linear transformations for HMM based speech recognition. Comput. Speech Lang. 1998, 12, 75–98. [Google Scholar] [CrossRef]
- Wu, J.; Huo, Q. Supervised adaptation of MCE-trained CDHMMs using minimum classification error linear regression. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Orlando, FL, USA, 13–17 May 2002; Volume I, pp. 605–608. [Google Scholar]
- He, X.; Chou, W. Minimum classification error linear regression for acoustic model adaptation of continuous density HMMs. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hong Kong, China, 6–10 April 2003; Volume I, pp. 556–559. [Google Scholar]
- Yu, K.; Gales, M.J.F.; Woodland, P.C. Unsupervised adaptation with discriminative mapping transforms. IEEE Trans. Audio Speech Lang. Process. 2009, 17, 714–723. [Google Scholar] [CrossRef]
- Gales, M.J. Model-Based Techniques for Noise Robust Speech Recognition. Ph.D. Thesis, Cambridge University, Cambridge, UK, 1995. [Google Scholar]
- Moreno, P.J. Speech Recognition in Noisy Environments. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 1996. [Google Scholar]
- Li, J.; Deng, L.; Haeb-Umbach, R.; Gong, Y.F. Robust Automatic Speech Recognition: A Bridge. to Practical Applications; Elsevier: AMS, NL, 2015; Chapter four: Processing in the feature and model domains. [Google Scholar]
- Candes, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Bouwmansa, T.; HadiZahzahb, E. Robust PCA via principal component pursuit: A review for a comparative evaluation in video surveillance. Comput. Vis. Image Understand. 2014, 122, 22–34. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, Q.; Wang, J.; Xie, J. Noise reduction based on robust principal component analysis. J. Comput. Inf. Syst. 2014, 10, 4403–4410. [Google Scholar]
- Wu, C.L.; Hsu, H.P.; Wang, S.S.; Hung, J.W.; Lai, Y.H.; Wang, H.M.; Tsao, Y. Wavelet speech enhancement based on robust principal component analysis. Proc. Interspeech 2017, 781, 439–443. [Google Scholar]
- Gavrilescu, M. Noise Robust Automatic Speech Recognition System by Integrating Robust Principal Component Analysis (RPCA) and Exemplar-Based Sparse Representation. In Proceedings of the International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Bucharest, Romania, 25–27 June 2015. [Google Scholar]
- Chen, Z.; Ellis, D.P.W. Speech enhancement by sparse, low-rank, and dictionary spectrogram decomposition. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 20–23 October 2013. [Google Scholar]
- Sun, P.; Qin, J. Low-rank and sparsity analysis applied to speech enhancement via online estimated dictionary. IEEE Signal Process. Lett. 2016, 23, 1862–1866. [Google Scholar] [CrossRef]
- Parihar, N.; Picone, J. Aurora Working Group: DSR Front. End LVSCR Evaluation au/384/02; Institute for Signal and Information Processing: Philadelphia, PA, USA, 2002. [Google Scholar]
- Paul, D.B.; Baker, J.M. The design for the wall street journal-based CSR corpus. In Proceedings of the workshop on Speech and Natural Language (HLT ’91), Harriman, NY, USA, 23–26 February 1992; pp. 357–362. [Google Scholar]
- The 4th CHiME Speech Separation and Recognition Challenge. Available online: http://spandh.dcs.shef.ac.uk/chime_challenge/chime2016/ (accessed on 14 August 2018).
| Set 1 | Sets 2–7 | Sets 8–14 | |
|---|---|---|---|
| Baseline | 4.75 | 51.58 | 67.92 |
| MN | 4.17 | 32.58 | 47.98 |
| MVN | 5.38 | 31.59 | 47.09 |
| RASTA | 5.53 | 30.04 | 45.72 |
| RPCA-SPC | 7.42 | 31.70 | 46.30 |
| Set 1 | Sets 2–7 | Sets 8–14 | |
|---|---|---|---|
| Baseline | 2.97 | 52.81 | 68.81 |
| MN | 2.62 | 28.81 | 44.60 |
| MVN | 2.97 | 26.54 | 43.12 |
| RASTA | 3.27 | 29.46 | 45.77 |
| RPCA-SPC | 3.79 | 27.33 | 38.82 |
| Set 1 | Sets 2–7 | Sets 8–14 | |
|---|---|---|---|
| Baseline | 4.75 | 51.58 | 67.92 |
| MN + RPCA-SPC | 6.43 | 28.01 | 41.43 |
| RPCA-SPC + MN | 6.52 | 29.24 | 42.16 |
| MVN + RPCA-SPC | 5.77 | 27.85 | 43.99 |
| RPCA-SPC + MVN | 6.48 | 31.68 | 49.60 |
| RASTA + RPCA-SPC | 7.08 | 29.08 | 43.99 |
| RPCA-SPC + RASTA | 7.58 | 28.02 | 41.51 |
| Set 1 | Sets 2–7 | Sets 8–14 | |
|---|---|---|---|
| Baseline | 2.97 | 52.81 | 68.81 |
| MN + RPCA-SPC | 3.19 | 20.69 | 33.15 |
| RPCA-SPC + MN | 3.46 | 27.63 | 36.89 |
| MVN + RPCA-SPC | 3.53 | 31.40 | 46.22 |
| RPCA-SPC + MVN | 3.89 | 25.79 | 36.81 |
| RASTA + RPCA-SPC | 4.76 | 24.17 | 34.43 |
| RPCA-SPC + RASTA | 4.97 | 22.47 | 31.97 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, J.-w.; Lin, J.-S.; Wu, P.-J. Employing Robust Principal Component Analysis for Noise-Robust Speech Feature Extraction in Automatic Speech Recognition with the Structure of a Deep Neural Network. Appl. Syst. Innov. 2018, 1, 28. https://doi.org/10.3390/asi1030028
Hung J-w, Lin J-S, Wu P-J. Employing Robust Principal Component Analysis for Noise-Robust Speech Feature Extraction in Automatic Speech Recognition with the Structure of a Deep Neural Network. Applied System Innovation. 2018; 1(3):28. https://doi.org/10.3390/asi1030028
Chicago/Turabian StyleHung, Jeih-weih, Jung-Shan Lin, and Po-Jen Wu. 2018. "Employing Robust Principal Component Analysis for Noise-Robust Speech Feature Extraction in Automatic Speech Recognition with the Structure of a Deep Neural Network" Applied System Innovation 1, no. 3: 28. https://doi.org/10.3390/asi1030028
APA StyleHung, J.-w., Lin, J.-S., & Wu, P.-J. (2018). Employing Robust Principal Component Analysis for Noise-Robust Speech Feature Extraction in Automatic Speech Recognition with the Structure of a Deep Neural Network. Applied System Innovation, 1(3), 28. https://doi.org/10.3390/asi1030028




