Influence of Rake Angles of Multi-Position Tool on Cutting Characteristics
Abstract
:1. Introduction
2. Experimental
2.1. Cutting Tool Design with Adjustable Angle
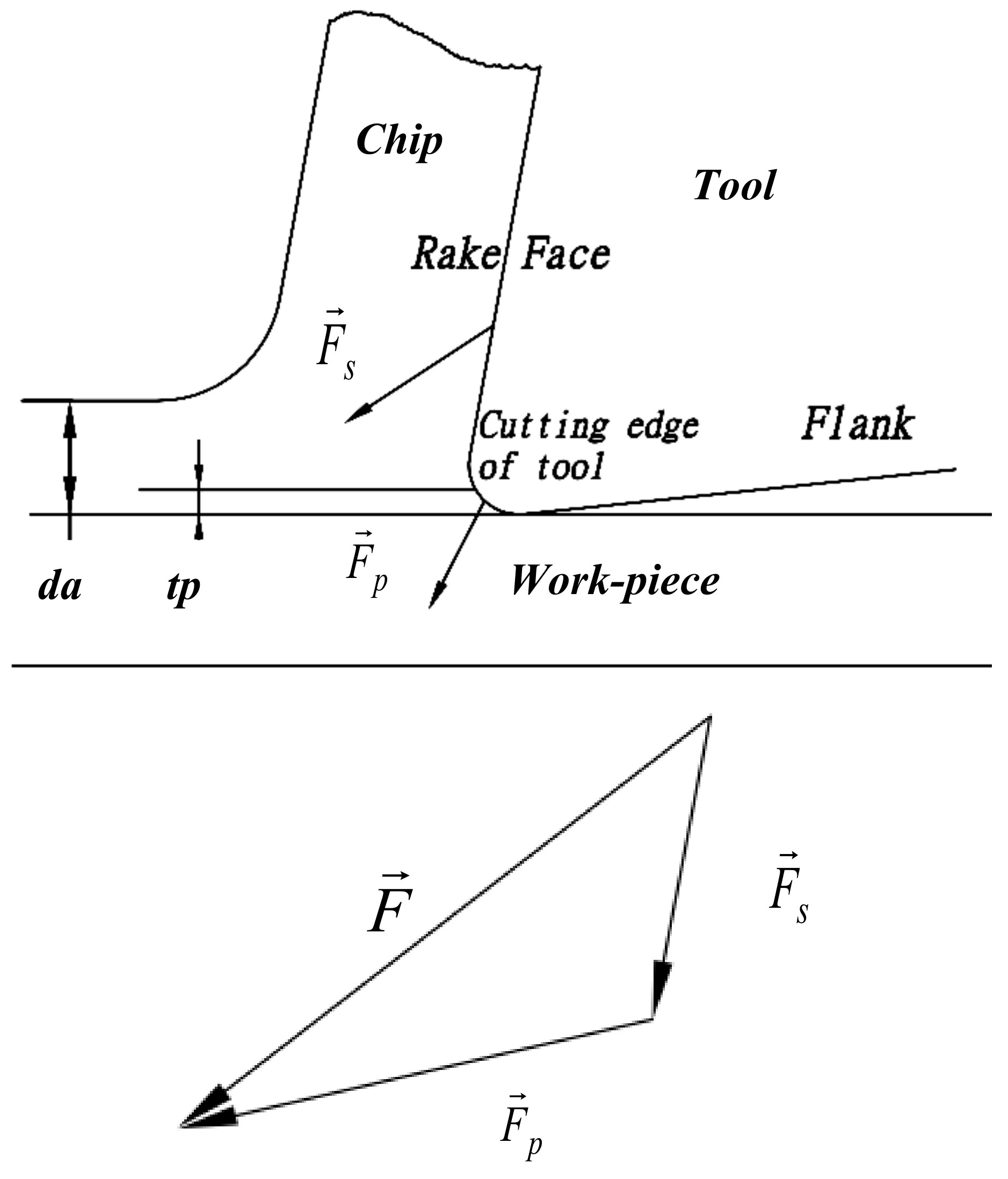
2.2. Mathematical Model Derivation
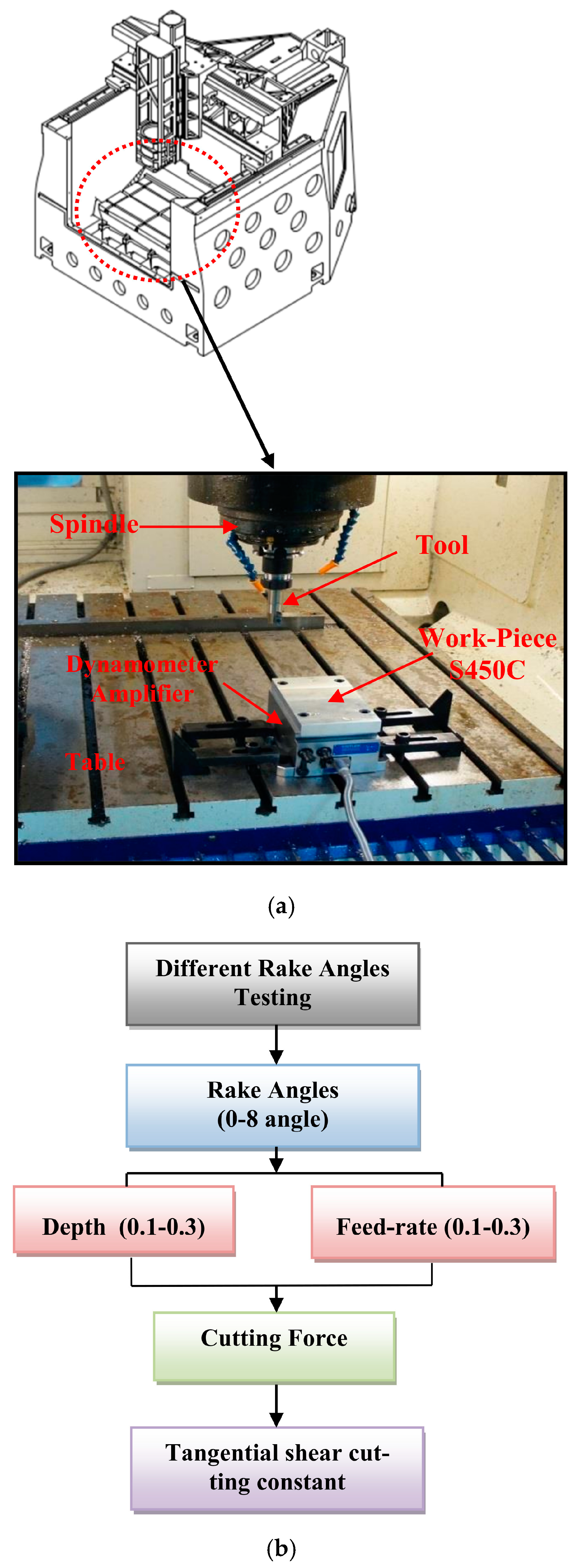
2.3. Equipment and Method
3. Discussion
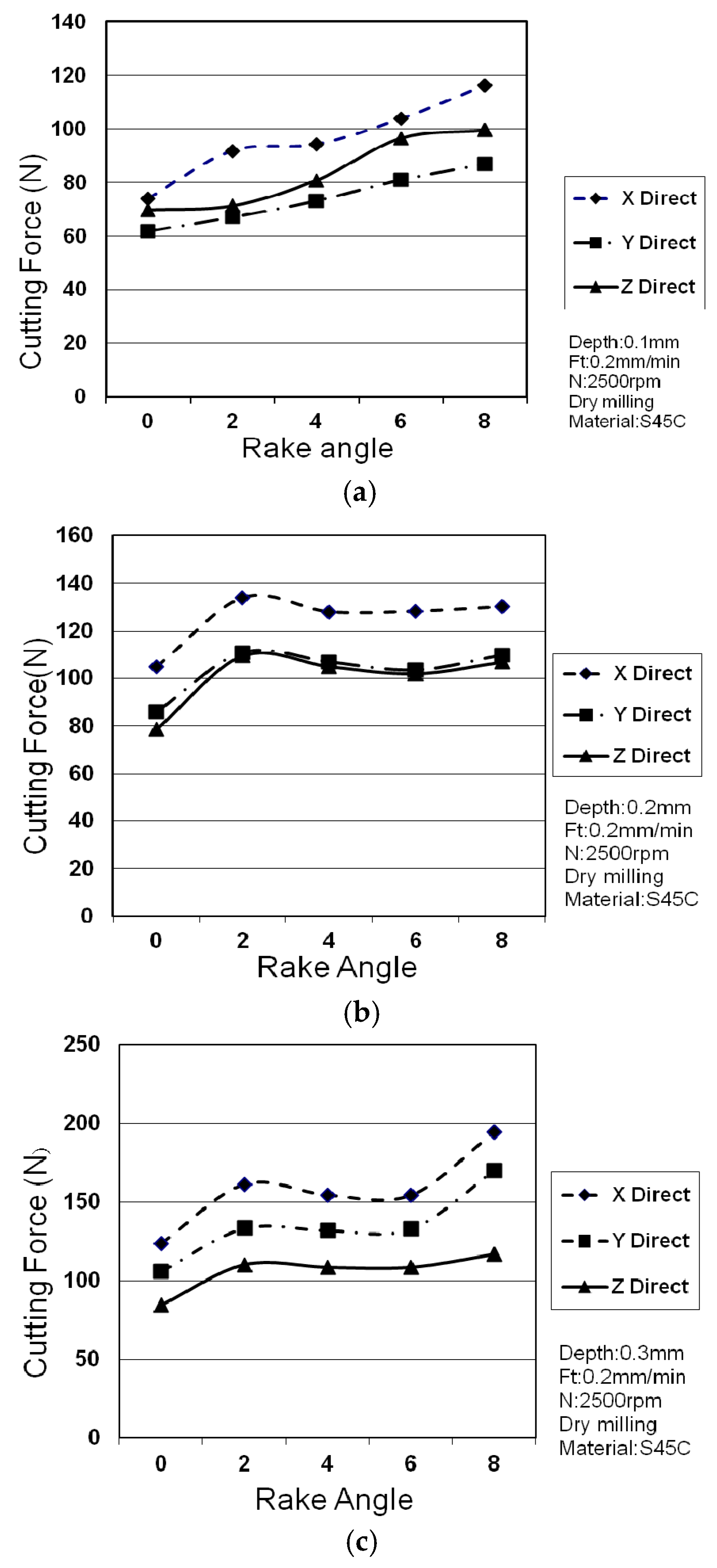
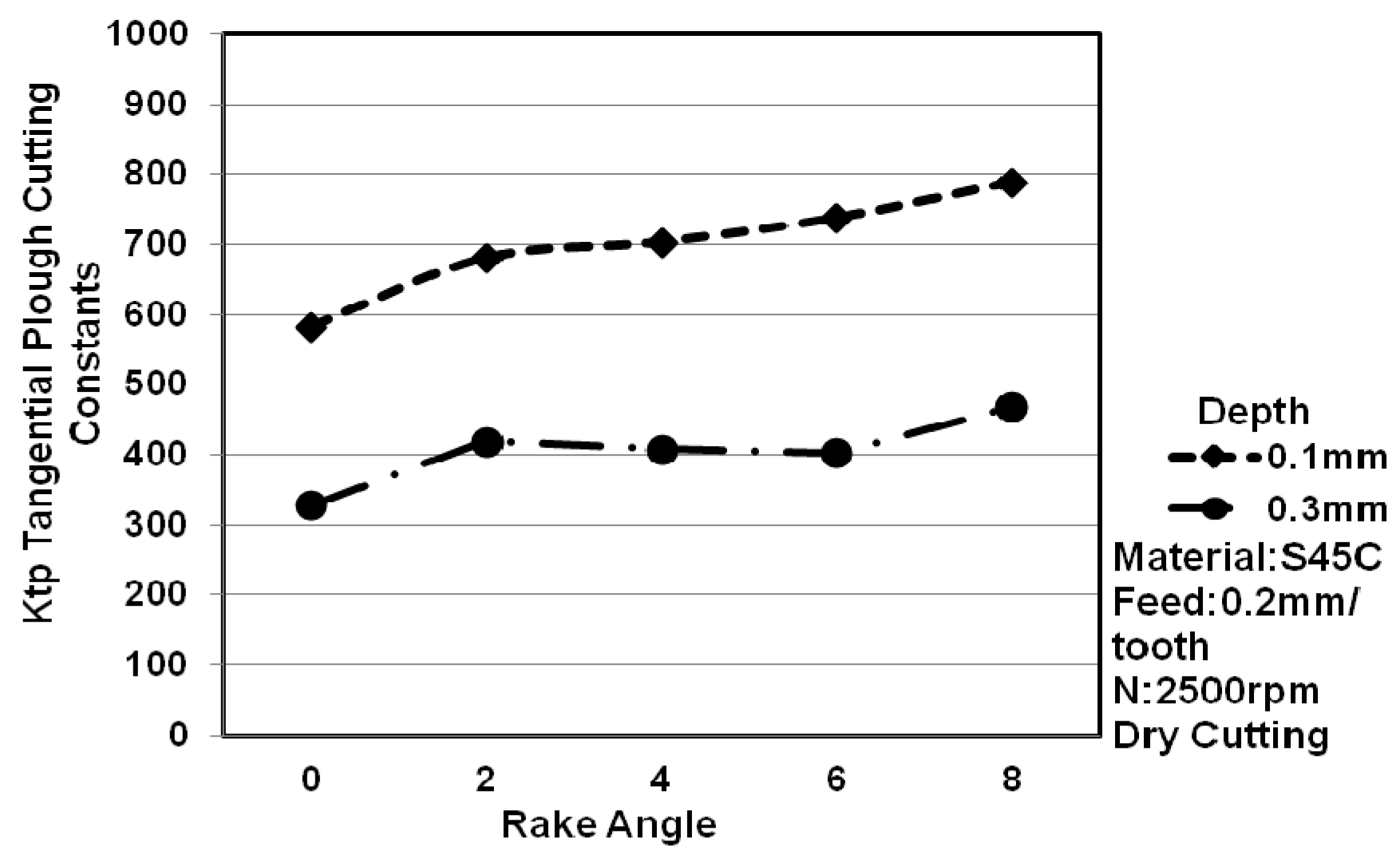
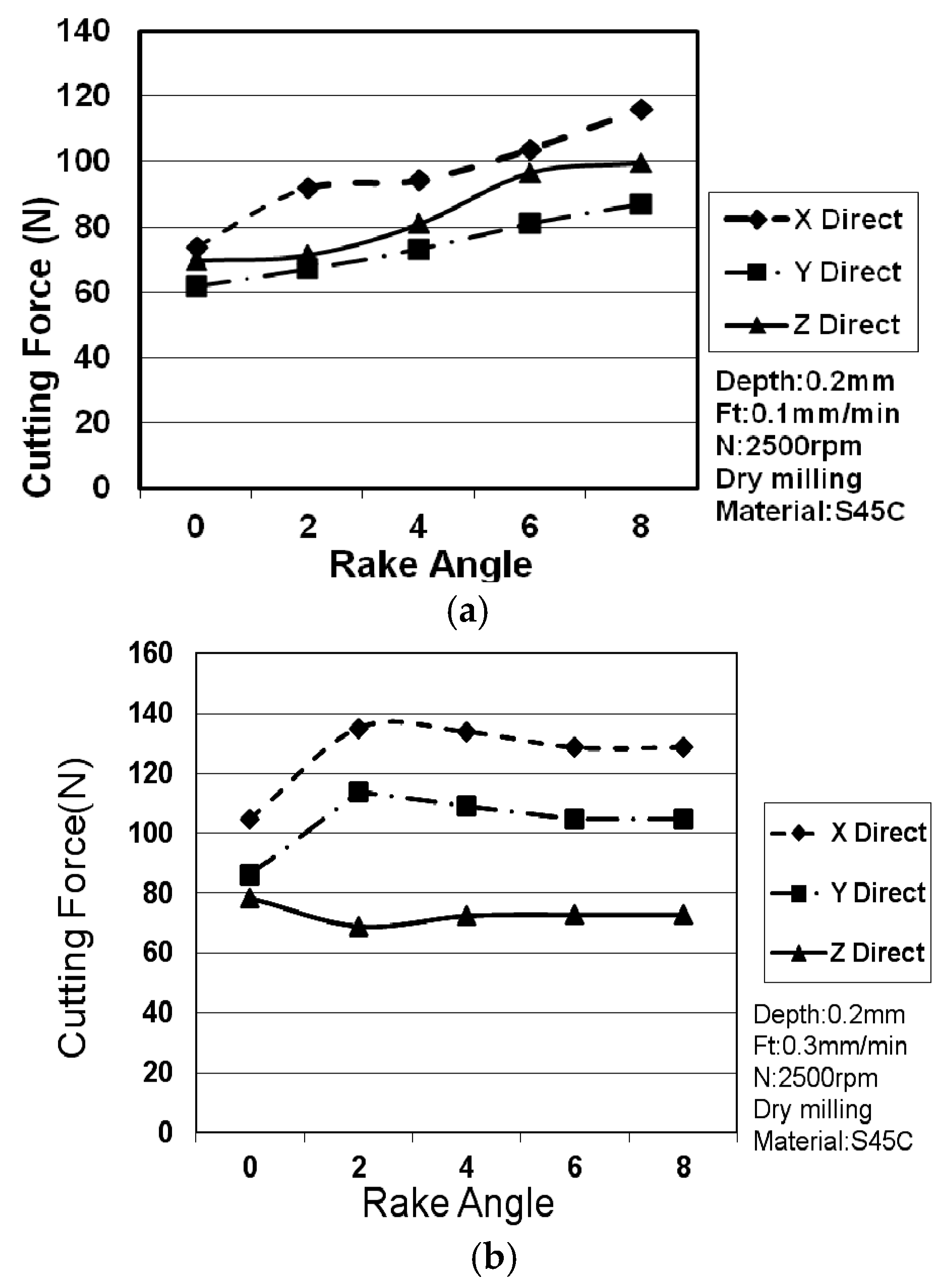
3.1. The Impact of Different Cutting Depths on Cutting Characteristics
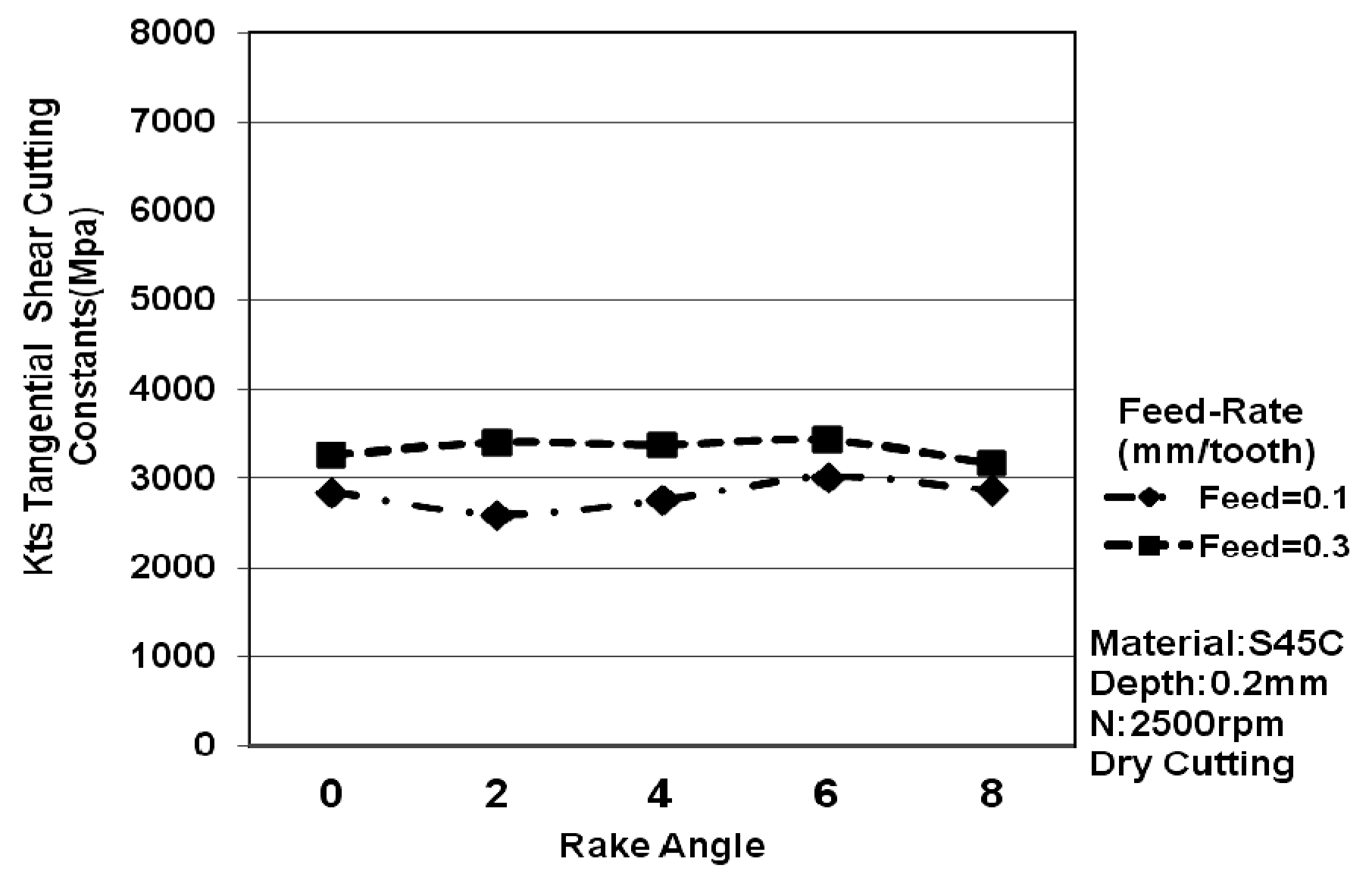
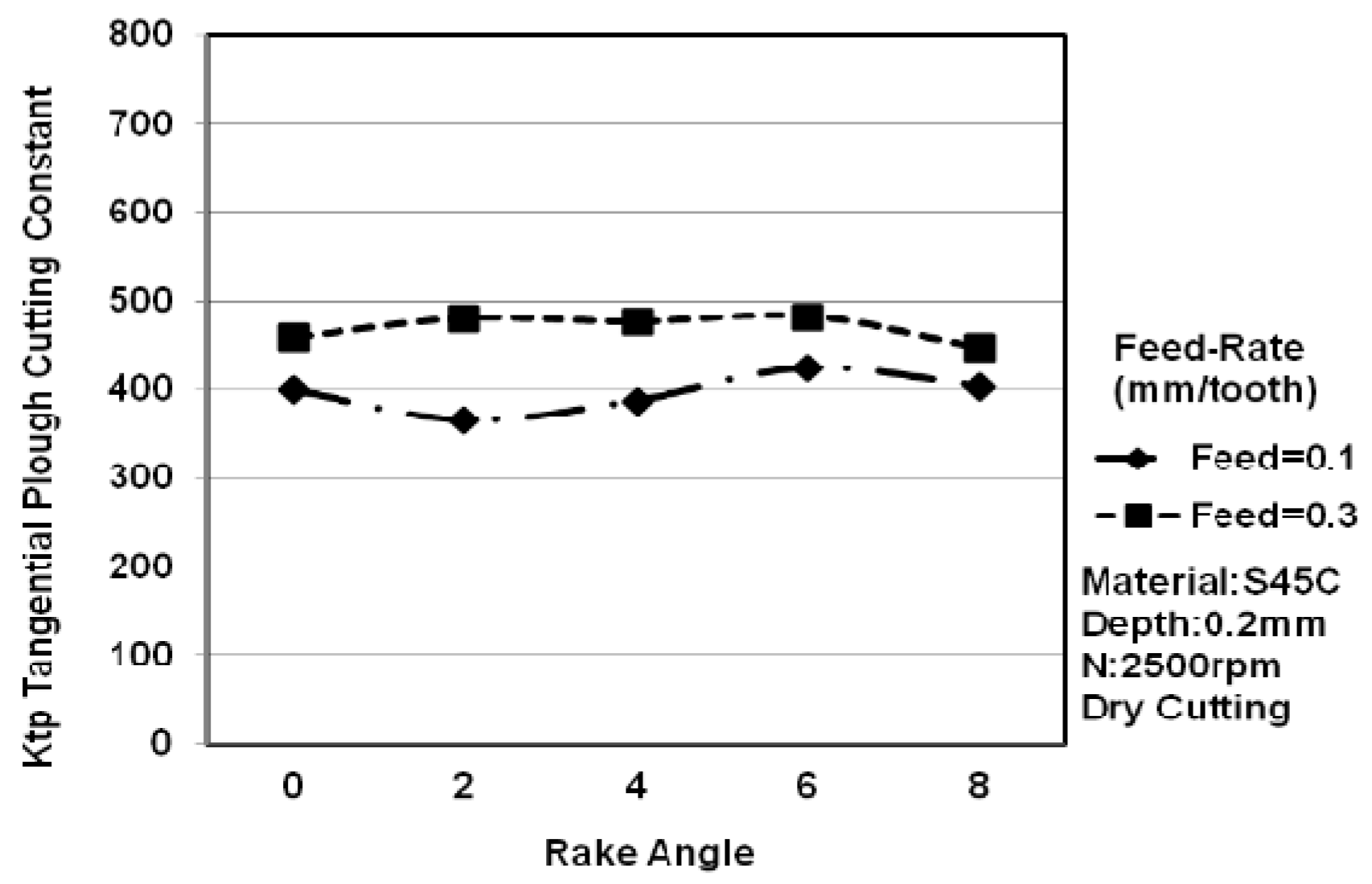
3.2. The Impact of Different Feed-Rates on Cutting Characteristics
4. Conclusions
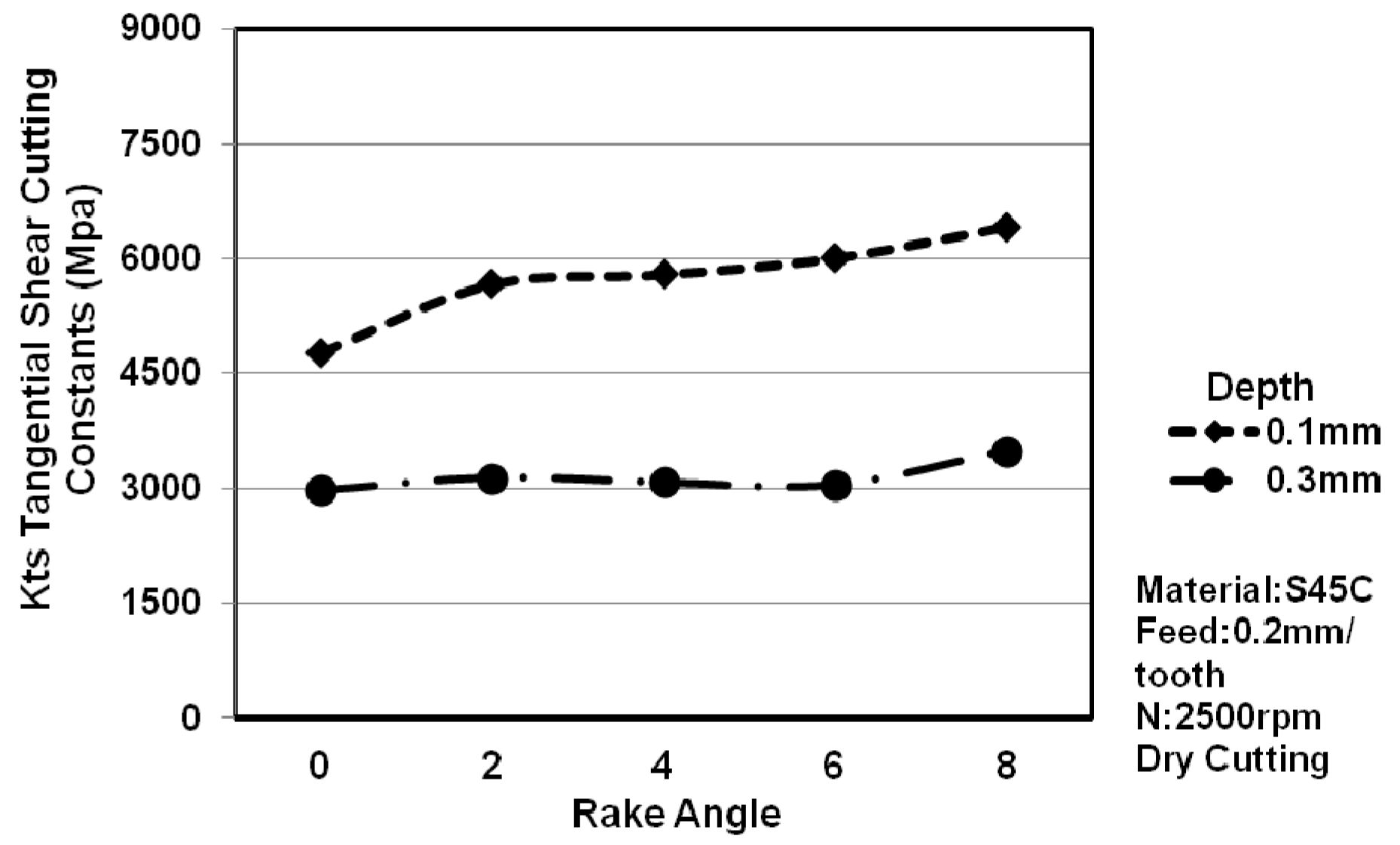
- In order to avoid increasing the tangential plough constant and the tangential shear constant of tools, which might increase the cutting force and further reduce the service life of tools, the clearance angle of the tools should be increased. This is because, as the cutting rake angle increases, when the rake angle is 0°, the cutting force in the X/Y/Z direction is the smallest.
- The smaller the cutting depth is, the bigger the tangential plough constant and the tangential shear constant are. The main reason for this is that the size effect causes the bigger tangential shear constant, and the contact length of the flank is the primary cause for the big tangential plough constant.
- When the cutting feed-rate is changed, the bigger the feed-rate is, the bigger the tangential plough constant and the tangential shear constant are. The main reason for this is that the removal rate per unit of time is big, however the effect is not too big and the impact on the different rake angle of tools is not obvious.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, Y.M.; Tai, C.C. A Coupled Thermal and Mechanical Finite Element Model of Orthogonal Metal Cutting with Deformable Cutting Tools. Master’s Thesis, Tatung University, Taipei, Taiwan, 2009. [Google Scholar]
- Huang, T.H. Study of Evaluation Criteria for Machinability of Steel; NCKU: Taipei, Taiwan, 2002. [Google Scholar]
- Dewes, R.C.; Aspinwall, D.K. A review of ultru high speed milling of hardened steels. J. Mater. Process. Technol. 1997, 69, 1–17. [Google Scholar] [CrossRef]
- Karandikar, J.; Mcleay, T.; Turner, S.; Schmitz, T. Tool wear monitoring using naive Bayes classifiers. Int. J. Adv. Manuf. Technol. 2014, 75, 5–8. [Google Scholar] [CrossRef]
- Koenigsberger, F.; Sabberwal, A.J.P. An investigation into the cutting force pulsations during milling operations. Int. J. Mach. Tool Des. Res. 1961, 1, 15–33. [Google Scholar] [CrossRef]
- Tlusty, J.; Macneil, P. Dynamics of cutting forces in end milling. CIRP Ann. 1975, 24, 21–25. [Google Scholar]
- Wang, J.J.; Zheng, C.M. On-line identification of shearing and plowing constants in end milling. ASME J. Manuf. Sci. Eng. 2003, 125, 58–65. [Google Scholar]
- Wang, J.J.; Zheng, C.M. An analytical force model with shearing and ploughing mechanisms for end milling. Int. J. Mach. Tools Manuf. 2002, 42, 761–771. [Google Scholar] [CrossRef]
- Wang, J.J.; Huang, C.Y. Analysis of Process Damping and System Dynamics in Milling; NCKU: Taipei City, Taiwan, 2006. [Google Scholar]
- Martellotti, M.E. An analysis of the milling process. Trans. ASME 1941, 63, 677–700. [Google Scholar]
- Engin, S.; Altintas, Y. Mechanics and dynamics of general milling cutters. Part I: Helical end mills. Int. J. Mach. Tools Manuf. 2001, 41, 2195–2212. [Google Scholar] [CrossRef]
- Ozel, T.; Altan, T. Process simulation using finite element method-prediction of cutting forces, tool stresses and temperatures in high—Speed flat end milling. Int. J. Mach. Tools Manuf. 2000, 40, 713–738. [Google Scholar] [CrossRef]
- Smith, S.; Tlusty, J. An overview of modeling and simulation of the milling process. J. Eng. Ind. 1991, 113, 169–175. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principle; Clarendon Press: New York, NY, USA, 1984; Chapter 14. [Google Scholar]
- Wang, J.J.; Liang, S.Y.; Book, W.J. Convolution analysis of milling force pulsation. ASME J. Eng. Ind. 1994, 116, 17–25. [Google Scholar] [CrossRef]
- Zheng, L.; Li, Y.; Liang, S.Y. A generalized model of milling forces. Int. J. Adv. Manuf. Technol. 1998, 14, 160–171. [Google Scholar] [CrossRef]
- Kline, W.A.; DeVor, R.E.; Snareef, I.A. The prediction of surface accuracy in end milling. J. Eng. Ind. 1982, 104, 272–278. [Google Scholar] [CrossRef]
- Schulz, H.; Moriwaki, T. High-speed machining. Ann. CIRP 1992, 41, 637–643. [Google Scholar] [CrossRef]
- Karandikar, J.; Schmitz, T.; Abbas, A. spindle speed selection for tool life testing using Bayesian inference. J. Manuf. Syst. 2012, 31, 403–411. [Google Scholar] [CrossRef]
- Otto, A.; Radons, G. The influence of tangential and tensional vibrations on the stability lobes in metal cutting. Nonlinear Dyn. 2015, 82, 1989–2000. [Google Scholar] [CrossRef]
- Ganesh babu, B.; Selladurai, V.; Shanmugam, R. Analytical modeling of cutting forces of end milling operation on aluminum silicon carbide particulate metal matrix composite material using response surface methodology. J. Eng. Appl. Sci. 2008, 3, 195–196. [Google Scholar]
- Wyen, C.-F.; Jaeger, D.; Wegener, K. Influence of cutting edge radius on surface integrity and burr formation in milling titanium. Int. J. Adv. Manuf. Technol. 2013, 67, 589–599. [Google Scholar] [CrossRef]
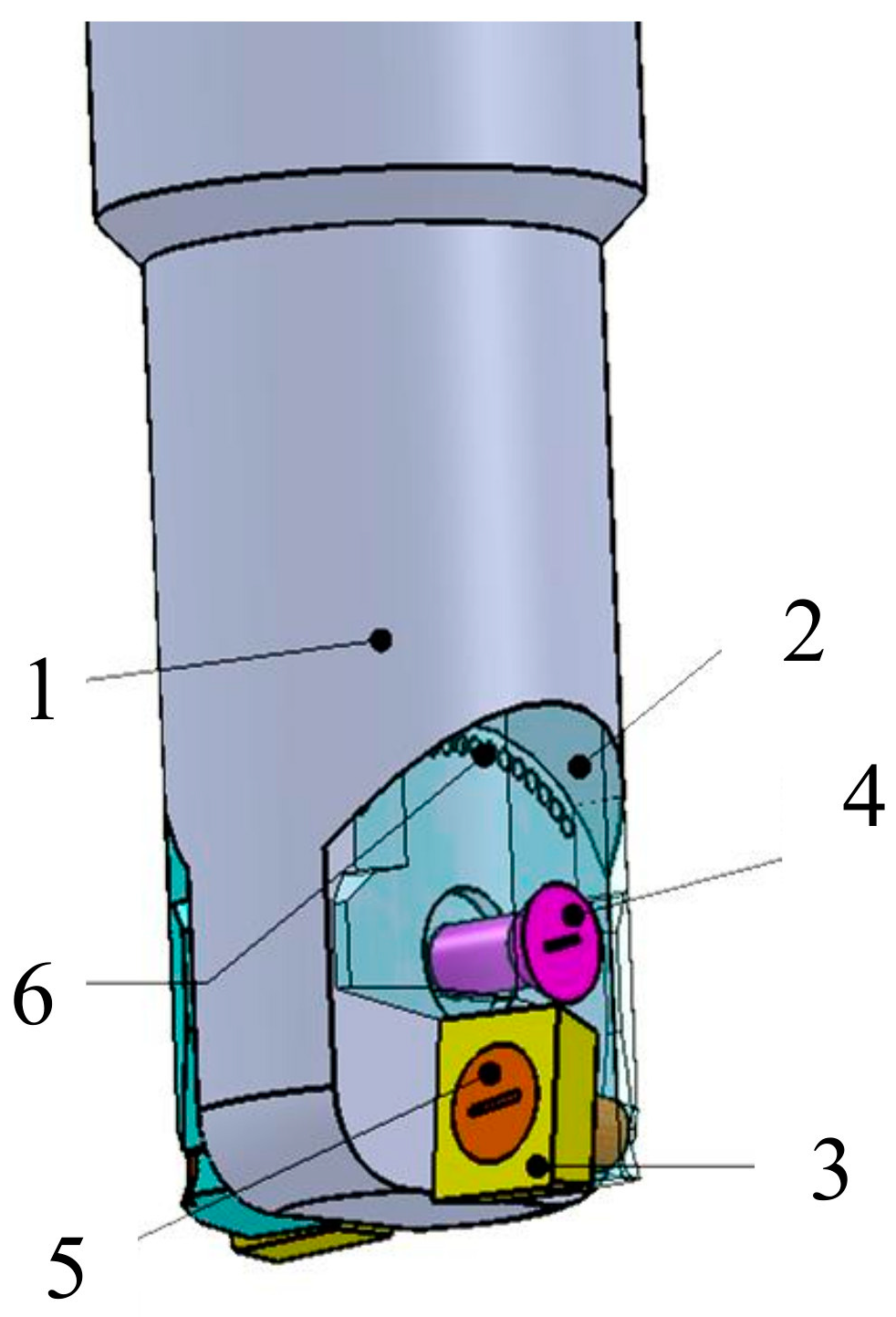
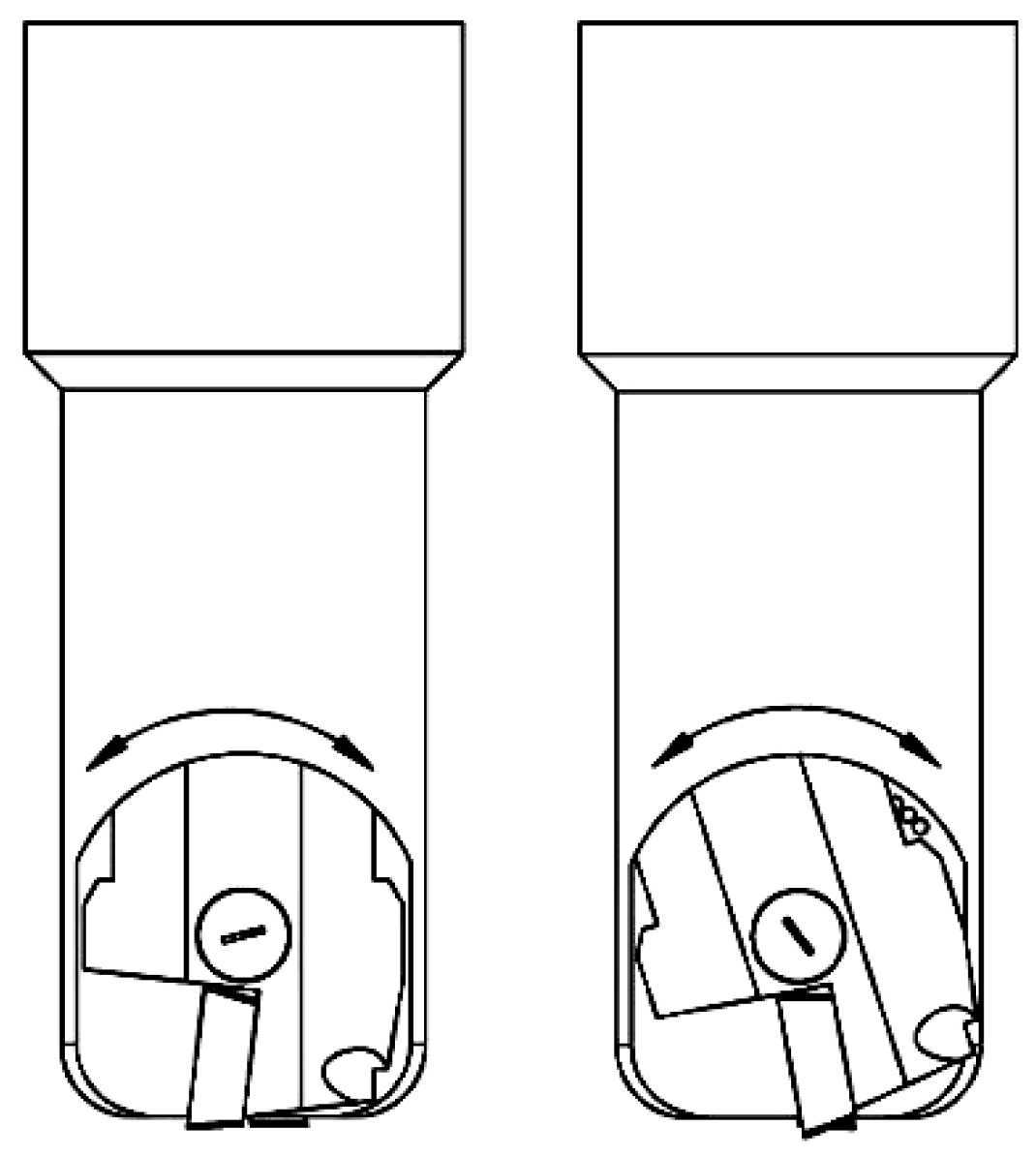
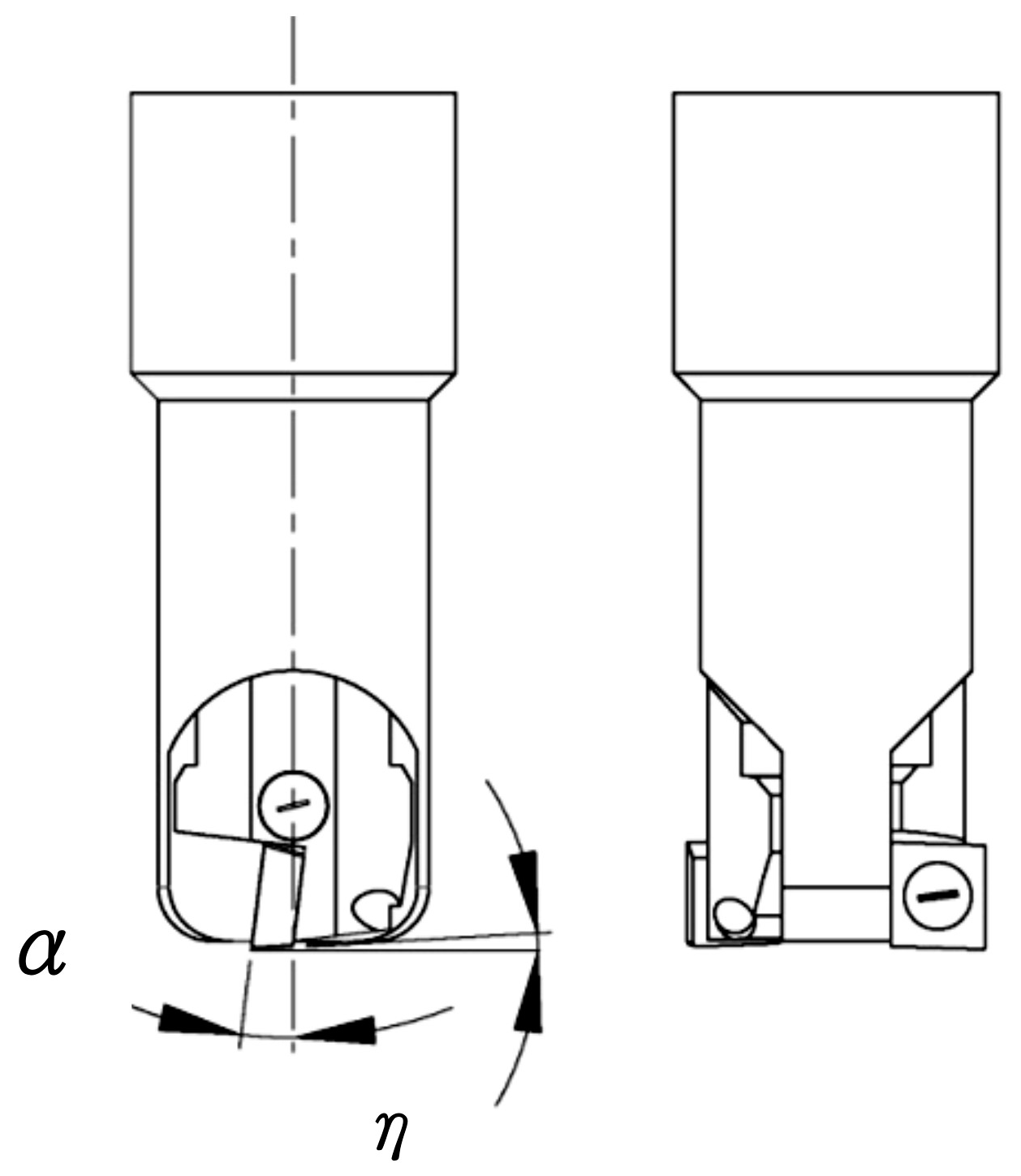
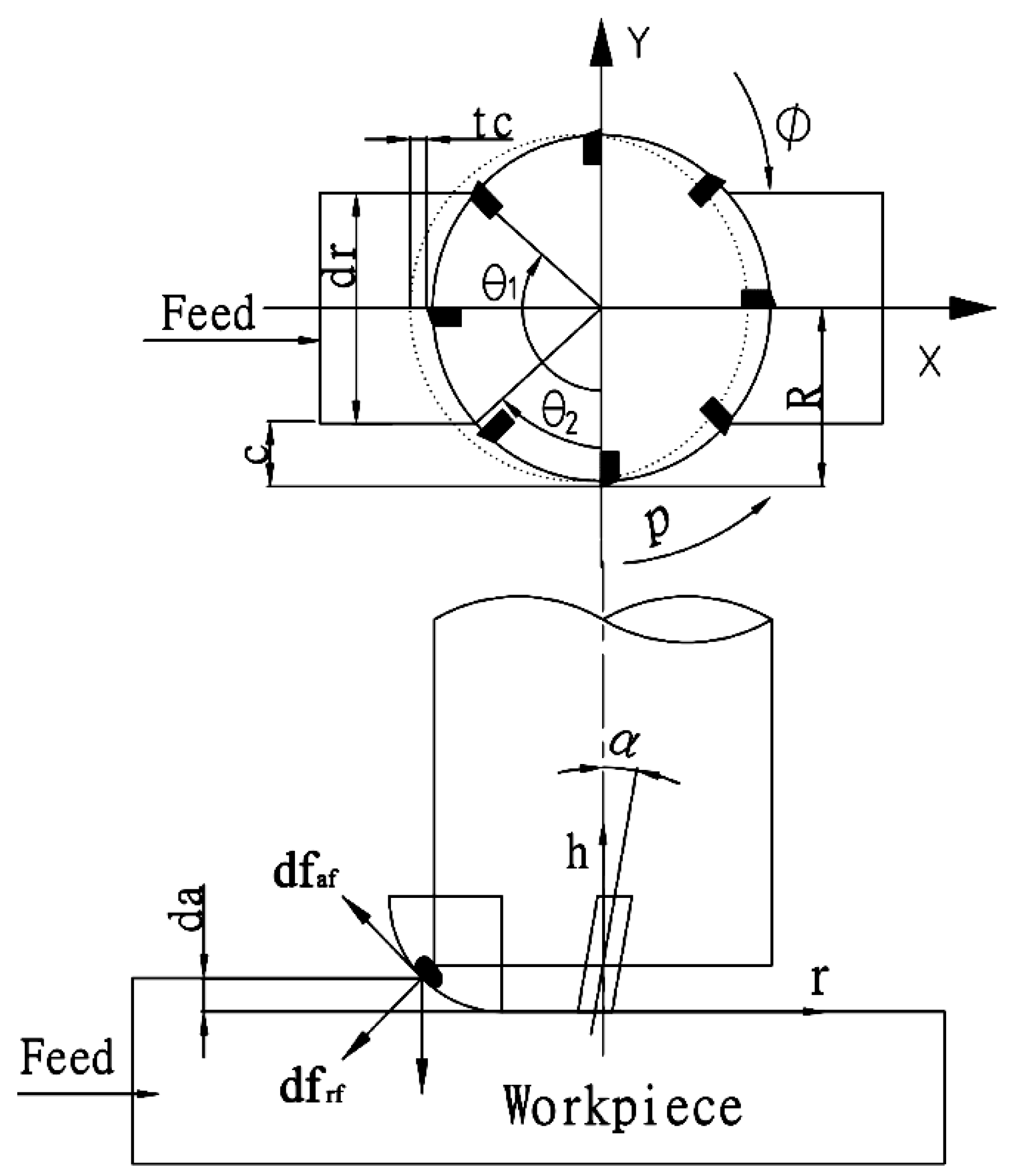
| Specification of Holder | Item No. of Blade | Material of Tool | Tooth Qty | Company |
|---|---|---|---|---|
| BXD4000R252SA25SA | XDGT1550PDER-G15 | Coated TiAlN | 2 | MITSUBISHI |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-H.; Pan, C.-H. Influence of Rake Angles of Multi-Position Tool on Cutting Characteristics. Appl. Syst. Innov. 2018, 1, 18. https://doi.org/10.3390/asi1020018
Chen S-H, Pan C-H. Influence of Rake Angles of Multi-Position Tool on Cutting Characteristics. Applied System Innovation. 2018; 1(2):18. https://doi.org/10.3390/asi1020018
Chicago/Turabian StyleChen, Shao-Hsien, and Chi-Hsiang Pan. 2018. "Influence of Rake Angles of Multi-Position Tool on Cutting Characteristics" Applied System Innovation 1, no. 2: 18. https://doi.org/10.3390/asi1020018
APA StyleChen, S.-H., & Pan, C.-H. (2018). Influence of Rake Angles of Multi-Position Tool on Cutting Characteristics. Applied System Innovation, 1(2), 18. https://doi.org/10.3390/asi1020018




