Climate During the Last Glacial Maximum in the Southern Sangre de Cristo Mountains, Colorado, U.S.A.
Abstract
1. Introduction
2. Regional Setting
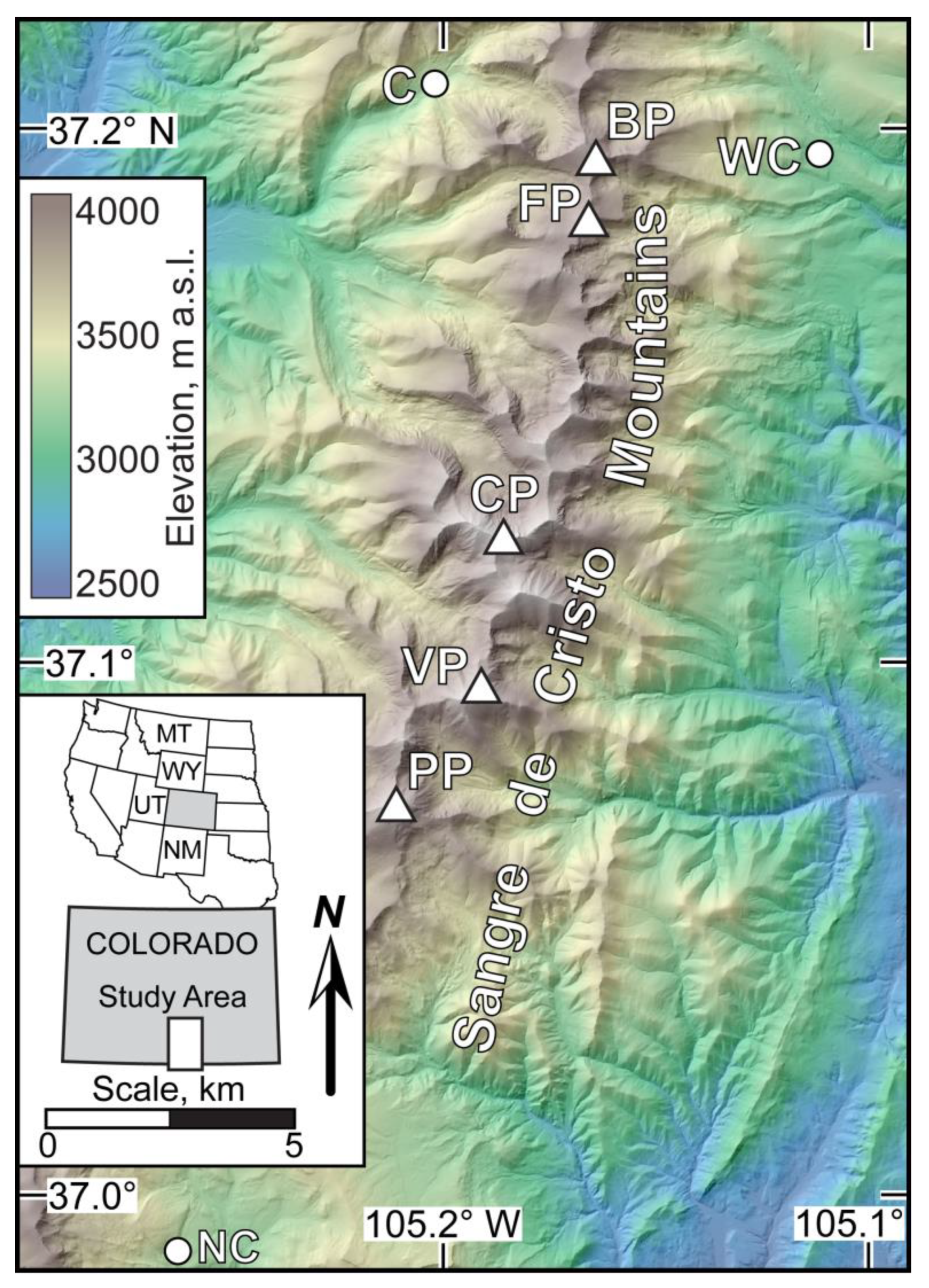
2.1. Geologic and Geomorphological Setting
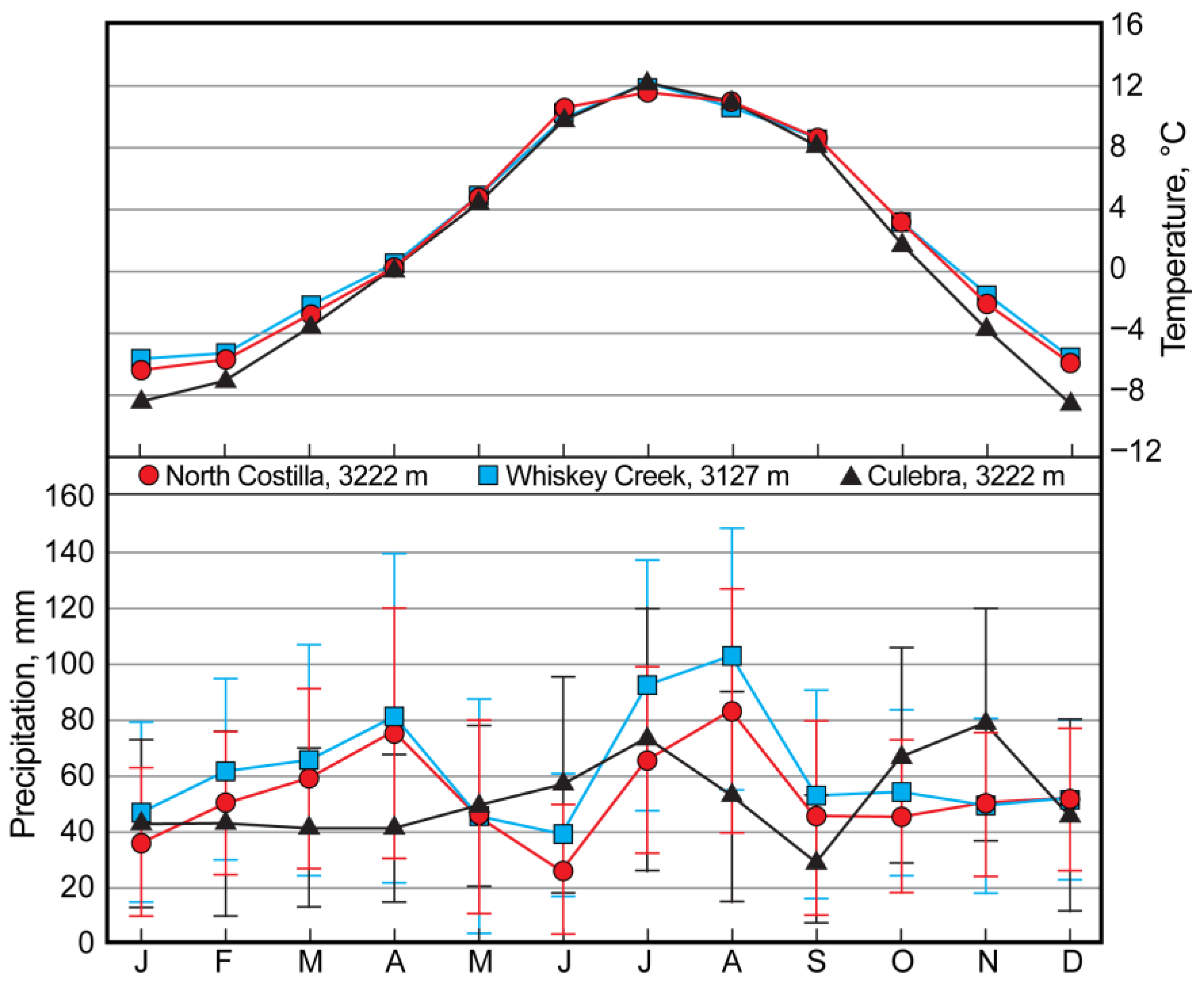
2.2. Modern Climatology
2.3. Timing of the Local LGM
3. Materials and Methods
3.1. Glacier Reconstruction
3.2. The Temperature-Index Model and Its Implementation
4. Results
4.1. Glacier Reconstruction and Equilibrium-Line Altitudes
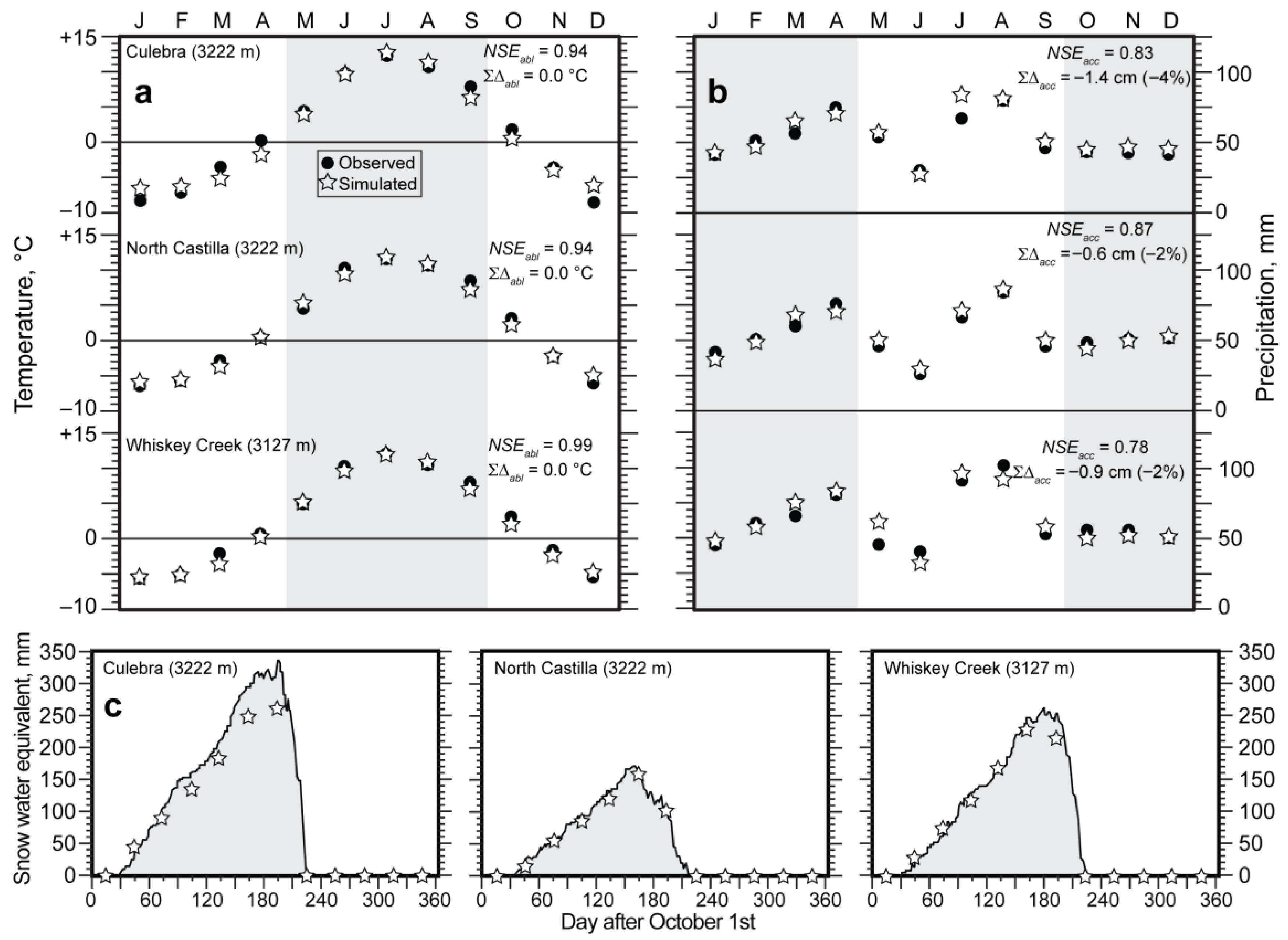
4.2. Temperature-Index Modeling: Model Skill
4.3. Steady-State Mass Balances of Paleoglaciers and Implications for LGM Climate
4.4. Uncertainties in the Estimates of LGM Temperature Depression
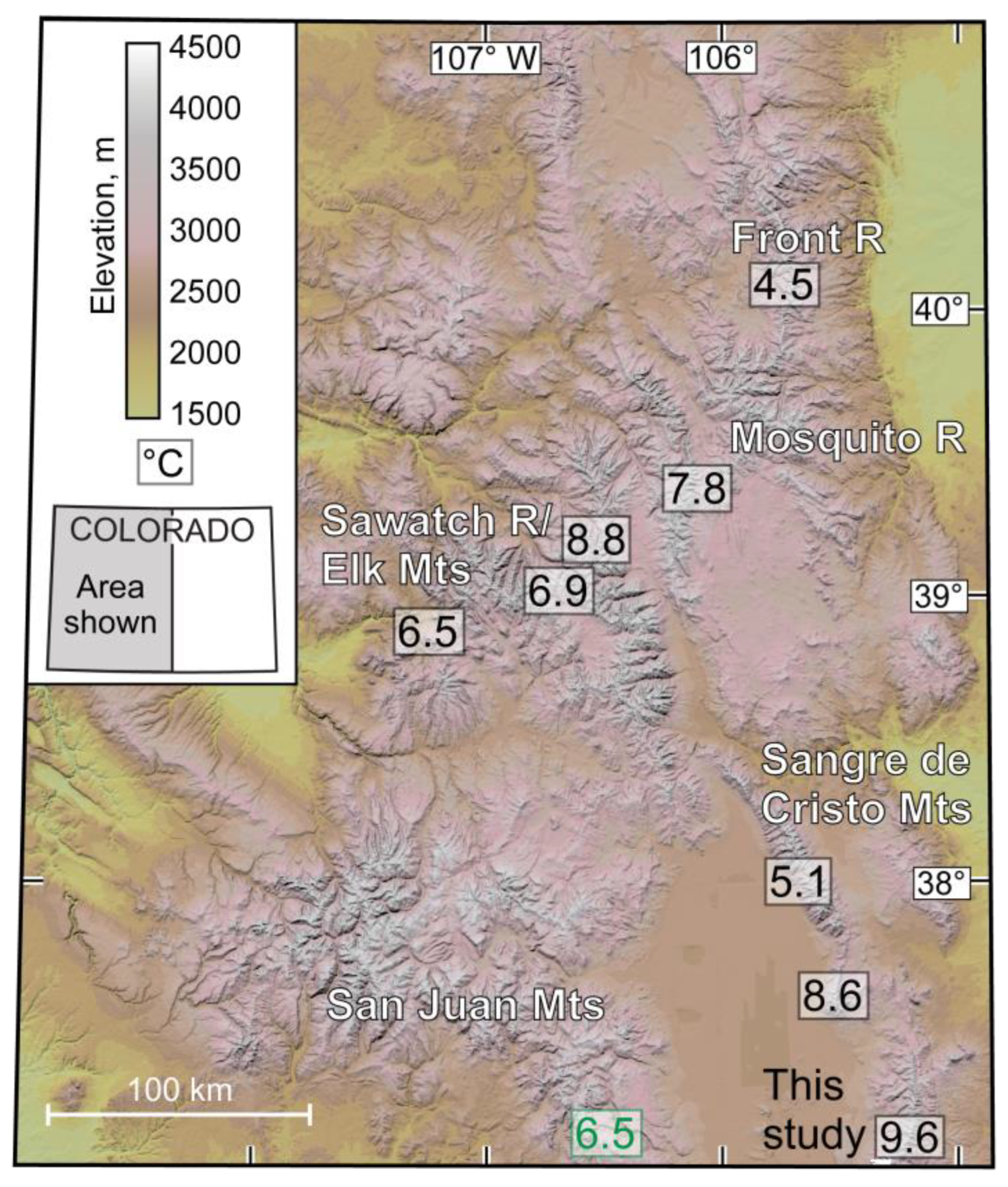
5. Discussion
6. Conclusions
- (1)
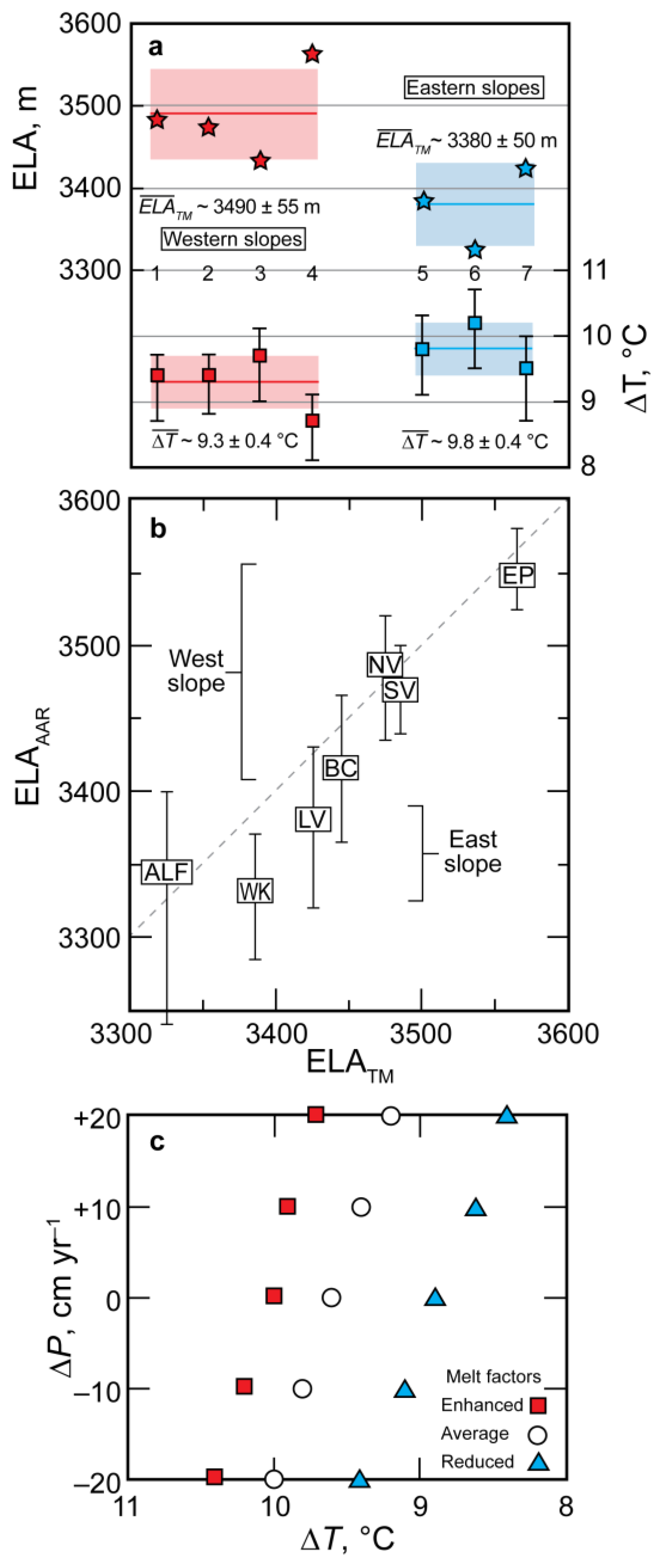
- At the glacier’s maximum LGM extents, ELAs on east-facing slopes were on average ~100 m lower than those on west-facing slopes. This east–west asymmetry in ELAs has been documented elsewhere in the Sangre de Cristo [25] and in the Mosquito Range farther north [15]. This is possibly a result of less insolation, and hence ablation, and/or mechanisms through which accumulation might have been enhanced via wind drift or snow advection [17,26,38] or late winter/early spring upslope precipitation events [24].
- (2)
- Temperature-index modeling was used to determine the temperatures and precipitation necessary to maintain steady-state mass balances of the glacier. Modeling suggests mean temperature depressions during the LGM of between 8.9 and 10.0 °C, this range being associated with different melt factors used in the model and if LGM precipitation did not differ from that today. Considering modest increases in precipitation, the magnitude(s) of temperature depressions is slightly reduced by ~0.3 °C, well within estimated uncertainties of ±1 °C. Under the most reasonably favorable glacial conditions, temperature depression could have been as small as 8.6 or even 7.6 °C incorporating uncertainty.
- (3)
- While the temperature depression obtained for the study area is significantly greater than some other estimates elsewhere in Colorado, it is consistent with those suggested by CHELSA-TraCE21k downscaling [56] and PMIP3 ensembles [2]. With due consideration of the associated uncertainties, it is also in agreement with the mean temperature depression determined for the nearby Blanca Massif [17] and the southernmost Sangre de Cristo Mountains in New Mexico [11].
- (4)
- Because of their dependence on knowledge of paleoprecipitation, models seeking to understand the nature of LGM temperature change in the Colorado Rocky Mountains would be better constrained by, and benefit from, new and/or improved precipitation proxies.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clark, P.U.; Dyke, A.S.; Shakun, J.D.; Carlson, A.E.; Clark, J.; Wohlfarth, B.; Mitrovica, J.X.; Hostetler, S.W.; McCabe, A.M. The Last Glacial Maximum. Science 2009, 325, 710–714. [Google Scholar] [CrossRef] [PubMed]
- Oster, J.L.; Ibarra, D.E.; Winnick, M.J.; Maher, K. Steering of westerly storms over western North America at the Last Glacial Maximum. Nat. Geosci. 2015, 8, 201–205. [Google Scholar] [CrossRef]
- Lora, J.M. Components and Mechanisms of Hydrologic Cycle changes over North America at the Last Glacial Maximum. J. Clim. 2018, 31, 7035–7051. [Google Scholar] [CrossRef]
- Ibarra, D.E.; Oster, J.L.; Winnick, M.J.; Caves Rugenstein, J.K.; Byrne, M.; Chamberlain, C.P. Warm and cold wet states in the western United States during the Pliocene-Pleistocene. Geology 2018, 46, 355–358. [Google Scholar] [CrossRef]
- Lora, J.M.; Ibarra, D.E. The North American hydrologic cycle through the last deglaciation. Quat. Sci. Rev. 2019, 226, 105991. [Google Scholar] [CrossRef]
- Laabs, B.J.; Plummer, M.A.; Mickelson, D.M. Climate during the last glacial maximum in the Wasatch and southern Uinta Mountains inferred from glacier modeling. Geomorphology 2006, 75, 300–317. [Google Scholar] [CrossRef]
- Refsnider, K.A.; Laabs, B.J.C.; Plummer, M.A.; Mickelson, D.M.; Singer, B.S.; Caffee, M.W. Last Glacial Maximum climate inferences from cosmogenic dating and glacier modeling of the western Uinta ice field, Uinta Mountains, Utah. Quat. Res. 2008, 69, 130–144. [Google Scholar] [CrossRef]
- Dühnforth, M.; Anderson, R.S. Reconstructing the glacial history of green lakes valley, North Boulder Creek, Colorado Front Range. Arct. Antarct. Alp. Res. 2011, 43, 527–542. [Google Scholar] [CrossRef]
- Leonard, E.M.; Laabs, B.J.C.; Plummer, M.A.; Kroner, R.K.; Brugger, K.A.; Spiess, V.M.; Refsnider, K.A.; Xia, Y.; Caffee, M.W. Late Pleistocene glaciation and deglaciation in the Crestone Peaks area, Sangre de Cristo Mountains, USA-chronology and paleoclimate. Quat. Sci. Rev. 2017, 158, 127–144. [Google Scholar] [CrossRef]
- Quirk, B.J.; Moore, J.R.; Laabs, B.J.C.; Plummer, M.A.; Caffee, M.W. Latest Pleistocene glacial and climate history of the Wasatch Range, Utah. Quat. Sci. Rev. 2020, 238, 106313. [Google Scholar] [CrossRef]
- Leonard, E.M.; Laabs, B.J.C.; Roberson, A.; Plummer, M.A.; Ibarra, D.E.; Caffee, M.W. Late Pleistocene glaciation in the southernmost Sangre de Cristo Mountains, New Mexico—Chronology and paleoclimate. Quat. Sci. Adv. 2023, 9, 100070. [Google Scholar] [CrossRef]
- Quirk, B.J.; Larsen, I.J.; Hidy, A.J. Latest Pleistocene glacial chronology and paleoclimate reconstruction for the East River watershed, Colorado, USA. Quat. Res. 2024, 119, 86–98. [Google Scholar] [CrossRef]
- Brugger, K.A. Late Pleistocene climate inferred from the reconstruction of the Taylor River glacier complex, southern Sawatch Range, Colorado. Geomorphology 2006, 75, 318–329. [Google Scholar] [CrossRef]
- Brugger, K.A. Climate in the southern Sawatch Range and Elk Mountains, Colorado, USA, during the Last Glacial Maximum: Inferences using a simple degree-day model. Arct. Antarct. Alp. Res. 2010, 42, 164–178. [Google Scholar] [CrossRef]
- Brugger, K.A.; Laabs, B.; Reimers, A.; Bensen, N. Late Pleistocene glaciation in the Mosquito Range, Colorado, USA: Chronology and climate. J. Quat. Sci. 2019, 34, 187–202. [Google Scholar] [CrossRef]
- Brugger, K.A.; Ruleman, C.A.; Caffee, M.W.; Mason, C.C. Climate during the Last Glacial Maximum in the Northern Sawatch Range, Colorado, USA. Quaternary 2019, 2, 36. [Google Scholar] [CrossRef]
- Brugger, K.A.; Leonard, E.M.; Refsnider, K.A.; Dolan, P. Climate on the Blanca Massif, Sangre de Cristo Mountains, Colorado, USA, during the Last Glacial Maximum. Quaternary 2021, 4, 27. [Google Scholar] [CrossRef]
- Shafer, S.L.; Bartlein, P.J.; Izumi, K. PMIP3/CMIP5 lgm Simulated Temperature Data for North America Downscaled to a 10-km Grid; U.S. Geological Survey data release; US Geological Survey: Reston, VA, USA, 2021. [Google Scholar] [CrossRef]
- Lindsey, D.A.; Caine, J.S. Thick- and thin-skinned contractional styles and the tectonic evolution of the northern Sangre de Cristo Mountains, Colorado, USA. Geosphere 2024, 20, 678–710. [Google Scholar] [CrossRef]
- Lindsey, D.A. The Geologic Story of Colorado’s Sangre de Cristo Range; US Geological Survey: Reston, VA, USA, 2010; 14p. [Google Scholar]
- Johnstone, S.A.; Hudson, A.M.; Nicovitch, S.; Ruleman, C.A.; Sare, R.M.; Thompson, R.A. Establishing chronologies for alluvial-fan sequences with analysis of high resolution topographic data: San Luis Valley, Colorado, USA. Geosphere 2018, 14, 2487–2504. [Google Scholar] [CrossRef]
- Nicovich, S.R.; Schmitt, J.G.; Gray, H.J.; Klinger, R.E.; Mahan, S.A. Construction and modification of debris-flow alluvial fans as captured in the geomorphic and sedimentary record: Example from the western Sangre Mountains, south-central Colorado. Geol. Soc. Am. Spec. Pap. 2023, 561, 47. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the coterminous United States. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Boatman, J.F.; Reinking, R.F. Synoptic and mesoscale circulation and precipitation mechanisms in shallow upslope storms over the western high plains. Mon. Weather Rev. 1984, 112, 1725–1744. [Google Scholar] [CrossRef]
- Refsnider, K.A.; Brugger, K.A.; Leonard, E.M.; McCalpin, J.P.; Armstrong, P.P. Last glacial maximum equilibrium-line altitude trends and precipitation patterns in the Sangre de Cristo Mountains, southern Colorado, USA. Boreas 2009, 38, 663–678. [Google Scholar] [CrossRef]
- Gutmann, E.D.; Rasmussen, R.M.; Lui, C.; Ikeda, K.; Gochis, D.J.; Clark, M.P.; Dudhia, J.; Thompson, G. A comparison of statistical and dynamical downscaling of winter precipitation over complex terrain. J. Clim. 2012, 25, 262–281. [Google Scholar] [CrossRef]
- Sheppard, P.R.; Comrie, A.C.; Packin, G.D.; Angerbach, K.; Hughes, M.K. The climate of the US Southwest. Clim. Res. 2002, 21, 219–238. [Google Scholar] [CrossRef]
- Brugger, K.A. Cosmogenic 10Be and 36Cl ages from late Pleistocene terminal moraine complexes in the Taylor River drainage basin, central Colorado, USA. Quat. Sci. Rev. 2007, 26, 494–499. [Google Scholar] [CrossRef]
- Young, N.E.; Briner, J.P.; Leonard, E.M.; Licciardi, J.M.; Lee, K. Assessing climatic and non-climatic forcing of Pinedale glaciation and deglaciation in the western United States. Geology 2011, 39, 171–174. [Google Scholar] [CrossRef]
- Schweinsberg, A.D.; Briner, J.P.; Licciardi, J.M.; Schroba, R.R.; Leonard, E.M. Cosmogenic 10Be exposure dating of Bull Lake and Pinedale moraine sequences in the upper Arkansas River valley Colorado Rocky Mountains, USA. Quat. Res. 2020, 97, 125–139. [Google Scholar] [CrossRef]
- Laabs, B.J.C.; Licciardi, J.M.; Leonard, E.M.; Munroe, J.S.; Marchetti, D.W. Updated cosmogenic chronologies of Pleistocene mountain glaciation in the western United States and associated paleoclimate inferences. Quat. Sci. Rev. 2020, 242, 106427. [Google Scholar] [CrossRef]
- Kirkham, R.M.; Lufkin, J.L.; Lindsay, N.R.; Dickens, K.E. Geologic Map of the La Valley Quadrangle; Colorado Geological Survey Open-File Report; Colorado Geological Survey: Costilla County, CO, USA, 2004; pp. 4–8. [Google Scholar]
- Kirkham, R.M.; Keller, J.W.; Price, N.R.; Lindsay, N.R. Geologic Map of the South Half of the Culebra Peak Quadrangle; Colorado Geological Survey Open-File Report; Colorado Geological Survey: Costilla and Las Animas Counties, CO, USA, 2005. [Google Scholar]
- Fridrich, C.J.; Kirkham, R.M. Preliminary Map of the Culebra Peak Area, Sangre de Cristo Mountains, Las Animas and Costilla Countaines; U.S. Geol. Surv. OFR 2007-1428; USA Geological Survey: Reston, VA, USA, 2007. [Google Scholar]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Elsevier: Boston, MA, USA, 2010. [Google Scholar]
- Nye, J.F. The flow of a glacier in a channel of rectangular, elliptic or parabolic cross-section. J. Glaciol. 1965, 5, 661–690. [Google Scholar] [CrossRef]
- Bindschadler, R.; Harrison, W.D.; Raymond, C.F.; Crossen, R. Geometry and dynamics of a surge-type glacier. J. Glaciol. 1977, 18, 181–194. [Google Scholar] [CrossRef]
- Brocklehurst, S.H.; MacGregor, K.R. The role of wind in the evolution of glaciated mountain ranges: Field observations and insights from numerical modelling. AGU Fall Meet. Abstr. 2005, 2005, H51C-0390. [Google Scholar]
- Lora, J.M.; Mitchell, J.L.; Tripati, A.E. Abrupt reorganization of North Pacific and western North American climate during the last glaciation. Geophys. Res. Lett. 2016, 43, 11796–11804. [Google Scholar] [CrossRef]
- Kim, S.-J.; Crowley, T.J.; Erickson, D.J.; Govindasamy, B.; Duffy, P.B.; Lee, B.Y. High-resolution climate simulation of the last glacial maximum. Clim. Dyn. 2008, 31, 1–16. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D.; Lang, X. Northern westerlies during the Last Glacial Maximum: Results from CMIP5 simulations. J. Clim. 2018, 31, 1135–1153. [Google Scholar] [CrossRef]
- Hu, Y.; Xia, Y.; Liu, Z.; Wang, Y.; Lu, Z.; Wang, T. Distorted Pacific-North American teleconnections at the Last Glacial Maximum. Clim. Past. 2020, 16, 199–209. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, Y.; Yan, Q.; Yao, T.; Wang, M.; Huang, H.; Hu, Y. The glacier-climate interaction over the Tibetan Plateau and its surroundings during the Last Glacial Maximum. Geophy. Res. Lett. 2023, 50, e2023GL103538. [Google Scholar] [CrossRef]
- Menking, K.M.; Anderson, R.; Shafike, N.; Syed, K.H.; Allen, B.D. Wetter or colder during the Last Glacial Maximum? Revisiting the pluvial lake question in southwestern North America. Quat. Res. 2004, 62, 280–288. [Google Scholar] [CrossRef]
- Asmerom, Y.; Polyak, V.; Burns, S. Variable winter moisture in the southwestern United States linked to rapid glacial climate shifts. Nat. Geosci. 2010, 3, 114–117. [Google Scholar] [CrossRef]
- Menking, K.M.; Polyak, V.J.; Anderson, R.Y.; Asmerom, Y. Climate history of the southwestern United States base on Estancia Basin hydrologic variability from 69 to 10 ka. Quat. Sci. Rev. 2018, 200, 237–252. [Google Scholar] [CrossRef]
- Menking, K.M.; Bixby, R.J.; Cutler, S.M. Diatom evidence for a groundwater divide that limited the extent of Lake Estancia, New Mexico, USA, highstands during the Last Glacial Maximum. GSA Bull. 2022, 135, 407–419. [Google Scholar] [CrossRef]
- Hudson, A.M.; Quade, J.; Holliday, V.T.; Fenerty, B.; Bright, J.E.; Gray, H.J.; Mahan, S.A. Paleohydrologic history of pluvial lake San Agustin, New Mexico: Tracking changing effective moisture in southwest North America through the last glacial transition. Quat. Sci. Rev. 2023, 310, 108110. [Google Scholar] [CrossRef]
- Lora, J.M.; Skinner, C.B.; Rush, W.D.; Baek, S.H. The hydrologic cycle and atmospheric rivers in CESM2 simulations of the Last Glacial Maximum. Geophy. Res. Lett. 2023, 50, e2023GL104805. [Google Scholar] [CrossRef]
- Kutzbach, J.E.; Wright, H.E., Jr. Simulation of the climate of 18,000 years BP: Results for the North American/North Atlantic/European sector and comparison with the geologic record of North America. Quat. Sci. Rev. 1985, 4, 147–187. [Google Scholar] [CrossRef]
- Lyle, M.; Heusser, L.; Ravelo, C.; Yamamoto, M.; Barron, J.; Diffenbaugh, N.S.; Herbert, T.; Andreasen, D. Out of the Tropics: The Pacific, Great Basin Lakes, and the late Pleistocene water cycle in the western United States. Science 2012, 337, 1629–1633. [Google Scholar] [CrossRef]
- Lora, J.M.; Mitchell, J.L.; Risi, C.; Tripati, A.E. North Pacific atmospheric rivers and their influence on western North America at the Last Glacial Maximum. Geophys. Res. Lett. 2017, 44, 1051–1059. [Google Scholar] [CrossRef]
- Morrill, C.; Lowry, D.P.; Hoell, A. Thermodynamic and dynamic causes of pluvial conditions during the last glacial maximum. Geophys. Res. Lett. 2018, 45, 335–345. [Google Scholar] [CrossRef]
- Tabor, C.; Lofverstrom, M.; Oster, J.; Wortham, B.; de Wet, C.; Montañez, I.; Rhoades, A.; Zarzycki, C.; He, C.; Liu, Z. A mechanistic understanding of oxygen isotope changes in the western United States at the Last Glacial Maximum. Quat. Sci. Rev. 2021, 274, 107255. [Google Scholar] [CrossRef]
- Amaya, D.J.; Seltzer, A.M.; Karnauskas, K.B.; Lora, J.M.; Zhang, X.; DiNezio, P.N. Air-sea coupling shapes North American hydroclimate response to ice sheets during the Last Glacial Maximum. Earth Planet. Sci Lett. 2022, 578, 117271. [Google Scholar] [CrossRef]
- Karger, D.N.; Nobis, M.P.; Normand, S.; Graham, C.H.; Zimmermann, N.E. CHELSA-TraCE21k-high resolution (1 km) downscaled transient temperature and precipitation data since the Last Glacial Maximum. Clim. Past 2023, 19, 439–456. [Google Scholar] [CrossRef]
- Quirk, B.J.; Huss, E.; Laabs, B.J.C.; Leonard, E.; Licciardi, J.; Plummer, M.A.; Caffee, M.W. Late Pleistocene glacial chronologies and paleoclimate in the northern Rocky Mountains. Clim. Past 2022, 18, 293–312. [Google Scholar] [CrossRef]
- Birkel, S.D.; Putnam, A.E.; Denton, G.H.; Koons, P.O.; Fastook, J.L.; Putnam, D.E.; Maasch, K.A. Climate inferences from a glaciological reconstruction of the Late Pleistocene Wind River ice cap, Wind River Range, Wyoming. Arct. Antarct. Alp. Res. 2012, 44, 265–276. [Google Scholar] [CrossRef]
- Marchetti, D.W.; Harris, M.S.; Bailey, C.M.; Cerling, T.E.; Bergman, S. Timing of glaciation and last glacial maximum paleoclimate estimates from the Fish Lake Plateaus, Utah. Quat. Res. 2011, 75, 183–195. [Google Scholar] [CrossRef]
- Todd, V.L.; Shanahan, T.M.; Johnson, B.G. Hydroclimate and ecosystem changes in the Colorado Rocky Mountains since the Last Glacial Maximum. Paleocean. Paleoclim. 2025, 40, e2024PA005049. [Google Scholar] [CrossRef]

| Glacier | Area | Length, km * | Average Ice | Maximum Ice | Driving Stresses, | AAR-Derived ELA, m † | ||
|---|---|---|---|---|---|---|---|---|
| km2 | km | Thickness, m *,† | Thickness, m *,† | kPa ** (Mean) | =0.65 | =0.70 | =0.60 | |
| Western slope | ||||||||
| South Vallejos | 7.02 | 5.8 | 105 | 130 | 53–118 (93) | 3470 | 3440 | 3500 |
| North Vallejos | 7.95 | 7.6 | 105 | 155 | 73–156 (95) | 3485 | 3435 | 3525 |
| Bernardino- | 14.23 | 7.5 | 105 | 150 | 83–131 (113) | 3415 | 3365 | 3465 |
| Carneros †† | 7.3 | 110 | 160 | 65–122 (91) | ||||
| El Perdido | 3.25 | 4.6 | 75 | 100 | 55–152 (90) | 3550 | 3525 | 3580 |
| Means | 3480 | 3440 | 3520 | |||||
| Eastern slope | ||||||||
| Wilkens | 4.65 | 6.1 | 105 | 130 | 66–135 (108) | 3330 | 3285 | 3370 |
| Abbot-Left | 6.87 | 7.0 | 60 | 80 | 50–154 (95) | 3345 | 3290 | 3400 |
| Fork Abbot †† | 5.1 | 60 | 100 | 52–187 (98) | ||||
| Las Vigas | 3.09 | 5.9 | 70 | 95 | 52–144 (98) | 3380 | 3320 | 3430 |
| Means | 3355 | 3305 | 3405 | |||||
| Elevation (n) * | ∑∆Tablation | NSEablation | ∑∆Paccumulation | NSEaccumulation |
|---|---|---|---|---|
| North and South Vallejos Valleys | ||||
| 3999 (3) | −0.6 | 0.98 | +23 (+4%) | 0.93 |
| 3801 (5) | +0.1 | 0.98 | −11 (−2%) | 0.97 |
| 3601 (5) | +0.2 | 0.98 | −12 (−3%) | 0.97 |
| 3398 (4) | +0.8 | 0.98 | +1 (<1%) | 0.99 |
| 3195 (6) | −0.2 | 0.97 | +7 (+2%) | 0.97 |
| 3001 (6) | −0.6 | 0.99 | −11 (−3%) | 0.92 |
| Means | 0.4 | 9 (2%) | ||
| Bernardino, Carneros, and El Perdido Valleys | ||||
| 3900 (3) | −0.6 | 0.98 | +22 (+4%) | 0.95 |
| 3750 (8) | +0.05 | 0.98 | +7 (+1%) | 0.99 |
| 3599 (3) | +0.6 | 0.98 | −50 (−10%) | 0.70 |
| 3450 (5) | +0.6 | 0.98 | −25 (−6%) | 0.91 |
| 3198 (4) | −0.6 | 0.98 | −1 (0%) | 1.00 |
| Means | 0.5 | 21 (4%) | ||
| Wilkens Valley | ||||
| 3865 (3) | −0.2 | 0.99 | +31 (+5%) | 0.91 |
| 3654 (4) | −0.6 | 0.98 | +25 (+5%) | 0.91 |
| 3291 (3) | +1.0 | 0.98 | +5 (+1%) | 1.00 |
| 3054 (3) | −0.2 | 0.98 | +2 (<1%) | 0.85 |
| Means | 0.5 | 16 (3%) | ||
| Abbot, Left Fork Abbot, and Las Vigas Valleys | ||||
| 3904 (4) | +0.7 | 0.98 | −6 (−1%) | 0.93 |
| 3771 (4) | −0.1 | 0.98 | +29 (+5%) | 0.85 |
| 3497 (6) | +0.4 | 0.98 | +39 (+9%) | 0.84 |
| 3299 (3) | +0.4 | 0.98 | +18 (+4%) | 0.94 |
| 2994 (6) | −0.2 | 0.99 | −20 (−6%) | 0.72 |
| Means | 0.4 | 22 (5%) |
| Glacier | ∆T (°C; ∆P = 0) | ∆P (mm) * | ELA † | |||||
|---|---|---|---|---|---|---|---|---|
| Average Melt | Reduced Melt | Enhanced Melt | +200 | +100 | −100 | −200 | ||
| West slope | ||||||||
| 1. South Vallejo | 9.4 | 8.7 | 9.7 | 9.0 | 9.2 | 9.5 | 9.7 | 3485 |
| 2. North Vallejo | 9.4 | 8.7 | 9.8 | 9.0 | 9.2 | 9.6 | 9.8 | 3475 |
| 3. Bernardino-Carneros | 9.7 | 9.0 | 10.1 | 9.3 | 9.5 | 9.9 | 10.2 | 3435 |
| 4. El Perdido | 8.7 | 8.1 | 9.1 | 8.4 | 8.5 | 8.9 | 9.1 | 3565 |
| Means | 9.3 | 8.6 | 9.7 | 8.9 | 9.1 | 9.5 | 9.7 | 3490 |
| East Slope | ||||||||
| 5. Wilkens | 9.8 | 9.1 | 10.3 | 9.5 | 9.7 | 10.0 | 10.3 | 3385 |
| 6. Abbot-Left | ||||||||
| Fork Abbot | 10.2 | 9.5 | 10.7 | 9.9 | 10.0 | 10.5 | 10.7 | 3325 |
| 7. Las Vigas | 9.5 | 8.8 | 10.0 | 9.1 | 9.3 | 9.8 | 10.0 | 3425 |
| Means | 9.8 | 9.1 | 10.3 | 9.5 | 9.7 | 10.1 | 10.3 | 3380 |
| Grand means | 9.5 | 8.8 | 10.0 | 9.2 | 9.3 | 9.7 | 10.0 | 3440 |
| Reduced melt, means | 8.4 | 8.6 | 9.1 | 9.3 | ||||
| Enhanced melt, means | 9.6 | 9.8 | 10.1 | 10.3 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brugger, K.A.; Feldman, A.; Anderson, L.S.; Sion, B. Climate During the Last Glacial Maximum in the Southern Sangre de Cristo Mountains, Colorado, U.S.A. Quaternary 2025, 8, 64. https://doi.org/10.3390/quat8040064
Brugger KA, Feldman A, Anderson LS, Sion B. Climate During the Last Glacial Maximum in the Southern Sangre de Cristo Mountains, Colorado, U.S.A. Quaternary. 2025; 8(4):64. https://doi.org/10.3390/quat8040064
Chicago/Turabian StyleBrugger, Keith A., Anthony Feldman, Leif S. Anderson, and Brad Sion. 2025. "Climate During the Last Glacial Maximum in the Southern Sangre de Cristo Mountains, Colorado, U.S.A." Quaternary 8, no. 4: 64. https://doi.org/10.3390/quat8040064
APA StyleBrugger, K. A., Feldman, A., Anderson, L. S., & Sion, B. (2025). Climate During the Last Glacial Maximum in the Southern Sangre de Cristo Mountains, Colorado, U.S.A. Quaternary, 8(4), 64. https://doi.org/10.3390/quat8040064






