Hydrological Regime of Rivers in the Periglacial Zone of the East European Plain in the Late MIS 2
Abstract
1. Introduction
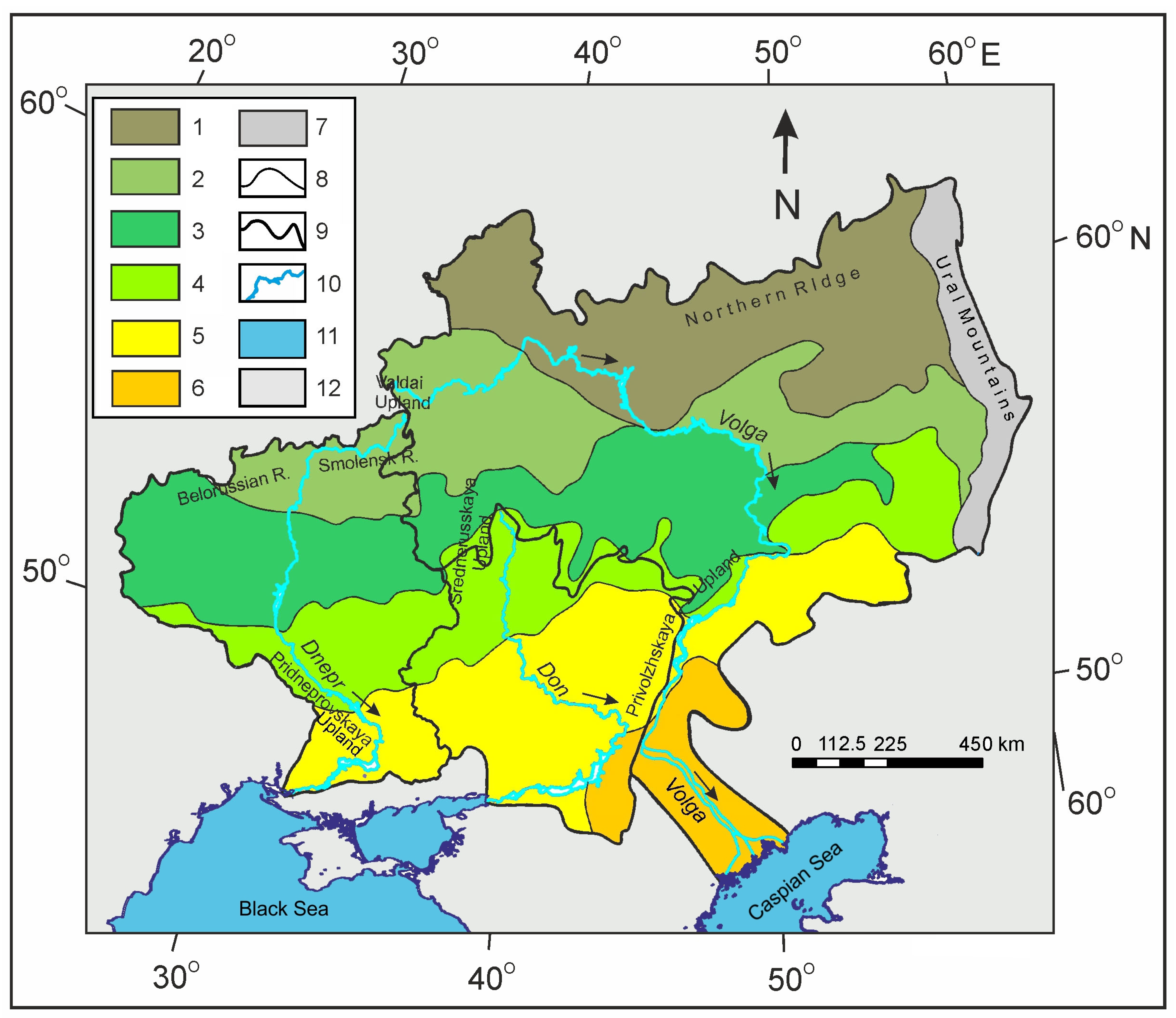
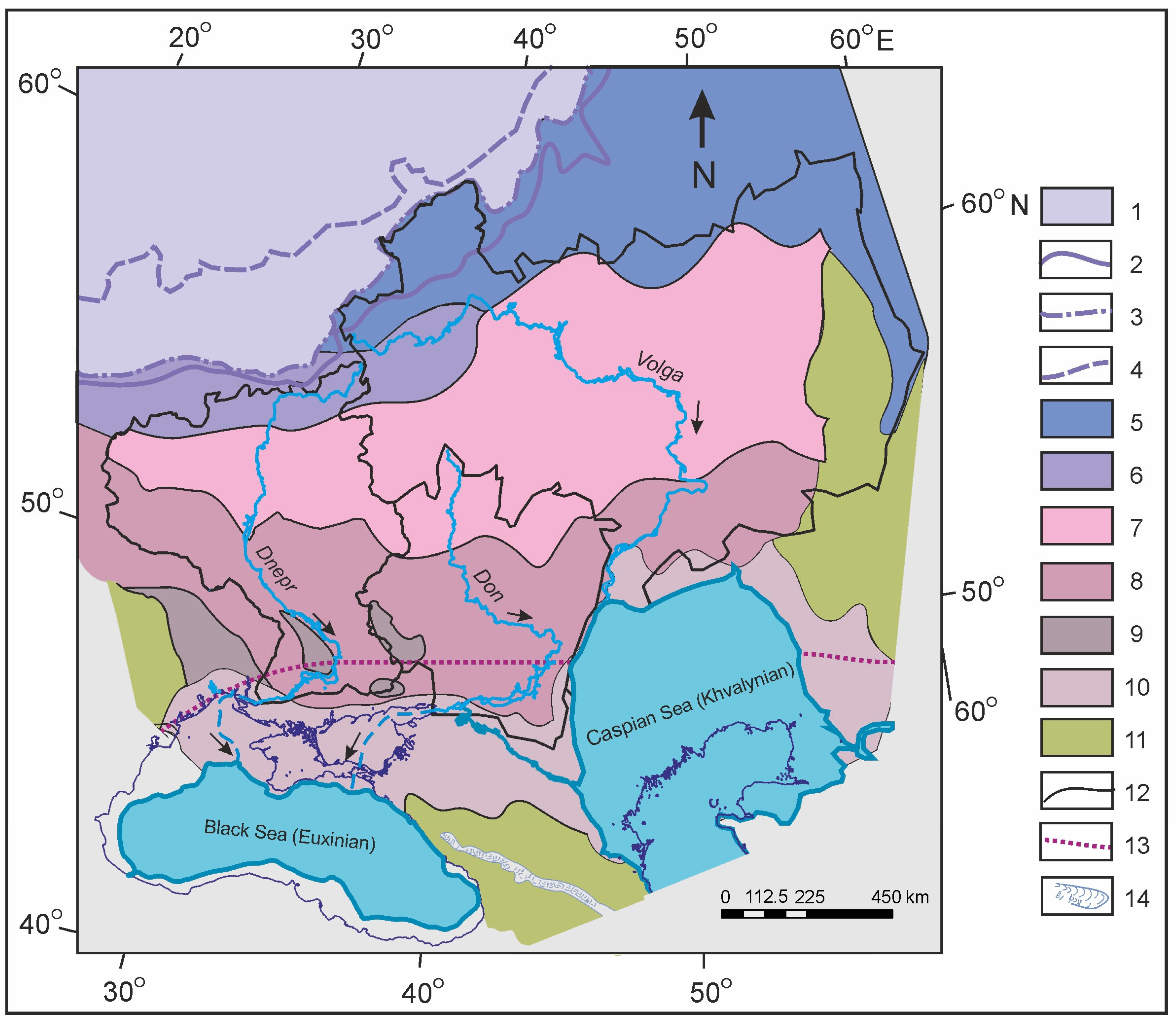
2. Study Area
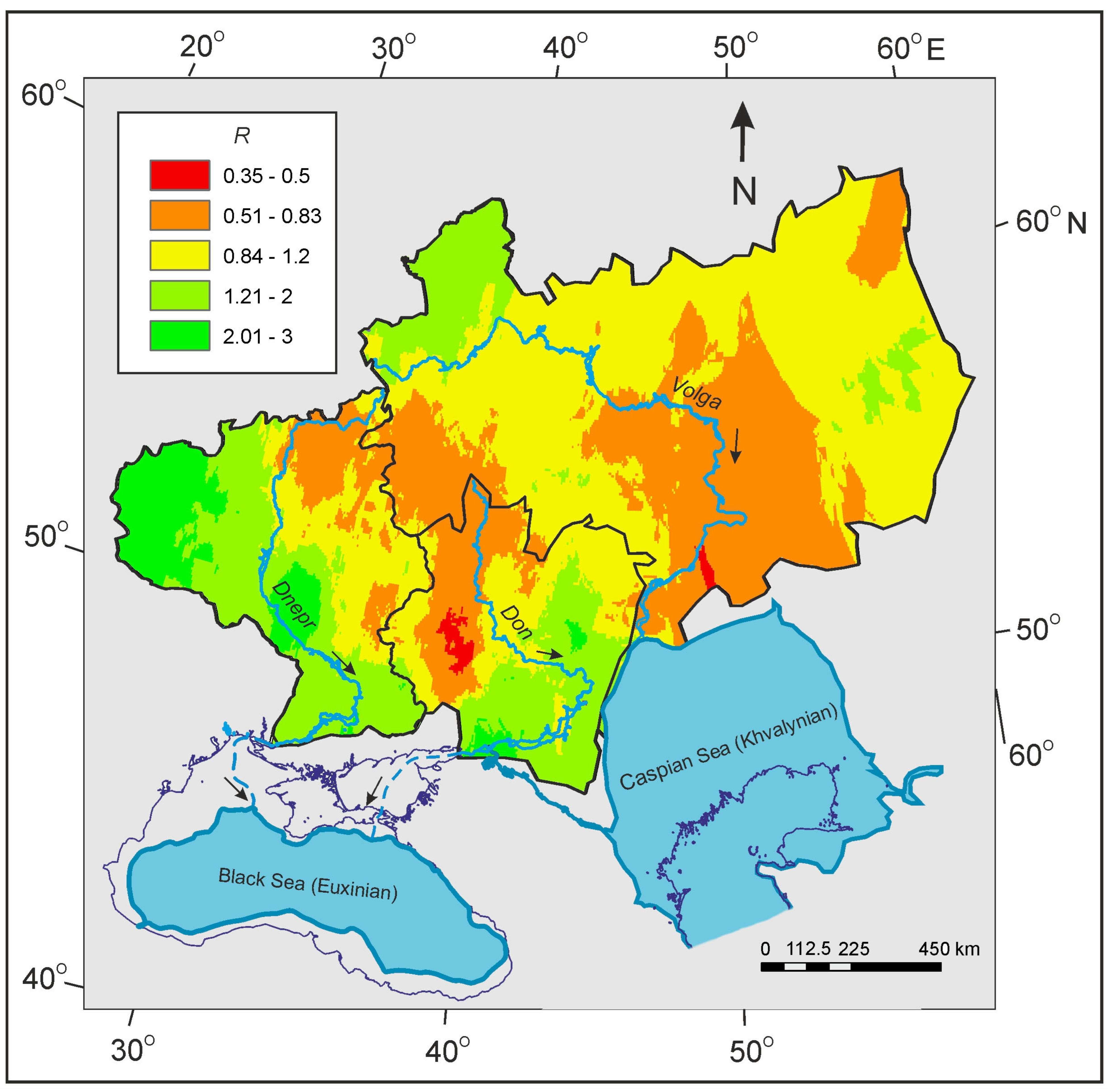
2.1. General Information
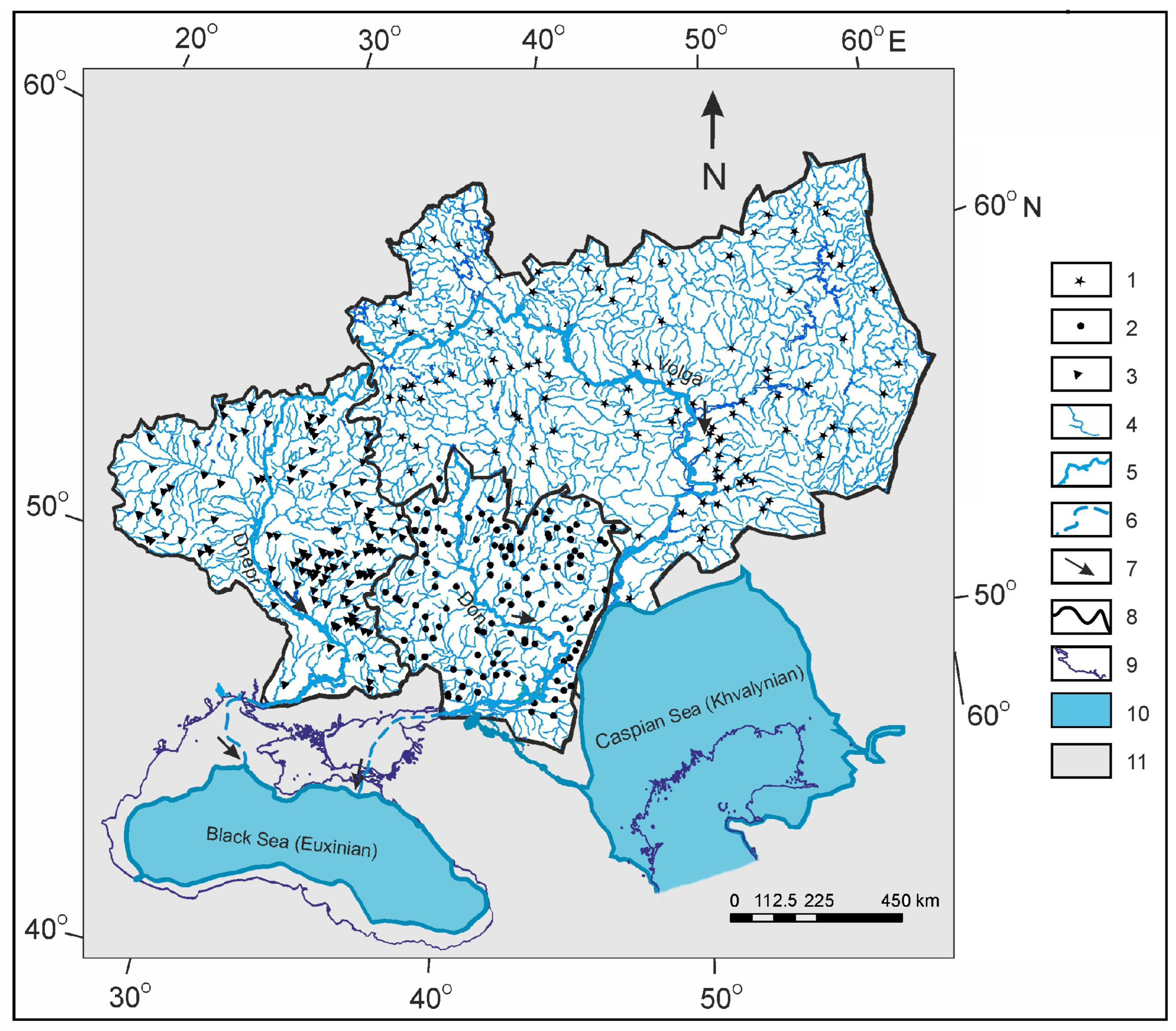
2.2. Large Ancient Meandering Rivers
2.3. Hydrological Data
3. Methods
3.1. Relationship between the Meander Wavelength and the Width of the Channel
3.2. Relationships between Water Flow and Channel Width
3.3. Relationships between Water Flows and Catchment Areas
4. Results
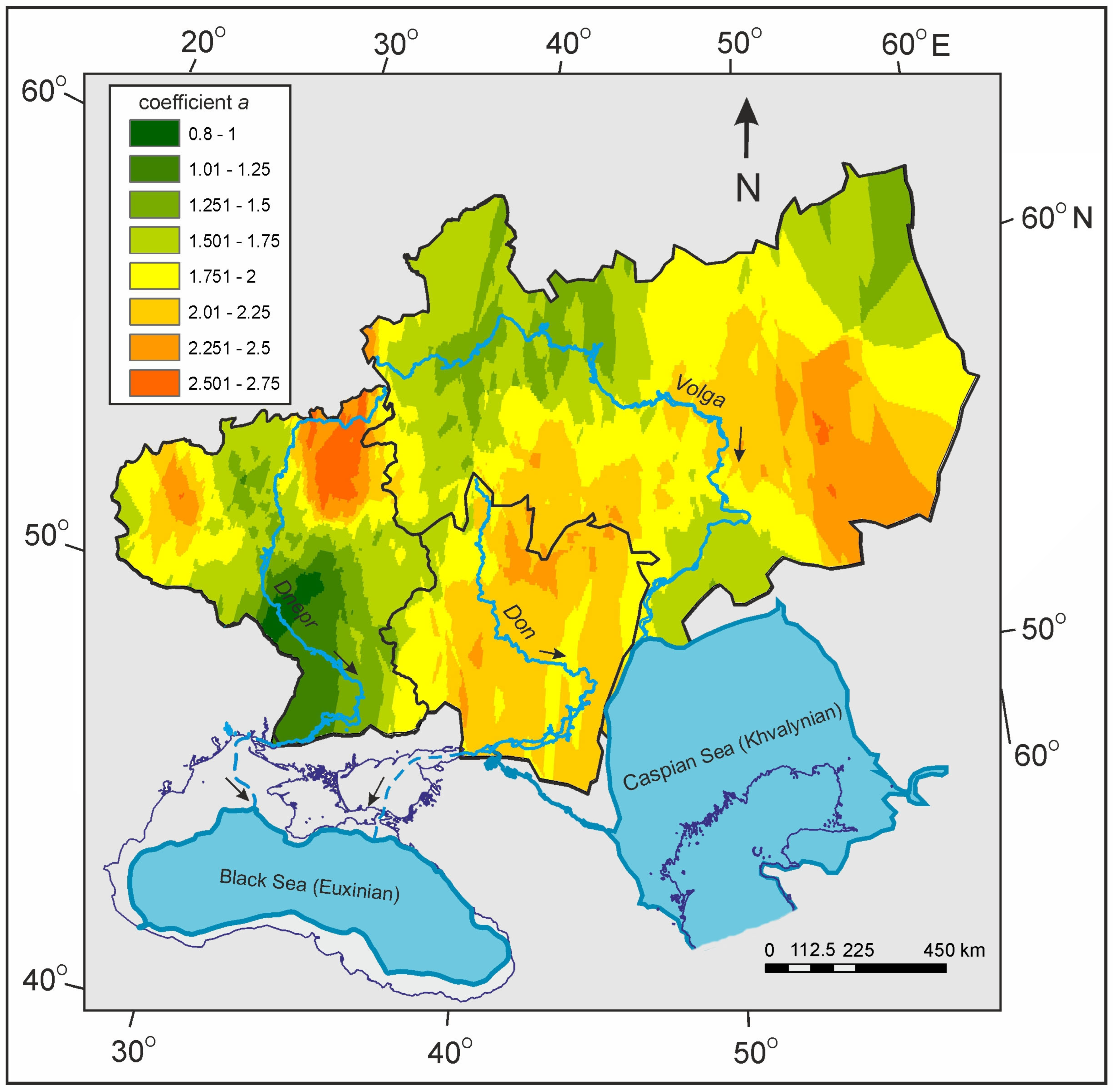
4.1. Channel Morphology
4.2. Paleohydrological Reconstructions
4.2.1. Paleo-Discharge Calculation with the Paleochannel Widths
4.2.2. The Maximum Discharge and Runoff Depth
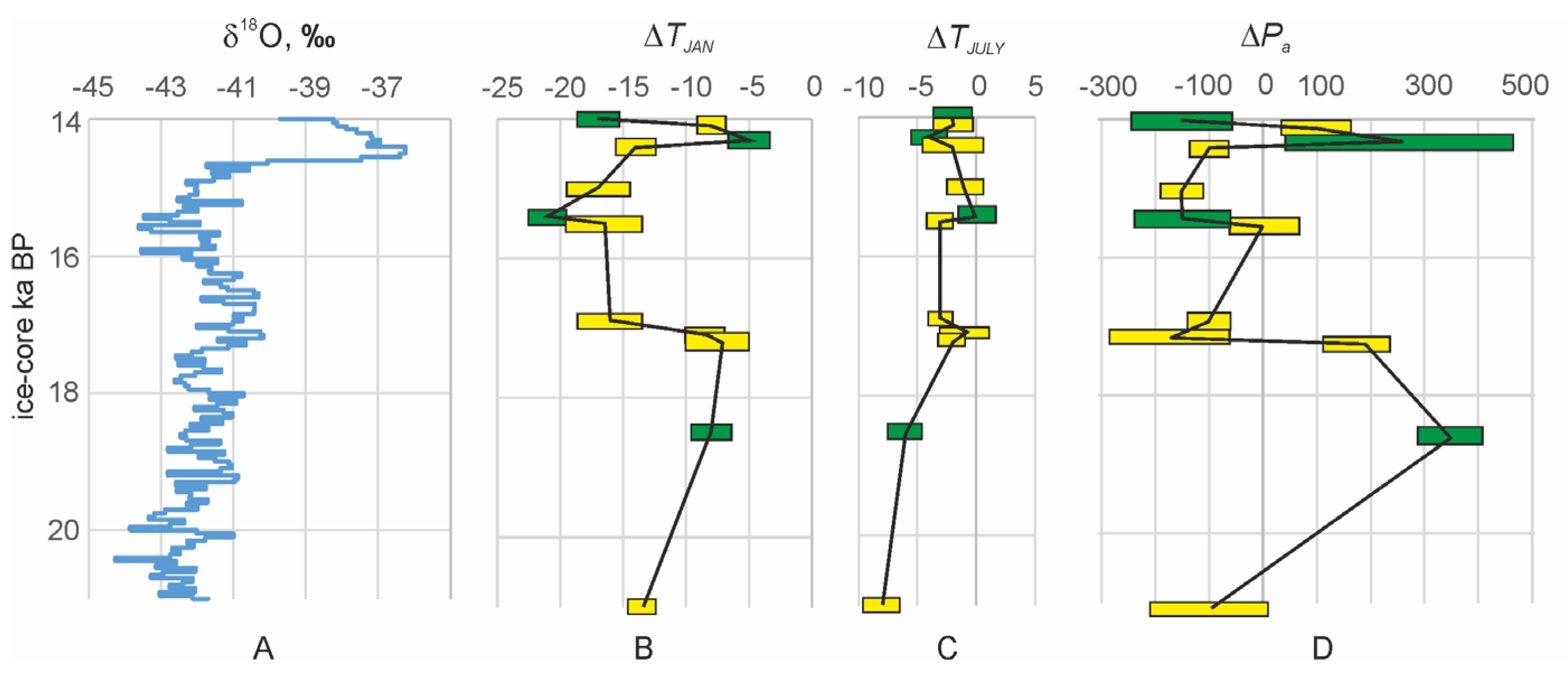
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dokuchaev, V.V. The Ways of the River Valleys Formation at the European Russia; Tipografiya V. Dermakova: St. Petersburg, Russia, 1878; p. 221. (In Russian) [Google Scholar]
- Davis, W.M. La Seine, la Meuse et la Moselle. Ann. Géographie 1895, 4, 25–49. [Google Scholar] [CrossRef]
- Dury, G.H. Principles of underfit streams. US Geol. Surv. Prof. Pap. 1964, 452, 67. [Google Scholar]
- Dury, G.H. Theoretical implication of underfit streams. US Geol. Surv. Prof. Pap. 1965, 442, 43. [Google Scholar]
- Schumm, S.A. Quaternary paleohydrology. In The Quaternary of the United States; Wright, H.E., Jr., Frey, D.G., Eds.; Princeton University Press: Princeton, NY, USA, 1965; pp. 783–794. [Google Scholar]
- Schumm, S.A. River Adjustment to Altered Hydrologic Regimen—Murrumbidgee River and Paleochannels. US Geol. Surv. Prof. Pap. 1968, 598, 65. [Google Scholar]
- Volkov, I.A. On the recent past of the rivers Ishim and Nura (O nedavnem proshlom rek Ishima i Nury). Tr. Lab. Aerometod. AN SSSR 1960, 9, 15–19. (In Russian) [Google Scholar]
- Makkaveev, N.I.; Khmeleva, N.V.; Gun, G. Changes in the pattern of meanders detected in some rivers. In Experimental Geomorphology; Moscow University Press: Moscow, Russia, 1969; Volume 2, pp. 52–62. (In Russian) [Google Scholar]
- Vandenberghe, J.; Sidorchuk, A. Large palaeomeanders in Europe: Distribution, formation process, age, environments and significance. In Palaeohydrology; Geography of the Physical Environment; Springer: Cham, Switzerland, 2019; pp. 169–186. [Google Scholar]
- Sidorchuk, A. The large rivers of the past in West Siberia: Unknown hydrological regimen. Water 2023, 15, 258. [Google Scholar] [CrossRef]
- Alayev, E.B.; Badenkov, Y.P.; Karavaeva, N.A. The Russian Plain. In The Earth as Transformed by Human Action; Turner, B.L., Clark, W.C., Kates, R.W., Richards, J.F., Mathews, J.T., Meyer, W.B., Eds.; Cambridge University Press: Cambridge, MA, USA, 1990; pp. 543–560. [Google Scholar]
- Borodko, A.V. (Ed.) National Atlas of Russia (Maps) (Natsional’nyi Atlas Rossii (Karty)); Roskartografiya: Moscow, Russia, 2004; Volume 2. (In Russian) [Google Scholar]
- Gribova, S.A.; Isachenko, T.I.; Lavrenko, E.M. (Eds.) Vegetation of the European Part of the USSR (Rastitel'nost' Yevropeyskoy Chasti SSSR); Nauka (Publ.): Leningrad, Russia, 1980; p. 429. (In Russian) [Google Scholar]
- Available online: https://earth.google.com (accessed on 20 June 2024).
- Available online: https://maps.yandex.ru/ (accessed on 20 June 2024).
- Velichko, A.A. (Ed.) Dynamics of Landscape Components and Internal Marine Basins of Northern Eurasia over the Past 130,000 Years: Atlas-Monograph. Part 2. Development of Landscapes and Climate of Northern Eurasia. Late Pleistocene—Holocene—Forecast Elements; GEOS: Moscow, Russia, 2002; p. 231. (In Russian) [Google Scholar]
- Panin, A.; Matlakhova, E. Fluvial chronology in the East European Plain over the last 20 ka and its palaeohydrological implications. Catena 2015, 130, 46–61. [Google Scholar] [CrossRef]
- Gelfan, A.; Panin, A.; Kalugin, A.; Morozova, P.; Semenov, V.; Sidorchuk, A.; Ukraintsev, V.; Ushakov, K. Hydroclimatic processes as the primary drivers of the Early Khvalynian transgression of the Caspian Sea: New developments. Hydrol. Earth Syst. Sci. 2024, 28, 241–259. [Google Scholar] [CrossRef]
- Sidorchuk, A.; Panin, A.; Borisova, O. Surface runoff to the Black Sea from the East European Plain during the Last Glaciation Maximum—Late Glacial time. In Geology and Geoarchaeology of the Black Sea Region: Beyond the Flood Hypothesis; Buynevich, I.V., Yanko-Hombach, V., Gilbert, A.S., Martin, R.E., Eds.; Geological Society of America: Boulder, CO, USA, 2011; Volume 473, pp. 1–25. [Google Scholar]
- Panin, A.V.; Sidorchuk, A.Y.; Ukraintsev, V.Y. The Contribution of Glacial Melt Water to Annual Runoff of River Volga in the Last Glacial Epoch. Water Resour. 2021, 48, 877–885. [Google Scholar] [CrossRef]
- Protasiev, M.S. (Ed.) Surface Water Resources of the USSR. Volume 7: Don Region; Gidrometeoizdat: Leningrad, Russia, 1973; p. 458. (In Russian) [Google Scholar]
- Velikanov, M.A. Channel Process: Basics of the Theory; Fizmatgiz: Moscow, Russia, 1958; p. 395. (In Russian) [Google Scholar]
- Sidorchuk, A.Y.; Borisova, O.K.; Panin, A.V. Fluvial response to the Late Valdai/Holocene environmental change on the East European Plain. Glob. Planet. Chang. 2001, 28, 303–318. [Google Scholar] [CrossRef]
- Sidorchuk, A.Y.; Panin, A.V.; Borisova, O.K. Climate-induced changes in surface runoff on the north-Eurasian plains during the Late Glacial and Holocene. Water Resour. 2008, 35, 386–396. [Google Scholar] [CrossRef]
- Inglis, C.C. Meanders and their bearing on river training. Inst. Civ. Eng. Mar. Waterw. Eng. Div. 1947, 7, 3–54. [Google Scholar]
- Leopold, L.B.; Wolman, M.G. River Channel Patterns: Braided, Meandering and Straight. US Geol. Surv. Prof. Pap. 1957, 282, 39–85. [Google Scholar]
- Frasson, R.P.; Pavelsky, T.M.; Fonstad, M.A.; Durand, M.T.; Allen, G.H.; Schumann, G.; Lion, C.; Beighley, R.E.; Yang, X. Global relationships between river width, slope, catchment area, meander wavelength, sinuosity, and discharge. Geophys. Res. Lett. 2019, 46, 3252–3262. [Google Scholar] [CrossRef]
- Leopold, L.B.; Maddock, T. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications. US Geol. Surv. Prof. Pap. 1953, 252, 57. [Google Scholar]
- Blom, A.; Arkesteijn, L.; Chavarrias Borras, V.; Viparelli, E. The equilibrium alluvial river under variable flow and its channel-forming discharge. J. Geophys. Res. Earth Surf. 2017, 122, 1924–1948. [Google Scholar] [CrossRef]
- Perdios, A.; Langousis, A. Revisiting the statistical scaling of annual discharge maxima at daily resolution with respect to the basin size in the light of rainfall climatology. Water 2020, 12, 610. [Google Scholar] [CrossRef]
- Yanina, T.A. Environmental variability of the Ponto-Caspian and Mediterranean basins during the last climatic macrocycle. Geogr. Environ. Sustain. 2020, 13, 6–23. [Google Scholar] [CrossRef]
- Matoshko, A.; Gozhik, P.; Ivchenko, A.S. The fluvial archive of the Middle and Lower Dnieper (a review). Neth. J. Geosci. 2002, 81, 339–355. [Google Scholar] [CrossRef]
- Ukraintsev, V.Y.; Zakharov, A.L. Dynamics of downcutting and accumulation in river valleys of the Volga basin during the Late Pleniglacial. Gidrosfera. Opasnyye Protsessy I Yavleniya 2023, 5, 147–159. (In Russian) [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Tinkler, K.J. Active valley meanders. Area 1973, 5, 41–43. [Google Scholar]
- Cogley, J.G. On runoff at the time of deglaciation. Area 1973, 5, 33–37. [Google Scholar]
- Nachtergaele, J.; Poesen, J.; Sidorchuk, A.; Torri, D. Prediction of concentrated flow width in ephemeral gully channels. Hydrol. Process. 2002, 16, 1935–1953. [Google Scholar] [CrossRef]
- Watts, W.A. Regional variation in the response of vegetation to Lateglacial climatic events in Europe. In Studies in the Lateglacial of North-West Europe; Lowe, J.J., Gray, J.M., Robinson, J.E., Eds.; Pergamon: Oxford, UK, 1980; pp. 1–22. [Google Scholar]
- Velichko, A.A. (Ed.) Paleoclimates and Paleoenvironments of Extra-Tropical Regions of the Northern Hemisphere. Late Pleistocene—Holocene. Atlas-Monograph; GEOS: Moscow, Russia, 2008; p. 120. (In Russian) [Google Scholar]
- Tarasov, P.E.; Peyron, O.; Guiot, J.; Brewer, S.; Volkova, V.S.; Bezusko, L.G.; Dorofeyuk, N.I.; Kvavadze, E.V.; Osipova, I.M.; Panova, N.K. Last Glacial Maximum climate of the former Soviet Union and Mongolia reconstructed from pollen and plant macrofossil data. Clim. Dyn. 1999, 15, 227–240. [Google Scholar] [CrossRef]
- Tarasov, P.E.; Volkova, V.S.; Webb, T.; Guiot, J.; Andreev, A.A.; Bezusko, L.G.; Bezusko, T.V.; Bykova, G.V.; Dorofeyuk, N.I.; Kvavadze, E.V.; et al. Last glacial maximum biomes reconstructed from pollen and plant macrofossil data from northern Eurasia. J. Biogeogr. 2000, 27, 609–620. [Google Scholar] [CrossRef]
- Johnsen, S.J.; Dahl-Jensen, D.; Gundestrup, N.S.; Steffensen, J.P.; Clausen, H.B.; Miller, H.; Masson-Delmotte, V.; Sveinbjörnsdóttir, A.E.; White, J. Oxygen isotope and palaeotemperature records from six Greenland ice-core stations: Camp Century, Dye-3, GRIP, GISP2, Renland and NorthGRIP. J. Quat. Sci. 2001, 16, 299–307. [Google Scholar] [CrossRef]
- NorthGRIP Members. High-resolution record of Northern Hemisphere climate extending into the Last Interglacial period. Nature 2004, 431, 147–151. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, S.O.; Andersen, K.K.; Svensson, A.M.; Steffensen, J.P.; Vinther, B.M.; Clausen, H.B.; Siggaard-Andersen, M.L.; Johnsen, S.J.; Larsen, L.B.; Dahl-Jensen, D.; et al. A new Greenland ice core chronology for the last glacial termination. J. Geophys. Res. Atmos. 2006, 111, D06102. [Google Scholar] [CrossRef]
- Luoto, T.P.; Kotrys, B.; Płóciennik, M. East European chironomid-based calibration model for past summer temperature reconstructions. Clim. Res. 2019, 77, 63–76. [Google Scholar] [CrossRef]
- Płóciennik, M.; Mroczkowska, A.; Pawłowski, D.; Kruk, A.; Wieckowska-Lüth, M.; Kurzawska, A.; Rzodkiewicz, M.; Okupny, D.; Szma´nda, J.; Mazurkevich, A.; et al. Summer temperature drives the lake ecosystem during the late weichselian and Holocene in eastern Europe: A case study from western Russia. Catena 2022, 214, 106–206. [Google Scholar] [CrossRef]
- Borisova, O.K. Landscape and climatic conditions in the central East European Plain in the last 22 thousand years: Reconstruction based on paleobotanical data. Water Resour. 2021, 48, 886–896. [Google Scholar] [CrossRef]
- Motovilov, Y. Hydrological simulation of river basins at different spatial scales: 1. Generalization and averaging algorithms. Water Resour. 2016, 43, 429–437. [Google Scholar] [CrossRef]
- Kapsch, M.-L.; Mikolajewicz, U.; Ziemen, F.; Schannwell, C. Ocean response in transient simulations of the last deglaciation dominated by underlying ice-sheet reconstruction and method of meltwater distribution. Geophys. Res. Lett. 2022, 49, e2021GL096767. [Google Scholar] [CrossRef]




| River Basin | Coefficient a | Exponent b | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | STD Err | +95.00% Cnf. Lmt | +95.00% Cnf. Lmt | Mean | STD Err | +95.00% Cnf. Lmt | +95.00% Cnf. Lmt | |
| Volga | 1.66 | 2.38 | 0.44 | 6.25 | 1.38 | 0.16 | 1.05 | 1.72 |
| Don | 1.74 | 1.29 | 1.02 | 2.95 | 1.37 | 0.1 | 1.17 | 1.57 |
| Dnepr | 1.3 | 1.25 | 0.83 | 2.04 | 1.37 | 0.06 | 1.24 | 1.49 |
| Modern | |||
|---|---|---|---|
| Basin Area | Landscape | Coefficient a1 | Exponent b1 |
| F ≤ 1000 km2 | Forest–steppe | 0.14 | 1 |
| F > 1000 | 1.6 | 0.65 | |
| F ≤ 1000 km2 | steppe | 0.082 | 1 |
| F > 1000 | 0.41 | 0.75 | |
| F ≤ 1000 km2 | Dry steppe | 0.063 | 1 |
| F > 1000 | 0.19 | 0.79 | |
| River Basin | Modern Rivers | Ancient Rivers | The Ratio Ancient/Modern | ||||
|---|---|---|---|---|---|---|---|
| Name | Basin Area for the Lowermost Gauging Stations, 103 km2 | Mean Daily Runoff Depth at the Unit Basin, mm | Mean Maximum Discharges for the Lowermost Gauging Stations m3/s | Mean Daily Runoff Depth at the Unit Basin, mm | Mean Maximum Discharges for the Lowermost Point, m3/s | Mean Daily Runoff Depth | Mean Maximum Discharges |
| Volga | 1360 | 8.3 | 25,100 | 46 | 98,300 | 5.5 | 3.9 |
| Don | 378 | 7.2 | 5620 | 45 | 32,000 | 6.3 | 5.7 |
| Dnepr | 459 | 4.9 | 7680 | 39 | 13,000 | 8 | 1.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidorchuk, A.; Panin, A.; Borisova, O. Hydrological Regime of Rivers in the Periglacial Zone of the East European Plain in the Late MIS 2. Quaternary 2024, 7, 32. https://doi.org/10.3390/quat7030032
Sidorchuk A, Panin A, Borisova O. Hydrological Regime of Rivers in the Periglacial Zone of the East European Plain in the Late MIS 2. Quaternary. 2024; 7(3):32. https://doi.org/10.3390/quat7030032
Chicago/Turabian StyleSidorchuk, Aleksey, Andrei Panin, and Olga Borisova. 2024. "Hydrological Regime of Rivers in the Periglacial Zone of the East European Plain in the Late MIS 2" Quaternary 7, no. 3: 32. https://doi.org/10.3390/quat7030032
APA StyleSidorchuk, A., Panin, A., & Borisova, O. (2024). Hydrological Regime of Rivers in the Periglacial Zone of the East European Plain in the Late MIS 2. Quaternary, 7(3), 32. https://doi.org/10.3390/quat7030032








