Effect of Dielectric Constant on Interaction Between Charged Macroions in Asymmetric Electrolyte
Abstract
1. Introduction
2. Model and Method
2.1. Model
2.2. Method and Simulation Settings
2.3. Mean Force and Potential of Mean Force
3. Results and Discussion
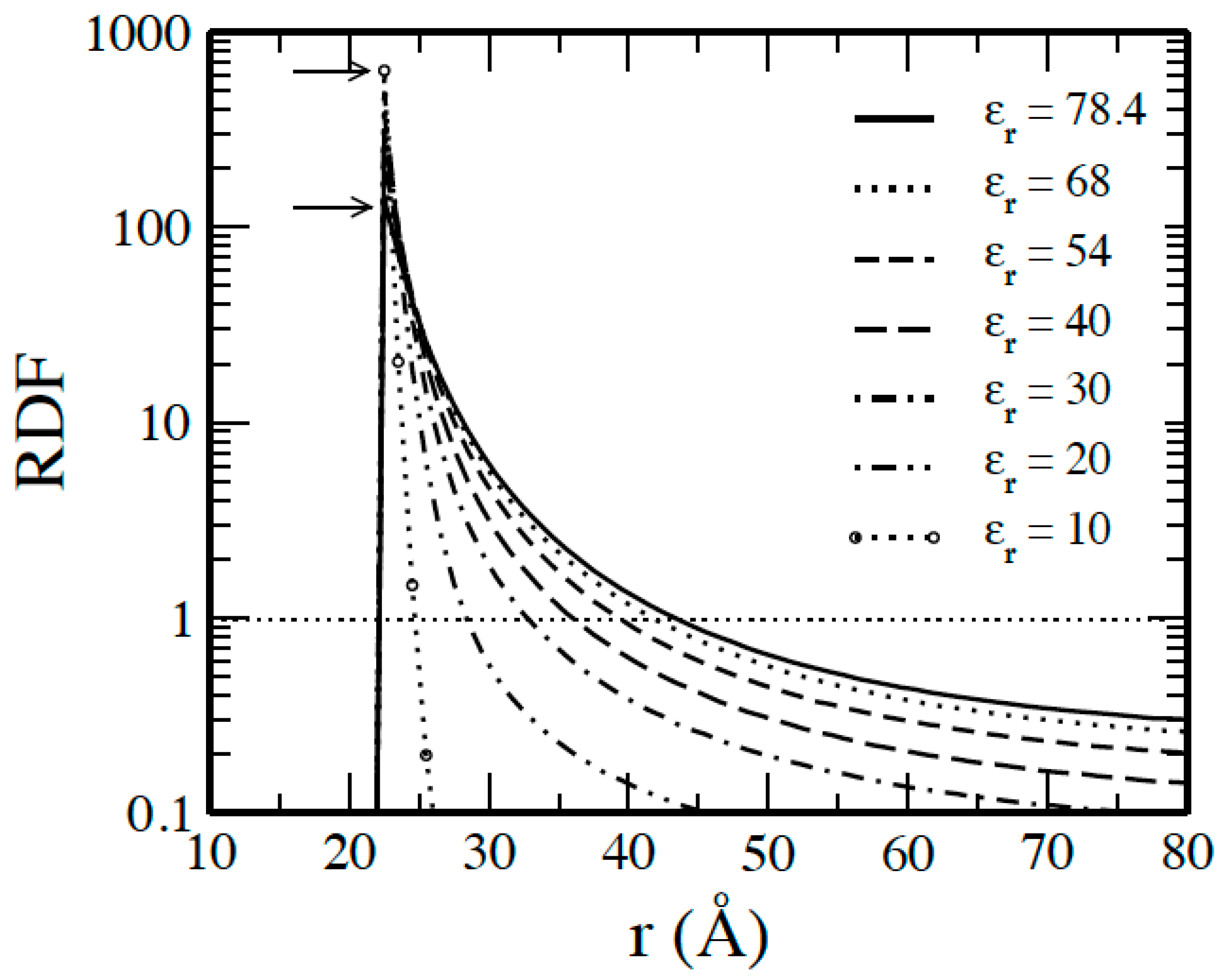
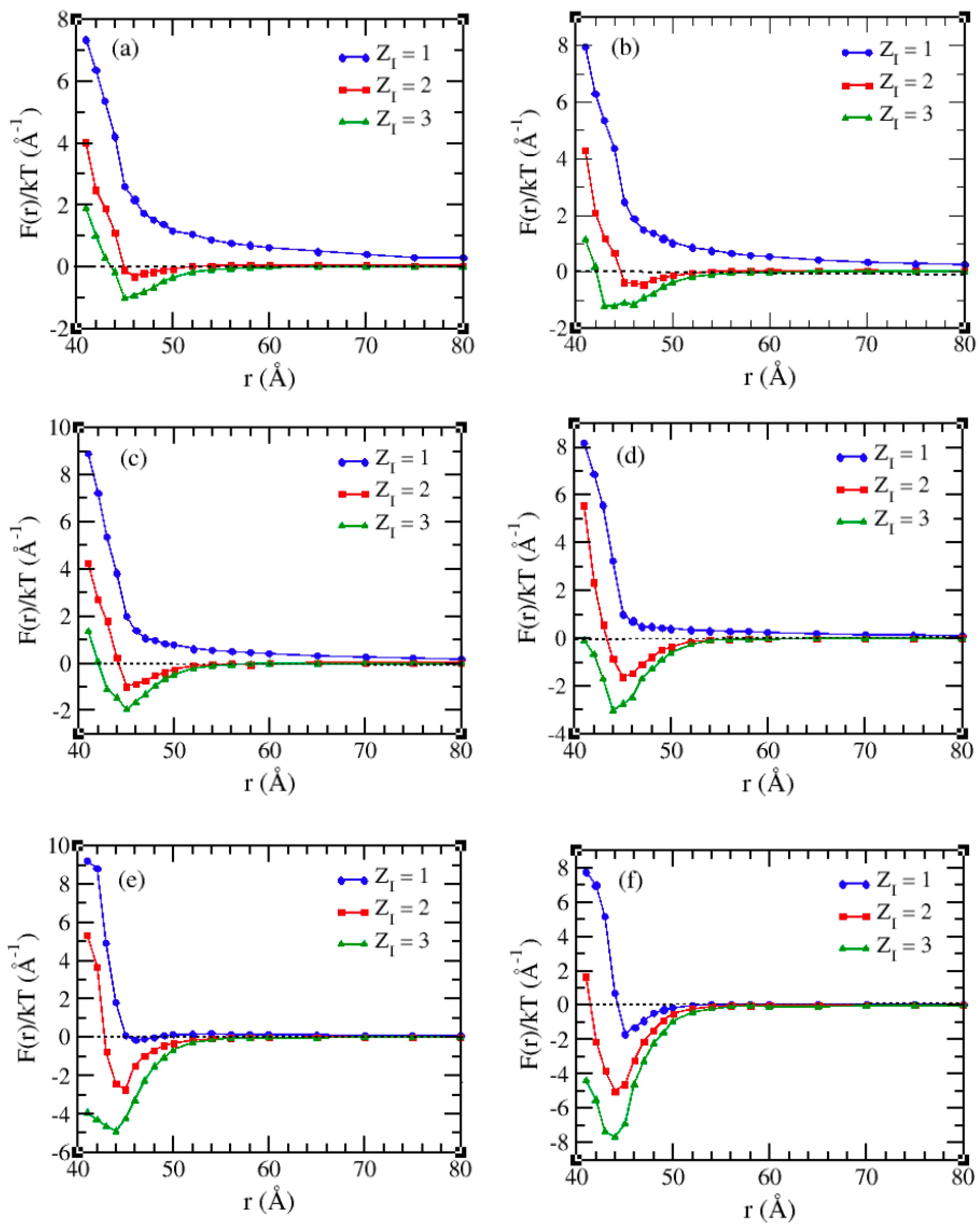
3.1. Salt-Free Solvents
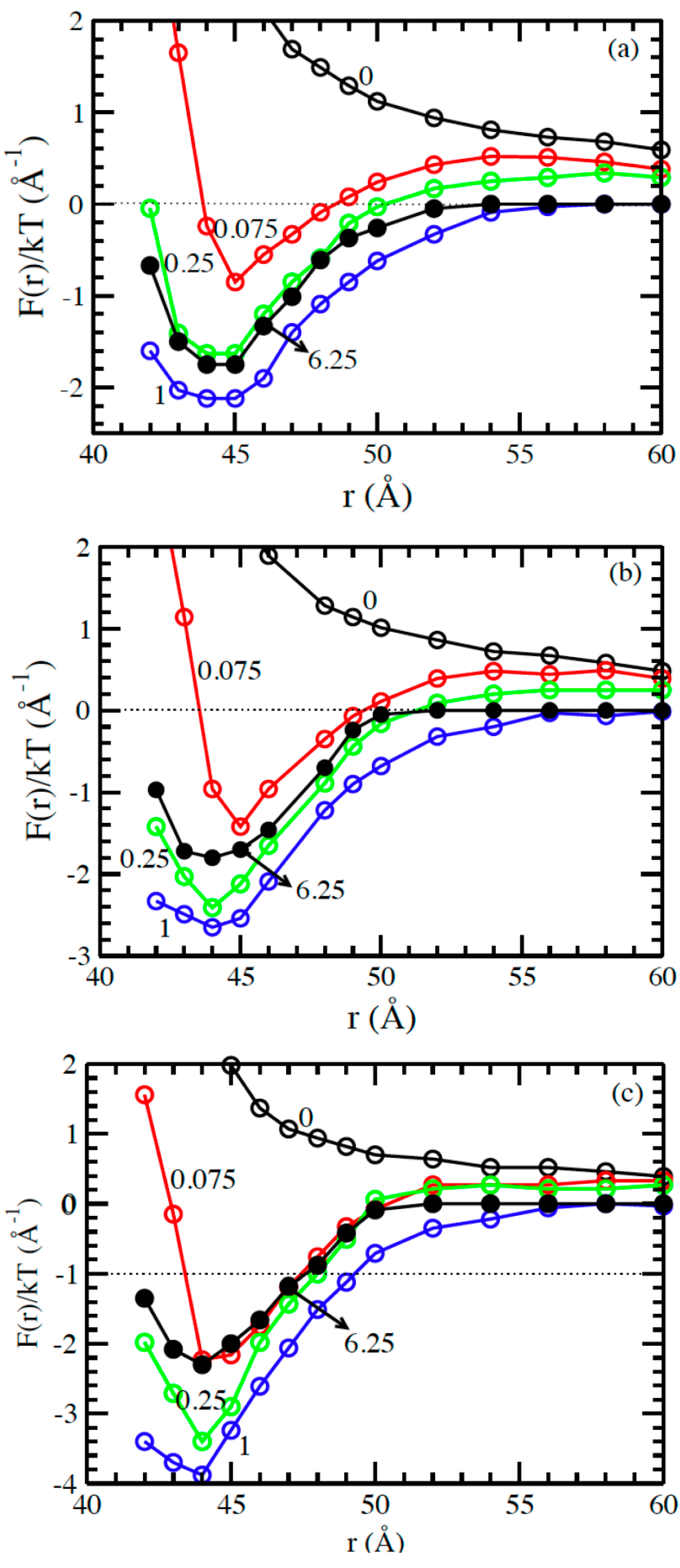
3.2. Solvents with the Presence of Added Salt
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Evans, D.; Wennerström, H. The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet, 2nd ed.; Wiley-VCH: Hoboken, NJ, USA, 1999. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Landau, L.D. Theory of the Stability of Strongly Charged Lyophobic Sols and the Adhesion of Strongly Charged Particles in Solutions of Electrolytes. Acta Physicochim. URSS 1941, 14, 633. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Guldbrand, L.; Jönsson, B.; Wennerström, H.; Linse, P. Electrical Double Layer Forces. A Monte Carlo Study. J. Chem. Phys. 1984, 80, 2221–2228. [Google Scholar] [CrossRef]
- Kjellander, R.; Marcelja, S. Correlation and Image Charge Effects in Electric Double Layers. Chem. Phys. Lett. 1985, 112, 49. [Google Scholar] [CrossRef]
- Strunk, W., Jr.; White, E.B. The Elements of Style, 4th ed.; Longman: New York, NY, USA, 2000. [Google Scholar]
- Bao, X.; Lee, H.; Qiu, S. Behavior of complex knots in single DNA molecules. Phys. Rev. Lett. 2003, 91, 265506. [Google Scholar] [CrossRef]
- Meiners, J.C.; Quake, S.R. Femtonewton Force Spectroscopy of Single Extended DNA Molecules. Phys. Rev. Lett. 2000, 84, 5014–5017. [Google Scholar] [CrossRef] [PubMed]
- Ong, G.M.C.; Gallegos, A.; Wu, J. Modeling Surface Charge Regulation of Colloidal Particles in Aqueous Solutions. Langmuir 2020, 36, 11918–11928. [Google Scholar] [CrossRef]
- Lobaskin, V.; Qamhieh, K. Effective Macroion Charge and Stability of Highly Asymmetric Electrolytes at Various Salt Conditions. J. Phys. Chem. B 2003, 107, 8022–8029. [Google Scholar] [CrossRef]
- Qamhieh, K.; Linse, P. Effect of discrete macroion charge distributions in solutions of like-charged macroions. J. Chem. Phys. 2005, 123, 104901. [Google Scholar] [CrossRef]
- Hansen, J.-P.; Löwen, H. Effective Interactions between Electric Double Layers. Annu. Rev. Phys. Chem. 2000, 51, 209–242. [Google Scholar] [CrossRef]
- Qamhieh, K.; Amleh, M.; Khaleel, M. Effect of Discrete Macroion Charge Distributions on Electric Double Layer of a Spherical Macroion. J. Dispers. Sci. Technol. 2013, 34, 1517–1525. [Google Scholar] [CrossRef]
- Linse, P. Electrostatics in the presence of spherical dielectric discontinuities. J. Chem. Phys. 2008, 128, 214505. [Google Scholar] [CrossRef]
- Bouyer, F.; Robben, A.; Yu, W.L.; Borkovec, M. Aggregation of colloidal particles in the presence of oppositely charged polyelectrolytes: Effect of surface charge heterogeneities. Langmuir 2001, 17, 5225–5231. [Google Scholar] [CrossRef]
- Rouzina, I.; Bloomfield, V.A. Macroion attraction due to electrostatic correlation between screening counterions. 1. Mobile surface-adsorbed ions and diffuse ion cloud. J. Phys. Chem. 1996, 100, 9977–9989. [Google Scholar] [CrossRef]
- Turesson, M.; Jönsson, B.; Labbez, C. Coarse-Graining Intermolecular Interactions in Dispersions of Highly Charged Colloids. Langmuir 2012, 28, 4926–4930. [Google Scholar] [CrossRef]
- Messina, R.; Holm, C.; Kremer, K. Strong attraction between charged spheres due to metastable ionized states. Phys. Rev. Lett. 2000, 85, 872–875. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, M.; Grosberg, A.Y. Electrophoresis of a charge-inverted macroion complex: Molecular-dynamics study. Eur. Phys. J. E 2002, 7, 371–379. [Google Scholar] [CrossRef] [PubMed]
- Martín-Molina, A.; Quesada-Pérez, M.; Galisteo-González, F.; Hidalgo-Álvarez, R. Looking into overcharging in model colloids through electrophoresis: Asymmetric electrolytes. J. Chem. Phys. 2003, 118, 4183–4189. [Google Scholar] [CrossRef]
- Besteman, K.; Zevenbergen, M.A.G.; Lemay, S.G. Charge inversion by multivalent ions: Dependence on dielectric constant and surface-charge density. Phys. Rev. E 2005, 72, 061501. [Google Scholar] [CrossRef]
- Allahyarov, E.; Zaccarelli, E.; Sciortino, F.; Tartaglia, P.; Löwen, H. Interaction between charged colloids in a low dielectric constant solvent. Europhys. Lett. 2007, 78, 38002. [Google Scholar] [CrossRef]
- Qamhieh, K. Effect of dielectric constant on the zeta potential of spherical electric double layer. Molecules 2024, 29, 2484. [Google Scholar] [CrossRef]
- Toukmaji, A.Y.; Board, J.A. Ewald Summation Techniques in Perspective: A Survey. Comput. Phys. Commun. 1996, 95, 73–92. [Google Scholar] [CrossRef]
- Linse, P. MOLSIM; Lund University: Lund, Sweden, 2004. [Google Scholar]
- Angelescu, D.G.; Linse, P. Monte Carlo simulation of the mean force between two like-charged macroions with simple 1:3 salt added. Langmuir 2003, 19, 9661–9668. [Google Scholar] [CrossRef]
- Linse, P. Mean force between like-charged macroions at high electrostatic coupling. J. Phys. Condens. Matter 2002, 14, 13449–13467. [Google Scholar] [CrossRef]
- Belloni, L. Colloidal interactions. J. Phys. Condens. Matter 2000, 12, R549–R587. [Google Scholar] [CrossRef]
- Wu, J.; Bratko, D.; Prausnitz, J.M. Interaction between like-charged colloidal particles in electrolyte solutions. Proc. Natl. Acad. Sci. USA 1998, 95, 15169–15172. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Nguyen, T.T.; Shklovskii, B.I. Colloquium: The Physics of Charge Inversion in Chemical and Biological Systems. Rev. Mod. Phys. 2002, 74, 329–345. [Google Scholar] [CrossRef]
- Angelini, T.E.; Liang, H.; Wriggers, W.; Olson, N.; Zlotnick, A.; Hagan, M.F.; Wong, G.C.L. Counterions Unlock Barriers to Virus Assembly. Proc. Natl. Acad. Sci. USA 2006, 103, 7962–7967. [Google Scholar] [CrossRef]
- Torchilin, V.P. Multifunctional and Stimuli-Sensitive Pharmaceutical Nanocarriers. Eur. J. Pharm. Biopharm. 2009, 71, 431–444. [Google Scholar] [CrossRef]
- Messina, R. Electrostatics in Soft Matter. J. Phys. Condens. Matter 2009, 21, 113102–113119. [Google Scholar] [CrossRef]




| 78.4 | 68 | 54 | 40 | 30 | 20 | 15 | 10 | |
|---|---|---|---|---|---|---|---|---|
| 7.1 | 8.23 | 10.36 | 14.0 | 18.657 | 27.986 | 37.315 | 55.973 |
| 78.4 | 68 | 54 | 40 | 30 | 20 | 15 | 10 | |
|---|---|---|---|---|---|---|---|---|
| (Å) | 7.1 | 8.2 | 10.4 | 14.0 | 18.6 | 28.0 | 37.3 | 56 |
| 0.8 | 0.9 | 1.1 | 1.5 | 2.0 | 3.0 | 4.1 | 6.1 | |
| 2.3 | 2.5 | 3.1 | 4.2 | 5.6 | 8.5 | 11.6 | 17.2 | |
| 4.1 | 4.7 | 5.7 | 7.8 | 10.4 | 15.6 | 21.3 | 31.7 | |
| 8.9 | 10.1 | 12.3 | 16.8 | 22.4 | 33.5 | 45.8 | 68.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qamhieh, K. Effect of Dielectric Constant on Interaction Between Charged Macroions in Asymmetric Electrolyte. Colloids Interfaces 2025, 9, 43. https://doi.org/10.3390/colloids9040043
Qamhieh K. Effect of Dielectric Constant on Interaction Between Charged Macroions in Asymmetric Electrolyte. Colloids and Interfaces. 2025; 9(4):43. https://doi.org/10.3390/colloids9040043
Chicago/Turabian StyleQamhieh, Khawla. 2025. "Effect of Dielectric Constant on Interaction Between Charged Macroions in Asymmetric Electrolyte" Colloids and Interfaces 9, no. 4: 43. https://doi.org/10.3390/colloids9040043
APA StyleQamhieh, K. (2025). Effect of Dielectric Constant on Interaction Between Charged Macroions in Asymmetric Electrolyte. Colloids and Interfaces, 9(4), 43. https://doi.org/10.3390/colloids9040043





