An Investigation of the Effect of pH on Micelle Formation by a Glutamic Acid-Based Biosurfactant
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Surfactant Synthesis
2.3. NMR Titrations
2.4. NMR Diffusion Experiments
2.5. Conductivity Experiments
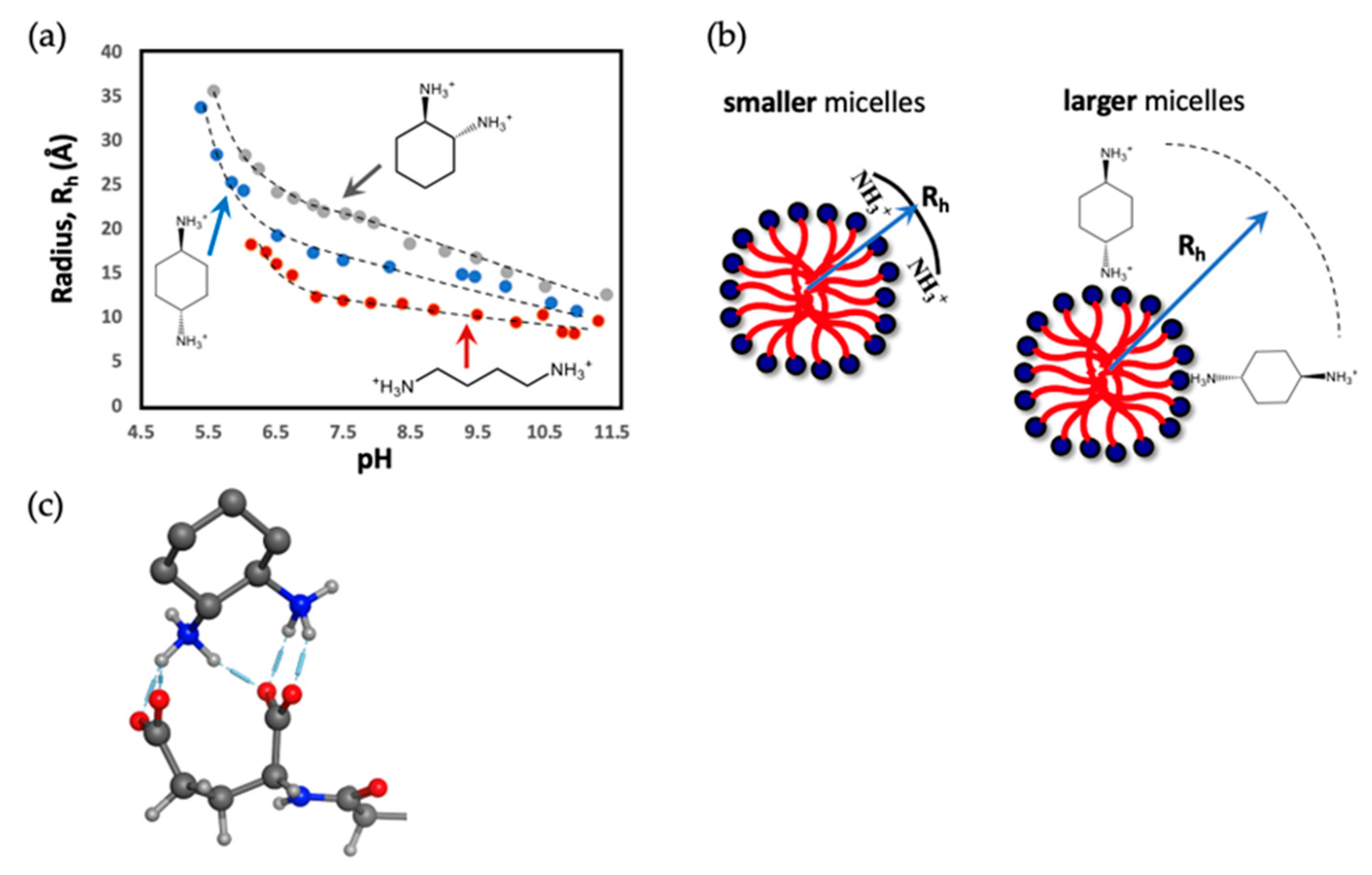
2.6. Molecular Modeling and Simulations
3. Results and Discussion
3.1. Headgroup pKa Measurements
3.2. Critical Micelle Concentration Measurements
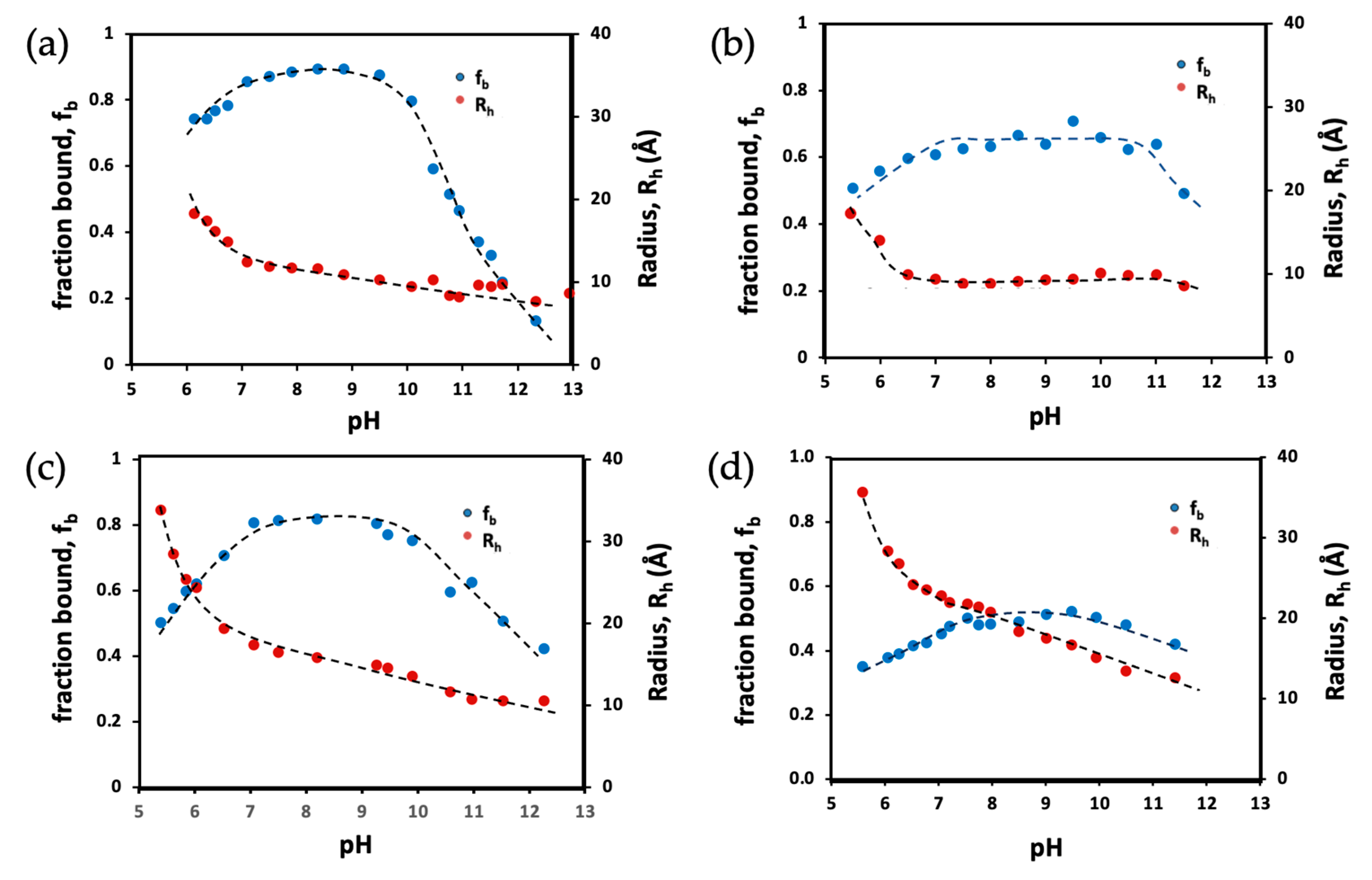
3.3. Micelle Radii and Counterion Binding
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bettenhausen, C. Switching to Sustainable Surfactants. Chem. Eng. News 2022, 100, 1–12. Available online: https://cen.acs.org/business/specialty-chemicals/Switching-sustainable-surfactants/100/i15 (accessed on 5 June 2024).
- Nagtode, V.S.; Cardoza, C.; Yasin, H.K.A.; Mali, S.N.; Tambe, S.M.; Roy, P.; Singh, K.; Goel, A.; Amin, P.D.; Thorat, B.R.; et al. Green Surfactants (Biosurfactants): A Petroleum-Free Substitute for Sustainability. Comparison, Applications, Market, and Future Prospects. ACS Omega 2023, 8, 11674–11699. [Google Scholar] [CrossRef]
- Pinheiro, L.; Faustino, C. Amino Acid-Based Surfactants for Biomedical Applications. In Application and Characterization of Surfactants; Najjar, R., Ed.; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Soni, S.; Agrawal, P.; Haider, T.; Singh, A.P.; Rohit, R.; Kumar Patra, R.K.; Dubey, H.; Namdeo, S.; Vishwakarma, M.; Soni, V. The Potential of Biosurfactants in the Pharmaceutical Industry: A Review. Bioequiv. Bioavailab. Int. J. 2022, 6, 1–15. [Google Scholar] [CrossRef]
- Takassi, M.A.; Zargar, G.; Madani, M.; Zadehnazari, A. The Preparation of an Amino Acid-Based Surfactant and its Potential Application as an EOR Agent. Petrol. Sci. Technol. 2017, 35, 385–391. [Google Scholar] [CrossRef]
- Madani, M.; Zargar, G.; Takassi, M.A.; Daryasafar, A.; Wood, D.A.; Zang, Z. Fundamental Investigation of an Environmentally-Friendly Surfactant Agent for Chemical Enhanced Oil Recovery. Fuel 2019, 238, 186–197. [Google Scholar] [CrossRef]
- Tackie-Otoo, B.N.; Mohammed, M.A.A. Experimental Investigation of the Behavior of a Novel Amino Acid-based Surfactant Relevant to EOR Application. J. Mol. Liq. 2020, 316, 133848. [Google Scholar] [CrossRef]
- Sharma, H.; Tyagi, R. Safer Surfactants, Based on Amino Acids for Cleaner Environment: A Review. J. Biochem. Int. 2018, 5, 28–56. Available online: www.ikprress.org/index.php/JOBI/article/view/4315 (accessed on 5 June 2024).
- Bhadani, A.; Kafle, A.; Ogura, T.; Akamatsu, M.; Sakai, K.; Sakai, H.; Abe, M. Current Perspective of Sustainable Surfactants based on Renewable Building Blocks. Curr. Opin. Colloid Interface Sci. 2020, 45, 124–135. [Google Scholar] [CrossRef]
- Mori, R. Replacing All Petroleum-based Chemical Products with Natural Biomass-Based Chemical Products: A Tutorial Review. RSC Sustain. 2023, 1, 179–212. [Google Scholar] [CrossRef]
- Gaudin, T.; Lu, H.; Fayet, G.; Berthauld-Drelich, A.; Rotureau, P.; Pourceau, G.; Wadouachi, A.; Van Hecke, E.; Nesterenko, A.; Pezron, I. Impact of the Chemical Structure on Amphiphilic Properties of Sugar-Based Surfactants: A Literature Overview. Adv. Colloid Interface Sci. 2019, 270, 87–100. [Google Scholar] [CrossRef]
- Tripathy, D.B.; Mishra, A.; Clark, J.; Farmer, T. Synthesis, Chemistry, Physiochemical Properties, and Industrial Applications of Amino Acid Surfactants: A Review. Comptes Rendus Chim. 2017, 2, 112–130. [Google Scholar] [CrossRef]
- Guo, J.; Sun, L.; Zhang, F.; Sun, B.; Xu, B.; Zhou, Y. Review: Progress in Synthesis, Properties and Application of Amino Acid Surfactants. Chem. Phys. Lett. 2022, 794, 139484–139499. [Google Scholar] [CrossRef]
- Bustelo, M.; Pinazoa, A.; Manresad, M.A.; Mitjansb, M.; Vinardellb, M.P.; Péreza, L. Monocatenary Histidine-based Surfactants: Role of the Alkyl Chain Length in Antimicrobial Activity and their Selectivity over Red Blood Cells. Colliods Surfaces A 2017, 532, 501–509. [Google Scholar] [CrossRef]
- Lewis, C.; Hughes, B.H.; Vasquez, M.; Wall, A.M.; Northrup, V.L.; Witzleb, T.J.; Billiot, E.J.; Fang, Y.; Billiot, F.H.; Morris, K.F. Effect of pH on the Binding of Sodium, Lysine, and Arginine Counterions to L-Undecyl Leucinate Micelles. J. Surfactants Deterg. 2016, 19, 1175–1188. [Google Scholar] [CrossRef]
- Rothbauer, G.A.; Rutter, E.A.; Reuter-Seng, C.; Vera, S.; Billiot, E.J.; Fang, Y.; Billiot, F.H.; Morris, K.F. Nuclear Magnetic Resonance Investigation of the Effect of pH on Micelle Formation by the Amino Acid-Based Surfactant Undecyl L-Phenylalaninate. J. Surfactants Deterg. 2018, 21, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Maynard-Benson, A.; Alekisch, M.; Wall, A.; Billiot, E.J.; Billiot, F.H.; Morris, K.F. Characterization of Micelle Formation by the Single Amino Acid-Based Surfactants Undecanoic L-Isoleucine and Undecanoic L-Norleucine in the Presence of Diamine Counterions with Varying Chain Lengths. Colloids Interfaces 2023, 7, 28. [Google Scholar] [CrossRef]
- Bonini, M.; Gabbani, A.; Del Buffa, S.; Ridi, F.; Baglioni, R.; Holmberg, K. Adsorption of Amino Acids and Glutamic Acid-Based Surfactants on Imogolite Clays. Langmuir 2017, 33, 2411–2419. [Google Scholar] [CrossRef]
- Ikeda, N.; Aramaki, K. Hydrogel Formation by Glutamic-acid-based Organogelator Using Surfactant-Mediated Gelation. J. Oleo Sci. 2022, 71, 1169–1180. [Google Scholar] [CrossRef]
- Zhang, N.; Chen, Y.; Ji, X.; Han, Y.; Wang, Y. Partition of Glutamic Acid-Based Single-Chain and Gemini Amphiphiles into Phospholipid Membranes. Langmuir 2018, 45, 13652–13661. [Google Scholar] [CrossRef]
- Ananthapadmanabhan, K.P. Amino-Acid Surfactants in Personal Cleansing (Review). Tenside Surfactants Deterg. 2019, 56, 378–386. [Google Scholar] [CrossRef]
- Ali, A.F.; Danielson, N.D. Liquid Chromatography of Short Chain Carboxylic Acids using a Glutamic Acid Surfactant Coated C18 Stationary Phase. Talanta 2020, 213, 120807. [Google Scholar] [CrossRef] [PubMed]
- Waters, D.; Yuan, M. Personal Care Compositions Comprising Naturally Derived Surfactant Systems; World Intellectual Property Organization: Geneva, Switzerland, 2021; WO2021245159. [Google Scholar]
- O’Lenick, A.J., Jr. Carboxylated Surfactants in Personal Care Applications. United. U.S. Patent US6642193, 11 November 2003. [Google Scholar]
- Arkhipov, V.P.; Arkhipov, R.V.; Filippov, A. Dynamic and Molecular Association in Premicellar Aqueous Solutions of Dicarboxylate Amino Acid-Based Surfactant as Studied by 1H NMR. Magn. Reson. Chem. 2021, 60, 359–368. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, J.; Mahant, G.; Witzleb, T.; Busche, R.; Garcia, M.; Fang, Y.; Billiot, E.J.; Billiot, F.H.; Morris, K.F. NMR Investigation of Counterion Binding to Undecyl LL-Leucinevalanate Micelles. J. Dispers. Sci. Technol. 2020, 45, 284–295. [Google Scholar] [CrossRef]
- Lépori, C.M.O.; Correa, N.M.; Silber, J.J.; Falcone, R.D.; López-López, M.; Moyá, M.L. Influence of the AOT Counterion Chemical Structure on the Generation of Organized Systems. Langmuir 2020, 36, 10785–10793. [Google Scholar] [CrossRef] [PubMed]
- Gnezdilov, O.I.; Zuev, Y.F.; Zueva, O.S.; Potarikina, K.S.; Us’yarov, O.G. Self-Diffusion of Ionic Surfactants and Counterions in Premicellar and Micellar Solutions of Sodium, Lithium, and Cesium Dodecyl Sulfates as Studied by NMR Diffusometry. Appl. Magn. Reson. 2010, 40, 91–103. [Google Scholar] [CrossRef]
- Bachofer, S.J. Micelle Formation of Tetradecyltrimethylammonium X-benzoate Surfactants: Benzoate Counterion Substituent Effects. J. Surfactants Deterg. 2023, 27, 259–267. [Google Scholar] [CrossRef]
- Li, Y.; Zou, A.; Ye, R.; Mu, B. Counterion-Induced Changes to the Micellization of Surfactin-C16 Aqueous Solution. J. Phys. Chem. B 2009, 113, 15272–15277. [Google Scholar] [CrossRef] [PubMed]
- Bodet, J.F.; Scheper, W.M.; Oglesby, J.L.; Murch, B.P.; Kacher, M.L. Dishwashing Detergent Compositions Containing Organic Polyamines; World Intellectual Property Organization: Geneva, Switzerland, 2000; WO2000063334. [Google Scholar]
- Gao, P.; Karim, A.; Hassan, F.; Forbes, J.C. Oral Pharmaceutical Compositions Comprising a Low-Water-Soluble Drug, a Solvent, a Fatty Acid and an Organic Amine; World Intellectual Property Organization: Geneva, Switzerland, 2002; WO2002083177. [Google Scholar]
- Perinelli, D.R.; Cespi, M.; Lorusso, N.; Palmieri, G.F.; Bonacucina, G.; Blasi, P. Surfactant Self-Assembling and Critical Micelle Concentration: One Approach Fits All? Langmuir 2020, 21, 5745–5753. [Google Scholar] [CrossRef] [PubMed]
- Han, G.E.; Priefer, R. A Systematic Review of Various pKa Determination Techniques. Int. J. Pharm. 2023, 635, 112783. [Google Scholar] [CrossRef]
- Lui, X.; Yu, Q.; Song, A.; Dong, S.; Hao, J. Progress in Nuclear Magnetic Resonance Studies of Surfactant Systems. Curr. Opin. Colloid Interface Sci. 2020, 45, 14–27. [Google Scholar] [CrossRef]
- Morris, K.F.; Becker, B.A.; Tarus, J.; Almeida, V.; Froberg, A.; Larive, C.K. Using NMR Spectroscopy to Develop Insights into the Intermolecular Interactions Underlying Electrokinetic Chromatography. Anal. Chem. 2005, 77, 254A–263A. [Google Scholar] [CrossRef][Green Version]
- Fritz, S.R. Characterization of Green Surfactants with Dicarboxylate Polar Head. Master’s Thesis, Texas A&M University-Corpus Christi, Corpus Christi, TX, USA, 2023. [Google Scholar]
- Piotto, M.; Saudek, V.; Skienar, V. Gradient-Tailored Excitation for Single-Quantum NMR Spectroscopy of Aqueous Solutions. J. Biomol. NMR 1992, 2, 661–665. [Google Scholar] [CrossRef] [PubMed]
- Stilbs, P. Diffusion and Electrophoretic NMR; Walter de Gruyter: Boston, MA, USA, 2019. [Google Scholar] [CrossRef]
- Wong, T.C. Micellar Systems: Nuclear Magnetic Resonance Spectroscopy. In Encyclopedia of Surface and Colloid Science; Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Wu, D.; Chen, A.; Johnson, C.S., Jr. An Improved Diffusion-Ordered Spectroscopy Experiment Incorporating Bipolar-Gradient Pulses. J. Magn. Reson. 1995, 115, 260–264. [Google Scholar] [CrossRef]
- Wilkins, D.K.; Grimshaw, S.B.; Receveur, V.; Dobson, C.M.; Jones, J.A.; Smith, L.J. Hydrodynamic Radii of Native and Denatured Proteins Measured by Pulse Field Gradient NMR Techniques. Biochemistry 1999, 38, 16424–16431. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Babin, V.; Berryman, J.T.; Betz, R.M.; Cai, Q.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Gohlke, H.; et al. AMBER 16; University of California: San Francisco, CA, USA, 2016. [Google Scholar]
- Rumble, J. CRC Handbook of Chemistry and Physics, 103rd ed.; CRC Press: Boca Rotan, FL, USA, 2022. [Google Scholar]
- Tao, L.; Han, J.; Tao, F. Correlations and Predictions of Carboxylic Acid pKa Values Using Intermolecular Structure and Properties of Hydrogen-Bonded Complexes. J. Phys. Chem. A 2008, 112, 775–782. [Google Scholar] [CrossRef]
- Huque, F.T.; Plats, J.A. The Effect of Intramolecular Interactions on Hydrogen Bond Acidity. Org. Biomol. Chem. 2003, 1, 1419–1424. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Ray, A.; Pramanik, N. Self-Assembly of Surfactants: An Overview on General Aspects of Amphiphiles. Biophys. Chem. 2020, 265, 106429. [Google Scholar] [CrossRef] [PubMed]
- Brycki, B.; Szulc, A.; Koenig, H.; Kowalczyk, I.; Pospieszny, T.; Górka, S. Effect of the Alkyl Chain Length on Micelle Formation for bis(N-alkyl-N,N-dimethylethylammonium)ether dibromides. Comptes Rendus Chim. 2019, 5, 386–392. [Google Scholar] [CrossRef]
- Hoque, J.; Gonuguntla, S.; Yarlagadda, V.; Aswal, V.; Haldar, J. Effect of Amide Bonds on the Self Assembly of Gemini Surfactants. Phys. Chem. Chem. Phys. 2014, 16, 11279–11288. [Google Scholar] [CrossRef]
- Armarego, W.L.F.; Chai, C.L.L. Purification of Lab Chemicals, 6th ed.; Elsevier: Burlington, VT, USA, 2009. [Google Scholar] [CrossRef]
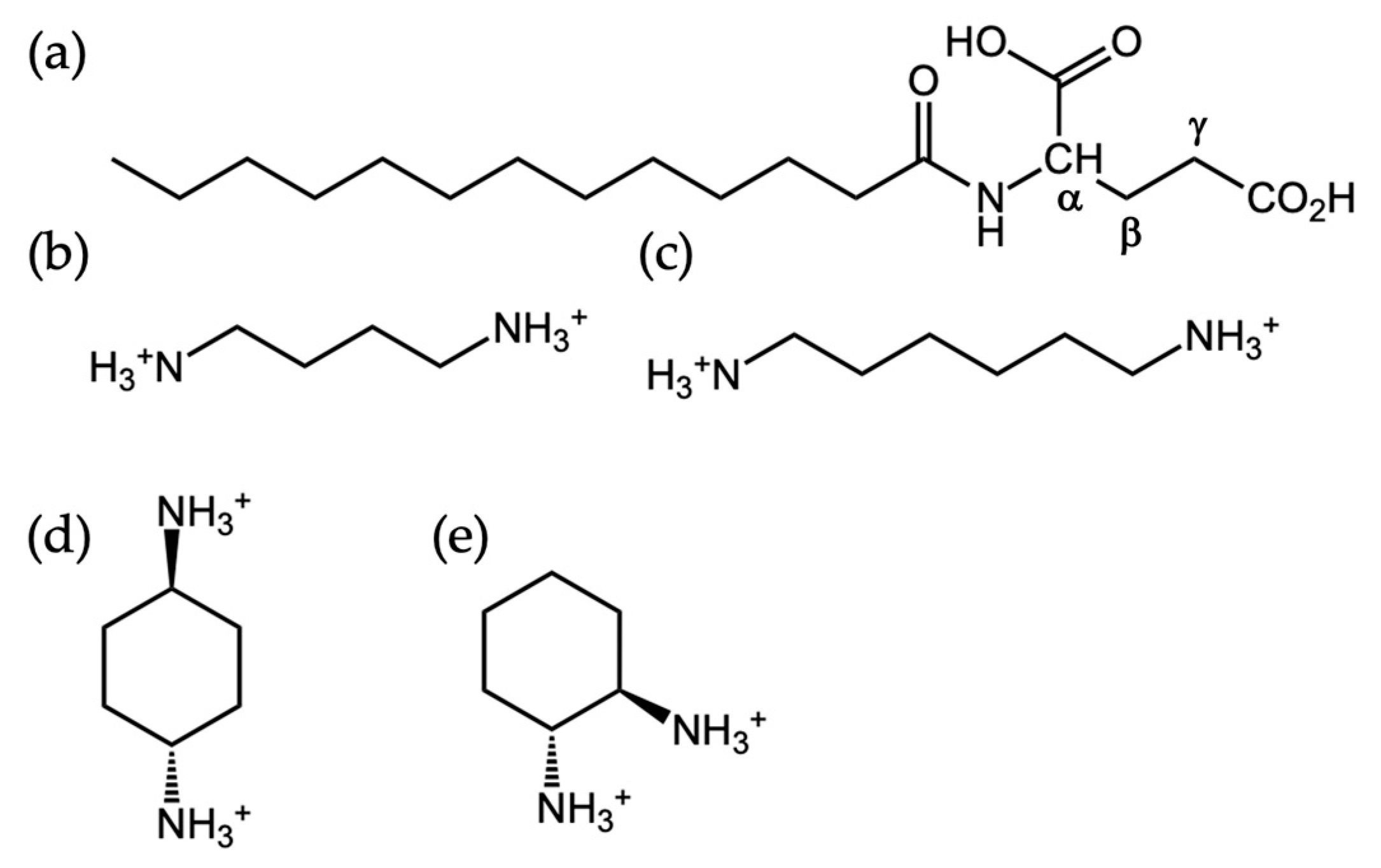
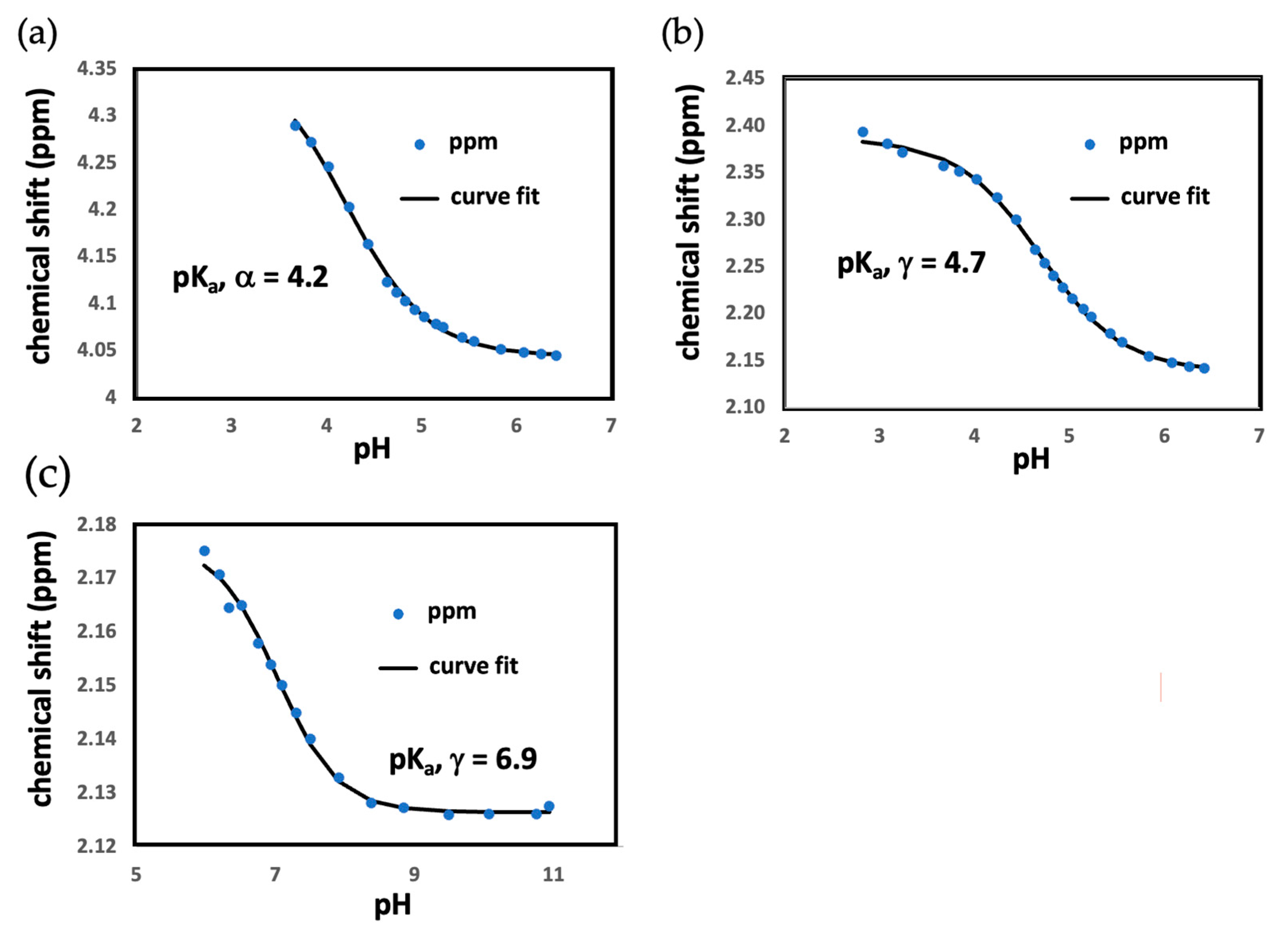


| Primary-CO2H | Gamma-CO2H | |
| L-Glutamic Acid | 2.2 | 4.3 |
| Tridecanoic-Glu Monomer | 4.2 ± 0.3 | 4.7 ± 0.4 |
| Tridecanoic-Glu Micelles | n/a | 6.9 ± 0.6 |
| Tridecanoic-Glutamic Acid | ||
|---|---|---|
| Counterion | CMC at pH 6.0 (mM) | CMC at pH 7.0 (mM) |
| 1,4-diaminobutane | 3.2 ± 0.1 | 6.8 ± 0.3 |
| 1,6-diaminohexane | 3.4 ± 0.6 | 6.3 ± 0.5 |
| trans-1,4-diamocyclohexane | 3.1 ± 0.1 | 6.2 ± 0.3 |
| trans-1,2-diamocyclohexane | 1.3 ± 0.2 | 2.1 ± 0.1 |
| Undecanoic-Glutamic Acid | ||
| Counterion | CMC at pH 6.0 (mM) | CMC at pH 7.0 (mM) |
| 1,4-diaminobutane | 22.1 ± 0.2 | 25.2 ± 0.5 |
| 1,6-diaminohexane | 19.6 ± 0.4 | 22.2 ± 0.5 |
| trans-1,4-diamocyclohexane | 17.5 ± 0.1 | 22.1 ± 0.2 |
| trans-1,2-diamocyclohexane | 11.9 ± 0.2 | 13.9 ± 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayer, J.D.; Rauscher, R.M.; Fritz, S.R.; Fang, Y.; Billiot, E.J.; Billiot, F.H.; Morris, K.F. An Investigation of the Effect of pH on Micelle Formation by a Glutamic Acid-Based Biosurfactant. Colloids Interfaces 2024, 8, 38. https://doi.org/10.3390/colloids8030038
Mayer JD, Rauscher RM, Fritz SR, Fang Y, Billiot EJ, Billiot FH, Morris KF. An Investigation of the Effect of pH on Micelle Formation by a Glutamic Acid-Based Biosurfactant. Colloids and Interfaces. 2024; 8(3):38. https://doi.org/10.3390/colloids8030038
Chicago/Turabian StyleMayer, Jacob D., Robert M. Rauscher, Shayden R. Fritz, Yayin Fang, Eugene J. Billiot, Fereshteh H. Billiot, and Kevin F. Morris. 2024. "An Investigation of the Effect of pH on Micelle Formation by a Glutamic Acid-Based Biosurfactant" Colloids and Interfaces 8, no. 3: 38. https://doi.org/10.3390/colloids8030038
APA StyleMayer, J. D., Rauscher, R. M., Fritz, S. R., Fang, Y., Billiot, E. J., Billiot, F. H., & Morris, K. F. (2024). An Investigation of the Effect of pH on Micelle Formation by a Glutamic Acid-Based Biosurfactant. Colloids and Interfaces, 8(3), 38. https://doi.org/10.3390/colloids8030038







