Evaporation of Small Sessile Drop Deposited on a Horizontal Solid Surface: New Exact Solutions and Approximations
Abstract
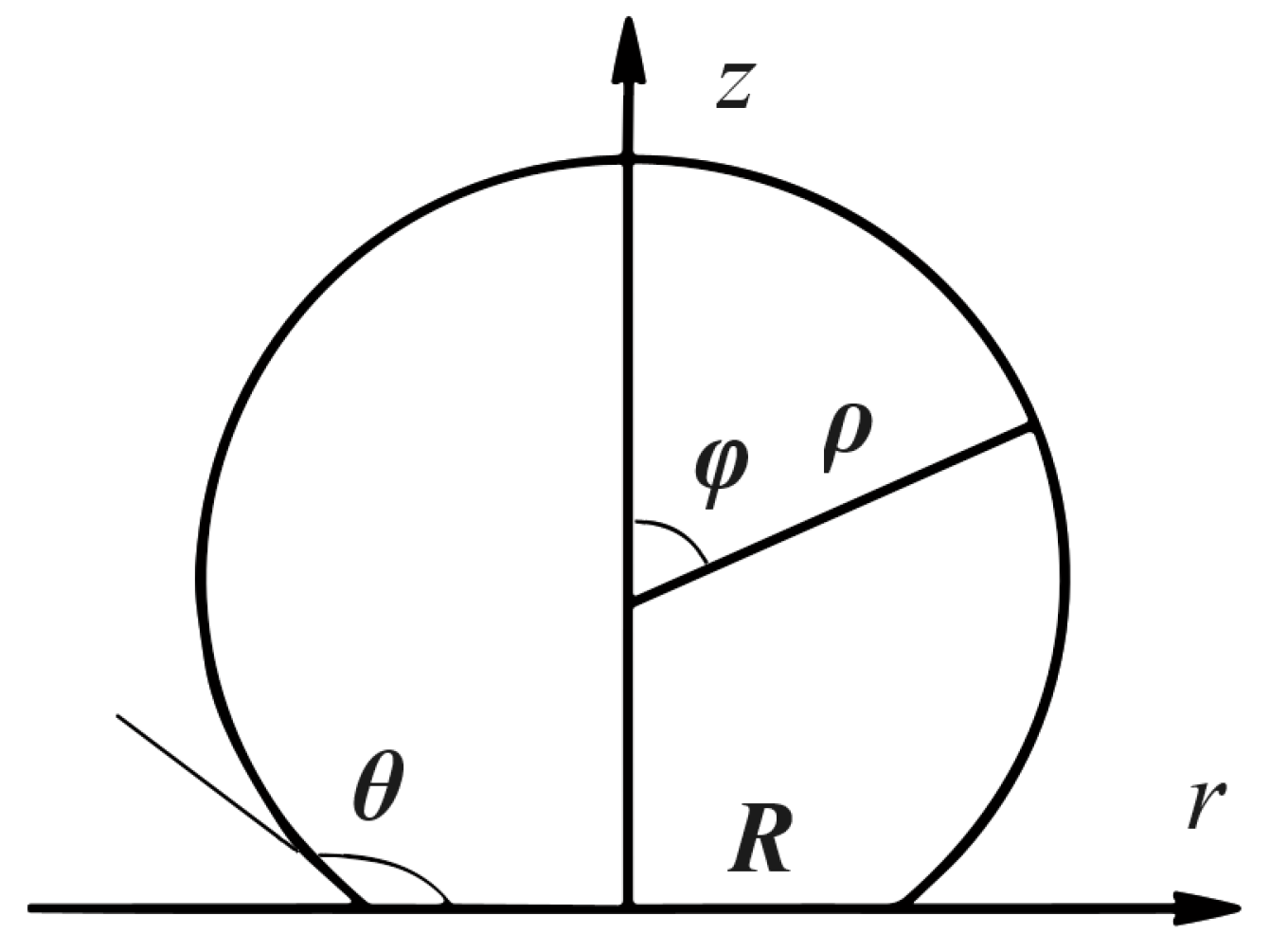
:1. Introduction
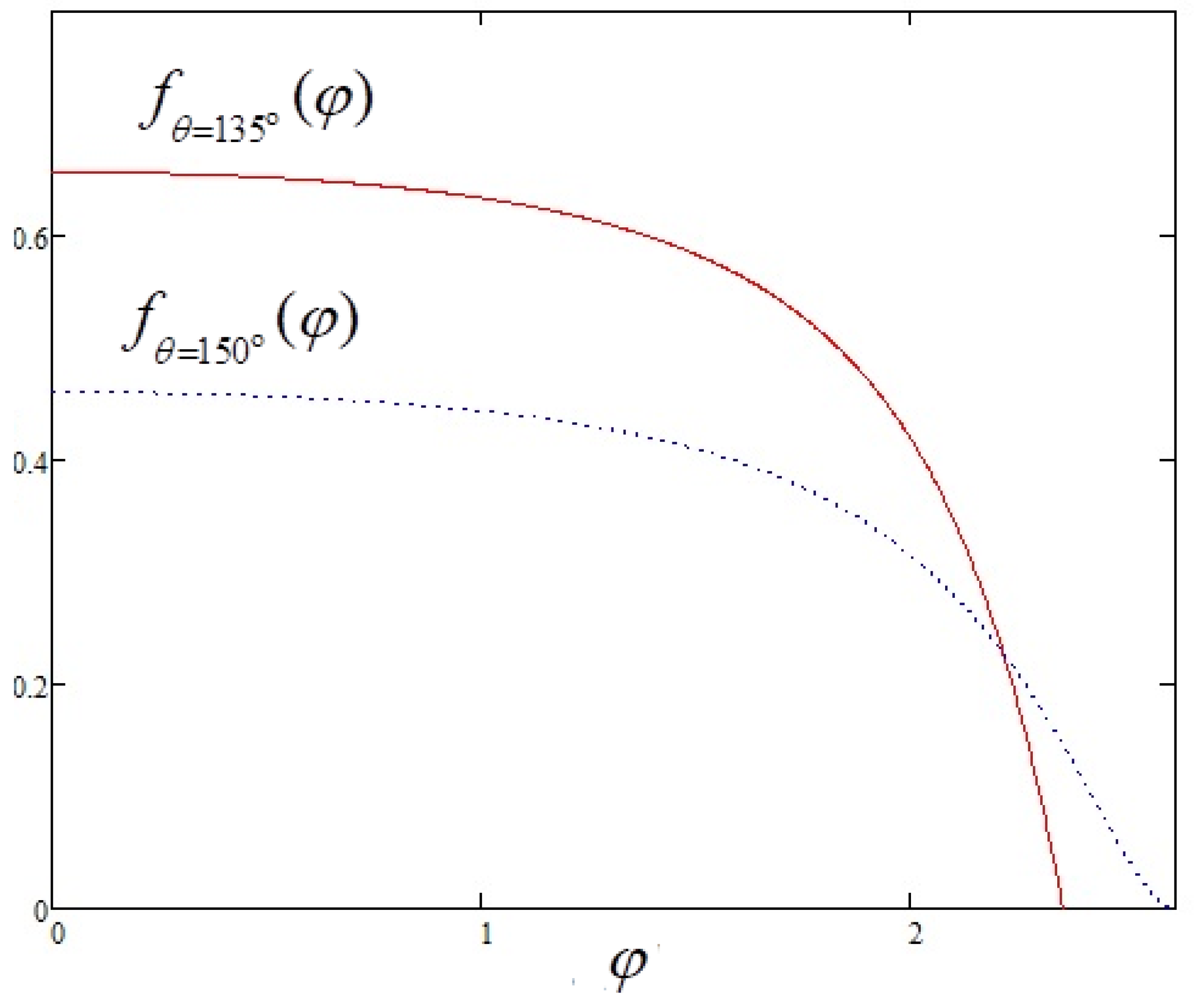
2. New Exact Solutions for Some Values of Contact Angles
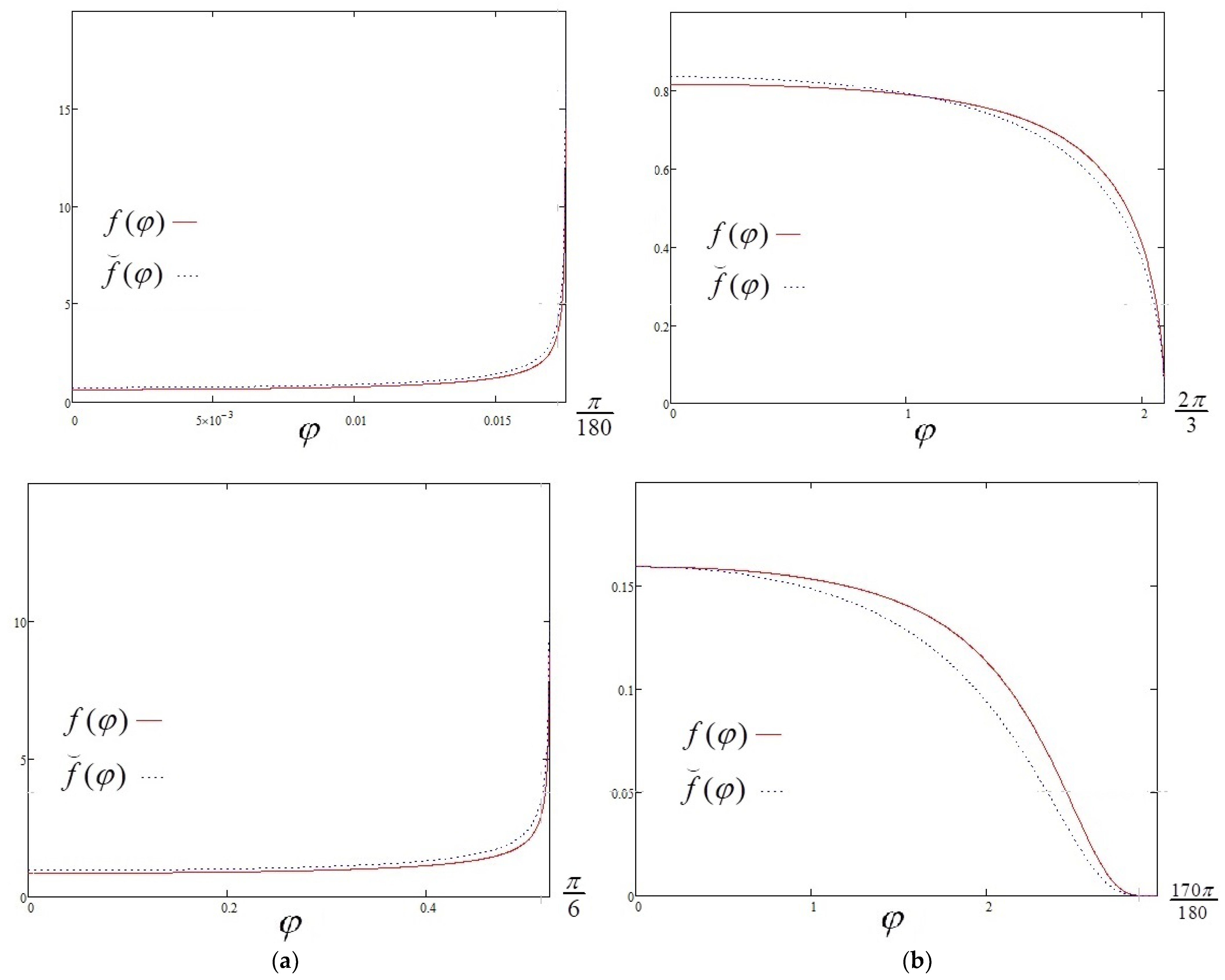
3. New Approximate Solutions
3.1. Total Evaporation Rate
3.2. Evaporation Flux Density for Acute and Obtuse Contact Angles
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brutin, D. Droplet Wetting and Evaporation; Elsevier Inc.: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Zang, D.; Tarafdar, S.; Tarasevich, Y.Y.; Choudhury, M.D.; Dutta, T. Evaporation of a droplet: From physics to applications. Phys. Rep. 2019, 804, 1–56. [Google Scholar] [CrossRef]
- Lebedev-Stepanov, P.; Vlasov, K. Simulation of self-assembly in an evaporating droplet of colloidal solution by dissipative particle dynamics. Coll. Surf. A Physicochem. Eng. Asp. 2013, 432, 132–138. [Google Scholar] [CrossRef]
- Kolegov, K.; Barash, L. Applying droplets and films in evaporative lithography. Adv. Colloid Interface Sci. 2020, 285, 102271. [Google Scholar] [CrossRef] [PubMed]
- Schnall-Levin, M.; Lauga, E.; Brenner, M.P. Self-assembly of spherical particles on an evaporating sessile droplet. Langmuir 2006, 22, 4547. [Google Scholar] [CrossRef] [PubMed]
- Kokornaczyk, M.O.; Bodrova, N.B.; Baumgartner, S. Diagnostic tests based on pattern formation in drying body fluids—A mapping review. Colloids Surf. B Biointerfaces 2021, 208, 112092. [Google Scholar] [CrossRef] [PubMed]
- Hamadeh, L.; Imran, S.; Bencsik, M.; Sharpe, G.R.; Johnson, M.A.; Fairhurst, D.J. Machine learning analysis for quantitative discrimination of dried blood droplets. Sci. Rep. 2020, 10, 3313–3326. [Google Scholar] [CrossRef] [PubMed]
- Lebedev-Stepanov, P.V.; Buzoverya, M.E.; Vlasov, K.O.; Potekhina, Y.P. Morphological analysis of images of dried droplets of saliva for determination the degree of endogenous intoxication. J. Bioinform. Genom. 2018, 4, 1–4. [Google Scholar]
- Boinovich, L.B.; Emelyanenko, A.M. Hydrophobic materials and coatings: Principles of design, properties and applications. Russ. Chem. Rev. 2008, 77, 583–600. [Google Scholar] [CrossRef]
- Lebedev-Stepanov, P.V. Introduction to Self-Organization and Self-Assembly of Ensembles of Nanoparticles; NRNU MEPhI: Moscow, Russia, 2015. (In Russian) [Google Scholar]
- Maxwell, J.C. Diffusion. In Collected Scientific Papers; Niven, W.D., Ed.; Cambridge University Press: Cambridge, UK, 2010; Volume 2, pp. 625–646. [Google Scholar]
- Wang, Y.; Ma, L.; Xu, X.; Luo, J. Combined effects of underlying substrate and evaporative cooling on the evaporation of sessile liquid droplets. Soft Matter 2015, 11, 5632–5640. [Google Scholar] [CrossRef]
- Sefiane, K.; Wilson, S.K.; David, S.; Dunn, G.J.; Duffy, B.R. On the effect of the atmosphere on the evaporation of sessile droplets of water. Phys. Fluids 2009, 21, 062101. [Google Scholar] [CrossRef]
- Sefiane, K.; Bennacer, R. An expression for droplet evaporation incorporating thermal effects. J. Fluid Mech. 2011, 667, 260–271. [Google Scholar] [CrossRef]
- Bin, L.; Bennacer, R.; Sefiane, K.; Steinchen, A. Transient Effects in Evaporating Sessile Drops: With and without Heating. J. Heat Transfer. 2016, 138, 091009. [Google Scholar] [CrossRef]
- Stefan, J. Über die dynamische Theorie der Diffusion der Gase. Sitzungsberichte Akad Wiss 1872, 65, 323–363. [Google Scholar]
- Fuchs, N.A. Evaporation and Droplet Growth in Gaseous Media; Pergamon Press: London, UK, 2013; pp. 1–80. [Google Scholar]
- Barash, L.Y.; Bigioni, T.P.; Vinokur, V.M.; Shchur, L.N. Evaporation and fluid dynamics of a sessile drop of capillary size. Phys. Rev. E 2009, 79, 046301. [Google Scholar] [CrossRef]
- Picknett, R.G.; Bexon, R. The evaporation of sessile or pendant drops in still air. J. Colloid Interface Sci. 1977, 61, 336. [Google Scholar] [CrossRef]
- Talbot, E.; Bain, C.; De Dier, R.; Sempels, W.; Vermant, J. Droplets Drying on Surfaces. In Fundamentals of Inkjet Printing; Hoath, S.D., Ed.; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2016; pp. 251–279. [Google Scholar]
- Wilson, S.K.; Duffy, B.R. Mathematical Models for the Evaporation of Sessile Droplets. In Drying of Complex Fluid Drops; Brutin, D., Sefiane, K., Eds.; The Royal Society of Chemistry: Croydon, UK, 2022; pp. 80–109. [Google Scholar]
- Brutin, D.; Starov, V. Recent advances in droplet wetting and evaporation. Chem. Soc. Rev. 2018, 47, 558–585. [Google Scholar] [CrossRef] [PubMed]
- Murisic, N.; Kondic, L. On evaporation of sessile drops with moving contact lines. J. Fluid Mech. 2011, 679, 219–246. [Google Scholar] [CrossRef]
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Contact line deposits in an evaporating drop. Phys. Rev. E 2000, 62, 756–765. [Google Scholar] [CrossRef] [PubMed]
- Popov, Y.O. Evaporative deposition patterns: Spatial dimensions of the deposit. Phys. Rev. E 2005, 71, 036313. [Google Scholar] [CrossRef] [PubMed]
- Lebedev-Stepanov, P. Sessile liquid drop evaporation: Analytical solution in bipolar coordinates. arXiv 2021, arXiv:2103.15582v3. [Google Scholar]
- Savenko, O.A.; Lebedev-Stepanov, P.V. Quasi-Stationary Evaporation of a Small Liquid Droplet on a Flat Substrate: Analytical Solution in Bipolar Coordinates. Colloid J. 2022, 84, 312–320. [Google Scholar] [CrossRef]
- Wilson, S.K.; D’Ambrosio, H.-M. Evaporation of Sessile Droplets. Annu. Rev. Fluid Mech. 2023, 55, 481–509. [Google Scholar] [CrossRef]
- Hu, H.; Larson, R.G.J. Evaporation of a sessile droplet on a substrate. J. Phys. Chem. B 2002, 106, 1334. [Google Scholar] [CrossRef]
- Grinberg, G.A. Selected Questions of Mathematical Theory of Electric and Magnetic Phenomena; Academy of Science Publishing: Moscow, Russia, 1948; p. 404. (In Russian) [Google Scholar]
- Lebedev-Stepanov, P.V. New exact solutions for the evaporation flux density of a small droplet on a flat horizontal substrate with a contact angle in the range of 135–180 degrees. arXiv 2023, arXiv:2306.02322v2. [Google Scholar]
- Dash, S.; Garimella, S.V. Droplet Evaporation Dynamics on a Superhydrophobic Surface with Negligible Hysteresis. Langmuir 2013, 29, 10785–10795. [Google Scholar] [CrossRef]


 ) indicates the lifetime of the drop for CCA mode calculated by Equation (50), and the blue line (
) indicates the lifetime of the drop for CCA mode calculated by Equation (50), and the blue line ( ) is the same for CCR mode calculated by Equation (49). Blue points (
) is the same for CCR mode calculated by Equation (49). Blue points ( ) are the experiment data from Ref. [32]. Gray (
) are the experiment data from Ref. [32]. Gray ( ) and yellow (
) and yellow ( ) points are the lifetimes for CCA and CCR modes, respectively, calculated by Popov’s Formula (6) that gives the exact solution, presented in Ref. [32].
) points are the lifetimes for CCA and CCR modes, respectively, calculated by Popov’s Formula (6) that gives the exact solution, presented in Ref. [32].
 ) indicates the lifetime of the drop for CCA mode calculated by Equation (50), and the blue line (
) indicates the lifetime of the drop for CCA mode calculated by Equation (50), and the blue line ( ) is the same for CCR mode calculated by Equation (49). Blue points (
) is the same for CCR mode calculated by Equation (49). Blue points ( ) are the experiment data from Ref. [32]. Gray (
) are the experiment data from Ref. [32]. Gray ( ) and yellow (
) and yellow ( ) points are the lifetimes for CCA and CCR modes, respectively, calculated by Popov’s Formula (6) that gives the exact solution, presented in Ref. [32].
) points are the lifetimes for CCA and CCR modes, respectively, calculated by Popov’s Formula (6) that gives the exact solution, presented in Ref. [32].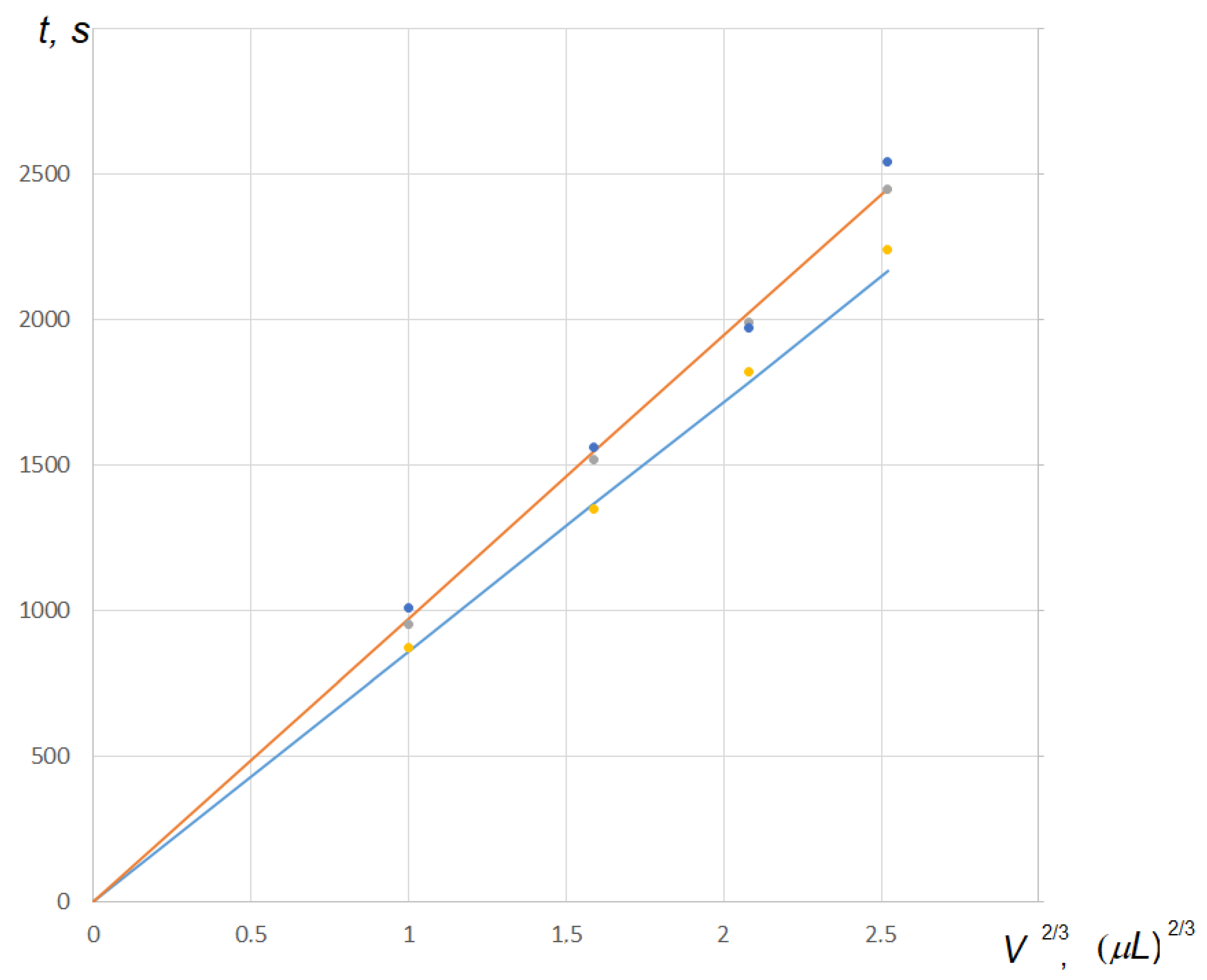
| j | J | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lebedev-Stepanov, P.; Savenko, O. Evaporation of Small Sessile Drop Deposited on a Horizontal Solid Surface: New Exact Solutions and Approximations. Colloids Interfaces 2024, 8, 2. https://doi.org/10.3390/colloids8010002
Lebedev-Stepanov P, Savenko O. Evaporation of Small Sessile Drop Deposited on a Horizontal Solid Surface: New Exact Solutions and Approximations. Colloids and Interfaces. 2024; 8(1):2. https://doi.org/10.3390/colloids8010002
Chicago/Turabian StyleLebedev-Stepanov, Peter, and Olga Savenko. 2024. "Evaporation of Small Sessile Drop Deposited on a Horizontal Solid Surface: New Exact Solutions and Approximations" Colloids and Interfaces 8, no. 1: 2. https://doi.org/10.3390/colloids8010002
APA StyleLebedev-Stepanov, P., & Savenko, O. (2024). Evaporation of Small Sessile Drop Deposited on a Horizontal Solid Surface: New Exact Solutions and Approximations. Colloids and Interfaces, 8(1), 2. https://doi.org/10.3390/colloids8010002







