3.1. Quartz Surface Tension
The wettability of the solids by different kinds of liquids or solutions, the measure of which is, among others, the contact angle (θ) on the solid surface, depends on the liquid or solution surface tension (
), the solid surface tension (
) and the solid-liquid (solution) interface tension (
) as well as the type of forces contributing to this tension. In turn,
is a function of
and
. The dependence between
,
,
and
can be expressed by the Young equation, having the form [
42,
43]:
Equation (1) shows that in order to determine the effect of the surface-active substances on the wettability of a solid, its surface tension should be known. In the case of quartz, it is difficult to use the literature data onits surface tension because, as mentioned above, many parameters affect this value. For this reason, the surface tension of quartz plates used to study the effect of ET, RL and TX165 wettability was determined. For the determination of
and its Lifshitz-van der Waals (LW) and acid-base (AB) components as well as the electron-acceptor (+) and electron-donor (−) parameters of AB component, the contact angles of W (
), F (
) and D (
) on the quartz surface were measured. Water, formamide and diiodomethane are applied as model liquids for the surface tension determination of many solids [
13].
The main problem in using Young’s equation (Equation (1)) to determine the surface tension of solids is the dependence of the solid-liquid interface tension on the surface tension of the solid and liquid. Most approaches dealing with this dependence are based on the equation proposed by Girifalco and Good [
44], which has the form:
where
is the parameter of the interactions across the interface.
Neumann et al. [
45,
46,
47] assumed that the
parameter is a linear function of the solid-liquid interface tension and proposed the following equation for
determination:
where
β is a constant.
In contrast to Neumann et al. [
45,
46,
47], Owens and Wendt [
48] as well as van Oss et al. proved that the parameter
depends on the kind of intermolecular interactions [
13,
49,
50,
51,
52]. In consequence, Owens and Wendt obtained the following expression [
48]:
where indices
d and
n refer to the dispersion and non-dispersion components of liquid and solid surface tension.
On the other hand, van Oss et al. [
13,
49,
50,
51,
52] derived an equation, which has the following form:
In fact, the dispersion component in the Owens and Wendt approach differs from the LW component of the solid surface tension in the van Oss et al. equation only by the definition [
53].
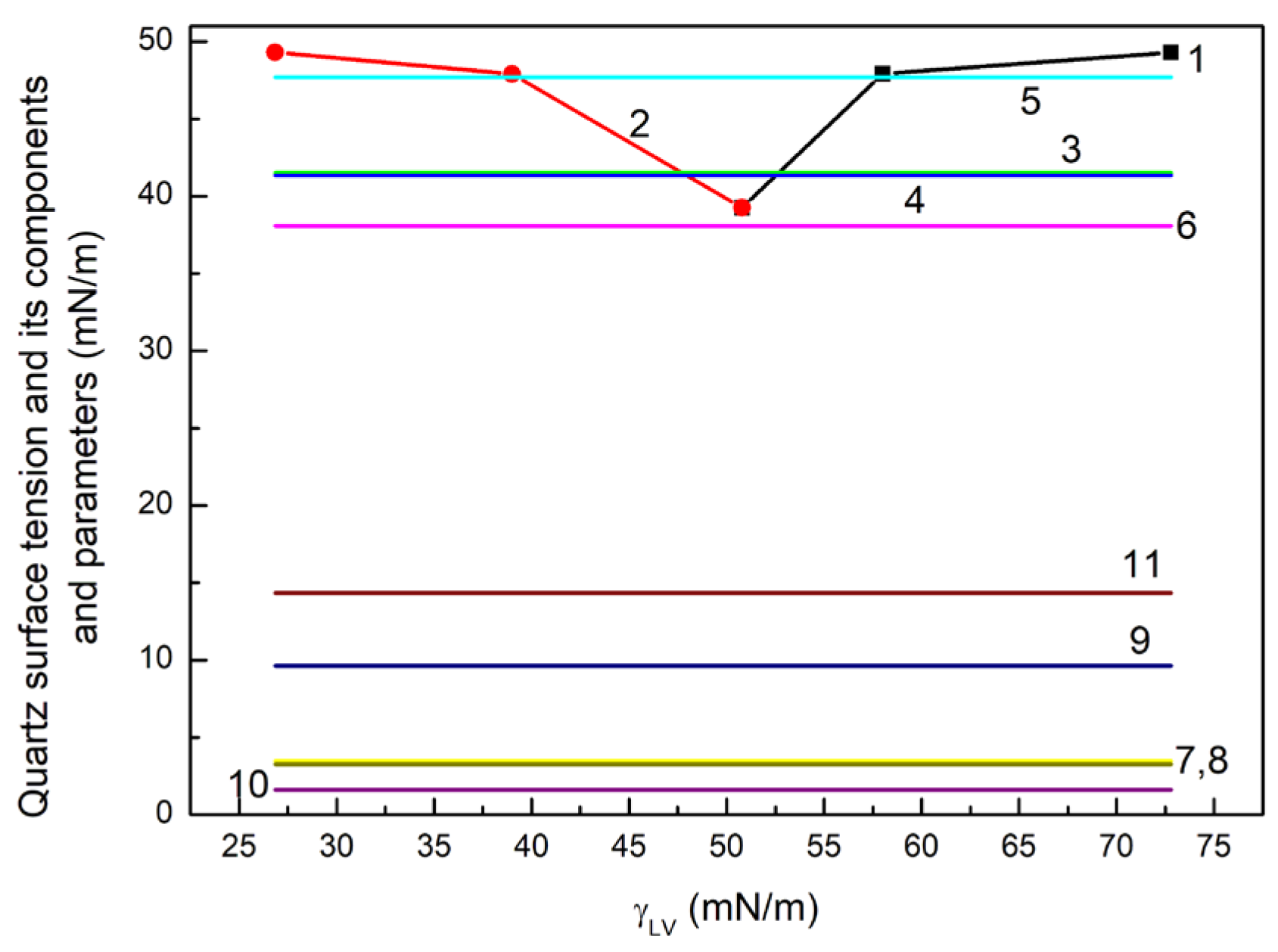
Equations (3)–(5) were used for quartz surface tension determination from
,
and
. It appeared that the
values of quartz calculated from the Neumann et al. equation [
45,
46,
47] increase with the increasing surface tension of liquids taken for calculations (
Figure 1).
It should be mentioned that with the decreasing surface tension in the order W, F, D the LW component of this tension increases. In the case of diiodomethane, its surface tension results only from LW intermolecular interactions [
13,
53]. Thus, it follows for D from Equations (4) and (5) that:
The values of
or
calculated from Equation (6) based on
are close to those of
determined from the Neumann equation (Equation (3)) (
Figure 1). This fact suggests that not total surface tension of liquids used for the contact angle measurements on the quartz surface but its components resulting from different kinds of intermolecular interactions decide about the value of contact angle, which is also related rather to the components of quartz surface tension than to its total value. On the other hand, it is possible that the value of
β in Equation (3) for quartz (Q) is not proper for all kinds of liquids or the properties of the water-specific layer on the quartz surface under a drop are different for each studied liquid. It is possible to obtain some information about the water layer properties from the calculations of the components and parameters of the quartz surface tension based on Equations (4) and (5) as well as from the
parameter calculated using the following expression:
For the calculation of components and parameters of the quartz surface tension from Equations (4) and (5), the values of
and
as well as
for water, formamide and diiodomethane, obtained only based on the contact angle of these liquids on the PTFE and PMMA surface, were used [
41].
From the calculations based on Equation (4), it results that the quartz surface tension and dispersion and non-dispersion components obtained from
and
are comparable to those obtained from
and
(
Figure 1). However, the
values calculated from Equation (4) are lower than those calculated from Equation (5), which are close to the
values determined from the Neumann et al. equation [
45,
46,
47] (
Figure 1). In turn, the
values calculated from Equation (7) using
ones obtained from Equation (5), which are higher than 1 for water and formamide, can suggest that the water layer on the Q surface is partially dissolved under the water and formamide drops. Nevertheless, it seems that the Q surface tension and its components and parameters calculated from the van Oss et al. [
49,
50,
51,
52] equation are the most appropriate to interpret the change in quartz wetting under the influence of ET, RL and TX165 and their mixture.
3.2. Wettability of Quartz by the Aqueous Solution of Ethanol, Rhamnolipid and Triton X-165
Some researchers suggest that in the case of liquids or aqueous solutions with a surface tension equal to that of a given solid, the contact angle is equal to zero [
13,
45,
46,
47,
49,
50,
51,
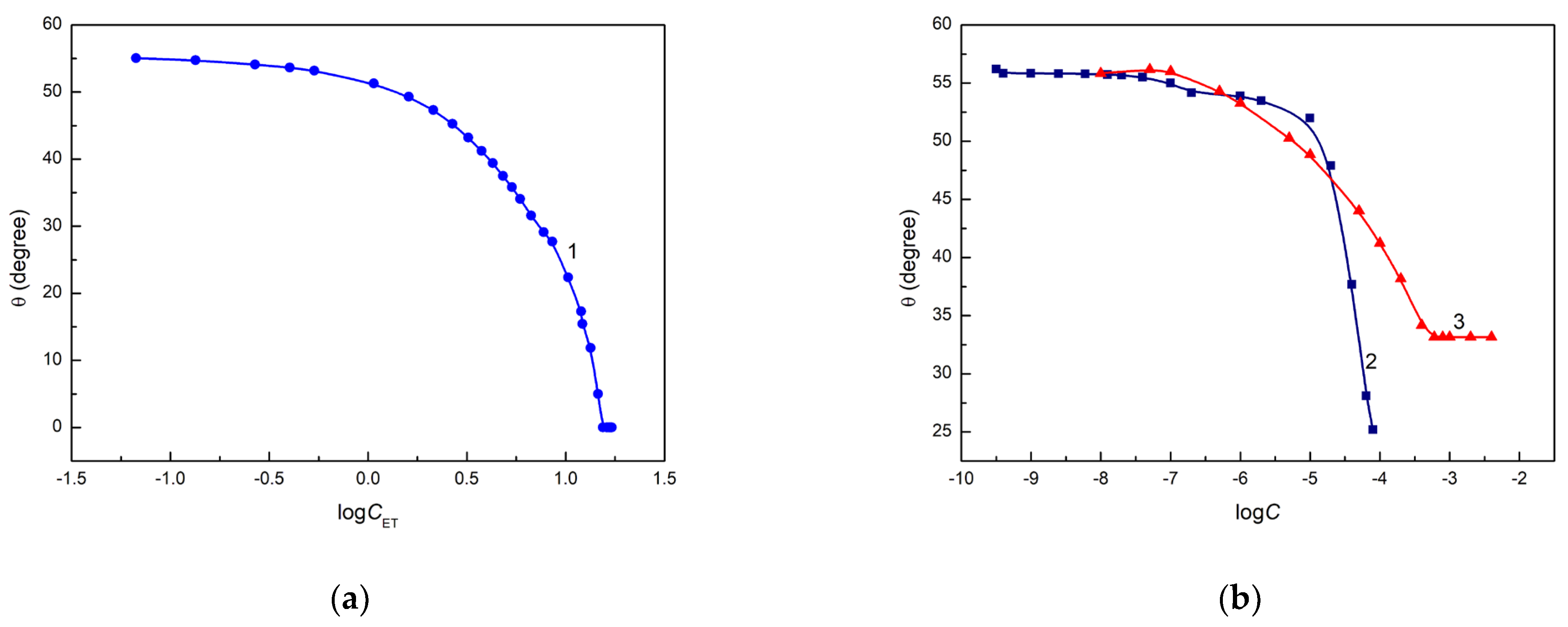
52]. Unfortunately, only in the case of an aqueous ET solution, its complete spreading is observed, but at a surface tension much lower than the quartz surface tension (
Figure 2a). The minimum of the surface tension of aqueous solution of RL and TX165 [
54,
55] is lower than the Q surface tension, but
is considerably higher than zero (
Figure 2b).
Therefore, the following question arises: what is the reason for this? From the Young-Dupre equation, it results that [
42,
43]:
where
is the adhesion work of liquid or solution to the solid surface.
However, only in the case of the aqueous solution of ET is there linear dependence between the cosine of the contact angle and the reciprocal of its surface tension in the range of ET concentration, in which the contact angle on the quartz surface is higher than zero (
Figure 3).
Unfortunately, Equation (8) is not satisfied because the slope of the linear relationship is not equal to
of the aqueous ET solution to the quartz surface. For the ET aqueous solution, the relationship between
and
satisfies the expression:
where
and
.
The changes in
as a function of
suggest that there is a different mechanism of the ET, RL and TX165 adsorption at interfaces including quartz. The LW and AB components of ET surface tension are considerably lower than these components of water surface tension. It seems that ET molecules are adsorbed on Q covered by a water layer surface in the whole range of its concentration. It is possible that at a high ET concentrations, only an ice-like layer of water is not destroyed, but the adsorbed water molecules are removed by the ET ones. In the case of RL and TX165, the mechanism of their adsorption at the interfaces including a quartz/water layer surface is more complicated that in the case of ET adsorption. According to van Oss and Constanzo [
56], the surface tension of a surfactant depends on the molecule orientation towards the air phase. If the molecules of surfactants are oriented by the hydrophobic group towards air, then the surfactant tension is treated as the tail surface tension, and if the hydrophilic group of surfactant molecules is oriented towards the water phase, then the surface tension is called the head surface tension. The tail surface tension of RL and TX165 is the same and close to the LW component of ET surface tension but lower than LW of water surface tension determined from
on hydrophobic surfaces [
41]. On the other hand, the head surface tension of RL and TX165 is higher than the tail surface tension and lower than that of water [
51]. Although the surface tension of RL and TX165 tails is similar to the ET surface tension, the hydrophobic interactions of surfactant molecules with the quartz/water layer surface are much greater than that of ET due to the much larger contact area [
38]. It should be remembered that RL is an anionic surfactant, and there may be repulsive electrostatic interactions between the RL molecules and the quartz/water layer surface. However, in the case of TX165, the hydrophilic group of its molecules is strongly hydrated, and it is possible that H
3O
+ ions are strongly bound to the oxyethylene groups in the TX165 molecule and, thus, attractive interactions between the TX165 molecules and the quartz surface may occur [
42]. The above facts indicate that the adsorption mechanism of RL and TX165 on the quartz surface covered with a layer of water is different, which is reflected in the differences in the relationship between
and
(
Figure 3).
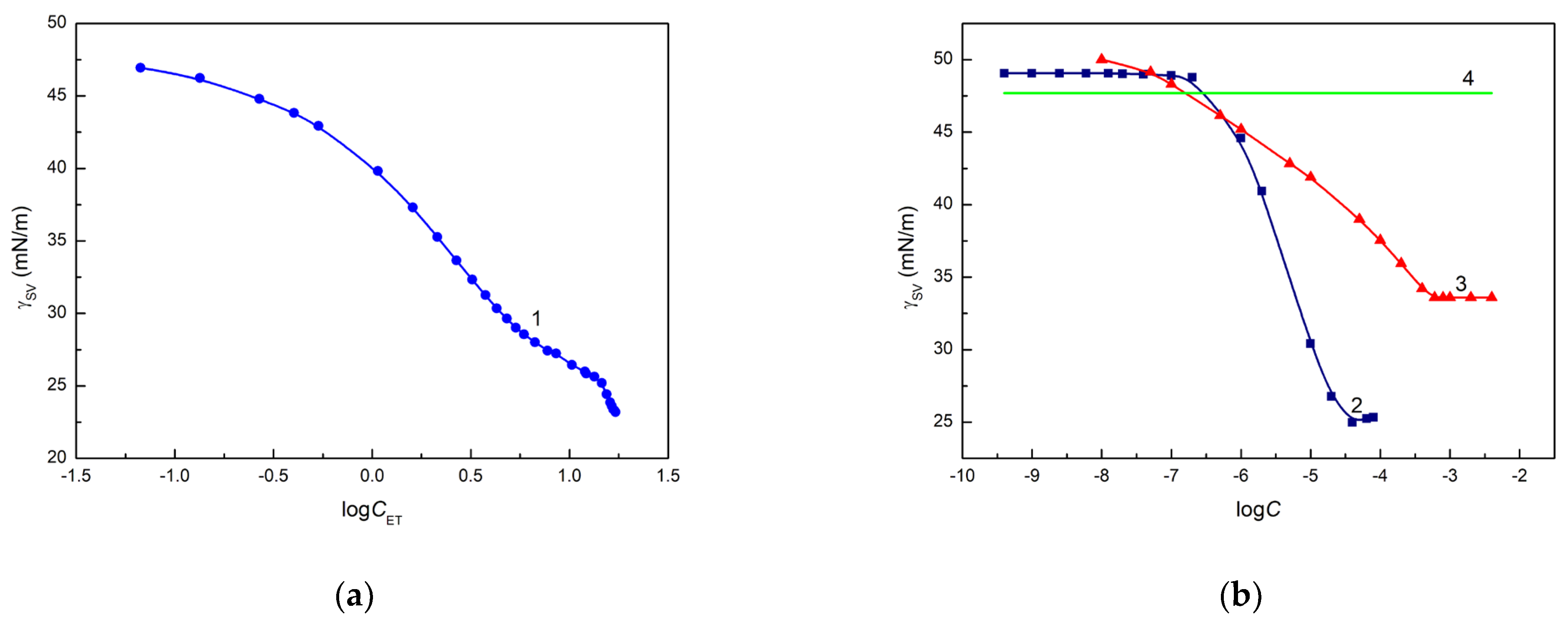
These differences for the ET, RL and TX165 solutions can also result from the change in the surface tension of the quartz after deposition of a solution drop on its surface as a function of the concentration of ET, RL and TX165. The confirmation of this suggestion can be the values of the quartz surface tension calculated from the Neumann et al. [
45,
46,
47] equation (Equation (3)) based on the contact angle of aqueous solutions of ET, RL and TX165 (
Figure 4a,b).
The calculated
values decrease as a function of solution concentration (
). It is interesting that the complete spreading of ET aqueous solution takes place when the surface tension of the solution is close to that of quartz calculated from Equation (3). In the case of the aqueous solution of RL and TX165, the values of
calculated from Equation (3) are lower than the minimal surface tension of these solutions and, probably for this reason, complete spreading of quartz by the solution of RL and TX165 is not observed (
Figure 2b). The
values calculated from Equation (3) based on the contact angle of aqueous solution of ET, RL and TX165 on the Q surface suggest that behind the solution drop settled on quartz, the layer of a given solute is formed, which decreases the quartz surface tension. The surface tension of the head and tail of RL and TX165 is lower than that of quartz [
38]. Thus, the adhesion work of ET, RL and TX165 is greater than their cohesion work, as opposed to water. Hence, the ET, RL and TX165 molecules have a greater ability to migrate along the quartz surface than water molecules, whose work of adhesion to quartz is smaller than that of cohesion. In the case of ET, there is a possibility of adsorption of its vapours behind a solution drop deposited on the quartz surface.
The possibility of formation of an ET, RL or TX165 layer behind a drop of their aqueous solutions deposited on quartz is confirmed by the values of the work of adhesion of these solutions to the quartz surface calculated from the Young-Dupre (
) and the van Oss et al. equations
[
49,
50,
51,
52] (
Figure S1a–c). For the calculation of
the measured values of the contact angle of aqueous solution of ET, RL and TX165 as well as the components and parameters of solution surface tension taken from the literature [
54,
55,
57] were used. There is a difference between the values of
calculated from the Young-Dupre and van Oss et al. equations. Probably, this difference corresponds to the pressure of the layer formed by the ET, RL or TX165 on the quartz surface (
). It is interesting that there is linear dependence between the
obtained from the Young-Dupre equation and
of aqueous solution of ET or TX165 but not for solution of RL (
Figure S1d). In the case of
calculated from the van Oss et al. [
49,
50,
51,
52] equation, its changes are not linear for solutions of surfactants and ET but can be described by one function. If we assume that the changes in the quartz surface tension calculated from the Neumann et al. equation (Equation (3)) [
45,
46,
47] are caused by the formation of the ET or RL or TX165 layer on the quartz surface, then the pressure of this layer should be equal to the difference between the quartz surface tension calculated from the contact angles for water and solution at the given concentration (
). It appeared that the pressure of the surfactants and ET layer on the quartz surface (
) determined by the two mentioned ways are similar (
Figure 5a,b).
Moreover, this pressure is close to half the difference between the surface tension of water (
) and the solution (
) (
Figure S1d). The presence of a layer of surfactants and ET on the quartz surface behind the deposited drop of their solution is also confirmed by the values of the parameter of intermolecular interactions across the quartz-solution interface calculated both on the basis of the contact angle and the components and parameters of the quartz surface tension (
Figure S2a,b).
The calculation of
based on Equation (7), in which the contact angles of aqueous solutions of ET, RL and TX165 were used, as well as the constant value of
equal to 47.7 mN/m and the variable values of
obtained from the Neumann et al. [
45,
46,
47] equation (
Figure S2a,b).
The other method of
calculation was based on the equation resulting from the equations of van Oss et al. [
49,
50,
51,
52] and Girifalco and Good [
44], which has the form:
It appeared that the values of
calculated from Equation (7) at the constant
decrease as a function of ET or surfactant concentration (
Figure S2a,b). Because the values of contact angle also decrease as a function of ET and surfactant concentration, it seems that the
values determined in such a way are not real. On the other hand, the
values increase as a function of ET, RL or TX165 concentration if, for its calculation from Equation (7), the variable values of
obtained from Equation (3) are used. These values are close to those obtained from Equation (10). This fact confirms the conclusion drawn above that the layer of ET, RL or TX165 is formed behind the solution-settled drop on the quartz surface, which influences the value of contact angle. Probably for this reason, the complete spreading of the aqueous solution of RL and TX165 is not observed, although the surface tension of the solution is lower than the quartz surface tension. On the other hand, in the case of the ET solution, its complete spreading over the quartz surface occurs at the solution concentration which corresponds to its surface tension equal to or lower than the surface tension of the quartz covered with the ET layer. Hence, the so-called critical surface tension of quartz wetting (
) is not equal to its surface tension but to the surface tension of quartz/layer of a surface-active substance. In such cases, the wetting properties of ET, RL and TX165 depend on the surface tension of ET, RL and TX 165 aqueous solution and its components and parameters as well as the surface tension of quartz covered by these substance layers. The
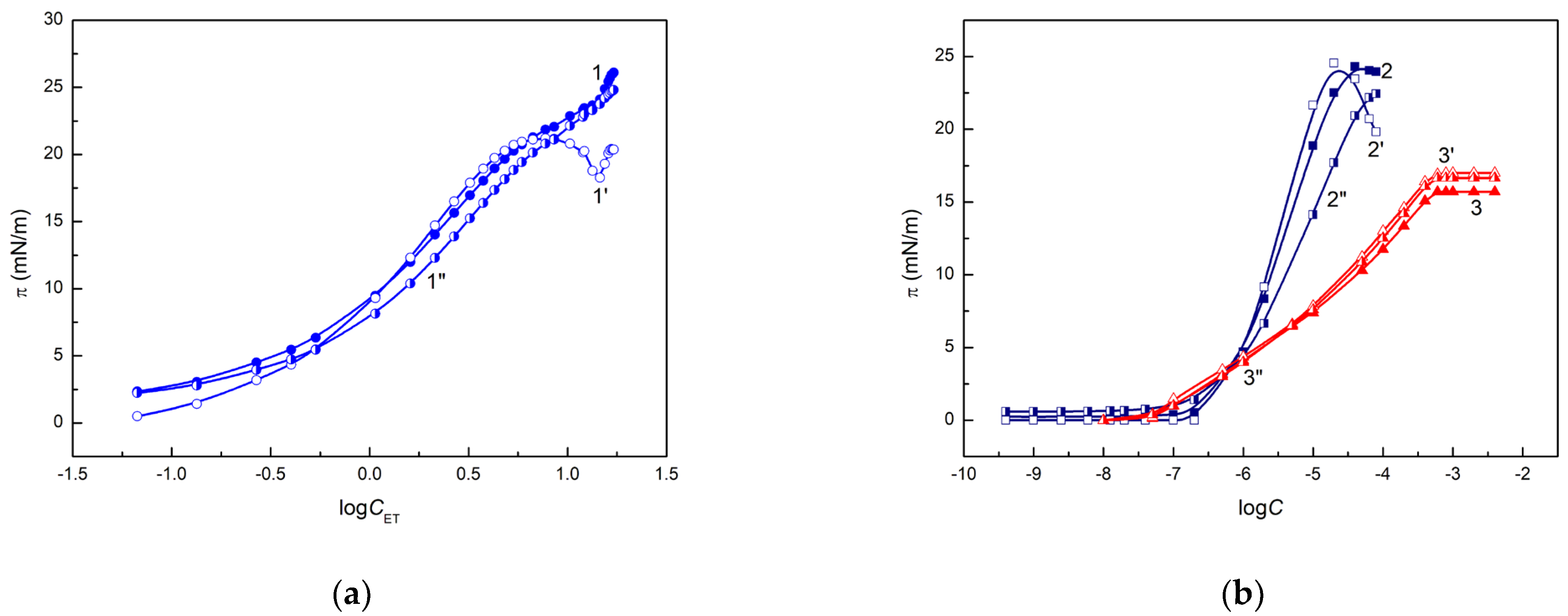
and
are only independent parameters influencing θ because
depends on these parameters. As follows from
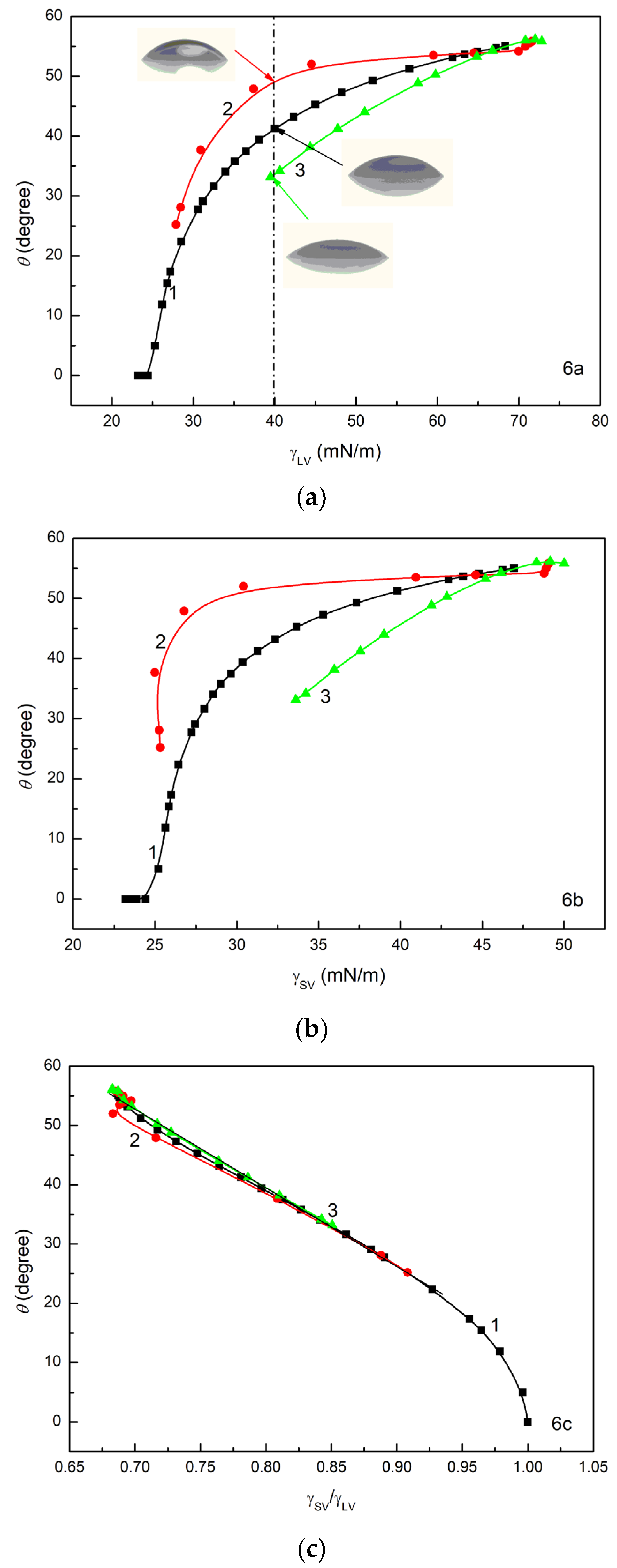
Figure 6, the wetting properties of ET, RL and TX165 are the same at a low concentration of their solution (large surface tension). However, with a decrease in the solution surface tension, differences in the wetting properties of ET, RL and TX165 are observed. At the same values of
(
Figure 6a) and
(
Figure 6b), the greatest θ is observed for RL and the smallest for TX165. This indicates that at a given surface tension of aqueous solution, the wetting properties of TX165 are the best but those for RL are the worst. This is probably associated with repulsive interactions between the electron-donor parameters of RL and TX165 head surface tension and the electron-donor parameter of quartz surface tension as well as with repulsive electrostatic interactions between the RL molecules and quartz surface. However, the contact angle at a given surface tension of ethanol solution is higher than that for TX165 solution at the same surface tension, although the electron-donor parameter of ET surface tension is considerably smaller than this parameter of the head of TX165 surface tension. Because the surface tension of the TX165 tail is close to ET, this effect results probably from attractive electrostatic interactions between the head of TX165 strongly hydrated by H
3O
+ ions with the negatively charged quartz surface. It is interesting that the ratio of
to
is almost the same for the aqueous solution of ET, RL and TX165. Moreover, the changes in θ as a function of
for RL and TX165 can be described by the linear equation in the whole range of their concentration in the solution (
Figure 6c). However, in the case of ET solution, the linear dependence between θ and
exists in the range of ET concentration at which the LW component of its solution surface tension is constant and close to the LW component of water surface tension [
57]. In fact, the value of
equal to unity indicates complete wetting of the quartz/surfactant layer by a given solution if
. It should be emphasized that the wettability of quartz, which, according to the concept of van Oss et al. [
49,
50,
51,
52], is treated as a bipolar solid, by the aqueous solutions of ET, RL and TX165, is different than, for example, for nylon 6, which is also a bipolar solid with components and surface tension parameters not much different from those of quartz. The reason for this is probably a highly ordered layer of water on the quartz surface, significantly changing its surface properties, which affects the adsorption mechanism of ET, RL and TX165 molecules at the quartz-air and quartz-solution interfaces.
Knowledge of the wettability of the quartz surface by the aqueous solution of ET, RL and TX165 reflected by the behaviour of their molecules at the solution-air, quartz-air and quartz-solution interfaces can contribute to a better understanding of the wetting properties of multicomponent surfactant mixtures containing anionic and nonionic surfactants and ethanol as additives. This is important from a practical point of view because, in practice, in most cases, mixtures but not individual surfactants are used.
3.3. Concentration of ET, RL and TX165 at the Quart-Air and Quartz-Solution Interfaces and the Gibbs Standard Free Energy of Adsorption
Knowing the pressure (
of ET, RL and TX165 layers at the quartz-air (Q-A) and quartz-solution (Q-S) interfaces, it is possible to determine their concentration (Γ) at these interfaces using, among others, the Frumkin equation, which has the form [
42]:
where
is the maximum concentration,
is the temperature and
is the gas constant.
One of the problems associated with applying Equation (11) to determine the concentrations of ET, RL and TX165 at the Q-A and Q-S interfaces is to determine their maximum concentrations at these interfaces. Since the ET aqueous solution can be treated as a two-component mixture, the maximum concentration of ET at these interfaces should be equal to its concentration in the bulk phase in terms of two-dimensional concentration [
42,
43]. Hence,
equal to 7.91 × 10
−6 mole/m
2 was taken in the calculations of Γ. In the case of RL and TX165, it appeared that there was linear dependence between
π and
(
is the mole concentration) in the range of the concentration close to their critical micelle concentration (CMC) [
54,
55]. Thus, it was possible to determine
for RL and TX165 at the Q-A and Q-S interfaces (
Table 1).
For the calculation of
at the Q-A interface, the values of
for ET, RL and TX165 solution obtained from the Neumann et al. [
45,
46,
47] equation as well as from the difference of
calculated from the van Oss et al. [
49,
50,
51,
52] and Young and Dupre equations were used. It proved that in the case of ET, its concentration at the Q-A interface is higher than at the Q-S one. However, the concentration of ET at the S-A interface is higher than that at Q-A and Q-S.
On the isotherm of ET concentration at the Q-S interface, the maximum is observed (
Figure S3a). The adsorption isotherm of ET suggests that at the quartz-air interface molecules of ET are rarely adsorbed on the quartz/monolayer surface compared with the “bare” quartz surface. However, at the ET concentration approaching its mole fraction in the bulk phase close to unity, the ethanol molecules destroy the ice-like structure of water, and a water-ethanol layer is formed. In consequence, the ET concentration at the quartz-solution interface decreases.
In the case of RL and TX165, their adsorption at the Q-S interface is about twice smaller than at the Q-A one (
Figure S3b). It should be added that at the Q-A and Q-S interfaces, RL and TX165 concentration is considerably lower than at the solution-air interface (
Figure S3b). Probably, this results from the strong Lewis acid-base interactions of water molecules with the head of RL and TX165 molecules. In the case of RL, some repulsive electrostatic interactions between the quartz surface and head of RL may take place. Behind the solution drop settled on the quartz surface, the interactions of RL and TX165 at the Q-A interface can be stronger than at the Q-S one due to the lack of competitive interactions of RL and TX165 molecules with water.
The measure of the tendency of a given substance to adsorb at any interface is the standard Gibbs free energy of adsorption (
). This energy is equal to the difference between the standard chemical potential of a given component of the solution in the bulk phase (
) and in the interface region (
). In the literature, it is possible to find various definitions of the chemical potential for a given component of the surface layer (
) [
43]. For an ideal mixed adsorption layer or a non-ideal one with a small concentration of a given component, its chemical potential can be represented, among others, by the following equation:
where
is the chemical potential of a given component of the mixed surface layer and
is the activity of a given component of the surface layer.
Because
, Equation (12) assumes the form:
where
is the fraction of the surface area occupied by molecules of a given compound at the interface and
is the activity coefficient of a given substance in the surface layer.
In turn, the chemical potential of the same component in the bulk phase (
), according to its asymmetric definition, can be expressed as:
where
is the activity of a given component of the bulk phase (
is the mole fraction of a given component and
is the activity coefficient).
It is known that in the thermodynamic equilibrium state
; then:
Taking into account that
, we obtain:
where
is the number of the moles of all components in solution in 1 dm
3.
If the solution in the bulk phase and in the surface layer can be treated as ideal, then:
In the case of aqueous solution of RL and TX165, their
C values are lower than 0.1 mole/dm
3 and
value can be treated as constant and equal to the number of water moles in 1 dm
3 of solution. Hence, the
can be treated as constant in the Langmuir isotherm and Szyszkowski equations [
42].
However, in the aqueous solution of ET, which should be rather treated as a mixture of water and ET , being the sum of ET and water moles in 1 dm3 of solution is changed as a function of ET concentration. This indicates that values for ET at the Q-A and Q-S interfaces should be changed more than RL and TX165 as a function of their concentration. To determine , and must be known.
For the surface monolayer,
can be determined based on the surface concentration of a given substance and the limiting area occupied by its molecule (
).
is correlated with the structure of a molecule of a given substance as well as its orientation at the interface. In the case of ET, it is easy to establish the
value because this value is the same at each possible orientation of the ET molecule at the interface and is equal to 21 Ǻ
2 [
38]. The
value for RL and TX165 depends on the orientation of their molecules towards the interface. At the perpendicular orientation of RL and TX165 molecules towards the interface, their
values are equal to 60.09 and 35.70 Ǻ
2, respectively [
38]. However, at the parallel orientation of the tail of RL and TX165 molecules, this area is equal to 87.30 for RL and 52.12 Ǻ
2 for TX165. Taking into account the above-mentioned
values and Γ, it is possible to determine
values using the expression:
where
is the Avogadro number.
The values of
determined for ET at both Q-A and Q-S interfaces are constant only in the range of low concentration, and there are small differences between
values for the Q-S and Q-A interfaces (
Figure S4a). For the Q-A interface and ET at its concentration from
= 1.07 mole/dm
3 to pure ET, almost linear dependence between
and
C takes place, and it does not depend on the method of ET layer pressure determination (see above). In the case of Q-S interface at the ET concentration range higher than its critical aggregation concentration [
57], there is a deviation from the linear dependence between
and
C. This confirms the suggestion that the adsorption behaviour of ET at the Q-S interface in a large concentration range is different from that at the Q-A interface. As mentioned above, the values of
depend on
of ET and, thus, from a thermodynamic point of view, it should be more interesting to show changes in the
ratio than
one as a function of
C (
Figure S4b). This proved that the changes in
are different from
as a function of
C, as expected. In the range of ET concentration from zero to the concentration at which the maximum of its Gibbs surface excess concentration takes place [
38,
57], the values of
for the Q-A and Q-S interfaces are the same and are slightly changed (
Figure S4b). On the basis of the data presented in
Figure S4a,b, it can be stated that only in a very low concentration range of ET approaching zero, at the first approximation,
and
are a little higher than the constant and directly associated with the standard Gibbs free energy of adsorption. As a matter of fact, in the whole range of ET concentration, this energy is related to
. To show the changes in
as a function of
for ET, it was assumed that for the lowest concentration of ET
. The values of
determined in such a way are presented in
Figure S4c. The changes in
as a function of concentration for both Q-A and Q-S interfaces can be successfully described by the exponential function of the second order.
The changes in
for RL and TX165 as a function of
are small in the range of RL as well as TX165 concentration lower than their CMC (
Figure S5a). These changes do not depend on the type of the interface. To confirm the suggestion resulting from
Figure S5a, the
values were determined in a similar way to the case of ET. For RL, the
values are equal to unity in its concentration range, corresponding to the RL unsaturated monolayer at the water-air interface and practically the same for the Q-A and Q-S interfaces as they do not depend on the limiting area of RL molecules (perpendicular and parallel orientations) taken for
determination (
Figure S5b). However, the
values for TX165 are constant only in its very low concentration range in the bulk phase. In fact, similar changes in
for the Q-S and Q-A interfaces of a given surfactant as a function of its concentration in the bulk phase do not indicate the same adsorption tendency at these interfaces. However, the
values equal to unity suggest that in a concentration range of the aqueous solution, the monolayer at the interfaces behaves as an ideal one. For this concentration range, the values of standard Gibb free energy (
) calculated based on the
values can be treated as real ones (
Figure S6a,b). It is difficult to establish, for ET, which values of
calculated from Equation (17) are real. It is possible to state that these values are similar for the Q-A and Q-S interfaces and a little different than at the water-air interface [
57]. In the case of RL, the absolute values of
for Q-S interface are lower than for the Q-A one, and both are lower than that at the water-air interface [
47,
55] (
Figure S6b). This fact suggests that there are repulsive electrostatic interactions between the quartz surface and RL molecules, which are more evident at the Q-A interface. The
values for TX165 for the Q-A interface are almost the same as for the water-air one. However, absolute values of
for the Q-A interface are higher than that at the Q-S one, similar to the case of RL. This indicates that for both RL and TX165, the tendency of their molecules to adsorb at the Q-A interface is greater than that of the Q-S interface. Probably, this results from smaller interactions between the surfactant molecules and air than between water ones. Therefore, the penetration of RL and TX165 molecules from the solution drop settled on the quartz surface causes a larger decrease in free energy of the quartz solution drop-air system than adsorption of these molecules at the quartz-water interface.