How Dimensionality Affects the Structural Anomaly in a Core-Softened Colloid
Abstract
1. Introduction
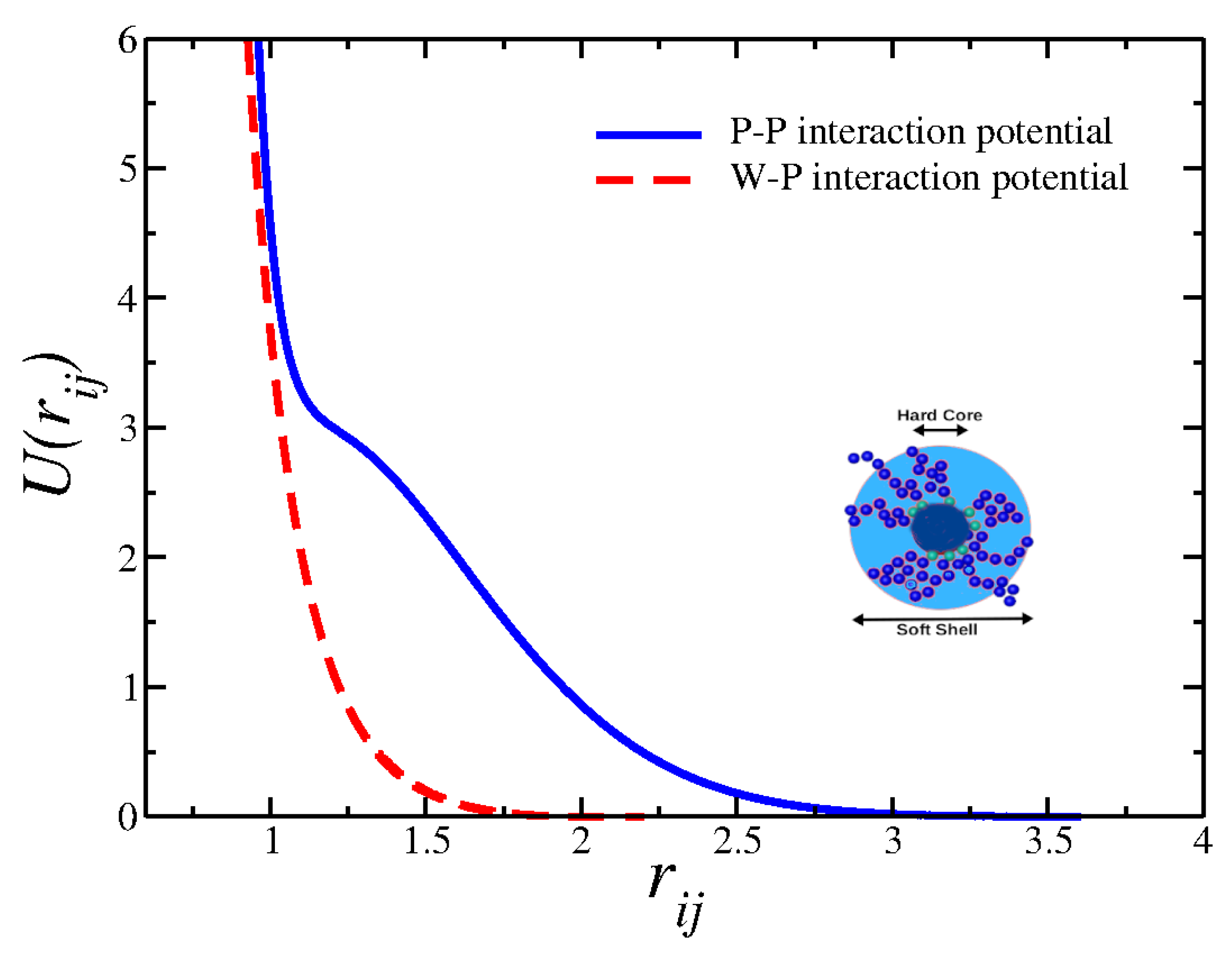
2. The Model
3. Methods and Simulation Details
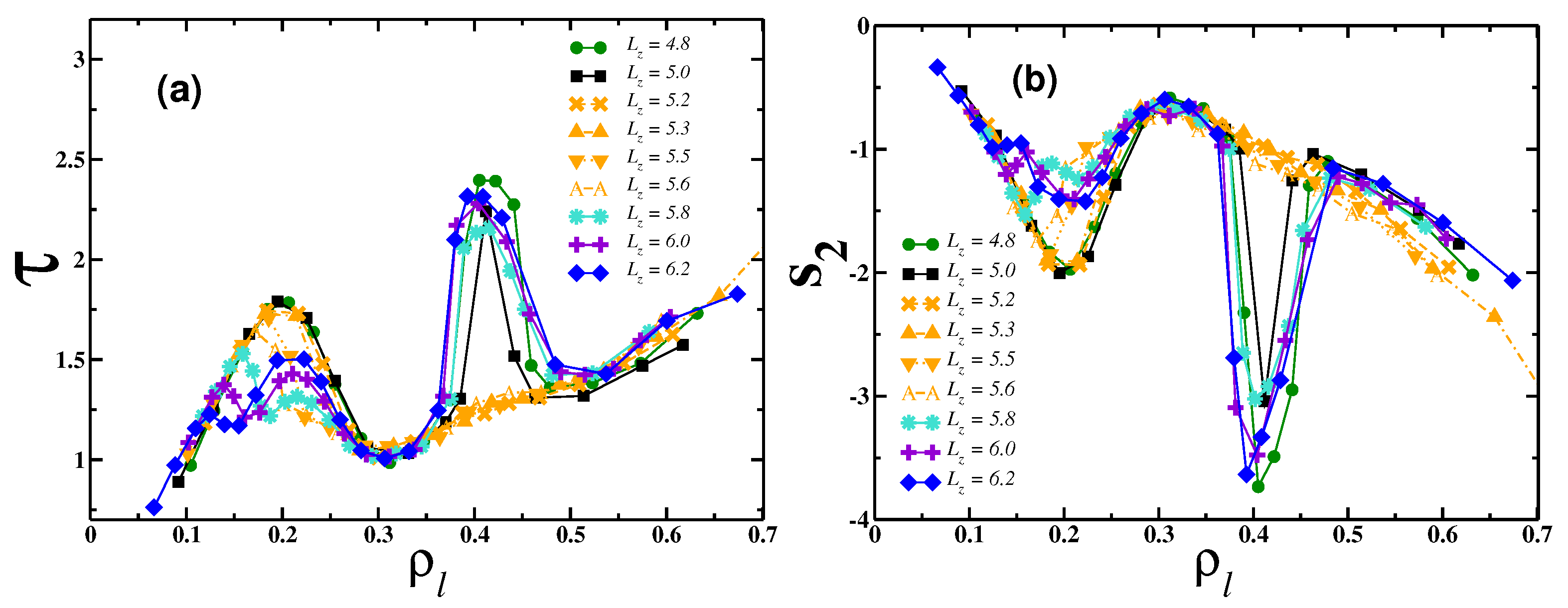
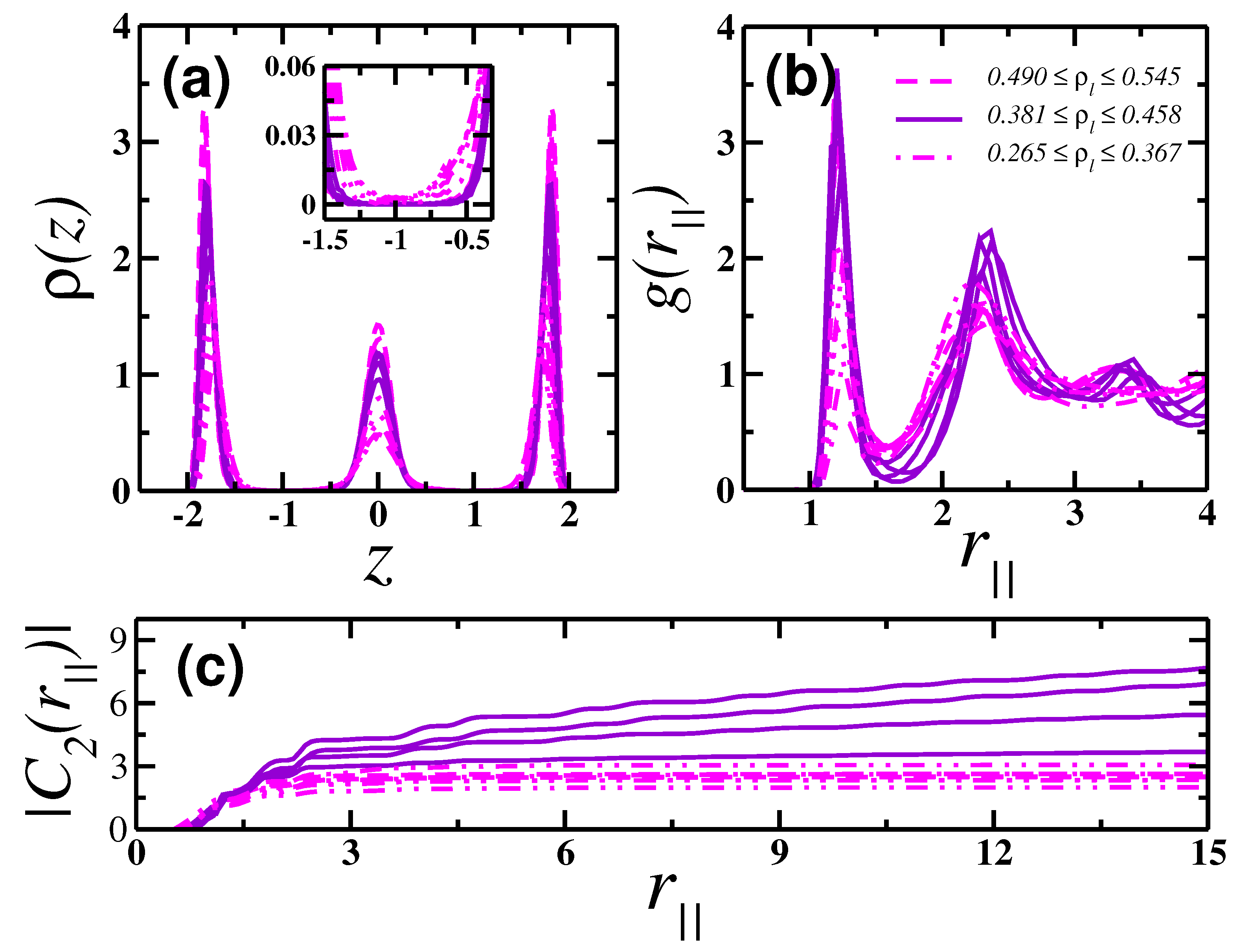
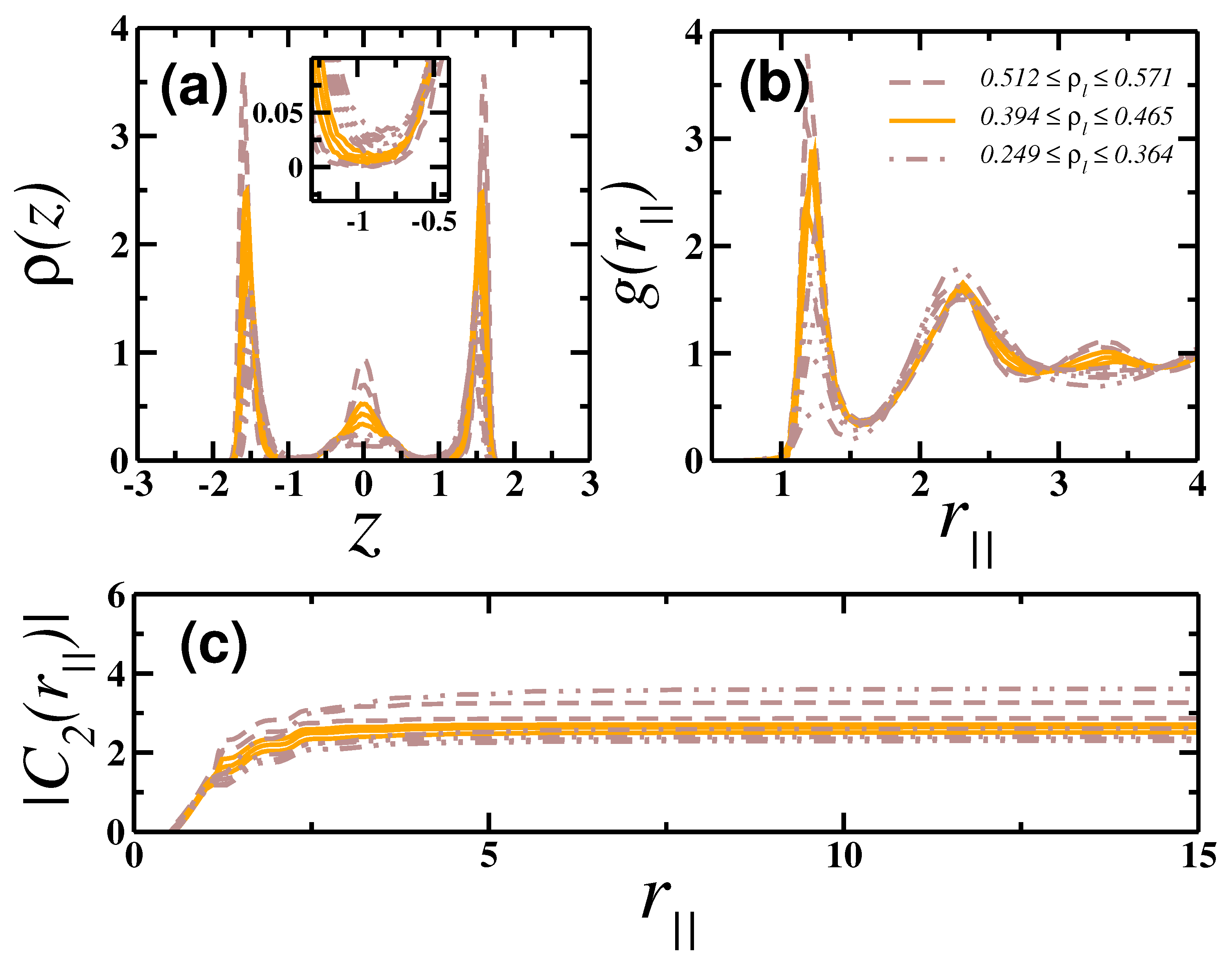
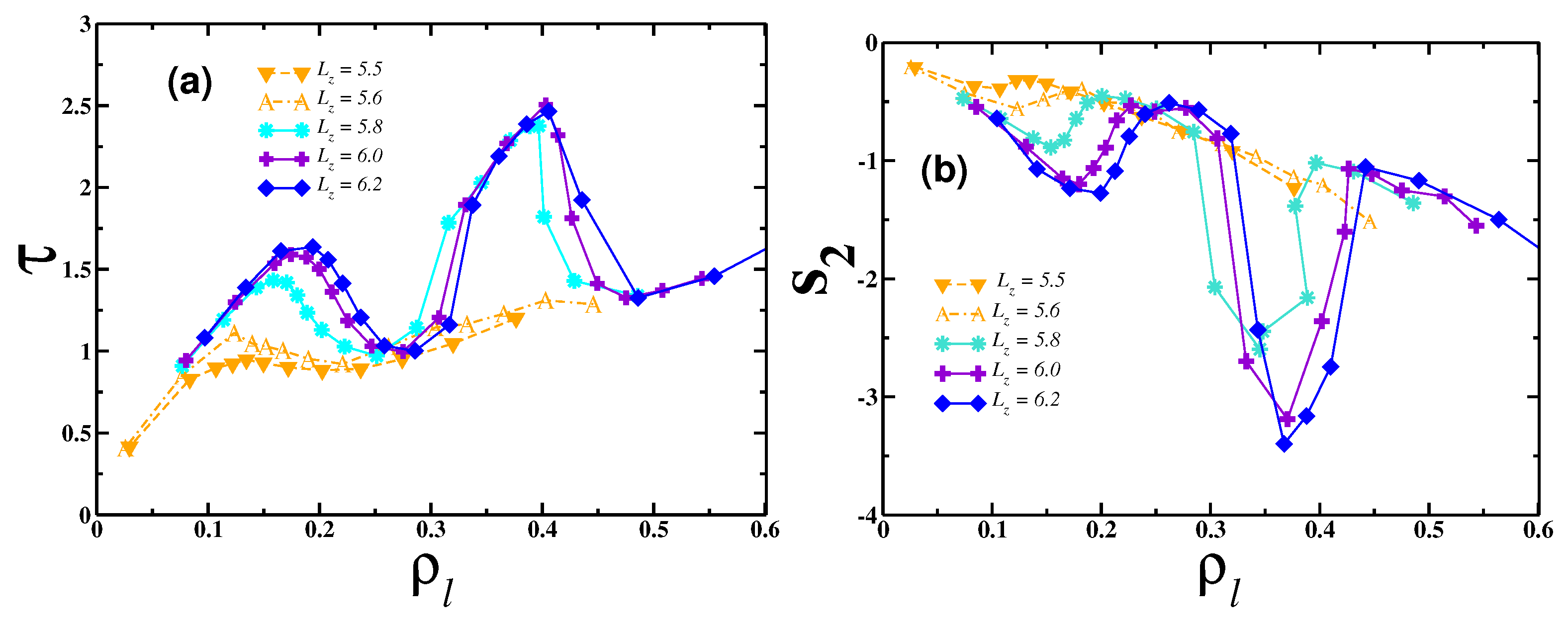
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vilaseca, P.; Franzese, G. Isotropic soft-core potentials with two characteristic length scales and anomalous behaviour. J. Non-Cryst. Solids 2011, 357, 419–426. [Google Scholar] [CrossRef]
- Ruiz-Franco, J.; Zaccarelli, E. On the Role of Competing Interactions in Charged Colloids with Short-Range Attraction. Annu. Rev. Condens. Matter Phys. 2021, 12, 51–70. [Google Scholar] [CrossRef]
- Shukla, A.; Mylonas, E.; Di Cola, E.; Finet, S.; Timmins, P.; Narayanan, T.; Svergun, D.I. Absence of equilibrium cluster phase in concentrated lysozyme solutions. Proc. Natl. Acad. Sci. USA 2008, 105, 5075–5080. [Google Scholar] [CrossRef]
- Yethiraj, A. Tunable colloids: Control of colloidal phase transitions with tunable interactions. Soft Matter 2007, 3, 1099. [Google Scholar] [CrossRef]
- Jagla, E.A. Phase behavior of a system of particles with core collapse. Phys. Rev. E 1998, 58, 1478. [Google Scholar] [CrossRef]
- Jagla, E.A. Minimum energy configurations of repelling particles in two dimensions. J. Chem. Phys. 1999, 110, 451–456. [Google Scholar] [CrossRef]
- Jagla, E.A. Core-softened potentials and the anomalous properties of water. J. Chem. Phys. 1999, 111, 8980–8986. [Google Scholar] [CrossRef]
- de Oliveira, A.B.; Netz, P.A.; Barbosa, M.C. Interplay between structure and density anomaly for an isotropic core-softened ramp-like potential. Physica A 2007, 386, 744–747. [Google Scholar] [CrossRef]
- Barbosa, M.A.; Salcedo, E.; Barbosa, M.C. Multiple liquid-liquid critical points and density anomaly in core-softened potentials. Phys. Rev. E 2013, 87, 032303. [Google Scholar] [CrossRef]
- Fomin, Y.D.; Tsiok, E.N.; Ryzhov, V.N. Inversion of sequence of diffusion and density anomalies in core-softened systems. J. Chem. Phys. 2011, 135, 234502. [Google Scholar] [CrossRef]
- Yan, Z.; Buldyrev, S.V.; Giovambattista, N.; Stanley, H.E. Structural Order for One-Scale and Two-Scale Potentials. Phys. Rev. Lett. 2005, 95, 130604. [Google Scholar] [CrossRef]
- Fomin, D.Y.; Gribova, N.V.; Ryzhov, V.N.; Stishov, S.M.; Frenkel, D. Quasibinary amorphous phase in a three-dimensional system of particles with repulsive-shoulder interactions. J. Chem. Phys. 2008, 129, 064512. [Google Scholar] [CrossRef]
- Lascaris, E.; Malescio, G.; Buldyrev, S.V.; Stanley, H.E. Cluster formation, water-like anomalies, and re-entrant melting for a family of bounded repulsive interaction potentials. Phys. Rev. E 2010, 81, 031201. [Google Scholar] [CrossRef] [PubMed]
- Buldyrev, S.V.; Malescio, G.; Angell, C.A.; Giovambattista, N.; Prestipino, S.; Saija, F.; Stanley, H.E.; Xu, L. Unusual phase behavior of one-component systems with two-scale isotropic interactions. J. Phys. Condens. Matter 2009, 21, 504106. [Google Scholar] [CrossRef]
- Saija, F.; Prestipino, S.; Malescio, G. Anomalous phase behavior of a soft-repulsive potential with a strictly monotonic force. Phys. Rev. E 2009, 80, 031502. [Google Scholar] [CrossRef]
- Malescio, G.; Saija, F. A Criterion for Anomalous Melting in Systems with Isotropic Interactions. J. Phys. Chem. B 2011, 115, 14091–14098. [Google Scholar] [CrossRef]
- Prestipino, S.; Saija, F.; Malescio, G. Anomalous phase behavior in a model fluid with only one type of local structure. J. Chem. Phys. 2010, 133, 144504. [Google Scholar] [CrossRef]
- Prestipino, S.; Saija, F.; Giaquinta, P.V. Hexatic phase and water-like anomalies in a two-dimensional fluid of particles with a weakly softened core. J. Chem. Phys. 2012, 137, 104503. [Google Scholar] [CrossRef] [PubMed]
- Coslovich, D.; Ikeda, A. Cluster and reentrant anomalies of nearly Gaussian core particles. Soft Matter 2013, 9, 6786–6795. [Google Scholar] [CrossRef]
- Quesada-Perez, M.; Moncho-Jorda, A.; Martinez-Lopez, F.; Hidalgo-Álvarez, R. Probing interaction forces in colloidal monolayers: Inversion of structural data. J. Chem. Phys. 2001, 115, 10897–10902. [Google Scholar] [CrossRef]
- Contreras-Aburto, C.; Méndez-Alcaraz, J.M.; Castañeda-Priego, R. Structure and effective interactions in parallel monolayers of charged spherical colloids. J. Chem. Phys. 2010, 132, 174111. [Google Scholar] [CrossRef] [PubMed]
- Haddadi, S.; Skepö, M.; Jannasch, P.; Manner, S.; Forsman, J. Building polymer-like clusters from colloidal particles with isotropic interactions, in aqueous solution. J. Colloid Interface Sci. 2020, 581, 669–681. [Google Scholar] [CrossRef] [PubMed]
- Grillo, F.; Fernandez-Rodriguez, M.A.; Antonopoulou, M.N.; Gerber, D.; Isa, L. Self-templating assembly of soft microparticles into complex tessellations. Nature 2020, 582, 219–224. [Google Scholar] [CrossRef] [PubMed]
- Ranganathan, V.T.; Bazmi, S.; Wallin, S.; Liu, Y.; Yethiraj, A. Is Ficoll a Colloid or Polymer? A Multitechnique Study of a Prototypical Excluded-Volume Macromolecular Crowder. Macromolecules 2022, 55, 9103–9112. [Google Scholar] [CrossRef]
- Marques, M.S.; Nogueira, T.P.O.; Dillenburg, R.F.; Barbosa, M.C.; Bordin, J.R. Waterlike anomalies in hard core–soft shell nanoparticles using an effective potential approach: Pinned vs adsorbed polymers. J. Appl. Phys. 2020, 127, 054701. [Google Scholar] [CrossRef]
- Lafitte, T.; Kumar, S.K.; Panagiotoulos, A.Z. Self-assembly of polymer-grafted nanoparticles in thin films. Soft Matter 2014, 10, 786–794. [Google Scholar] [CrossRef]
- Bos, I.; van der Scheer, P.; Ellenbroek, W.G.; Sprakel, J. Two-dimensional crystals of star polymers: A tale of tails. Soft Matter 2019, 15, 615–622. [Google Scholar] [CrossRef]
- Angell, C.A. Two phases? Nat. Mater. 2014, 13, 673–675. [Google Scholar] [CrossRef]
- Gallo, P.; Amann-Winkel, K.; Angell, C.A.; Anisimov, M.A.; Caupin, F.; Chakravarty, C.; Lascaris, E.; Loerting, T.; Panagiotopoulos, A.Z.; Russo, J.; et al. Water: A Tale of Two Liquids. Chem. Rev. 2016, 116, 7463–7500. [Google Scholar] [CrossRef]
- Gallo, P.; Bachler, J.; Bove, L.E.; Böhmer, R.; Camisasca, G.; Coronas, L.E.; Corti, H.R.; de Almeida Ribeiro, I.; de Koning, M.; Franzese, G.; et al. Advances in the study of supercooled water. Eur. Phys. J. E 2021, 44, 143. [Google Scholar] [CrossRef]
- Chaplin, M. Anomalous Properties of Water. 2023. Available online: http://www.lsbu.ac.uk/water/anmlies.html (accessed on 16 February 2023).
- Kellu, G.S. Density, thermal expansivity, and compressibility of liquid water from 0.deg. to 150.deg. Correlations and tables for atmospheric pressure and saturation reviewed and expressed on 1968 temperature scale. J. Chem. Eng. Data 1975, 20, 97–105. [Google Scholar] [CrossRef]
- Errington, J.R.; Debenedetti, P.D. Relationship between structural order and the anomalies of liquid water. Nature 2001, 409, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Buldyrev, S.V.; Giovambattista, N.; Debenedetti, P.G.; Stanley, H.E. Family of tunable spherically symmetric potentials that span the range from hard spheres to water-like behavior. Phys. Rev. E 2006, 73, 051204. [Google Scholar] [CrossRef] [PubMed]
- Gibson, H.M.; Wilding, N.B. Metastable liquid-liquid coexistence and density anomalies in a core-softened fluid. Phys. Rev. E 2006, 73, 061507. [Google Scholar] [CrossRef]
- Vilaseca, P.; Franzese, G. Softness dependence of the anomalies for the continuous shouldered well potential. J. Chem. Phys. 2010, 133, 084507. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Giovambattista, N.; Buldyrev, S.V.; Debenedetti, P.G.; Stanley, H.E. Waterlike glass polyamorphism in a monoatomic isotropic Jagla model. J. Chem. Phys. 2011, 134, 064507. [Google Scholar] [CrossRef] [PubMed]
- Reisman, S.; Giovambattista, N. Glass and liquid phase diagram of a polyamorphic monatomic system. J. Chem. Phys. 2013, 138, 064509. [Google Scholar] [CrossRef] [PubMed]
- Das, G.; Gnan, N.; Sciortino, F.; Zaccarelli, E. Unveiling the complex glassy dynamics of square shoulder systems: Simulations and theory. J. Chem. Phys. 2013, 138, 134501. [Google Scholar] [CrossRef]
- Krott, L.B.; Bordin, J.R.; Barraz, N.M.; Barbosa, M.C. Effects of confinement on anomalies and phase transitions of core-softened fluids. J. Chem. Phys. 2015, 142, 134502. [Google Scholar] [CrossRef]
- Luo, J.; Xu, L.; Angell, C.A.; Stanley, H.E.; Buldyrev, S.V. Physics of the Jagla model as the liquid-liquid coexistence line slope varies. J. Chem. Phys. 2015, 142, 224501. [Google Scholar] [CrossRef]
- Bordin, J. Waterlike features, liquid-crystal phase and self-assembly in Janus dumbbells. Phys. A Stat. Mech. Appl. 2016, 459, 1–8. [Google Scholar] [CrossRef]
- Pinheiro, L.; Furlan, A.; Krott, L.; Diehl, A.; Barbosa, M. Critical points, phase transitions and water-like anomalies for an isotropic two length scale potential with increasing attractive well. Phys. A Stat. Mech. Appl. 2017, 468, 866–879. [Google Scholar] [CrossRef]
- de Haro, M.L.; Rodríguez-Rivas, A.; Yuste, S.B.; Santos, A. Structural properties of the Jagla fluid. Phys. Rev. E 2018, 98, 012138. [Google Scholar] [CrossRef] [PubMed]
- Higuchi, S.; Kato, D.; Awaji, D.; Kim, K. Connecting thermodynamic and dynamical anomalies of water-like liquid-liquid phase transition in the Fermi–Jagla model. J. Chem. Phys. 2018, 148, 094507. [Google Scholar] [CrossRef]
- Ryzhov, V.N.; Tareyeva, E.E.; Fomin, Y.D.; Tsiok, E.N. Complex phase diagrams of systems with isotropic potentials: Results of computer simulations. Physics-Uspekhi 2020, 63, 417. [Google Scholar] [CrossRef]
- Martín-Roca, J.; Martinez, R.; Martínez-Pedrero, F.; Ramírez, J.; Valeriani, C. Dynamical anomalies and structural features of active Brownian particles characterized by two repulsive length scales. J. Chem. Phys. 2022, 156, 164502. [Google Scholar] [CrossRef]
- Bretonnet, J.L.; Bomont, J.M. Analytical treatment of the structure for systems interacting via core-softened potentials. Chem. Phys. 2022, 555, 111445. [Google Scholar] [CrossRef]
- Nogueira, T.; Bordin, J.R. Patterns in 2D core-softened systems: From sphere to dumbbell colloids. Phys. A Stat. Mech. Appl. 2022, 605, 128048. [Google Scholar] [CrossRef]
- Bordin, J.R.; Krott, L.B.; Barbosa, M.C. Self-Assembly and Water-like Anomalies in Janus Nanoparticles. Langmuir 2015, 31, 8577–8582. [Google Scholar] [CrossRef]
- Bordin, J.R.; Krott, L.B. How Competitive Interactions Affect the Self-Assembly of Confined Janus Dumbbells. J. Phys. Chem. B 2017, 121, 4308–4317. [Google Scholar] [CrossRef]
- Jiménez-Millán, S.; García-Alcántara, C.; Ramírez-Hernández, A.; Sambriski, E.; Hernández, S. Self-Aassembly of core-corona colloids under cylindrical confinement: A Monte Carlo study. J. Mol. Liq. 2021, 335, 116219. [Google Scholar] [CrossRef]
- Pérez-Figueroa, S.E.; Gallegos-Lozano, A.; Mendoza, C.I. Packing core–corona particles on a spherical surface. Soft Matter 2022, 18, 6812–6824. [Google Scholar] [CrossRef]
- Isa, L.; Buttinoni, I.; Fernandez-Rodriguez, M.A.; Vasudevan, S.A. Two-dimensional assemblies of soft repulsive colloids confined at fluid interfaces(a). Europhys. Lett. 2017, 119, 26001. [Google Scholar] [CrossRef]
- Wang, J.; Mbah, C.F.; Przybilla, T.; Englisch, S.; Spiecker, E.; Engel, M.; Vogel, N. Free Energy Landscape of Colloidal Clusters in Spherical Confinement. ACS Nano 2019, 13, 9005–9015. [Google Scholar] [CrossRef] [PubMed]
- Osterman, N.; Babič, D.; Poberaj, I.; Dobnikar, J.; Ziherl, P. Observation of Condensed Phases of Quasiplanar Core-Softened Colloids. Phys. Rev. Lett. 2007, 99, 248301. [Google Scholar] [CrossRef]
- Villada-Balbuena, A.; Jung, G.; Zuccolotto-Bernez, A.B.; Franosch, T.; Egelhaaf, S.U. Layering and packing in confined colloidal suspensions. Soft Matter 2022, 18, 4699–4714. [Google Scholar] [CrossRef]
- Kang, C.; Honciuc, A. Self-Assembly of Janus Nanoparticles into Transformable Suprastructures. J. Phys. Chem. Lett. 2018, 9, 1415–1421. [Google Scholar] [CrossRef]
- Wu, D.; Honciuc, A. Design of Janus Nanoparticles with pH-Triggered Switchable Amphiphilicity for Interfacial Applications. ACS Appl. Nano Mater. 2018, 1, 471–482. [Google Scholar] [CrossRef]
- Rafael Bordin, J. Distinct self-assembly aggregation patters of nanorods with decorated ends: A simple model study. Fluid Phase Equilibria 2019, 499, 112251. [Google Scholar] [CrossRef]
- Bordin, J.R. Distinct aggregation patterns and fluid porous phase in a 2D model for colloids with competitive interactions. Phys. A Stat. Mech. Appl. 2018, 495, 215–224. [Google Scholar] [CrossRef]
- Cardoso, D.S.; Hernandes, V.F.; Nogueira, T.; Bordin, J.R. Structural behavior of a two length scale core-softened fluid in two dimensions. Phys. A Stat. Mech. Appl. 2021, 566, 125628. [Google Scholar] [CrossRef]
- Fonseca, E.R.; Mendoza, C.I. Self-assembly of core-corona particles confined in a circular box. J. Phys. Condens. Matter 2019, 32, 015101. [Google Scholar] [CrossRef]
- Marques, M.S.; Bordin, J.R. Interplay between adsorption, aggregation and diffusion in confined core-softened colloids. JCIS Open 2021, 4, 100029. [Google Scholar] [CrossRef]
- Pekalski, J.; Bildanau, E.; Ciach, A. Self-assembly of spiral patterns in confined systems with competing interactions. Soft Matter 2019, 15, 7715–7721. [Google Scholar] [CrossRef]
- Serna, H.; Noya, E.G.; Góźdź, W.T. Confinement of Colloids with Competing Interactions in Ordered Porous Materials. J. Phys. Chem. B 2020, 124, 10567–10577. [Google Scholar] [CrossRef] [PubMed]
- Pant, S.; Ghorai, P.K. Structural anomaly of core-softened fluid confined in single walled carbon nanotube: A molecular dynamics simulation investigation. Mol. Phys. 2016, 114, 1771–1777. [Google Scholar] [CrossRef]
- Bordin, J.R.; Krott, L.B. Confinement effects on the properties of Janus dimers. Phys. Chem. Chem. Phys. 2016, 18, 28740–28746. [Google Scholar] [CrossRef]
- Dobnikar, J.; Fornleitner, J.; Kahl, G. Ground states of model core-softened colloids. J. Phys. Condens. Matter 2008, 20, 494220. [Google Scholar] [CrossRef]
- Bildanau, E.; Pękalski, J.; Vikhrenko, V.; Ciach, A. Adsorption anomalies in a two-dimensional model of cluster-forming systems. Phys. Rev. E 2020, 101, 012801. [Google Scholar] [CrossRef]
- Tsiok, E.; Fomin, Y.D.; Ryzhov, V. The effect of confinement on the solid–liquid transition in a core-softened potential system. Phys. A Stat. Mech. Appl. 2020, 550, 124521. [Google Scholar] [CrossRef]
- Fomin, Y.D.; Ryzhov, V.N.; Tsiok, E.N. Interplay between freezing and density anomaly in a confined core-softened fluid. Mol. Phys. 2020, 118, e1718792. [Google Scholar] [CrossRef]
- Fomin, Y.D. Between two and three dimensions: Crystal structures in a slit pore. J. Colloid Interface Sci. 2020, 580, 135–145. [Google Scholar] [CrossRef]
- Barros de Oliveira, A.; Netz, P.A.; Colla, T.; Barbosa, M.C. Thermodynamic and dynamic anomalies for a three-dimensional isotropic core-softened potential. J. Chem. Phys. 2006, 124, 084505. [Google Scholar] [CrossRef]
- de Oliveira, A.B.; Netz, P.A.; Colla, T.; Barbosa, M.C. Structural anomalies for a three dimensional isotropic core-softened potential. J. Chem. Phys. 2006, 125, 124503. [Google Scholar] [CrossRef] [PubMed]
- Bordin, J.R.; de Oliveira, A.B.; Diehl, A.; Barbosa, M.C. Diffusion enhancement in core-softened fluid confined in nanotubes. J. Chem. Phys. 2012, 137, 084504. [Google Scholar] [CrossRef]
- Krott, L.B.; Barbosa, M.C. Anomalies in a water-like model confined between plates. J. Chem. Phys. 2013, 138, 084505. [Google Scholar] [CrossRef]
- Bordin, J.R.; Diehl, A.; Barbosa, M.C. Relation Between Flow Enhancement Factor and Structure for Core-Softened Fluids Inside Nanotubes. J. Phys. Chem. B 2013, 117, 7047–7056. [Google Scholar] [CrossRef] [PubMed]
- Krott, L.B.; Barbosa, M.C. Model of water-like fluid under confinement for hydrophobic and hydrophilic particle-plate interaction potentials. Phys. Rev. E 2014, 89, 012110. [Google Scholar] [CrossRef] [PubMed]
- Krott, L.B.; Bordin, J.R. Distinct dynamical and structural properties of a core-softened fluid when confined between fluctuating and fixed walls. J. Chem. Phys. 2013, 139, 154502. [Google Scholar] [CrossRef]
- Bordin, J.R.; Krott, L.B.; Barbosa, M.C. High pressure induced phase transition and superdiffusion in anomalous fluid confined in flexible nanopores. J. Chem. Phys. 2014, 141, 144502. [Google Scholar] [CrossRef]
- Bordin, J.R.; Krott, L.B.; Barbosa, M.C. Surface Phase Transition in Anomalous Fluid in Nanoconfinement. J. Phys. Chem. C 2014, 118, 9497–9506. [Google Scholar] [CrossRef]
- Krott, L.B.; Bordin, J.R.; Barbosa, M.C. New Structural Anomaly Induced by Nanoconfinement. J. Phys. Chem. B 2015, 119, 291–300. [Google Scholar] [CrossRef] [PubMed]
- Bordin, J.R.; Barbosa, M.C. Waterlike anomalies in a two-dimensional core-softened potential. Phys. Rev. E 2018, 97, 022604. [Google Scholar] [CrossRef] [PubMed]
- Dudalov, D.E.; Fomin, Y.D.; Tsiok, E.N.; Ryzhov, V.N. How dimensionality changes the anomalous behavior and melting scenario of a core-softened potential system? Soft Matter 2014, 10, 4966–4976. [Google Scholar] [CrossRef]
- Bordin, J.R.; Krott, L.B. Solid-amorphous transition is related to the water-like anomalies in a fluid without liquid–liquid phase transition. J. Chem. Phys. 2023, 158, 134501. [Google Scholar] [CrossRef] [PubMed]
- Allen, P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Dzugutov, M. Universal scaling law for atomic diffusion in condensed matter. Nature 1996, 381, 137–139. [Google Scholar] [CrossRef]
- Dyre, J.C. Perspective: Excess-entropy scaling. J. Chem. Phys. 2018, 149, 210901. [Google Scholar] [CrossRef]
- Bell, I.; Dyre, J.; Ingebrigtsen, T. Excess-entropy scaling in supercooled binary mixtures. Nat. Commun. 2020, 2020, 015012. [Google Scholar] [CrossRef]
- Galliero, G.; Boned, C.; Fernández, J. Scaling of the viscosity of the Lennard-Jones chain fluid model, argon, and some normal alkanes. J. Chem. Phys. 2011, 134, 064505. [Google Scholar] [CrossRef]
- Raveché, H.J. Entropy and Molecular Correlation Functions in Open Systems. I. Derivation. J. Chem. Phys. 1971, 55, 2242–2250. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. Direct entropy calculation from computer simulation of liquids. Phys. Rev. A 1989, 40, 3817–3822. [Google Scholar] [CrossRef] [PubMed]
- Klumov, B.A.; Khrapak, S.A. Two-body entropy of two-dimensional fluids. Results Phys. 2020, 17, 103020. [Google Scholar] [CrossRef]
- Shell, M.S.; Debenedetti, P.G.; Panagiotopoulos, A.Z. Molecular structural order and anomalies in liquid silica. Phys. Rev. E 2002, 66, 011202. [Google Scholar] [CrossRef]
- Errington, J.E.; Debenedetti, P.G.; Torquato, S. Quantification of Order in the Lennard-Jones System. J. Chem. Phys. 2003, 118, 2256–2263. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krott, L.B.; Bordin, J.R. How Dimensionality Affects the Structural Anomaly in a Core-Softened Colloid. Colloids Interfaces 2023, 7, 33. https://doi.org/10.3390/colloids7020033
Krott LB, Bordin JR. How Dimensionality Affects the Structural Anomaly in a Core-Softened Colloid. Colloids and Interfaces. 2023; 7(2):33. https://doi.org/10.3390/colloids7020033
Chicago/Turabian StyleKrott, Leandro B., and José Rafael Bordin. 2023. "How Dimensionality Affects the Structural Anomaly in a Core-Softened Colloid" Colloids and Interfaces 7, no. 2: 33. https://doi.org/10.3390/colloids7020033
APA StyleKrott, L. B., & Bordin, J. R. (2023). How Dimensionality Affects the Structural Anomaly in a Core-Softened Colloid. Colloids and Interfaces, 7(2), 33. https://doi.org/10.3390/colloids7020033





