Abstract
The population balance is an indispensable tool for studying colloidal, aerosol, and, in general, particulate systems. The need to incorporate spatial variation (imposed by flow) to it invokes the reduction of its complexity and degrees of freedom. It has been shown in the past that the method of moments and, in particular, the log-normal approximation can serve this purpose for certain phenomena and mechanisms. However, it is not adequate to treat gravitational deposition. In the present work, the ability of the particular method to treat diffusional and convective diffusional depositions relevant to colloid systems is studied in detail.
1. Introduction
The population balance equation with terms of coagulation, particle growth, and particle removal is the main tool for the simulation of a variety of processes. It can be used for the study of colloidal systems, aerosol reactors, atmospheric aerosols, and for the study of the precipitation of solids from solutions. Although there are accurate numerical methods for the solution of the population balance [1], the need for space–time simulations involving complex flows [2] renders them computationally intractable. However, the well-known method of moments is ideally suited to this problem because of its low computational requirements. Furthermore, McGraw et al. [3] showed that the method of moments is capable of describing the integral properties of the distribution even if the initially assumed distribution is quite different from the real one. Barret and Jheeta [4], as well as Mc Graw [5] developed two different hierarchies of moment methods in which the accuracy increases with the number of unknowns. Over the last decade, several novel methods of moments appeared in the literature [6,7]. The full exploitation of low-order moment methods is necessary because the key point in complex applications is not the very high accuracy but the computational requirements. In this context, Kielkiewicz [8], as well as Barret and Jheeta [4] have shown that the simple log-normal method of moments has a poor performance for the gravitational removal of particles. In the present work, it will be shown that this simple moment method gives very good results for the more important case of pure or convective diffusional removal. In conjunction with the well-known ability of the log-normal distribution to simulate Brownian coagulation and growth processes, it is concluded that this method of moments is capable of simulating systems that obey the above mentioned population balance equation.
2. Theoretical Analysis
In order to facilitate the presentation, it is convenient to use dimensionless variables. Thus, assuming that xo is the mean volume of the initial particle size distribution and N is the initial number concentration, the following non-dimensionalization is made:
where R(x) is the removal rate, x is the particle volume, τ is the time, and f(x,τ) is the number-density particle volume distribution. The evolution equation for the particle size distribution has the following dimensionless form.
with the initial condition .
The solution of the above equation is . Assuming a typical removal rate of power type , the evolution of the first (dimensionless) moments of the distribution is obtained from the following relations.
where, by construction, Mo(0) = M1(0) = 1. The dispersity of the particle size distribution can be found from the following relation.
According to the method of moments with log-normal distribution, it is assumed that the particle size distribution retains a log-normal form with its main parameters evolving in time. After some algebra, the method results in the following system of ordinary differential equations for the first two moments and dispersity of the distribution [9]:
The initial distribution is assumed to be log-normal with dispersity so. In summary, the exact solution for the moments can be found from integral (3), whereas the approximations are obtained from system (4). Integration is performed by an explicit Runge–Kutta integrator [10]. The prespecified relative accuracy is set equal to 10−5. It is noted here that the application of the log-normal method is not restricted to removal rates, for which a closure of the moment equation can be achieved. In the case of a general complex form of the removal rate, system (4) contains integrals over the log-normal profile. These integrals can be readily integrated numerically through the Gauss–Hermite quadrature. The log-normal method is one with three degrees of freedom. In certain complex applications, moment methods of even lower orders are employed (e.g., monodisperse with two degrees of freedom) [11,12].
3. Results and Discussion
A very interesting solution of the removal problem arises when m = 0, i.e., the removal rate is independent of the particle size. In this case, the moments are given simply as Mi = Mi(0)e−t and the size distribution is self-preserving, i.e., it does not change with time after it has been transformed using the self-similarity variables, which are extensively used in coagulation literature (e.g., see [13]). In this particular case, the method of moments leads to the exact result, which can be confirmed by setting m = 0 in Equation (4). Another limiting case is that of zero dispersity (monodisperse initial distribution). The distribution remains monodisperse at all times and Mi = e−t. This behavior is also exactly predicted by the method of moments (Equation (4)).
In generalizing the above observations, it is possible to say that in assuming a m-σo plane (or rather a hemiplane because sο is always positive), the method of moments becomes more accurate as we move towards the axis m = 0 and it becomes exact on this axis. This statement is compatible with an observation of Williams [14] who compared a moments method (two parameter Gamma distribution) with the analytical solution of the growth-removal population balance. According to this author, considering all the other conditions identical, the accuracy of the moments method is greater for the removal exponent m = −1/3 than for m = 2/3. Before proceeding to more quantitative results, the range of exponent m must be considered, for which the accuracy of the method of moments must be studied. Assuming the general case of fractal particles with fractal dimension df and using the well-known relation for the diffusivity D∝, one obtains that for pure diffusional deposition m = −1/df. In the more important case of convective diffusional deposition from turbulent flows, the exponent m takes the value −2/(3df) [9]. This type of removal is relevant to the simulation of aerosol reactors, of precipitation of sparingly soluble salt processes, and of colloidal particle deposition, while gravitational deposition is relevant to the simulation of atmospheric aerosols or industrial settling processes. A typical range of df is 2 to 3; thus, the range of m worth studying is 0 to −1/2, with special interest in the range of −2/9 to −1/3, which represents the removal by convection/diffusion.
In Figure 1, the relative error of the moments method for the total particle mass is shown at the time when the remaining total particle mass is 10% of its initial value. The procedure to construct this graph is the following: First, Equation (3) with i = 1 and M1 = 0.1 is solved with the Newton–Raphson method to find the required time τ and then system (4) is integrated over this time to find the approximate value of M1. The relative error is given as (M1/0.1 − 1). This error is shown versus exponent m for three values of sο, as depicted in Figure 1. As it is expected, the greater the sο, the larger the error. A characteristic of the negative exponent m is that, consistently, Mo < M1, whereas for the gravitational removal (m > 0), it is always M1 < Mo. The computation showed that the corresponding Figure 1 error for the Mo is much smaller than that of M1. The assumed extent of the process is rather large (90% of the total mass deposited) and covers all the possible applications of the method. For larger extents, the total mass of the particles remaining in the flow is too small to require a highly accurate computation. In other words, if the relative error in Figure 1 was transformed to an absolute error (fraction of the initial total mass), it would be 10-times smaller.
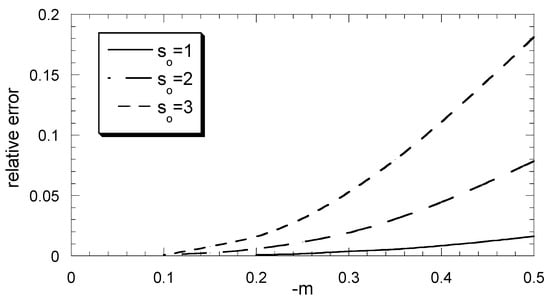
Figure 1.
Relative error of the method of moment in computation of M1 (in time such that the exact value of M1 is 0.1) versus exponent m for three values of the initial dispersity so.
The evolution of the dispersity of the distribution is shown in Figure 2 for m = −1/3 and for several initial dispersities sο. The exact results are compared to those obtained with the method of moments. The time range appeared in Figure 2 corresponds more than 95% of the initial mass finally removed. According to this figure, only for large initial dispersities and large times there is a considerable difference between the method of moments and the exact results. The corresponding results for m = −2/9 are of the same general form as in Figure 2 but with smaller discrepancies between the two methods.
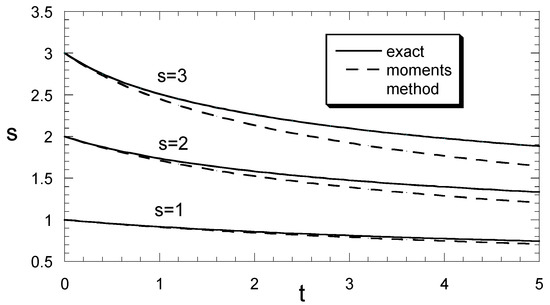
Figure 2.
Exact and computed results with the method of moments dispersities versus dimensionless time for three values of the initial dispersity so.
According to the literature, Brownian coagulation generates particle-size distributions with rather small dispersities (s = 0.693 in the continuum regime irrespective of df [15]). Additionally, the growth process has the tendency to further sharpen the distribution. Other coagulation mechanisms, such as turbulent coagulation, are capable of producing distributions with large dispersities but it is known that the log-normal version of the method of moments is inadequate for this coagulation mechanism [16]. For large dispersities where the accuracy of the log-normal distribution method for particle removal deteriorates, the same occurs for particle growth as well [17]. However, as discussed above, Brownian coagulation and growth retains the dispersity minimally, thus the log-normal method can be accurately used for the above phenomena in combination with the diffusional or convective-diffusional removal of particles. There are many other further methods of moments apart from the log-normal method but we believe that it is a very attractive choice in terms of simplicity, accuracy, stability, and distribution reconstruction ability, at least for particular mechanisms, such as those examined here.
4. Conclusions
This work shows that in cases where the log-normal distribution approximation is adequate for the simulation of other phenomena (i.e., coagulation and growth), it is also adequate for the simulation of diffusional (convective or molecular) deposition. This includes the majority of practical cases, especially in the precipitation of sparingly soluble salts where instantaneous nucleation is relevant and the final colloidal particle size is too small for the turbulent coagulation to prevail. An application of the moments method to a practical problem that includes particle deposition can be found in [18]. Due to well-known difficulties in the numerical solution of the population balance, the moments method solution to the abovementioned cases is usually comparably accurate to some of the more computationally demanding methods that are based on particle-size discretization [19,20].
Author Contributions
Conceptualization, M.K. and T.D.K.; methodology, M.K.; validation, M.K.; writing—original draft preparation, M.K. and T.D.K.; writing—review and editing, M.K. and T.D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research study received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization-III. Nucleation, growth and aggregation of particles. Chem. Eng. Sci. 1997, 52, 4659–4679. [Google Scholar] [CrossRef]
- Jurcik, B.J.; Brock, J.R. Numerical simulation of particle formation and growth in rapidly expanding axisymmetric flows. J. Phys. Chem. 1993, 97, 323–331. [Google Scholar] [CrossRef]
- McGraw, R.; Nemesure, S.; Schwartz, S.E. Properties and evolution of aerosol with size distributions having identical moments. J. Aerosol Sci. 1998, 29, 761–772. [Google Scholar] [CrossRef]
- Barret, J.C.; Jheeta, J.S. Improving the accuracy of the moments method for solving the aerosol general dynamic equation. J. Aerosol Sci. 1996, 27, 1135–1142. [Google Scholar] [CrossRef]
- McGraw, R. Description of atmospheric aerosol dynamics by the quadrature method of moments. Aerosol Sci. Technol. 1997, 27, 255–265. [Google Scholar] [CrossRef]
- Yu, M.; Liu, Y.; Lin, J.; Seipenbusch, M. Generalized TEMOM scheme for solving the population balance equation. Aerosol Sci. Technol. 2015, 49, 1021–1036. [Google Scholar] [CrossRef] [Green Version]
- Falola, A.; Borissova, A.; Wang, X.Z. Extended method of moment for general population balance models including size dependent growth rate, aggregation and breakage kernels. Comp. Chem. Eng. 2013, 56, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Kielkiewicz, M. Accuracy of the moments method. Ann. Nucl. Energy 1994, 21, 189–193. [Google Scholar] [CrossRef]
- Williams, M.M.R.; Loyalka, S.K. Aerosol Science: Theory and Practice; Pergamon Press: New York, NY, USA, 1991. [Google Scholar]
- Press, W.; Flannery, B.; Teukolski, S.; Vetterling, W. Numerical Recipes; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Kostoglou, M.; Karabelas, A.J. On modeling incipient crystallization of sparingly soluble salts in frontal membrane filtration. J. Colloid Interface Sci. 2011, 362, 202–214. [Google Scholar] [CrossRef] [PubMed]
- Kostoglou, M.; Karapantsios, T.D. Population balance modeling of flotation pulp: The route from process frequency functions to spatially distributed models. Comp. Chem. Eng. 2021, 155, 107506. [Google Scholar] [CrossRef]
- Friedlander, S.K. Smoke, Dust and Haze; Wiley Interscience: New York, NY, USA, 1977. [Google Scholar]
- Williams, M.M.R. The time-dependent behavior of aerosols with growth and deposition I. Without coagulation. J. Colloid Interface Sci. 1983, 93, 252–263. [Google Scholar] [CrossRef]
- Jain, S.; Kodas, T.T. Asymptotic widths of size distributions resulting from collisional growth assuming log-normally distributed fractal aggregates. J. Aerosol Sci. 1998, 29, 259–261. [Google Scholar] [CrossRef]
- Williams, M.M.R. On the modified Gamma distribution for representing the size spectra of coagulating aerosol particles. J. Colloid Interface Sci. 1985, 103, 516–527. [Google Scholar] [CrossRef]
- Tsang, T.H.; Rao, A. Comparison of different numerical schemes for condensational growth of aerosols. Aerosol Sci. Technol. 1988, 9, 271–277. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karabelas, A.J. Comprehensive modeling of precipitation and fouling in turbulent pipe flow. Ind. Eng. Res. Chem. 1998, 37, 1536–1550. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karabelas, A.J. Evaluation of numerical methods for simulating an evolving particle size distribution in growth processes. Chem. Eng. Comm. 1995, 136, 177–199. [Google Scholar] [CrossRef]
- Kostoglou, M. Extended cell average technique for the solution of coagulation equation. J. Colloid Interface Sci. 2007, 306, 72–81. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).