Diffusiophoresis in Suspensions of Charged Soft Particles
Abstract
1. Introduction
2. Electrokinetic Equations
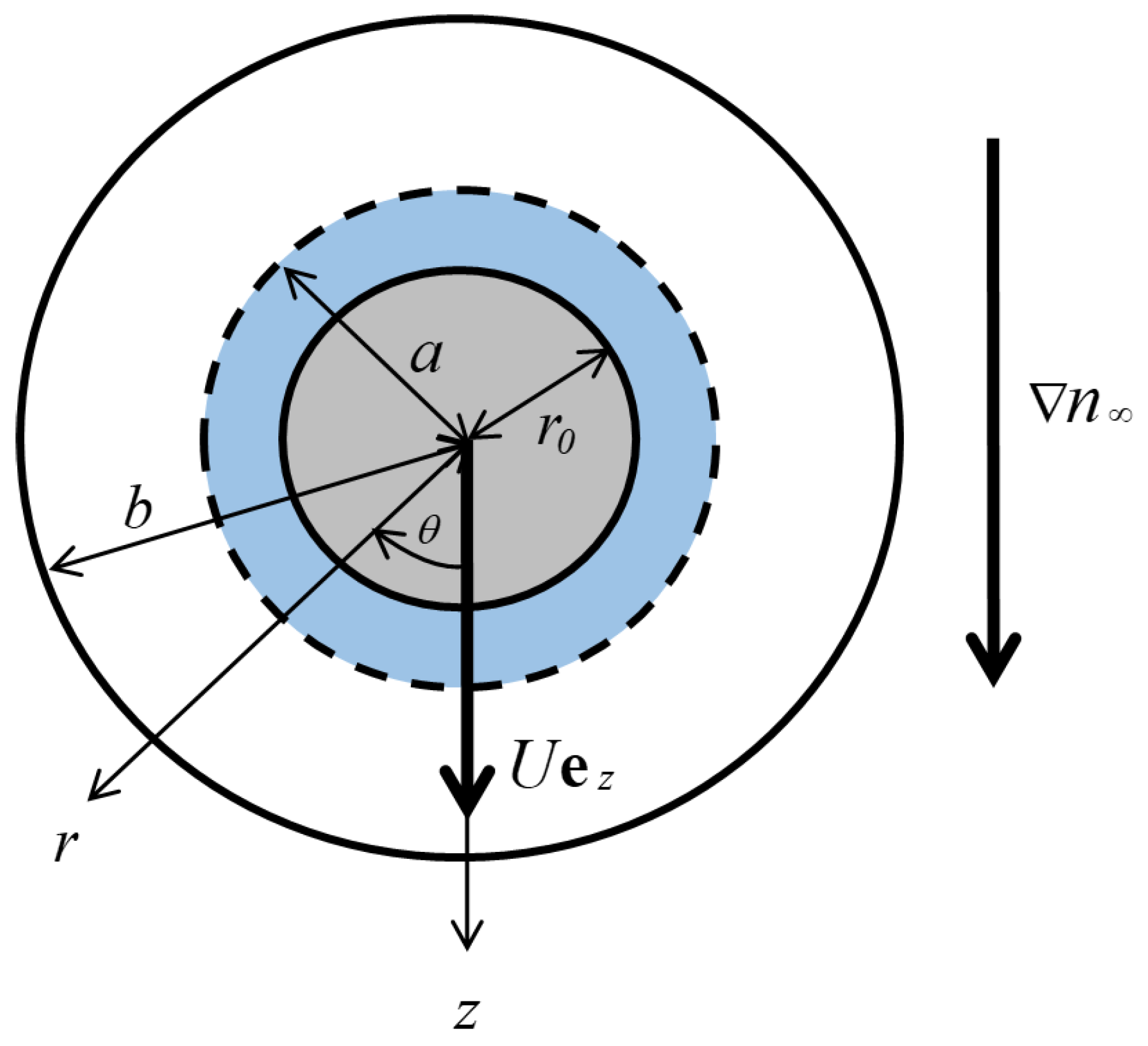
2.1. Governing Equations
2.2. Boundary Conditions
3. Solution for the Diffusiophoretic Velocity
3.1. Equilibrium Electric Potential
3.2. Solution to Electrokinetic Equations
3.3. Forces Exerted on the Particle
3.4. Velocity of the Particle
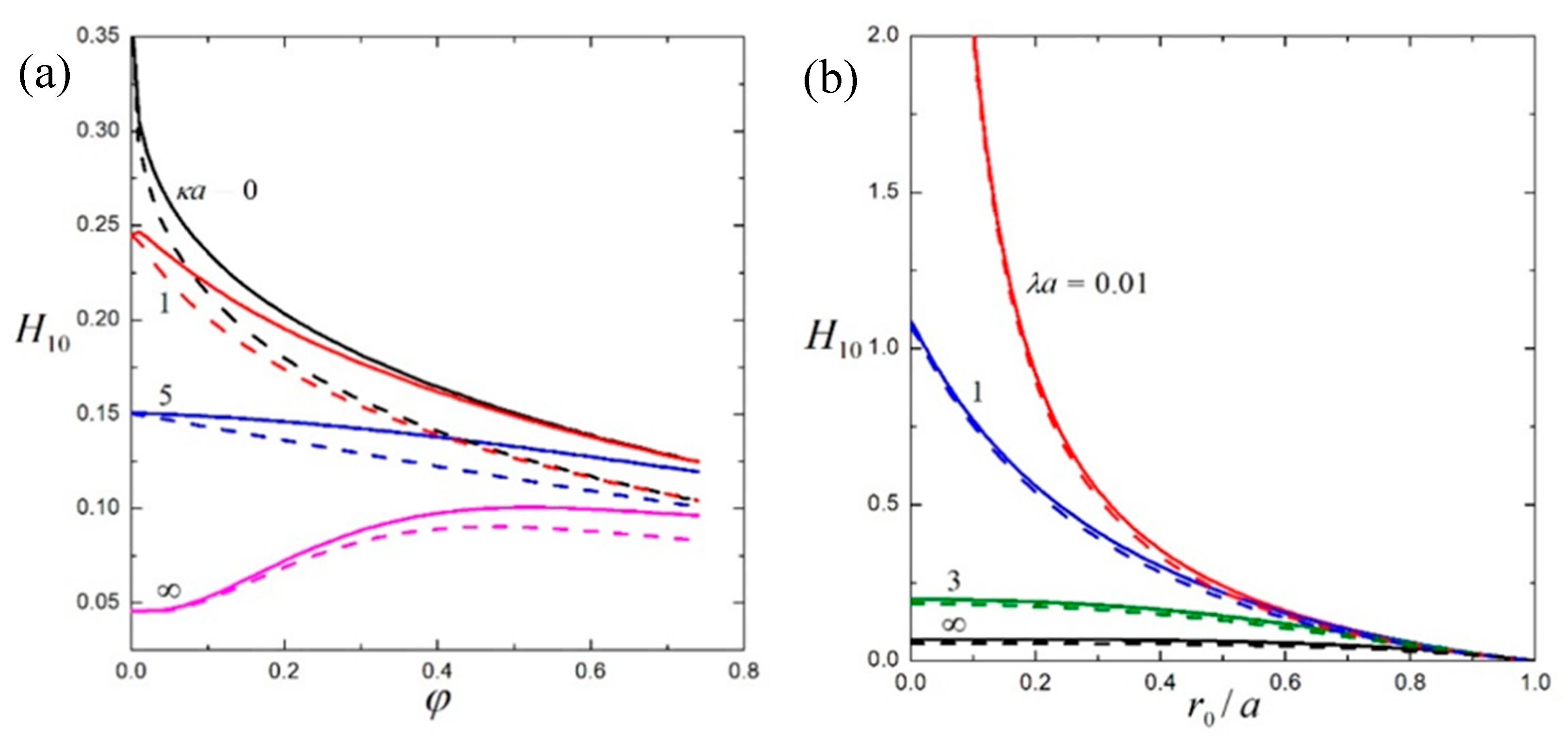
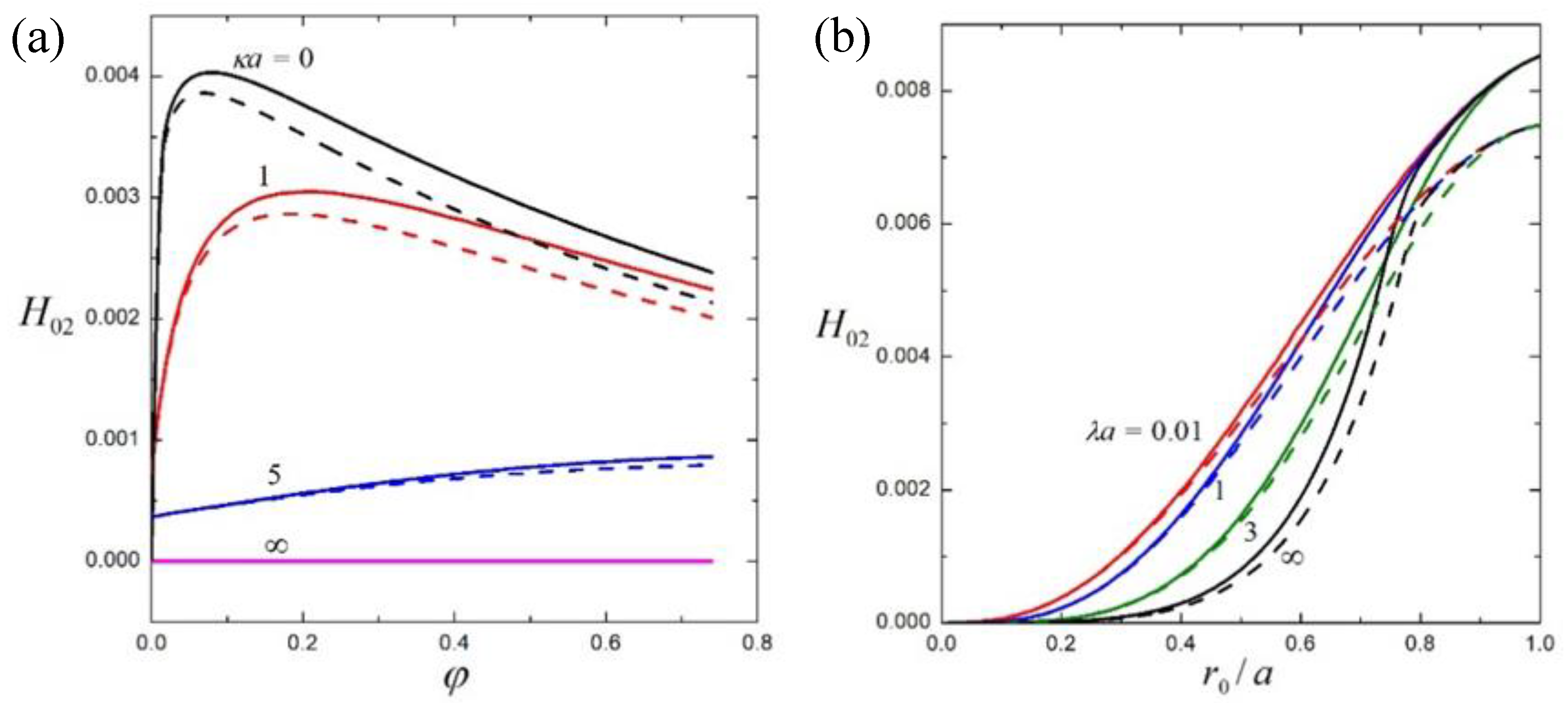
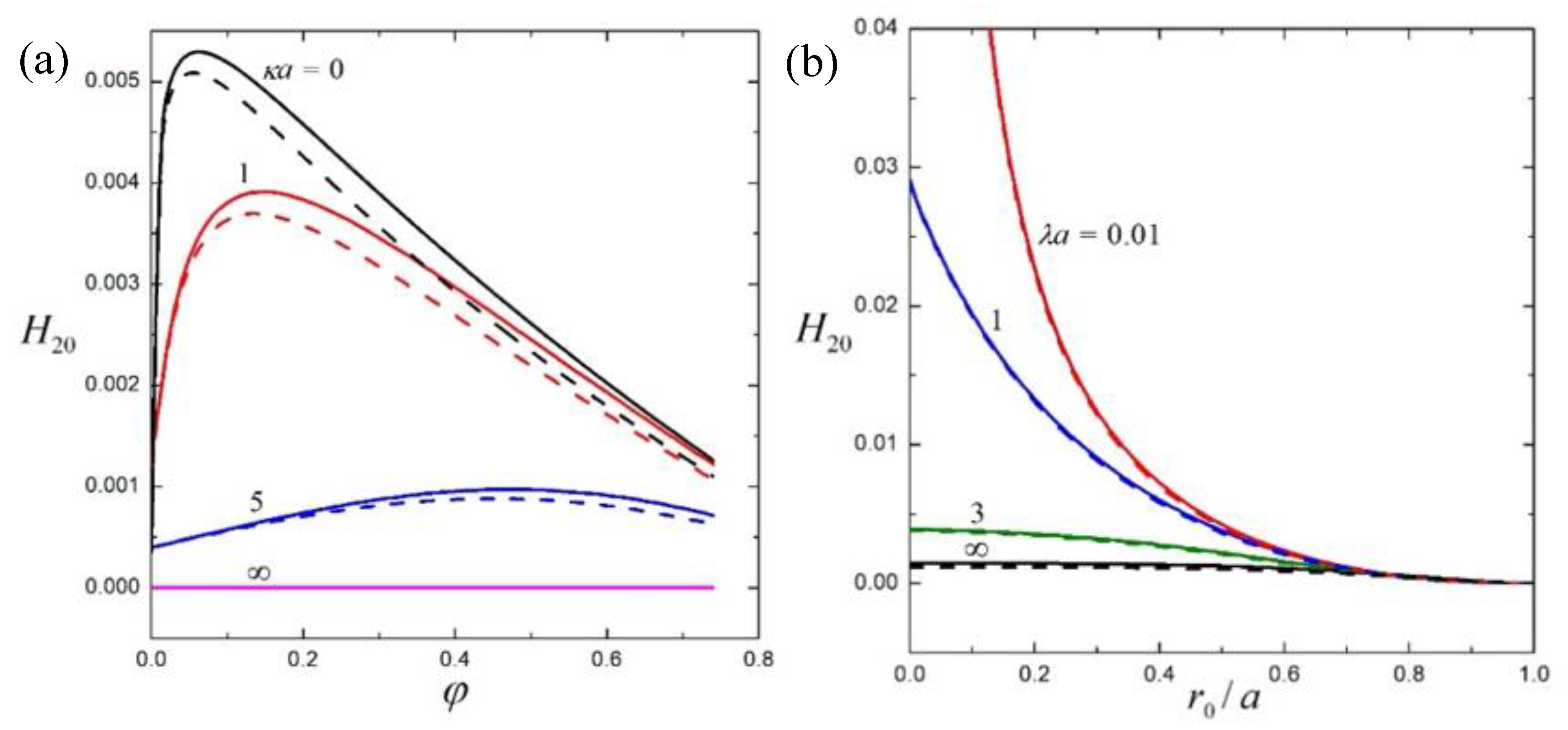
4. Results and Discussion
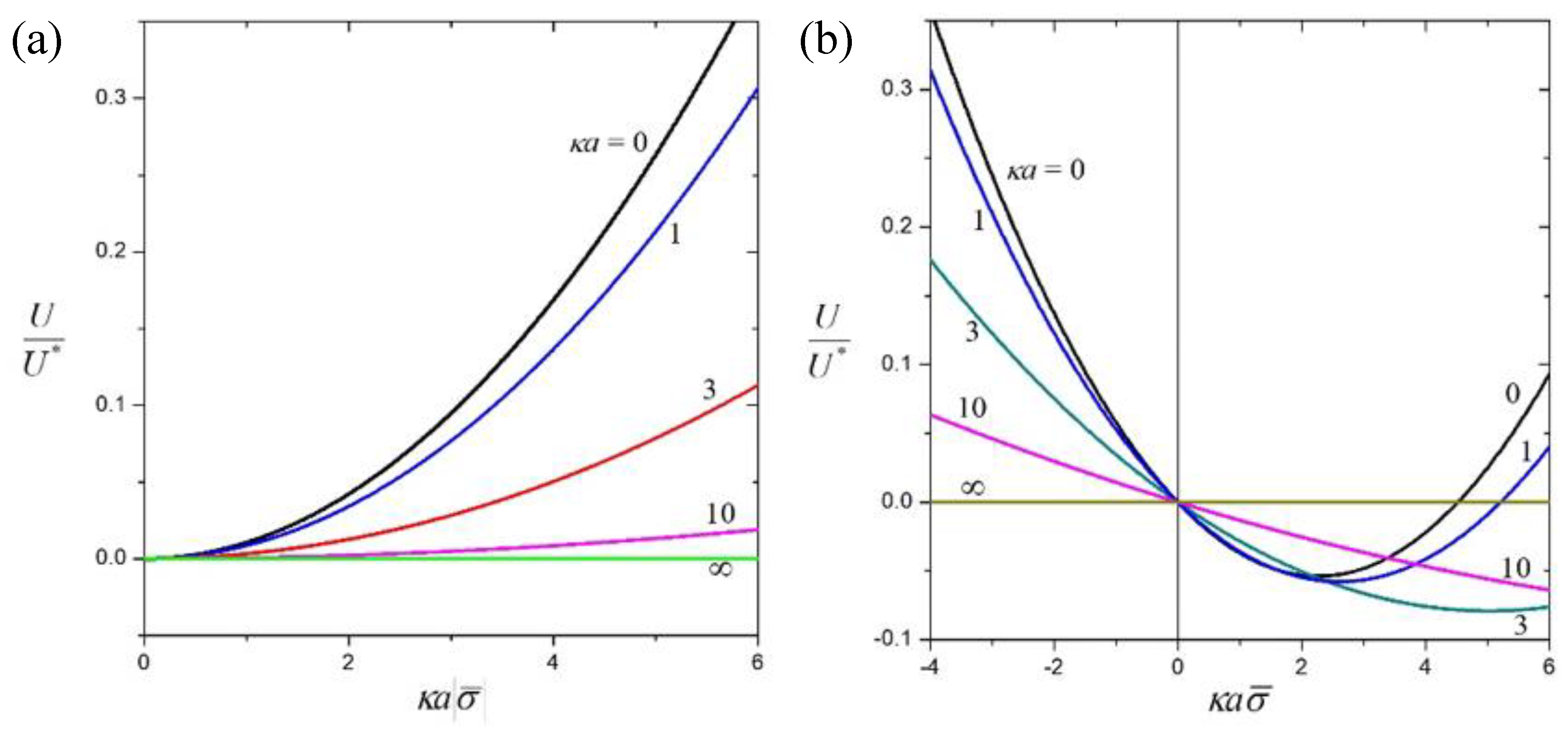
4.1. Suspension of Hard Spheres
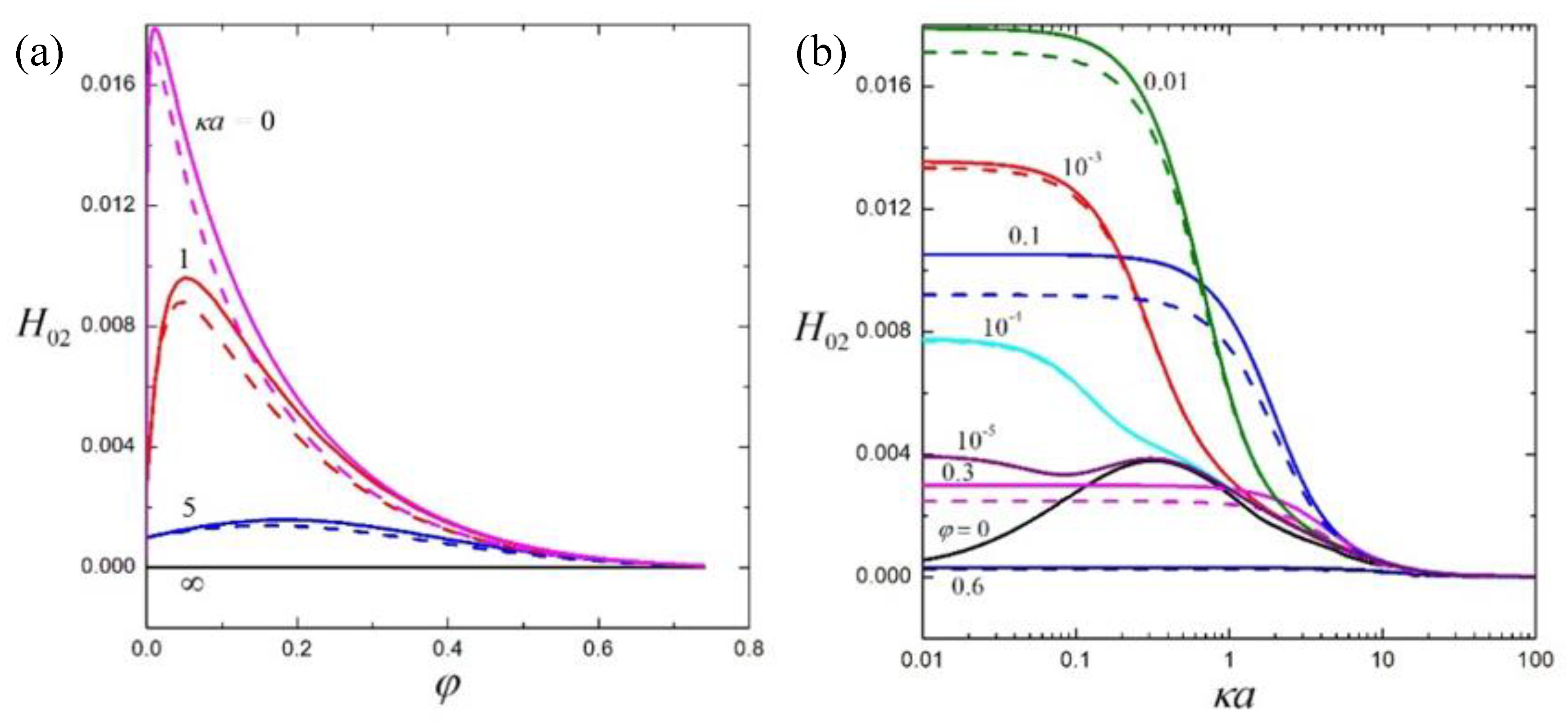
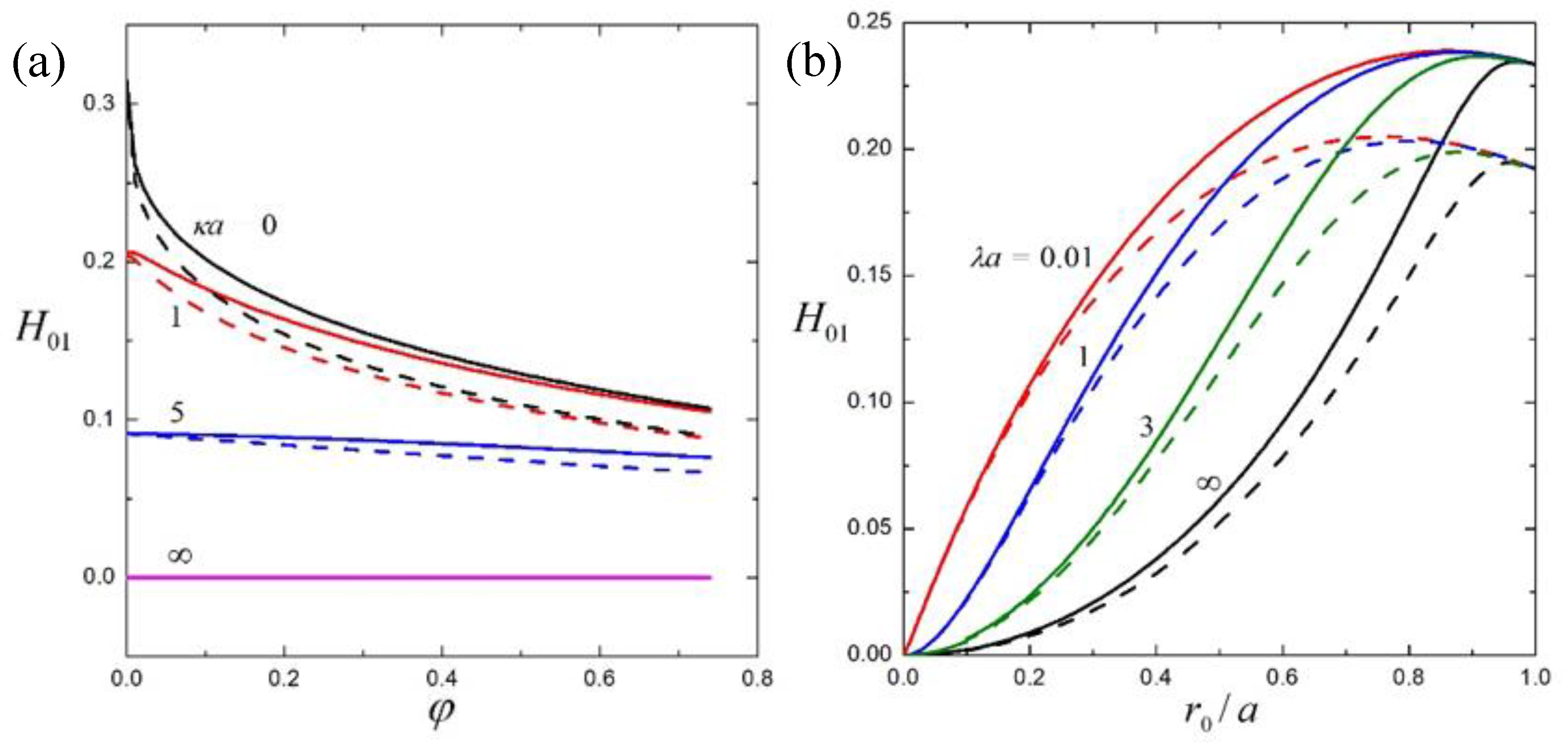
4.2. Suspension of Soft Spheres
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Dukhin, S.S.; Derjaguin, B.V. Electrokinetic Phenomena. In Surface and Colloid Science; Matijevic, E., Ed.; Wiley: New York, NY, USA, 1974; Volume 7. [Google Scholar]
- Prieve, D.C.; Anderson, J.L.; Ebel, J.P.; Lowell, M.E. Motion of a particle generated by chemical gradients. Part 2. Electrolytes. J. Fluid Mech. 1984, 148, 247–269. [Google Scholar] [CrossRef]
- Zhang, X.; Hsu, W.-L.; Hsu, J.-P.; Tseng, S. Diffusiophoresis of a soft spherical particle in a spherical cavity. J. Phys. Chem. B 2009, 113, 8646–8656. [Google Scholar] [CrossRef] [PubMed]
- Joo, S.W.; Lee, S.Y.; Liu, J.; Qian, S. Diffusiophoresis of an elongated cylindrical nanoparticle along the axis of a nanopore. ChemPhysChem 2010, 11, 3281–3290. [Google Scholar] [CrossRef] [PubMed]
- Keh, H.J. Diffusiophoresis of charged particles and diffusioosmosis of electrolyte solutions. Curr. Opin. Colloid Interface Sci. 2016, 24, 13–22. [Google Scholar] [CrossRef]
- Chang, Y.C.; Keh, H.J. Diffusiophoresis of a colloidal cylinder at small finite Péclet numbers. Colloids Interfaces 2019, 3, 44. [Google Scholar] [CrossRef]
- Smith, R.E.; Prieve, D.C. Accelerated deposition of latex particles onto a rapidly dissolving steel surface. Chem. Eng. Sci. 1982, 37, 1213–1223. [Google Scholar] [CrossRef]
- Oshanin, G.; Popescu, M.N.; Dietrich, S. Active colloids in the context of chemical kinetics. J. Phys. A Math. Theor. 2017, 50, 134001. [Google Scholar] [CrossRef]
- Gupta, A.; Rallabandi, B.; Stone, H.A. Diffusiophoretic and diffusioosmotic velocities for mixtures of valence-asymmetric electrolytes. Phys. Rev. Fluids 2019, 4, 043702. [Google Scholar] [CrossRef]
- Hatlo, M.M.; Panja, D.; van Roij, R. Translocation of DNA molecules through nanopores with salt gradients: The role of osmotic flow. Phys. Rev. Lett. 2011, 107, 68101. [Google Scholar] [CrossRef]
- Shin, S.; Um, E.; Sabass, B.; Ault, J.T.; Rahimi, M.; Warren, P.B.; Stone, H.A. Size-Dependent control of colloid transport via solute gradients in dead-end channels. Proc. Natl. Acad. Sci. USA 2016, 113, 257–261. [Google Scholar] [CrossRef]
- Wilson, J.L.; Shim, S.; Yu, Y.E.; Gupta, A.; Stone, H.A. Diffusiophoresis in Multivalent Electrolytes. Langmuir 2020, 36, 7014–7020. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.L. Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 1989, 21, 61–99. [Google Scholar] [CrossRef]
- Abécassis, B.; Cottin-Bizonne, C.; Ybert, C.; Ajdari, A.; Bocquet, L. Boosting migration of large particles by solute contrasts. Nat. Mater. 2008, 7, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Williams, I.; Azevedo, R.N.; Helgeson, M.E.; Squires, T.M. Soluto-Inertial phenomena: Designing long-range, long-lasting, surface-specific interactions in suspensions. Proc. Natl. Acad. Sci. USA 2016, 113, 8612–8617. [Google Scholar] [CrossRef]
- Velegol, D.; Garg, A.; Guha, R.; Kar, A.; Kumar, M. Origins of concentration gradients for diffusiophoresis. Soft Matter 2016, 12, 4686–4703. [Google Scholar] [CrossRef]
- Pawar, Y.; Solomentsev, Y.E.; Anderson, J.L. Polarization effects on diffusiophoresis in electrolyte gradients. J. Colloid Interface Sci. 1993, 155, 488–498. [Google Scholar] [CrossRef]
- Tu, H.J.; Keh, H.J. Particle interactions in diffusiophoresis and electrophoresis of colloidal spheres with thin but polarized double layers. J. Colloid Interface Sci. 2000, 231, 265–282. [Google Scholar] [CrossRef]
- Prieve, D.C.; Roman, R. Diffusiophoresis of a rigid sphere through a viscous electrolyte solution. J. Chem. Soc. Faraday Trans. 2 1987, 83, 1287–1306. [Google Scholar] [CrossRef]
- Keh, H.J.; Wei, Y.K. Diffusiophoretic mobility of spherical particles at low potential and arbitrary double-layer thickness. Langmuir 2000, 16, 5289–5294. [Google Scholar] [CrossRef]
- Wei, Y.K.; Keh, H.J. Diffusiophoretic mobility of charged porous spheres in electrolyte gradients. J. Colloid Interface Sci. 2004, 269, 240–250. [Google Scholar] [CrossRef]
- Huang, P.Y.; Keh, H.J. Diffusiophoresis of a spherical soft particle in electrolyte gradients. J. Phys. Chem. B 2012, 116, 7575–7589. [Google Scholar] [CrossRef] [PubMed]
- Yeh, Y.Z.; Keh, H.J. Diffusiophoresis of a charged porous shell in electrolyte gradients. Colloid Polym. Sci. 2018, 296, 451–459. [Google Scholar] [CrossRef]
- Levine, S.; Neale, G.; Epstein, N. The prediction of electrokinetic phenomena within multiparticle systems II. Sedimentation potential. J. Colloid Interface Sci. 1976, 57, 424–437. [Google Scholar] [CrossRef]
- Ohshima, H. Sedimentation potential in a concentrated suspension of spherical colloidal particles. J. Colloid Interface Sci. 1998, 208, 295–301. [Google Scholar] [CrossRef]
- Carrique, F.; Arroyo, F.J.; Delgado, A.V. Sedimentation velocity and potential in a concentrated colloidal suspension. Effect of a dynamic Stern layer. Colloids Surfaces A 2001, 195, 157–169. [Google Scholar] [CrossRef]
- Ding, J.M.; Keh, H.J. Sedimentation velocity and potential in a suspension of charge-regulating colloidal spheres. J. Colloid Interface Sci. 2001, 243, 331–341. [Google Scholar] [CrossRef]
- Keh, H.J.; Chen, W.C. Sedimentation velocity and potential in concentrated suspensions of charged porous spheres. J. Colloid Interface Sci. 2006, 296, 710–720. [Google Scholar] [CrossRef]
- Chiu, Y.S.; Keh, H.J. Sedimentation velocity and potential in a concentrated suspension of charged soft spheres. Colloids Surfaces A 2014, 440, 185–196. [Google Scholar] [CrossRef]
- Levine, S.; Neale, G.H. The prediction of electrokinetic phenomena within multiparticle systems I. Electrophoresis and electroosmosis. J. Colloid Interface Sci. 1974, 47, 520–529. [Google Scholar] [CrossRef]
- Zharkikh, N.I.; Shilov, V.N. Theory of collective electrophoresis of spherical particles in the Henry approximation. Colloid J. USSR Engl. Transl. 1982, 43, 865–870. [Google Scholar]
- Ohshima, H. Electrophoretic mobility of spherical colloidal particles in concentrated suspensions. J. Colloid Interface Sci. 1997, 188, 481–485. [Google Scholar] [CrossRef]
- Zholkovskiy, E.K.; Masliyah, J.H.; Shilov, V.N.; Bhattacharjee, S. Electrokinetic phenomena in concentrated disperse systems: General problem formulation and spherical cell approach. Adv. Colloid Interface Sci. 2007, 134, 279–321. [Google Scholar] [CrossRef] [PubMed]
- Keh, H.J.; Ding, J.M. Electrophoretic mobility and electric conductivity of suspensions of charge-regulating colloidal spheres. Langmuir 2002, 18, 4572–4583. [Google Scholar] [CrossRef]
- Carrique, F.; Arroyo, F.J.; Jimenez, M.L.; Delgado, A.V. Influence of double-layer overlap on the electrophoretic mobility and DC conductivity of a concentrated suspension of spherical particles. J. Phys. Chem. B 2003, 107, 3199–3206. [Google Scholar] [CrossRef]
- Huang, H.Y.; Keh, H.J. Electrophoretic mobility and electric conductivity in suspensions of charge-regulating porous particles. Colloid Polym. Sci. 2015, 293, 1903–1914. [Google Scholar] [CrossRef]
- Liu, H.C.; Keh, H.J. Electrophoresis and electric conduction in a suspension of charged soft particles. Colloid Polym. Sci. 2016, 294, 1129–1141. [Google Scholar] [CrossRef]
- Ohshima, H. Electrical conductivity of a concentrated suspension of spherical colloidal particles. J. Colloid Interface Sci. 1999, 212, 443–448. [Google Scholar] [CrossRef]
- Miller, N.P.; Berg, J.C. Experiments on the electrophoresis of porous aggregates. J. Colloid Interface Sci. 1993, 159, 253–254. [Google Scholar] [CrossRef]
- Wei, Y.K.; Keh, H.J. Diffusiophoresis in a suspension of spherical particles with arbitrary double-layer thickness. J. Colloid Interface Sci. 2002, 248, 76–87. [Google Scholar] [CrossRef]
- Huang, H.Y.; Keh, H.J. Diffusiophoresis in suspensions of charged porous particles. J. Phys. Chem. B 2015, 119, 2040–2050. [Google Scholar] [CrossRef]
- Koplik, J.; Levine, H.; Zee, A. Viscosity renormalization in the Brinkman equation. Phys. Fluids 1983, 26, 2864–2870. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Nijhoff: Leiden, The Netherlands, 1983. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.C.; Keh, H.J. Diffusiophoresis in Suspensions of Charged Soft Particles. Colloids Interfaces 2020, 4, 30. https://doi.org/10.3390/colloids4030030
Lin WC, Keh HJ. Diffusiophoresis in Suspensions of Charged Soft Particles. Colloids and Interfaces. 2020; 4(3):30. https://doi.org/10.3390/colloids4030030
Chicago/Turabian StyleLin, Wei C., and Huan J. Keh. 2020. "Diffusiophoresis in Suspensions of Charged Soft Particles" Colloids and Interfaces 4, no. 3: 30. https://doi.org/10.3390/colloids4030030
APA StyleLin, W. C., & Keh, H. J. (2020). Diffusiophoresis in Suspensions of Charged Soft Particles. Colloids and Interfaces, 4(3), 30. https://doi.org/10.3390/colloids4030030





