Pickett Equation for the Description of Adsorption on Arbitrary Surfaces

Abstract

The theory of multilayer adsorption of gases, namely the Pickett equation, has been developed to the case of adsorption on arbitrary surfaces in a molecular and a topological approach. We present the prediction of the fractal dimension for the surface of an adsorbent and for the set of interfaces generated by the growing of layers. The theoretical models correctly predict quantities and qualitative features of the experiment for two systems: adsorption of water vapor (T = 298 K) on the sample of lunar regolith and of nitrogen (T = 77 K) on a coal sample.

1. Introduction

Physical chemists use adsorption isotherms for:

(1)

measuring the surface areas of porous materials;

(2)

obtaining information on the pore size distribution of porous materials.

For measuring surface areas, the BET theory (Brunauer, Emmett, Teller) was suggested [1]. The BET theory is based on the multilayer adsorption. The BET theory predicts five types of adsorption isotherms [2]. Nevertheless, many questions remain unanswered. The problem of the theory application to surfaces with energetic heterogeneity is solved partly. Moreover, the BET theory does not account for the geometric disorder. Both kinds of disorder, namely, energetic heterogeneity and geometric disorder, can be related and distinguished from each other. The geometric environment of an adsorption site (or a domain) is a function of the morphology of the surface and thus of its fractal character [3]. The fractal concept is based on a mathematical study of a low-dimensional physical object embedded in a high-dimensional space. The study of the surfaces of adsorbents is based on fractal random measures and is able to describe the physical and chemical behavior of arbitrary surfaces. The fractal model takes both the enthalpy and the entropy of the system strictly into account [4].

In spite of all criticisms, the multilayer BET theory is applicable to fractal surfaces. The influence of the fractal character of the surface on the adsorption isotherms has been studied from two viewpoints:

(1) The first one is founded on a molecular description of the adsorption process [4]. The molecular description of the process of the multilayer adsorption on a fractal surface is based on the two-parameter equation of BET [1].

(2) The second one has a topological character [5]. The topological-based fractal BET theory is based on the three-parameter equation. As shown by Pfeifer et al., this equation has a number of drawbacks [6]. Both approaches employ the fundamental principles of the BET theory.

Pickett has shown that the three-parameter equation does not describe the BET isotherm at high pressures. Pickett and independently Dallies received an extremely simple three-parameter equation for multilayer adsorption [7,8]. This equation better describes the isotherm of adsorption on the Euclidean surface at high pressures. The purpose of this paper is to extend the analytical equation of Pickett to fractal surfaces.

2. Theory

The BET theory is expressed by the following equation [1]:

$$a=a_{m}c{{\displaystyle \sum }}_{n=1}^{\infty }n{x}^n/\left(1+c{{\displaystyle \sum }}_{n+1}^{\infty }{x}^n\right).$$

(1)

For a planar surface, the summation in Equation (1) gives the classical two-parameter equation of BET:

$$a=a_m \frac{cx}{\left(1-x\right)\left(1-x+cx\right)}=a_{BET-2}$$

(2)

$$c=\left(\frac{a_1}{b_1} g\right)exp\left(\frac{E_1-E_L}{RT}\right)$$

(3)

$$g=\frac{b_2}{a_2}=\frac{b_3}{a_3}=\cdots \cdots =\frac{b_n}{a_n}$$

(4)

where x = p/p₀, p and p₀ are the pressure of the adsorbate in the bulk phase and the saturation vapor pressure, respectively; a and a_m are the adsorption at a pressure p and the adsorption in the monolayer; E₁ and E_L are the heat of evaporation in the first layer and the heat of liquefaction of the condensate; and a_n and b_n are constants determining the rate of condensation and evaporation in the n-th layer. In the derivation of the equation, g = const. was assumed. The difference E₁ − E_L is usually termed as the heat of adsorption, and the ratio $\left(a_n{b}_{n+1}\right)/\left(b_n{a}_{n+1}\right)$ is usually termed as the entropy of adsorption [1]. The range of relative pressure x, for which Equation (1) describes the adsorption isotherm, depends on the type of isotherm. Thus, for an isotherm of Type II after the Brunauer Deming Deming Teller (BDDT) classification [2], Equation (1) is valid for $0.05\le x\le 0.35$. However, the value of the admissible interval x may vary in each case.

If adsorption occurs within the pores of the adsorbent, it is necessary to limit the number of layers. In the approximation of an ideal slit pore, a three-parameter BET equation is obtained [1]:

$$a_{BET-3}=\frac{a_{m }cx}{\left(1-x\right)}\frac{1-\left(n-1\right)x^n+n{x}^{n+1}}{1+\left(c-1\right)x+c{x}^{n+1}}.$$

(5)

Equation (5) provides two important limiting effects. For $n\to \infty$, Equation (5) reduces to Equation (2). When n = 1, it transforms to the Langmuir equation. However, the main disadvantage of Equation (5) is that, as it has been shown by Pickett [7], it incorrectly describes the isotherm at $p\to p_0$. To remove this deficiency, Pickett made following assumption, according to which for the last layer the ratio $b_n/a_n$ obeys equation $b_n/a_n=g\left(1-x\right)$, rather than $g=b_n/a_n$ [7]. With this assumption, Equation (1) amended by Pickett can be written in the following form:

$$a=a_m\left[\frac{c\left({{\displaystyle \sum }}_{n=1}^{n-1}n{x}^n+\frac{n{x}^n}{1-x}\right)}{1+c{{\displaystyle \sum }}_{n=1}^{\infty }{x}^n}\right].$$

(6)

The limit of summation in the numerator is finite. However, the summation in the denominator should be performed indefinitely. This is due to the need for considering the adsorption system in the thermodynamic limit. The summation leads to the following equation [7,8]:

$$a=a_m\frac{cx\left(1-x^n\right)}{\left(1-x\right)\left(1-x+cx\right)}.$$

(7)

Equation (7) describes the experimental data better than Equation (5). Additionally, Equation (7) is significantly simpler to apply to the analysis of experimental adsorption isotherms. In the analysis of the adsorption process, it is convenient to use a relative width of the pores $H=h/\sigma$, where h corresponds to pore width and σ corresponds to the van der Waals diameter of the adsorbate molecule [9]. For slit-shaped pores in the interval $1<H\le 1.6$ the volume filling of pores occurs. The adsorption process is described by the theory of volume filling of micropores (VFM) [10]. The upper limit micropores of the considered sample of coal satisfy the relation $h/\sigma \le 1.6$.

It should be emphasized that in the theory of adsorption, the film thickness is defined as the ratio of the amount of adsorption a and the amount of adsorption in the monolayer a_m. The ratio a/a_m is referred to as θ. The ratio $\theta \sim H$ is strictly correct under the assumption that $a\sim h$ and $a_m\sim \sigma$ [11]. In the article, the authors have chosen following designation for the number of layers in the condensation film n with $n=\theta =a/a_m$. For H > 1.6, a stable film of condensate is formed on the walls of the pores. Multilayer filling starts, which is described by the BET or Frenkel–Halsey–Hill (FHH) equation. FHH is used conveniently to determine the effect of the adsorption potential of the walls.

We now consider the multilayer adsorption on a fractal surface with two different approaches.

2.1. The molecular Approach

The approximate molecular description of the multilayer adsorption on a fractal surface is based on a comparison of the magnitudes of adsorption on the Euclidean surface and on the fractal surface. When calculating the adsorption isotherms for the rigorous evaluation of the fractal surface, the following correlation factor is introduced [5]:

$$f_n=\frac{a_F molecular content of i-th layer}{a_m}$$

(8)

In this formula, f_n is a function of n and the dimension D with f < 1 and $n\ge 2$. As a result of numerical experiments, the relationship between f_n, n and D was established [4]:

$$f_n=n^{2-D}$$

(9)

Equation (9) was the basis for the derivation of the equation for the fractal BET surface. In the molecular approximation, the fractal BET equation is given as follows [4]:

$$\frac{a}{a_m}=\frac{c{{\displaystyle \sum }}_{n=1}^n{n}^{2-D}\left({{\displaystyle \sum }}_{n=1}^n{x}^n\right)}{1+c{{\displaystyle \sum }}_{n=1}^n{x}^n}$$

(10)

The numerator in Equation (10) is

$${\displaystyle \sum }_{n=1}^n{x}^n+2^{\left(2-D\right)}{\displaystyle \sum }_{n=2}^n{x}^n+\cdots \cdots +n^{\left(2-D\right)}{x}^n$$

(11)

Equation (10) reduces to the classical BET Equation (1) if D = 2. A practical application of Equation (10) can be realized only by numerical methods [4].

In calculating the fractal dimension in a molecular approach, one should take into consideration the following circumstances.

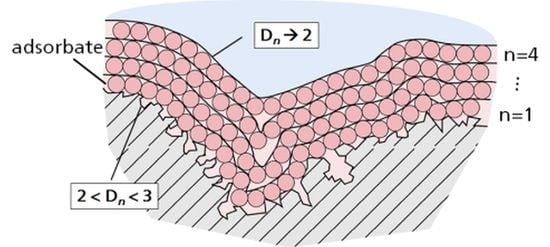
The set of surfaces generated by growing a coating of n layers can be characterized within the scale σ by a family of apparent fractal dimensions D_n such as [4]:

$$2 \le D_{n }\le D$$

(12)

$$D_{n }\le D_{n-1}$$

(13)

Let us denote the surface area of the Euclidean surface as S. Let S_n be the fractal surface area, which is measured in the units of σ.

Let us consider the multilayer adsorption on both the Euclidean and the fractal surface. We will determine the number of layers formed at the completion of the multilayer formation as a ratio of the total value of adsorption a to the monolayer adsorption a_m. In the classical BET theory, the value a_m of each monolayer remains the same and equal to the amount of adsorption in the first monolayer. When the monolayer is formed on the fractal surface, the adsorption value in each monolayer is related to the adsorption in the first monolayer by Formula (14).

$$a_F=f_n{a}_m$$

(14)

You can consider the surface of the pore as Euclidean or as fractal, and in both cases, you gain different results in the form of $n_{BET}$ and $n_F$. Let $n_{BET}$ and $n_F$ be the number of layers formed on the Euclidean surface and on the fractal surface, respectively. Then, from Equations (9) and (14), we obtain:

$$n_F^{\left(3-D\right)}=n_{BET}$$

(15)

In Formula (15), $n_F \mathrm{and} n_{BET}$ are defined as the ratio of the adsorption a at an arbitrary value of x to the values $a_F \mathrm{and}{a}_m$, respectively:

$$n_F=\frac{a}{a_F}\mathrm{and} n_{BET}=\frac{a}{a_m}$$

We define $n_{BET}$ for each of the considered isotherms and the corresponding value of the relative pressure of the adsorbate in the bulk phase x and denote this value as $x_{BET}$. According to this value of $x_{BET}$, the number of layers formed during adsorption on the fractal surface can be determined from Equations (2) and (7):

$$a=a_{BET-2}\left(1-x_{BET}^n\right)$$

(16)

By taking the logarithms, the following equation is received for fractal surfaces:

$$n_F\ast \ln x_{BET}=\ln (1-\frac{a}{a_{BET-2}})$$

(17)

$$n_F=ln\left(1-\frac{a}{a_{BET-2}}\right){\left(\ln x_{BET}\right)}^{-1}$$

(18)

From Equation (15), we determine the fractal dimension value

$$D=3-\frac{ln{n}_{BET}}{ln{n}_F}$$

(19)

Equation (19) determines the fractal dimension of the adsorbent in the molecular approach.

2.2. The Topological Approach

We now proceed to the description of the multilayer adsorption on a fractal surface in the topological approximation. Consider the surface, which is characterized by the fractal dimension D, and the fractal dimension describes the volume filling due to the fractal structure. As the fractal dimension can be estimated from the pore size distribution, a fractal surface can be represented as an equivalent system of independent pores. The filling process is considered in the BET theory as the adsorption between two parallel walls [8]. The adsorption volume across the surface is defined as the total volume of all adsorption pores. Thus, D can be treated as the characteristic of the pores’ distribution over the fractal surface. The adsorption isotherm for a single pore is determined by Equations (5) and (7). Now, we consider the multilayer adsorption in the topological approach.

Equation (5) as the basis of the fractal BET equation results in a topological approximation:

$$a=a_m\frac{cx}{\left(1-x\right)}\left(D-2\right)\underset{n=1}{\overset{\infty }{{\displaystyle \int }}}{n}^{1-D}h\left(x\right)dn \wedge 2\le D\le 3$$

(20)

Equation (20) is an integral equation for the adsorption isotherm on a fractal surface. The integrand is given by the three-parameter BET equation (Equation 5). Equation (5) contains a factor $a_{m }\frac{cx}{1-x}$ that does not depend on n. This factor is taken outside the integral sign.

The function h (x) is given as: $h\left(x\right)\equiv \frac{1-\left(n-1\right)x^n+n{x}^{n+1}}{1\mp \left(c-1\right)x+c{x}^{n+1}}$.

In Equation (20), there is no singularity for D = 2 because of the limit of the product of (D-2) and the integral when D = 2 is finite. Equation (20) is studied in detail in [6]. However, its practical application is related to computational difficulties. Therefore, we consider the Pickett equation (6) more attentively.

In Equation (7), n is an integer. However, the analysis of numerous experimental data shows that n is not an integer. This is due to the fractal properties of the adsorbent surface [12]. The only way for higher layers to be more stable is to have higher entropy than the liquid. This produces fluctuations in film thickness (the coexistence of patches of different thicknesses). The coverage of the surface is extremely non-uniform. In this case, the entropy of the adsorbed phase for the n-th layer in a fractal mode no longer corresponds to the adsorption in the Euclidean space.

The amendment in the Pickett equation (6) creates the conditions for the last layer of stabilization. This amendment was introduced for the process of adsorption on the Euclidean surface.

In case of adsorption on the fractal surface, the Pickett amendment can be written as follows:

$$\frac{b_{n }}{a_n}=g{\left(1-x\right)}^{D-1}$$

(21)

For D = 2, the amendment (Equation 21) is transformed into the amendment of Pickett, which is introduced to the three-parameter Equation (7).

Then, the fractal mode in Equation (6) should be written as:

$$a=a_{m }\left[\frac{c{{\displaystyle \sum }}_{n=1}^{n-1}n{x}^n+\frac{n{x}^n}{1-x}{\left(1-x\right)}^{2-D}}{1+c{{\displaystyle \sum }}_{n=1}^{\infty }{x}^n}\right]$$

(22)

If D = 2, Equation (22) reduces to Equation (6). After performing the summation in Equation (22), we obtain the fractal form of the Pickett equation:

$$a=a_m\frac{cx}{\left(1-x\right)\left(1-x+cx\right)}\left\{1-x^n\left[1+\frac{n\left(1-x\right)}{x}-\frac{n{\left(1-x\right)}^{3-D}}{x}\right]\right\}$$

(23)

For D = 2, Equation (23) reduces to the Pickett equation (7).

In Equation (23), we distinguish a part corresponding to the two-parameter BET equation and denote:

$$a_{BET-2}=\frac{a_{m}cx}{\left(1-x\right)\left(1-x+cx\right)}$$

(24)

Using Equation (24), we can write Equation (23) as follows:

$$\frac{a}{a_{BET-2}}=1-x^n\left\{1+\frac{n\left(1-x\right)}{x} \left[1-{\left(1-x\right)}^{2-D}\right]\right\}$$

(25)

The value of the fractal dimension D is determined by Equation (26) as:

$$D=2-\frac{ln\left\{\left[1-\left(1-\frac{a}{a_{BET-2}}\right)\frac{1}{x^n}\right]\frac{x}{n\left(1-x\right)}+1\right\}}{\ln \left(1-x\right)}$$

(26)

3. Results and Discussion

As an example, we consider the adsorption of water vapor (T = 298 K) on the sample of lunar regolith 12001.922 [13,14] and the adsorption of nitrogen (T = 77 K) on the sample of coal [15]. Both isotherms are of Type II in the BDDT classification [1]. According to the IUPAC (International Union of Pure and Applied Chemistry) classification, the type of a hysteresis loop is associated in a certain manner with the geometry of an adsorbent porous structure. H3 type hysteresis loops can be observed virtually upon adsorption on adsorbents with a lamellar structure. These adsorbents are characterized by the presence of slit-like pores and are often nonrigid.

In an ideal pore model, the pore walls are taken as plane, smooth, and parallel to each other. The adsorbate–gas (vapor) interface in the pores of such a structure is not curved. During adsorption at pressures lower than saturation, the pore walls are covered with a film by the physical adsorption mechanism. When the state of an adsorption layer is considered in disregard of the influence of an opposite wall, the thickness of an adsorption film can be comparable to that of the film on a nonporous adsorbent surface.

Once a pore has been completely filled via the adsorption mechanism, a cylindrical meniscus emerges in it. In this case, the capillary evaporation is regulated by this meniscus. Thus, two different mechanisms should be considered: multilayer adsorption in direct processes and capillary evaporation in reverse processes.

However, clear separation of the condensation into the adsorption mechanism and capillary evaporation for slit-like pores is possible only in a particular range of adsorbate relative pressures in the bulk phase. In a slit-like pore, the capillary condensation in an entirely filled pore can proceed at very high values of adsorbate relative pressures in the bulk phase. The effect of the features of the porous structure of the adsorbent on the form of an isotherm is conveniently analyzed based on the t-curve, for which the adsorption magnitude is determined along the ordinate axis, and the thickness of the adsorption film is determined along the abscissa axis. The value of the adsorbate relative pressure at which the adsorption film loses its stability and condensation takes place can be defined as the point on the t-curve after which a t-line curves downward. At this value of adsorbate relative pressure in the bulk phase, the stabilizing effect of the wall potential on the condensate film becomes negligible, and the film loses its stability. Under real conditions, the loss of film stability does not occur at the exact point but rather proceeds for some finite interval of adsorbate relative pressures in the bulk phase.

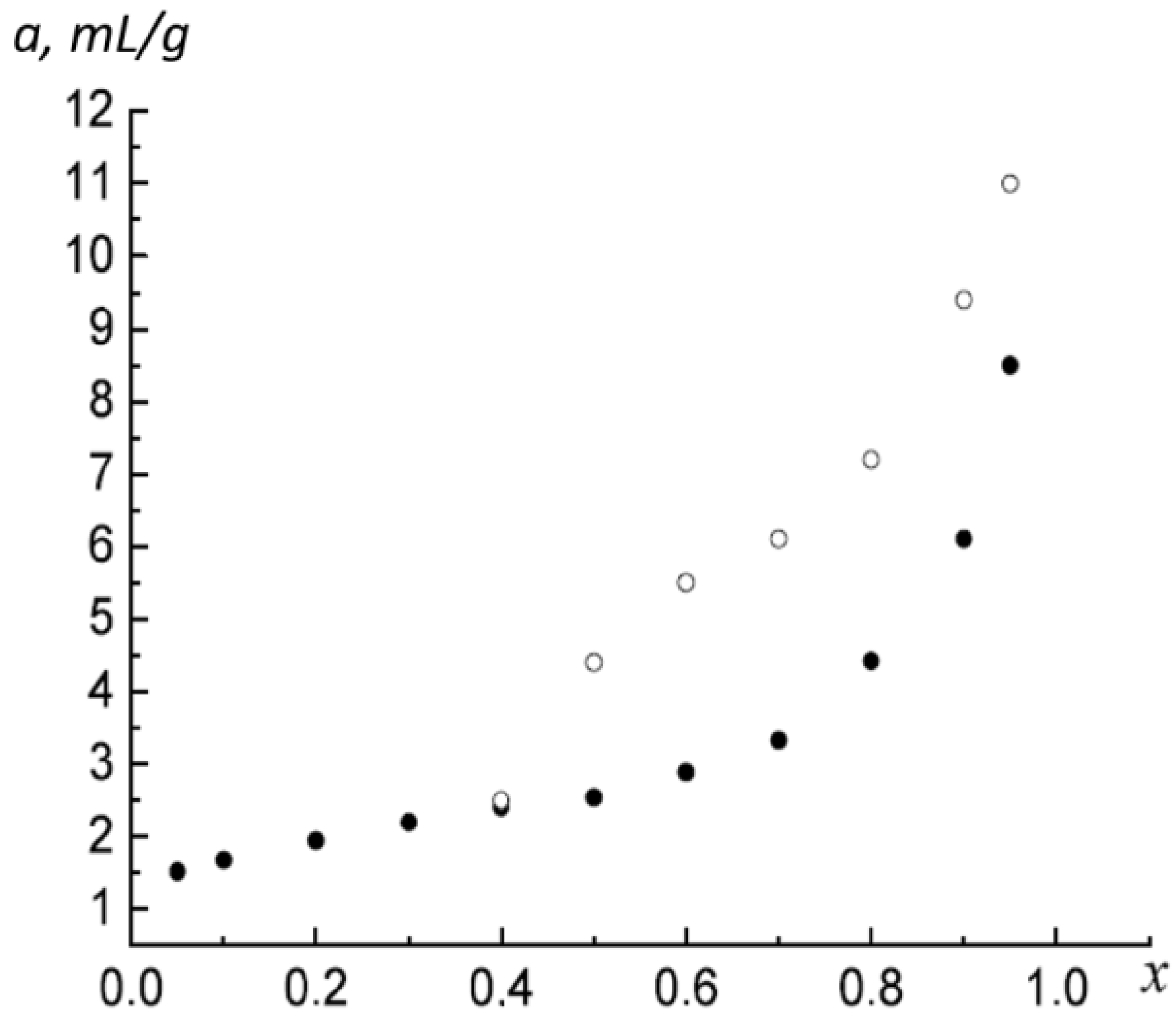
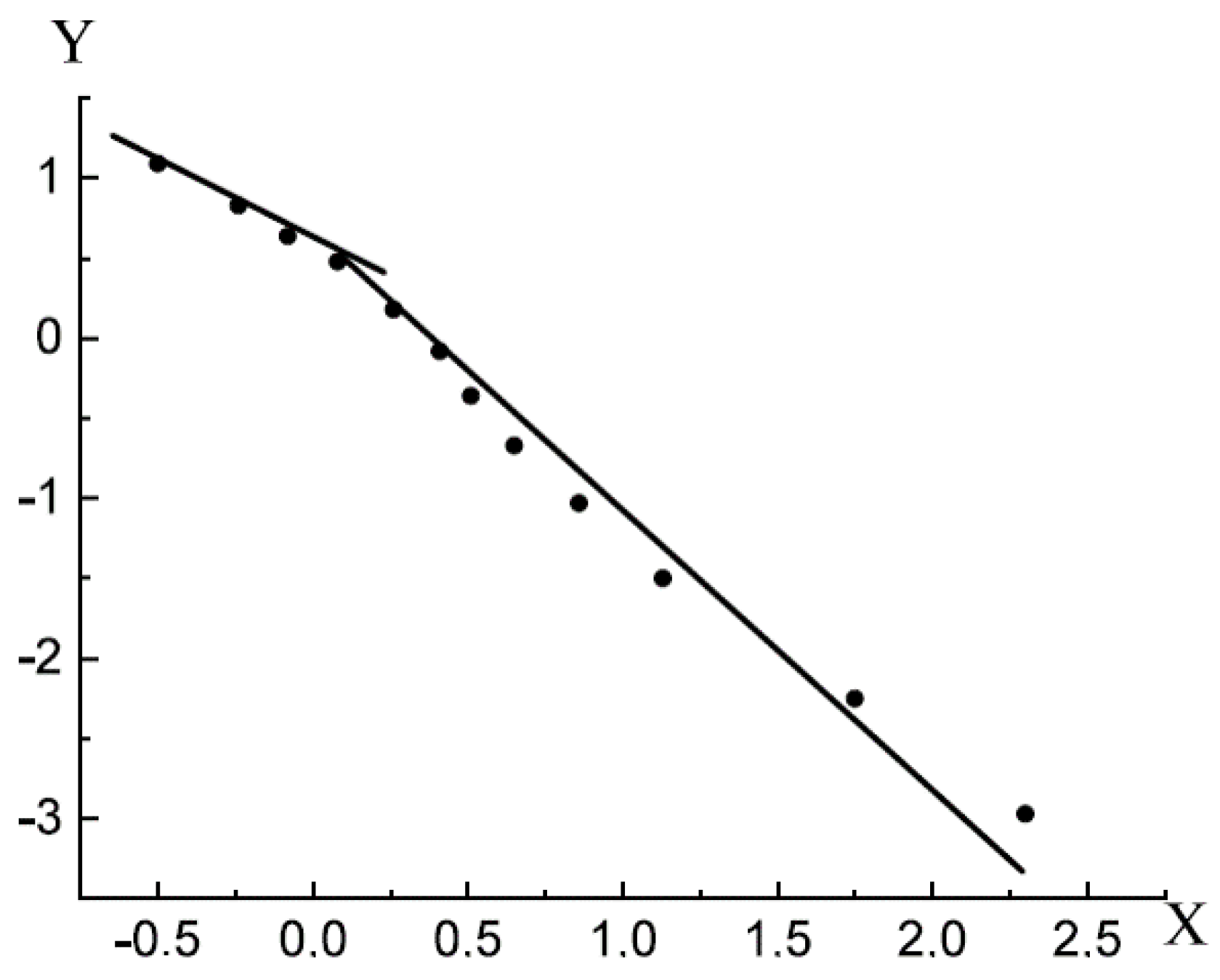
For example, consider a low-temperature nitrogen adsorption isotherm on a sample of coal BD3, Figure 1 [15].

Figure 2 shows the t-curve of the considered isotherm. In the range of the relative pressure of the adsorbate in the bulk phase 0.07 ≤ x ≤ 0.95, the t-curve is a straight line. This characteristic t-curve indicates that in this range (0.07 ≤ x ≤ 0.95), the multilayer pore filling extends.

On the other hand, to differentiate the regions of multilayer formation and capillary condensation in greater pores, we describe the isotherm by the equation considered by Frenkel–Halsey–Hill (FHH) [16]:

$$a=a_m{\left(\frac{b}{-ln x}\right)}^{\alpha }$$

(27)

In Equation (27), b and α are the parameters of the FHH theory. In the FHH theory, α has a value of 1/3 [17] for Euclidean surfaces. For a fractal surface, $\alpha \ne 1/3$ [16].

In the analysis of the experimental data, the isotherm in Equation (27) is converted to the form:

$$ln\left(-lnx\right)=f(lna/a_m)$$

(28)

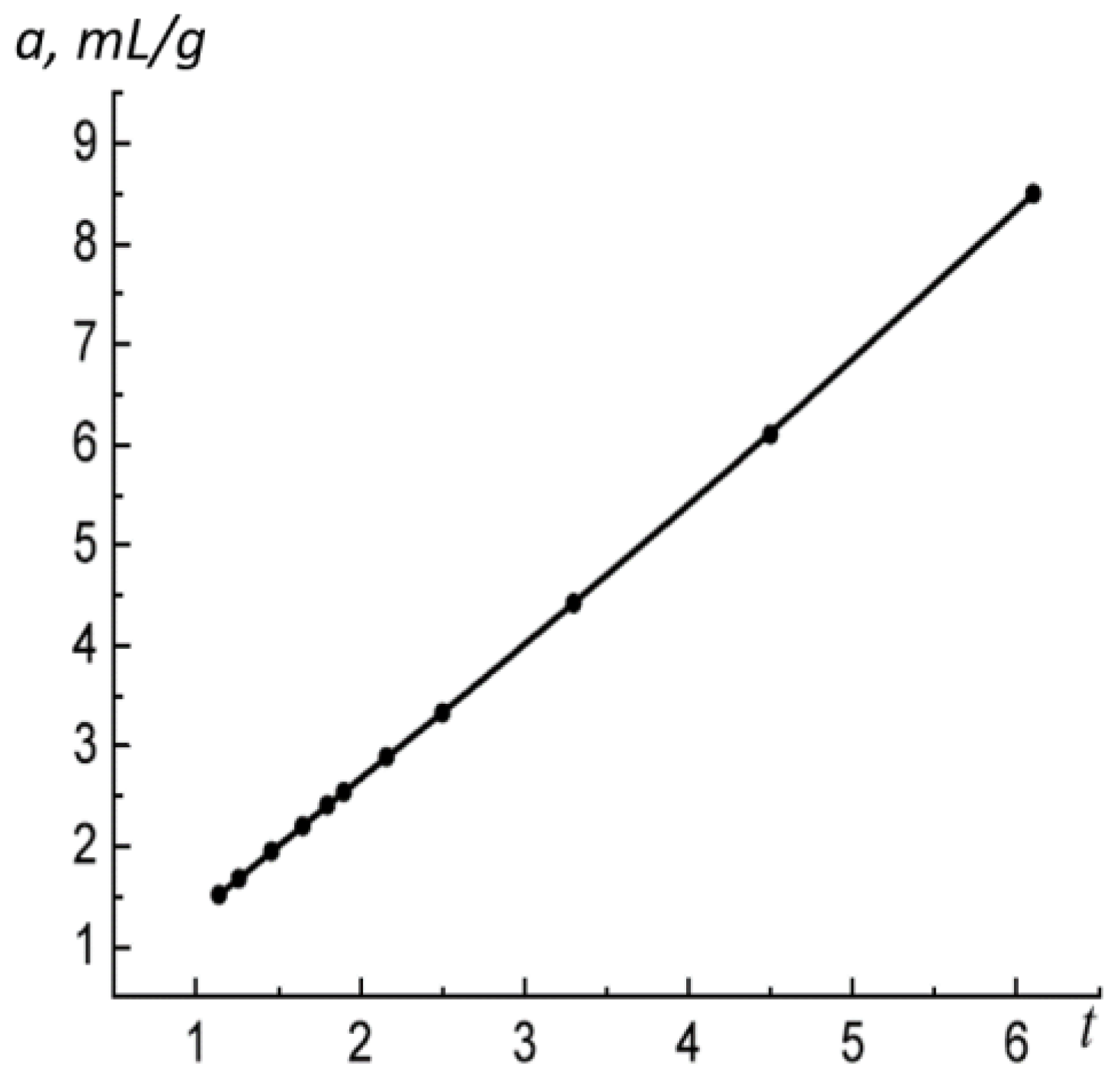
Figure 3 shows the adsorption isotherm of nitrogen on the coal sample in the coordinates of Equation (28).

By analyzing Figure 3, one can determine the parameters of Equation (28) for the adsorption of nitrogen on the sample of coal: $a_m=1.34 c{m}^3/g;b=4.1; \alpha =0.41$. The point with coordinates $a_m=1.34 c{m}^3/g;x=0.066$ determines the monolayer adsorption. The FHH equation describes the process of adsorption for $0.07<x\le 0.95$ with a maximum deviation of $\pm \delta =7.8\%$. The region of multilayer formation preserves its stability up to the saturation pressure. Such a mechanism of the adsorption is characteristic for slit-shaped pores.

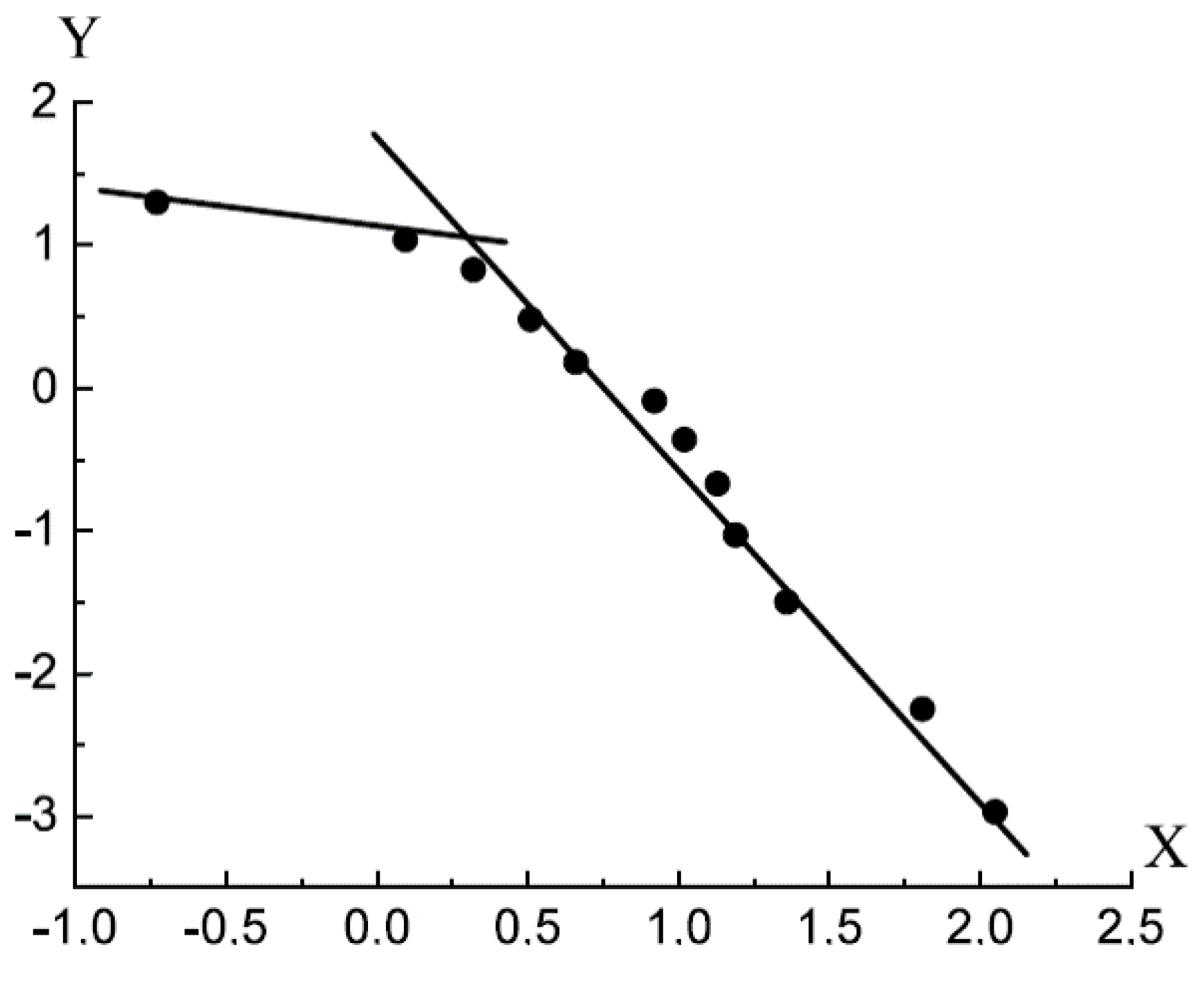
Figure 4 shows the adsorption isotherm of water on the lunar soil sample [13,14] in the coordinates of Equation (28).

For the adsorption isotherm of water on the lunar soil sample, the following parameters of the FHH equation were obtained: $a_m=9.6\ast {10}^{-3}c{m}^3/g;b=1.37; \alpha =0.58$. In the case of adsorption of water on the sample of lunar soil, the stable multilayer film exists in the interval $0.4<x<0.9$. In this interval, Equation (28) describes the isotherm with the maximum relative deviation of $\pm \delta =8.3\%$. The capillary condensation can proceed only at very high values of adsorbate relative pressures in the bulk phase (x > 0.90).

For further calculations, it is necessary to determine the parameters of the considered BET equation for the isotherms. According to the standard procedure [9], the following values were obtained: for the adsorption of nitrogen on carbon $a_m=1.34 c{m}^3/g;c=68.2$; for the adsorption of water vapor on the sample of lunar soil, $a_m=9.6\ast {10}^{-3} c{m}^3/g;c=13.3$.

Now, we determine the fractal characteristics of these adsorbents. First, we calculate the fractal dimension of the adsorbent within the molecular approach (Equation (19)). For the calculated values $n_{BET}$ and $n_F$, Formula (19) yields the corresponding values of the fractal dimension D, which are listed in

Table 1. Results of calculations of the fractal dimension with Equations (19) and (26).

	Sample 1		Sample 2
${\mathit{n}}_{\mathit{B}\mathit{E}\mathit{T}}$	From (19)	From (26)	From (19)	From (26)
2	2.51	2.60	2.47	2.50
3	2.20	2.21	2.39	2.45
4	2.14	2.16	2.37	2.35
5	2.07	2.11	2.34	2.32
6			2.32	2.30
	sample 1 [15]		sample 2 [13,14]

.

Now, consider the calculation of the fractal dimension within the topological approximation (equation (26)). Formula (26) is obtained as the solution of Equation (25) with respect to the parameter D. If D = 2, Equation (26) becomes Equation (25), in which Equation (7) is taken into account. Equation (7) is the Pickett equation for the Euclidean surface. Consequently, in Equation (26), we must take $n=n_{BET}$, $x=x_{BET}$. The results of calculations by means of Formulas (19) and (26) are presented in Table 1.

Here, we must remember that the stability of the film is formed upon condition $n\ge 1.6$. The value of n = 2 corresponds to the first layer of stable condensate film in the pore [11]. The calculated fractal dimension is the fractal dimension of the inner surface of the adsorbent [18]. For n > 2, Table 1 shows the values of the fractal dimension of the interface. These facts are explained further in [5].

Now, let us consider the growth of the BET-type multilayer. On a non-planar surface, the adsorbed film–vapor interface is determined by the gas–solid potential and by the surface tension. The fractal character of the surface is scanned by the adsorptive molecules only in the first-layer. Our results are in good agreement with the results of Pfeifer, who examined in detail the growth of the BET-type multilayer on a fractal surface. [19].

The steady state of the adsorbate film is determined by competition between the gas–solid potential and the surface tension. By the growing thickness of the layer, the gas–solid potential is reduced. The surface tension may modify the shape of the interface. The surface tension minimizes the area of the interface and for the fractal dimension of the interface applies $D_s \to 2$ [5].

In order to describe the growth of the BET-type multilayer, simulation experiments were carried out [5]. The set of surfaces S_n generated by growing coverage with n layers can be characterized by the apparent fractal dimension D_n [5].

The table shows the results of calculations of the dependence of the fractal dimension D_n on the layer number n. For the dependence of D_n on n, the following formula was obtained:

$$D_n=\frac{n}{k_{1}n-k_2}$$

(29)

The isotherm of nitrogen adsorption on the coal sample is $k_1=0.54; k_2=0.3$; the isotherm of adsorption of water on the lunar regolith is $k_1=0.44; k_2=0.072$.

As can be seen in the table, the fractal dimension of the interface decreases as the number of layers increases.

4. Conclusions

We have given a discussion of the fractal BET theory, namely the Pickett equation, on an arbitrary surface. It should be stressed that the results of the topological and molecular approaches agree for both isotherms. The molecular and the topological approach provide similar results corresponding to the fractal dimension of the adsorbent and the adsorbate vapor interface. With an increasing number of adsorbed layers, the fractal dimension of the interface decreases.